An Experimental Evaluation of Summarisation-Based Frequent Subgraph Mining for Subgraph Searching

Abstract

The subgraph searching is a fundamental operation for the analysis and exploration of graphs. Nowadays, molecular databases are nearing close to one hundred million molecules. Since finding all the data graphs in a graph database that contain the query graph using subgraph isomorphism is an NP-complete problem, indexes are built and processed. Further, to assist the formulation of the query by a user, the visual exploratory subgraph query paradigm proposes a graphical user interface and leverages exploration time to reduce query processing time. However, state-of-the-art approaches need to scale better to dynamic graph databases and suffer from efficiency problems. In addition, the existing Summarisation-based frequent subgraph mining for visual exploratory subgraph searching (SuMExplorer) is lacking implementation and evaluation study for handling visual subgraph similarity search and modify operations. In this paper, we present a novel index structure, which aids the subgraph searching using the summarised-based weighted frequent subgraph mining on data graphs. By the structure-preserving, we exploit the indexes to support similarity and modify operations. We conduct extensive performance studies on both real-world and synthetic datasets to evaluate the overall performance of the extended SuMExplorer to the recent visual exploratory FERRARI and traditional subgraph search algorithms (such as the gIndex and the GRAPES-DD). Our results showed that our indexes can query up to 3 times faster in comparison to the FERRARI while reducing the storage footprint by 2 orders of magnitude.

Introduction

Recent advances in biological network analysis have resulted in the dominance of graph databases for graph modelling and storage. Typically, chemical datasets have been growing rapidly for tens of billions of molecules, for example in the Zinc dataset. As a result, the need for a modern graph database to handle complex queries has arisen. Some popular queries in graph database are subgraph and similarity searching. For example, many researchers are interested in (1) finding network motifs (small subgraphs that are recurrent and statistically significant) [21, 30], (2) identifying and comparing similarities between two biological graphs [16, 22], and (3) discovering active regions of molecules that interact with biological targets [24].

Given a graph database, denoted by ${\mathcal{G}}=\{G_1, G_2,\ldots , G_n\},$ containing numbers of medium-sized graphs called the data graph and a query graph, denoted by Q,  then assume that Q is derived from ${\mathcal{G}}.$ In the case of subgraph containment, we need to identify all the data graphs that contain a query graph. The subgraph similarity problem involves finding all the labelled graphs that approximately contain Q. Hence, the similarity distance function is $dist(G_i, Q) \le \theta ,$ where $\theta$ is the subgraph similarity distance threshold. When $\theta =0,$ the subgraph similarity becomes a subgraph containment problem.

However, the subgraph containment and similarity problem is a challenging issue. The classical solution to a subgraph containment query is to use subgraph isomorphism, which is an NP-complete problem [7]. Whilst we can overcome the drawbacks of subgraph isomorphism by using indices to filter noncandidate data graphs, they are not always efficient in terms of indexing time and storage usage.

Existing approaches propose solutions based on subgraph isomorphism and use the concept of mining to extract frequent subgraphs and perform filtering to obtain candidate graphs. [9, 15, 26] are some of the recent works proposing indices for optimising subgraph searching. However, these methods are incapable of supporting exploratory subgraph searching where the query graph evolves.

Motivating example. The subgraph containment problem is of paramount importance for chemists when searching for chemical compounds. A graph is a natural abstraction of chemical compounds. For example, chemical graphs can be represented as data graphs in a graph database called the transactional graph database. We model atoms in chemical compounds as nodes and bonds between them as edges in the data graph. In Fig. 1, we illustrate the subgraph containment problem; here, our interest lies in identifying and reporting all the structural motifs or subgraphs within the chemical database [27]. In Fig. 1a, we provide an example for a transactional graph database, and in (b), we illustrate an example of the query graph that undergoes refinement with one edge at a time. Suppose the user adds a new edge at time $t_1,$ whereby the query graph is constructed and hence denoted by $Q_{1}.$ Next, at time $t_2,$ the user adds another edge connecting vertex $v_1$ to a new node $v_2,$ thereby forming $Q_{2}.$ Subsequently, an edge is removed between $v_1$ and $v_2$ at time $t_3.$ Followed by the new edge addition at time $t_4$ between the existing vertex $v_1$ and the new vertex $v_2.$ We can observe that at time $t_1,$ the $Q_1$ is contained in $G_1, G_3,$ and $G_4.$ At time $t_2,$ the $Q_2$ is contained in $G_1.$ Finally, at time $t_4,$ the $Q_4$ is contained in $G_3$ and $G_4.$

Fig. 1

A running example of data graphs and query graph for subgraph searching. The database is composed of four data graphs, $G_1,G_2,G_3,G_4$ and $G_5.$ The query graphs are generated at $t_1,t_2,t_3,$ and $t_4$ with the addition of new edges or modification of existing edges, as highlighted by red-colored edges or crosses, respectively

Challenges and contributions. In this paper, we tackle the issues related to similarity containment by introducing a new framework for query processing using summarised graphs. Our previous effort, Summarisation-based frequent subgraph mining for visual exploratory subgraph searching (SuMExplorer) [27], focussed on efficiently solving the visual subgraph searching problem using graph summarisation and weighted frequent subgraph mining. Thus, when the query graph evolves from a frequent to an infrequent subgraph, and it is not present within the indexed graph database, the query processing operation will result in an empty result set. Therefore, it is important to perform a similarity search in such a scenario [10]. We focus on the implementation and improvement of similarity searches and modification operations for the SuMExplorer framework. More precisely, we make the following contributions.

• 1. We leverage summarisation-based, weighted frequent subgraph mining for efficient subgraph similarity searching. Furthermore, we implement modules for modification operations to support the deletion of an edge(s) and an evolving graph database in “Summarise and Search Framework (SuMExplorer)”.

• 2. We revisit the heuristic algorithms for subgraph containment in “Related Work” and “Summarise and Search Framework (SuMExplorer)”.

• 3. We empirically compare various algorithms using real-world and synthetic datasets in “Experimental Analysis”. We vary the graph properties and algorithmic parameters for an in-depth analysis of algorithms on the basis of the characteristics of the data graphs and query graphs.

Outline. The remainder of this paper is organised as follows. Firstly, in “Notation, Background, and Problem Statement”, we discuss the notations and provide definitions related to the graph database that we use throughout the paper. Subsequently, in “Related Work”, we review related works. In “Summarise and Search Framework (SuMExplorer)”, we provide an overview of our framework and describe the subgraph similarity and modification operations. Consequently, we present the extensive experimental evaluation and analyse the results in “Experimental Analysis”. In “Summary of Results”, we summarise the key insights acquired from our evaluations. Finally, in “Conclusions and Future Work”, we conclude our paper and outline some potential future work.

Notation, Background, and Problem Statement

In this section, we provide the formal definitions for the labelled data graph, query graph, path-to-path mapping, and subgraph isomorphism. For consistency, we use “node” for objects in the index and “vertex” for entities in the graph.

The chemical database contains chemical compounds that occur in either the SMILES or SDF formats. We parse these chemicals in simple graphs without loops and that have a multiplicity of 1. Now, we define the labelled data graph as follows.

Definition 1

(Labelled Data Graph) A labelled data graph is a graph in the transactional graph database, denoted by $G=\{V_G, E_G, \sigma _G\},$ where $G \in {\mathcal{G}}.$ The graph has $|V_G|$ vertices, $|E_G|$ edges and $|\sigma _G|$ labels. We have vertex and edge labeling functions. The vertex labeling function, $L_G (V): v_i \mapsto \sigma _G,$ assigns a label to each vertex $v_i \in V_G$ (where $0 \le i \le |V_G|).$ Similarly, the edge labeling function, $L_G(E): e_r \mapsto 0,$ assigns 0 to each edge $e_r \in E_G$ (where $0 \le r \le |E_G|).$ We ignore the edge labels as was done in [25]. We define the degree of the graph as the total number of edges incident to each vertex in the graph. We denote the degree of the graph as $d_G=\sum _{i=0}^{|V_G|} d_G (v_i),$ where $d_G(v_i)=|\{v_j:(v_j,v_i) \in E_G\}|.$ An edge connecting a vertex to itself is called a loop (or reflexive edge). An edge is considered to be a multi-edge if its multiplicity is more than 1. As mentioned before, we only deal with a simple graph, therefore, loops and multiplicity are ignored.

In the context of the graph database, we denote the average number of vertices, edges, and labels as $V_{{\mathcal{AVG}}({\mathcal{G}})},$ $E_{{\mathcal{AVG}}({\mathcal{G}})},$ and $\sigma _{{\mathcal{AVG}}({\mathcal{G}})},$ respectively. Now, we define the subgraph, which is also a query graph in our setting. The primary assumption is that a given labelled graph contains the formulated query graph.

Definition 2

(Subgraph) We say that a graph, H,  is a subgraph of the graph G,  if the vertices and edges in H are a subset of the vertices in G,  denoted as $V_H \subseteq V_{G}$ and $E_{H} \subseteq E_{G}.$ The labelling of the vertices in H is the same as the labelling of the corresponding vertices in G,  i.e. $L_H(v) = L_{G}(v) \ \forall v \in V_H.$

The subgraph containment and similarity problem involves searching for a query graph within the transactional graph database. Here, we consider a query graph that is obtained from the labelled data graphs. Hence, the query graph is also a simple, labelled graph. We elaborate extensively on the process of generating query workloads in “Real-World Datasets”.

Definition 3

(Subgraph Isomorphism [14]) Given a query graph, Q,  and data graph, G,  an embedding of Q in G is a mapping $M :V_Q \rightarrow V_G$ such that:

• 1. M is injective, i.e. $M(u) \ne M(u') \text{ for } u \ne u' \in V_Q).$

• 2. The labels match, i.e. $L_Q(u) = L_G(M(u))$ for every $u \in V_Q.$

• 3. All edges of Q exist in G,  i.e. $(M(u), M(u')) \in E_G \ \ \forall (u,u') \in E_Q.$

We say that graph Q is subgraph-isomorphic to G,  denoted by $Q \subseteq G$ if there exists an embedding of Q in G. We present the notations used in this paper in Table 1.

Table 1 Notation overview

Related Work

In this section, we provide a generalised understanding of the “filter-then-verify” framework that uses subgraph-based graph indexing techniques to facilitate subgraph searching within the transactional graph database. It is important to note here that the considered graph database contains multiple instances of graphs instead of a single massive graph within the database. The subgraph-based graph indexing embeds particular subgraphs (or features) extracted from the graph, such as paths, trees, or subgraphs, in a specialised index structure. The filter-then-verify framework comprises two steps: (1) index construction, an offline process of extracting subgraphs from the graph and building inverted indices between the subgraphs and the identifiers (ids) of the labelled graphs in which the subgraph appears, and (2) query processing, a process involving three steps: enumerating the built graph index for each subgraph observed in a query graph, thus maintaining the candidate graph set, and finally performing subgraph isomorphism on the graph ids appearing in the candidate set.

Given the transactional graph database and a query graph, the query processing time, denoted as $T_{QPT},$ is formulated as follows [29]:

$$\begin{aligned} T_{QPT} = T_{\text{filter}} + \sum _{C_Q \in {\mathcal{G}}} T_{\text{ISO}}(G) \end{aligned}$$

(1)

$T_{QPT}$ is the time taken to process a query graph, $|C_Q|$ is the cardinality of candidate data graphs containing a query graph, and $T_{ISO}$ is the time taken for isomorphism testing. Furthermore, the index size is proportional to the number of data graphs [29].

We shall now provide reviews on the related works associated with graph indexing, i.e. the gIndex, the FERRARI, and graph summarisation. We begin by reviewing the above-mentioned graph indexing methods because it is necessary to choose which graph structure for the index meets our requirements for efficient and effective indexing.

Graph Indexing

As previously mentioned, the subgraphs (or features) are generally paths, trees or subgraphs. The path is the simplest subgraph for indexing graphs, hence, it is easier to manipulate than other structures, thus leading to a shorter construction time. The main limitation of using a path as a subgraph is the loss of structural information due to the decomposition of the graph into a large number of paths. The existing works that incorporate subgraphs, such as the GraphGrep [8], the GraphGrepSX [5], the GRAPES [9], and the CT-Index [15], despite exhibiting good performance, are limited to only static graph databases. The only graph indexing method that supports a dynamic graph database is the gIndex [29]. According to an extensive benchmark conducted for subgraph searching problem [13], most of the non-mining-based approaches, such as GraphGrepSX and GRAPES, have performed superior to CT-Index in terms of indexing and query processing time. In the experimental evaluation of FERRARI, we observe that FERRARI has already been compared to the above-mentioned state-of-the-art subgraph indexing methods and, in fact, outperforms the above algorithms. Furthermore, our work includes a benchmark against another baseline, GRAPES-DD, which is the state-of-the-art non-mining-based approach. Its experimental analysis shows that this approach outperforms both GRAPES and CT-Index. This is the reason why we have not considered CT-Index as our baseline. We can conclude from our study that our work is superior to state-of-the-art methods, thereby bound to be superior to CT-Index.

Considering that the nature of the problem requires an index structure that supports a dynamic graph database, we chose to use the gIndex for our investigations. Now, we shall specifically focus on an elaborate discussion of the gIndex since our work, the W-Index, is an extension of the gIndex.

gIndex

The gIndex was the first method to introduce a novel, frequent subgraph mining algorithm based on a pattern growth approach that overcomes the drawbacks of Apriori-based frequent subgraph mining. In addition, a new canonical labelling method for graphs called Depth-first Search code (DFS code) was introduced. DFS code is a graph sequentialisation method, that represents a graph as a string sequence translating to the edge sequences in the graph. We can obtain DFS code through the depth-first search method and this is ordered based on the lexicographic order of the vertices label. We chose the minimal DFS code for this study. For in-depth understanding, we refer to [28]. The main aim of gIndex is to prune redundant subgraphs and only index those that are discriminative. The discriminative subgraphs are then maintained in an inverted index, that utilises a hash table structure. The key in the hash table is the canonical labelling of the frequent, discriminative subgraphs using DFS code. Furthermore, in its development, authors of the gIndex mapped each key to a unique identifier for a discriminative subgraph. Thus, they used another hash table to map the unique identifier of the subgraph to the list of graph identifiers that contain these discriminative structures. However, the pruning power of the gIndex ignores the weights on the edges and does not consider using a summary graph to reduce the query processing time. In addition, if gIndex were to be used for a visual exploratory subgraph searching (VESS) problem, then when the user adds an edge stream, the gIndex structure may not detect the subgraphs in the query graph. This is because it indexes only discriminative subgraphs which results in the need to perform expensive subgraph isomorphism testing. Moreover, even if we can search the subgraphs of the query graph within the gIndex, it would require building multiple index structures for the query graphs to facilitate VESS.

GRAPES-DD

Recently, the GRAPES-DD [18] has significantly reduced the complexity of the index-building phase and has outperformed the state-of-the-art GRAPES in terms of both indexing and query processing. Unlike in frequent subgraph indexing, in the GRAPES-DD, the paths of maximum length (denoted as $l_p)$ are extracted from the data graphs and then indexed within the Multi-Terminal Multi-way Decision Diagram (MTMDD), a type of decision diagram¹ [6]. MTMDD is a rooted directed acyclic graph. The GRAPES-DD method applies the heuristics of embedding common portions of the paths and efficiently storing their occurrence counts in a multiset. However, this approach suffers from the complexity of identifying the optimal variable order to optimise the index size, which is considered an NP-Complete problem [4]. As mentioned earlier, the GRAPES-DD is proposed for a static graph database where neither the data graphs nor the query graph grow. Furthermore, the GRAPES-DD does not exploit graphical user interface (GUI) latency during VESS.

FERRARI

The user inputs the query, as in the case of exploratory subgraph searching, through the GUI. In particular, the user facilitates the latter type of query to build the graph model and obtain answers to their query with a simple drag-and-drop operation. The main drawback of the existing query processing system is that it is limited to those knowledge users who can formulate complex syntax.

The FERRARI [25] framework is the foremost work providing a visual exploratory subgraph searching tool. This framework maintains an index structure for storing both frequent and discriminative infrequent subgraphs obtained through graph mining, VACCINE. Furthermore, it supports querying through building another index for the query graph called the ADVICE. On the other hand, the framework suffers mainly from longer construction times and query processing due to the large input graphs and multiple index structures. In contrast, our framework introduces graph summarisation as a solution to solve exploratory similarity searching. Instead of mining and indexing data graphs, we generate a summary of the data graphs and perform weighted frequent subgraph mining on the summary graphs. This novel work proposed a generic framework and, hence, is limited to static graph databases. Unfortunately, the number of chemicals in the graph database is growing rapidly; for instance, PubChem datasets have reached close to one hundred million molecules. Therefore, in order to support the evolution of the graph database, we have to re-mine the updated graph database and build a new index from scratch. This approach is, indeed, inefficient in terms of memory and time. In contrast to the FERRARI, in our work, we equip our framework to handle updates on the graph database.

Graph Summarisation

The input for the graph summarisation algorithm consists of static, labelled data graphs in the transactional graph database. We transform these simple, labelled dynamic query graphs into a condensed form during query processing. The input graph undergoes a transformation into a summary graph by aggregating the vertices into supervertices based on the graph’s structural properties and vertex attributes, and creating an edge between two supervertices. Furthermore, the summary graph retains important structural information from the original graph including the vertices, edges, labels, and counts. However, this process results in a multigraph.

Summarise and Search Framework (SuMExplorer)

In this section, we describe the summarise and search framework, the SuMmarisation-based frequent subgraph mining for visual exploratory subgraph searching (SuMExplorer) [27]. The SuMExplorer is derived based on inspiration from the classical approaches of a dual, step-based generalised framework called “filter-then-verify” [29].

In Fig. 2, we present the workflow of the SuMExplorer. Given an input graph database ${\mathcal{G}},$ we describe the overall process for subgraph query processing on SuMExplorer as follows:

• 1. The first step involves using the graph loader to preprocess and store the textual datasets by modelling them as data graphs.

• 2. Next, we summarise the data graphs in the transactional graph database $G \in {\mathcal{G}}.$

• 3. Then, we mine the weighted frequent and the discriminative infrequent subgraphs and edges from the intermediate summary graph. We then encode each weighted frequent and infrequent subgraph, $f \in F_h,$ using a canonical label called DFS code.

• 4. Subsequently, we must preserve parent–children information in the prebuilt offline index structure to facilitate efficient query processing. Hence, we store the mined subgraphs in the radix tree data structure sequentially, where the edges represent the parent-descendant relationship. We provide a detailed discussion on the process of maintaining the parent-descendants in the W-Index later (see “Global Index Structure (W-Index)”). Once we have built the global index structure, the W-Index, which we build only once and is immutable in nature, we can carry out the add(), modify(),  and run() operations on the query graph.

• 5. Finally, with an input query from the user endpoint $e_{Q_t},$ we can search for the seed edge $e_{Q_t}$ in the W-Index. We progress by finding the matching index node’s identifier in the W-Index which contains the current query input with $id=MatchNode(e_{Q_t}),$ and then check whether the id is already indexed in the M-Index with SearchNode(id). If SearchNode(id) contains the id,  we update the new node in the M-Index with $UpdateNode(id, e_{Q_t}),$ otherwise, we index the node in the M-Index with $AddNode(id, e_{Q_t}).$

• 6. Now, to find each frequent subgraph in the query graph $H \in Q_t$ that contains $e_{Q_t},$ we can perform a search in the W-Index using the parent–child relationship associated with the previously found index node in the W-Index that has the identifier id. We can then retrieve the identifier of the matching child node in the W-Index with $id=MatchChild(Q_t, id,e_{Q_t})$ and update or add a new node to the M-Index using the $AddNode(id, e_{Q_t})$ function. Consequently, we maintain the candidate set of data graphs by intersecting the graph identifiers associated with the leaf nodes in the M-Index.

• 7. Ultimately, when the user invokes the run() operation, we verify the partial results by performing a subgraph isomorphism algorithm on the candidate graph sets and return the final results to the user.

We formally define the above-mentioned list of functions below. The node matching in the W-Index involves searching for the matching canonical label within the W-Index.

Definition 4

(Node matching in the W-Index) Given the label of an indexed node in the W-Index, denoted as $C_h,$ and the canonical label as the DFS code (refer to the “gIndex”) of $e_{Q_t},$ we say that $e_{Q_t}$ matches a node with label $C_h,$ denoted as $MatchNode(e_{Q_t}),$ if $DFS code(e_{Q_t})=C_h.$ Recall that $e_{Q_t}$ is the new or seed edge which is added to query graph $Q_{t-1},$ which is constructed at time $t-1.$ We can retrieve the matching index node’s identifier as an id with the node matching function.

Example 1

(An example of node matching in the W-Index) In Fig. 4, suppose we have already built W-Index containing the extracted frequent subgraphs as observed in Fig. 3. Now referring to Fig. 1b, let us assume that the user adds a seed edge $e_{Q_1}$ connecting vertices $v_0$ and $v_1,$ thereby constructing the first query graph $Q_{t_1}$ at time $t_1.$ With this, the node matching function performs a look-up in the W-Index to observe if the root node contains any children with the label $C_h$ matching the DFSCode of $e_{Q_1}.$

As a consequence of node matching in the W-Index, we can obtain the id for the matching node. Based on the matching node, we can traverse the child nodes to search for the matching child in the W-Index that has the frequent subgraph $f \in F_h$ which contains $e_{Q_t}.$

Definition 5

(Child matching in the W-Index) Given the whole query graph $Q_t,$ the new edge $e_{Q_t}$ and the identifier of the matched index node in the W-Index that contains $e_{Q_t},$ we say that the child of the matched index node in the W-Index matches H,  denoted as $MatchChild(Q_t, id, e_{Q_t}),$ if $MatchChild(Q_t, id, e_{Q_t})=H$ where H is a subgraph of $Q_t$ and $e_{Q_t} \in$ $E_H$. With this function, given a matched index node identified by the id within the W-Index, we can retrieve its child node that contains $e_{Q_t}.$

We can perform node matching in the M-Index based on the identifier of the stored, previously matched, $e_{Q_t}$ in the M-Index.

Definition 6

(Node matching in the M-Index) Given the identifier of an indexed node in the M-Index, denoted as $\gamma _{id},$ and the identifier to search the id,  we say that id matches a node in the M-Index with an identifier $\gamma _{id},$ denoted as SearchNode(id),  if $\gamma _{id}=id.$ We can retrieve the matching index node’s id with the node matching function in the M-Index.

Fig. 2

Overview of the SuMExplorer workflow. We represent the workflow using a sequence diagram. The solid arrowhead shows the interaction between the user and the SuMExplorer. We represent the response from the SuMExplorer to the user using a dashed line. Additionally, we signify the interaction between the global index and query processing with self-messages (either recursive or simple)

In the following section, we shall elaborate on the solution for weighted frequent subgraph mining, however, before that, we will introduce the necessary definitions related to graph mining.

Frequent Subgraph Mining for Weighted Graphs

In order to reduce the longer query processing time associated with the stand-alone subgraph isomorphism, it is necessary to filter non-candidate labelled graphs. Hence, we need to identify interesting subgraphs, such as frequent subgraphs, to provide sufficient conditions for improving the filtering power. Next, we formally define a frequent subgraph as follows:

Definition 7

(Frequent Subgraph) A frequent subgraph is a subgraph, H,  in a labelled graph whose support cardinality in the transactional graph database, $Sup(H, {\mathcal{G}}),$ is greater than a specified threshold, $min_{sup}.$

We can compute the support of a subgraph, H,  in a labelled graph, $G_i,$ as follows:

$$\begin{aligned} Sup(H, G_i) = \left\{ \begin{array}{ll} 1 &{} \quad \text{if } H\subseteq G_i \\ 0 &{} \quad \text{otherwise}. \end{array}\right. \end{aligned}$$

(2)

Furthermore, we can compute the support of a subgraph, H,  in a transactional graph database, ${\mathcal{G}},$ as follows:

$$\begin{aligned} Sup(H, {\mathcal{G}})= \sum _{i=1}^{n} Sup(H, G_i). \end{aligned}$$

(3)

Here, n is the size of the transactional graph database.

Therefore, we formally define all the subgraphs, H,  that satisfy the following condition as frequent subgraphs:

$$\begin{aligned} Sup(H, {\mathcal{G}}) \ge min_{sup} \cdot |{\mathcal{G}}|. \end{aligned}$$

(4)

The frequency of the subgraphs in a graph is an important property in frequent subgraph mining. In this section, we focus on weighted subgraph mining since an intermediate summary graph results in a labelled graph with weights assigned to its edges. The weights on the edges provide additional structural information to improve the pruning power. However, these weights do not support the anti-monotonicity property (see Definition 8) that is the basis for frequent subgraph mining. Therefore, we must either ensure that the weights support the anti-monotonicity or apply heuristics based on weights and frequency separately. The latter is shown to require considerable computational time and to have poor filtering power. Hence, we now introduce our novel weighting function influenced by weighted association rule mining.

We first define the term anti-monotonicity property as follows:

Definition 8

(Anti-monotonicity property) The size l subgraph is frequent, if and only if its size ${l-1}$ subgraphs are frequent. Hence, $Sup(H_l, {\mathcal{G}}) \le Sup(H_{l-1}, {\mathcal{G}}).$

The first question concerning weighted frequent subgraph mining is which weight should be used to characterise the local structural information. Here, we can derive the current weights on the edges from the graph summarisation method. We can obtain weights through the interrelationships between the subgraphs. Therefore, we chose local structural information based on (1) computational efficiency and (2) how well it can embed local information.

Definition 9

Given the intermediate summary graph, $G_i,$ consisting of $\{w_1, w_2,\ldots ,w_k\}$ mapped to graph edges, we can compute the average total weight, $W_{avg},$ as follows:

$$\begin{aligned} W_{avg}(G_i)=\frac{\sum _{r=1}^{k} w_r}{k}. \end{aligned}$$

(5)

Here, k refers to the total number of edges in the summary graph. Thus, we can compute the total weight of a transactional database, denoted as $W_{sum}({\mathcal{G}}),$ as follows:

$$\begin{aligned} W_{sum}({\mathcal{G}})=\sum _{i=1}^{n} W_{avg}(G_i). \end{aligned}$$

(6)

Suppose that a subgraph, H,  occurs in a set of labelled graphs, denoted as $Occ_H,$ then we can define the weight of H with respect to ${\mathcal{G}}$ as follows:

$$\begin{aligned} W_{avg}(H)=\frac{\sum _{i\in Occ_H} w_{avg}(G_i)}{W_{sum}({\mathcal{G}})}. \end{aligned}$$

(7)

Next, we can compute the weighted support of a subgraph, H,  as follows:

$$\begin{aligned} {W}_{sup}(H)&= {W}_{avg}(H) \cdot Sup(H, {\mathcal{G}}) \\ &= \frac{{W}_{avg}(H) \cdot |Occ_{H}|}{|{\mathcal{G}}|}. \end{aligned}$$

(8)

Global Index Structure (W-Index)

In this section, we describe the offline, global index structure for data graphs in the transactional graph database. We call this index structure the Weighted-Index (W-Index) [27]; this is necessary for supporting subgraph searches during the query processing phase.

The W-Index is a memory-resident index structure. Our space-efficient optimisation enables us to store our index structure within the memory without requiring extra input/output costs to fetch the data from the disk. The W-Index is an N-ary tree rooted at node $\gamma _0$ that progressively grows index nodes in a levelwise manner based on the number of edges in the frequent subgraph |E|. We denote each index node in the W-Index as $\gamma _u \in \gamma ,$ where $0 \le u \le N_w$ and $N_w$ represent the total number of nodes in the W-Index.

The index node in the W-Index is a tuple with four elements, $\gamma =\langle id, C_h, p, G_I \rangle ,$ where id is the unique identifier of the index node in the W-Index and $C_h$ is the canonical label of the frequent or discriminative infrequent subgraph that we store in the index node. To determine whether the index node contains frequent or infrequent subgraphs, we maintain a boolean variable p,  where we store 1 if the subgraph is frequent, or 0 otherwise. In each index node of the W-Index, we maintain the references of the graph identifiers that contain the associated frequent or discriminative infrequent subgraph. We connect two index nodes with an edge to indicate the parent-descendant relationship, where the descendant node is a proper subgraph of the parent node. First, we store all the 1-edge frequent and infrequent subgraphs as a child to the root node. Subsequently, we store all the subgraphs containing l-edges at the lth level of the index structure. The index node in level l is connected to an index node of level $l-1$ with an edge. This edge is called the parent-descendant relationship which we formally define as follows:

Definition 10

(Parent–descendant relationship) Given two frequent or infrequent subgraphs, $H_1$ and $H_2,$ the numbers of edges in $H_1$ and $H_2$ is |E| and $|E|+1,$ respectively. In addition, $H_1 \subseteq H_2.$

Example 2

In Fig. 4a, we show the physical structure of an inner node. With the canonical labelling of the frequent (or infrequent) subgraph stored in the index node, we denote $H_j,$ where $1 \le j \le N_w.$ The set of graph identifiers associated with each index node, which we have shown as a black dot, is stored physically in a compressed bitmap index.

Example 3

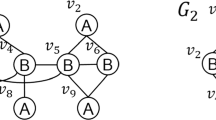
(An example of the W-Index) We note here that due to graph summarisation, the subgraphs extracted from the labelled graphs contain self-loops. The algorithm merges the common vertices, thereby reducing the number of subgraphs. Furthermore, the filtering operation is now a Boolean AND query. In Fig. 3, we foremost present the subgraphs extracted from the given labelled graphs $G_1, G_2, G_3, G_4,$ and $G_5$ that are present in the motivational example (see Fig. 1). Based on Definition 8, we classify the listed subgraphs as either frequent or infrequent subgraphs. Subsequently, we show the overall structure of the W-Index for the extracted subgraphs. We use white and grey nodes to discriminate between the frequent and infrequent subgraphs, as indicated by the boolean variable p. Each node of the W-Index contains a extracted subgraph’s id and its corresponding canonical label $C_h.$ For the sake of clarity, we do not present the canonical label but instead present the subgraph $H_{id}$ since canonical label is unique to the subgraph, similar to the unique identifier id. The node id is shown in square brackets. Furthermore, each node stores their graph identifier as a bitmap of size $|{\mathcal{G}}|$ where a value 1 in position j indicates the presence of the subgraph $H_i$ in the jth data graph. Here, j is an identifier of a data graph.

In contrast to the VACCINE’s memory-based frequent index (MF-Index) and disk-based frequent index (DF-Index), we maintain only the memory resident index for the offline, global index. This is because our graph summarisation and weighted frequent subgraph mining algorithm enable us to achieve a reduction in space usage.

Fig. 3

Graphical representation of frequent subgraphs generated from Fig. 1

Fig. 4

Graphical representation of the structure of the W-Index

Maintainable Index (M-Index)

In this section, we provide a description of the online index structure for incrementally maintaining the query graph. This index structure is called the Maintainable-Index (M-Index) [27]. The M-Index is a hash-based radix tree whose node contains a tuple with three elements $\lambda _m=\langle id, C_h, E \rangle ,$ where $1 \le m \le N_m.$ Here, we represent the total number of nodes in the M-Index as $N_m.$ The term $C_h$ represents the canonical label of the subgraph in the query graph. The integer id is associated with the matching node in the W-Index containing $C_h.$ Here, E is the set of edge sets that are contained in the subgraph. Now, let us first formalise the concept of a query graph since it is essential to understand how we create query graphs on GUI and subsequently construct the M-Index.

In the initial stage of visual exploratory query processing, we construct a new query graph by adding a new edge to the query panel on the visual interface. A query graph, $Q_t,$ is a labelled graph that we build incrementally through multiple query operations such as add(),  modify(),  and run().

We distinguish between the three types of operations on the query graph as follows:

• 1. add(): this indicates the user’s insertion of a node, edge, or template pattern² [25] into the query panel; hence, this is the modified query graph. The addition of a node itself is not considered when maintaining the M-Index. Only after connecting the new node to an existing node in the query graph is the modified query graph created.

• 2. modify(): this represents the user’s action to delete nodes, edges, or template patterns from the query graph. Node removal does not influence the modification of the query graph. The removal of its edges must accompany node removal.

• 3. run(): this triggers the execution of the whole query by the user.

The add() and modify() operations on the template pattern can be treated as a series of operations on the edge stream [25].

Query Construction Operation

The construction of the index for maintaining partial results of the query graph involves taking as an input a new edge $e_{Q_t},$ the current query graph $Q_t,$ and the prebuilt the W-Index. This process returns as an output the updated M-Index that matches the new edge and frequent or discriminative subgraphs containing the new edge in the M-Index. We depict an example of the M-Index construction in Fig. 5.

Example 4

(An example of the M-Index) Given the W-Index depicted in Fig. 4, we initiate the process of constructing the query graph in VESS with a single edge at time $t=1$ and proceed to add edges one at a time. Consider an edge $(C-C)$ in Fig. 3 as the seed edge. With the support of the node matching function $MatchNode(e_{Q_t})$ (see Definition 4), we foremostly look up in the W-Index to check for the matching node in the W-Index based on the canonical label of the queried edge. Since $\gamma _3$ with the node $id=3$ is the match, we now store the id of $\gamma _3$ as the label in the first node of the M-Index. Suppose we now add another edge $(C-O),$ which is stored in the W-Index with the node identifier 1. Consequently, we expand it in a levelwise manner by using the child matching function $MatchChild(Q_t, id, e_{Q_t})$ (see Definition 5) to search for the child of the matched index node that contains $e_{Q_t}.$ Going back to the example, we discover index nodes with identifiers 8 and 9 as matching children in the W-Index.

Observe that the above example results in four costs: (1) identifying the matching index node in the W-Index that contains the seed edge $e_{Q_t}$ $(MatchNode(e_{Q_t})),$ (2) maintaining the new edge, $e_{Q_t},$ to the query graph and the identifier of the matching index node in the M-Index (AddNode(id) or UpdateNode(id)),  (3) identifying all the subgraphs created by the query operation on the partial query graph $(MatchChild(id, e_{Q_t})),$ and (4) maintaining the matching index node’s identifier in the W-Index of the resulting subgraphs due to all the combinations of the new edge, $e_{Q_t},$ and the existing vertices in $Q_{t-1}$ (AddNode(id) or UpdateNode(id)).

Fig. 5

Graphical representation of the structure of the M-Index

We extend our initial proposal, the SuMExplorer, in the following five aspects: (1) supporting similarity searches, (2) enabling query modification, (3) enhancing the graph database to accommodate evolution, (4) exploiting compressed bitmaps for graph references, and (5) replacing the VF2 algorithm with an improved version provided by the CT-Index [15] implementation.

As previously mentioned in the related work section, our prior research primarily focused on addressing graph summarisation for visual exploratory subgraph searching. However, the effectiveness of this optimization was not thoroughly examined concerning similarity search (Experiment 4) and modification operations (Experiment 5) in our previous work. Furthermore, our previous work lacked extensive analysis of various parameters and their impact on indexing time and size, which we aim to investigate further in this paper as evident in Experiment 1 to 4. While the existing work [19] has proposed compressed bitmaps for path indexing to address subgraph searching, our focus lies in solving visual exploratory subgraph searching, where both the query graph and the graph database are dynamic and growing. The state-of-the-art approach FERRARI has already demonstrated in their work the inefficiency of traditional subgraph searching methods in solving visual exploratory subgraph search problems. However, our contribution is the first to propose the use of compressed bitmaps to optimise visual exploratory subgraph searching. We leverage optimisation methods proposed for the subgraph search to address this challenge for VESS. With this we iterate that rather than absolutely neglecting traditional subgraph search method for VESS, we emphasise on the importance of utilising knowledge gained to further optimise the index structure for the VESS.

Like the PICASSO [10], when adding a query and no exact matches are found in the W-Index with the candidate set $C_Q=0,$ we prompt the user with two choices: (1) modify the query or (2) perform similarity-based searching. The query modification involves deleting an edge. In the case of similarity-based searching, we can utilise the W-Index to facilitate the search.

Query Modification Operation

To elaborate further on the query modification operation, a critical condition is that while deleting an edge, we must avoid disconnecting the modified query graph. Currently, our system supports only one single query graph at a time. Thus, disconnecting the query graph would result in multiple queries. As mentioned earlier, users have the flexibility to modify the current query by formulating a new query when the current query graph has no exact matches. In addition, the user can modify the query to rectify the mistakenly added edges.

Similar to [25], our process for query modification consists of simple steps: (1) for each node in the M-Index, we check whether any edge sets in ${\mathcal{E}}$ contain the deleted edge and, subsequently, remove them. We can visit each node in our M-Index by using the depth-first-search algorithm and then remove the deleted edge by setting its bit position to 0 in the associated edge set, and (2) if ${\mathcal{E}}$ becomes empty as a result, then we remove the node from the M-Index. This operation has a ${\mathcal{O}}(N_m)$ complexity because we need to visit each node in the M-Index to check if it contains the deleted edges. Recall that the M-Index has $N_m$ number of nodes.

In contrast to our existing work, the SuMExplorer, our modification algorithm now allows the user to modify the query graph and efficiently update the M-Index.

Example 5

(An example of the modification operation) Suppose we want to delete an edge $(C-O)$ with the edge identifier $e_i=1.$ Referring to the M-Index in Fig. 5, we traverse through all the nodes and explicitly set the value at bit position 1 of each edge set in E to 0. Now, let us consider another edge to delete, for instance, an edge $(C-C)$ with the edge identifier $e_i=2.$ At this point, we notice that the edge set of node $\lambda _2$ is empty. Consequently, we proceed to delete node $\lambda _2.$

Query Processing Operation

The processing of a query, $Q_t,$ leveraging the W-Index and the M-Index involves two cases: $C_Q \ne 0$ or $C_Q=0.$

• 1. When $C_Q \ne 0,$ the problem is a subgraph containment problem. Here, $Q_t$ can be either a frequent or discriminative frequent subgraph which is indexed within the W-Index. The data graph identifiers associated with this matching node already contain $Q_t$ and, therefore, would require no further verification. On the other hand, if $Q_t$ is neither a frequent nor discriminative subgraph, we collect the leaf nodes of the W-Index. Finally, we perform an intersection operation on the data identifiers associated with the leaf nodes and verify the results using the extended VF2 algorithm. This method is based on the FG-Index.

• 2. When $C_Q=0,$ the problem shifts to similarity subgraph containment. Following [25], we iteratively remove edges from the query graph. Subsequently, we compute all the subgraph similarities based on $\theta$ between the modified query graphs, $Q_t,$ and their corresponding M-Index matching nodes. Finally, we perform similarity verification on top of the similarity candidates using an extended VF2. This idea involves an exhaustive enumeration of modified queries by considering all the possible combinations of edges in the query graph based on $\theta$ that can be removed without causing the query graph to become disconnected. Simultaneously, for each edge that is considered for removal from the query graph, we perform a modification operation on the M-Index to maintain the corresponding modified M-Index. Consequently, for each $1 \le k \le \theta ,$ we obtain a list of pairs consisting of modified query graphs and their corresponding modified M-Index. Ultimately, for each of these pairs, we perform an intersection operation on the graph identifiers associated with the leaf nodes of the modified M-Index, followed by subgraph isomorphism using extended VF2.

Experimental Analysis

In the proof-of-concept evaluation, we implemented our framework, the SuMExplorer, in the Java programming language on the system specified in Table 2. We integrated our framework with the user interface of the Java-based gBlend software to support user interaction. Furthermore, we implemented and extended the PARMoL’s gSpan [20] algorithm to support weighted frequent subgraph mining.

Table 2 System specification

We turn to study how our approach compares to the state-of-the-art visual exploratory subgraph search algorithm the FERRARI in terms of efficiency and effectiveness for three query operations (add(), modify(),  and run()). For brevity, we chose $min_{sup}=0.1$ and maximum subgraph size $\beta =8$ as described in the previous experiments [12, 25]. In this paper, we do not study the empirical analysis of varying $\beta$ because prior work [11] has already confirmed that it does not impact index time and size. Both FERRARI and SuMExplorer indexes all the frequent subgraphs in the memory regardless of the maximum subgraph size $\beta .$ Therefore, varying the value of $\beta$ does not affect the index time or size. Similarly, the subgraph and similarity query processing time is also independent of $\beta .$ In contrast to PICASSO, which required access to either memory or disk access depending on $\beta ,$ both FERRARI and SuMExplorer only consider filtering time in context to an in-memory access.

Furthermore, to extract frequent subgraphs, the FERRARI uses the gSpan algorithm implemented in [29]. Both our framework and the FERRARI use a graphical user interface (GUI) from gBlend. We present the results using 3 metrics: the index construction time and query processing time (measured in seconds (s)), and the index size (in megabytes (MB)). Furthermore, we used two different types of datasets (real-world and synthetic) and queries. The two different types of queries are as follows: one is formulated by the user, and the other is generated through a synthetic query graph simulator.

In our experimental study, we seek to answer the following research questions:

• 1. Effectiveness: how effective is our SuMExplorer framework in comparison to the state-of-the-art VESS and traditional filter-then-verify based methods?

• 2. Scalability: how do SuMExplorer’s index time, index size, and query time grow with respect to the parameter values?

Real-World Datasets

We used six real datasets, namely human immunodeficiency virus confirmed active (HIV-CA), cancer (CANS2DA99), antiviral screen (AIDS), public chemical database (PubChem), anticancer drug screen (NCI), and predictive toxicology (PTC) datasets, to show the effectiveness of our indexing algorithm. In Table 3, we list all the datasets and their characteristics, such as average number of nodes $V_{{\mathcal{AVG}}({\mathcal{G}})},$ average number of edges $E_{{\mathcal{AVG}}({\mathcal{G}})},$ average degree of the graphs $D_{{\mathcal{AVG}}({\mathcal{G}})},$ and labels $\sigma _{{\mathcal{AVG}}({\mathcal{G}})}.$ Considering the graph database, ${\mathcal{G}},$ is composed of several data graphs, denoted as ${G_1, G_2,\ldots , G_n}$ where each data graph has a number of vertices and edges, we obtain the average values for the mentioned characteristics. We present a detailed description of all the datasets as follows:

• HIV-CA: this dataset is popular and was used in more than 11 experiments [3]. In this collection, molecular compounds related to human immunodeficiency viruses were present. The HIV-CA contains 423 molecules with $V_{{\mathcal{AVG}}({\mathcal{G}})}=40, E_{{\mathcal{AVG}}({\mathcal{G}})}=42, \text{ and } \sigma _{{\mathcal{AVG}}({\mathcal{G}})}=21.$ We specifically selected 50 labelled graphs from the original dataset.

• CANS2DA99: these molecules are involved in carcinogenic tumours. CANS2DA99 consists of 32,557 molecular graphs with $V_{{\mathcal{AVG}}({\mathcal{G}})}=21, E_{{\mathcal{AVG}}({\mathcal{G}})}=22,$ and $\sigma _{{\mathcal{AVG}}({\mathcal{G}})}=82.$ We selected a subset from the original dataset with 600 labelled graphs.

• AIDS: this consists of approximately 40,000 chemical compounds with $V_{{\mathcal{AVG}}({\mathcal{G}})}=45, E_{{\mathcal{AVG}}({\mathcal{G}})}=46.95,$ and $\sigma _{{\mathcal{AVG}}({\mathcal{G}})}=62.$ From this dataset, we selected a subset containing 10,000 labelled graphs.

• PubChem: this is yet another chemical compound dataset published by the PubChem Project. It contains 200,000 to 50 million chemical compounds and is considerably larger than existing chemical datasets. From this dataset, we selected a subset containing 18,771 labelled graphs.

• NCI: this dataset includes a bioassay task for anticancer activity prediction against 10 types of cancer. It contains 250,251 chemical compounds from various sources with $V_{{\mathcal{AVG}}({\mathcal{G}})}=21, E_{{\mathcal{AVG}}({\mathcal{G}})}=22,$ and $\sigma _{{\mathcal{AVG}}({\mathcal{G}})}=82.$ We selected a subset from the original dataset containing 25,000 labelled graphs.

• PTC: this consists of the carcinogenic records of 342 chemical compounds tested on 4 animal models. In our case, we utilised the complete dataset since it contained a smaller number of graphs.

We retrieved the AIDS dataset from [1], acquired the PubChem dataset from [23], and obtained the remaining datasets (PTC, HIV-CA, CANS2DA99, and NCI) from [3]. First, we parsed the chemical graphs using SmilesGraphParser and then serialised them into the LineGraphParser format. Both graph parsers are available in the ParMol package [20]. Subsequently, we obtained frequent and infrequent subgraphs using our weighted frequent subgraph mining algorithm. In contrast to our approach of weighted frequent subgraph mining, FERRARI employs the gSpan algorithm³ without assigning weights to the edge labels.

Table 3 Characteristics of the real-world datasets

Now, we present our empirical findings (construction time, index size, and query response time) of our SuMExplorer framework for real-world datasets. To verify our claim that our W-Index and M-Index are efficient approaches for reducing computational resources, we conducted a comparative analysis. This involved the assessment of the W-Index’s index size and time and the M-Index’s query time to that of the FERRARI and the gIndex. Our method utilises a summary graph with fewer vertices and edges and employs weighted frequent subgraph mining to improve its effectiveness. The results of our comparison demonstrate that our approach is, indeed, effective, as evidenced by its smaller index size and faster building time.

By demonstrating the effectiveness of our the W-Index, we can highlight that using an efficient graph summarisation and an effective weighted frequent subgraph mining can significantly impact the index building time.

Experiment 1: Effectiveness of Indexing in the W-Index

In Fig. 6, we show the index time of our W-Index compared to the gIndex, and FERRARI’s VACCINE for the HIV-CA, PTC, CANS2DA99, AIDS, PubChem, and NCI datasets. As observed in Fig. 6, independent of the complexity of the graphs, the index building time for the W-Index and the gIndex are faster than the VACCINE for all the datasets. The usage of optimisation, such as graph summarisation and weighted frequent mining, led to a faster construction time for the W-Index than for the gIndex and the FERRARI. However, in the experimental results of the W-Index and the gIndex, we discerned that as the number of graphs in the dataset increased, denoted as $|{\mathcal{G}}|,$ the indexing times became approximately equivalent. This phenomenon is likely due to the summarisation overhead for each data graph in the database since the mining and index building time of the W-Index are comparatively less than those of the gIndex. Overall, we can deduce that reducing the complexity of the graph is the key factor for the superior performance of the W-Index across various biochemical graphs.

Fig. 6

Exp 1: Comparison of construction time in seconds (s) for various techniques (the W-Index, the gIndex, the FERRARI, and the GRAPES-DD) using a log-scale

In Fig. 7, we present the memory cost of the aforementioned index structures. We observed that for all the datasets, both the W-Index and the gIndex have similar memory consumption. In contrast to the W-Index and the gIndex, the FERRARI requires noticeably more memory.

Fig. 7

Exp 1: Comparison of the index size (MB) for various techniques (the W-Index, the gIndex, the FERRARI, and the GRAPES-DD) using a log-scale

Experiment 2: Effectiveness of Query Processing

Next, we show the effect of $min_{sup}$ on the query processing time when the user invokes the run() operation on the PubChem dataset with $|{\mathcal{G}}|=300{,}000.$ For this experiment, we varied the values of $min_{sup}$ as 0.05, 0.1,  and 0.2 and evaluated the query processing time for $Q_1$ to $Q_3.$ In addition, we evaluated the impact of varying $min_{sup}$ by setting 0.1, 0.2,  and 0.3 on the AIDS dataset with $|{\mathcal{G}}|=40{,}000$ for $Q_{10}$ and $Q_{11}.$ Based on Eq. 1, the query processing time $(\text{QPT})$ relies on the filtering time that consists of intersecting multiple graph identifier sets associated with the leaf nodes. Furthermore, it includes the verification time of the resulting candidate sets.

As illustrated in Fig. 8, the run() operation exhibits an approximately inversely proportional relationship between the query time and varying values of $min_{sup}.$ Since decreasing the values of $min_{sup}$ leads to the discovery of more frequent subgraphs, this increases the filtering time for both the FERRARI and the SuMExplorer. Due to the efficiency of our intersection operation and the use of the extended VF2 subgraph isomorphism method, the SuMExplorer is at the most 3.29 and 9.89 times faster compared to the execution of the run() operation on the FERRARI for the queries $Q_2$ $(min_{sup}=0.2)$ and $Q_{10}$ $(min_{sup}=0.3)$ on PubChem and AIDS, respectively. While SuMExplorer achieves 3.2 and 8.4 times faster, respectively, for the above-mentioned queries in contrast to FERRARI + Optimised VF2. The FERRARI + Optimised VF2 is FERRARI integrated with extended VF2. Due to the speed-up of optimised VF2 in comparison to VF2, we use FERRARI with extended VF2 for the subsequent experiments.

Fig. 8

Exp 2: Comparison of query processing time in milliseconds (ms) between the M-Index and the ADVICE for different values of $min_{sup}$

Experiment 3: Scalability of Subgraph Indexing

To analyse the scalability of the subgraph indexes, we first investigated the impact of varying $min_{sup}$ on the number of frequent subgraphs. In addition, we studied the effect of varying $|{\mathcal{G}}|$ on $min_{sup}.$ In the case of a mining-based subgraph index, the index construction time involves conducting frequent subgraph mining from data graphs and indexing time for the extracted frequent subgraphs. The resulting index structure mainly captures these extracted subgraphs. For instance, the W-Index for the SuMExplorer includes weighted frequent and discriminative infrequent subgraphs. In the case of FERRARI, frequent and discriminative infrequent subgraphs are stored in the VACCINE. On the other hand, the GRAPES-DD is a non-mining-based method and is not reliant on $min_{sup}$ and, therefore, we left it out for this experiment.

The $min_{sup}$ is approximately inversely proportional to the number of frequent subgraphs discovered. This is because we expect that a decrease in $min_{sup}$ will result in selecting an infrequent subgraph as frequent. Ultimately, the number of frequent subgraphs increases with decreasing in $min_{sup}.$ Conversely, an increase in $min_{sup}$ should result in pruning many infrequent subgraphs, and, therefore, a lesser number of frequent subgraphs would be discovered.

Moreover, the number of frequent subgraphs generated has a proportional correlation with the size of the transactional graph database $|{\mathcal{G}}|.$ Based on the principle of the size-increasing support function⁴ [29], $\psi (l) \propto min_{sup} \times N \propto N,$ we expect that for all the methods the index time scales approximately linearly with the number of data graphs.

To verify our prediction, we analysed the effect of different values of $min_{sup}$ (0.05, 0.1,  and 0.2) on the index building time and memory consumption for different methods the (SuMExplorer and the FERRARI with a varying number of data graphs (100,000, 200,000, 400,000, 500,000, 800,000 and 1000,000) on the PubChem dataset.

In Fig. 9a and b, we present the indexing time and memory cost, respectively. The FERRARI uses non-weighted frequent subgraph mining. We found that the W-Index was approximately 75% faster than the VACCINE. Our W-Index requires less space than the FERRARI. Recall that the W-Index utilises weighted frequent subgraph mining and graph summarisation. Hence, this approach speeds up subgraph mining and improves the pruning power. Thus, fewer numbers of frequent subgraphs are generated in comparison to the FERRARI.

Regarding larger datasets, we demonstrate the efficient construction of the SuMExplorer by benchmarking on the PubChem dataset with up to $|{\mathcal{G}}|=1000{,}000$ data graph entries. However, FERRARI cannot be constructed after 400,000 graph entries for $\alpha =0.05$ due to encountering memory issues. Similarly, for a database containing more than 450,000 graph entries, FERRARI stops executing across different $\alpha$ values.

Fig. 9

Exp 3: Comparison of a indexing time in seconds (s) and b memory consumption in Megabytes (MB), respectively, between the W-Index and the VACCINE for different values of $min_{sup}$ and the number of data graphs $|{\mathcal{G}}|$ of the PubChem dataset using a log-scale

Experiment 4: Effectiveness of Modification Operation

Now, we turn to analyse the effect of varying $|{\mathcal{G}}|$ on the efficiency of modifying the M-Index. For this experiment, after performing sequences of add() operations on the queries $Q_1, Q_2, Q_4$ and $Q_5$ for the PubChem dataset, we deliberately deleted the first edge. Similarly, we carried out the modify() operation on the queries $Q_1, Q_3, Q_6$ and $Q_7$ for the AIDS dataset. This ensured that we maintained the worst-case scenario. Subsequently, we measured the maximal response time required for the modification [25].

Recall that the expected modification time is linear to the number of nodes in the M-Index, denoted as $N_m$ (refer to “Query Modification Operation”). Furthermore, the upper bound of the number of nodes in the M-Index is $min(N_w, 2^{|E_Q|}-1)$ [27]. This implies that the modification time is linear with the number of nodes in the W-Index, thus, representing the weighted frequent and discriminate infrequent subgraphs extracted from the data graphs. In addition, following the same intuition explained in “Experiment 3: Scalability of Subgraph Indexing”, the number of frequent subgraphs is expected to increase proportionally with the number of data graphs $|{\mathcal{G}}|.$ In conclusion, we expected a linear correlation between $|{\mathcal{G}}|$ and the modification time. This is supported by Fig. 10, which almost perfectly matches this prediction. Nevertheless, the modification time also depends on the structure of the query graph.

In Fig. 10, we present our update time for the M-Index while varying the number of data graphs (10,000, 20,000, 30,000, and 40,000) for the AIDS dataset and (100,000, 200,000, 300,000, and 400,000) for the PubChem dataset. Our modification time is negligible due to the fewer nodes in the M-Index. We can observe that for PubChem, the SuMExplorer has an approximately 70% maximal response time reduction compared to the FERRARI for all the queries $Q_1, Q_2, Q_4$ and $Q_5$ at $|{\mathcal{G}}|=400{,}000.$ In the case of AIDS, the SuMExplorer has an approximately 97.60% maximal response time reduction compared to the FERRARI for query $Q_6$ at $|{\mathcal{G}}|=40{,}000.$

Fig. 10

Exp 4: Comparison of the maximal response time (modification operation) in milliseconds (ms) between the SuMExplorer and the FERRARI for different numbers of data graphs $|{\mathcal{G}}|$

Experiment 5: Effectiveness of the Similarity Searching Operation

Here, we compute the QPT to execute the similarity searching algorithm on the SuMExplorer and the FERRARI. We analysed the efficiency of algorithms for different values of similarity distance $\theta \in [1, 4].$ In Fig. 11, we illustrate the experimental observations of the query processing time on the PubChem for queries $Q_4$ to $Q_6$ and AIDS for queries $Q_1$ to $Q_3.$ Similarly, we also evaluated the QPT for similarity searching with the above-mentioned different values of $\theta$ for the AIDS dataset. As it was already stated, $min_{sup}=0.1$ and for PubChem dataset we have $|{\mathcal{G}}|=300{,}000$ and for AIDS dataset we have $|{\mathcal{G}}|=40{,}000.$

Our results show that the QPT of the SuMExplorer increases with the increase in $\theta$ values and ${\mathcal{G}}.$ This is expected since the number of candidate values to be verified should increase with the variation in model parameters because, when ${\mathcal{G}}$ increases, the number of frequent subgraphs should also increase. Nevertheless, the pruning power of our discriminative and weighted frequent subgraphs can significantly reduce the candidate size, thereby reducing the overall similarity verification time.

To elaborate further, based on the Eq. 1, we derive the overall query processing time. In the case of similarity search, the filtering time is $T_{{\text{filter}\, (\text{similarity})}}=T_{\text{filter}(\text{exact})}+(\sum _{k=1}^{\theta } \left( {\begin{array}{c}|Q_E|\\ k\end{array}}\right) ) \cdot T_{modification} \cdot T_{\text{intersection}}).$ As explained in “Query Processing Operation”, the first step to query processing is to check if the query graph is contained in data graphs. Thus, $T_{\text{filter}(\text{exact})}$ represents the time taken to obtain to check the current query graph for subgraph containment. Only then will the algorithm proceed with similarity containment if $C_Q=0.$ Now, the similarity search involves finding similar subgraphs to the query graph for each $\theta$ value by enumerating all possible combinations of $Q_E$ whose removal from the query graph will not cause disconnection. Hence, we have $( \sum _{k=1}^{\theta } \left( {\begin{array}{c}|Q_E|\\ k\end{array}}\right) )$ total number of possible combination of selecting k edges from $Q_E$ where k is restricted by $\theta$ value. Subsequently, for each exhaustive enumeration, we have to perform a modification operation, which is $T_{modification}={\mathcal{O}} (N_m)$ to obtain corresponding modified M-Index. With the obtained pairs of modified query graph and modified M-Index according to $\theta$ value, we now have to perform the intersection of the graph identifier references in the leaf nodes of the modified M-Index. Assume each intersection operation takes $T_{intersection}$ time. Hence, similarity search processing time will increase linearly with the increase in $\theta$ because of the increasing number of combinations to remove edges from the query graph and its corresponding query index, followed by performance of subgraph isomorphism between the modified query graph and the graph identifiers associated with the leaf nodes of the modified query index. As a result, we can observe three costs associated with similarity processing time: (1) query modification cost, (2) intersection operation, and (3) subgraph isomorphism cost. As demonstrated in Experiment 4, our algorithm proves more powerful for the modification operation, which ultimately reduces the filtering time for similarity search time. The cost reduction for SuMExplorer is incurred during the similarity verification time due to efficient intersection operation and pruning ability of the weighted, summarised mining aside from integration of state-of-the-art subgraph isomorphism. Both the algorithms, FERRARI and SuMExplorer are incorporated with extended VF2. Noticeably, the out-performance of SuMExplorer can reach one to two times faster with respect to the FERRARI for all of the queries.

Fig. 11

Exp 5: Comparison of the query processing time (similarity operation) in seconds w.r.t. (s) between the SuMExplorer and the FERRARI for values of distance $\theta$ on the $(Q_1{-}Q_3) \text{AIDS}$ and $(Q_4{-}Q_6) \text{PubChem}$ datasets

Synthetic Datasets

We generated data graphs and synthetic query graphs with a well-known G(n, p) random graph model using the implementation of the NetworKit⁵ [2]. The undirected G(n, p) model produces graphs with n nodes and adds each of the $\left( {\begin{array}{c}n\\ 2\end{array}}\right)$ possible edges independently with probability p. Since G(n, p) graphs are not assigned vertex labels, we independently assigned labels to the vertices uniformly at random.

In contrast to real-world datasets, the objective of benchmarking on synthetic datasets is to analyse the effect of varying parameter values on the evaluation metrics. We illustrate the synthetic query workloads in Fig. 12.

Fig. 12

Synthetic query workloads

Experiment 6: Effectiveness of Indexing in M-Index

In this subsection, we first evaluate the impact of the number of data graphs on the performance of the algorithm for querying synthetic datasets. To analyse this experiment, we measured the query processing time and memory consumption of the M-Index for evaluating the query graph. We expect the query processing time to scale linearly to the number of data graphs since the complexity of the graph is unaffected [29]. Nevertheless, when the data graphs become dense, more data graphs are highly likely to contain the given query graph. Therefore, the prospective number of candidate data graphs $|C_Q|$ and, ultimately, the query processing time increase.

As mentioned above, we incrementally built the query graph through multiple add() operations on the edge streams. We maintained the same values for the parameters as specified in “Experimental Analysis”, with $min_{sup}=0.1$ and $\beta =8.$ In addition, we varied the number of graphs linearly, from 30,000 to 60,000 for the Gilbert graph. Subsequently, we executed run() operations on the whole query graph and recorded the runtime for the given queries (i.e. $Q_1$ to $Q_{4})$ in the order specified by the edge label in Fig. 12.

In Fig. 13a, we compared the performance query processing of both algorithms on the synthetically generated queries. Our SuMExplorer has a compact index structure of summary graphs and benefits from the succinct nature of an improvised, compressed bitmap for storing graph references. In contrast, the FERRARI stores the subgraphs obtained from the original dataset within the index structure and their corresponding graph references in an uncompressed list. The efficiency of compressed bitmaps over lists has already been studied in various studies [17, 19]. Thus, the filtering time is efficiently reduced in our SuMExplorer. In addition, the use of a state-of-the-art subgraph isomorphism effectively decreases the verification time for both SuMExplorer and FERRARI. Our results provide compelling evidence since the query processing time scales linearly with the increasing number of graphs and is fastest for all the queries, with an approximately 70% reduction in the processing time.

In Fig. 13b, we report the compression gain obtained by our M-Index. Our M-Index has an average indexing compression ratio of 1 with respect to the FERRARI’s ADVICE. We computed the ratio by dividing the peak memory consumption measured for the radix tree structure of the M-Index by that registered for the Directed Acyclic Graph of the ADVICE. Despite sharing the same complexity, the number of nodes in our M-Index is sufficiently less than that in the ADVICE due to the adoption of graph summarisation and weighted frequent subgraph mining for the W-Index.

Experiment 7: Scalability of Subgraph Indexing and Query Processing

Similar to Experiment 2, we investigated the impact of $min_{sup}$ on the performance of the query processing time, this time using the synthetic dataset. While varying $min_{sup}$ to 0.05, 0.1,  and 0.2,  we recorded the query processing time for the G(n, p) generated graphs with $|{\mathcal{G}}|=60{,}000.$

Consistent with our prior analysis, as shown in Fig. 8, the SuMExplorer is faster than the FERRARI on the synthetic dataset. We measured a speedup of 2 times in contrast to the FERRARI (Fig. 14).

Fig. 13

Exp 6: a Query processing time (ms) for varying the number of data graphs on the synthetic dataset using a log-scale. b Comparison of memory consumption (MB) for various techniques (the W-Index, the gIndex, and the FERRARI) on the synthetic dataset

Fig. 14

Exp 7: Query processing time (ms) for varying the values for $min_{sup}$ on the synthetic dataset using a log-scale

Summary of Results

Overall, from our experimental study we gained the following insights:

• 1. In the context of the scalability of subgraph indexes, our first hypothesis is that given fixed parameters, the index time and memory consumption should linearly increase with the size of the database ${\mathcal{G}}.$ This was verified in both “Experiment 1: Effectiveness of Indexing in the W-Index” and Experiment 3: Scalability of Subgraph Indexing”. Despite an overhead from graph summarisation as $|{\mathcal{G}}|$ increases, our SuMExplorer emerges as the clear winner for both the real-world and synthetic datasets. Our SuMExplorer can be constructed 75% faster than FERRARI while reducing the size of the index by a factor of 2 orders of magnitude.

• 2. The run() operation of the SuMExplorer and the FERRARI distinctly outperforms traditional methods such as the GRAPES-DD and the gIndex. In particular, due to heuristic methods such as graph summarisation, the use of compressed bitmaps for faster intersection operations, and an extended VF2 algorithm, the SuMExplorer surpasses the FERRARI by at least 3 times faster for all queries.

• 3. Consistent with the observations of the FERRARI, the updating time of SuMExplorer is considerably negligible. Nevertheless, our method achieves a performance up to 70% faster, as observed in “Experiment 4: Effectiveness of Modification Operation”.

• 4. The similarity verification workload is expected to increase with an increase in distance since the number of verification tasks will increase. Our results from “Experiment 5: Effectiveness of the Similarity Searching Operation” matches our predictions for both the FERRARI and the SuMExplorer. However, the SuMExplorer outperforms FERRARI due to its efficient index structure, effectively reducing the filtering time with faster intersection operations, despite both employing state-of-the-art subgraph isomorphism.

Conclusions and Future Work

We propose a new framework of “summarise and search” to evaluate visual exploratory subgraph searching efficiently. We aimed to optimise visual exploratory subgraph processing and modification operations. We have introduced two index structures to evaluate the evolving query graph. The first index method is W-Index to embed the subgraphs mined from the data graphs compactly using summarisation and weighted frequent-based optimisation. The proposed structure is implemented using a radix tree. The second approach is M-Index; this is designed to reduce the search space during query processing and is built during runtime. To reduce the query processing time, we replace inefficient graph identifier lists associated with each node in the W-Index with a compressed bitmap and use a state-of-the-art subgraph isomorphism algorithm.

We have conducted extensive experiments on real-world and synthetic datasets with various workloads to compare four subgraph query processing algorithms belonging to (1) traditional non-mining based subgraph searching approach (such as the GRAPES-DD), (2) traditional mining based subgraph searching approach (such as the gIndex), and (3) the VESS methods (such as the FERRARI and the SuMExplorer). Our results demonstrate that the SuMExplorer can optimise the scalability of index construction with a speed-up of 75% in contrast to the FERRARI for the PubChem dataset. Our framework is capable of efficiently solving both exact visual exploratory subgraph searching and answering similarity search queries up to 3 and 1 times, respectively, faster than the FERRARI. Furthermore, it can support both query and database modification operations. As predicted, in case of modification operation, SuMExplorer outperforms FERRARI by approximately 70% and 90% for PubChem and AIDS respectively.

Our future work involves extending our approach to other complex graphs.