Delay Performance of a Two-User Broadcast Channel with Security Constraints

Abstract

In this paper, we consider the two-user broadcast channel with security constraints. We assume that a source broadcasts packets to two receivers, and that one of them has secrecy constraints, i.e., its packets need to be kept secret from the other receiver. The receiver with secrecy constraint has full-duplex capability, allowing it to transmit a jamming signal to increase its secrecy. We derive the average delay per packet and provide simulations and numerical results, where we compare different performance metrics for the cases when both receivers treat interference as noise, when the legitimate receiver performs successive decoding, and when the eavesdropper performs successive decoding. The results show that successive decoding provides better average packet delay for the legitimate user. Furthermore, we define a new metric that characterizes the reduction on the success probability for the legitimate user that is caused by the secrecy constraint. The results show that secrecy poses a significant amount of packet delay for the legitimate receiver when either receiver performs successive decoding. We also formulate an optimization problem, wherein the throughput of the eavesdropper is maximized under delay and secrecy rate constraints at the legitimate receiver. We provide numerical results for the optimization problem, where we show the trade-off between the transmission power for the jamming and the throughput of the non-legitimate receiver. The results provide insights into how channel ordering and encoding differences can be exploited to improve performance under different interference conditions.

Introduction

Due to the broadcast nature of the wireless medium, communication over a wireless channel is susceptible to eavesdropping. Secure communication is one of the critical issues for current and future wireless networks, and physical layer secrecy has emerged as a promising approach for ensuring secure communication over wireless channels in the last decade.

Most of the works in physical layer secrecy assume that users have always data to transmit. However, in many practical scenarios, the arrival of data is bursty in nature and the notion of stable throughput or region becomes a meaningful measure for such scenarios [2,3,4,5,6]. However, the exact characterization of delay is rather difficult, even in small multiple access networks, and remains unexplored in most cases [6].

Fig. 1

The system model where queue $Q_1$ has bursty traffic with arrival rate $\lambda _1$ and a queue $Q_2$ which is saturated. Receiver $D_1$ transmits a jamming signal of power $P_J$ to receiver $D_2$ to hinder eavesdropping

Related Work

The broadcast channel has been studied extensively with and without secrecy constraints in the existing literature [7,8,9,10,11]. In [7], the problem of secure communication is investigated for the broadcast channel, where the transmitter needs to send a confidential message to one of the receivers and also needs to send a common message to both of the receivers. The role of cooperation for secure communication when using a broadcast channel is studied in [9]. The effects on the capacity of the broadcast channel without secrecy constraints are studied in [10, 11]. However, characterizing the capacity and communication latency of a broadcast channel, even without secrecy constraints, is still an open problem.

The role of fading in secure communication has been explored in [8, 12]. In [8], the problem of secure communication is considered over a wiretap channel where the channel between different communicating nodes undergo quasi-static fading. In [8], it is shown that in the presence of fading, the legitimate transmitter can communicate securely even when the eavesdropper has a better SNR than the legitimate receiver. The impact of fading on the secrecy capacity of the broadcast channel has been explored in [12]. The effect of fading on secrecy for other communication models can be found in [13,14,15].

The problem of secure communication over multihop wireless networks has also been investigated [16,17,18,19]. Lai and Garnal [16] explores security enhancement through the use of relay nodes. In [17], it is shown how the intrinsic properties of multilevel wireless networks can be exploited to support network secrecy. The impact of secrecy constraints on the throughput of large-scale decentralized network has been analyzed in [18]. In [19], the scalability of physical layer-based approaches, which exploit the dynamics of wireless fading channels, is studied for a large wireless network.

Recently, there has been rapid growth in the area of supporting real-time applications, which means that there is a need to provide delay-based guarantees. For many future wireless networks, security and delay are required to be considered jointly for the performance analysis of the networks. At the same time, decoding ability of the users can impact the performance of the users significantly. To explore the impact of security and delay constraint on the performance, we have considered a two-user broadcast channel (BC) under various decoding schemes. The transmitter has two queues, where one of the queues has confidential data and the other queue has non-confidential data. The work also considers different traffic conditions at the queues. In particular, the delay performance is analyzed for the BC with secrecy constraint under various decoding schemes such as both the receivers treat interference as noise and one of the receivers treat interference as noise and the other receiver performs successive decoding.

Contribution

In this paper, we study the average delay performance of a two-user broadcast channel with security constraints and different traffic conditions at the queues. It is assumed that the receiver whose packets require secrecy has full-duplex capability. Hence, the receiver can send a jamming signal to hinder decoding of the sensitive information at the non-legitimate receiver. However, the full-duplex operation of the receiver results in self-interference at its own receiver, which can hamper decoding of its own message. The delay performance of the system depends on the secrecy constraint as well as on the jamming power and degree of self-interference cancelation at the receiver. The main contribution of this paper is to characterize the average delay performance for the legitimate receiver; in addition, we introduce a new metric that characterizes the reduction on the success probability for the legitimate user that is caused by the secrecy constraint. This metric can also characterize the tradeoff between secrecy and achieved throughput without secrecy. The paper also formulates an optimization problem, where the throughput of the receiver that does not have a secrecy constraint is maximized under delay and secrecy rate constraints for the legitimate receiver. To the best of our knowledge, the delay performance of a two-user broadcast channel with security constraints using different decoding schemes and different queue conditions (saturated queue and non-saturated queue), and a metric that characterizes the trade-off between secrecy and throughput performance has not been explored in the existing literature. In this work, we show how different decoding schemes can affect performance metrics such as average packet delay, saturated throughput, and the average queue size.

Structure of the Paper

The remainder of this paper is organized as follows. In the next section, we present some prior work used in the proposed method. In the subsequent section, we introduce the throughput analysis for different decoding schemes, and traffic at the source, followed by which we characterize the delay performance of the legitimate user. Before the concluding section, we provide numerical and simulation results, where we compare different performance metrics for different decoding schemes, and traffic at the source. Finally, we conclude the paper.

System Model

We consider a two-user broadcast channel (BC), where a single source S sends packets from two separate queues $Q_i$ to two different users (receivers) $D_i$, where $i = 1,2$, as shown in Fig. 1. Here, we use $Q_i$ to denote both the queue size of the queue that holds the packets for receiver $D_i$ and to refer to the queue itself. Queue $Q_1$ holds sensitive information; thus, these packets must be kept secret from $D_2$. In contrast, queue $Q_2$ contains non-sensitive packets intended for receiver $D_2$. Time is assumed to be slotted.

The arrival process at $Q_1$ is assumed to be Bernoulli with mean $\lambda _1$; thus, within a given time slot, a packet arrives with probability $\lambda _1$. Queue $Q_2$ is assumed to be saturated, thus it can capture the case of heavy traffic scenario, where $Pr(Q_2=0) \approx 0$, thus it can overestimate the interference that is caused to the other transmission.

When queue $Q_1$ is non-empty, source S transmits two messages in a single time slot using superposition coding. When queue $Q_1$ is empty, source S sends the packet intended for receiver $D_2$, with power $P_2$. The total power budget at the source is $P_{\max }$. The capacity of both queues is infinite, i.e., there is no packet dropping. Moreover, it is assumed that packets not successfully transmitted in a time slot will be re-transmitted until they are received by their intended destination. Packet transmission occurs at the beginning of the time slot. Finally, the packet arrivals happen at the end of the time slot. It is assumed that the transmission of acknowledgement (ACKs) is instantaneous and error free.

We assume that the legitimate receiver $D_1$ has full-duplex capability, i.e., it can receive and transmit simultaneously. Hence, receiver $D_1$ can send a jamming signal to receiver $D_2$ to prevent $D_2$ from decoding the packet that is intended for $D_1$. Thus, we assume that $D_1$ transmits a jamming signal when $Q_1 \ne 0$, otherwise is silent. In this work is assumed that $D_1$ is aware of the state of its intended queue, this can be achieved by the transmission of a control packet only when that queue is empty. We assume that this transmission is instantaneous and error free. The simultaneous transmission and reception at $D_1$ causes self-interference. It is assumed that the self-interference cancelation at receiver $D_1$ is imperfect and that the residual self-interference is modelled as a scalar g, where $g \in [0,1]$. For $g=0$, we have perfect self-interference-based cancelation, whereas for $g=1$, there is no cancelation at receiver $D_1$ [20,21,22].

We assume that the channel between source S and receiver $D_i$ is subject to Rayleigh fading. The signals that are received at the receivers, when both queues are non-empty, are as follows:

$$\begin{aligned} y_1[t]&= h_1x[t] + gx_J[t] + z_1[t], \nonumber \\ y_2[t]&= h_2x[t] + h_{12}x_{J}[t] + z_2[t], \end{aligned}$$

(1)

where $z_i$ ($i=1,2$) is additive white Gaussian noise with zero mean and unit variance, $h_i$ is the channel gain from source S to receiver $D_i$, $h_{12}$ is the channel gain from $D_1$ to $D_2$, $x_i$ is the signal that the source S transmits to the receiver $D_i$, $x_J$ is the jamming signal, and g is the self-interference cancelation coefficient. Note that $x_1$ and $x_2$ are independent. Due to the transmission of the jamming signal, the self-interference affects the reception of the sensitive information by the legitimate receiver. The source transmits the signal $x[t] = x_1[t] + x_2[t]$, when both queues have packet, t indicates the time slot. When queue $Q_1$ is empty, the transmitted signal is $x[t] = x_2[t]$. We also assume that both receivers have multipacket reception (MPR) capabilities. Specifically, a receiver can decode its intended transmission even when both queues are active and two packets are transmitted in a time slot based on the received signal-to-interference and noise ratio (SINR)/signal-to-noise ratio (SNR).

The probability that the legitimate receiver can successfully decode the packets originated by queue $Q_1$ and that the eavesdropper cannot decode the packet is denoted by $Pr(D_{1/T}^s)$, where T denotes the set of the queues containing messages, and s indicates the event that a message intended for receiver $D_1$ contains confidential information. Moreover, $Pr(D_{2/T})$ represents the probability that the eavesdropper can successfully decode the packets transmitted by queue $Q_2$. The mentioned probabilities depend on the decoding scheme and in the next section we will provide their exact characterization.

Throughput Analysis

We consider two schemes to decode the packets that are intended for receiver $D_i$: successive decoding and treating interference as noise. In the successive decoding scheme, the receiver first decodes the unintended packet and cancels its effect before decoding the intended packet. In the case of treating interference as noise, the receiver decodes the intended packet by treating the other packet as noise. Based on the different decoding schemes at the receivers, we consider three cases. In the first case, we consider that both of the receivers treat interference as noise. In the second case, we assume that receiver $D_1$ performs successive decoding and receiver $D_2$ treats interference as noise. In the third case, receiver $D_2$ performs successive decoding and receiver $D_1$ treats interference as noise. Finally, we note that the case where both receivers $D_1$ and $D_2$ perform successive decoding is infeasible in terms of power allocation for the two receivers as shown in [4]. In the following, the aforementioned cases are presented with different traffic assumptions at $Q_1$ and $Q_2$, in contrast with [5], where the case where one queue has bursty traffic and other queue has saturated traffic is not considered.

Queue $Q_1$ Has Bursty Traffic, While Queue $Q_2$ Is Saturated

In this case, the average service probabilities for queues $Q_1$ and $Q_2$ are given, respectively, by

$$\begin{aligned} \mu _1=\, & Pr(D^s_{1/1,2}), \end{aligned}$$

(2)

$$\begin{aligned} \mu _2=\, & Pr(Q_1 > 0) Pr(D_{2/1,2}) + Pr(Q_1 = 0) Pr(D_{2/2}). \end{aligned}$$

(3)

The probability of success $Pr(D_{2/2})$ is given by

$$\begin{aligned} Pr(D_{2/2}) = Pr\{ \textit{SNR}_2 \ge \gamma _2\}=\exp \left( -\frac{\gamma _2 d_2^\alpha }{P_2} \right) , \end{aligned}$$

(4)

where $\textit{SNR}_2 = P_2 \left| h_2\right| ^2d_2^{-\alpha }$, with $P_2$ being the transmit power, $h_2$ being the Rayleigh block fading channel gain from source S to receiver 2, $d_2$ being the distance between source S and receiver $D_2$, and $\alpha$ being the path loss exponent. When both queues $Q_1$ and $Q_2$ are non-empty, the probability that the $\textit{SINR}$ requirement is satisfied depends on the decoding scheme. Table 1 summarizes the notations used in the following equations.

The probability that queue $Q_1$ is empty is given by

$$\begin{aligned} Pr(Q_1 = 0) = 1 - \frac{\lambda _1}{Pr(D_{1/1,2}^s)}. \end{aligned}$$

(5)

From (2) and (5), we can obtain the service probability for queue $Q_2$, given by

$$\begin{aligned} \mu _2 = Pr(D_{2/2}) - \frac{Pr(D_{2/2}) - Pr(D_{2/1,2})}{Pr(D_{1/1,2}^s)}\lambda _1. \end{aligned}$$

(6)

Table 1 List of notations

Below we present the three cases regarding the decoding schemes at the receivers and provide the success probabilities.

Case 1 (Both receivers treat interference as noise) The probability of success that the legitimate receiver decodes the packet transmitted by source S to the legitimate receiver is given by

$$\begin{aligned} Pr(D_{1/1,2}^s)= \,& \exp \left( -\frac{\gamma _1 d_1^\alpha }{P_1 - \gamma _1 P_2} \big (1 + P_Jg^2 \big ) \right) \\ \nonumber&\times \left\{ 1 - \exp \left( -\frac{\gamma _1 d_2^\alpha }{P_1 - \gamma _1 P_2}\right) [ 1 + \gamma _1 \frac{P_J}{P_1 - \gamma _1 P_2} \left( \frac{d_2}{d_{12}}\right) ^\alpha ]^{-1} \right\} , \end{aligned}$$

(7)

with $P_1$ being the transmit power for the legitimate receiver, $h_{1}$ being the Rayleigh block fading channel gain from source S to receiver $D_1$, $d_1$ being the distance between source S and receiver $D_1$, $P_2$ being the transmit power for the eavesdropper, $\alpha$ being the path loss exponent, $P_J$ being the jamming power, g being the residual self-interference, $h_{12}$ being the Rayleigh block fading channel gain between the two receivers, and $d_{12}$ being the distance between receiver $D_1$ and receiver $D_2$. Equation (7) is nonzero when $\frac{P_1}{P_2} > \gamma _1$.

The probability of success that the legitimate receiver can decode the packets intended for it without the secrecy constraint, $Pr(D_{1/1,2})$, is given by

$$\begin{aligned} Pr(D_{1/1,2}) = \exp \left( -\frac{\gamma _1 d_1^\alpha }{P_1 - \gamma _1 P_2} \right) , \end{aligned}$$

(8)

when $P_1 > \gamma _1 P_2$.

The probability of success $Pr(D_{2/1,2})$ is given by

$$\begin{aligned} \begin{aligned} Pr(D_{2/1,2}) = \frac{ \exp \left( -\frac{\gamma _2d_2^\alpha }{P_2 - \gamma _2 P_1}\right) }{1 + \gamma _2 \frac{P_J}{P_2 - \gamma _2 P_1} \left( \frac{d_2}{d_{12}}\right) ^\alpha }, \end{aligned} \end{aligned}$$

(9)

and it is nonzero when $\frac{P_2}{P_1} > \gamma _2$. If we want to consider the system without secrecy constraints, then we replace $P_J=0$ in (9). The derivations for (7) and (9) are based on the Rayleigh fading assumption [5].

Case 2 (Receiver $D_1$ performs successive decoding and receiver $D_2$ treats interference as noise) In this case, $Pr(D_{1/1,2}^s)$ is given by

$$\begin{aligned} Pr(D_{1/1,2}^s)= \,& \exp \left( -\max \left\{ \frac{\gamma _2(1 + g^2P_J)d_1^\alpha }{P_2 - \gamma _2P_1},\right. \right. \\ \nonumber&\left. \left. \frac{\gamma _1(1 + g^2P_J)d_1^\alpha }{P_1} \right\} \right) \times \left[ 1 - \exp \left( -\frac{\gamma _1d_2^\alpha }{P_1 - \gamma _1P_2} \right) \right. \\ \nonumber&\left. \times \left\{ 1 + \gamma _1 \frac{P_J}{P_1 - \gamma _1P_2} \left( \frac{d_2}{d_{12}} \right) ^\alpha \right\} ^{-1} \right] . \end{aligned}$$

(10)

The details of the proof can be found in [5].

The probability of success $Pr(D_{1/1,2})$ that the legitimate receiver can decode the packets intended for it without secrecy is given by

$$\begin{aligned} Pr(D_{1/1,2}) = Pr \left( \frac{P_2 \left| h_1\right| d_1^{-\alpha }}{1 + P_1 \left| h_1\right| d_1^{-\alpha }} \ge \gamma _2, P_1 \left| h_1\right| d_1^{-\alpha } \ge \gamma _1 \right) . \end{aligned}$$

(11)

After some simplifications, $Pr(D_{1/1,2})$ is given by

$$\begin{aligned} Pr(D_{1/1,2}) = {\left\{ \begin{array}{ll} \exp \left( -\frac{\gamma _2 d_1^{\alpha }}{P_2 - \gamma _2 P_1} \right) , \text { if } \gamma _2P_1 < P_2 \le P_1 \frac{\gamma _2(1+\gamma _1)}{\gamma _1}, \\ \exp \left( - \frac{\gamma _1 d_1^{\alpha }}{P_1} \right) , \text { if } P_2>P_1\frac{\gamma _2(1+\gamma _1)}{\gamma _1}. \end{array}\right. } \end{aligned}$$

(12)

Case 3 (Receiver $D_1$ treats interference as noise and receiver $D_2$ performs successive decoding) In this case we consider that receiver $D_2$ has the capability to perform successive decoding. Since the eavesdropper has the capability to perform successive decoding, then if it fails, it makes sense to assume that it will try to decode the packet by treating interference as noise. Thus, by following the same methodology as in [5], $Pr(D_{1/1,2}^s)$ is given by

$$\begin{aligned} \begin{aligned} Pr(D_{1/1,2}^s) =&\exp \left( -\frac{\gamma _1 d_1^\alpha }{P_1 - \gamma _1P_2}(1 + P_J g^2) \right) \\&\times \left[ \frac{\exp \left( \frac{-\gamma _2 d_2^\alpha }{P_2 - \gamma _2 P_1} \right) }{1 + \frac{\gamma _2 P_J}{P_2 - \gamma _2 P_1} \left( \frac{d_2}{d_{12}} \right) ^\alpha } - \frac{\exp (\frac{-\gamma _1d_2^\alpha }{P_1})}{1 + \gamma _1 \frac{P_J}{P_1} \left( \frac{d_2}{d_{12}}\right) ^\alpha }\right] \\&+ \exp \left( - \frac{\gamma _1 d_1^\alpha }{P_1 - \gamma _1P_2}( 1 + P_Jg^2) \right) \\&\times \left( 1 - \exp \left( -\frac{d_2^\alpha }{\max \{\frac{P_2}{\gamma _2} - P_1, \frac{P_1}{\gamma _1} - P_2\} } \right) \right. \\&\left. \times \left\{ 1 + \frac{d_2^\alpha }{{\max \{\frac{P_2}{\gamma _2} - P_1, \frac{P_1}{\gamma _1} - P_2\} }} P_J d_{12}^{-\alpha } \right\} ^{-1} \right) . \end{aligned} \end{aligned}$$

(13)

The probability of success $Pr(D_{1/1,2})$ that the legitimate receiver can decode its packets without secrecy constraints is given by

$$\begin{aligned} Pr(D_{1/1,2}) = Pr \left( \frac{P_1 \left| h_1 \right| ^2 d_1^{-\alpha }}{ 1 + P_2 \left| h_1 \right| ^2 d_1^{-\alpha }} \ge \gamma _1 \right) , \end{aligned}$$

(14)

and its expression is given by (8).

In the following, we will provide the expression for the success probability for receiver 2. Here, receiver 2 first attempts to decode its intended packet by successive decoding. If this fails, it decodes by treating interference as noise. Following the same, methodology as in [5] we obtain

$$\begin{aligned} \begin{aligned} Pr(D_{2/1,2}) =&\exp \left( -\frac{\gamma _2d_2^\alpha }{P_2-\gamma _2P_1} \right) \left[1 + \gamma _2 \right.\\&\left.\frac{P_J}{P_2-\gamma _2P_1}\left( \frac{d_2}{d_{12}}\right) ^\alpha \right]^{-1} + \frac{\exp (-\gamma _2')}{1 + \gamma _2'P_Jd_{12}^{-\alpha }}\\&- \frac{\exp (-\gamma _2'')}{1 + \gamma _2''P_Jd_{12}^{-\alpha }}, \end{aligned} \end{aligned}$$

(15)

where $\gamma _2' \triangleq \min \left\{ \frac{\gamma _1d_2^{\alpha }}{P_1-\gamma _1P_2}, \frac{\gamma _2d_2^{\alpha }}{P_2} \right\}$ and $\gamma _2'' = \frac{\gamma _2d_2^{\alpha }}{P_2-\gamma _2P_1}$. The probability of success $Pr(D_{2/2})$ is given by (4).

Remark 1

Previously we provided the success probabilities for both cases of secrecy and without secrecy constraints for the legitimate user for several decoding schemes. It is interesting to show the reduction on the success probability for the legitimate user that is caused by the secrecy constraint. Thus, we define the following function f

$$\begin{aligned} f = 1-\frac{Pr(D^s_{1/1,2})}{Pr(D_{1/1,2})}. \end{aligned}$$

(16)

This function can also model the tolerance on the loss of secrecy to increase the throughput performance, in our case this can be achieved by adjusting the jamming power or the power allocation at the transmitter. This function provides a design factor for our system since it allows to tune the percentage of throughput loss we are willing to sacrifice to impose security constraints for the legitimate user. As $P(D_{1/1,2}^s) \le P(D_{1/1,2})$, following holds $0 \le f \le 1$. In this case, we assume that the feasibility conditions are satisfied so that we do not encounter the case where $P(D_{1/1,2}) = 0$. When f = 0, there is no loss due to the secrecy constraints when both the queues have data to send.

Remark 2

The expression for f can be obtained for various decoding schemes using the results in this section. In the following, the expression for f is obtained when both the receivers treat interference as noise. Thus, f is given by

$$\begin{aligned} f= \,& 1-\exp \left( -\frac{\gamma _1 d_1^\alpha P_Jg^2}{P_1 - \gamma _1 P_2} \right) \nonumber \\&\times \left\{ 1 - \frac{\exp \left( -\frac{\gamma _1 d_2^\alpha }{P_1 - \gamma _1 P_2}\right) }{1 + \frac{\gamma _1P_J}{P_1 - \gamma _1 P_2} \left( \frac{d_2}{d_{12}}\right) ^\alpha } \right\} . \end{aligned}$$

(17)

If $P_J=0$, then we have

$$\begin{aligned} f = \exp \left( -\frac{\gamma _1 d_2^\alpha }{P_1 - \gamma _1 P_2}\right) . \end{aligned}$$

(18)

In this case, f reduces to the probability that the eavesdropper can decode correctly the packet of the legitimate user if we did not impose security constraint.

In Sect. 4, we will utilize function f as a constraint in an optimization problem.

Both Queues Have Bursty Traffic

In this case, we consider that the queue $Q_2$ is no longer saturated, but instead has bursty traffic with arrival rate $\lambda _2$. The average service probabilities for queues $Q_1$ and $Q_2$ when they have both bursty traffic are given, respectively, by

$$\begin{aligned} \mu _1&= Pr(Q_2 > 0) Pr(D^s_{1/1,2}) + P(Q_2 = 0) Pr(D^s_{1/1}), \end{aligned}$$

(19)

$$\begin{aligned} \mu _2&= Pr(Q_1 > 0) Pr(D_{2/1,2}) + Pr(Q_1 = 0) Pr(D_{2/2}). \end{aligned}$$

(20)

As we can see, the average service rate given by (19) and (20) depends on the queue size of $Q_2$ and $Q_1$ respectively. Thus, queues $Q_1$ and $Q_2$ are coupled, which makes it difficult to compute the average service rates $\mu _1$ and $\mu _2$. The coupling of the queues can be tackled by applying the stochastic dominance technique, as in [2]. The stochastic dominance technique is based on the construction of dominant systems, where the queue with no packets transmits “dummy” packets and the other one behaves as in the original system. After applying the stochastic dominance technique we can obtain the stability conditions, which was the study of the work in [5]. Here, we focus on the delay performance of this system and more specifically on the delay performance for the legitimate user with secrecy constraints when queue $Q_2$ does not empty, thus it can overestimate the interference that is caused to the other transmission.

Delay Analysis for the Legitimate User

In this section, we will characterize the delay performance of the legitimate user. Delay has two components, the queueing delay and the transmission delay.

The average transmission delay of a packet from queue $Q_1$ when it is transmitted by source S to the legitimate receiver is given by

$$\begin{aligned} {\bar{D}}_{T} = \frac{1}{\mu _1}, \end{aligned}$$

(21)

where $\mu _1$ is the probability of departure for a packet waiting in queue $Q_1$.

The average queue size $Q_1$, if the queue is stable, is given by

$$\begin{aligned} {\bar{Q}}_1 = \frac{\lambda _1}{\mu _1 - \lambda _1} (1-\lambda _1). \end{aligned}$$

(22)

Proof: See “Appendix A”.

By Little’s law, the average waiting time of a packet in queue $Q_1$ is given by

$$\begin{aligned} {\bar{D}}_{Q_1} = \frac{{\bar{Q}}_1}{\lambda _1} = \frac{\frac{\lambda _1}{\mu _1-\lambda _1} (1-\lambda _1)}{\lambda _1} = \frac{1}{\mu _1 - \lambda _1}(1-\lambda _1). \end{aligned}$$

(23)

The average packet delay for the legitimate receiver is given by

$$\begin{aligned} {\bar{D}}_1 = {\bar{D}}_{Q_1} + {\bar{D}}_T = \frac{1}{\mu _1 - \lambda _1} (1-\lambda _1) + \frac{1}{\mu _1}. \end{aligned}$$

(24)

Optimization Problem

Here, we will consider the maximization of the throughout of the eavesdropper with delay constraints for the legitimate receiver and also a constraint regarding the f function defined in (16). The throughput for the eavesdropper is given by (6). The decision variables for the optimization problem are $P_1$, $P_2$, and $P_J$. Since $P_1 + P_2 = P_{\max }$, the optimization variables are reduced to $P_1$ and $P_J$. Then, the optimization problem is defined as follows

$$\begin{aligned} \begin{array}{ll} \underset{P_1, P_J}{\text{max}} &{} \text{Pr}(\text{D}_{2/2}) - \frac{\text{Pr}(\text{D}_{2/2}) - \text{Pr}(\text{D}_{2/1,2})}{\text{Pr}(\text{D}^{\text{s}}_{1/1,2})}\lambda _1 \\ \text {s.t} &{} {\bar{D}}_1 \le D^{*}, \\ &{} f \le f^{*}, \\ &{} 0\le P_1\le P_{\max }, \\ &{} 0\le P_J\le P_{\max }^{\prime }, \end{array} \end{aligned}$$

(25)

where ${\bar{D}}_1 \le D^{*}$ is the average delay constraint for the legitimate user, $f^{*}$ is the threshold for the function f given by (16), and the constraint $f \le f^{*}$ denotes that the success probability loss due to secrecy for the legitimate user cannot be above $f^{*}$. Furthermore, we assume that the arrival probability for the traffic of the legitimate user is fixed and equals to $\lambda _1$. The expressions for the success probabilities depend on the decoding schemes as presented in the previous section.

This optimization problem can model the case where a base station serves simultaneously two users with different secrecy requirements. We want to maximize the throughput seen by the user without secrecy requirements and at the same time to keep the delay for the user with secrecy requirements below a threshold. We also tune the secrecy tolerance depending on the requirements of the legitimate user.

The optimization problem in (25) is nonlinear due to the exponential factors in the equations for the success probabilities. We solve it numerically in the next section by utilizing the MATLAB solver (fmincon).

Numerical and Simulation Results

In this section, we provide numerical evaluation of the analytical results presented in the previous sections, in addition, we confirm the accuracy of our analysis with simulation results. Specifically, we study the impact of the jamming power $P_J$, the transmission power $P_1$, and the arrival rate $\lambda _1$ on the average packet delay ${\bar{D}}_1$, given in (24), on the saturated throughput $\mu _2$, given in (6), on the probability that queue $Q_1$ is empty, given in (5), and on the average queue size, given in (22). The average packet delay is a significant metric in a physical layer security application with partial jamming; it determines how often the legitimate receiver transmits a jamming signal in order to preserve the secrecy of its packets from an eavesdropper. When the legitimate receiver transmits a jamming signal frequently, the saturated throughput decreases, since the legitimate receiver causes interference to the eavesdropper. Even in the case where the eavesdropper does not receive the packets intended for the legitimate receiver, the legitimate receiver transmits a jamming signal because is has no knowledge about the channel state of the eavesdropper. The saturated throughput is another important metric; it has the maximum value if the legitimate receiver does not transmit jamming signals to the eavesdropper. The saturated throughput decreases as the jamming signal is transmitted more often. It is desirable that the probability that queue $Q_1$ is empty has a high value and a small average queue size for a given arrival probability, since the goal is to transmit all the packets from queue $Q_1$ to the legitimate receiver.

For our evaluation, we performed numerical evaluation and simulations in MATLAB R2016a. We consider the scenario where queue $Q_1$ has bursty traffic, while queue $Q_2$ is saturated. Under the aforementioned scenario, we consider three cases, and all numeric results are presented together with the corresponding simulation results when queue $Q_2$ is saturated. In the first case, both receivers treat interference as noise. Here, the distances between source S and the two receivers are $d_1 = 10$ m, $d_2 = 11$ m, and $d_{12} = 11$ m. In the second case, receiver $D_1$ performs successive decoding since it is closest to source S, and receiver $D_2$ treats interference as noise. In the third case, receiver $D_1$ treats interference as noise, and receiver $D_2$ performs successive decoding. Here, the distances between source S and the receivers are $d_1 = 11$ m, $d_2 = 10$ m, $d_{12} = 11$ m, where receiver $D_2$ is closest to source S and performs successive decoding.

The reason why we consider the first topology is that we have that the distance between the legitimate user and the transmitter is shorter than the distance between the eavesdropper and the transmitter. Furthermore, as also explained in [5], we need to have an asymmetric setup to reveal gains from the superposition coding and the successive decoding. In the second case, we consider the case where the eavesdropper is closer to the transmitter compared to the legitimate user, and also the eavesdropper can perform successive decoding, so satisfying the secrecy requirements is more challenging in this case. Thus, this case can stress the secrecy performance of the legitimate user.

For each of the aforementioned experiments, we have three sub-cases. First, we change the jamming power at the legitimate receiver, while keeping the transmission power to the legitimate receiver and the eavesdropper constant ($P_1=P_2 =20$ dB) for different values of $\lambda _1$ and $\beta$. Second, we change the transmission power to the legitimate receiver and the eavesdropper, while the jamming power at the legitimate receiver is kept constant ($P_J = 20$ dB) for different values of $\lambda$ and $\beta$. In the third case, we change $\lambda _1$ while keeping the transmission power constant for both the legitimate receiver and the eavesdropper ($P_1=P_2=20$ dB) for different values of $P_J$. For our simulation results, each simulation was run 10 times, with each simulation lasting over $10^7$ time slots, and the average value of the performance metrics were then reported. The simulation parameters are shown in Table 2. For each experiment, the sum of the transmission powers to the legitimate receiver and the eavesdropper are equal to the total power budget, $P_{\max }$. We measure the residual self-interference in dB ($\beta \triangleq -10 \log g^2$). The arrival probabilities are chosen such that $\lambda _1 < \mu _1$, which means that the system is stable.

We summarize the key points from the numerical and simulation results as following:

• Increasing the jamming power affects negatively both the delay performance and the saturated throughput regardless the decoding scheme.

• The delay performance can considerably be improved in the case when receiver $D_1$ performs successive decoding, while receiver $D_2$ treats interference as noise, since receiver $D_1$ is closer to the source in this decoding scheme.

• Another way to increase the saturated throughput is by lowering the secrecy level, in other words, by increasing the value of $f^*$ in the case when receiver $D_1$ performs successive decoding, while receiver $D_2$ treats interference as noise. Receiver $D_2$ can also benefit by achieving a higher throughput when the value of $D^*$ is small in the aforementioned decoding scheme.

Table 2 List of simulation parameters

Both Receivers Treat Interference as Noise

In Figs. 2, 3, 4, 5, 6, 7, 8 and 9, both receivers treat interference as noise, and queue $Q_2$ is saturated. In Figs. 2, 3 and 4, we change $P_J$ when both queues treat interference as noise. Figure 2 presents the average packet delay vs. the jamming power at the legitimate receiver for different values of $\lambda _1$ and $\beta$. The average packet delay decreases as the jamming power increases since the service probability increases as the jamming power increases as shown by (7) and (24). It should be noted that the simulation results validate the analytic expressions. To illustrate the uncertainty in the simulation values, Table 3 presents confidence intervals for the case $\lambda _1 = 0.09$ and $\beta = 40$ dB. Since the confidence intervals are also relatively tight, we have decided not to show these for the rest of the results in this paper. Instead, we only report average values from the simulations. Moreover, we can see that the average packet delay increases as the arrival probability at $Q_1$ increases. This happens because the waiting time of packets at queue $Q_1$ increases. The average packet delay also increases when $\beta$ is small, which means that the self-interference cancelation technique is insufficient, resulting in retransmissions of the packets. Figure 3 presents the saturated throughput vs. the jamming power at the legitimate receiver for different values of $\lambda _1$ and $\beta$. An increase in jamming power leads to a decrease in the saturated throughput, as shown by (6). We can also see that the saturated throughput increases as the arrival rate at $Q_1$ decreases, since the legitimate receiver transmits a jamming signal more often as the number of packets entering queue $Q_1$ increases. We can also see that the saturated throughput increases as $\beta$ increases, which means that a small self-interference residual (g) leads to an increase in the saturated throughput. In Fig. 4, we measure the probability that $Q_1$ is empty vs. $P_J$. We observe that the probability of $Q_1$ being empty increases as $P_J$ increases. The reason is that a high $P_J$ contributes to high service probability due to security constraints that are satisfied. We can also see that a high $\beta$ corresponds to a higher probability that queue $Q_1$ is empty. The reason is that a large $\beta$ means that the self-interference residual (g) is small, which in turn means that there are fewer retransmissions of the confidential packets.

Table 3 T confidence intervals

In Figs. 5 and 6, we change the transmission power of the legitimate receiver. The average packet delay vs. the transmission power at the legitimate receiver and the average queue size vs. the transmission power at the legitimate receiver are presented for different values of $\lambda _1$ and $\beta$. The transmission powers are in the range [19.29, 20.00] because they satisfy the constraints $\frac{P_1}{P_2} > \gamma _1$ and $\frac{P_2}{P_1} > \gamma _2$ in (7) and (9), respectively. The average packet delay decreases as the transmission power at the legitimate receiver increases, since source S uses more power for the transmission. We can also see that the average packet delay increases as $\lambda _1$ increases, since there are more packets in queue $Q_1$ waiting for transmission. Another observation is that the average packet delay is higher when $\beta$ is smaller. Thus, the average packet delay is higher due to more packet retransmissions, since the self-interference cancelation is not sufficient. In Fig. 6, we see that the average queue size decreases as the transmission power increases. This is reasonable since the more power source S uses to transmit the packets, the greater the likelihood that they will be received successfully. As $\lambda _1$ increases, the number of packets entering queue $Q_1$ also increases, thereby increasing the average queue size. The average queue size is also higher in the case where $\beta$ is small, meaning that the self-interference cancelation is insufficient. In Fig. 7, we can see the penalty on the delay performance due to secrecy constraints in comparison to the case when there is not secrecy constraints and both receivers treat interference as noise. Specifically, we note that the average packet delay is higher in the case where there is secrecy. This happens due to retransmission of packets.

Fig. 2

Average packet delay vs. jamming power at the legitimate receiver when both receivers treat interference as noise

Fig. 3

Average saturated throughput vs. jamming power at the legitimate receiver when both receivers treat interference as noise

Fig. 4

Probability that $Q_1$ is empty vs. jamming power at the legitimate receiver when both receivers treat interference as noise

Fig. 5

Average packet delay vs. transmission power at the legitimate receiver when both receivers treat interference as noise

Fig. 6

Average queue size vs. transmission power at the legitimate receiver when both receivers treat interference as noise

Fig. 7

Average packet delay vs. transmission power at the legitimate receiver when both receivers treat interference as noise

We also evaluate the optimization problem in (25), in which both receivers treat interference as noise. In Fig.  8, the optimal saturated throughput vs. the delay threshold is presented. For obtaining the optimal saturated throughput, we get the optimal jamming power for $f^{*} = 0.2$ and different values of $D^{*}$ and $\lambda _1$ in Table 4. Since $f^{*} = 0.2$, it means that the required secrecy level is high. We can see that the optimal saturated throughput increases as the delay threshold increases. This happens because as $D^{*}$ increases, the probability that receiver $D_1$ transmits a jamming signal decreases. In Fig.  9, the optimal saturated throughput vs. the f threshold is presented. For obtaining the optimal saturated throughput, we get the optimal jamming power for $D^{*} = 50$ timeslots and different values of $f^{*}$ and $\lambda _1$ in Table 5. The optimal saturated throughput increases as $f^*$ increases, since smaller $f^*$ implies less secrecy.

Fig. 8

Optimal saturated throughput vs. delay threshold when both receivers treat interference as noise and $f^* = 0.2$

Table 4 Optimal ${\bar{P}}_J$ for $f^{*} = 0.2$ and different values of $D^{*}$ and $\lambda _1$ when both receivers treat interference as noise

Fig. 9

Optimal saturated throughput vs. f threshold when both receivers treat interference as noise and $D^* = 50$ timeslots

Table 5 Optimal ${\bar{P}}_J$ for $D^{*} = 50$ time slots and different values of $f^{*}$ and $\lambda _1$ when both receivers treat interference as noise

Receiver $D_1$ Performs Successive Decoding and Receiver $D_2$ Treats Interference as Noise

In Figs. 10, 11, 12, 13, 14, 15, 16 and 17, receiver $D_1$ performs successive decoding and receiver $D_2$ treats interference as noise. In Figs. 10, 11 and  12, we change $P_J$ for different values of $\lambda _1$ and $\beta$. In Fig. 10, we observe that the average packet delay decreases as $P_J$ decreases and it increases as $\lambda _1$ increases as shown by (10), (24), and (21). Comparing Fig. 2 with Fig. 10, we can see that the successive decoding for receiver $D_1$ leads to smaller average packet delay in comparison with the case where both receivers treat interference as noise for the same $\lambda _1$ and $P_J$. In Fig. 11, we see that the saturated throughput decreases as $P_J$ increases. In contrast with Fig. 3, we see that the saturated throughput with the same values of $\lambda _1$ and $P_J$ is higher in the case where receiver $D_1$ performs successive decoding. This is justified by the fact that the service probability is higher in this case due to the successive decoding. In Fig. 12, we see the probability that the queue $Q_1$ is empty vs. $P_J$, where it increases as $P_J$ increases and it increases as $\lambda _1$ decreases as shown by (5) and (10). If we compare this figure with the respective one in the case where both receivers treat interference as noise in Fig. 4, we can see that the probability is higher when using successive decoding. This is justified by the fact that receiver $D_1$ has a better link.

In Figs. 13 and 14, we see the average packet delay vs. the transmission power at receiver $D_1$ and the average queue size vs. the transmission power at receiver $D_1$ when $D_1$ performs successive decoding and $D_2$ treats interference as noise, respectively. The transmission powers are in the range [19.29, 20.00] because they satisfy the constraints $\frac{P_1}{P_2} > \gamma _1$ and $\frac{P_2}{P_1} > \gamma _2$ in (7) and (9) respectively. In Fig. 13, we see that the average packet delay decreases slightly at $P_1 = 19.60$ dB and it increases for $P_1 > 19.60$ dB. Moreover, we observe that the average packet delay increases as $\lambda _1$ increases and as $\beta$ decreases. The reason is that higher arrival probability leads to increasing packets in queue $Q_1$ and small $\beta$ implies a limited ability to cancel out self-interference, which leads to an increase in the average packet delay due to packet retransmissions. Comparing Figs. 5 and 13, we see that the average packet delay decreases as $P_1$ increases in the case of where both receivers treat interference as noise. Another observation is that we have significantly smaller average packet delay when successive decoding is used, which is due to better channel between source S and receiver $D_1$. In Fig. 14, we see that the average queue size decreases slightly at $P_1 = 19.60$ dB and it increases as $P_1$ increases as shown in (10) and (22). Furthermore, we see that the average queue size increases for larger values of $\lambda _1$ and for smaller values of $\beta$. Comparing Fig. 6 with Fig. 14, we can see that, when the receiver performs successive decoding, the average queue size increases as $P_1$ increases, while in the case when both receivers treat interference as noise, the average queue size decreases as $P_1$ increases.

In Fig. 15, we can see that the average packet delay is higher as $P_1$ increases when there is secrecy, but decreases when there is no secrecy. The reason is that since receiver $D_1$ is closer to the source, a high transmission power leads to a low average packet delay when there is no secrecy.

Fig. 10

Average packet delay vs. jamming power at the legitimate receiver when $D_1$ performs successive decoding and $D_2$ treats interference as noise

Fig. 11

Saturated throughput vs. jamming power at the legitimate receiver when $D_1$ performs successive decoding and $D_2$ treats interference as noise

Fig. 12

Probability that $Q_1$ is empty vs. jamming power at the legitimate receiver when $D_1$ performs successive decoding and $D_2$ treats interference as noise

Fig. 13

Average packet delay vs. transmission power when $D_1$ performs successive decoding and $D_2$ treats interference as noise

Fig. 14

Average queue size vs. transmission power when $D_1$ performs successive decoding and $D_2$ treats interference as noise

Fig. 15

Average packet delay vs. transmission power when $D_1$ performs successive decoding and $D_2$ treats interference as noise

We also evaluate the optimization problem in (25) when receiver $D_1$ performs successive decoding and receiver $D_2$ treats interference as noise. In Fig. 16, the optimal saturated throughput vs. the delay threshold is presented. For obtaining the optimal saturated throughput, we get the optimal jamming power for $f^{*} = 0.2$ and different values of $D^{*}$ and $\lambda _1$ in Table 6. Since $f^{*} = 0.2$, it means that there is high secrecy at receiver $D_2$. We can see that the optimal saturated throughput, increases as the delay threshold increases, since the probability receiver $D_1$ transmits a jamming signal to receiver $D_2$ decreases. Figure 17 presents the optimal saturated throughput vs. f threshold. For obtaining the optimal saturated throughput, we get the optimal jamming power for $D^{*} = 50$ time slots and different values of $f^{*}$ and $\lambda _1$ in Table 7. We see that the optimal saturated throughput increases as f increases, because higher $f^*$ means that there is less secrecy.

Fig. 16

Optimal saturated throughput vs. delay threshold when receiver $D_1$ performs successive decoding and receiver $D_2$ treats interference as noise and $f^* = 0.2$

Table 6 Optimal ${\bar{P}}_J$ for $f^{*} = 0.2$ and different values of $D^{*}$ and $\lambda _1$ when receiver $D_1$ performs successive decoding and receiver $D_2$ treats interference as noise

Fig. 17

Optimal saturated throughput vs. f threshold when receiver $D_1$ performs successive decoding and receiver $D_2$ treats interference as noise and $D^* = 50$ timeslots

Table 7 Optimal ${\bar{P}}_J$ for $D^{*} = 50$ timeslots and different values of $f^{*}$ and $\lambda _1$ when receiver $D_1$ performs successive decoding and receiver $D_2$ treats interference as noise

Receiver $D_1$ Treats Interference as Noise and Receiver $D_2$ Performs Successive Decoding

In Figs. 18, 19, and 20, we change $P_J$ for different values of $\lambda _1$ in the case where receiver $D_1$ treats interference as noise while receiver $D_2$ is more powerful and performs successive decoding. Specifically, in Fig. 18, we see that the average packet delay decreases as $P_J$ increases and it increases as $\lambda _1$ increases as shown in (13), (21), and (24). Comparing Figs. 2 and 10 with Fig. 18, we can see that the case when receiver $D_2$ performs successive decoding has a higher average packet delay than the other two cases. Figure 19 presents the saturated throughput vs. jamming power. As we can see, the saturated throughput decreases quickly as $P_J$ increases and it decreases as $\lambda _1$ increases as shown in (6) and (13). Comparing Figs. 3 and 11 with Fig. 19, we can see that the case where receiver $D_2$ performs successive decoding achieves the highest saturated throughput of the three cases. This can be justified since receiver $D_2$ is geographically closer to source S, and thus it has a better channel. In Fig. 20, the probability that $Q_1$ is empty vs. jamming power is presented. The probability increases as $P_J$ increases and as $\beta$ increases, and decreases as $\lambda _1$ increases as shown in (5) and (13). When we compare Figs. 4 and 12 with Fig. 20, we see that the probability has the lowest value in the case where receiver $D_2$ performs successive decoding.

In Figs. 21 and 22, we have the average packet delay vs. the transmission power at source S for receiver $D_1$ and the average queue size vs. the transmission power at source S for receiver $D_1$ when $D_2$ performs successive decoding and $D_1$ treats interference as noise. The transmission powers are in the range [19.29, 20.00] because they satisfy the constraints $\frac{P_1}{P_2} > \gamma _1$ and $\frac{P_2}{P_1} > \gamma _2$ in (7) and (9), respectively. In Fig. 21, we can see the average packet delay vs. the transmission power $P_1$ for different values of $\lambda _1$ and $\beta$. As we can notice, the average packet delay decreases as $P_1$ increases and increases as $\lambda _1$ increases as shown in (13), (21), and (24). In Fig. 22, we can see the average queue size vs. the transmission power $P_1$ for different values of $\lambda _1$ and $\beta$. We can see that the average queue size decreases as $P_1$ and $\lambda _1$ increase, and increases as $\beta$ decreases as shown in (13), and (22). Comparing Figs. 6 and 14 with Fig. 22, we observe that the average queue size decreases as $P_1$ increases when both receivers treat interference as noise and when receiver $D_1$ treats interference as noise and receiver $D_2$ performs successive decoding, but increases as $P_1$ increases when receiver $D_1$ performs successive decoding.

In Fig. 23, we see that the average packet delay is higher in the case where there is no secrecy. Specifically, we can see that when receiver $D_2$ performs successive decoding and, thus is closer to the source, the average packet delay for receiver $D_1$ is considerably higher in the case where there is secrecy.

We also evaluate the optimization problem in (25) when receiver $D_1$ treats interference as noise and receiver $D_2$ performs successive decoding. In Fig. 24, the optimal saturated throughput vs. the delay threshold is presented. For obtaining the optimal saturated throughput, we get the optimal jamming power for $f^{*} = 0.2$ and different values of $D^{*}$ and $\lambda _1$ in Table 8. We can see that the optimal saturated throughput is constant between [5, 10] timeslots, but it increases when $D^{*}> 10$ timeslots. The reason is that the probability that receiver $D_1$ transmits a jamming signal to receiver $D_2$ decreases, as a result optimal saturated throughput increases. Figure 25 presents the optimal saturated throughput vs. f threshold. For obtaining the optimal saturated throughput, we get the optimal jamming power for $D^{*} = 50$ timeslots and different values of $f^{*}$ and $\lambda _1$ in Table 9. We see that the optimal saturated throughput increases as f increases, because as $f^*$ increases there is less secrecy.

Fig. 18

Average packet delay vs. jamming power at the legitimate user when $D_1$ treats interference as noise and $D_2$ performs successive decoding

Fig. 19

Saturated throughput vs. jamming power at the legitimate user when $D_1$ treats interference as noise and $D_2$ performs successive decoding

Fig. 20

Probability that $Q_1$ is empty vs. jamming power at the legitimate user when $D_1$ treats interference as noise and $D_2$ performs successive decoding

Fig. 21

Average packet delay vs. transmission power when $D_1$ treats interference as noise and $D_2$ performs successive decoding

Fig. 22

Average queue size vs. transmission power when $D_1$ treats interference as noise and $D_2$ performs successive decoding

Fig. 23

Average packet delay vs. transmission power when $D_1$ treats interference as noise and $D_2$ performs successive decoding

Fig. 24

Optimal saturated throughput vs. delay threshold when receiver $D_1$ treats interference as noise and receiver $D_2$ performs successive decoding and $f^* = 0.2$

Table 8 Optimal ${\bar{P}}_J$ for $f^{*} = 0.2$ and different values of $D^{*}$ and $\lambda _1$ when receiver $D_1$ treats interference as noise and receiver $D_2$ performs successive decoding

Fig. 25

Optimal saturated throughput vs. f threshold when receiver $D_1$ treats interference as noise and receiver $D_2$ performs successive decoding and $D^* = 50$ timeslots

Table 9 Optimal ${\bar{P}}_J$ for $D^{*} = 50$ timeslots and different values of $f^{*}$ and $\lambda _1$ when receiver $D_1$ treats interference as noise and receiver $D_2$ performs successive decoding

Conclusion

This paper presents an analysis of delay for a two-receiver broadcast scenario with security constraints. Specifically, a source transmits both confidential and non-confidential data to two receivers, while the legitimate receiver transmits a jamming signal to the eavesdropper in order to prevent the latter from decoding the former’s packets. A delay analysis is provided and the saturated throughput is maximized with packet delay and secrecy rate constraints for the legitimate receiver. We provide numerical results where we show that the use of successive decoding at the legitimate receiver outperforms the cases where the eavesdropper performs successive decoding and when both receivers treat interference as noise. Thus, different decoding schemes affect the performance metrics differently. This allows us to exploit the channel ordering to provide better performance. For example, in cases where the interference from the other receiver is strong, performing successive decoding is desirable, and when the interference is sufficiently weak it is better to treat the interference as noise.

Appendices

Appendix A

Markov Chain

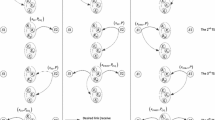
The Markov chain (DTMC) that describes the queue evolution is presented in Fig. 26. Each state represents the number of packets in the queue $Q_1$. At each time slot, the departures take place before the arrivals. The queue stays in state 0, when no arrivals happen. When a new packet arrives in queue $Q_1$, there is a transition to state 1 with probability $\lambda _1$. The transition from state 1 to state 0 happens with probability $\mu _1(1-\lambda _1)$, where a packet departure happens but no packet arrives in the current time slot. The queue length remains in the same state with probability $\kappa = \lambda _1\mu _1 + (1-\lambda _1)(1-\mu _1)$, where both a packet arrival and a packet departure happen, or where neither happens. The transition for packet arrivals to state 2 happens with a probability $\lambda _1(1-\mu _1)$, where a packet arrives in the queue but there is no packet departure. The same applies for packet arrivals for the rest of the states. Next, we derive the steady-state distribution of the Markov chain.

Fig. 26

The discrete time Markov Chain (DTMC) for the evolution of $Q_1$

To compute the steady-state distribution $\pi$, we have to solve for $\pi = \pi P$, where P is the transition matrix, which is equivalent to

$$\begin{aligned} {} \pi _i= \,& \pi _{i-1}P_{i-1,i} + \pi _iP_{ii} + \pi _{i+1}P_{i+1,i}, \quad i>0, \end{aligned}$$

(26)

$$\begin{aligned} \pi _0=\, & \pi _0P_{00} + \pi _1P_{1,0}. \end{aligned}$$

(27)

For $i=0$, we obtain $\pi _0 = \pi _0P_{00} + \pi _1P_{1,0} \Rightarrow \pi _1 = \frac{\lambda _1}{\mu _1(1-\lambda _1)}\pi _0$. For $i=1$, we get $\pi _1 = \pi _{0}P_{0,1} + \pi _1P_{11} + \pi _{2}P_{2,1} \Rightarrow \pi _2 = \frac{\lambda _1}{\mu _1(1-\lambda _1)} \left[ \frac{\lambda _1(1-\mu _1)}{\mu _1(1-\lambda _1)}\right] \pi _0$. For $i=2$, it is $\pi _2 = \pi _{2}P_{1,2} + \pi _2P_{22} + \pi _{3}P_{3,2} \Rightarrow \pi _3 = \frac{\lambda _1}{\mu _1(1-\lambda _1)} \left[ \frac{\lambda _1(1-\mu _1)}{\mu _1(1-\lambda _1)}\right] ^2 \pi _0$.

In addition, the above equations have to satisfy the constraint $\sum _{i} \pi _i=1$. By substituting the aforementioned expressions for the steady-state distribution to the above constraint, we obtain $\pi _0 + \frac{\lambda _1}{\mu _1(1-\lambda _1)}\pi _0 + \frac{\lambda _1}{\mu _1(1-\lambda _1)} \left[ \frac{\lambda _1(1-\mu _1)}{\mu _1(1-\lambda _1)}\right] \pi _0 + \frac{\lambda _1}{\mu _1(1-\lambda _1)} \left[ \frac{\lambda _1(1-\mu _1)}{\mu _1(1-\lambda _1)}\right] ^2 \pi _0 + \cdots = 1$. Solving for $\pi _0$, we get the stationary probability of being in the state 0, which is given by $\pi _0 = 1 - \frac{\lambda _1}{\mu _1}$. Thus, the steady-state distribution is given by

$$\begin{aligned} \pi _i={\left\{ \begin{array}{ll} \frac{\lambda _1}{\mu _1(1-\lambda _1)} \left[ \frac{\lambda _1(1-\mu _1)}{\mu _1(1-\lambda _1)}\right] ^{i-1} \pi _0, \qquad i>0, \\ 1 - \frac{\lambda _1}{\mu _1}, \quad i=0. \end{array}\right. } \end{aligned}$$

(28)

The average queue size can be calculated by

$$\begin{aligned} {} \begin{aligned} E[Q_1]&= \sum _{i=0}^\infty i \pi _i \\&= \sum _{i=1}^\infty i \frac{\lambda _1}{\mu _1(1-\lambda _1)} \left[ \frac{\lambda _1(1-\mu _1)}{\mu _1(1-\lambda _1)}\right] ^{i-1}\pi _0 \\&= \pi _0 \sum _{i=1}^\infty i \frac{\lambda _1}{\mu _1(1-\lambda _1)} \left[ \frac{\lambda _1(1-\mu _1)}{\mu _1(1-\lambda _1)}\right] ^{i-1} \\&= \left( 1-\frac{\lambda _1}{\mu _1}\right) \sum _{i=1}^\infty i\frac{\lambda _1}{\mu _1(1-\lambda _1)} \left[ \frac{\lambda _1(1-\mu _1)}{\mu _1(1-\lambda _1)}\right] ^{i-1} \\&= \left( 1-\frac{\lambda _1}{\mu _1}\right) \frac{\lambda _1}{\mu _1(1-\lambda _1)} \sum _{i=1}^\infty i \left[ \frac{\lambda _1(1-\mu _1)}{\mu _1(1-\lambda _1)}\right] ^{i-1} \\&= \left( 1-\frac{\lambda _1}{\mu _1}\right) \frac{\lambda _1}{(1-\lambda _1)} \frac{1}{\left[ 1 - \frac{\lambda _1(1-\mu _1)}{\mu _1(1-\lambda _1)}\right] ^2}. \end{aligned} \end{aligned}$$

(29)

After some simplifications, (29) takes the form

$$\begin{aligned} E[Q_1] = \frac{\lambda _1}{\mu _1-\lambda _1} (1-\lambda _1). \end{aligned}$$

(30)