Coordinate-Adaptive Integration of PDEs on Tensor Manifolds

Abstract

We introduce a new tensor integration method for time-dependent partial differential equations (PDEs) that controls the tensor rank of the PDE solution via time-dependent smooth coordinate transformations. Such coordinate transformations are obtained by solving a sequence of convex optimization problems that minimize the component of the PDE operator responsible for increasing the tensor rank of the PDE solution. The new algorithm improves upon the non-convex algorithm we recently proposed in Dektor and Venturi (2023) which has no guarantee of producing globally optimal rank-reducing coordinate transformations. Numerical applications demonstrating the effectiveness of the new coordinate-adaptive tensor integration method are presented and discussed for prototype Liouville and Fokker-Planck equations.

1 Introduction

Developing efficient numerical methods to solve high-dimensional partial differential equations (PDEs) is a central task in many areas of engineering, physical sciences, and mathematics. Such PDEs are often written in the form of an abstract initial/boundary value problem

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{\partial u(\varvec{x},t)}{\partial t} = G_{\varvec{x}}(u(\varvec{x},t)) , \qquad t \in [0,T], \\ u(\varvec{x},0) = u_0(\varvec{x}), \end{array}\right. } \end{aligned}$$

(1)

which governs the time evolution of a quantity of interest $u(\varvec{x},t)$ (high-dimensional field) over a compact domain $\Omega \subseteq {\mathbb {R}}^d$ ($d \gg 1$) and has temporal dynamics generated by the nonlinear operator $G_{\varvec{x}}$. The subscript “$\varvec{x}$” in $G_{\varvec{x}}$ indicates that the operator can explicitly depend on the variables $\varvec{x}\in \Omega$. For instance,

$$\begin{aligned} G_{\varvec{x}}(u) = \varvec{f}(\varvec{x}) \cdot \nabla u +\nabla \cdot ( \sigma (\varvec{x}) \nabla u) +R(u), \end{aligned}$$

(2)

where R(u) is a nonlinear reaction term. The PDE (1) may involve tens, hundreds, or thousands of independent variables, and arises naturally in a variety of applications of kinetic theory, e.g., the Liouville equation, the Fokker-Planck equation, the Bogoliubov-Born-Green-Kirkwood-Yvon (BBGKY) PDF hierarchy [2, 7, 8, 26] or the Lundgren-Monin-Novikov (LMN) PDF hierarchy [16, 20, 24, 37]. These equations allow us to perform uncertainty quantification in many different physical systems including non-neutral plasmas, turbulent combustion, hypersonic flows, and stochastic particle dynamics.

Several general-purpose algorithms, e.g., based on tensor networks [9,10,11,12,13, 22, 31] and physics-informed machine learning [21, 29, 30], have recently been proposed to integrate the PDE (1). Tensor networks can be seen as factorizations of entangled objects such as multivariate functions or operators into networks of simpler objects which are amenable to efficient representation and computation. The vast majority of tensor algorithms currently available to approximate functions, operators and PDEs on tensor manifolds rely on canonical polyadic (CP) decomposition [3, 5, 6, 10], Tucker tensors, or tensors corresponding to binary trees such as functional tensor train (FTT) [4, 12, 27] and hierarchical Tucker tensors [14, 17, 32, 34]. A compelling reason for using binary tensor trees is that they allow the tensor expansion to be constructed via spectral theory for linear operators, in particular the hierarchical Schmidt decomposition [11, 12, 18].

Regardless of the chosen tensor format, the efficiency of tensor algorithms for high-dimensional PDEs depends heavily on the rank of the solution and the PDE operator in the chosen format. Indeed, the computational cost of tensor approximation algorithms scales linearly with the dimension of the system, e.g., the number of independent variables d in the PDE (1), and polynomially with the rank. To address the rank-related unfavorable scaling, we recently developed a new tensor rank reduction algorithm based on coordinate transformations that can significantly increase the efficiency of high-dimensional tensor approximation algorithms [13]. Given a multivariate function or operator, the algorithm determines a coordinate transformation so that the function, the operator, or the operator applied to the function in the new coordinate system has a smaller tensor rank. In [13] we considered linear coordinate transformations, which yield a new class of functions that we called tensor ridge functions. Tensor ridge functions can be written analytically as

$$\begin{aligned} v_{\varvec{s}}(\varvec{x},t) = u_{\varvec{r}}(\varvec{A}\varvec{x},t), \end{aligned}$$

(3)

where $u_{\varvec{r}}$ is a given FTT tensor, and $v_{\varvec{s}}$ is an FTT tensor with smaller rank, i.e., $|\varvec{s}| \leqslant |\varvec{r}|$. To compute the unknown matrix $\varvec{A}$ (which enables tensor rank reduction), we developed a Riemannian gradient descent algorithm on some matrix manifold (e.g., $\varvec{A} \in \text {SL}_d({\mathbb {R}})$) that minimizes the non-convex cost functional

$$\begin{aligned} C(\varvec{A})=S\left[ u_{\varvec{r}}(\varvec{A}\varvec{x},t)\right] , \end{aligned}$$

(4)

where S is the Schatten 1-norm. The numerical results we obtained in the recent paper [13] suggest that rank reduction based on linear coordinate transformations can significantly speed up tensor computations for PDEs while retaining accuracy.

In this paper, we propose a new algorithm for reducing the tensor rank of the solution to (1) by constructing a time-dependent coordinate transformation via a sequence of convex optimization problems. The new algorithm improves upon the non-convex algorithm we recently proposed in [13], which has no guarantee of producing globally optimal rank-reducing coordinate transformations. The main idea of the new algorithm is to select an infinitesimal generator of the coordinate transformation at each time which minimizes the component of the PDE operator (expressed in intrinsic coordinates) that is normal to the tensor manifold where we approximate the PDE solution. This generates a time-dependent nonlinear coordinate transformation (hereafter referred to as a coordinate flow) directly from the PDE via a convex optimization problem. The Euler-Lagrange equations arising from this time-dependent variational principle (TDVP) allow us to determine an optimal coordinate flow that controls/minimizes the tensor rank of the solution during time integration. This approach can be combined with the algorithm we proposed in [13], e.g., to compute a low-rank coordinate transformation for the initial condition before time integration begins.

This paper is organized as follows. In Sect. 2 we develop the theory for coordinate-adaptive tensor integration of PDEs via rank-reducing coordinate flows. To this end, we begin with general nonlinear coordinate flows (diffeomorphisms) and formulate a new convex functional that links the PDE generator to the geometry of the tensor manifold and the flow (Sect. 2.1). We then restrict our attention to linear coordinate flows, i.e., ridge tensors, and develop the corresponding coordinate-adaptive tensor integration scheme. In Sect. 3 we demonstrate the effectiveness of the new tensor integrators by applying them to prototype Liouville and Fokker-Planck equations. Our findings are summarized in Sect. 4.

2 Coordinate-Adaptive Time Integration of PDEs on Tensor Manifolds

We begin by representing the solution $u(\varvec{x},t)$ to the PDE (1) with another function

$$\begin{aligned} v(\varvec{y}(\varvec{x},t),t) = u(\varvec{x},t), \end{aligned}$$

(5)

defined on a time-dependent curvilinear coordinate system $\varvec{y}(\varvec{x}, t)$ [1, 33, 35] with $\varvec{y}(\varvec{x}, 0)=\varvec{x}$. It is assumed that $\varvec{y}(\varvec{x},t)$ is a diffeomorphism¹ which we will refer to as coordinate flow. To simplify notation we may not explicitly write the dependence of $\varvec{y}$ on $\varvec{x}$ (and viceversa the dependence of $\varvec{x}$ on $\varvec{y}$), or the dependence of $\varvec{x}$, $\varvec{y}$ on t. However, it is always assumed that $\varvec{x}$ and $\varvec{y}$ are related via a (time-dependent) diffeomorphism. Next, we define two distinct time derivatives of $v(\varvec{y}(\varvec{x},t),t)$. The first represents a change in v at fixed location $\varvec{y}$, i.e., a derivative of v with respect to time with $\varvec{y}$ constant, which we denote by $\partial v(\varvec{y}(\varvec{x},t),t)/\partial t$. The second represents a change in v along the coordinate flow $\varvec{y}$, i.e., a derivative of v with respect to time with $\varvec{x}$ constant, which we denote by ${\rm D} v(\varvec{y}(\varvec{x},t),t)/{\rm D}t$. The derivative ${\rm D} v(\varvec{y}(\varvec{x},t),t)/{\rm D}t$ is known as the material derivative [1, 25], or the convective derivative [35, 36]. Of course these time derivatives are related via the equation

$$\begin{aligned} \frac{{\rm D} v(\varvec{y}(\varvec{x},t),t)}{{\rm D} t} = \frac{\partial v(\varvec{y}(\varvec{x},t),t)}{\partial t} + \frac{\partial \varvec{y}(\varvec{x},t)}{\partial t} \cdot \nabla _{\varvec{y}} v(\varvec{y}(\varvec{x},t),t). \end{aligned}$$

(6)

Since $u(\varvec{x},t)$ is a solution to (1), v is related to u by (5), and $\varvec{y}(\varvec{x},0) = \varvec{x}$, it follows immediately that v satisfies the PDE

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{{\rm D} v(\varvec{y},t)}{{\rm D} t} = G_{\varvec{y}}(v(\varvec{y},t)) , \qquad t \in [0,T], \\ v(\varvec{y},0) = u_0(\varvec{y}), \end{array}\right. } \end{aligned}$$

(7)

where the operator $G_{\varvec{y}}$ can be derived by writing $G_{\varvec{x}}$ in coordinates $\varvec{y}$ using standard tools of differential geometry [1, 35, 36]. Combining (6) and (7) we obtain²

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{\partial v(\varvec{y},t)}{\partial t} = Q_{\varvec{y}}(v(\varvec{y},t),\dot{\varvec{y}}), \qquad t \in [0,T], \\ v(\varvec{y},0) = u_0(\varvec{y}), \end{array}\right. } \end{aligned}$$

(8)

where

$$\begin{aligned} Q_{\varvec{y}}(v(\varvec{y},t),\dot{\varvec{y}})=G_{\varvec{y}}(v(\varvec{y},t)) - \dot{\varvec{y}}(\varvec{x},t) \cdot \nabla _{\varvec{y}} v(\varvec{y},t) \end{aligned}$$

(9)

and $\dot{\varvec{y}}(\varvec{x},t)=\partial \varvec{y}(\varvec{x},t)/\partial t$. Of course $\dot{\varvec{y}}(\varvec{x},t)$ can be expressed in coordinates $\varvec{y}$ via the inverse map $\varvec{x}(\varvec{y},t)$. Moreover, the PDE domain $\Omega$ is mapped into

$$\begin{aligned} \Omega _y(t) =\left\{ \varvec{z}\in {\mathbb {R}}^d\!\!: \varvec{z}=\varvec{y} (\varvec{x},t), \,\varvec{x}\in \Omega \right\} \end{aligned}$$

(10)

by the coordinate flow $\varvec{y}(\varvec{x},t)$.

2.1 Dynamic Tensor Approximation

Denote by ${\mathcal {M}}_{\varvec{r}}(t) \subseteq {\mathcal {H}}(\Omega _y(t))$ a tensor manifold embedded in the Hilbert space

$$\begin{aligned} {\mathcal {H}}(\Omega _y(t))=L^2(\Omega _y(t)) \end{aligned}$$

(11)

of functions defined on the time-dependent domain $\Omega _y(t)\subseteq {\mathbb {R}}^d$. Such manifolds include hierarchical tensor formats such as the hierarchical Tucker and the tensor train formats [15, 32]. We approximate the solution $v(\varvec{y},t)$ to the PDE (8) with an element $v_{\varvec{r}}(\varvec{y},t)$ belonging to ${\mathcal {M}}_{\varvec{r}}(t)$. We allow the tensor manifold to depend on t so that the solution rank can be chosen adaptively during time integration to ensure an accurate approximation. At each point $v_{\varvec{r}} \in {\mathcal {M}}_{\varvec{r}}$ the function space ${\mathcal {H}}(\Omega _y)$ can be partitioned as a direct sum of two vector subspaces [11]

$$\begin{aligned} {\mathcal {H}}(\Omega _y) = T_{v_{\varvec{r}}} {\mathcal {M}}_{\varvec{r}} \oplus N_{v_{\varvec{r}}} {\mathcal {M}}_{\varvec{r}}, \end{aligned}$$

(12)

where $T_{v_{\varvec{r}}} {\mathcal {M}}_{\varvec{r}}$ (resp. $N_{v_{\varvec{r}}} {\mathcal {M}}_{\varvec{r}}$) denotes the tangent space (resp. normal space) relative to the manifold ${\mathcal {M}}_{\varvec{r}}$ at the point $v_{\varvec{r}}$. Assuming the solution to (8) at time t can be represented by an element of the tensor manifold ${\mathcal {M}}_{\varvec{r}}(t)$, we utilize the direct sum (12) to decompose the right-hand side of the PDE (8) into a tangential component and a normal component relative to ${\mathcal {M}}_{\varvec{r}}(t)$

$$\begin{aligned} Q_{\varvec{y}}(v_{\varvec{r}},\dot{\varvec{y}}) = {\mathcal {P}}_{T}({v}_{\varvec{r}})Q_{\varvec{y}}(v_{\varvec{r}},\dot{\varvec{y}}) + {\mathcal {P}}_{N}({v}_{\varvec{r}})Q_{\varvec{y}}(v_{\varvec{r}},\dot{\varvec{y}}), \qquad v_{\varvec{r}}\in {\mathcal {M}}_{\varvec{r}}(t), \end{aligned}$$

(13)

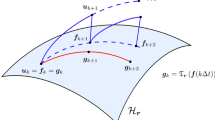
where ${\mathcal {P}}_{T}({v}_{\varvec{r}})$ and ${\mathcal {P}}_{N}({v}_{\varvec{r}})={\mathcal {I}}-{\mathcal {P}}_{T}({v}_{\varvec{r}})$ denote, respectively, the orthogonal projections onto the tangent and normal space of ${\mathcal {M}}_{\varvec{r}}(t)$ at the point $v_{\varvec{r}}$ (see Fig. 1). Projecting the initial condition in (8) onto ${\mathcal {M}}_{\varvec{r}}(0)$ with a truncation operator $\mathfrak {T}_{\varvec{r}}(\cdot )$ and using only the tangential component of the PDE dynamics for all $t \in [0,T]$ we obtain the projected PDE

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{\partial v_{\varvec{r}}(\varvec{y},t)}{\partial t} ={\mathcal {P}}_{T}(v_{\varvec{r}}) Q_{\varvec{y}}(v_{\varvec{r}}(\varvec{y},t),\dot{\varvec{y}}), \qquad t \in [0,T], \\ v_{\varvec{r}}(\varvec{y},0) = \mathfrak {T}_{\varvec{r}} (u_0(\varvec{y})) \end{array}\right. } \end{aligned}$$

(14)

with solution $v_{\varvec{r}}(\varvec{y},t)$ which remains on the tensor manifold ${\mathcal {M}}_{\varvec{r}}(t)$ for all $t \in [0,T]$. We have previously shown [11] that the approximation error

$$\begin{aligned} \epsilon (t)= \left\| v(\varvec{y},t) - v_{\varvec{r}} (\varvec{y},t)\right\| _{{\mathcal {H}}(\Omega _y(t))} \end{aligned}$$

(15)

can be controlled by selecting the rank $\varvec{r}(t)$ at each t so that the norm of the normal component in (13) remains bounded by some user-defined threshold $\varepsilon$, i.e.,

$$\begin{aligned} \left\| {\mathcal {P}}_{N}(v_{\varvec{r}})Q_{\varvec{y}}(v_{\varvec{r}} (\varvec{y},t),\dot{\varvec{y}}) \right\| _{{\mathcal {H}} (\Omega _y(t))} < \varepsilon . \end{aligned}$$

(16)

Therefore the normal component determines the increase in solution rank required to maintain an accurate approximation during time integration. On the other hand, rank decrease during time integration can be interpreted as the tangential component of the PDE operator guiding the solution to a region of the manifold ${\mathcal {M}}_{\varvec{r}}(t)$ with higher curvature. In fact, recall that the smallest singular value of $v_{\varvec{r}}$ is inversely proportional to the curvature of the manifold ${\mathcal {M}}_{\varvec{r}}(t)$ at the point $v_{\varvec{r}}$ [23].

2.2 Variational Principle for Rank-Reducing Coordinate Flows

Leveraging the geometric structure of the tensor manifold ${\mathcal {M}}_{\varvec{r}}(t)$ described in Sect. 2.1, we aim at generating a coordinate flow $\varvec{y}(\varvec{x},t)$ that minimizes the rank of the PDE solution $v_{\varvec{r}}(\varvec{y},t)$ to (14) while maintaining an accurate approximation to (7). Since the approximation error (15) is controlled by the normal component of the PDE operator we select an infinitesimal generator for the coordinate flow $\dot{\varvec{y}}$ that minimizes such normal component, i.e., that minimizes the left-hand side of (16). This idea results in a convex optimization problem over the Lie algebra $\mathfrak {g}$ of infinitesimal coordinate flow generators $\dot{\varvec{y}}$ at time t

$$\begin{aligned} \min _{\dot{\varvec{y}} \in \mathfrak {g}}\left\| {\mathcal {P}}_{N}(v_{\varvec{r}}) Q_{\varvec{y}}(v_{\varvec{r}},\dot{\varvec{y}}) \right\| _{{\mathcal {H}} (\Omega _y(t))}^2 = \min _{\dot{\varvec{y}} \in \mathfrak {g}} \left\| {\mathcal {P}}_{N}(v_{\varvec{r}})\left[ G_{\varvec{y}}(v_{\varvec{r}}) - \dot{\varvec{y}}(\varvec{x},t) \cdot \nabla _{\varvec{y}} v_{\varvec{r}} \right] \right\| _{{\mathcal {H}}(\Omega _y(t))}^2 . \end{aligned}$$

(17)

Fig. 1

Sketch of the tensor manifold ${\mathcal {M}}_{\varvec{r}}(t)\subset {\mathcal {H}}(\Omega _y(t))$. Shown are the normal and tangent components of $Q_{\varvec{y}} (v_{\varvec{r}},\dot{\varvec{y}})$ (PDE operator in (9)) at $v_{\varvec{r}}\in {\mathcal {M}}_{\varvec{r}}(t)$. The manifold ${\mathcal {M}}_{\varvec{r}}(t)$ has multilinear rank that depends on the coordinate flow $\varvec{y}(\varvec{x},t)$ (see [13]). The variational principle (17) minimizes the component of $Q_{\varvec{y}}$ normal to the tensor manifold ${\mathcal {M}}_{\varvec{r}}(t)$ at each time, i.e., the component of $Q_{\varvec{y}}$ that is responsible for the rank increase, relative to arbitrary variations of the coordinate flow generator. This mitigates the tensor rank increase when integrating (14) using the rank-adaptive tensor methods we recently developed in [11, 31]

Note that this is a convex optimization problem since the cost functional is the norm of an affine functional, hence convex, and the search space is a linear space (in particular a Lie algebra). We also emphasize that the functional (17) is not optimizing the projection of $\dot{\varvec{y}}\cdot \nabla v_{\varvec{r}}$ onto the tangent space of the tensor manifold at $v_{\varvec{r}}$. In principle, it is possible to construct a related functional that facilitates tensor rank decrease by making the tangential component of $Q_{\varvec{y}}$ point toward a region of the tensor manifold with higher curvature.³

Proposition 1

Let $\varvec{f}$ be a solution of the convex optimization problem (17). Then $\varvec{f}$ satisfies the linear system of equations

$$\begin{aligned} {\mathcal {P}}_N(v_{\varvec{r}}) \left[ \varvec{f} \cdot \nabla v_{\varvec{r}}\right] \nabla v_{\varvec{r}} = {\mathcal {P}}_N(v_{\varvec{r}})\left[ G_{\varvec{y}}(v_{\varvec{r}}) \right] \nabla v_{\varvec{r}} . \end{aligned}$$

(18)

Proof

Due to the convexity of (17) any critical point of the cost functional

$$\begin{aligned} C(\dot{\varvec{y}})= \left\| {\mathcal {P}}_{N}(v_{\varvec{r}}) \left[ G_{\varvec{y}}(v_{\varvec{r}}) - \dot{\varvec{y}}(\varvec{x},t) \cdot \nabla _{\varvec{y}} v_{\varvec{r}} \right] \right\| _{{\mathcal {H}} (\Omega _y(t))}^2 \end{aligned}$$

(19)

in the Lie algebra $\mathfrak {g}$ is necessarily a global solution to the optimization problem (17). The first variation of C with respect to $\dot{y}_i$ is easily obtained as

$$\begin{aligned} \delta _{\dot{y}_i} C \eta _i&= 2 \int _{\Omega _y(t)} {\mathcal {P}}_{N}(v_{\varvec{r}}) \left[ G_{\varvec{y}}(v_{\varvec{r}}) - \dot{\varvec{y}} \cdot \nabla v_{\varvec{r}} \right] {\mathcal {P}}_{N}(v_{\varvec{r}}) \left[ - \frac{\partial v_{\varvec{r}}}{\partial y_i} \eta _i \right] {\text d}\varvec{y} \nonumber \\&= 2 \int _{\Omega _y(t)} {\mathcal {P}}_{N}(v_{\varvec{r}}) \left[ G_{\varvec{y}}(v_{\varvec{r}}) - \dot{\varvec{y}} \cdot \nabla v_{\varvec{r}} \right] \left( - \frac{\partial v_{\varvec{r}}}{\partial y_i} \eta _i \right) {\text d}\varvec{y}, \end{aligned}$$

(20)

where $\eta _i \in \mathfrak {g}$ is an arbitrary perturbation. To obtain the second equality in (20) we used the fact that the orthogonal projection ${\mathcal {P}}_N(v_{\varvec{r}})$ is symmetric with respect to the inner product in $L^2(\Omega _y(t))$ and idempotent. Setting (20) equal to zero for arbitrary $\eta _i$ yields the Euler-Lagrange equations

$$\begin{aligned} {\mathcal {P}}_{N}(v_{\varvec{r}}) \left[ \dot{\varvec{y}} \cdot \nabla v_{\varvec{r}}\right] \frac{\partial v_{\varvec{r}}}{\partial y_i} ={\mathcal {P}}_{N}(v_{\varvec{r}}) \left[ G_{\varvec{y}}(v_{\varvec{r}})\right] \frac{\partial v_{\varvec{r}}}{\partial y_i} , \qquad i = 1,2,\cdots , d. \end{aligned}$$

(21)

Writing the preceding system of equations in vector notation proves the Proposition.

Note that if $\nabla v_{\varvec{r}}$ is non-zero then from the optimality conditions we obtain ${\mathcal {P}}_N(v_{\varvec{r}}) \left[ \varvec{f} \cdot \nabla v_{\varvec{r}}\right] = {\mathcal {P}}_N(v_{\varvec{r}}) G_{\varvec{y}}(v_{\varvec{r}})$. In this case the normal component of $v_{\varvec{r}}(\varvec{y},t)$, i.e., the right-hand side of (16), is zero along the optimal coordinate flow and therefore the rank of $v_{\varvec{r}}$ never increases during time integration.

With the infinitesimal generator $\varvec{f}(\varvec{y},t)$ solving the convex optimization problem (17) available (i.e., the generator satisfying the linear system (18)), we can now compute a coordinate transformation $\varvec{y}(\varvec{x},t)$ via the dynamical system

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{\partial \varvec{y}}{\partial t} = \varvec{f}(\varvec{y},t) , \\ \varvec{y}(\varvec{x},0) = \varvec{x}. \end{array}\right. } \end{aligned}$$

(22)

Such coordinate transformation allows us to solve the PDE (14) along a coordinate flow that minimizes the projection of $Q_{\varvec{y}}$ onto the normal component of the tensor manifold in which the solution lives, henceforth minimizing the rank increase of $v_{\varvec{r}}$ during time integration. The corresponding evolution equation along the rank reducing coordinate flow is obtained by coupling the ODE (22) with (14) as

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{\partial v_{\varvec{r}}(\varvec{y},t)}{\partial t} = {\mathcal {P}}_T(v_{\varvec{r}})\left[ G_{\varvec{y}}(v_{\varvec{r}}(\varvec{y},t)) - \varvec{f}(\varvec{y},t) \cdot \nabla _{\varvec{y}} v_{\varvec{r}}(\varvec{y},t) \right] , \\ v_{\varvec{r}}(\varvec{y}(\varvec{x},0),0) = \mathfrak {T}_{\varvec{r}}(u_0(\varvec{y})). \end{array}\right. } \end{aligned}$$

(23)

The coupled system of (17), (22), and (23) allows us to devise a time integration scheme for the PDE (1) that leverages diffeomorphic coordinate flows to control the component of $Q_{\varvec{y}}$ that is normal to tensor manifold ${\mathcal {M}}_{\varvec{r}}$, and therefore control the rank increase of the PDE solution $v_{\varvec{r}}$ in time.

To describe the scheme in more detail let us discretize the temporal domain [0, T] into $N+1$ evenly spaced time instants

$$\begin{aligned} t_k = k \Delta t, \qquad \Delta t = \frac{T}{N}, \qquad k = 0,1,\cdots ,N. \end{aligned}$$

(24)

To integrate the solution and the coordinate flow from time $t_k$ to time $t_{k+1}$ we first solve the linear system of equations (18). This gives us an optimal infinitesimal coordinate flow generator $\varvec{f}(\varvec{y},t_k)$ at time $t_k$. Using the evolution equations (22) and (23) we then integrate both the coordinate flow $\varvec{y}(\varvec{x},t)$ and the PDE solution along the coordinate flow $v_{\varvec{r}}(\varvec{y}(\varvec{x},t),t)$ from time $t_k$ to time $t_{k+1}$. Finally we update the PDE operator $G_{\varvec{y}}$ to operate in the new coordinate system.

The proposed coordinate flow time marching scheme comes with two computational challenges. The first challenge is computing the optimal infinitesimal generator $\varvec{f}(\varvec{y},t_k)$, i.e., solving the linear system (18) at each time step. If we represent $\varvec{f}(\varvec{y},t_k)$ in the span of a finite-dimensional basis then (18) yields a linear system for the coefficients of the expansion. The size of such a linear system depends on the dimension of the chosen space. For instance, in the case of linear coordinate flows we obtain a $d^2\times d^2$ system. The second challenge is representing the PDE operator in coordinates $\varvec{y}(\varvec{x},t)$, i.e., constructing $G_{\varvec{y}}$. For a general nonlinear coordinate transformation $\varvec{y}(\varvec{x},t)$ the operator $G_{\varvec{y}}$ includes the metric tensor of the transformation which can significantly complicate the form of $G_{\varvec{y}}$ (see, e.g., [1, 25]). Hereafter we narrow our attention to linear coordinate flows and derive the corresponding time integration scheme which does not suffer from the aforementioned computational challenges.

2.2.1 Linear Coordinate Flows

Any coordinate flow $\varvec{y}(\varvec{x},t)$ that is linear in $\varvec{x}$ at each time t can be represented by a time-dependent invertible $d \times d$ matrix $\varvec{\Gamma }(t)$

$$\begin{aligned} \varvec{y}(\varvec{x},t) = \varvec{\Gamma }(t) \varvec{x}. \end{aligned}$$

(25)

Here we consider arbitrary matrices $\varvec{\Gamma }(t)$ belonging to the collection of all⁴$d \times d$ invertible matrices with real entries, denoted by $\text {GL}_d({\mathbb {R}})$. The corresponding collection of infinitesimal coordinate flow generators is the vector space of all $d \times d$ matrices with real entries. In this setting the time-dependent tensor approximation of $u(\varvec{x},t)$ in coordinates $\varvec{y}$ takes the form

$$\begin{aligned} v_{\varvec{r}}(\varvec{\Gamma }(t) \varvec{x}, t) \approx u(\varvec{x},t). \end{aligned}$$

(26)

This is known as a (time-dependent) generalized tensor ridge function [13, 28]. The time-dependent optimization problem (17) that generates the optimal linear coordinate flow can be now written as

$$\begin{aligned} \min _{\dot{\varvec{\Gamma }} \in M_{d\times d}({\mathbb {R}})} C\left( \dot{\varvec{\Gamma }} \varvec{y}\right) , \end{aligned}$$

(27)

where $C(\cdot )$ is the cost function defined in (19).

Proposition 2

Let $\varvec{\Sigma }(t)$ be a solution of the optimization problem (27) at time t. Then $\varvec{\Sigma }(t)$ satisfies the symmetric $d^2 \times d^2$ linear system

$$\begin{aligned} \varvec{A} \textrm{vec}(\varvec{\Sigma }(t)) = \varvec{b} , \end{aligned}$$

(28)

where $\textrm{vec}(\varvec{\Sigma }(t))$ is a vectorization of the $d \times d$ matrix $\varvec{\Sigma }(t)$,

$$\begin{aligned} \varvec{A} = \int _{\Omega _{y(t)}} {\mathcal {P}}_{N}(v_{\varvec{r}}) \left[ \textrm{vec}(\varvec{c}(\varvec{y}))\right] \textrm{vec} (\varvec{c}(\varvec{y}))^{\textrm{T}} {\rm d} \varvec{y}, \qquad \varvec{b} = \int _{\Omega _{y(t)}} {\mathcal {P}}_{N}(v_{\varvec{r}}) \left[ G_{\varvec{y}}(v_{\varvec{r}}(\varvec{y},t))\right] \textrm{vec}(\varvec{c}(\varvec{y})) {\rm d} \varvec{y}, \end{aligned}$$

(29)

and $\varvec{c}(\varvec{y})$ is the $d \times d$ matrix with entries

$$\begin{aligned} c_{ij}(\varvec{y}) = \frac{\partial v_{\varvec{r}}(\varvec{y},t)}{\partial y_i} y_j, \qquad i,j=1,2,\cdots ,d. \end{aligned}$$

(30)

Proof

First note that the cost function $C\left( \dot{\varvec{\Gamma }} \varvec{y}\right)$ is convex in $\dot{\varvec{\Gamma }}$ and the search space $M_{d\times d}({\mathbb {R}})$ is linear. Hence, any critical point of the cost function is necessarily a global minimum. To find such a critical point we calculate the derivative of $C(\dot{\varvec{\Gamma }}\varvec{y})$ with respect to each entry of the matrix $\dot{\varvec{\Gamma }}$ directly

$$\begin{aligned} \frac{\partial C(\dot{\varvec{\Gamma }} \varvec{y})}{\partial \dot{\Gamma }_{ij}}&= 2 \int _{\Omega _y(t)} {\mathcal {P}}_{N}(v_{\varvec{r}}) \left[ G_{\varvec{\Gamma }} (v_{\varvec{r}}) - (\dot{\varvec{\Gamma }} \varvec{y}) \cdot \nabla v_{\varvec{r}}\right] {\mathcal {P}}_{N}(v_{\varvec{r}}) \left[ -y_j \frac{\partial v_{\varvec{r}}}{\partial y_i} \right] {\rm d} \varvec{y} \nonumber \\&= 2 \int _{\Omega _y(t)} {\mathcal {P}}_{N}(v_{\varvec{r}}) \left[ G_{\varvec{\Gamma }}(v_{\varvec{r}}) - (\dot{\varvec{\Gamma }} \varvec{y}) \cdot \nabla v_{\varvec{r}}\right] \left( -y_j \frac{\partial v_{\varvec{r}}}{\partial y_i} \right) {\rm d} \varvec{y} \end{aligned}$$

(31)

for all $i,j=1,2,\cdots ,d$, where in the second line we used the fact that the orthogonal projection ${\mathcal {P}}_N(v_{\varvec{r}})$ is symmetric with respect to the inner product in $L^2(\Omega _y(t))$ and idempotent. The critical points are then obtained by setting $\partial C(\dot{\varvec{\Gamma }})/\partial \dot{\Gamma }_{ij} = 0$ for all $i,j = 1,2,\cdots ,d$, resulting in a linear system of equations for the entries of the infinitesimal linear coordinate flow generator $\dot{\varvec{\Gamma }}$

$$\begin{aligned} \sum _{k,p=1}^d \dot{\Gamma }_{kp} \int _{\Omega _y(t)} {\mathcal {P}}_{N}(v_{\varvec{r}}) \left( y_p \frac{\partial v_{\varvec{r}}}{\partial y_k} \right) y_j \frac{\partial v_{\varvec{r}}}{\partial y_i}{\rm d} \varvec{y} = \int _{\Omega _y(t)} {\mathcal {P}}_{N}(v_{\varvec{r}}) \left[ G_{\varvec{y}}(v_{\varvec{r}}) \right] y_j \frac{\partial v_{\varvec{r}}}{\partial y_i} {\rm d} \varvec{y} \end{aligned}$$

(32)

for $i = 1,2,\cdots , d$. We obtain (28) by writing the linear system (32) in matrix notation.

The linear system of equations (32) can also be obtained directly from the Euler-Lagrange equations (21) by substituting $\dot{\varvec{y}} = \dot{\varvec{\Gamma }} \varvec{y}$ and projecting onto $y_j$ for $j = 1,2,\cdots ,d$.

A few remarks are in order regarding the linear system (28). The matrix $\varvec{A}$ is a $d^2 \times d^2$ symmetric matrix which is determined by $(d^4 + d^2)/2$ entries and the vector $\varvec{b}$ has length $d^2$. Computing each entry of the matrix $\varvec{A}$ and the vector $\varvec{b}$ requires evaluating a d-dimensional integral. Therefore computing $\varvec{A}$ and $\varvec{b}$ to set up the linear system at each time t requires evaluating a total of $(d^4 + 3d^2)/2$ d-dimensional integrals. Since $v_{\varvec{r}}$ is a low-rank tensor these high-dimensional integrals can be computed by applying one-dimensional quadrature rules to the tensor modes. By orthogonalizing the low-rank tensor expansion (e.g., tensor train) it is possible to reduce the number one-dimensional integrals needed to compute $\varvec{A}$. If the matrix $\varvec{A}$ is singular then the solution to the linear system of equations is not unique. In this case any solution will suffice for generating a coordinate flow.

For linear coordinate transformations it may be advantageous to consider the related functional

$$\begin{aligned} C_2(\dot{\varvec{\Gamma }} \varvec{y})&= \left\| \frac{\partial v_{\varvec{r}}}{\partial t}\right\| _{{\mathcal {H}}(\Omega _y(t))}^2\nonumber \\&= \left\| Q_{\varvec{y}}(v_{\varvec{r}}) \right\| _{{\mathcal {H}}(\Omega _y(t))}^2 \nonumber \\&= \left\| {\mathcal {P}}_T(v_{\varvec{r}})Q_{\varvec{y}}(v_{\varvec{r}}, \dot{\varvec{y}}) \right\| _{{\mathcal {H}}(\Omega _y(t))}^2 +\left\| {\mathcal {P}}_N(v_{\varvec{r}}) Q_{\varvec{y}}(v_{\varvec{r}}, \dot{\varvec{y}}) \right\| _{{\mathcal {H}}(\Omega _y(t))}^2. \end{aligned}$$

(33)

The linear coordinate flow minimizing (33) aims at “undoing” the action of the operator $G_{\varvec{y}}$ in coordinates $\varvec{y}$. More precisely the PDE solution $u(\varvec{x},t)$ as seen in coordinate $\varvec{y}(\varvec{x},t)=\varvec{\Gamma }(t)\varvec{x}$, i.e., $v_{r}(\varvec{\Gamma }(t)\varvec{x},t) \approx u(\varvec{x},t)$, varies in time as little as possible. In the third equality of (33) we used the fact that ${\mathcal {P}}_T(v_{\varvec{r}})$ and ${\mathcal {P}}_N(v_{\varvec{r}})$ are orthogonal projections. Following similar steps used to prove Proposition 2 it is straightforward to show that the critical points $\varvec{\Sigma }(t)$ of (33) satisfy the linear system (28) with

$$\begin{aligned} \varvec{A} = \int _{\Omega _y(t)} \textrm{vec}(\varvec{c}(\varvec{y})) \textrm{vec}(\varvec{c}(\varvec{y}))^{\textrm{T}} {\rm d} \varvec{y}, \qquad \varvec{b} = \int _{\Omega _y(t)} G_{\varvec{y}}(v_{\varvec{r}}(\varvec{y},t)) \textrm{vec}(\varvec{c}(\varvec{y})) {\rm d} \varvec{y}. \end{aligned}$$

(34)

With the optimal coordinate flow generator $\varvec{\Sigma }(t)$ available we can compute the matrix $\varvec{\Gamma }(t)$ appearing in (25) by solving the matrix differential equation

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{{\rm d} \varvec{\Gamma }(t)}{{\rm d} t} = \varvec{\Sigma }(t) \varvec{\Gamma }(t), \\ \varvec{\Gamma }(0) = \varvec{I}_{d \times d}. \end{array}\right. } \end{aligned}$$

(35)

Correspondingly, the PDE (23) can be written along the optimal rank-reducing linear coordinate flow (25) as

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{\partial v_{\varvec{r}}(\varvec{\Gamma }(t) \varvec{x},t)}{\partial t} = G_{\varvec{y}}(v_{\varvec{r}}(\varvec{y},t),\varvec{y}) - \left( \varvec{\Sigma }(t)\varvec{y}(\varvec{x},t)\right) \cdot \nabla _{\varvec{y}} v_{\varvec{r}}(\varvec{y}(\varvec{x},t),t), \\ v_{\varvec{r}}(\varvec{x},0) = \mathfrak {T}_{\varvec{r}}(u_0(\varvec{x})). \end{array}\right. } \end{aligned}$$

(36)

Using the linear system (28), the matrix differential equation (35), and the PDE (36), we can specialize the time integration scheme described in Sect. 2.2 for nonlinear coordinate flows to linear coordinate flows. In Algorithm 1, we provide the pseudo-code for PDE time stepping with linear coordinate flows. In Algorithm 1, $\textrm{TDVP}$ denotes a subroutine that solves the optimization problem (27) (e.g., by solving the symmetric $d^2 \times d^2$ linear system of equations (28)) and $\textrm{LMM}$ denotes any time stepping scheme.

Algorithm 1

PDE integrator with rank-reducing linear coordinate flow

3 Numerical Examples

We demonstrate the proposed coordinate-adaptive time integration scheme based on linear coordinate flows (Algorithm 1) on several prototype PDEs projected on FTT manifolds ${\mathcal {M}}_{\varvec{r}}$ [12].

3.1 Liouville Equation

Consider the d-dimensional Liouville equation

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{\partial u(\varvec{x},t)}{\partial t} = \varvec{f}(\varvec{x}) \cdot \nabla u(\varvec{x},t), \\ u(\varvec{x},0) = u_0(\varvec{x}), \end{array}\right. } \end{aligned}$$

(37)

where $\varvec{f}(\varvec{x})$ is a divergence-free vector field. We set the initial condition to be a product of independent Gaussians

$$\begin{aligned} u_0(\varvec{x}) = \frac{1}{m} \exp \left( - \sum _{j=1}^d \frac{1}{\beta _{j}} \left( x_j + t_{j} \right) ^2 \right) , \end{aligned}$$

(38)

where $\beta _j > 0$, $t_j\in {\mathbb {R}}$, and m is the normalization factor

$$\begin{aligned} m = \left\| \exp \left( - \sum _{j=1}^d \frac{1}{\beta _{j}} \left( x_j + t_{j} \right) ^2 \right) \right\| _{L^1\left( {\mathbb {R}}^d\right) }. \end{aligned}$$

3.1.1 Two-Dimensional Simulation Results

We first consider the Liouville on a two-dimensional flat torus $\Omega \subset {\mathbb {R}}^2$ with velocity vector $\varvec{f}(\varvec{x})=(f_1(\varvec{x}),f_2(\varvec{x}))$ consisting of

$$\begin{aligned} f_1(\varvec{x}) = \frac{\partial \psi }{\partial x_2}, \qquad f_2(\varvec{x}) = -\frac{\partial \psi }{\partial x_1} \end{aligned}$$

(39)

generated via the two-dimensional stream function [38]

$$\begin{aligned} \psi (x_1,x_2) = \Theta (x_1) \Theta (x_2) \end{aligned}$$

(40)

with

$$\begin{aligned} \Theta (x) = \frac{\cos (\alpha x/L)}{\cos (\alpha /2)} -\frac{\cosh (\alpha x/L)}{\cosh (\alpha /2)}, \end{aligned}$$

(41)

$L=30$, and $\alpha = 4.73$. This yields a two-dimensional measure-preserving (divergence-free) velocity vector $\varvec{f}(\varvec{x})$. In the initial condition (38) we set $\varvec{\beta } = \begin{bmatrix} 1/4&2 \end{bmatrix}$ and $\varvec{t} = \begin{bmatrix} 3&3 \end{bmatrix}$ resulting in a rank-1 initial condition.

Fig. 2

Two-dimensional advection PDE. a Initial condition. b Solution in Cartesian coordinates at time $t=35$. c Solution in time-dependent adaptive coordinates at time $t=35$

Note that this is the same problem we recently studied in [13] using coordinate-adaptive tensor integration based on non-convex relaxations of the rank minimization problem. We discretize the PDE with the Fourier pseudo-spectral method [19] using 200 points in each spatial variable $x_i$ and integrate the PDE from $t=0$ to $t=35$ using the two-step Adams-Bashforth scheme (AB2) with time step size $\Delta t = 10^{-3}$. To demonstrate rank reduction with coordinate flows, we run three distinct simulations. In the first simulation, we integrate the PDE on a full two-dimensional tensor product grid in Cartesian coordinates for all time resulting in our benchmark solution. In the second simulation, we construct a low-rank representation of the solution in fixed Cartesian coordinates with the rank-adaptive step-truncation time integration scheme [31] built upon the AB2 integrator using relative tensor truncation tolerance $\delta = 10^{-8}$. The third simulation demonstrates the low-rank tensor format in adaptive coordinates generated by Algorithm 1 (using the cost function (33)) with a step-truncation time integration scheme built upon the AB2 integrator using relative tensor truncation tolerance $\delta = 10^{-8}$.

In Fig. 2, we plot the low-rank solution at time $t=0$ (a), $t=35$ computed in fixed Cartesian coordinates (b), and $t=35$ computed in adaptive coordinates (c). We notice that the time-dependent coordinate system in the adaptive simulation captures the affine components (i.e., translation, rotation, and stretching) of the dynamics generated by the PDE operator. In Fig. 3d, we plot the rank versus time of the solution computed in fixed Cartesian coordinates and the solution computed in adaptive time-dependent coordinates. We also plot the norm of the normal components, i.e., the left-hand side of (16), versus time in Cartesian coordinates and in adaptive coordinates. Since the linear coordinate flow is minimizing the normal component of the PDE operator we observe that the red dashed line increases at a slower rate than the blue dashed line. Once the norm of the normal component reaches a threshold depending on the relative tensor truncation tolerance $\delta$ set on the solution and time step size $\Delta t$, the rank-adaptive criterion discussed [11] is triggered which results in an increase of the solution rank. At the subsequent time step, the normal component is reduced due to the addition of a tensor mode.

Fig. 3

Two-dimensional advection PDE. a Rank versus time and b norm of the normal component of PDE dynamics versus time for the low-rank solution in Cartesian coordinates (blue solid line) and in adaptive coordinates (red dashed line)

At time $t = 35$ we check the $L^{\infty }$ error of the low-rank tensor solution computed in Cartesian coordinates and the low-rank solution computed using adaptive coordinates (for the adaptive solution we map it back to Cartesian using a two-dimensional interpolant) and find that both errors are bounded by $1.5 \times 10^{-5}$.

3.1.2 Three-Dimensional Simulation Results

Next we consider the Liouville equation (37) on a three-dimensional flat torus $\Omega \subset {\mathbb {R}}^3$ with velocity vector

$$\begin{aligned} \varvec{f}(\varvec{x}) =\begin{bmatrix} x_2 \\ -x_1 \\ x_2 \\ \end{bmatrix}. \end{aligned}$$

(42)

This allows us to test our coordinate-adaptive algorithm for a problem in which we know the optimal ridge matrix. We set the parameters of the initial condition (38) as $\varvec{\beta } = \begin{bmatrix} 4&1/4&4 \end{bmatrix}$ and $\varvec{t} = \begin{bmatrix} 1&-1&1 \end{bmatrix}$ resulting in the FTT rank $\varvec{r}(0)=\begin{bmatrix} 1&1&1&1 \end{bmatrix}$. Due to the choice of coefficients (42), the analytical solution to the PDE (37) can be written as a ridge function in terms of the PDE initial condition

$$\begin{aligned} u(\varvec{x},t) = u_0\left( {\text e}^{t\varvec{B}} \varvec{x} \right) , \end{aligned}$$

(43)

where

$$\begin{aligned} \varvec{B} = \begin{bmatrix} 0 &{} 1 &{} 0 \\ -1 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 \end{bmatrix}. \end{aligned}$$

(44)

Thus (43) is a tensor ridge solution to the three-dimensional Liouville equation (37) with the same rank as the initial condition, i.e., in this case there exists a tensor ridge solution at each time with an FTT rank equal to $\begin{bmatrix} 1&1&1&1 \end{bmatrix}$.

To demonstrate the performance of the rank-reducing coordinate flow algorithm, we ran two low-rank simulations of the PDE (37) up to $t = 1$ and compared the results with the analytic solution (43). The first simulation is computed using the rank-adaptive step-truncation methods discussed in [11, 31] with relative truncation accuracy $\delta = 10^{-5}$, Cartesian coordinates, and time step size $\Delta t = 10^{-3}$. The second simulation demonstrates the performance of the rank-reducing coordinate flow (Algorithm 1) and is computed with the same step-truncation scheme as the simulation in Cartesian coordinates. For this example the coordinate flow is constructed by minimizing the functional (33).

In Fig. 4a we plot the 1-norm of the FTT solution rank versus time. We observe that the FTT solution rank in Cartesian coordinates grows rapidly while the FTT-ridge solution generated by the proposed Algorithm  1 recovers the optimal time-dependent low-rank tensor ridge solution, which remains constant rank for all time at $\left\| \varvec{r}(t)\right\| _{1} = 4$. We also map the FTT ridge solution back to Cartesian coordinates using a three-dimensional trigonometric interpolant every 100 time steps and compare both low-rank FTT solutions to the benchmark solution. In Fig. 4b we plot the $L^{\infty }$ error versus time. The solution computed in adaptive coordinates does not change in time and therefore is about one order of magnitude more accurate than the solution computed in Cartesian coordinates. In this case the proposed algorithm outperforms our previous algorithm proposed in [13] which does not recover the optimal linear coordinate transformation due to the non-convexity of the cost function used to generate the time-dependent coordinate system.

Fig. 4

Three-dimensional advection equation (37). a Rank versus time and b $L^{\infty }$ error of the low-rank solutions relative to the benchmark solution

For this example the PDE operator has separation rank (CP-rank) 3 in Cartesian coordinates and CP-rank 9 in a general linearly transformed coordinate system.

3.2 Fokker-Planck Equation

Finally we consider the Fokker-Planck equation

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{\partial u(\varvec{x},t)}{\partial t} =- \nabla \cdot \left( \varvec{f}(\varvec{x}) u(\varvec{x},t)\right) +\sum _{i,j=1}^d \frac{\partial ^2}{\partial x_i \partial x_j} \left( D_{ij}(\varvec{x}) u(\varvec{x},t)\right) , \\ u(\varvec{x},0) = u_0(\varvec{x}) \end{array}\right. } \end{aligned}$$

(45)

in three spatial dimensions ($d=3$) on a flat torus $\Omega \subseteq {\mathbb {R}}^3$. We set the drift vector $\varvec{f}$ as in (42), and the diffusion tensor

$$\begin{aligned} \varvec{D} = \sigma \begin{bmatrix} \exp \left( -x_2^2\right) &{} 0 &{} 0 \\ 0 &{} \exp \left( -x_3^2\right) &{} 0 \\ 0 &{} 0 &{} \exp \left( -x_1^2\right) \end{bmatrix} \end{aligned}$$

(46)

with $\sigma = 1/4$. We use the same initial condition as in Sect. 3.1.2.

Once again, to demonstrate the performance of the rank-reducing coordinate flow algorithm, we ran three simulations of the PDE (45) up to $t = 1$. The first simulation is computed with a three-dimensional Fourier pseudo-spectral method on a tensor product grid with 200 points per dimension and AB2 time stepping with $\Delta t = 10^{-4}$. This yields an accurate solution benchmark. The second simulation is computed using the rank-adaptive step-truncation methods discussed in [11, 31] using relative truncation accuracy $\delta = 10^{-5}$, fixed Cartesian coordinates, and time step size $\Delta t = 10^{-3}$. The third simulation demonstrates the performance of the rank-reducing coordinate flow (Algorithm 1) and is computed with the same step-truncation scheme as the simulation in Cartesian coordinates. For this example the coordinate flow is constructed by minimizing the functional (33).

Fig. 5

Three-dimensional Fokker-Planck equation (45). Time snapshots of the solution at $t=0.1,0.5,1.0$ in Cartesian coordinates (top row) and adaptive coordinates (bottom row). The adaptive coordinate system generated by Algorithm 1 effectively captures the affine effects (i.e., rotation, stretching, translation) of the transformation generated by the Fokker-Planck equation (45)

In Fig. 5 we plot three time snapshots of the low-rank solutions to (45) in fixed Cartesian coordinates (top row) and rank-reducing adaptive coordinates (bottom row). We observe that the rank-reducing adaptive coordinate transformation effectively captures the affine effects of the transformation generated by the PDE (45) even in the presence of diffusion. In Fig. 6a we plot the 1-norm of the FTT solution rank versus time. We observe that the FTT solution rank in Cartesian coordinates grows rapidly while the FTT-ridge solution generated by Algorithm 1 grows significantly slower. We also map the FTT ridge solution back to Cartesian coordinates using a three-dimensional trigonometric interpolant every 100 time steps and compare both low-rank FTT solutions to the benchmark solution. In Fig. 6b we plot the $L^{\infty }$ error of Cartesian and coordinate-adaptive low-rank solutions relative to the benchmark solution versus time. We observe that the process of solving the PDE in transformed coordinates and mapping the transformed solution back to Cartesian coordinates incurs negligible error.

Fig. 6

Three-dimensional Fokker-Planck equation (45). a Rank versus time and b $L^{\infty }$ error of the low-rank solutions relative to the benchmark solution

4 Conclusions

We proposed a new tensor integration method for time-dependent PDEs that controls the rank of the PDE solution in time using diffeomorphic coordinate transformations. Such coordinate transformations are generated by minimizing the normal component of the PDE operator (written in intrinsic coordinates) relative to the tensor manifold that approximates the PDE solution. This minimization principle is defined by a convex functional which can be computed efficiently and has optimality guarantees. The proposed method significantly improves upon and may be used in conjunction with the coordinate-adaptive algorithms we recently proposed in [13], which are based on non-convex relaxations of the rank minimization problem and Riemannian optimization. We demonstrated the proposed coordinate-adaptive time-integration algorithm for linear coordinate transformations on prototype Liouville and Fokker-Planck equations in two and three dimensions. Our numerical results clearly demonstrate that linear coordinate flows can capture the affine component (i.e., rotation, translation, and stretching) of the transformation generated by PDE operator very effectively. In general, one cannot expect linear coordinate flow (or even nonlinear coordinate flows) to fully control the rank of the solution generated by an arbitrary nonlinear PDE. Yet, the proposed method allows us to solve certain classes of PDEs at a computational cost that is significantly lower than standard temporal integration on tensor manifolds in Cartesian coordinates. In general, overall computational cost of the proposed method is not only determined by the tensor rank of the solution but also the rank of the PDE operator $G_{\varvec{y}}$, as discussed in [13]. Further research is warranted to determine if the efficiency of the proposed coordinate-adaptive methodology can be improved by including conditions on the tangent projection of $\dot{\varvec{y}} \cdot \nabla v_{\varvec{r}}$ in (17), or by simultaneously controlling the PDE solution and operator rank during time integration.