A new thinning-based INAR(1) process for underdispersed or overdispersed counts

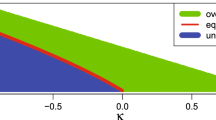
Abstract

Underdispersed and overdispersed phenomena are often observed in practice. To deal with these phenomena, we introduce a new thinning-based integer-valued autoregressive process. Some probabilistic and statistical properties of the process are obtained. The asymptotic normality of the estimators of the model parameters, using conditional least squares, weighted conditional least squares and modified quasi-likelihood methods, are presented. One overdispersed real-data example and one underdispersed real-data example are given to show the flexibility and superiority of the new model.

Appendix

As we mentioned in the third paragraph of Sect. 2, the infinite sum in the mean and variance for GSC($\alpha$, $\theta$) are convergent, where $\alpha <1$, $\alpha \ne 0$ and $0<\theta <1$. We illustrate it, as follows:

Let $\alpha <0$. Denote $S_n=\sum _{s=1}^{n}\log (1-\alpha \theta ^{s})$. Then, we have

$$\begin{aligned} 0{\le }\lim _{n\rightarrow \infty }\sup _{p{>}0}|S_{n+p}{-}S_n|{=}\lim _{n\rightarrow \infty }\sup _{p{>}0}\sum _{s{=}n+1}^{n+p}\log (1{-}\alpha \theta ^{s}){\le }\lim _{n\rightarrow \infty }\sup _{p{>}0} [p\log (1{-}\alpha \theta ^{n})]{=}0. \end{aligned}$$

By the Cauchy criterion of series, the infinite sum $\sum _{s=1}^{\infty }\log (1-\alpha \theta ^{s})$ are convergent.

Denote $S_n^{'}=\sum _{s=1}^{n}(2s-1)\log (1-\alpha \theta ^{s})$. Then, we have

$$\begin{aligned} 0&\le \lim _{n\rightarrow \infty }\sup _{p>0}|S_{n+p}^{'}-S_n^{'}|=\lim _{n\rightarrow \infty }\sup _{p>0}\sum _{s=n+1}^{n+p}(2s-1)\log (1-\alpha \theta ^{s})\\&\le \lim _{n\rightarrow \infty }\sup _{p>0}p\cdot 2(n+p)\log (1-\alpha \theta ^{n+1})\le \lim _{n\rightarrow \infty }\sup _{p>0}2p(n+p)(-\alpha )\theta ^{n+1}=0, \end{aligned}$$

using $x\ge \log (1+x)$ for $x\ge 0$. By the Cauchy criterion of series, the infinite sum $\sum _{s=1}^{\infty }(2s-1)\log (1-\alpha \theta ^{s})$ are convergent. Following the same way, we can see that the two infinite sum are convergent when $0<\alpha <1$. $\square$

Proof of Proposition 1

We have (i) and (iii), i.e.,

$$\begin{aligned} \mathrm {E}(X_{t}|X_{t-1})=\mathrm {E}(\alpha \diamond X_{t-1}+\epsilon _{t}|X_{t-1})=\phi X_{t-1}+\mu _{\epsilon } \end{aligned}$$

and

$$\begin{aligned} \mathrm {Var}(X_{t}|X_{t-1})&=\mathrm {Var}(\alpha \diamond X_{t-1}+\epsilon _{t}|X_{t-1})\\&=\mathrm {Var}(\alpha \diamond X_{t-1}|X_{t-1})+\mathrm {Var}(\epsilon _{t}|X_{t-1})\\&=\beta X_{t-1}+\sigma _{\epsilon }^2. \end{aligned}$$

Then, we get

$$\begin{aligned} \mathrm {E}(X_{t})=\mathrm {E}[\mathrm {E}(X_{t}|X_{t-1})]=\phi \mathrm {E}(X_{t-1})+\mu _{\epsilon } \end{aligned}$$

and

$$\begin{aligned} \mathrm {Var}(X_{t})&=\mathrm {Var}[\mathrm {E}(X_{t}|X_{t-1})]+\mathrm {E}[\mathrm {Var}(X_{t}|X_{t-1})]\\&=\mathrm {Var}(\phi X_{t-1}+\mu _{\epsilon })+\mathrm {E}(\beta X_{t-1}+\sigma _{\epsilon }^2)\\&=\phi ^2\mathrm {Var}(X_{t-1})+\beta \mathrm {E}(X_{t-1})+\sigma _{\epsilon }^2, \end{aligned}$$

which yield (ii) and (iv), due to the stationarity; $\mathrm {E}(X_{t})=\mathrm {E}(X_{t-1})$ and $\mathrm {Var}(X_{t})=\mathrm {Var}(X_{t-1})$. Moreover, we have (v), i.e.,

$$\begin{aligned} \mathrm {Cov}(X_{t},X_{t+k})&=\mathrm {Cov}(X_{t}, \underbrace{\alpha \diamond \cdots \diamond \alpha }_{k}\diamond X_{t})+\mathrm {Cov}(X_{t},\sum _{j=0}^{k-1} \underbrace{\alpha \diamond \cdots \diamond \alpha }_{j} \diamond \epsilon _{t+k-j})\\&=\mathrm {E}\{\mathrm {E}[X_{t}(\underbrace{\alpha \diamond \cdots \diamond \alpha }_{k}\diamond X_{t})|X_{t}]\} -\mathrm {E}(\underbrace{\alpha \diamond \cdots \diamond \alpha }_{k}\diamond X_{t})\cdot \mathrm {E}(X_{t})\\&=\phi ^k\{\mathrm {E}(X_t^2)-[\mathrm {E}(X_t)]^2\}\\&=\phi ^k\mathrm {Var}(X_t). \end{aligned}$$

$\square$

Proof of Theorem 1

We first introduce a random sequence $\{X_{t}^{(n)}\}$,

$$\begin{aligned} X_{t}^{(n)}=\left\{ \begin{array}{ll} 0,&{} \quad n<0,\\ \epsilon _t,&{} \quad n=0,\\ \alpha \diamond X_{t-1}^{(n-1)}+\epsilon _{t},&{} \quad n>0,\\ \end{array} \right. \end{aligned}$$

where $\mathrm {Cov}(X_{s}^{(n)},\epsilon _t)=0$ when $s<t$ for any n.

As in Li et al. (2015), we can verify: existence of $\{X_t\}$ satisfying (5), i.e., (A1) $X_{t}^{(n)}\in L^2$, $n>0$, (A2) $X_t^{(n)}$ is a Cauchy sequence, (A3) $\{X_t\}$ satisfies (5), uniqueness, strict stationarity and ergodicity. The details are omitted here to save space. $\square$

Proof of Theorem 2

From (6), solving $\partial Q_1(\varvec{\eta })/\partial \alpha =0$ and $\partial Q_1(\varvec{\eta })/\partial \mu _{\epsilon }=0$ lead to the CLS estimators of $\alpha$ and $\mu _{\epsilon }$. Now, let $\mathcal {F}_n=\sigma \{X_0,X_1,\ldots ,X_n\}$, $M_{n}^{(1)}=-\frac{1}{2}(\partial Q_1(\varvec{\eta })/\partial \alpha )=\sum _{t=1}^{n}\dot{\phi }X_{t-1}\big (X_t-\phi X_{t-1}-\mu _{\epsilon }\big )$, $M_0^{(1)}=0$. Also, $M_{n}^{(2)}=-\frac{1}{2}(\partial Q_1(\varvec{\eta })/\partial \mu _{\epsilon })=\sum _{t=1}^{n}\big (X_t-\phi X_{t-1}-\mu _{\epsilon }\big )$, $M_0^{(2)}=0$. Then, it is easy to see that $\{M_{n}^{(1)},\mathcal {F}_n\}_{n\ge 0}$ and $\{M_{n}^{(2)},\mathcal {F}_n\}_{n\ge 0}$ are martingales. The martingale central limit theorem and Cramer-Wold’s device imply that

$$\begin{aligned} n^{-1/2}(M_n^{(1)},M_n^{(2)})^{'}\mathop {\longrightarrow }\limits ^{d}N(\mathbf {0},\varvec{V_{CLS}}). \end{aligned}$$

Using Taylor’s expansion, we have

$$\begin{aligned} \mathbf {0}{=-}\frac{1}{2\sqrt{n}}\frac{\partial Q_1(\widehat{\varvec{\eta }}_{CLS})}{\partial \varvec{\eta }}{=-}\frac{1}{2\sqrt{n}}\frac{\partial Q_1(\varvec{\eta })}{\partial \varvec{\eta }} -\frac{1}{2n}\frac{\partial ^2 Q_1(\varvec{\eta })}{\partial \varvec{\eta }\partial \varvec{\eta ^{'}}}\sqrt{n}(\widehat{\varvec{\eta }}_{CLS}{-}\varvec{\eta }){+}o_p(n^{-1/2}). \end{aligned}$$

Since we have proved that $-\frac{1}{2\sqrt{n}}\frac{\partial Q_1(\varvec{\eta })}{\partial \varvec{\eta }} \mathop {\longrightarrow }\limits ^{d}N(\mathbf {0},\varvec{V_{CLS}})$, after some algebra, we have

$$\begin{aligned} \sqrt{n}(\widehat{\varvec{\eta }}_{CLS}-\varvec{\eta })\mathop {\longrightarrow }\limits ^{d}N(\mathbf {0},\varvec{H_{CLS}}^{-1}\varvec{V_{CLS}}\varvec{H_{CLS}}^{-1}). \end{aligned}$$

This completes the proof. $\square$

Proof of Theorem 4

Following Zheng et al. (2007), we firstly suppose $\varvec{\tau }$ is known. Let

$$\begin{aligned} L_{n}^{(1)}(\varvec{\tau },\varvec{\eta })&=\sum _{t=1}^{n}\mathrm {V_{\varvec{\tau }}^{-1}}(X_t| X_{t-1})\dot{\phi }X_{t-1}\big (X_t-\phi X_{t-1}-\mu _{\epsilon }\big ),~L_{0}^{(1)}(\varvec{\tau },\varvec{\eta })=0,\\ L_{n}^{(2)}(\varvec{\tau },\varvec{\eta })&=\sum _{t=1}^{n}\mathrm {V_{\varvec{\tau }}^{-1}}(X_t|X_{t-1})\big (X_t-\phi X_{t-1}-\mu _{\epsilon }\big ),~L_{0}^{(2)}(\varvec{\tau },\varvec{\eta })=0. \end{aligned}$$

Similar to Theorem 2, we have

$$\begin{aligned} n^{-1/2}\big (L_{n}^{(1)}(\varvec{\tau },\varvec{\eta }),L_{n}^{(2)}(\varvec{\tau },\varvec{\eta })\big )^{'} \mathop {\longrightarrow }\limits ^{d} N(\mathbf {0},\varvec{V_{MQL}}). \end{aligned}$$

Now, we replace $V_{\varvec{\tau }}^{-2}(X_t|X_{t-1})$ by $V_{\varvec{\widehat{\tau }}}^{-2}(X_t|X_{t-1})$, where $\varvec{\widehat{\tau }}$ is a consistent estimator of $\varvec{\tau }$. Then we want

$$\begin{aligned} n^{-1/2}\big (L_{n}^{(1)}(\varvec{\widehat{\tau }},\varvec{\eta }),L_{n}^{(2)}(\varvec{\widehat{\tau }},\varvec{\eta })\big )^{'} \mathop {\longrightarrow }\limits ^{d} N(\mathbf {0},\varvec{V_{MQL}}). \end{aligned}$$

For this we need to prove that $\frac{1}{\sqrt{n}}L_{n}^{(i)}(\varvec{\widehat{\tau }},\varvec{\eta })- \frac{1}{\sqrt{n}}L_{n}^{(i)}(\varvec{\tau },\varvec{\eta })\mathop {\longrightarrow }\limits ^{P}0,~i=1,2$ [its proof is omitted here, since the argument is the same as in Zheng et al. (2007)]. Following the proof of Theorem 2, by Taylor’s expansion and some algebra, we have

$$\begin{aligned} \sqrt{n}(\widehat{\varvec{\eta }}_{MQL}-\varvec{\eta })\mathop {\longrightarrow }\limits ^{d}N(\mathbf {0},\varvec{H_{MQL}}^{-1}\varvec{V_{MQL}}\varvec{H_{MQL}}^{-1}). \end{aligned}$$

This completes the proof. $\square$