1 Introduction

Concrete (rigid) pavement is becoming increasingly popular in tropical monsoon climate regions like the coastal region of Karnataka state, India, due to its longevity, improved load-carrying capacity, low maintenance cost and high resilience to persistent rainfall damage. The top surface of concrete pavement is typically a rigid pavement quality concrete (PQC) slab, a structural member, anticipated to withstand stresses induced from wheel loads, temperature, and moisture fluctuations. Ordinary Portland Cement (OPC), coarse aggregate (CA), fine aggregate (FA), and water make up the majority of the PQC combination. Concerns over the depleting aggregate resources, as well as the environmental impact of cement manufacture on the environment, have prompted pavement technologist and road construction experts to investigate sustainable alternatives for PQC materials. Construction and industrial wastes, as well as used tyres, plastics, waste glass and many more are now being considered as CA and FA alternatives. In addition, novel cementitious composites such as alkali activated materials (AAM) and geopolymer-based cement (GC) are being explored as ecologically benign alternatives to OPC.

Davidovits created the term “geopolymer” in 1978 [1, 2]. It is a one-of-a-kind binder made mostly of aluminosilicate materials such fly ash (f-ash), ground granulated blast furnace slag (GGBS), and metakaolin clay. These minerals are mixed in specified quantities with alkaline solutions including sodium hydroxide (NaOH) or potassium hydroxide (KOH) and sodium silicate (Na2SiO3) or potassium silicate (K2SiO3) to produce cement by geopolymerisation process [3, 4]. Geopolymerisation is a four-stage process that is impacted by preparation technique [4, 5], alkaline activator (AA) content [6,7,8,9,10], and raw material chemical composition [11,12,13,14,15]. It entails aluminosilicate monomer dissolution and release of Si–O and Al–O tetrahedral monomers, tetrahedral monomers diffusion into the reaction system, polycondensation generating amorphous structures (–Si–O–Al–O–) or zeolite crystals, and final hardening of the geopolymer concrete (GPC) with water removal [16].

Because of their availability in large volumes and, high silica (SiO2) and alumina (Al2O3) concentrations in fly ash and CaO in GGBS, these materials are often utilised in geopolymer concrete [17,18,19,20,21]. Furthermore, GPC developed based on these components cure ambiently [22,23,24,25,26,27], eliminating the need for heat curing and making it ideal for field applications such as rigid pavement construction [28, 29]. The primary reaction products of f-ash and GGBS-based GPC are calcium silicate hydrate (CSH) gel, calcium aluminosilicate hydrate (CASH) gel, and sodium alumino silicate hydrate (NASH) gel, all of which have a major impact on mechanical strength and durability [30,31,32,33,34]. Precursor materials such as lateritic soil [35], red mud [36, 37], metakaolin [38], volcanic pumice dust [39] and mining tiles [40] have been explored for production of GPC. Many studies conducted thus far demonstrate that GC exhibits comparable performance to OPC [41], suggesting that it could be considered a viable binding material in the construction sector [42].

The Federal Highway Administration of the United States has emphasised the need of GPC meant for paving [43], that has reasonable setting time, hardens at room temperature like OPC, and is cost-effective. Subsequently, in 2014, the first-ever functioning GPC greenfield pavement for the airport in Brisbane, Australia, was constructed [44]. Several studies have investigated GPC's function and features, including as its mechanical strengths and appropriateness for paving applications [45,46,47], slip-form paving [48], and pavement repair operations [49]. Largely, these findings indicate the GPC as a feasible choice for road construction.

Wheel loads, temperature, and moisture all have a substantial impact on GPC performance if used as a road material. Variations in temperature and moisture condition create vertical and horizontal displacements, while wheel loads cause fatigue in the GPC pavement. Fatigue is defined as persistent microstructural degradation caused by repetitive loads on the pavement [50, 51]. OPC pavement fatigue performance is influenced by factors such as bonds at the aggregate–cement interface [52,53,54], concrete’s microstructure depending on additives such as f-ash [55], silica fume, and metakaolin clay [56], presence of fibre types like: steel—plain, corrugated and crimped [56, 57], polypropylene [58], and hybrid [59,60,61]. These factors may significantly affect PQGC also. Hence, study of fatigue behaviour of PQGC becomes important.

River sand is largely used in mortar and concrete. More than 12 million tonnes of natural aggregates are consumed globally by the construction industry to produce concrete [62]. The demand for RS is increasing because of infrastructure development. Considering the depletion of RS supply, the substitution of RS with acceptable alternatives in high-quality GPC for paving would ultimately boost its environmental friendliness. While manufactured sand (M-sand) has been considered as a potential substitute, its use in paving GPC is equally unsustainable due to the environmental harm caused by crushing stones to create M-sand. Some studies [62] have focussed on utilising industrial wastes such as coal bottom ash (CBF) [63], waste foundry sand (WFS) [64, 65], ferrochrome slag (FS) [66], precious slag ball (PSB) [29], copper slag (CuS) [67], recycled glass [68], waste glass and limestone [69] and others as alternatives to RS in OPC. Blast furnace slags are widely generated among different types of metallurgical slags, as blast furnaces are responsible for more than 60% of iron smelting worldwide [70]. Properly harnessing blast furnace slag materials in the construction sector has the potential to conserve millions of tons of natural resources. Currently, the cement industry utilises granulated blast furnace slag (GBS) and GGBS to either produce cement or enhance its quality. However, processed granulated blast furnace slag (PGBS) or slag sand (SS), produced by processing GBS, is considered suitable for use in mortar as a replacement for RS [71]. PGBS exhibits properties similar to RS, such as blunt particles and grain size, while also having improved dry bulk density and mild pozzolanic characteristics, albeit with higher water absorption [70, 71]. The presence of PGBS in mortar is found not to alter the flow property of the mortar. Moreover, studies have shown that mortar specimens containing PGBS exhibit improved mechanical strengths as a result of formation of CSH gel in OPC concrete matrix and improved bonding between cement and PGBS particles [70,71,72]. In addition, PGBS is more cost-effective than RS within proximity of 300–400 km from its production source [73, 74].

2 Research Significance

To address the growing concern for environmental sustainability and the need for sustainable alternatives to traditional river sand (RS) in paving applications, a new type of GPC that incorporates an alternative to RS developed. Previous studies have explored the use of various materials such as PSB [29], CuS [75] and waste glass [76] as potential substitutes for RS in PQGC. However, there is limited research specifically focussed on the use of slag sand (SS) in GPC designed for pavement. To fill this research gap, a novel PQGC that replaces river sand with slag sand was prepared. Different proportions of SS (25%, 50%, 75%, and 100% of RS) were incorporated into the PQGC. The study primarily focussed on investigating the fatigue behaviour of PQGC containing SS. In addition, the researchers also examined the fresh state characteristics and hardened state properties under static loadings before conducting fatigue analysis.

3 Materials Used and Their Properties

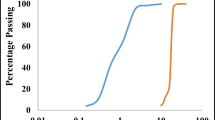
The f-ash, GGBS, 10 M NaOH solution, Na2SiO3 solution, RS, CA, SS, and potable water were the ingredients used to manufacture PQGC. Class F ultra-fine f-ash of UPCL thermal power plant was purchased from an Udupi-based Ash-tech India Pvt. Ltd. The particles of f-ash were mostly ceno-spherical in shape with a smooth-textured, see Fig. 1a, with diameters ranging from 0.03 micron to 3.57 micron and having a mean diameter of 0.67 micron. The JSW GGBS was obtained from a retailer in Mangalore. The GGBS particles, as shown in Fig. 1b, are majorly irregular in shape with sharp edges and rough texture. Locally available RS as FA, and virgin granite stone passing 20 mm was used as CA. JSW slag sand (commercial name of PGBS) as FA was used to replace RS in 25%, 50%, 75% and 100% replacement levels in the PQGC mixes. The SS appeared grey with a surface rough texture having intragranular surface microcavities and micro-fleeces, as depicted in Fig. 2. The manufacturing process of SS at JSW is pictorially presented in Fig. 3. Particle size distribution of the RS and SS were identical, as shown in Fig. 4, and both fall under zone II of IS:2386-Part I, 1963 [77] classifications.

Fig. 1
figure 1

a Fly ash and b GGBS

Full size image
Fig. 2
figure 2

Slag sand

Full size image
Fig. 3
figure 3

Manufacturing process of slag sand [84]

Full size image
Fig. 4
figure 4

Particle size distribution of RS, SS and CA

Full size image

The physical properties of all the ingredients of the PQGC mix were determined as per the relevant Indian Standard (IS) code presented in Table 1. The chemical composition of f-ash, GGBS and SS is presented in Table 2. The ratio of Si and Al in f-ash, GGBS and SS was found to be 2.4, 2.6 and 2.1, respectively. Any precursor materials having a Si to Al ratio in the range of 2 to 3.5 is suitable for pavement applications [78,79,80,81]. The 10 M NaOH and Na2SiO3 solution in a 1:2.5 ratio was used as alkaline activator (AA) solution. NaOH solution of 10 M was prepared by dissolving 97% pure NaOH crystal in 1 l of water. Na2SiO3 solution contained Na2O—13.54%, SiO2—32.46%, and H2O—54.0% as its composition.

Table 1 Physical properties of ingredients used in PQGC
Full size table
Table 2 Chemical composition of ingredients used in PQGC
Full size table

4 Preparation of PQGC Mixes

The PQGC used in this study was a stiff mix with a targeted slump value of 25 ± 10 mm and a compressive strength of 40 MPa. Five PQGC blends, designated as GRS, GS1, GS2, GS3, and GS4, were developed in agreement with the specifications of IRC:44-2017 [82] and Rangan’s Geopolymer concrete mix design guidelines [28, 83]. Consequently, the quantities of ingredients of the PQGC mixes that arrived are tabulated in Table 3. GRS contained 100% RS as fine aggregate whereas in other PQGC mixes, SS replaced the RS in the order of 25%, 50%, 75%, and 100%, respectively, in GS1, GS2, GS3, and GS4.

Table 3 Estimated quantities of ingredients used in PQGC
Full size table

The blending of PQGC was mixed in a drum-type concrete mixer. Initially, the f-ash, GGBS, CA, and RS/SS were thoroughly mixed for the first 5 min. AA was added later, and the mixing process continued for the next 5 min. After achieving a homogeneous mixture, an appropriate amount of water was added and stirred for an additional 2 min. The workability of the prepared mix was assessed using the slump cone test. Subsequently, the fresh concrete was poured into cylindrical, rectangular, and cubical moulds and left to harden for 24 h. The hardened PQGC specimens were then removed from the moulds and placed in an open-air environment for curing periods of 7, 14, 28, and 56 days. The mixing, placing, and curing procedures of the PQGC mixes were conducted under typical Manipal summer conditions (March to April), with a temperature of 36 degrees Celsius and a relative humidity of 74%.

5 Results and Discussion

5.1 Effect of Slag Sand on Setting Times and Consistency of PQGC Mixes

PQGC setting behaviour is a vital trait that affects the entire sequence of PQGC operations, from manufacture to transportation to application. In the present study the setting times of PQGC mixes were determined as per specifications of IS: 4031 Part 5-1988. The results of the test are depicted in Fig. 5. Accordingly, all the PQGC mixes have shown an initial and final setting times as 70 and 90 min, respectively. This shows that the SS in 25–100% of RS has no impact on the setting times of PQGC mixes.

Fig. 5
figure 5

Initial and final setting time of PQGC mixes

Full size image

To ensure that a PQC is laid using slip form or pavers, it is crucial to maintain a consistent slump. Therefore, a stiff concrete mix with a slump range of 25–50 mm is preferred for pavement applications [88, 89]. The slump cone test on PQGC mixes was conducted according to the specification stipulated in IS:1199-1959 [90]. The results of the slump test, presented in Fig. 6, indicate that the slump values of GRS and GS series mixes ranged from 25 to 26 mm, meeting the requirement for paving. All PQGC mixes exhibited a stiffer consistency, which is a typical characteristic of f-ash and GGBS-based GPC due to the combined effect of the viscosity of Na2SiO3, the molar concentration of NaOH solution, and GGBS content [79, 91]. Comparison of slumps of GRS and GS series mixes suggesting that the replacement of RS with SS from 25 to 100% did not affect the slump of the PQGC mixes.

Fig. 6
figure 6

Slump of PQGC mixes

Full size image

5.1.1 SEM Micrographs Analysis of PQGC Mixes

Figure 7a–e shows the SEM micrographs of the GRS and GS series mixes obtained after the 28-day ambient curing. All the micrographs were taken at the central instrumentation facility located in the MIT Manipal campus. As the developed PQGC is a blend of f-ash and GGBS, it primarily comprises CSH [21, 92] alongside CASH and NASH [93,94,95,96] as geopolymer gels nomenclated as GG in all SEM images. SEM image of GRS mix, shown in Fig. 7a, depicts reaction compounds by the process of geopolymerisation with many large and small unreacted or partially reacted f-ash and GGBS particles which are being found held between the reaction compounds. Further, the GRS mix appeared more porous with sizeable number of cracks occurring in unreacted larger f-ash particles. This had a determinantal effect on the mechanical strengths of GRS with respect to the GS series mixes. The replacement levels of RS by SS increasing from 25 to 100% in PQGC instigated a gradual reduction of pores and lowered the number of unreacted f-ash and GGBS particles, which is evident in Fig. 7b–e. In the GS1 mix, Fig. 7b, with 25% RS replacement by SS led to the synthesis of some of f-ash and GGBS particle. However, a few un-synthesised GGBS particles along with several unreacted mid- and small-sized f-ash particles were also identified, whereas GS2, GS3 and GS4 mixes with SS content of 50%, 75% and 100%, respectively, had improved the geopolymer gel compounds in the hardened mass-producing dense and amorphous microstructure with decreased un-synthesised micro f-ash particles as depicted in Fig. 7c–e. All these consequently increased the mechanical strengths under both static and repeated loadings particularly for GS4 mix when compared to GRS mix.

Fig. 7
figure 7

a–e SEM micrographs of PQGC mixes

Full size image

5.1.2 Effect of Slag Sand on Compressive Strength

The compressive strength of hardened concrete is the most crucial factor in meeting structural requirements and serves as a metric for measuring paving concrete performance and quality. Figure 8 presents the results of a compressive strength test conducted on hardened samples of GRS and GS series mixes, following the standards set by IS:516 Part-1/Sec-1 2021 [97]. Figure 8 illustrates an increasing trend in compressive strength from 7 to 56 days of open-air curing. At 7 days, the GRS mix exhibited 58% of its 28-day compressive strength, while the GS series mixes showed at least 66% of its compressive strength at 28 days. The synthesis of CaO from GGBS initially produce the hydration product CSH, later the formation of NASH and CASH compounds, as commonly observed reaction chemistry in fly ash and GGBS-blended GPC [33, 34] is the primary reason for the early gain and increase of compressive strength in PQGC. The discontinuous line in Fig. 8 represents the minimum compressive strength requirement (40 MPa) according to IRC 58:2015 [88] for pavement concrete to be opened for vehicular traffic. Interestingly, both GRS and GS series mixes exceed the minimum compressive strength requirement of 40 MPa by 10% and 15%, respectively, at 14 days of open-air curing. In contrast, achieving a compressive strength of 40 MPa or higher with Portland cement concrete as a binder would typically require at least 28 days under normal circumstances. Hence, it can be inferred that concrete roads made with GRS and GS series mixes would practically facilitate the early opening of roadways to traffic. Furthermore, the 28-day compressive strength results of GRS and GS series mixes indicate that all mixes achieved a compressive strength above 56 MPa, which is at least 37% higher than 40 MPa. In addition, comparing the compressive strength of GRS (56.3 MPa), GS1 (56.8 MPa), and GS2 (56.8 MPa) reveals a marginal variation in strength, suggesting that replacing up to 50% of RS with SS in PQGC has no significant impact on compressive strength. However, GS3 (58.2 MPa) and GS4 (60.6 MPa) demonstrated a 3.4% and 7.0% improvement in compressive strength, respectively, when compared to the GRS mix. This enhancement can be attributed to the reduced unreacted fly ash and GGBS particles as a result of contribution of CaO from SS [70, 72] producing refined microstructure, as shown in Fig. 7d, e. In addition, the quantity of fine particles of SS also increases with higher content of SS which further aided in improving compressive strength of GS3 and GS4 by filling the intergranular pores [72]. On the other hand, there was only a 3% improvement in compressive strength from 28 to 56 days, indicating a minimal rate of geopolymerisation in the GRS and GS series after 28 days.

Fig. 8
figure 8

Compressive strength of PQGC mixes

Full size image

5.1.3 Effect of Slag Sand on Flexural Strength

Structures such as rigid pavement need to possess sufficient flexural strength (FS) for increased fatigue resistance and longer lifespans. According to IRC 58:2015 [88] guidelines, rigid pavements should have a minimum flexural strength of 4.5 MPa, determined after a 28-day curing period (depicted by the discontinuous line in the figure). To determine the flexural strength of GRS and GS series PQGC mixes, a two-point bending test was conducted on hardened beams measuring 500 mm × 100 mm × 100 mm, following the specifications of IS:516 Part-1/Sec-1 2021 [97]. The test was carried out at 7, 14, and 28 days of open-air curing. The results of the flexural strength test are presented in Fig. 9. The figure indicates that, for the initial 7 and 14 days of curing, the flexural strength of GS series mixes remains lower than that of GRS mixes. This suggests that PQGC mixes with SS exhibit less initial bending strength during initial days of curing. However, after 28 days of curing, the flexural strength of GRS (5.4 MPa), GS1 (5.3 MPa), GS2 (5.2 MPa), GS3 (5.3 MPa), and GS4 (6.3 MPa) exceeds the minimum requirement of 4.5 MPa, representing an overall increase of 22%. It appears that, the flexural strength of GS1, GS2, and GS3 closely aligns with that of GRS, indicating that the incorporation of SS in PQGS up to a 75% level has no considerable influence on flexural strength. PQGC containing 100% SS, GS4, exhibited 16.7% enhancement in flexural strength w.r.t GRS. In addition to enhanced geopolymer reaction products and improved microstructure (Fig. 7e), the rough texture and blunt shape of SS particle may have led to the development of physical bond between the binder and SS particles that improved the flexural strength of GS4 [72, 98].

Fig. 9
figure 9

Flexural strength of PQGC mixes

Full size image

5.1.4 Splitting Tensile Strength of PQGC Mixes

The splitting tensile strength of concrete is a measure of hardened concrete’s tensile behaviour under circumferential tensile loading. The splitting tensile strength was conducted as per IS:516 Part-1/Sec-1 2021 [97] and the result of the test is presented in Fig. 10. The figure demonstrates the variation in splitting tensile strength of GRS and GS series mixes for 7, 14 and 28 days followed the similar trend as that of flexural strength gain. At 28 days of curing, variation of splitting tensile strength between GS1, GS2, GS3 and GRS was marginal, whereas GS4 mix registering an improved splitting strength of 8.3% w.r.t GRS. It is the rough textured of the SS particles that may have caused development of strong bond between the binder and SS particle, therefore, improving the tensile behaviour of GS4 [72].

Fig. 10
figure 10

Splitting tensile strength of PQGC mixes

Full size image

According to the results of the mechanical strength tests, the PQGC mix with 100% SS, i.e. GS4, outperformed the other PQGC mixes. In summary, better synthesis of fly ash and GGBS particles, refined microstructure, filling of pores by fine slag sand particles, and bonding between the binder and slag sand particle benefited GS4 in obtaining enhanced characteristics. As a result, for subsequent study, only GRS and GS4 mixtures are compared.

5.1.5 Relationship Between Compressive Strength and Flexural Strength of GRS and GS4 Mix

There are well-established equations that can predict the relationship between the compressive strength (fc) and flexural strength (fs) of OPC. These equations are based on empirical correlations and are commonly used in the construction industry. The relationship between fc and fs of GPC is complex and depends on various factors, including the precursor, mix design, curing conditions, and the type and concentration of alkali activators used. As a result, there is no standardised relationship is established so far to predict flexural strength of GPC from compressive strength. In this study, Eqs. (1) and (2) were developed, using square root model [99] of the form \(fs=b{fc}^{1/2}\), to establish the relationship between compressive and flexural strength for GRS and GS4 mixes. The coefficients ‘b = 0.72’ and ‘b = 0.85’, respectively, for GRS and GS4 mixes were determined by fitting the data of flexural strength and square root of compressive strength and using power function. The coefficient b for OPC varies from 0.62 to 0.69 according to certain codes and standards [99,100,101]. Contrary, some studies suggest higher b value for GPC as 0.93 [102] and PQGC as 0.82 [103] and 0.93 [29]:

$${f}_{\mathrm{GRS}}=0.72\times \sqrt{{f}_{c\_\mathrm{GRS}}}$$
(1)
$${f}_{\mathrm{GS}4}=0.85\times \sqrt{{f}_{c\_\mathrm{GS}4}}$$
(2)

where fGRS and fGS4 are the flexural strength in MPa and fc_GRS and fc_GS4 are the compressive strength in MPa.

The proposed models were compared with existing correlation equations found in the literature and codes, as depicted in Fig. 11. From the figure, it is evident that the predicted flexural strength using the proposed Eqs. (1) and (2) for GRS and GS4 mixes, respectively, were greater than the flexural strength calculated for OPC concrete using the formulae provided in codes such as IS 456 (2007) [104], ACI 318-14 (2014) [100], BS-8110 and NZS3101 [105]. In addition, the projected flexural strength obtained from the equations developed by researchers of PQGC mixes GC1 [103] and GC2 [106] were higher than the predicted flexural strength for GRS using the proposed Eq. (1). Furthermore, for every level of compressive strength, the flexural strength of the GS4 mix computed using the proposed Eq. (2) remained higher than the flexural strength of GC1 and GC2.

Fig. 11
figure 11

Comparison of correlation between the compressive strength and flexural strength of PQGC and PQC

Full size image

5.1.6 Analysis of Fatigue Behaviour of GRS and GS4 Mix

Figure 12 illustrates the MTS SERVO equipped, 5-ton loading capacity, two-point repetitive load testing equipment. In view of the results of flexural strength and the benefit to the environment in terms of conservation of RS, the PQGC mix GS4 was considered for fatigue response study, and the results are compared with the GRS mix to know the effect of 100% replacement of RS by SS. The 35 beams each for GRS and GS4, of dimension 500 mm × 100 mm × 100 mm, were subjected to cyclic loading for a constant amplitude and a frequency of 10 Hz with stress levels (it is the ratio of applied stress to the modulus of rupture [FS]) ranging from 0.9 to 0.6. This study used a cyclic load threshold of 3,00,000 cycles since fatigue testing is a time-consuming and expensive procedure that necessitates the inspection of numerous samples. When the specimen failed, or the threshold point was reached, the application of cyclic loads on the beam was stopped. The results of the fatigue failure data were analysed mainly by the S–N curve and probabilistic approaches.

Fig. 12
figure 12

Repetitive loading set up

Full size image

5.1.7 S–N Curves of GRS and GS4 Mixes

The S–N curves are regarded as the backbone of fatigue data analysis from the beginning of fatigue behavioural studies. It provides the most basic information about concrete specimen fatigue behaviour [107]. S–N curves show structural degradation and bond breakdown in general. Engineering studies almost primarily use the most common scale, linear stress levels, SL versus log of fatigue life, N. The fatigue test data of GRS and GS4 mixes are tabulated in Table 4. The figure depicts that the fatigue life increased as the stress level decreased for both GRS and GS4 mixes. Comparing the fatigue life of both blends for all stress levels indicates that the GS4 mix exhibits higher fatigue endurance than the GRS mix. For instance, at a peak stress level of 0.9, the minimum and maximum fatigue cycles for the GRS mix were 170 and 730. Whereas for the GS4 mix, the minimum and maximum fatigue cycles was 1522 and 16,102. Similarly, at the lowest stress level of 0.6, the GRS mix sustained a minimum of 87,370 and a maximum of 199,342 fatigue cycles. At the same time, GS4 mix borne a minimum of 97,000 and a maximum of 265,001 fatigue cycles. This enhancement in the fatigue life of the GS4 mix can be attributed to the intragranular micro cavity present on the surface of SS. The GC paste fills this intragranular micro cavity wholly or partially, thus improving the bond strength in GS4. At the same time, with 100% SS in GS4, the synthesis of f-ash and GGBS particles is found to be maximum, as indicated in Fig. 7e, which also improved the hardened properties of GS4. The data of the fatigue test were utilised to plot the S–N diagram, as shown in Fig. 13. Correspondingly, liner fitting models given in Table 5 for GRS and GS4 mixes were proposed. These proposed models reasonably estimate the fatigue life cycles at any given value of stress level. Thus, the proposed models can be used for designing of PQGC pavement with or without SS.

Table 4 Fatigue life of GS4 and GRS mixes
Full size table
Fig. 13
figure 13

S–N curve for GRS and GS4 mixes

Full size image
Table 5 Proposed S–N models for GRS and GS4 mixes
Full size table

The fatigue life estimated from the proposed S–N models for GRS and GS4 were compared with the fatigue cycles obtained from models for PQC, viz. PCA/IRC [88]and ERES/COE FFM [108, 109], and for special concretes such as mixed fibre-reinforced PQC [110], AAC with copper slag FA and AAC with PS ball FA [111]. The comparative analysis has been pictorially presented in Fig. 14. It can be perceived from the figure that the GRS and GS4 mix showed higher fatigue strength w.r.t PQC and AAC with PS ball FA. In contrast, w.r.t mixed fibre-reinforced PQC and AAC with copper slag FA, the fatigue strength of both GRS and GS4 remained lower after a stress level of 0.80.

Fig. 14
figure 14

Comparison of fatigue lives of GRS and GS4 with different concretes

Full size image

5.1.8 Probabilistic Analysis of GRS’s and GS4’s Fatigue Failure Data

The S–N curve is obtained by fitting fatigue data with the least square method, and its failure probability is close to 50% [112]. Since PQGC is a heterogeneous material with variable fatigue loading, the flexural fatigue lifetimes of PQGC are distinct. However, to achieve sufficient fatigue resistance, an acceptable flexural fatigue strength must be selected throughout the design phase, and the fatigue strength must reflect the uncertainty in the fatigue behaviour. This form of uncertainty can be effectively dealt with using probabilistic reliability theory, but a proper mathematical model must be chosen. The Weibull distribution model is the best suited model to represent the distribution of the flexural fatigue life of PQGC, considering the real service circumstances and variability of PQGC for paving applications.

The two parameters of Weibull probability’s cumulative distribution function, Pf(n) are represented by Eq. (3):

$${P}_{\mathrm{f}}\left(n\right)=1- \mathrm{exp}{\left[-\left(\frac{n-n\text{0,s}}{\mu -n\text{0,s}}\right)\right]}^{\alpha }$$
(3)

where n is the random variable of N’s particular value; α is the shape parameter or Weibull slope at stress level S; µ is the scale parameter or characteristic life at stress level S; and n0, s is the location parameter or minimal life at stress level S.

The Weibull shape and scale parameters can be estimated using the graphical approach, the method of moments, or the maximum likelihood estimator. The graphical method of calculating Weibull parameters, on the other hand, is easy and was used in this study to estimate the Weibull parameters. Accordingly, the Eq. (3) can be deduced to an equation of form Y = dependent variable, x = independent variable, m = slope, c = constant, Y = mx ± c, as follows:

$$\mathrm{ln}\left[\mathrm{ln}\left(\frac{1}{{L}_{\mathrm{R}}}\right)\right]= \alpha \mathrm{ln}\left(n\right)- \alpha \mathrm{ln}\left(\upmu \right)$$
(4)

where we have

$$Y=\mathrm{ln}\left[\mathrm{ln}\left(\frac{1}{{L}_{\mathrm{R}}}\right)\right]$$
(5)
$$X=\mathrm{ ln}(n)$$
(6)
$$B= \alpha \mathrm{ln}\left(\upmu \right)$$
(7)

The two Weibull parameters ‘α’ and ‘µ’ are estimated using the graphical method as follows. First, the fatigue data of each stress level are arranged in ascending order. Then, the survival-ship function ‘LR’ is calculated by Eq. (8):

$${L}_{\mathrm{R}}=1-\frac{i}{k+1}$$
(8)

where i is the failure order number, and k is the number of data points in a data sample under consideration at a particular stress level. The values empirical survival ship function LR for i = 1 to 5 at stress level = 0.90 is presented in Table 6.

Table 6 Fatigue life and empirical survival-ship at SL = 0.9 for GRS mix
Full size table

The procedure above is extended to other values of stress levels, viz.0.85, 0.80, 0.75, 0.70, 0.65 and 0.60 of both GRS and GS4 mixes, and the graph between ln [ln(1/LR)] and ln(n) is plotted as shown in Fig. 15. The slope of the line gives the value of α whereas µ is determined from the Eq. (7) for the known value of B obtained from the graphs. Weibull parameters were estimated as tabulated in Table 7.

Fig. 15
figure 15

Graphical analysis of fatigue life at SL = 0.9 for a GRS and b GS4 mixes

Full size image
Table 7 Estimated values of Weibull parameters by graphical method
Full size table

5.1.9 K–S Goodness of Fit Test

It is clear from the previous session that the graphical method accurately estimates the Weibull parameters, as revealed by correlation coefficient values ranging from 0.90 to 0.98 for stress levels ranging from 0.90 to 0.60. In addition, a goodness of fit test is performed to demonstrate the significance of the graphical method for estimating the Weibull parameter. For this purpose, the K–S test method is appropriate because flexural fatigue life is a one-dimensional random variable. The theoretical distribution of a small sample size is a completely known continuous distribution.

If F≠(ni) and F(ni) represent observed cumulative distribution and hypothesised cumulative distribution according to Eq. (3). Then, the fitting model is said to be significant and accepted when \({D}_{t}={\mathrm{max}}_{i}^{k}\left\{\left|{{\varvec{F}}}^{\ne }\left({n}_{i}\right)-{\varvec{F}}\left({n}_{i}\right)\right|\right\}\) is less than \({D}_{\mathrm{c}}\left(i, \beta \right)\), where Dt and Dc are tabulated and critical values, respectively, whereas \(i\) and \(\beta\) are the order number of data points and significance level, respectively. It can be found from Table 8 that for i = 5 and β = 0.05, the graphical method satisfactorily estimates the Weibull parameter.

Table 8 K–S test for fatigue life of GRS and GS4 mixes
Full size table

5.1.10 Probability of Survival (P s) of GRS and GS4 Mixes

Equation (3) can be rearranged into Eq. (9) by substituting LR = 1 − Pf, which allows for the determination of survival probability (Ps) for any given failure probability (Pf). As per IRC:58 2015, Expressways and National Highways pavement design require accounting for a failure margin of 10%. Thus, the survival probability curves for GRS and GS4 were determined at Pf = 10% and are compared with the PQC survival probability curve (obtained from the equation given in IRC: 58 2015 for Pf = 10%) in Fig. 16. The comparison reveals that both GRS and GS4 exhibit a better chance of survival than the PQC:

Fig. 16
figure 16

Probability of survival of PQC, GRS and GS4 mixes

Full size image
$$n={\mathrm{ln}}^{-1}\left[\frac{\mathrm{ln}\left\{\mathrm{ln}\left(\frac{1}{1-Pf}\right)\right\}+\alpha *\mathrm{ln}(\upmu )}{\alpha }\right]$$
(9)

5.1.11 Endurance Limit (EL) of GRS and GS4 PQGC Mixes

Repeated traffic loads can subject PQGC pavement to fatigue stress, causing it to fail at a stress level lower than its maximum stress under static loading. Therefore, it is practical to determine the fatigue stress level in terms of endurance limit (EL). EL is defined as the maximum stress value a material can withstand under loading cycles without undergoing fatigue failure. The EL value for rigid pavement is typically 20,00,000 cycles [107, 113]. To determine the stress levels corresponding to EL of 20,00,000 fatigue cycles for GRS and GS4 mixes, SN curves were plotted using the proposed models presented in Table 5, between stress levels 0.445 and 0.55. As shown in Fig. 17, the EL occurs at stress levels of 46.6% and 56.7% for GRS and GS4, respectively. These stress levels in terms of actual flexural stress correspond to 2.93 MPa for GRS and 2.94 MPa for GS4. Table 9 provides the details of the occurrence of EL for GRS, GS4, and other types of PQC.

Fig. 17
figure 17

Endurance limit of GRS and GS4

Full size image
Table 9 Occurrence of EL for GRS, GS4 and other types of PQC
Full size table

Table 9 clearly shows that GRS and GS4 mixes required higher stress levels to achieve 20,00,000 fatigue cycles than PQC made with OPC. However, GRS and GS4 sustained lower stress levels to reach EL than steel fibre-reinforced PQC. The presence of steel fibres in concrete bridges the cracks and delays their propagation, thereby enhancing EL. Consequently, steel fibre-reinforced PQC exhibits better endurance than GRS and GS4. Moreover, the stress levels at EL for GRS were found to be comparable to those of AAC containing PBS as FA. On the other hand, GS4 required a higher stress level to reach EL when compared to AAC containing PBS as FA.

6 Conclusion

The study investigated the effects of replacing river sand with slag sand on the hardening time, workability, and hardened properties of PQGC. The outcome of the present study is given as follows:

  • Physical properties such as specific gravity and particle size distribution of river sand and slag sand were found to be similar which suggests that slag sand can be used for pavement grade concrete. Also no effect on setting character and workability is found.

  • Strength gain is faster as the designated strengths were achieved in 14 days for PQGC as against 28 days for PQC. Strength gain after 28 days was minimal.

  • Flexural and split tensile performance were similar for all PQGC mixes irrespective of replacement levels of steel slag. 28 day cured PQGC mix with 100% slag sand performed best among the samples tested.

  • Comparative analysis of fatigue lives of PQC, GRS and GS4 indicate that the slag sand improved the fatigue endurance of PQGC. The fatigue endurance were of the order GS4 > GRS > PQC. The improved bond between the binder and slag sand, maximum synthesis of fly ash and GGBS particles aggregate, refined microstructure all enhanced the fatigue durability of PQGC having 100% slag sand.

  • Incorporation of slag sand partially or fully in PQGC reduces dependency on river sand and makes road construction economical particularly in the region located near to slag sand production.

  • Overall, slag sand in PQGC makes it even more environment friendly, promotes utilisation of industrial waste, reduces river sand demand and has major impact on overall economy.