1 Introduction

Screening ground-borne vibrations generated by large hammers, rail and road traffic, and machinery sources is one of the most important geotechnical problems in recent years. Rayleigh waves are propagated near the ground surface and transmit most proportion of the vibratory energy. To screen these induced vibrations, different approaches, such as the construction of in-filled or open trenches, thin-wall barriers, expanded polystyrene (EPS) blocks, and pile barriers, have been proposed. Also, the induced vibration can affect the mechanical behavior of buried structures, such as pipelines [1,2,3,4,5,6,7,8,9,10].

On the one hand, vibration mitigation has generally been investigated by considering the source of vibrations in the forms of train loading, impact loading, and especially sinusoidal loading. Among these types of loading, the least attention was paid to the impact loading. Liyanapathirana and Ekanayake [11] showed that a wave barrier should have a depth of at least two-thirds of a Rayleigh wavelength to be effective in screening seismic surface waves. However, using open trenches has several limitations in practical applications. For instance, due to the localized collapse, installation and maintenance of the open trenches are difficult. There are also safety issues and accidental filling because of rainfall, and therefore, in-filled trenches should be considered. Woods [12] indicated that in-filled trenches with appropriate sizes were effective but in no case were as effective as an open trench of the same size.

Richart et al. [13] illustrated that the waves reaching the interface of in-filled trenches would undergo different mechanisms such as reflection, refraction, scattering, and diffraction. While both P and S waves are transmitted at a solid–solid interface, only P waves are transmitted in the solid–fluid interface. Also, at a solid-void interface, no waves are transmitted. Zoccali et al. [14] investigated the mitigation of train-induced vibrations using in-filled trenches and concluded that this mitigation was strongly influenced by the properties of in-filled materials. Also, the authors stated that the concrete had a positive performance in most of the frequency ranges but was not a cost-efficient in-filled material that might even increase the vibration in some frequency ranges, and therefore, it should be studied based on critical frequencies of the receiver. On the other hand, El-Naggar and Chehab [15] investigated the vibration barriers for shock-producing equipment and concluded that soft wave barriers were more effective than stiff ones. Also, the researchers showed that the effectiveness of a wave barrier increased as the ratio of trench depth to the wavelength increased. Furthermore, Ekanayake et al. [16] studied the performance of in-filled trenches with water and geofoam and concluded that geofoam was a more effective fill in the attenuation of ground-borne vibrations.

Massarsch and Fellenius [17] focused on the ground vibration induced by impact pile driving and proposed a model to study the vibration force that can be transmitted along with the soil-pile transmission. Jayawardana et al. [18] investigated the effectiveness of in-filled trenches in screening the ground vibrations induced by pile driving impacts and summarized that the open and water-filled trenches had a better performance compared to other in-filled trenches. The authors also indicated that soft in-filled materials contributed more towards vibration reduction compared to stiffer materials.

Jaya et al. [19] and Ulgen and Toygar [20] conducted field tests to investigate the performance of trenches in mitigating vibrations induced by impact loading. Jaya et al. [19] concluded that the geometry of the trench had an influence on the protective performance of an in-filled trench. The researchers found that reducing the length of a trench to half resulted in a 20% decrease in its efficiency, while doubling the depth of a trench led to a 33% increase in its efficiency. Moreover, Ulgen and Toygar [20] reported that a trench depth of 4.5 m could reduce the vibrations by 50%.

Baziar et al. [15] conducted centrifuge model tests to investigate the performance of geofoam barriers in mitigating the vibrations induced by surface impact loading on underground structures. The authors found that the geofoam was a proper material that could reduce the effects of blast loading, and this effectiveness greatly influenced by its location. In other words, geofoam can better mitigate the vibration when it is located near the structure than when it is located close to the explosive charge.

On the other hand, Ahmad and Al-Hussaini [21] used Rayleigh wavelength to normalize the dimensions and location of the trench to perform a dimensionless study. This assumption was subsequently used in other research articles in this field [e.g., 22, 23]. Based on this assumption, the previous publications were focused on normalization by only one wavelength, and therefore, the results were specifically obtained for that wavelength. The subtle point in the suggestion of Ahmad and Al-Hussaini’s work [21] is that researchers did not specify a range that the results can be extended. In the study, two sets of data were provided having the same values of normalized dimensions and location of the trench for two different wavelengths (Fig. 1). In this figure, \(W\) is the width of the trench, \({\lambda }_{R}\) is the Rayleigh wavelength, \(\vartheta\) is the soil Poisson’s ratio, and \({A}_{m}\) is the average amplitude reduction ratio. By comparing the results of Fig. 1a and b, it can be seen that the results for the given two cases were not the same. This differentiation happened when the Rayleigh wavelength just decreased at a very small amount: from 5.0 to 4.8 m, and therefore, more diverse results can be observed from normalized trench dimensions under the situation of larger or smaller values of Rayleigh wavelengths. In other words, it can be concluded that the results obtained for a wavelength in a given condition are not the same as the results obtained for another wavelength, even with the same normalized dimensions (see Sect. 3.1.1). It should be mentioned that while previous studies investigated the change of loading frequency on trench effectiveness, the reported design charts were based on only normalized dimensions, and their general approach neglected the effect of Rayleigh wavelength on the effect of normalized dimension on trench performance. It means that the investigation of trench performance should be based on the coupling effect of Rayleigh wavelength and normalized dimensions. This conclusion can also be deduced from the results reported in other studies [e.g., 24–26], as was shown here for the results of Ahmad and Al-Hussaini [21]. Therefore, this study aims to investigate the trench efficiency based on the coupling effect of normalized dimension and Rayleigh wavelength.

Fig. 1
figure 1

Effect of normalized trench dimensions on trench performance for different Rayleigh wavelengths a \({\lambda }_{R}\) = 5.0 m b \({\lambda }_{R}\) = 4.8 m [21]

Full size image

As aforementioned, most of the previous studies performed on vibration mitigation concentrated on sinusoidal harmonic loading, and there are limited studies available in the literature considering the impact loading as a source of vibration. This loading is one of the frequent types of loading induced by machine foundations. In this study, the influence of impact loading, and subsequently, the effects of the open trench and geofoam trench have been investigated. Also, the regular approach for investigating the trench performance adopted to study the effectiveness of a trench neglected the coupling effect of normalized dimension and Rayleigh wavelength. In the present study, at the first step, it would be shown that investigating the barrier effectiveness using normalized dimensions and locations of the trench for just a single wavelength is not a comprehensive choice, and the trench effectiveness for different values of \({\lambda }_{R}\) cannot be the same. Then, the effectiveness of open trench, geofoam trench, and double and multiple geofoam trench was investigated for different values of Rayleigh wavelengths. Finally, several charts were proposed which could be adopted for designing the geofoam trench for different Rayleigh wavelengths.

2 Methodology and Modeling

The efficiency of any wave barriers are typically expressed as an amplitude reduction factor, \({A}_{r}\) [27], which is given as Eq. (1). The values of \({A}_{r}\) may not be uniform beyond the trench (as can be seen in Fig. 4). Therefore, to have an idea of the overall performance of the trench, an average value of the amplitude reduction factors was computed over the trench influence zone, x, represented by the average amplitude reduction ratio (\({A}_{m}\)) (Eq. 2).

Since the model system is discrete, it is necessary to average the grid points available in the domain of trench efficiency. Furthermore, overall system efficiency or effectiveness (\({E}_{f}\)) could be evaluated as Eq. (3).

$${A}_{r}=\frac{\mathrm{Vertical \, velocity \, amplitude \, of \, ground \, surface \, with \, barrier} }{\mathrm{Vertical \, velocity \, amplitude \, of \, ground \, surface \, without \, barrier}},$$
(1)
$${A}_{m}=\frac{1}{x}\int {A}_{r} \cdot dx= \frac{\sum {A}_{r}}{\mathrm{Number \, of \, grid \, points \, in \, the \, domain \, of \, trench \, efficiency}},$$
(2)
$${E}_{f}=(1-{A}_{m})\times 100.$$
(3)

Furthermore, Eq. (4) has been used to calculate Rayleigh wavelength (\({\lambda }_{R})\):

$${\lambda }_{R}=\frac{{V}_{R}}{f}.$$
(4)

In this equation, \({V}_{R}\) stands for velocity of Rayleigh wave (unit: m/s), and \(f\) (unit: Hz) is the frequency induced by the loading presented in Fig. 3.

2.1 Scheme of Finite-Difference Modeling

In this study, FLAC software [28] was adopted to investigate the efficiency and behavior of open and in-filled (geofoam) trenches in mitigating the ground-borne vibration due to the impact loadings generated by machine foundations or other sources. Many researchers have used the axisymmetric model to obtain a realistic model of wave propagation and to evaluate the effect of trenches on mitigating these ground-borne vibrations [18, 22, 23, 29]. Therefore, the axisymmetric condition for such types of impact loadings was considered in the present study. In this study, the domain of trench efficiency in Eq. (2) (observation area) is investigated for the range beyond the trench to a distance of 40 m from the source of vibration (see Fig. 2a). This 40 m is an assumption to have a specified point for the end of the observation area, and not other logics exist behind this assumption. Beyond this observation area, the assurance length of \({L}_{A}\) has been considered (see Fig. 2a). This length was different in each analysis depending on the impact-induced shear wave velocity, with this consideration that the first pulse of the loading must not reach the right side boundary. This length can avoid any wave reflection from the right side boundary to the body of the model.

Fig. 2
figure 2

a Schematic of the vibration isolation system and boundary conditions. b Schematic 3D view

Full size image

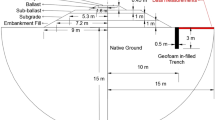
Also, the height of the model is considered to be equal to 20 m. Furthermore, based on Lysmer and Kuhlemeyer [30] suggestions, the viscous boundaries were assumed on both the bottom and right sides of the mesh to absorb body waves reaching these boundaries without any reflection of the waves. Consequently, these viscous boundaries can model semi-infinite soil. The sensitivity analyses on these boundary sizes (model width from 1.1 to 2 times of the calculated size introduced in Fig. 2a, and model height from 10 to 50 m) with considering maximum and minimum of Rayleigh wavelengths used in this study showed that this model domain minimized the boundary effects, and larger domain size is not necessary. The results of the sensitivity analyses were not reported to avoid this paper being lengthier. Three considerations have been used to determine good element sizes used in this study. First of all, FLAC manual [28] suggests that the mesh elements should be 4 nodded with a maximum aspect ratio of 5. Second, Kuhlemeyer and Lysmer [31] suggested that the maximum size of the elements should be smaller than one-tenth of the shortest Rayleigh wavelength. Third, to use Eq. (2), the x-dimension of the elements along the x-direction in the observation area must be equal. Otherwise, it will not be possible to use Eq. (2) to average between different grid points. Based on these three factors, the mesh elements of the in-filled trench and soil in the present study are chosen to be squares with the size of 10 cm × 10 cm all over the model. Since the shortest Rayleigh wavelength (\({\lambda }_{R}\)) studied in the present study is equal to \(2.0 \, \mathrm{m}\), this element sizes are smaller than half of the dimensions suggested by Kuhlemeyer and Lysmer [31], which can provide sufficient confidence about the element dimensions. Figure 2 shows an example of viscous boundaries and the mesh sizes used in the present study. In this figure, \(L\) is the distance of the beginning of the trench from the source of vibration, while \(D\) and \(W\) are the depth and width of the trench, respectively.

Wave propagations in soils having open or in-filled trenches usually generate small strains. Therefore, several researchers considered linear elastic behavior for the soil without significant loss of accuracy [e.g., 22, 29]. Connolly et al. [32] conducted some field tests and concluded that such simplification was realistic. Therefore, this study considers the same assumption, and the linearly elastic constitutive law was implemented in the model. Linear elastic criterion requires using soil elastic modulus (\({E}_{\mathrm{soil}}\)), unit weight (\({\gamma }_{s}\)), and Poisson’s ratio (\({\vartheta }_{s}\)). In this study, the unit weight and the Poisson’s ratio of the soil were assumed to be 18 kN/m3 and 0.25, respectively. Also, the soil elastic modulus varied between 20 and 150 MPa in different analyses, and the Rayleigh damping coefficient (\({\varepsilon }_{s}\)) of soil and in-filled material were considered to be both equal to 5%, which was defined by mass and stiffness coefficients calculated according to the exciting frequency. This value has been used by several researchers [e.g., 21, 23, 29].

2.2 Loading

Figure 3 shows the impact loading considered in this study which includes 12 triangular impulses with a maximum magnitude of 100 kN; however, it is evident that the magnitude of loading does not affect the efficiency of trenches due to the nature of linear elastic constitutive law. This loading would be vertically applied at the top left corner of the model. For practical purposes, the footing carrying the vibrating loads was not considered in the model because it did not considerably affect the results [33].

Fig. 3
figure 3

Pattern of impact loading used in this study

Full size image

The explicit dynamic analyses were performed by choosing automatic time intervals calculated by FLAC, which are accurate and calculation time minimizer. However, time intervals equal to one-tenth of the automatic time interval result in the same value of vibration velocities. Moreover, the total time considered for the analyses was calculated based on the time needed for the first impact pulse to reach the right boundary. This time is equal to the time required by the last impact pulse to cross the observation area (due to the choice of \({L}_{A}\)). Another important point is that the frequency of this loading has been considered equal to \(\frac{1}{t}\) and the Rayleigh wavelength has been computed based on this frequency. It should be mentioned that the aim of this study is to evaluate the trench efficiency, and the discussion on the frequency content of the impact loading is out of the scope of this paper.

2.3 Verification

At first, the numerical model was verified by the data reported by Ahmad and Al-Hussaini [21] and Saikia [22]. For this purpose, an open trench with depth \(D=3 \, \mathrm{m}\), width \(W=0.3 \, \mathrm{m}\), and distance between trench and source of vibration of \(L=15 \, \mathrm{m}\) was considered. This is to say that the trench is installed at a distance of 15 m from the source load. Soil elastic modulus \({(E}_{s})\), Poisson’s ratio \({(\vartheta }_{s})\), unit weight (\({\gamma }_{s})\), and damping coefficient \({(\varepsilon }_{s})\) were assumed to be the same as given by Ahmad and Al-Hussaini [21] and Saikia [22], and were considered as 46 MPa, 0.25, 18 kN/m3, and 5%, respectively. The source of vibration was taken to be a periodic sinusoidal harmonic load of magnitude 1 kN vibrating vertically at a frequency of 31 Hz. Figure 4a plots the variation in \({A}_{r}\) with distance beyond the source of vibration. Good agreement was found between the results of this study and those reported by Ahmad and Al-Hussaini [21] and Saikia [22].

Fig. 4
figure 4

Agreement between the present study results and the reported data in the literature. a Open trench. b Free field. c Open trench. d In-filled geofoam trench

Full size image

The numerical results obtained in the present study were also compared with the field measurements reported by Alzawi and El-Naggar [29]. In this regard, geofoam trench, open trench, and free field considered by Alzawi and El-Naggar [29] were numerically modeled. Figure 4b–d plots the variation in normalized soil particle vertical velocities with distance beyond the source of vibration. The results obtained in this study are in good agreement with those reported by Alzawi and El-Naggar [29]. It should be noted that in this case, the trenches were assumed to be located at a distance of 2.5 m from the source of vibration, which was vibrating with a frequency of 40 Hz. The differences in some cases could be due to variability and anisotropy in soil properties of the site reported by Alzawi and El-Naggar [29].

3 Results and Discussion

3.1 Performance of Open Trenches in Vibration Isolation

3.1.1 Effect of Soil Condition and Loading

To find a suitable factor for considering the effects of the soil shear wave velocity and loading, Cases 1–8, provided in Table 1, were compared (Fig. 5a). These cases have the same value for Rayleigh wavelength, which is equal to \({\lambda }_{R}=5.0 \, \mathrm{m}\). It should be mentioned that the values of the parameter \(t\) (time) were intended to generate the desired Rayleigh wavelengths. Also, the frequencies induced by the values of \(t\) presented in Table 1 are in the range of 12–33 Hz (low-frequencies), which is the range of frequencies induced by railway traffic. In Fig. 5a, the values of \({E}_{f}\) for Cases 1–4 (shown in green) and also Cases 5–8 (presented in blue) are almost equal. This means that the performance of trenches is a function of Rayleigh wavelength (\({\lambda }_{R}\)), and a separate investigation of the effect of soil condition described as shear wave velocity and also loading speed (loading frequency) is not necessary. Lower values of \(t\) [i.e., higher frequencies (e.g., 200 and 300 Hz)] have been investigated in this study, and the same results as the results obtained from lower frequencies were observed for trench performances (not shown in this paper as a matter of brevity). Therefore, this study uses different values of \({\lambda }_{R}\) to consider the effect of both soil condition and loading speed (frequency). The Rayleigh wavelengths (\({\lambda }_{R})\) used in this study ranged from 2.0 to 13.0 m. For instance, this range can cover the ground elastic modulus from 2.5 to 90 MPa for frequency of 10 Hz, 22.5–810 MPa for 30 Hz, or 1–36 GPa (useful for rock environment) for 200 Hz. It means that the condition of high frequencies such as 100 Hz or 200 Hz in regular soils elastic modulus is out of the scope of this study.

Table 1 Different conditions of soil, trench, and loading speed
Full size table
Fig. 5
figure 5

Effect of soil shear wave velocity and loading speed (details of different cases were described in Table 1). a Checking whether it is possible to consider Rayleigh wavelength for investigation instead of considering soil properties and excitation frequency. b Checking whether barrier effectiveness of trenches with the same normalized dimensions and locations for different Rayleigh wavelengths are equal

Full size image

It should be noted that the unit weight and the Poisson’s ratio of soil were assumed to be 18 kN/m3 and 0.25, respectively. Therefore, the value of soil shear wave velocity (\({V}_{\mathrm{s}\_\mathrm{soil}}\)) is only related to the \({E}_{\mathrm{soil}}\).

As mentioned in the Introduction, to perform a dimensionless study, some previous studies used Rayleigh wavelength to normalize dimensions and location of the trench. Based on this assumption, the general approach in previous publications was based on normalization by only one wavelength, and therefore, the results were specifically obtained for that wavelength.

Therefore, Cases 9–12 presented in Table 1 were chosen to determine if the values of barrier effectiveness of trenches with the same normalized dimensions and locations for different Rayleigh wavelengths are equal. The normalized depth \(\left(\frac{D}{{\lambda }_{R}}\right)\), normalized width \(\left(\frac{W}{{\lambda }_{R}}\right)\), and normalized distance \(\left(\frac{L}{{\lambda }_{R}}\right)\) of these cases are equal to 1.0, 0.2, and 4.0, respectively. According to Fig. 5b, the values of trench effectiveness for Cases 9–12 are not the same. Therefore, it can be concluded that investigating the barrier effectiveness using normalized dimensions and locations of the trench for just a single wavelength is not a comprehensive choice since the trench effectiveness for a given \({\lambda }_{R}\) cannot be used for another value of \({\lambda }_{R}\). This is also in agreement with those of the results provided in Fig. 1.

Thus, this study used the normalized dimensions and location of the trench for different values of \({\lambda }_{R}\). It should be mentioned that the results of researchers that used only normalized dimensions are correct for the assumed Rayleigh wavelength; still, the results cannot be used for other Rayleigh wavelengths. Hence, this study aims to investigate barrier effectiveness using the same normalized dimensions and locations of the trench, but for several Rayleigh wavelengths. It means that the approach of this study is based on considering the coupling effect of normalizd dimension and location of the trench together with Rayleigh wavelength.

3.1.2 Sensitivity Analysis on the Dimension and Location of the Open Trench

The three variables that define an open trench (as shown in Fig. 1) are the distance of the beginning of the trench from the source of vibration (\(L\)), depth of the tench (\(D\)), and width of the trench (\(W\)), which affect the trench performance. Figure 6 demonstrates the effects of the above-mentioned parameters of the trench on trench efficiency (\({E}_{f}\)). In Fig. 6a and b, the value of normalized length \(\left(\frac{L}{{\lambda }_{R}}\right)\) is equal to 2.0. Additionally, in Fig. 6c, the values of normalized depth \(\left(\frac{D}{{\lambda }_{R}}\right)\) and normalized width \(\left(\frac{W}{{\lambda }_{R}}\right)\) and are equal to 1.0 and 0.5, respectively.

Fig. 6
figure 6

Effect of location and dimensions of the open trench on its performance. a Effect of normalized depth on open trench effectiveness for the condition of normalized distance equal to \(2, {\lambda }_{R}=2.0 \, \mathrm{m}\). b Effect of normalized depth on open trench effectiveness for the condition of normalized distance equal to \(2, {\lambda }_{R}=8.0 \, \mathrm{m}\). c Effect of normalized distance on open trench effectiveness for the condition of normalized depth equal to \(1.0\), normalized width equal to 0.5

Full size image

Figure 6a plots the effect of trench depth for different values of trench width for the condition of \({\lambda }_{R}=2.0 \, \mathrm{m}\) (\({E}_{\mathrm{soil}}=20 \, \mathrm{MPa}\) and \(t=82 \, \mathrm{ms}\)). This figure shows that the width of the open trench does not have any effect on the performance of the trench, except for a shallow trench with normalized depth of less than \(0.7\), in which a very slight effect can be observed. This was also shown previously by Woods [27].

Figure 6b, which is associated with the condition of \({\lambda }_{R}=8.0 \, \mathrm{m}\) (\({E}_{\mathrm{soil}}=100 \, \mathrm{MPa}\) and \(t=58 \, \mathrm{ms}\)), illustrates that the trench effectiveness associated with different values of width is the same. Figure 6c indicates that for normalized distance of less than \(1.0\), the system effectiveness improves for the larger trench distance from the source of vibration. The reason is that in a trench located close to the source of vibration, the body waves have a dominant role. If a trench is located near the source, a major portion of the body waves can pass beneath the trench, and therefore, the trench efficiency decreases. However, the surface waves take control for greater distances, and the wave barrier screen this type of wave [32]. Therefore, the trenches should be installed at a minimum distance equal to the Rayleigh wavelength (\({\lambda }_{R}\)) from the source of vibration. This applies to all Rayleigh wavelengths, as can be seen in Fig. 6c.

Furthermore, Fig. 6c shows that the results of the trench effectiveness for the same normalized dimensions and location of the trench for different values of \({\lambda }_{R}\) are not the same, and they increase with an increase in \({\lambda }_{R}\). This can also be observed by comparing Fig. 6a and b, and therefore, this is in agreement with results indicated in Sect. 3.1.1. Moreover, comparing Fig. 6a–c reveals that the trench depth is the key parameter controlling trench efficiency, and this is true for all wavelengths.

Figure 6a also indicates that a trench with a normalized depth of 1.5 (equal to a trench depth of 3.0 m) can mitigate the vibration by 70% in the case of \({\lambda }_{R}=2.0 \, \mathrm{m}\). However, the normalized depth needed for this value of vibration screening is 0.5 (equal to a trench depth of 4.0 m) for a wavelength of \({\lambda }_{R}=8.0 \, \mathrm{m}\) (Fig. 6b).

3.2 Performance of In-Filled (Geofoam) Trenches in Vibration Isolation

3.2.1 Effect of Dimensions and Location of the In-Filled (Geofoam) Trench

In this study, the effectiveness of the in-filled geofoam (EPS) trench was also investigated. The properties of the geofoam material are \({E}_{\mathrm{foam}}=10 \, \mathrm{MPa}\), \({\vartheta }_{\mathrm{foam}}=0.1\), and \({\rho }_{\mathrm{foam}}=30 \, \frac{\mathrm{kg}}{{\mathrm{m}}^{3}}\). Figure 7 plots the effects of the dimensions and location of the trench on its effectiveness (\({E}_{f}\)). In Fig. 8a and b, the value of normalized distance is equal to 2.0. Additionally, in Fig. 7c, the values of normalized depth and normalized width are equal to 1.0 and 0.5, respectively.

Fig. 7
figure 7

Effect of location and dimensions of the in-filled (geofoam) trench on its performance. a Effect of normalized depth on geofoam trench effectiveness for the condition of \({\lambda }_{R}=2.0 \, \mathrm{m}\). b Effect of normalized depth on geofoam trench effectiveness for the condition of \({\lambda }_{R}=8.0 \, \mathrm{m}\). c Effect of normalized distance on geofoam trench effectiveness for the condition of normalized depth and normalized width equal to 1.0 and 0.5, respectively

Full size image
Fig. 8
figure 8

Effect of slenderness ratio and cross-sectional area of the in-filled (geofoam) trench on its performance. a \({\lambda }_{R}=2.0 \, \mathrm{m}\), b \({\lambda }_{R}=4.0 \, \mathrm{m}\), c \({\lambda }_{R}=8.0 \, \mathrm{m}\), d \({\lambda }_{R}=13.0 \, \mathrm{m}\)

Full size image

Based on Fig. 7, both the width and depth of the geofoam trench significantly affect the performance of the trench. Unlike the open trench that the absorption does not have a role and the waves generally reflect from the sides of the trench wall, this phenomenon can have a substantial effect on vibration mitigation of in-filled trenches. Therefore, the trench width plays a significant role in the in-filled trenches. The reason is that the waves can cross through the in-filled material (unlike the open trenches), and therefore, having larger width can result in more absorbance and damping of the wave within the in-filled material [26]. Figure 7a and b show that in the cases of normalized depth less than \(1\), the system efficiency increases with an increase in the geofoam trench-normalized depth, and after that, increasing the normalized depth does not change the trench effectiveness. Also, Fig. 7a indicates the significant effect of normalized width on system efficiency for \({\lambda }_{R}=2.0 \, \mathrm{m}\). However, this effect decreases with an increase in \({\lambda }_{R}\) to 8.0 m (Fig. 7b). According to Fig. 7c, it can be concluded that the trench effectiveness for normalized distance less than \(1.0\) increases with an increase in normalized distance \(\left(\frac{L}{{\lambda }_{R}}\right)\). However, this parameter does not change \({E}_{f}\) for cases with normalized distance larger than \(1.0\). This is the same as what was observed for open trenches (Fig. 7c).

As mentioned before, the results obtained based on normalized dimensions should be interpreted carefully. For example, it may seem that the trenches can mitigate the vibration more effectively for larger wavelengths than for the smaller ones; the system efficiency for \({\lambda }_{R}=8.0 \, \mathrm{m}\) reaches up to 80% (Fig. 7b) and this maximum value for \({\lambda }_{R}=2.0 \, \mathrm{m}\) is about 66% (Fig. 7a). But, it should be noted that the depth and width required to mitigate the vibration by 80% for \({\lambda }_{R}=8.0 \, \mathrm{m}\) are 8.0 m and 4.0 m, respectively. However for \({\lambda }_{R}=2.0 \, \mathrm{m}\), a trench with width and depth both equal to 2.0 can generate an efficiency of about 60%. As another instance, for \({\lambda }_{R}=8.0 \, \mathrm{m}\), the depth and width of 1.5 m (normalized depth and normalized width are both equal to \(0.2\)) result in the effectiveness of 25%, but for \({\lambda }_{R}=2.0 \, \mathrm{m}\), the depth and width of 1.0 m (normalized depth and normalized width are both equal to \(0.5\)) result in system efficiency of 37%. Therefore, for practical situations, in which choosing the width and depth is limited, another approach should be considered that is discussed in the next section.

3.2.2 Trench Effectiveness for the Specific Cross-Sectional Area

Figure 8 presents the combined effects of trench slenderness ratio \(\left(\frac{D}{W}\right)\) and cross-sectional area (\(A\)) on the effectiveness of trench installed at a normalized distance equal to \(1\) from the source of vibration. The value of normalized distance was chosen to avoid the negative influence of trench nearness to the source of vibration on the barrier effectiveness, as can be seen in Fig. 7c. The cross-sectional area varies in the range of 1–10 m2. Furthermore, for each area, the barrier slenderness ratio \(\left(\frac{D}{W}\right)\) is gradually increased from 0.2 to 5.0. These values of cross-sectional areas are chosen based on a wide range of trenches that can be found in practice. In addition, the Rayleigh wavelengths vary between 2.0 and 13.0 m (see Fig. 8).

Figure 8 indicates that the optimum trench effectiveness occurs at a slenderness ratio of \(1.0\le \frac{D}{W}\le 2.0\) and deeper trenches do not enhance the trench efficiency, except for small cross-sections of \(A=1.0 \, {\mathrm{m}}^{2}\) for \({\lambda }_{R}=8.0 \, \mathrm{m}\) and \(13 \, \mathrm{m}\). This result can be seen for all cross-sectional areas in all Rayleigh wavelengths. However for \({\lambda }_{R}=2.0 \, \mathrm{m}\), thin barriers with slenderness ratios of more than 1.0 lead to the reduction of the effectiveness. Therefore, for small values of \({\lambda }_{R}\), the trench slenderness ratio should be carefully chosen to reach the optimum efficiency of the barrier, and this optimum value is equal to the \(\frac{D}{W}=1.0\).

Another point that can be observed from Fig. 8 is that for \(\frac{D}{W}<1.0\), the trench effectiveness enhances with an increase in the slenderness ratio. The trenches with a depth smaller than their width \(\left(\frac{D}{W}<1.0\right)\) are known as wave-impeding blocks. Hense, the wave-impeding blocks do not perform better than the barriers with slenderness ratios of \(\frac{D}{W}\ge 1.0\), except for small values of \({\lambda }_{R}\) such as 2.0. By the way, more investigations are required to decide which one is more efficient.

Furthermore, by comparing Fig. 8a–d, it can be concluded that a specific cross-sectional area of the trench is more effective for lower values of Rayleigh wavelengths than the larger ones. The maximum system efficiency of a trench with \(A=10 \, {\mathrm{m}}^{2}\) is equal to 70% for \({\lambda }_{R}=2.0 \, \mathrm{m}\), and decreases to a value of about 50% for \({\lambda }_{R}=13 \, \mathrm{m}\).

4 Conclusions

A numerical finite-difference analysis was carried out using the FLAC program to investigate the behavior of open and in-filled geofoam (EPS) trenches when used as wave barriers to attenuate the ground-borne vibrations induced by impact loading. A novel approach was used in this study to investigate the trench performance with the same normalized dimensions and location obtained from several Rayleigh wavelengths (i.e., coupling effect of normalized dimensions and location of the trench together with Rayleigh wavelength). The conclusions obtained in the present research are as follows:

  1. 1.

    Trenches with equal normalized dimensions and locations with respect to the Rayleigh wavelength had not the same effectiveness for different values of Rayleigh wavelengths. Therefore, it is necessary to study both normalized lengths and Rayleigh wavelength together (coupling effect).

  2. 2.

    For open trenches, while the normalized depth \(\left(\frac{D}{{\lambda }_{R}}\right)\) was the key parameter controlling the trench efficiency, the normalized width \(\left(\frac{W}{{\lambda }_{R}}\right)\) had not a noticeable effect, except in shallow trench (normalized depth less than \(0.7\)) installed for the condition of a low wavelength such as \({\lambda }_{R}=2.0 \, \mathrm{m}\).

  3. 3.

    In in-filled geofoam trenches, the system effectiveness depended on both normalized depth and normalized width; however, the effect of normalized width was larger for the case of low values of wavelength such as \({\lambda }_{R}=2.0 \, \mathrm{m}\), and this effect decreased with an increase in \({\lambda }_{R}\). Also, the optimum value of the slenderness ratio was found to be equal to \(\frac{D}{W}=1.0\) for \({\lambda }_{R}=2.0 \, \mathrm{m}\) and \(4.0 \, \mathrm{m}\), and \(\frac{D}{W}=2.0\) in \({\lambda }_{R}=8.0 \, \mathrm{m}\) and \(13.0 \, \mathrm{m}\) irrespective of cross-sectional area.

  4. 4.

    For both open and geofoam trenches, the trench should be installed at a normalized distance equal to at least \(1\).