1 Introduction

In recent years, poor air quality has diverted the scientific community’s interests toward Electric Vehicles (EVs), which can potentially reduce fuel costs and overpower the current energy crisis. Electric motors play a crucial role among the various components of the Battery Electric Vehicles (BEV’s) architecture. Electric motors are expected to provide maintenance-free operation, high power density, wide-speed range, and high efficiency [1, 2]. Because of excellent reliability and low-cost traditional motors, the induction machine is still extensively acknowledged [3]. However, conventional control approaches in EVs cannot deliver the requisite performance. Conventional motors can also perform well with the current drive designs, but they are less viable with their inefficiencies in the lower speed ranges. The reason behind it is high losses and limited constant power range [4]. Nowadays, Permanent magnet motors are more competitive, especially permanent magnet brushless direct current (PMBLDC) motors that have a wide range of applications [5]. Fortunately, there have been many positive reviews on PMBLDC motors available in the literature, especially in the category of commutator-less machines. This motor has many features like simple structure, good mechanical characteristics, high efficiency, lightweight, low rotary inertia, high control precision and operates at low speed. However, demagnetization and cogging torque are some of the limitations of this motor [6,7,8,9].

Selection of materials, dimensions and design variations are essential parameters usually considered for motors. The first step for executing good design is to thoroughly understand the design process and make amendments as per the required applications. With the increasing use of high-power computing systems, the development of computational electromagnetics is also energized. Before performing things in the real world, these electromagnetic investigations of problems through computation will save time and money [10]. Numerical methods are used to solve the behavioural equations of electrical machines. The finite element method (FEM) numerical technique is one of the most reliable, flexible, and worthwhile for analyzing performance of electrical machines. Electromagnetic analysis of machines allows the determination of flux leakage distributions in a steady state at the areas of concern. As regards the magnetic vector potential, the magnetic field of electrical machines is analyzed using FEM, which allows for simple flux and flux density determination [11,12,13,14]. The reason is that complex geometries can easily be modelled and analyzed, which is impossible with other numerical techniques. Without significant knowledge of applied mathematics, this technique can be used to determine electromagnetic field distribution and critical parameters in the design of the rotating machine. Extensive research has been done on the design of motors using FEM [15,16,17].

From recent literature- The permanent magnet motor surface-mounted was designed by selecting an appropriate combination of pole arc coefficient, rotor pole, and stator slot with the help of FEM. Losses of the motor were determined based on electromagnetic torque [18]. The author mentioned a light electric vehicle drive system. The flux switching outer rotor type permanent magnet machine of 6 slots in the stator and 19 poles on the rotor with 188 W and 120 rpm combination was built for the application using a sizing equation and based on a finite element approach. The calculation of magnetic field distribution and machine parameters was done, and then performance was analyzed by the current vector strategy [19]. The authors illustrated motor design for application of three-wheeler. The results are obtained using a computer-aided finite element analysis tool to get the electromagnetic features of the motor [4]. In another study, the author proposed the design of BLDC, where pole arc coefficient and air gap length were optimized for medium-speed electric vehicles. Two-dimensional models were analyzed using Ansys Maxwell [20]. The author proposed the design of the motor and generator based on the three design variables. The thermal analysis was conducted, and fabrication of the structure was completed [21]. The author proposed some changes in the prior winding, which enhanced the performance of the motor depending on the material used and losses occurring in set up reduced considerably [22]. The Axial Flux type BLDC motor on Surface mounted type (AFSPMBLDC) motor was designed using a genetic algorithm. The aim of this analysis was to give the best possible combination of design variables acquired by employing the optimization technique genetic algorithm (GA), and the motor design depends on these optimized design factors. The validation at the end was carried out with 3D type finite element analysis (FEA) [23]. The author proposed the design for the motor for the micro-electric vehicle with the help of electromagnetic analysis [2]. The author proposed a BLDC motor design for light electric vehicles. This summarized that the proposed design type has the best result for the required application [24]. In another study, the author proposed a new method which includes superposition and subdomain methods to determine the cogging torque with rotor eccentricity of the permanent magnet motor. Using Maxwell stress tensor, cogging torque and effectiveness had been illustrated with FEA on 9slot/8pole and 12slot/10pole motor [25]. In this paper, author has emphasized only on wind power permanent synchronous generators with static and rotating eccentricity. In another paper [26], the authors proposed the design of a BLDC motor by applying the Artificial Neural Network and FEM method. The ratio of pole arc to pole pitch and values of offset were altered to achieve the required result of the motor. The authors in this paper have mainly concentrated their efforts on fast optimization of solutions based on Particle Swarm Optimization and Imperialist Competitive Algorithm. Still, they have not discussed the practical implications caused by dynamic conditions.

The present work deals with the parameter estimation of the PMBLDC motor with emphasis on reducing cogging torque and improving average torque of motor used in two-wheelers battery electric vehicles. The matching material and pole-slot combination are selected for the motor, which yields low cogging torque. PMBLDC model has been simulated considering the distinct values of the pole embrace factor design variable using a computational electromagnetic tool, i.e., Ansys Maxwell. Further, the paper’s focus is to carry out the improvements in design by performing parametric analysis. The final model offers a reduction in torque ripple with improved average torque. Because of the finite element adaptive approach, the design variable gets updated if changes are observed in computed and reference parameters of the motor. In the later part of the manuscript, simulation results and comparisons between the base design [24] and the proposed motor design have been discussed.

2 Parameter Matching of BEV

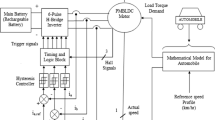
The dynamic equations are taken to match the performance of the BEV with the PMBLDC motor. The EV characteristics can be used to calculate the vehicle’s driving resistive forces along with the help of initial assumed parameters. Based on dynamic vehicle equations, the torque and power requirements have been derived for the specific driving condition [27, 28]. The forces acting on the vehicle are shown in the schematic presentation Fig. 1.

Fig. 1
figure 1

Representation of forces acting on a vehicle

Full size image

2.1 Kinematic Dynamic Equations

Equations regarding different kinds of forces acting on the vehicle and tractive power and torque have been briefly discussed.

2.1.1 Aerodynamic Drag Force

The aerodynamic drag force (Fa) in (1) is because of the friction of the vehicle moving through the air. The drag coefficient is Cd, the vehicle’s velocity is v, and rho (δ) is the air density at sea level. This force is directly square to a vehicle’s velocity, frontal area, and body shape.

$${\text{F}}_{\mathrm{a}}= \frac{1}{2}{\updelta }\quad \text{A} \quad{\text{C}}_{\mathrm{d}}{\text{v}}^{2}$$
(1)

2.1.2 Rolling Resistance Force

The rolling resistance force (Frr) in (2) depends on the tire’s selection. The rolling resistance coefficient is urr, the gravitational force is g, and the gradient angle is Ɵ. This force is directly proportional to the coefficient of rolling coefficient.

$${\text{F}}_{\mathrm{r}\text{r}}=\text{m} \text{g}\; {{\mu }}_{\mathrm{r}\text{r}} \;\text{C}\text{o}\text{s}\theta$$
(2)

2.1.3 Climbing Force

The climbing force (Fc) in (3) is needed to propel the vehicle up a slope where the vehicle’s gross weight is m.

$${\text{F}}_{\mathrm{c}}=\text{m} \text{g}\; \text{S}\text{i}\text{n}\theta$$
(3)

2.1.4 Total Tractive Force

The total tractive force (Ftrac) in (4) combines all the resistive forces needed to overcome the friction.

$$\text F_\text{trac}=\text F_\text a+\text F_\text {rr}+\text F_\text c$$
(4)

2.1.5 Tractive Power

The tractive power in (5) can be calculated and represented as (Ptrac)

$${\text{P}}_{\mathrm{t}\text{r}\text{a}\text{c}}={\text{F}}_{\mathrm{t}\text{r}\text{a}\text{c}} \text{v}$$
(5)

2.1.6 Tractive Torque

The force in (6) calculates the tractive torque (Ttrac) on the vehicle wheel. Here rwheel is the radius of the vehicle wheel.

$${\text{T}}_{\mathrm{t}\text{r}\text{a}\text{c}}={\text{F}}_{\mathrm{t}\text{r}\text{a}\text{c}}\text{*}{\text{r}}_{\mathrm{w}\text{h}\text{e}\text{e}\text{l}}$$
(6)

The reference vehicle taken is a two-wheeler having values of the parameters like gross weight, air drag coefficient and rolling coefficient, etc., as shown in Table 1.

Table 1 Specifications of Initially selected parameters for BEV
Full size table

The Indian driving cycle (IDC) selected for this vehicle is shown in Fig. 2.

Fig. 2
figure 2

Graphical representation of two-wheeler-IDC

Full size image

3 Mathematical Modelling of PMBLDC Motor

The sizing for electrical machine design is given by (7).

$$\text{S}=11. {\text{k}}_{\mathrm{w}1}.\text{B}.\text{a}\text{c}.\left({\frac{\text{D}}{100}}^{2}\right).\frac{\text{L}}{1000}.\text{n}$$
(7)

where S is motor apparent power in VA, kw1 is winding factor, B is magnetic specific loading, electrical specific loading is ac, L is stack length, D is stator diameter, n is rated speed of the motor. The modelling of the PMBLDC motor is proposed keeping in view that undesirable cogging torque that leads to inefficient operation. In the PMBLDC motor, the cogging torque affects average torque and generates unwanted torque ripple. The cogging torque as stated in (8) must be lowered to reduce noise and vibration [29, 30].

$${\text{T}}_{\mathrm{cog}} = \frac{{1}}{{2}}{\theta}_{\mathrm{g}}^{{2}}\frac{\text{dR}}{\text{d}\theta}$$
(8)

where air gap flux is \({\theta}_{\mathrm{g}}\) and change in air gap reluctance (as a rotor angle depends) is \(\frac{\text{dR}}{\text{d}\theta}\). The cogging torque will be reduced by reducing \(\frac{\text{dR}}{\text{d}\theta}\) as they are directly proportional to each other. The calculation of the cogging torque is based on changing one mechanical degree of angular rotation. It’s worth noting that most cogging torque-reduction solutions also diminish the effective back electro-motive force (emf), resulting in the generation of mutual torque. The voltage equation of three-phase a, b and c of PMBLDC motor equivalent circuit in matrix form is shown in (9).

$$\left\{ {\begin{array}{*{20}c} {{\text{V}}_{{\text{a}}} = \;{\text{i}}_{{\text{a}}} {\text{R}} + {\text{L}}\frac{{{\text{di}}_{{\text{a}}} {\text{(t)}}}}{{{\text{dt}}}} + {\text{e}}_{{\text{a}}} } \\ {{\text{V}}_{{\text{b}}} = \;{\text{i}}_{{\text{b}}} {\text{R}} + {\text{L}}\frac{{{\text{di}}_{{\text{b}}} {\text{(t)}}}}{{{\text{dt}}}} + {\text{e}}_{{\text{b}}} } \\ {{\text{V}}_{{\text{c}}} {\text{ = }}\;{\text{i}}_{{\text{c}}} {\text{R}} + {\text{L}}\frac{{{\text{di}}_{{\text{c}}} {\text{(t)}}}}{{{\text{dt}}}} + {\text{e}}_{{\text{c}}} } \\ \end{array} } \right.$$
(9)

In compact form the equation can be expressed in (10) where \(\widehat{V}\) is the phase voltage, \(\widehat{I}\) is phase current and \(\varDelta \widehat{I}\) is the change in phase current with respect to time.

$$\widehat{\text{V}}=\text{f} \left[\widehat{\text{I}}, \varDelta \widehat{\text{I}}\right]$$
(10)

The back-EMF values are affected by the number of rotations, rotor speed, and magnetic field intensity. There is a phase difference of 120° between each phase of the three-phase system. If the back-EMF constant is λ, then the back-EMF for each phase’s value is described as in (11).

$$\begin{aligned} e_{a} & = \quad \omega \lambda (\theta ) \\ e_{b} & = \omega \lambda \left( {\theta - \frac{{2\pi }}{3}} \right) \\ e_{c} & = \omega \lambda \left( {\theta + \frac{{2\pi }}{3}} \right) \\ \end{aligned}$$
(11)

Accordingly, back-EMF and phase current multiplication, considering all losses, is the instantaneous power supplied. The motor’s input and output power can be expressed as in (12) and (13).

$${\text{P}}_{\mathrm{i}} = {\text{i}}_{\mathrm{a }}{\text{e}}_{\mathrm{b}} + {\text{i}}_{\mathrm{b}}{\text{e}}_{\mathrm{b}} + {\text{i}}_{\mathrm{c}}{\text{e}}_{\mathrm{c}}$$
(12)
$${\text{P}}_{\mathrm{o}}={\text{ P}}_{\mathrm{i}}- ({\text{P}}_{\mathrm{fw}} + {\text{P}}_{\mathrm{cua}} + {\text{P}}_{\mathrm{t}}\text{+}{\text{ P}}_{\mathrm{fe}}\text{)}$$
(13)

where \({\text{P}}_{\mathrm{i}}\) is the input power, Pfe, Pt, Pcua, and Pfw are losses like iron, transistor/diode, stator copper, windage, and frictional losses respectively. The efficiency expression is stated in (14) and is computed by factoring output and input power along with losses.

$$\eta = \frac{{{\text{P}}_{{\text{o}}} }}{{{\text{P}}_{{\text{o}}} {\text{ + P}}_{{{\text{fw}}}} {\text{ + P}}_{{{\text{cua}}}} {\text{ + P}}_{{\text{t}}} {\text{ + P}}_{{{\text{fe}}}} }}$$
(14)

Stray losses are approximately 1% of the Mechanical Power [31] and therefore these have not been considered in calculations.

The torque \(\tau\) is obtained as shown in (15) is the ratio of power to the angular speed. The torque at any instant of rotor T(θ)is the arithmetic sum of average torque, and torque ripple is represented in (16). The motor’s average torque and torque ripple can be stated as in (17) and (18).

$$\tau {\text{ = P}}_{{\text{o}}} /\omega$$
(15)
$$\text{T}\left({\uptheta }\right)={\text{T}}_{\mathrm{a}\text{v}\text{g}}+ {\text{T}}_{\mathrm{r}\text{i}\text{p}\text{p}\text{l}\text{e}}$$
(16)
$${\text{T}}_{\mathrm{a}\text{v}\text{g}}=\frac{1}{{{\uptheta }}_{1}^{{\prime }}- {{\uptheta }}_{1}}\underset{{{\uptheta }}_{1}}{\overset{{{\uptheta }}_{1}^{{\prime }}}{\int }}\text{T}\left({\uptheta }\right)$$
(17)
$${\text{T}}_{\mathrm{r}\text{i}\text{p}\text{p}\text{l}\text{e}}= \frac{{\text{T}}_{\mathrm{m}\text{a}\text{x}}- {\text{T}}_{\mathrm{m}\text{i}\text{n}}}{{\text{T}}_{\mathrm{a}\text{v}\text{g}}}$$
(18)

where ω represents mechanical rotation/speed in rad/s, (\({{\uptheta }}_{1}^{{\prime }}\) −θ1) represents the complete electrical cycle of the PMBLDC motor. The cogging torque can be minimized by selecting the best value of the rotor pole embrace factor. The pole embrace factor is the ratio of rotor pole pitch (β) pole arc (γ) in a permanent magnet motor, as shown in Fig. 3. Generally, its value is less than unity [32].

Fig. 3
figure 3

Rotor pole embrace factor diagram

Full size image

4 Design of PMBLDC Motor

A designer can reduce demagnetizing effect and cogging torque with the appropriate selection of permanent magnet materials. Cogging torque generates noise, causes backlash in bearings, and disturbs rotor eccentricity. Table 2 lists the parameters of the permanent magnet materials [33]. Among three materials, the rare earth materials Neodymium Iron and Boron (NdFeB) rare earth magnet material are very high in demand because of greater magnetic field density, better magnetic field residual density and due to low curie temperature. Samarium Cobalt (SmCo) is the second-strongest magnet material after NdFeB but is the most expensive. Low-cost ceramic magnet materials are easily available and have very low magnetic field density due to poor retentivity. Mostly NdFeB and SmCo are being used for the motors used in EV’s. Alnicos have low coercive forces, which get demagnetized easily. Rare-earth permanent magnet materials have opened up new PMBLDC motor design and application options. The selection of magnet materials is purely based on the type of application [33,34,35]. Airgap length affects the motor performance and hence in addition to mechanical and thermal concerns, choosing the optimum airgap length depends on the objectives of the design and type of applications. In case of EV the increase in air gap length decreases the torque ripple content, while the increased thickness of the magnet helps to avoid demagnetization [21].

Table 2 Properties of Permanent magnet material
Full size table

The magnitude and frequency of the cogging torque also affect the selection of pole/slot combination. Motors with slot/pole/phase ratio value 1 or higher are integral-slot motors. In fractional-slot motors, as the slot/pole ratio decreases, the magnitude of cogging torque and frequency increases. In other terms, fractional slot motors have reduced cogging torque compared to integral slot motors. As a result, the amplitude of cogging torque reduces and to ensure mechanical utility, a 24/18 (slots/pole) combination is selected for the design having slots/pole/phase ratio less than 0.5 [24].

Fig. 4
figure 4

Flow chart of adaptive finite element process on motor

Full size image

The design procedure of the BLDC motor is shown in Fig. 4. The outer rotor PMBLDC motor has been designed using ANSYS Maxwell software. Figure 4 depicts the implementation of the adaptive finite element process on the PMBLDC motor. Rmxprt tool of Ansys Maxwell has been used as the designing platform. As per the Indian Driving Cycle (IDC) the motor specifications are selected to propel the cargo weight of EV and overcome the resistive forces. There are three stages of the finite element process in the flow chart. The mesh definition comes under the pre-processing stage of finite element procedure. The motor region under consideration is discretized using different kinds of finite elements, which in our case are the first order triangular elements. Parametric analysis comes under the processing stage of the finite element procedure, whereas different kinds of refinement strategies come under the post-processing stage. Error analysis to get the optimum design of the motor is also a part of the post-processing stage. In this paper h-adaptivity refinement strategy has been used and preferred over the p-type and hp type refinement strategies. The dimensional parameters of the motor once fixed are not altered, however the changes as per the feedback received from the post-processing stage are incorporated under “Define and Set variable” block to make the adaptive process. Optimum selection of rotor embrace factor and airgap length reduces the cogging torque. Dimensional specification of the PMBLDC motor is tabulated in Table 3 [24]. The 24/18 slot/pole combination of this reference paper has been selected over the other slot/pole combinations because less number of slots and poles make motor structure compact and cost-effective. Same slot/pole combination has been considered for the design and analysis of the motor in the present work. For designing a motor, the rotor pole embrace factor is selected as the variable.

Table 3 Dimensional specifications of PMBLDC motor
Full size table

The material used for the winding is copper while silicone steel material M27_26G is used for the stator and rotor core. The BH curve of the material is shown in the Fig. 5, B is the magnetic field density in tesla and H is magnetic field intensity in A_per_meter.

Fig. 5
figure 5

BH curve of M27_26G silicone steel

Full size image

5 Parameter Optimization

The cogging torque of the motor must be decreased for a smooth operation. The motor performance can be analyzed from a variety of perspectives. Efficiency is one of the most important characteristics of PMBLDC motor design. This motor is designed for the two-wheeler BEV at a constant power region of 3.5 kW. The variable rotor pole embrace factor has a considerable influence on the cogging torque and efficiency of the motor. The parametric approach is applied to guide the selection of the pole embrace factor in the design. In the parametric process of optimizing the rotor pole embrace factor values, region of interest must be considered, where efficiency is maximum and cogging torque is minimum. It is not necessary to achieve highest value of efficiency and lowest value of cogging torque at same value of variable. Sometimes the value between different regions needs to be selected. To achieve the optimum values of performance keeping in consideration the size of the motor, the pole embrace factor referred as ‘p’ is varied from 0.4 to 0.6, considering it as a lower limit and upper limit having 0.02 step size. The cogging torque, rated torque and efficiency with the change in the rotor pole embrace factor value are obtained by parametric scanning as shown in Figs. 6 and 7 respectively. At value 0.5, the cogging torque is least, and its value is 0.0353% of rated torque. Cogging torque is highest at 0.4 and its value is 28.27% of rated torque and at 0.52 its value is 6.1% of rated torque. The graph depicts that cogging torque is lowest at point 0.5 and at the same point efficiency of the motor is approx. 92.1%. The graphical representation also shows the lowest and intermediate values of the cogging torque and efficiency. The efficiency is highest i.e., 92.37% at pole embrace factor of 0.4 and is lowest i.e., 91.81% at value of 0.6.

Fig. 6
figure 6

Graphical representation of cogging torque and rated torque with reference to rotor pole embrace factor

Full size image
Fig. 7
figure 7

Graphical representation of efficiency with reference to rotor pole embrace factor

Full size image

The cogging torque variation in respect to the position of rotor is shown in Fig. 8. As shown in the graph the smaller value of cogging torque is 0.005 Nm at point 0.5 and the highest value of cogging torque is 3.967 Nm at point 0.4. The smaller value of cogging torque indicates less speed fluctuations, and better running stability.

Fig. 8
figure 8

Variation of cogging torque versus rotor angle in degree

Full size image

The comparison of performance parameters for various values of embrace factor is shown in Table 4. For the propulsion of an electric vehicle at low speed, initially high rated torque is required with enough air gap density. As evident in Table 4 the value of airgap flux density is highest at 0.4 value of embrace factor with less loss. But at some point, the effect of cogging torque is high. Besides, the lowest value occurred at 0.6 embrace factor with maximum losses. With less value of cogging torque and compromising the efficiency of the motor, the optimum intermediate value selected is 0.5 for air gap flux density and average value current. At this value the change in air gap density does not lead to extreme change in winding average current value. Permanent magnet may get demagnetized with abrupt and extreme variations of current and therefore due attention must be given on this parameter. No significant changes in average input current have been noticed while varying the pole embrace factor from 0.4 to 0.6. Most optimum values have been observed at pole embrace factor of 0.5, keeping in view the requirements of battery electric vehicles.

Table 4 Comparison of performance of the PMBLDC motor at various pole embrace factor
Full size table

The air gap flux density, average current and rated torque is determined parametrically with change in the embrace factor illustrated in Fig. 9.

Fig. 9
figure 9

Graphical representation of air gap flux density, average current and rated torque with rotor pole embrace factor

Full size image

6 Finite Element Based Magnetic Field Analysis of PMBLDC Motor

After electrical analysis, the FEM motor model is created using ANSYS Maxwell using the periodic boundary condition of the motor’s inner magnetic field distribution. The FEM model of motor is designed for optimum embrace value of 0.5. A discrete time simulation has been tuned for a time step of 2 ms and a range of 0 to 60 ms. This is subjected to transient analysis at rated load and rated speed. It generates the distribution profile of magnetic field at particular instant of time and rotor position. The structure design of the motor is shown in Fig. 10 and the mesh plot for full fraction model of the design is shown in Fig. 11.

Fig. 10
figure 10

Structure diagram of the motor

Full size image
Fig. 11
figure 11

Mesh refinement of the motor

Full size image

  • The distribution of magnetic field density of the motor is shown in Fig. 12 and the magnetic forces acting on the surfaces/edges of the motor is shown in Fig. 13. This elucidates that no saturation occurs in the motor and the maximum density of the magnetic flux exists in the stator tooth tip.

Fig. 12
figure 12

Magnetic flux density distribution of motor

Full size image
Fig. 13
figure 13

Vector Potential of the motor

Full size image

For the optimum design the graph for electromagnetic torque is shown in Fig. 14. The maximum peak value is 57.87 Nm, minimum is 5.06 Nm whereas the average torque value is 50.16 Nm. The value of the ripple torque is 1.25 Nm. The ripple content of the motor at this value is less in comparison to other values which enhance the life span of the motor with less requirement of maintenance. The efficiency of the motor has improved by 1.05%, compared to earlier reported design [24].

Fig. 14
figure 14

Plot showing variation torque and time at specific speed

Full size image

The variations in pole embrace factors of rotor led to the variation in unaligned position air gaps and thus providing more flux linkage at aligned position. The phase winding flux linkage and current for rated speed with time is shown in Figs. 15 and 16.

Fig. 15
figure 15

Winding flux linkage at rated speed

Full size image
Fig. 16
figure 16

Winding current for rated speed

Full size image

7 Conclusion

The present work in this paper represents the influence of rotor pole embrace factor on the performance of the motor for battery electric vehicle applications. With the help of a kinematic equation, the parameter matching with the PMBLDC motor has been deduced. Parametric analysis with optimetrics has been applied to accomplish the selection of suitable embrace factors with minimum ripples and maximum efficiency. Finite element based electromagnetic field analysis is performed based on the optimal value of pole embrace factor. The smaller improvement of efficiency has a good impact on the state of health of the battery, which is powering the vehicle. The reduction in cogging torque in the proposed design of the motor has a significant role to ensure the smooth drive and overall performance of the electric vehicles. The electromagnetic torque generated by the motor is enough to propel the vehicle. Consequently, a reduction in torque ripple reduces acoustic noise and vibrations of the motor and, in turn, lowers the motor’s eccentricity disbalancing issue, thereby extending the life span of battery electric vehicles.