Deep learning for quadratic hedging in incomplete jump market

Abstract

We propose a deep learning approach to study the minimal variance pricing and hedging problem in an incomplete jump diffusion market. It is based on a rigorous stochastic calculus derivation of the optimal hedging portfolio, optimal option price, and the corresponding equivalent martingale measure through the means of the Stackelberg game approach. A deep learning algorithm based on the combination of the feed-forward and LSTM neural networks is tested on three different market models, two of which are incomplete. In contrast, the complete market Black–Scholes model serves as a benchmark for the algorithm’s performance. The results that indicate the algorithm’s good performance are presented and discussed. In particular, we apply our results to the special incomplete market model studied by Merton and give a detailed comparison between our results based on the minimal variance principle and the results obtained by Merton based on a different pricing principle. Using deep learning, we find that the minimal variance principle leads to typically higher option prices than those deduced from the Merton principle. On the other hand, the minimal variance principle leads to lower losses than the Merton principle.

1 Introduction

Many jump diffusion models have been extensively studied in the past. Of particular interest to us is the Merton model proposed by Merton (1976), where the jump distribution is log-normal. Merton derived a closed-form solution to the hedging problem for the European option, assuming diversifiabilty of the jump component. There are also other popular jump diffusion models. Kou (2002) proposed an alternative approach where double exponential jump distribution is assumed. The variance gamma model proposed in Madan and Seneta (1990) also supports the inclusion of jumps.

Regarding the use of machine learning in stochastic control theory, there have been a lot of new developments in the past few years. With new techniques, it has now become possible to solve problems that do not obtain closed-form solutions numerically. In Han et al. (2016), a deep learning approach for solving stochastic control problems was proposed. The idea is that one discretizes time and, at each timestep, approximates the control with a feed-forward neural network. In the papers Buehler et al. (2019) and Carbonneau and Godin (2021), the authors extend these results to reinforcement learning algorithms for hedging in high dimensions. Methods proposed in Han et al. (2016) also provide a strong tool for finding the numerical solutions to high-dimensional partial differential equations. In a seminal paper (Han et al., 2018) and later on in Beck et al. (2019) and Chan-Wai-Nam et al. (2019), the authors transform PDEs to backward stochastic differential equations and use deep learning to solve the associated stochastic control problem.

Since control problems related to hedging rely heavily on time series dynamics, it is convenient to consider recurrent neural networks (RNN) instead of feed-forward ones. These types of networks were proposed in Rumelhart et al. (1986). The recurring nature of the network can contain cycles, which makes them suitable for problems that have sequential inputs. A particular case of RNN called long short-term memory (LSTM) was first introduced in Hochreiter and Schmidhuber (1997) and became very prominent in the last few years for time series modeling. The main advantage over RNN is LSTM’s ability to provide a memory structure that can store information over a large number of timesteps. It has been heavily used in financial time series prediction; for instance, see Cao et al. (2019), Selvin et al. (2017), Siami-Namini et al. (2018). One of the main advantages of LSTM networks is that they can also be used for non-Markovian models. In particular, Han et al. used them in (2021) to apply the methods proposed in Han et al. (2016) to stochastic control problems with delay. Deep learning for mean-field stochastic control has been studied by Agram et al. (2020) where the initial state was a part of the control process and then extended to mean-field systems with delay in Agram et al. (2022). Lai et al. (2022) also used LSTM networks to develop a data-driven approach for options market making.

Since our main concern is hedging in an incomplete market, we also refer to Fecamp et al. (2020), where Fecamp et al. present several deep learning algorithms for discrete-time hedging, where the sources of incompleteness are illiquidity, non-tradable risk factors, and transaction costs. They propose a modified global LSTM approach where a single LSTM net is used that takes the whole time series as an input. The above approach was adopted in Gao et al. (2021), where they study the double exponential jump distribution model proposed in Kou (2002).

Furthermore, we do not consider the calibration of SDEs to fit market data in this paper. For promising approaches, one can check (Boursin et al., 2022; Remlinger et al., 2022) where generative adversarial networks are used. Another approach could feature neural SDEs. A good survey is Kidger et al. (2021).

In what follows, let us describe our purpose in the present paper.

We consider a financial market where the underlying price of a risky asset follows a jump diffusion process:

$$\begin{aligned} {\text {d}}S(t)&=S(t^{-})\left[ \alpha (t){\text {d}}t+\sigma (t){\text {d}}B(t)+\int _{ \mathbb {R^*} }\gamma (t,\zeta )\widetilde{N}({\text {d}}t,{\text {d}}\zeta )\right] ,\quad S(0) >0, \end{aligned}$$

(1.1)

with $\mathbb {R}^{*}=\mathbb {R}{\setminus } \{0\}$, and $S_{0}(t)=1$ for all t denotes the value of a risk-free money market account.

Suppose now that the interest rate in the risk-free asset equals 0 and the time to maturity is finite and denoted by T.

For simplicity of notation, we will write S(t) instead of $S(t^{-})$ in the following.

Here, $\alpha (t) \in \mathbb {R}, \sigma (t)=(\sigma _1(t),\ldots , \sigma _m(t)) \in \mathbb {R}^{m},$ $\gamma (t,\zeta )=(\gamma _1(t,\zeta ),\ldots , \gamma _k(t,\zeta )) \in \mathbb {R}^{k}$, and $B(t)=(B_1(t),\ldots , B_m(t))^{'} \in \mathbb {R}^{m}$ and $\widetilde{N}(\textrm{d}t,\textrm{d}\zeta )=(\widetilde{N}_1(\textrm{d}t,\textrm{d}\zeta ),\ldots , \widetilde{N}_k(\textrm{d}t,\textrm{d}\zeta ))^{'} \in \mathbb {R}^{k}$ are independent Brownian motions and compensated Poisson random measures, respectively, defined on a complete filtered probability space $(\Omega ,\mathcal {F},\mathbb {F}=\{\mathcal {F}_t\}_{t\ge 0},P)$, where $\mathbb {F}=\{\mathcal {F}_{t}\}_{t\ge 0}$ is the filtration generated by $\{B(s)\}_{s\le t}$ and $\{N(s,\zeta )\}_{s\le t}$. We are using the matrix notation, that is

$$\begin{aligned} \sigma (t)\textrm{d}B(t)&:=\sum _{i=1}^{m} \sigma _i(t)\textrm{d}B_i(t), \qquad\gamma (t,\zeta )\widetilde{N}(\textrm{d}t,\textrm{d}\zeta )= \sum _{j=1}^{k}\gamma _j(t,\zeta )\widetilde{N}_j(\textrm{d}t,\textrm{d}\zeta ), \end{aligned}$$

and we assume that

$$\begin{aligned} \gamma (t,\zeta )>-1 \quad \text { and } \quad \sigma ^2(t) +\int _{ \mathbb {R^*} } \gamma ^2(t,\zeta ) \nu (\textrm{d}\zeta ) > 0, \quad \text { for a.a. } t, \text { a.s.} \end{aligned}$$

(1.2)

The coefficients $\alpha ,\sigma$ and $\gamma$ are supposed to be deterministic and bounded.

The results in this paper can easily be extended to an arbitrary number of risky assets, but since the features of incomplete markets we are dealing with, can be fully illustrated by one jump diffusion risky asset only, we will for simplicity concentrate on this case in the following. We emphasize, however, that we deal with an arbitrary number m of independent Brownian motions and an arbitrary number k of independent Poisson random measures in the representation (1.1).

Let $z\in \mathbb {R}$ be an initial endowment and let $\pi (t)\in \mathbb {R}$ be a self-financing portfolio, representing the fraction of the total wealth $X(t)=X_{z,\pi }(t)$ invested in the risky asset at time t. We say that $\pi$ is admissible if in addition $\pi$ is a predictable process in $L^{2}(\textrm{d}t \times dP)$. The set of admissible portfolios is denoted by $\mathcal {A}$. We associate to an admissible portfolio $\pi$ the wealth dynamics

$$\begin{aligned} \textrm{d}X(t) =X(t)\pi (t)\left[ \alpha (t)\textrm{d}t+\sigma (t)\textrm{d}B(t)+\int _{ \mathbb {R^*} }\gamma (t,\zeta )\widetilde{N}(\textrm{d}t,\textrm{d}\zeta )\right] , \quad X(0) =z. \end{aligned}$$

(1.3)

Here and in the following, we write for notational simplicity X(t) instead of $X(t^{-})$, in agreement with our convention for S(t).

Fix T be the time to maturity and let F be a given T-claim, i.e., $F \in L^2(P)$ is an $\mathcal {F}_{T}$-measurable random variable, representing the payoff at that time. Then, for each initial wealth $z\in \mathbb {R}$ and each portfolio $\pi \in \mathcal {A}$, we want to minimize the expected squared hedging error

$$\begin{aligned} J(z,\pi )=E\left[ \frac{1}{2}\left( X_{z,\pi }(T)-F\right) ^{2}\right] . \end{aligned}$$

Then, the problem we consider is the following.

Problem 1.1

Find the optimal initial endowment $\widehat{z}\in \mathbb {R}$ and the optimal portfolio $\widehat{\pi }\in \mathcal {A}$, such that

$$\begin{aligned} \underset{z,\pi }{\inf }J(z,\pi )=J(\widehat{z},\widehat{\pi }). \end{aligned}$$

Heuristically, this means that we define the price of the option with payoff F to be the initial endowment $\widehat{z}$ needed to get the terminal wealth X(T) as close as possible to F in quadratic mean by an admissible portfolio $\widehat{\pi }$.

We may regard the minimal variance problem (Problem 1.1) as a Stackelberg game, in which the first player chooses the initial endowment z, followed by the second player choosing the optimal portfolio $\pi$ based on this initial endowment. Knowing this response $\pi =\pi _{z}$ from the follower, the first player chooses the initial endowment $\widehat{z}$ which leads to a response $\pi =\pi _{\widehat{z}}$ which is optimal, in the sense that $J(\widehat{z},\pi _{\widehat{z}}) \le J(z,\pi )$ over all admissible pairs $(z,\pi )$.

For a general (discontinuous) semimartingale market, this is already a known result; we refer, for example, to Černý and Kallsen (2007) where the authors have proved that the optimal quadratic hedging strategy $\widehat{\pi }$ can first be characterized in a linear feedback form which is independent of the initial endowment z, and that $\widehat{z}$ can then be identified in a second step. Therefore, the results of Sect. 2 of the current paper might be derived from already existing results in the literature (Černý & Kallsen, 2007), but we found it convenient for the reader to find explicit expressions of the optimal quadratic hedging problem for a jump diffusion market (Lévy process).

Schweizer (1996) proves (under some conditions, including a non-arbitrage condition) that there exists a signed measure $\tilde{P}$, called the variance-optimal measure, such that

$$\begin{aligned} \widehat{z}= E_{\tilde{P}}[F]. \end{aligned}$$

(1.4)

We consider in the present paper a jump diffusion market and we show that $\tilde{P}$ is a positive measure and we find it explicitly.

In the next section, we prove the existence of the optimal hedging strategy and the optimal initial endowment for jump diffusion market.

We show that the minimal variance price can be represented as the expected value of the option’s (discounted) payoff under some equivalent martingale measures (which is given explicitly). The analysis concludes with looking at specific examples of jump diffusion market models.

Section 3 is devoted to the deep learning approach. Since the option price and the optimal hedging portfolio can not always be computed explicitly, or it is not feasible, we need to use some other numerical methods. We propose a deep learning algorithm that approximates option price and hedging portfolio. We propose a joint feed-forward and multilayered LSTM network that adopts the "online" approximation approach proposed in Han et al. (2016), where a neural network is used at each timestep to predict the control process.

First, we test this algorithm in the case of a complete market, namely in the case of the Black–Scholes (BS) model. This is done to estimate its performance, since both option price and hedging portfolio can be obtained explicitly in the BS case.

Then, we apply it to models that assume an incomplete market. First, a continuous model where the underlying asset depends on multiple independent Brownian motions is used to study the algorithm’s scalability to multi-dimensional inputs. The same is then also done for the jump diffusion Merton model.

We show the algorithm’s success in all three models and discuss its performance. Since Merton’s reasoning behind his hedging strategy is not consistent with the behavior of financial markets, we also compare our results to those obtained by Merton and discuss how the approaches differ. In particular, we show how the minimal variance approach provides a safer hedging strategy compared to the one proposed by Merton. Finally, the algorithm’s performance is also tested for another jump diffusion model, namely the Kou model.

2 Optimal quadratic hedging portfolio/optimal initial endowment

In this section, we find the optimal strategy pair to Problem 1.1.

2.1 Equivalent martingale measures (EMMs)

Since EMMs play a crucial role in our discussion, we start this section by recalling that an important group of measures $Q\in \mathbb {M}$ can be described as follows (we refer to Chapter 1 in Øksendal and Sulem (2007) for more details):

Let $\theta _{0}(t)$ and $\theta _{1}(t,\zeta )>-1$ be $\mathbb {F}$-predictable processes, such that

$$\begin{aligned} \alpha (t)+\theta _{0}(t)\sigma (t)+\int _{ \mathbb {R^*} }\theta _{1}(t,\zeta )\gamma (t,\zeta )\nu (\textrm{d}\zeta )=0\text {, } \quad t\ge 0. \end{aligned}$$

(2.1)

Define the local martingale $Z(t)=Z^{\theta _{0},\theta _{1}}(t)$, by

$$\begin{aligned} \textrm{d}Z(t) =Z(t)\left[ \theta _{0}(t)\textrm{d}B(t)+\int _{\mathbb {R^*} }\theta _{1}(t,\zeta )\widetilde{N}(\textrm{d}t,\textrm{d}\zeta )\right] , \quad Z(0) =1, \end{aligned}$$

that is

$$\begin{aligned} Z(t)&=\exp \left( \int _{0}^{t}\theta _{0}(s)\textrm{d}B(s)-\frac{1}{2}\int _{0} ^{t}\theta _{0}^{2}(s)\textrm{d}s\right. +\int _{0}^{t}\int _{\mathbb {R^*} }\left\{ \ln (1+\theta _{1}(s,\zeta ))-\theta _{1}(s,\zeta )\right\} \nu (\textrm{d}\zeta )\textrm{d}s\nonumber \\&\quad \left. +\int _{0}^{t}\int _{\mathbb {R^*} }\ln (1+\theta _{1}(s,\zeta ))\widetilde{N}(\textrm{d}s,\textrm{d}\zeta \textrm{d}\zeta )\right) . \end{aligned}$$

A sufficient condition for $Z(\cdot )$ being a true martingale is

$$\begin{aligned} E\Bigg [\exp \Bigg (\frac{1}{2}\int _0^T \theta _0^2(s)\textrm{d}s + \int _0^T\int _{\mathbb {R^*}}\theta _1^2(s,\zeta ) N(\textrm{d}s,\textrm{d}\zeta )\Bigg )\Bigg ] < \infty . \end{aligned}$$

(2.2)

For proof, see Kallsen and Shiryaev (2002). Then, the measure $Q^{\theta _{0},\theta _{1}}$ defined by

$$\begin{aligned} \textrm{d}Q^{\theta _{0},\theta _{1}}(\omega )=Z(T)dP(\omega )\text { on }\mathcal {F}_{T} \end{aligned}$$

is in $\mathbb {M}$.

2.2 The optimal portfolio

Assume as before that the wealth process $X(t)=X_{z, \pi }(t)$, corresponding to an initial wealth z and a self-financing portfolio $\pi$, is given by

$$\begin{aligned} \textrm{d}X(t)=X(t)\pi (t)\Bigg [\alpha (t) \textrm{d}t + \sigma (t) \textrm{d}B(t) + \int _{ \mathbb {R^*} }\gamma (t,\zeta )\widetilde{N}(\textrm{d}t,\textrm{d}\zeta )\Bigg ],\quad X(0)=z. \end{aligned}$$

Let F be a given T-claim representing the terminal payoff of the option. By the Itô/martingale representation theorem for jump diffusions (see Løkka (2004)), we can write $F=F(T)$, where the martingale $F(t):=E[F|\mathcal {F}_t],$ $t \in [0,T]$ has the Itô–Lévy representation

$$\begin{aligned} \textrm{d}F(t)=\beta (t)\textrm{d}B(t) + \int _{ \mathbb {R^*} } \kappa (t,\zeta ) \widetilde{N}(\textrm{d}t,\textrm{d}\zeta ), \quad E[F]= F(0), \end{aligned}$$

for unique $\mathbb {F}$-predictable processes $\beta (t) \in L^2(\lambda _0 \times P), \kappa (t,\zeta ) \in L^2(\lambda _0 \times \nu \times P)$, where $\lambda _0$ denotes Lebesgue measure.

Note that $\beta$ and $\kappa$ depend linearly on F (they can be given in terms of Malliavin derivatives of F).

Then, by the Itô formula for jump diffusions (see, e.g., Theorem 1.14 in Øksendal and Sulem (2007)), we get

$$\begin{aligned} \textrm{d}(X(t)F(t))&= X(t) \textrm{d}F(t) + F(t) \textrm{d}X(t) + \textrm{d}[X,F]_t \nonumber \\&= X(t)\Big [\beta (t)\textrm{d}B(t) + \int _{ \mathbb {R^*} } \kappa (t,\zeta )\widetilde{N}(\textrm{d}t,\textrm{d}\zeta )\Big ]\nonumber \\&\quad +X(t)F(t)\Big [\pi (t)\alpha (t) \textrm{d}t + \pi (t) \sigma (t) \textrm{d}B(t) + \int _{ \mathbb {R^*} } \pi (t)\gamma (t,\zeta )\widetilde{N}(\textrm{d}t,\textrm{d}\zeta )\Big ]\nonumber \\&\quad + X(t)\Big [\pi (t)\sigma (t)\beta (t) \textrm{d}t + \int _{ \mathbb {R^*} } \pi (t)\gamma (t,\zeta )\kappa (t,\zeta )\widetilde{N}(\textrm{d}t,\textrm{d}\zeta )\nonumber \\&\quad + \int _{ \mathbb {R^*} } \pi (t)\gamma (t,\zeta )\kappa (t,\zeta )\nu (\textrm{d}\zeta )\textrm{d}t\Big ]. \end{aligned}$$

Hence

$$\begin{aligned} E[X(T)F(T)]&=z F(0)+\int _0^T E\Big [ X(t)\Big \{F(t)\pi (t)\alpha (t) + \pi (t)\sigma (t)\beta (t) \nonumber \\&\quad + \int _{ \mathbb {R^*} } \pi (t)\gamma (t,\zeta )\kappa (t,\zeta )\nu (\textrm{d}\zeta )\Big \}\Big ]\textrm{d}t. \end{aligned}$$

Similarly

$$\begin{aligned} E[X^2(T)]= z^2 + \int _0^T E\Big [ X^2(t)\Big \{2 \pi (t)\alpha (t) + \pi ^2(t)\sigma ^2(t) + \int _{ \mathbb {R^*} } \pi ^2(t) \gamma ^2(t,\zeta ) \nu (\textrm{d}\zeta )\Big \} \Big ]\textrm{d}t, \end{aligned}$$

and

$$\begin{aligned} E[F^2(T)]=F(0)^2+\int _0^TE\Big [\beta ^2(t) + \int _{ \mathbb {R^*} }\kappa ^2(t,\zeta ) \nu (\textrm{d}\zeta )\Big ]\textrm{d}t. \end{aligned}$$

This gives

$$\begin{aligned} J(\pi )&=E\Big [\frac{1}{2} (X(T) -F)^2\Big ]= \frac{1}{2}\Big (E[X^2(T)] - 2E[X(T)F(T)]+E[F^2(T)]\Big )\nonumber \\&=\frac{1}{2}(z-F(0))^2 + \frac{1}{2}E\Big [\int _0^T\Big \{2 X^2(t)\pi (t)\alpha (t) + X^2(t)\pi ^2(t) \Big (\sigma ^2(t)+\int _{ \mathbb {R^*} } \gamma ^2(t,\zeta ) \nu (\textrm{d}\zeta )\Big )\nonumber \\&\quad -2X(t)\pi (t)\Big (F(t) \alpha (t) + \sigma (t)\beta (t) +\int _{ \mathbb {R^*} }\gamma (t,\zeta )\kappa (t,\zeta ) \nu (\textrm{d}\zeta )\Big )\nonumber \\&\quad +\beta ^2(t) + \int _{ \mathbb {R^*} }\kappa ^2(t,\zeta ) \nu (\textrm{d}\zeta )\Big \} \textrm{d}t\Big ]. \end{aligned}$$

We can minimize $J(\pi )$ by minimizing the $\textrm{d}t$-integrand pointwise for each t. This gives the following result:

Theorem 2.1

Recall that we have made the assumption (1.2).

(a) For given initial value $X(0)=z > 0$, the portfolio $\widehat{\pi }=\widehat{\pi }_{z}$ which minimizes

$$\begin{aligned} \pi \mapsto E\Big [\frac{1}{2}(X_{z,\pi }(T)-F)^2\Big ] \end{aligned}$$

is given in feedback form with respect to $X(t)=X_{z,\widehat{\pi }}$ by

$$\begin{aligned} \widehat{\pi }(t)&=\widehat{\pi }(t,X(t))= \frac{F(t)\alpha (t) +\sigma (t)\beta (t)+\int _{ \mathbb {R^*} }\gamma (t,\zeta )\kappa (t,\zeta )\nu (\textrm{d}\zeta ) - X(t)\alpha (t)}{X(t) \Bigg ( \sigma ^2(t) + \int _{ \mathbb {R^*} } \gamma ^2(t,\zeta ) \nu (\textrm{d}\zeta ) \Bigg )}, \end{aligned}$$

(2.3)

or equivalently

$$\begin{aligned} \widehat{\pi }(t)X(t)=G(t)[X(t)-F(t)]+\frac{\sigma (t)\beta (t)+\int _{\mathbb {R^*}}\gamma (t,\zeta )\kappa (t,\zeta )\nu (\textrm{d}\zeta )}{\sigma ^2(t)+\int _{\mathbb {R^*}}\gamma ^2(t,\zeta )\nu (\textrm{d}\zeta )}, \end{aligned}$$

where

$$\begin{aligned} G(t)=-\alpha (t)\Bigg (\sigma ^2(t)+\int _{\mathbb {R^*}} \gamma ^2(t,\zeta ) \nu (\textrm{d}\zeta )\Bigg )^{-1}. \end{aligned}$$

(2.4)

(b) Given an initial value $z>0$, the corresponding optimal wealth $X_{\widehat{\pi }}(t)=\widehat{X}(t)$ solves the SDE

$$\begin{aligned} \textrm{d}\widehat{X}(t)&=\widehat{X}(t)\widehat{\pi }(t,\widehat{X}(t))\Bigg [\alpha (t) \textrm{d}t + \sigma (t) \textrm{d}B(t) + \int _{ \mathbb {R^*} }\gamma (t,\zeta )\widetilde{N}(\textrm{d}t,\textrm{d}\zeta )\Bigg ]\nonumber \\&=\frac{F(t)\alpha (t) +\sigma (t)\beta (t)+\int _{ \mathbb {R^*} }\gamma (t,\zeta )\kappa (t,\zeta )\nu (\textrm{d}\zeta ) - X(t)\alpha (t)}{\sigma ^2(t) + \int _{ \mathbb {R^*} } \gamma ^2(t,\zeta ) \nu (\textrm{d}\zeta )}\nonumber \\&\quad \times \Bigg [\alpha (t) \textrm{d}t + \sigma (t) \textrm{d}B(t)+\int _{ \mathbb {R^*} }\gamma (t,\zeta )\widetilde{N}(\textrm{d}t,\textrm{d}\zeta )\Bigg ]. \end{aligned}$$

(2.5)

2.3 The optimal initial endowment

Completing the Stackelberg game, we now proceed to find the initial endowment $\widehat{z}$ which leads to a response $\widehat{\pi }=\pi _{\widehat{z}}$ that is optimal for Problem 1.1, in a sense that $J(\widehat{z},\widehat{\pi }) \le J(z,\pi )$ over all pairs $(z,\pi )$. We shall first find the explicit solution for X.

Writing $X=\widehat{X}$ for notational simplicity, Eq. (2.5) is of the form

$$\begin{aligned} \textrm{d}X\left( t\right) = C\left( t\right) \textrm{d}\Lambda _{t}+X\left( t\right) d\Gamma _{t};\quad X\left( 0\right) = z, \end{aligned}$$

(2.6)

where

$$\begin{aligned} C\left( t\right)= & {} \frac{F\left( t\right) \alpha \left( t\right) +\sigma \left( t\right) \beta \left( t\right) +\int _{ \mathbb {R^*} }\gamma \left( t,\zeta \right) \kappa \left( t,\zeta \right) \nu \left( \textrm{d}\zeta \right) }{ \sigma ^{2}\left( t\right) +\int _{ \mathbb {R^*} }\gamma ^{2}\left( t,\zeta \right) \nu \left( \textrm{d}\zeta \right) }, \end{aligned}$$

(2.7)

$$\begin{aligned} \textrm{d}\Lambda _{t}= & {} \alpha \left( t\right) \textrm{d}t+\sigma \left( t\right) \textrm{d}B\left( t\right) +\int _{ \mathbb {R^*} }\gamma \left( t,\zeta \right) \widetilde{N}\left( \textrm{d}t,\textrm{d}\zeta \right) , \\ \textrm{d}\Gamma _{t}= & {} \alpha _{1}\left( t\right) \textrm{d}t+\sigma _{1}\left( t\right) \textrm{d}B\left( t\right) +\int _{ \mathbb {R^*} }\gamma _{1}\left( t,\zeta \right) \widetilde{N }\left( \textrm{d}t,\textrm{d}\zeta \right) ,\nonumber \end{aligned}$$

(2.8)

with

$$\begin{aligned} \alpha _{1}\left( t\right) =G\left( t\right) \alpha \left( t\right) ; \quad \sigma _{1}\left( t\right) =G\left( t\right) \sigma \left( t\right) ; \quad \gamma _{1}\left( t,\zeta \right) =G\left( t\right) \gamma \left( t,\zeta \right) . \end{aligned}$$

We rewrite (2.6) as

$$\begin{aligned} \textrm{d}X\left( t\right) -X\left( t\right) \textrm{d}\Gamma _{t}=C\left( t\right) \textrm{d}\Lambda _{t}, \end{aligned}$$

(2.9)

and multiply this equation by a process of the form

$$\begin{aligned} Y_{t}=Y_{t}^{\left( \rho ,\lambda ,\theta \right) }=\exp \left( A_{t}^{\left( \rho ,\lambda ,\theta \right) }\right) , \end{aligned}$$

with

$$\begin{aligned} A_{t}^{\left( \rho ,\lambda ,\theta \right) }=\int _{0}^{t}\rho \left( s\right) \textrm{d}s+\int _{0}^{t}\lambda \left( s\right) \textrm{d}B\left( s\right) +\int _{0}^{t}\int _{ \mathbb {R^*} }\theta \left( s,\zeta \right) \widetilde{N}\left( \textrm{d}s,\textrm{d}\zeta \right) , \end{aligned}$$

where $\rho ,\lambda$ and $\theta$ are processes to be determined.

Then, (2.9) gets the form

$$\begin{aligned} Y_{t}\textrm{d}X\left( t\right) -Y_{t}X\left( t\right) \textrm{d}\Gamma _{t}=Y_{t}C\left( t\right) \textrm{d}\Lambda _{t}. \end{aligned}$$

(2.10)

We want to choose $\rho ,\lambda$ and $\theta$, such that $Y_t$ becomes an integrating factor, in the sense that

$$\begin{aligned} \textrm{d}\left( Y_{t}X\left( t\right) \right) =Y_{t}\textrm{d}X\left( t\right) -Y_{t}X\left( t\right) \textrm{d}\Gamma _{t}+\text {terms not depending on }X. \end{aligned}$$

To this end, note that by the Itô formula for Lévy processes, we have

$$\begin{aligned} \textrm{d}Y_{t}= & {} Y_{t}\left[ \rho \left( t\right) \textrm{d}t+\lambda \left( t\right) \textrm{d}B\left( t\right) \right] +\frac{1}{2}Y_{t}\lambda ^{2}\left( t\right) \textrm{d}t\\{} & {} \quad +\int _{ \mathbb {R^*} }\left\{ \exp \left( A_{t}+\theta \left( t,\zeta \right) \right) -\exp \left( A_{t}\right) -\exp \left( A_{t}\right) \theta \left( t,\zeta \right) \right\} \nu \left( \textrm{d}\zeta \right) \textrm{d}t \nonumber \\{} & {} \quad +\int _{ \mathbb {R^*} }\left\{ \exp \left( A_{t}+\theta \left( t,\zeta \right) \right) -\exp \left( A_{t}\right) \right\} \widetilde{N}\left( \textrm{d}t,\textrm{d}\zeta \right) \nonumber \\= & {} Y_t \left[ \left\{ \rho \left( t\right) +\frac{1}{2}\lambda ^{2}\left( t\right) +\int _{ \mathbb {R^*} }\left( e^{\theta \left( t,\zeta \right) }-1-\theta \left( t,\zeta \right) \right) \nu \left( \textrm{d}\zeta \right) \right\} \textrm{d}t\right. \nonumber \\{} & {} \quad \left. +\lambda \left( t\right) \textrm{d}B\left( t\right) +\int _{ \mathbb {R^*} }\left( e^{\theta \left( t,\zeta \right) }-1\right) \widetilde{N}\left( \textrm{d}t,\textrm{d}\zeta \right) \right] . \nonumber \end{aligned}$$

Therefore, again by the Itô formula, using (2.6)

$$\begin{aligned} d\left( Y_{t}X\left( t\right) \right)= & {} Y_{t}\textrm{d}X\left( t\right) +X\left( t\right) \textrm{d}Y_{t}+d\left[ X,Y\right] _{t} \\= & {} Y_{t}\textrm{d}X\left( t\right) +Y_{t}X\left( t\right) \left[ \left\{ \rho +\frac{1 }{2}\lambda ^{2}+\int _{ \mathbb {R^*} }\left( e^{\theta \left( t,\zeta \right) }-1-\theta \left( t,\zeta \right) \right) \nu \left( \textrm{d}\zeta \right) \right\} \textrm{d}t\right. \nonumber \\{} & {} \quad \left. +\lambda \left( t\right) \textrm{d}B\left( t\right) +\int _{ \mathbb {R^*} }\left( e^{\theta \left( t,\zeta \right) }-1\right) \widetilde{N}\left( \textrm{d}t,\textrm{d}\zeta \right) \right] \nonumber \\{} & {} \quad +Y_{t}X\left( t\right) \left[ \left\{ \lambda \left( t\right) \sigma _{1}\left( t\right) +\int _{ \mathbb {R^*} }\left( e^{\theta \left( t,\zeta \right) }-1\right) \gamma _{1}\left( t,\zeta \right) \nu \left( \textrm{d}\zeta \right) \right\} \textrm{d}t\right. \nonumber \\{} & {} \quad \left. +\int _{ \mathbb {R^*} }\left( e^{\theta \left( t,\zeta \right) }-1\right) \gamma _{1}\left( t,\zeta \right) \widetilde{N}\left( \textrm{d}t,\textrm{d}\zeta \right) \right] +Y_{t}C\left( t\right) \textrm{d}K_{t}, \nonumber \end{aligned}$$

where

$$\begin{aligned} \textrm{d}K_{t}=\left\{ \lambda \left( t\right) \sigma \left( t\right) +\int _{ \mathbb {R^*} }\left( e^{\theta \left( t,\zeta \right) }-1\right) \gamma \left( t,\zeta \right) \nu \left( \textrm{d}\zeta \right) \right\} \textrm{d}t+\int _{ \mathbb {R^*} }\left( e^{\theta \left( t,\zeta \right) }-1\right) \gamma \left( t,\zeta \right) \widetilde{N}\left( \textrm{d}t,\textrm{d}\zeta \right) . \end{aligned}$$

(2.11)

This gives

$$\begin{aligned}&\textrm{d}\left( Y_{t}X\left( t\right) \right) -Y_{t}\textrm{d}X\left( t\right) +Y_{t}X\left( t\right) \textrm{d}\Gamma _{t} \\&\quad =Y_{t}X\left( t\right) \Big [ \Big \{ \rho +\alpha _{1}+\frac{1}{2}\lambda ^{2}+\lambda \sigma _1+\int _{ \mathbb {R^*} }\left( e^{\theta \left( t,\zeta \right) }-1-\theta \left( t,\zeta \right) \right) \nu \left( \textrm{d}\zeta \right) \Big \}\textrm{d}t \nonumber \\&\qquad + \left( \lambda \left( t\right) +\sigma _{1}\left( t\right) \right) \textrm{d}B\left( t\right) +\int _{ \mathbb {R^*} }\left( e^{\theta \left( t,\zeta \right) }-1\right) \gamma _{1}\left( t,\zeta \right) \nu \left( \textrm{d}\zeta \right) \textrm{d}t \nonumber \\&\qquad +\int _{ \mathbb {R^*} }\Big \{ \left( e^{\theta \left( t,\zeta \right) }-1\right) \left( 1+\gamma _{1}\left( t,\zeta \right) \right) +\gamma _{1}\left( t,\zeta \right) \Big \} \widetilde{N}\left( \textrm{d}t,\textrm{d}\zeta \right) \nonumber \\&\qquad +Y_{t}C\left( t\right) \textrm{d}K_t. \nonumber \end{aligned}$$

Choose $\theta \left( t,\zeta \right) =\widehat{\theta }\left( t,\zeta \right)$, such that

$$\begin{aligned} ( e^{\theta \left( t,\zeta \right) }-1) \left( 1+\gamma _{1}\left( t,\zeta \right) \right) +\gamma _{1}\left( t,\zeta \right) =0, \end{aligned}$$

that is

$$\begin{aligned} \widehat{\theta }\left( t,\zeta \right) =-\ln \left( 1+\gamma _{1}\left( t,\zeta \right) \right) . \end{aligned}$$

Next, choose $\lambda \left( t\right) =\widehat{\lambda }\left( t\right)$, such that

$$\begin{aligned} \widehat{\lambda }\left( t\right) =-\sigma _{1}\left( t\right) . \end{aligned}$$

Finally, choose $\rho \left( t\right) =\widehat{\rho }\left( t\right)$, such that

$$\begin{aligned} \widehat{\rho }( t)&=-\Big [ \alpha _{1}( t) +\frac{1}{ 2}\sigma _{1}^{2}( t) -\sigma _1^2(t)+\int _{ \mathbb {R^*} }\Bigg ( e^{\widehat{\theta }( t,\zeta ) }-1-\widehat{\theta }( t,\zeta ) +( e^{ \widehat{\theta }( t,\zeta ) }-1) \gamma _{1}( t,\zeta ) \Bigg ) \nu \textrm{d}\zeta ) \Bigg ]\nonumber \\&=-\left[ \alpha _{1}\left( t\right) -\frac{1}{ 2}\sigma _{1}^{2}\left( t\right) +\int _{ \mathbb {R^*} }\Bigg ( \ln (1+\gamma _1(t,\zeta )) - \gamma _1(t,\zeta ) \Bigg ) \nu ( \textrm{d}\zeta ) \right] . \end{aligned}$$

Then

$$\begin{aligned} \widehat{A}_t&:=A_t^{(\widehat{\rho },\widehat{\lambda },\widehat{\theta })}\nonumber \\&=-\Bigg [\int _0^t\{ \alpha _1(s)-\frac{1}{2} \sigma _1^2(s) + \int _{ \mathbb {R^*} }(\ln (1+\gamma _1(s,\zeta ))-\gamma _1(s,\zeta ))\nu (\textrm{d}\zeta )\} \textrm{d}s \nonumber \\&\quad +\int _0^t \sigma _1(s)\textrm{d}B(s)+\int _0^t \int _{ \mathbb {R^*} } \ln (1+\gamma _1(s,\zeta ))\widetilde{N}(\textrm{d}s,\textrm{d}\zeta ) \Bigg ], \end{aligned}$$

(2.12)

with $\widehat{Y}_{t}=Y_{t}^{\left( \widehat{\rho },\widehat{\lambda }, \widehat{\theta }\right) } = \exp (\widehat{A}_t)$, we have, by (2.11)

$$\begin{aligned} \textrm{d}\left( \widehat{Y}_{t}X\left( t\right) \right) -\widehat{Y}_{t}\textrm{d}X\left( t\right) +\widehat{Y}_{t}X\left( t\right) \textrm{d}\Gamma _{t} =\widehat{Y}_{t}C\left( t\right) \textrm{d}K_{t}. \end{aligned}$$

Substituting this into (2.10), we get

$$\begin{aligned} \textrm{d}\left( \widehat{Y}_{t}X\left( t\right) \right) -\widehat{Y}_{t}C\left( t\right) \textrm{d}K_{t}=\widehat{Y}_{t}C\left( t\right) \textrm{d}\Lambda _{t}, \end{aligned}$$

which we integrate to since $\widehat{Y}_0=1$

$$\begin{aligned} \widehat{Y}_{t}X\left( t\right) =z+\int _{0}^{t}\widehat{Y}_{s}C\left( s\right) \textrm{d}\left( K_{s}+\Lambda _{s}\right) . \end{aligned}$$

Solving for $X\left( t\right)$, we obtain the following:

Theorem 2.2

Given initial value z, the corresponding optimal wealth process $\widehat{X}_z(t)$ is given by

$$\begin{aligned} \widehat{X}_z(t)&=z\widehat{Y}_{t}^{-1}+\widehat{Y}_{t}^{-1}\int _{0}^{t} \widehat{Y}_{s}C( s) \textrm{d}( K_{s}+\Lambda _{s}) \nonumber \\&=z\exp ( -\widehat{A}_t) +\exp ( -\widehat{A}_t)\int _{0}^{t}\exp (\widehat{A}_s) C\left( s\right) \textrm{d}\left( K_{s}+\Lambda _{s}\right) . \end{aligned}$$

(2.13)

In particular, note that

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}z}\widehat{X}_{z}\left( t\right) =\exp ( -\widehat{A}_{t}). \end{aligned}$$

(2.14)

Going back to our problem, choose $z \in \mathbb {R}$ and let $\widehat{\pi }_z$ be the corresponding optimal hedging portfolio given by (2.3) and let $\widehat{X}_z$ be the corresponding optimal wealth process given by (2.5) and (2.13), respectively. Then

$$\begin{aligned} \inf _{z,\pi }J(z,\pi )=\inf _{z,\pi }E\Bigg [\frac{1}{2}(X_{z,\pi }(T)-F)^2\Bigg ]=\inf _{z}E\Bigg [\frac{1}{2}(X_{z,\widehat{\pi }_z}(T) -F)^2\Bigg ]=\inf _{z}E\Bigg [\frac{1}{2}(\widehat{X}_{z}(T) -F)^2\Bigg ]. \end{aligned}$$

Note that, if we define

$$\begin{aligned} R_t&:=\exp (-\widehat{A}_t)=\exp \Bigg [\int _0^t\Bigg \{ \alpha _1(s)-\frac{1}{2} \sigma _1^2(s) + \int _{ \mathbb {R^*} }\Big (\ln (1+\gamma _1(s,\zeta ))-\gamma _1(s,\zeta )\Bigg )\nu (\textrm{d}\zeta )\Bigg \} \textrm{d}s \nonumber \\&\quad +\int _0^t \sigma _1(s)\textrm{d}B(s)+\int _0^t \int _{ \mathbb {R^*} } \ln (1+\gamma _1(s,\zeta ))\widetilde{N}(\textrm{d}s,\textrm{d}\zeta ) \Bigg ], \end{aligned}$$

and

$$\begin{aligned} Z^*(t)&:=\exp \Bigg (-\int _0^t \alpha _1(s)\textrm{d}s\Bigg )R_t\\&=\exp \Bigg [\int _0^t\Big \{-\frac{1}{2} \sigma _1^2(s) + \int _{\mathbb {R^*}}(\ln (1+\gamma _1(s,\zeta ))-\gamma _1(s,\zeta ))\nu (\textrm{d}\zeta )\Bigg \} \textrm{d}s \nonumber \\&\quad +\int _0^t \sigma _1(s)\textrm{d}B(s)+\int _0^t \int _{ \mathbb {R^*} } \ln (1+\gamma _1(s,\zeta ))\widetilde{N}(\textrm{d}s,\textrm{d}\zeta ) \Bigg ], \end{aligned}$$

then we can verify by the Itô formula that

$$\begin{aligned} \textrm{d}R_t&=R_t\Bigg (\alpha _1(t)\textrm{d}t + \sigma _1(t) \textrm{d}B(t) + \int _{ \mathbb {R^*} } \gamma _1(t,\zeta ) \widetilde{N}(\textrm{d}t,\textrm{d}\zeta )\Big )\nonumber \\&=R_t G(t)\Bigg (\alpha (t)\textrm{d}t + \sigma (t) \textrm{d}B(t) + \int _{ \mathbb {R^*} } \gamma (t,\zeta ) \widetilde{N}(\textrm{d}t,\textrm{d}\zeta )\Bigg )\nonumber \\&= R_t G(t) S^{-1}(t)\textrm{d}S(t), \end{aligned}$$

and

$$\begin{aligned} \textrm{d}Z^{*}(t)&=Z^{*}(t) G(t)\Bigg ( \sigma (t) \textrm{d}B(t) + \int _{ \mathbb {R^*} } \gamma (t,\zeta ) \widetilde{N}(\textrm{d}t,\textrm{d}\zeta )\Bigg ). \end{aligned}$$

(2.15)

Proposition 2.3

$Z^{*}(\cdot )$ is a P-martingale. (See (2.2).) In particular, it follows that $Q^{*}$ defined by:

$$\begin{aligned} \textrm{d}Q^{*}(\omega )=Z^{*}(T) \textrm{d}P(\omega ) \text{ on } \mathcal {F}_T \end{aligned}$$

(2.16)

is an EMM for $S(\cdot )$.

Proof

To see this, we verify that the coefficients $\theta _0(t):=G(t)\sigma (t)$ and $\theta _1(t,\zeta ):=G(t)\gamma (t,\zeta )$ satisfy condition (2.1)

$$\begin{aligned}&\alpha (t)+\theta _{0}(t)\sigma (t)+\int _{ \mathbb {R^*} }\theta _{1}(t,\zeta )\gamma (t,\zeta )\nu (\textrm{d}\zeta )\nonumber \\&\quad =\alpha (t)-\frac{\alpha (t)}{\sigma ^2(t) + \int _{ \mathbb {R^*} } \gamma ^2(t,\zeta ) \nu (\textrm{d}\zeta )}\sigma ^2(t) -\frac{\alpha (t)}{\sigma ^2(t) + \int _{ \mathbb {R^*} }\gamma ^2(t,\zeta ) \nu (\textrm{d}\zeta )}\int _{ \mathbb {R^*} }\gamma ^2(t,\zeta ) \nu (\textrm{d}\zeta )\nonumber \\&\quad = \alpha (t) -\alpha (t)=0\text {, }\quad t\ge 0. \end{aligned}$$

Using this, we obtain the following, which is the main result in this section:

Theorem 2.4

(i) The unique minimal variance price $\widehat{z}$ of a European option with terminal payoff F at time T is given by

$$\begin{aligned} \widehat{z}= \frac{E\Bigg [ \exp (-\widehat{A}_T)\Bigg (F - \exp (-\widehat{A}_T) \int _0^T \exp (\widehat{A}_s)C\left( s\right) \textrm{d}\left( K_{s}+\Lambda _{s}\right) \Bigg )\Bigg ]}{E[\exp (-2\widehat{A}_T)]}, \end{aligned}$$

(2.17)

where $\widehat{A}_T$ is given by (2.12), $C(s), \Lambda _s$ are given by (2.7), (2.8), respectively, and K is given by (2.11).

(ii) Assume that the coefficients $\alpha (t)$, $\sigma (t)$, and $\gamma (t,\zeta )$ are bounded and deterministic functions. Then

$$\begin{aligned} \widehat{z}=E_{Q^{*}}[F], \end{aligned}$$

(2.18)

where $Q^{*}$ is the EMM measure given by (2.16).

Proof

(i) To minimize $J_0(z):= E\Big [\frac{1}{2} (\widehat{X}_{z}(T)-F)^2\Big ]$ with respect to z, we get by (2.13) and (2.14) that

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}z} J_0(z)&=E\Bigg [(\widehat{X}_{z}(T) -F)\frac{\textrm{d}}{\textrm{d}Z}\widehat{X}_{z}(T)\Bigg ] \nonumber \\&=E[(\widehat{X}_z(T) -F)\textrm{exp}(-\widehat{A}_T)] \\&=E\Bigg [\Bigg (z\textrm{exp}(-\widehat{A}_T) +\textrm{exp}(-\widehat{A}_T)\int _0^T \exp (\widehat{A}_s)C\left( s\right) \textrm{d}\left( K_{s}+\Lambda _{s}\right) -F\Bigg )\exp (-\widehat{A}_T)\Bigg ].\nonumber \end{aligned}$$

(2.19)

This is 0 if and only if (2.17) holds.

(ii) By (2.19), we get

$$\begin{aligned}&E[\widehat{X}_z(T)\exp (-\widehat{A}_T)]=E[F \exp (-\widehat{A}_T)],\nonumber \\ \text { i.e., }\nonumber \\&\quad E\Bigg [\widehat{X}_z(T)\exp \Big (\int _0^T \alpha _1(s)\textrm{d}s\Bigg ) Z^{*}(T)\Bigg ]=E\Bigg [F\exp \Bigg (\int _0^T \alpha _1(s)\textrm{d}s\Bigg ) Z^{*}(T)\Bigg ]. \end{aligned}$$

If $\alpha _1$ is deterministic, we cancel out the factor $\exp \Bigg (\int _0^T \alpha _1(s)\textrm{d}s\Bigg )$ and (2.18) follows.

Remark 2.5

In particular, if F is a deterministic constant. Then, $F(t)=F=E[F]$ for all t, and $\beta =\kappa =0$. Hence, the optimal portfolio is given in feedback form by

$$\begin{aligned} \widehat{\pi }(t)X(t)=G(t)[X(t)-F]. \end{aligned}$$

Assume, for example, that $\alpha (t) > 0$. Then, $G(t) < 0$, and we see that if $X(t) < F$, then $\widehat{\pi }(t)X(t) >0$, and hence, the optimal portfolio pushes X(t) upwards toward F. Similarly, if $X(t) > F$, then $\widehat{\pi }(t)X(t) < 0$ and the optimal push of X(t) is downwards toward F. This is to be expected, since the portfolio tries to minimize the terminal variance $E[(X(T)-F)^2]$.

Moreover, if we start at $z=X(0)=F$, we can choose $\pi =0$ and this gives $J(z,\pi )=J(F,0)=E[\frac{1}{2}(X(T)-F)^2]=E[\frac{1}{2}(F-F)^2]=0$, which is clearly optimal. By uniqueness of $(\widehat{z},\widehat{\pi })$, we conclude that $(\widehat{z},\widehat{\pi })=(F,0)$ is the optimal pair in this case.

Remark 2.6

The price $\widehat{z}$ is an arbitrage-free price of F, follows by Theorem 2.4 (ii).

Remark 2.7

Note that, as remarked earlier, the coefficients $\beta$ and $\kappa$ depend linearly on F. Therefore, it follows from the formula (2.17) that the map $\Phi : L^2(P,\mathcal {F}_T) \mapsto \mathbb {R}$ defined by:

$$\begin{aligned} \Phi (F)= \widehat{z}; \quad F \in L^2(P,\mathcal {F}_T) \end{aligned}$$

is linear and bounded. By the Riesz representation theorem, this map can be represented by a random variable $Z \in L^2(P,\mathcal {F}_T)$, in the sense that

$$\begin{aligned} \widehat{z}=E[ ZF]; \quad F \in L^2(P,\mathcal {F}_T). \end{aligned}$$

Therefore, if we define the (signed) measure $\tilde{Q}$ on $\mathcal {F}_T$ by

$$\begin{aligned} \textrm{d}\tilde{Q}=Z \textrm{d}P, \end{aligned}$$

then

$$\begin{aligned} \widehat{z}=E_{\tilde{Q}}[F]. \end{aligned}$$

Comparing with the Schweizer variance-optimal pricing measure $\tilde{P}$ (1.4), we conclude the following:

Corollary 2.8

• (i) $\tilde{P}=\tilde{Q}$. In particular, $\tilde{P}$ always exists in this market, without any non-arbitrage conditions.

• (ii) Moreover, we have $\tilde{P}=Q^{*}$, which is a positive EMM.

2.4 Example: European call option

We give some details about how to compute the minimal variance price $\widehat{z}$ explicitly in the case of a European call option that will used in Sect. 3.

• (i) Note that the term C(s) in Theorem 2.4 depends on the coefficients $\beta$ and $\kappa$ in the Itô representation of F. These coefficients can for example be found using the generalized Clark–Ocone formula for Lévy processes, extended to $L^2(P)$. See Theorem 12.26 in Di Nunno et al. (2008). Let us find these coefficients in the case of a European call option, where

  $$\begin{aligned} F=(S(T)-K)^{+}, \end{aligned}$$

  where K is a given exercise price. In this case, $F(\omega )$ represents the payoff at time T (fixed) of a (European call) option which gives the owner the right to buy the stock with value $S(T,\omega )$ at a fixed exercise price K. Thus, if $S(T,\omega )>K$, the owner of the option gets the profit $S(T,\omega )-K$, and if $S(T,\omega )\le K$, the owner does not exercise the option and the profit is 0. Hence, in this case

  $$\begin{aligned} F(\omega )=(S(T,\omega )-K)^{+}. \end{aligned}$$

  Thus, we may write

  $$\begin{aligned} F(\omega )=f(S(T,\omega )), \end{aligned}$$

  where

  $$\begin{aligned} f(x)=(x-K)^{+}. \end{aligned}$$

  The function f is not differentiable at $x=K$, so we cannot use the chain rule directly to evaluate $D_tF$. However, we can approximate f by $C^1$ functions $f_n$ with the property that

  $$\begin{aligned} f_n(x)=f(x) \quad \text { for } \quad |x-K| \ge \frac{1}{n}, \end{aligned}$$

  and

  $$\begin{aligned} 0\le f'_n(x)\le 1 \text { for all } x. \end{aligned}$$

  Putting

  $$\begin{aligned} F_n(\omega )=f_n(S(T,\omega )), \end{aligned}$$

  we see

  $$\begin{aligned} D_tF(\omega )=\lim _{n \rightarrow +\infty } D_tF_n(\omega ). \end{aligned}$$

  We get

  $$\begin{aligned} \beta (t)= E[D_t F | \mathcal {F}_t],\qquad \kappa (t,\zeta )=E[D_{t,\zeta }F | \mathcal {F}_t], \end{aligned}$$

  where $D_t F$ and $D_{t,\zeta } F$ denote the generalized Malliavin derivatives (also called the Hida–Malliavin derivative) of F at t and $(t,\zeta )$, respectively, with respect to $B(\cdot )$ and $N(\cdot ,\cdot )$, respectively. Combining this with the chain rule for the Hida–Malliavin derivative and the Markov property of the process $S(\cdot )$, and assuming for simplicity that $\sigma$ is constant and $\gamma (t,\zeta )=\gamma (\zeta )$ does not depend on t, we obtain the following for $\beta$:

  $$\begin{aligned} \beta (t)&= E^{S_0}\Big [\mathbbm {1}_{[K,\infty )}(S(T))\sigma S(T) \Big |\mathcal {F}_t\Big ]\nonumber \\&=E^{S(t)}\Bigg [\mathbbm {1}_{[K,\infty )}(S(T-t))\sigma S(T-t)\Bigg ]. \end{aligned}$$

  (2.20)

  To find the corresponding result for $\kappa$, we first use the chain rule for $D_{t,\zeta }$ and get

  $$\begin{aligned} D_{t,\zeta }S(T)&=D_{t,\zeta }\Bigg [S_0 \exp \Bigg (\alpha T -\frac{1}{2}\sigma ^2 T+ \sigma B(T) +\int _{\mathbb {R^*}}(\log (1+\gamma (\zeta ))-\gamma (\zeta ))\nu (\textrm{d}\zeta )T\nonumber \\ {}&\quad +\int _0^t\int _{\mathbb {R^*}}\ln (1+\gamma (\zeta ))\widetilde{N}(\textrm{d}s,\textrm{d}\zeta ) \Bigg )\Bigg ]=S(T)\gamma (\zeta ). \end{aligned}$$

  Then, we obtain

  $$\begin{aligned} \kappa (t,\zeta )&=E^{S_0}\Bigg [\mathbbm {1}_{[K,\infty )}(S(T)+D_{t,\zeta }S(T))-\mathbbm {1}_{[K,\infty )}(S(T)) \Bigg |\mathcal {F}_t\Bigg ]\nonumber \\&=E^{S_0}\Big [\mathbbm {1}_{[K,\infty )}(S(T)+\gamma (\zeta )S(T)) -\mathbbm {1}_{[K,\infty )}(S(T)) \Bigg |\mathcal {F}_t\Bigg ] \nonumber \\ {}&=E^{S(t)}\Bigg [\mathbbm {1}_{[K,\infty )}(S(T-t)+\gamma (\zeta )S(T-t)) - \mathbbm {1}_{[K,\infty )}(S(T-t))\Bigg ], \end{aligned}$$

  (2.21)

  where in general $E^{y}[h(S(u))]$ means $E[h(S^{y}(u))]$, i.e., expectation when S starts at y.

• (ii) Since the coefficients $\alpha , \sigma$ and $\gamma$ of the process S are deterministic and bounded, we compute numerically the minimal variance price

  $$\begin{aligned} \widehat{z}=E\Big [(S(T)-K)^{+}Z_T^{*}\Big ] \end{aligned}$$

  of a European call option with payoff

  $$\begin{aligned} F=(S(T)-K)^{+}= E[F]+\int _0^T \beta (t)\textrm{d}B(t)+\int _0^T \int _{\mathbb {R^*}} \kappa (t,\zeta ) \widetilde{N}(\textrm{d}t,\textrm{d}\zeta ), \end{aligned}$$

  where $\beta ,\kappa$ are given by (2.20), (2.21), respectively, and we use the Itô formula combined with (2.15) to obtain

  $$\begin{aligned} \widehat{z}=E[F Z_T^{*}]=E[F]+ \int _0^T G(t)\Big \{\sigma (t) E[Z_t^{*}\beta (t)] + \int _{\mathbb {R^*}}\gamma (t,\zeta ) E[\kappa (t,\zeta ) Z_t^{*}] \nu (\textrm{d}\zeta )\Big \} \textrm{d}t, \end{aligned}$$

  where G(t) is given by (2.4).

2.4.1 Application to Black–Scholes market with two independent Brownian motions

In this example, we consider a market driven by two independent Brownian motions, $B_1(t), B_2(t)$

$$\begin{aligned} \textrm{d}S(t)=S(t)[\alpha _0\textrm{d}t +\beta _1 \textrm{d}B_1(t) + \beta _2)\textrm{d}B_2(t)],\quad S(0) > 0, \end{aligned}$$

where the coefficients $\alpha _0,\beta _1,\beta _2$ are assumed to be bounded constants. For a self-financing portfolio $\pi$ and an initial wealth z, we have a wealth dynamic

$$\begin{aligned} \textrm{d}X(t)=X(t)\pi (t)[\alpha _0\textrm{d}t +\beta _1\textrm{d}B_1(t) + \beta _2\textrm{d}B_2(t)],\quad X(0)=z. \end{aligned}$$

We want to find the pair $(\widehat{z},\widehat{\pi })$ which minimizes the expected squared hedging error

$$\begin{aligned} E\Bigg [\frac{1}{2}(X(T)-F)^2\Bigg ]. \end{aligned}$$

(2.22)

Corollary 2.9

From Theorem 2.4 (ii), we conclude that

$$\begin{aligned} E_{Q^{*}}[F] = E[FZ^*(T)], \end{aligned}$$

(2.23)

where

$$\begin{aligned} Z^*(t) =&\exp \Bigg (-\frac{1}{2} G^2( \beta _1^2+ \beta _2^2)t + G\beta _1 B_1(t)+ G \beta _2B_2(t)\Bigg ), \end{aligned}$$

and

$$\begin{aligned} G = -\frac{\alpha _0}{\beta _1^2 + \beta _2^2}. \end{aligned}$$

(2.24)

Looking at the above corollary, we can see that process $Z^*$ coincides with the one in the Black–Scholes setting, where the volatility coefficient of the single Brownian motion B(t) is given by $\beta = \sqrt{\beta _1^2 + \beta _2^2}$. Since processes $\beta B(t)$ and $\beta _1 B_1(t) + \beta _2 B_2(t)$ have the same distribution, so do the option payoffs. This yields that the minimal variance European call option price in an incomplete market with two independent Brownian motions $E_{Q^{*}}[F]$ coincides with the unique Black–Scholes price in a single Brownian motion case for volatility $\beta = \sqrt{\beta _1^2 + \beta _2^2}$.

Furthermore, we know that the hedging portfolio in the BS model is only a function of time and the underlying asset. Since for the choice of volatility parameter as above, the stocks in both BS and two-Brownian motion model follow the same distribution, we can deduce that for initial endowment $E_{Q^{*}}[F]$ from Eq. (2.23) and for the BS hedging portfolio, we get

$$\begin{aligned} {E\Bigg [\frac{1}{2}(X(T)-F)^2\Bigg ] = 0.} \end{aligned}$$

The above can, of course, be extended to the arbitrary number of Brownian motions.

2.5 Application to Merton model

Here, we consider the special case of the Merton model first proposed in Merton (1976). It deals with European options in the market modeled by jump diffusion. More precisely, the market consists of

• (i) a risk-free asset, with unit price $S_{0}(t)=1$ for all t;

• (ii) a risky asset, with price S(t) given by

  $$\begin{aligned} \textrm{d}S(t)=S(t)\Big [\alpha _0 \textrm{d}t + \sigma _0 \textrm{d}B(t) +(y-1)\tilde{N}(\textrm{d}t,\textrm{d}y) \Big ], \quad S(0)=S_0 > 0. \end{aligned}$$

  (2.25)

Here, $\tilde{N}$ is a compensated Poisson random measure corresponding to the compound Poisson process with intensity $\lambda$ and jump sizes $y = \exp (Y)$, where $Y \sim \mathcal {N}(\mu , \delta ^2),$ independent of B and jump times. Heuristically speaking, y represents the absolute jump size, while $\gamma _0(t,y) = y-1$ equals the relative jump size. The coefficients $\alpha _0$ and $\sigma _0$ are assumed to be bounded and deterministic.

If we denote $k = E[y-1] = \exp (\mu + \frac{\delta ^2}{2}) -1$ and observe that $y-1 > -1$ a.s., we can use Itô formula and obtain the explicit solution

$$\begin{aligned} S(t)&=S_0 \exp \left( \{\alpha _0-\frac{\sigma _0^2}{2}-\lambda k \}t+\sigma _0 B(t)+\sum ^{N(t)}_{i=1} Y_i\right) . \end{aligned}$$

Merton then proceeds to argue that the jumps in the asset price are not systemic and, therefore, the risk related to the jumps is diversifiable. In other words, this means that all the properties of the jump component of $S(\cdot )$ under the risk neutral measure are the same as under the natural measure. This argument yields the choice $\theta _0 = \frac{\alpha _0}{\sigma _0}$ and $\theta _1(y) = 0$ which results in EMM ${Q}^M$ corresponding to the Radon–Nikodým derivative

$$\begin{aligned} Z^M(t) = \exp \left( -\frac{\alpha _0^2}{2\sigma _0^2} t - \frac{\alpha _0}{\sigma _0} B(t) \right) \end{aligned}$$

and enables Merton to obtain the option price as

$$\begin{aligned} E_{{Q}^M}[ F] = \sum _{j\ge 0} \frac{e^{- \lambda (k+1)T} ((\lambda (k+1)T)^j}{j!} BS \left( 0,S_0, \sqrt{\sigma _0^2+\frac{j\delta ^2}{T}}, \frac{j\mu + j \delta ^2/2}{T}- \lambda k\right) , \end{aligned}$$

(2.26)

where $BS(t, S(t),\sigma _0,r)$ denotes the price of the European call option under the BS model at time t, with stock price S(t), volatility $\sigma$, and interest rate r.

This approach results in a non-symmetric loss. Merton argues that if no jump occurs, then the owner of the option collects a small profit. However, in a rare case when a jump does occur, the option holder suffers a significant loss. The non-symmetric loss distribution can, in some instances, be nondesirable. Apart from that, the assumption of diversifiabilty of the jump risk does not hold in practice; for example, market indexes do experience occasional jumps in price.

Using the results from the previous section, we can obtain the optimal portfolio, optimal wealth process, and the unique minimal variance price given by (2.3), (2.13), and (2.17), respectively. To evaluate these expressions, one has to compute coefficients $\beta (t)$ and $\kappa (t,y)$ given by Eqs. (2.20) and (2.21). If we denote $L(t) = S(t) \exp \big (( \alpha - \frac{\sigma ^2}{2} - \lambda k)(T-t) \big ),$ $H(t) = \sigma B(t) + \sum _{i=1}^{N(t)} Y_i$, we get

$$\begin{aligned} \beta (t)&= E^{S(t)}\Big [\mathbbm {1}_{[K,\infty )}(S(T-t))\sigma S(T-t)\Big ] \\&= \sigma L(t) E[\mathbbm {1}_{[K L(t)^{-1},\infty )}(e^{H(T-t)})e^{H(T-t)}] \\&= \sigma L(t) \sum _{j=0}^{\infty } E[\mathbbm {1}_{[K L(t)^{-1},\infty )}(e^{H(T-t)})e^{H(T-t)} \Big | N(T-t) = j] {P}(N(T-t) = j) \\&= \sigma L(t) \sum _{j=0}^{\infty } \exp \Big (j \mu + \frac{j \delta ^2 + \sigma ^2(T-t)}{2} \Big ) \cdot \\&\quad \cdot \Phi \Big (\frac{j \mu + j \delta ^2 + \sigma ^2(T-t) - \log (K) + \log (L(t))}{\sqrt{j \delta ^2 + \sigma ^2 (T-t)}} \Big ) \cdot \frac{(\lambda (T-t))^j \exp (-\lambda (T-t))}{j!},\\ \kappa (t,y)&= E^{S(t)}\Big [\mathbbm {1}_{[K,\infty )}(S(T-t)+\gamma (y)S(T-t)) - \mathbbm {1}_{[K,\infty )}(S(T-t))\Big ] \\&= E^{S(t)}\Big [\mathbbm {1}_{[K,\infty )}(S(T-t)+(y-1)S(T-t)) - \mathbbm {1}_{[K,\infty )}(S(T-t))\Big ] \\&= E^{S(t)}\Big [\mathbbm {1}_{[K,\infty )}(yS(T-t)) - \mathbbm {1}_{[K,\infty )}(S(T-t))\Big ] \\&= \mathbb {P}\Big (e^{H(T-t)}> \frac{K}{y L(t)} \Big ) - \mathbb {P}\Big (e^{H(T-t)} > \frac{K}{L(t)} \Big ) \\&= \sum _{j=0}^{\infty } \Bigg ( \Phi \Big (\frac{\log (K) - \log ( L(t)) -j \mu }{\sqrt{j \delta ^2 + \sigma ^2 (T-t)}} \Big ) \\&\quad - \Phi \Big (\frac{\log (K) - \log (y L(t)) -j \mu }{\sqrt{j \delta ^2 + \sigma ^2 (T-t)}} \Big ) \Bigg ) \cdot \frac{(\lambda (T-t))^j \exp (-\lambda (T-t))}{j!}, \end{aligned}$$

where we use the fact that $H(t) | \big \{ N(t) = j \big \} \sim \mathcal {N}\big ( j \mu , \sigma ^2(T-t) + j\delta ^2 \big ).$ Unfortunately, this representation is not enough to obtain the desired results explicitly. However, we may observe the following. The Lévy measure associated with the compound process in Eq. (2.25) equals $\lambda \mu _y$, where $\mu _y$ is the law of log-normally distributed random variable y. Hence, even though the coefficient $\gamma _0$ is stochastic, we have that $m = \int _{\mathbb {R}^*} \gamma _0(y)^2 \nu (\textrm{d}y)$ is deterministic. Since $\alpha _0$ and $\sigma _0$ are also deterministic, so is

$$\begin{aligned} G = - \frac{\alpha _0}{\sigma _0^2 + \lambda m}. \end{aligned}$$

(2.27)

By part (ii) of the Theorem 2.4, we have an explicit representation of the EMM $Q^*$ and the corresponding Radon–Nikodým derivative given by

$$\begin{aligned} Z^{*}(t)=\exp \left( \left\{ -\frac{1}{2}G^2\sigma _0^2 -\lambda G k\right\} t+G \sigma _0 B(t)+ \sum _{i=1}^{N(t)} \ln (1+G (y_i-1)) \right) . \end{aligned}$$

Moreover, the minimal variance price $\widehat{z}$ of an option with payoff F at time T is

$$\begin{aligned} \widehat{z}=E_{Q^{*}}(F)= E[F Z^{*}(T)]. \end{aligned}$$

(2.28)

Fig. 1

One realization of $Z^M$ and $Z^*$ for the choice of parameters specified in Sect. 3.3.3

Remark 2.10

It must be stated that, in theory, we do not have a guarantee that $G(y_i -1) > -1$, since log-normal distribution takes values on the whole positive line. Consequently, the logarithm may not be defined, in which case we use the alternative formulation

$$\begin{aligned} Z^*(t) = \left( \prod _{i=1}^{N(t)} 1+G (y_i-1) \right) \exp \left( \left\{ -\frac{1}{2}G^2\sigma _0^2 -\lambda G k\right\} t+G \sigma _0 B(t) \right) \end{aligned}$$

from Lamberton and Lapeyre (2011). This results in a signed measure $Q^*$. Nonetheless, in practice, for a reasonable choice of parameters, $G(y_i -1) > -1$ holds with probability practically equal to 1, and we do not need to worry about this technical problem.

We can not derive the same formula as in (2.26), since the distribution of $\ln (1+G (y-1))$ is unknown; however, we can use the Monte Carlo approach to obtain the option price. This option price obviously differs from Merton’s, as does the hedging portfolio that also considers the risk coming from the jumps and results in a symmetric loss. Using the Euler–Maruyama discretization rule, we simulate one realization of $Z^M$ and $Z^*$ and present it in Fig. 1. We can see that $Z^*$ has upward jumps, which are not present in $Z^M.$

In Figs. 2 and 3, we can see how the price of the European option changes for both models depending on the parameters $\lambda , \, \mu , \, \sigma , \, \delta .$ The option price in both models grows together with the absolute value of the parameters. Note that option prices coincide with the exclusion of jumps, namely when $\lambda = 0$, since the Merton model devolves into the BS model. It must be noted how the changes in prices are higher in the case described by Fig. 2, where we consider the dependence on parameters $\lambda$ and $\mu$, than in Fig. 3, where $\sigma$ and $\delta$ are taken into consideration, due to those parameters’ effect on stock and wealth dynamics. Large values of parameters $\lambda$ and $\mu$ change dynamics directly, while $\sigma$ and especially $\delta$ do it indirectly. In Fig. 2, it is shown how model prices are similar for small absolute values of parameters. When parameters grow, minimal variance price grows faster; however, the difference stabilizes. As a matter of fact, the difference appears to be most significant when $\lambda$ is relatively small, while $|\mu |$ is large. This is because once $\lambda$ is large, the compensated part of the jump component, which is taken into account in both hedging strategies, takes over.

To continue with observations for the other two parameters, we can see that even though absolute differences are smaller, relatively speaking, models differ more when $\sigma$ and $\delta$ parameters are modified, as shown in Fig. 3. The difference between the prices seems to be biggest when jump sizes are constant, while volatility in the model is large.

Fig. 2

Option price comparison depending on parameters $\lambda$ and $\mu$, where $S_0 = 1$, $K=0.5,$ $\sigma = 0.2$, and $\delta = 0.05$

Fig. 3

Option price comparison depending on parameters $\sigma$ and $\delta$, where $S_0 = 1$, $K=0.5,$ $\lambda = 10$, and $\mu = -0.2$

Numerical methods for obtaining the optimal portfolio are presented in the next section.

3 Deep learning approach

Here, we present the algorithm using deep learning methods that returns both the optimal initial value and the optimal portfolio. In Fecamp et al. (2020), different types of neural networks (NN) are compared when studying hedging in discrete-time incomplete markets. It turns out that long short-term memory (LSTM) networks, which are the particular case of Recurrent neural networks (RNN), outperform standard feed-forward NN. Because the model discussed in the aforementioned paper does not incorporate jumps in the price dynamics, we also conducted a comparison between the performance of LSTM and feed-forward neural networks. However, we detected no significant difference between the two approaches. A possible intuitive reason for the good performance of the LSTM network in the jump diffusion models could be its ability to learn the jump dynamics from the previous jump occurrences. Furthermore, RNN and, in particular, LSTM networks seem to be the most natural approach when working with time series data and, importantly, allow generalization to non-Markovian models. Hence, we opted to focus exclusively on the LSTM model in the subsequent work. In particular a possible extension that would benefit from the use of LSTM networks is if we consider stochastic volatility models. Historical information that LSTM keeps or forgets would help us to store and use knowledge about the behavior of the volatility parameter.

The performance of our network is to be tested on four models. First, we consider the BS model, where the market is complete. The reason for that is that both option value and hedging portfolio are known and can be compared to our results. Then, we consider three cases of incomplete markets. We start with the BS model with multiple independent Brownian motions and continue with two jump diffusion models, Merton and Kou double exponential models.

3.1 Data generation

To generate the data, we discretize time interval [0, T] into R equidistant points $t_i$ at a distance $\Delta _t$. We denote different realizations of the process with (j) in superscript, where $j = [M]$ and M denotes the batch size. When the superscript is omitted, we assume the vector notation. Additionally, we here assume the most general case with $d_B$ dimensional Brownian motion and $d_N$ dimensional Poisson random measure.

For initial wealth $x_0$, we construct under portfolio $\pi$ the wealth process at time $t_i$ using the update rule

$$\begin{aligned} x_{i+1} = x_{i} + x_i\pi _i\big [ (\alpha _0-\lambda {^\top } k) \Delta _t + \sqrt{\Delta _t}B_i {\sigma _0} + \gamma _0 J_i \big ], \qquad i \in [R-1]. \end{aligned}$$

(3.1)

Here, $\alpha _0\in \mathbb {R}$ and $\sigma _0 \in \mathbb {R}^{d_B}$ are drift and volatility parameters, respectively. Parameter $\gamma _0 \in \{0,1\}$ serves as a dummy variable that indicates whether a model is continuous or not. Moreover, $B_i$ are $M {\times d_B}$ dimensional independent $\mathcal {N}(0,1)$ random variables, while $J_i {= \sum _{l=1}^{d_N} J_i^l,}$ where $J_i^l$ are independent and given by

$$\begin{aligned} J_{i}{^l} = {\left\{ \begin{array}{ll} e^{Y_i{^l}} - 1, &{} N{^l}(t) \text { has a jump in } [t_i,t_{i+1}] \\ 0,&{} \text {otherwise}, \end{array}\right. } \end{aligned}$$

where $Y_i{^l}$ is M dimensional $\mathcal {N}(\mu {_l},\delta ^2{_l})$ and N(t) is an $M { \times d_N}$ dimensional homogeneous Poisson process with intensity $\lambda {\in \mathbb {R}_+^{d_N}}$ and independent components $N^l(t).$ Parameter k in Eq. (3.1) has $d_N$ components $k{^l} = \exp (\mu {_l} + \frac{\delta ^2{_l}}{2}) - 1.$

This discretization coincides with continuous time SDEs in the Merton model described in Sect. 2.5 and in the BS model when $\gamma _0=0$ and Brownian motion is one dimensional.

To obtain a discrete stock process s, which we need to compute the loss function later on, we choose the initial stock value $s_0$ and set $\pi = 1$ in Eq. (3.1).

For option strike price K, we first compute option’s $t_R$ claim as $F^{(j)} = (s^{(j)}_R - K)^+.$ Then, we can define loss as

$$\begin{aligned} \textrm{loss}(s_R,x_R) = \frac{1}{2}\frac{1}{M} \sum _{j=1}^{M} (x^{(j)}_R - F^{(j)})^2. \end{aligned}$$

(3.2)

Note that here we still, for brevity’s sake, assume that the interest rate $r=0,$ since all the proceeding computations can be done with the same amount of accuracy.

3.2 Network architecture and algorithm

As mentioned above, we make use of the LSTM networks. A feed-forward network approach was also tested. However, it resulted in worse performance; hence, we decided to stick with LSTM to allow more generality. We divide our learning task into two parts. First, we need to find the initial wealth value $x_0.$ This is a relatively simple task, so a simple one-layer linear feed-forward NN with hidden dimension d given by

$$\begin{aligned} L(y) = A y + b, \qquad y \in \mathbb {R}^d, A \in \mathbb {R}^{M \times d}, b \in \mathbb {R}^M \end{aligned}$$

(3.3)

is used. Recall that we interpret initial wealth $x_0$ as an option price, a deterministic quantity. Hence, $x_0^j = x_0$ for each $j \in [M]$ and we may use a vector of initial stock prices $y= [s_0, \ldots , s_0]^\top$ as an input for NN L. Since the wealth process in Eq. (1.3) is a geometric jump diffusion where a positive initial value is assumed, we use the softplus activation function $f(x) = \log (1+e^x).$

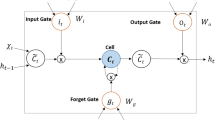
In the second part of the learning process, we strive to find the optimal portfolio $\pi$. We use a stacked LSTM network with two layers. Each layer is built from LSTM cells, one at each timestep. We do not give a detailed description of LSTM cells here. An interested reader can find more information in Hochreiter and Schmidhuber (1997). At each time step, the update rule (3.1) is used to obtain the wealth state $x_i$, which we feed as an input for the first LSTM layer, as shown in Fig. 4. It is important to note that learning the optimal portfolio $\pi$ is a challenging problem, since the portfolio at each timestep depends indirectly on the previous portfolio values. Our network architecture captures this dependency through hidden states $h_i^j$ and cell states $c_i^j$ for $i \in [R]$ and $j = 1,2.$ Second LSTM layer is used mainly to take into account the non-linearity of our problem and consequently the non-linearity of the solution $\pi$. After the second LSTM layer returns its hidden state $h_i^2 \in \mathbb {R}^d$, we feed it to another linear network of the form (3.3), which at last yields $\pi _i$. To summarize, our network takes as input the initial stock value $[s_0, \ldots , s_0]^\top \in \mathbb {R}^d$, Brownian motion increments $B \in \mathbb {R}^{M \times d_B \times R}$ and jump increments $J \in \mathbb {R}^{M \times d_N \times R}$ and returns an output $(x_0,\pi ) \in \mathbb {R}^{M \times R+1},$ where we can interpret $x_0$ as option price and $\pi$ as hedging portfolio.

Fig. 4

Neural network architecture with two LSTM layers. Dashed lines represent the update rule in Eq. (3.1)

Once done, we compute loss$(s_R,x_R)$ and use backpropagation to update the weights. In particular, the Adam optimizer is used. It feels befit to note here how the backpropagation approach to modifying the weights connects naturally to the theoretical control problem we solve in Sect. 2. Recall, in the Stackelberg game approach, we first determine the optimal portfolio $\hat{\pi }_z$ given arbitrary initial state z, and only after that do we also find the optimal initial state $\hat{z}$ where behavior under the above portfolio is assumed. Similarly, we start with an arbitrary initial state and portfolio when taking the deep learning approach. Then, once the loss is computed, we modify weights in a backward manner. Hence, we first modify weights responsible for the selection of portfolio $\pi _{x_0}$ given (at the moment arbitrary) initial wealth $x_0$, and only after that do we also modify the weights associated with the initial wealth.

Remark 3.1

Since the control process $\pi$ is $\mathbb {F}$-adopted, one may feel inclined to use the Brownian motion sequence $(B_i)_{i=1}^R$ as an input for the LSTM network. Indeed, it holds $\mathcal {F}^X_t \subseteq \mathcal {F}_t$, so it may happen that using the sequence $(x_i)_{i=1}^R$ as an input may result in sub-optimal controls. However, as it is shown in Eq. (2.3), the optimal control is of the feedback form; hence, the choice of $(x_i)_{i=1}^R$ as the data input is reasonable. Apart from that, as discussed in Han and Ruimeng (2021), taking $(B_i)_{i=1}^R$ as an input, does not improve the performance.

To summarize, let us present our Algorithm 1 in a more compact way.

3.3 Numerical results

Here, we present the numerical results obtained using Algorithm 1. For calculations, we used the PyTorch library from Python. The hidden dimension is set to 512, batch size to 256, and the learning rate to 0.0005. Unless stated otherwise, we set time maturity $T=1$. To assess the results, an evaluation set of size 10,000 is used. The programming code can be found on the GitHub repository: https://github.com/janrems/DeepLearningQHedging.

We examine four market models: the standard Black–Scholes (BS) model, the BS model with multiple independent Brownian motions, the Merton model, and the Kou double exponential jump diffusion model. Our analysis focuses on the convergence of losses in all these models. For the first three models, we explore the convergence of initial values toward the specified option price, as well. Additionally, we compare the predicted hedging portfolio to its analytical counterpart for both variations of the BS model. Furthermore, we assess the algorithm’s performance as the input dimension increases. In the continuous case, we achieve this by comparing results from the two studied BS variations. In jump models, we test scalability concerning the input dimension in a Merton case. Finally, we investigate the scalability of the algorithm in the temporal dimension, specifically when adjusting the timestep parameter R and maturity T.

3.3.1 Black–Scholes market model

For the BS model, we take the number of time steps $R=80$. Recall that the BS model is a case of the complete market model, which means that there exist initial wealth and optimal hedging portfolio that, at least in a continuous case, assures $loss = 0.$ Apart from that, we have nice analytic solutions for both option price and hedging portfolio.

We consider a case where in Eq. (3.1), we set $\alpha _0= 0.3,$ $\sigma _0=0.2,$ $\gamma _0=0$, and $\lambda =0$, while we put $s_0 = 1$ and $K=0.5.$ Different choices of listed parameters result in different training times but do not affect the model’s accuracy. For this particular choice of parameters, we compute 6000 epochs.

Fig. 5

Convergence of loss and initial values and one market realization for the BS model

All the results presented here and in the other models are obtained in the following way. At the epoch where the minimal loss is achieved, we save the network weights. Then, using those weights, we evaluate our model on a larger evaluation set of size 10,000.

The first two outputs of the algorithm are the optimal initial wealth $\hat{x}_0$ and the minimal obtained loss $\textrm{loss}_\textrm{min}$. Both of them can be found in Table 1. In Fig. 5a, b, we can see how loss and initial value $x_0$ both converge toward 0 and theoretical BS option price 0.5, respectively.

Now, let us take a look at our algorithm’s other output, namely hedging portfolio $\pi .$ Unlike initial value $x_0$ which is deterministic, portfolio $\pi$ differs over different market realizations. We select portfolio realizations obtained on the evaluation set and denote them with $\hat{\pi }.$ We also wish to determine how close $\hat{\pi }$ is to theoretical portfolio given by the BS model. To obtain its discrete version from our discrete stock process $s_{i \in [R]}$, we define

$$\begin{aligned} d_i = \frac{1}{\sigma _0 \sqrt{t_R-t_i}}\Bigg ( \log \bigg (\frac{s_i}{K} \bigg ) + \frac{\sigma _0^2}{2}(t_R-t_i) \Bigg ), \end{aligned}$$

and put

$$\begin{aligned} \varphi _i = \Phi (d_i)\frac{s_i}{x_i}, \end{aligned}$$

where $\Phi$ stands for the standard normal cumulative distribution function.

We define and estimate the distance between $\hat{\pi }$ and $\varphi$ as a discrete $L^2$ distance estimate, namely

$$\begin{aligned} \textrm{d}(\hat{\pi }, \varphi ) = E\bigg [ \Vert \hat{\pi } - \varphi \Vert _{L^2} \bigg ] \approx \frac{1}{M} \sum _{j \in [M]}\sqrt{ \sum _{i \in [R]} (\hat{\pi }_i^{(j)} - \varphi _i^{(j)})^2 \Delta _t}. \end{aligned}$$

(3.4)

We can see one instance of market realization, namely the stock process s, state process x, computed portfolio $\hat{\pi }$, theoretical portfolio $\varphi$, and option payoff at terminal time F in Fig. 5c.

The estimated portfolio follows the theoretical one closely. Moreover, as expected, we manage for the terminal wealth to be almost exact to the option payoff.

Table 1 Comparison of theoretical and numerical results in BS model

3.3.2 Black–Scholes market with multiple independent Brownian motions

In contrast to the classical Black–Scholes market with one Brownian motion, here the noise in the model comes from multiple independent Brownian options. In turn, this results in a non-complete market model. Let us recall that this means that there is no guarantee that the terminal wealth $X_T$ equals the option payoff F almost surely. Besides, there is, in general, a continuum of possible option prices. However, as it was discussed in Sect. 2.4.1, in the case of the European call option, following the minimal variance hedging approach, we end up with the price and the optimal hedging strategy coming from the classical Black–Scholes market with single Brownian motion and corresponding volatility coefficient equal to the norm of volatility coefficients of multi-dimensional Brownian motion.

This gives us a nice opportunity to study how our algorithm scales in the presence of multi-dimensional noisy input. We choose the same parameters as in the previous section, the only difference being the volatility coefficient, which is now, of course, multi-dimensional and given by $\sigma _0 = [0.11, 0.16, 0.05].$ Note that we have $\Vert \sigma _0 \Vert = 0.2$.

Fig. 6

Convergence of loss and initial values and one market realization in the BS model with multiple Brownian motions

Comparing both results in Table 2 and graphs in Fig. 6 with their counterparts in Sect. 3.3.1, we can see that our algorithm scales well with the increased size of the input. Even though the results in both tables differ a bit, it is only natural because of the random nature of our machine learning algorithm.

Table 2 Comparison of theoretical and numerical results for the BS model with multiple Brownian motions (BSMB)

3.3.3 Merton market model

In our particular example of the Merton model, we follow the setting from Sect. 2.5 and again use Algorithm 1, where we set parameters to $\alpha _0= 0.2,$ $\sigma _0=0.2,$ $\gamma _0=1,$ $s_0 = 1$ and $K=0.5.$ For the log-normally distributed jumps, we set expected value $\mu = -0.2$ and standard deviation $\delta = 0.05,$ while jump intensity $\lambda =5.$ Because of the downward jumps, we need to work with finer discretization to avoid negative wealth and stock values. Hence, we choose $R=150$, which in turn leads to longer training time, since we now have 150 times 2 LSTM cells in our NN. As the stock process is noisier than the one in the BS case, so is the portfolio, which in turn also means a harder learning task. We use 7000 epochs and disregard the training rounds where negative jumps occur.

In Fig. 7c, we see one market realization at the epoch at which the lowest loss was obtained.

The portfolio is much more dynamic, which, as discussed, results in slower learning. Furthermore, we see a more significant gap between terminal wealth and option payoff.

Fig. 7

Convergence of loss and initial values and one market realization for the Merton model

As we can see in Fig. 7a, b, both losses and initial values converge toward desired quantities. However, we can see that convergence becomes slow after just 3000 epochs. Tackling the plateau problem with, for instance, scheduling the learning rate is one of the tasks for future work. Notice there are a few spikes in both of these graphs. We believe that they are due to computational errors that occur when the wealth process takes values close to zero, which is more often than in the previous two cases due to downward jumps.

The option price for the case of the Merton model is given by Eq. (2.28). Using the Monte Carlo approach, we get an estimation $\hat{z} = 0.519$. Here, we again emphasize that this price differs from the one presented by Merton in Eq. (2.26), which equals 0.515 for our particular choice of parameters. This means that the difference between the option price proposed in Merton (1976) and the minimal variance price is nontrivial in practice. In Fig. 8, we can see how the distribution of the differences between terminal wealth and option payoff in Merton’s and our approach differ. We can see that using Merton’s portfolio, one usually observes small gains, which are balanced with occasional large losses. On the other hand, the distribution is symmetric around zero using our approach. Apart from that, we are able to avoid large losses entirely, which is an advantage. Consequently, using a minimal variance hedging strategy is more costly, as discussed in Sect. 2.5.

Fig. 8

Distribution of the difference between terminal wealth and option payoff under Merton’s and our approach in 1000 realizations

The performance of our deep learning algorithm for the Merton model is presented in Table 3. Compared to the performance in the BS case, the error of price prediction is around ten times higher, which is due to the increased volatility in the model.

Table 3 Comparison of theoretical and numerical results in Merton model

In the case of both complete and incomplete markets, we showed that the deep learning algorithm performs well by comparing the results with cases where explicit solutions or at least Monte Carlo estimates are available.

To analyze the scalability of the algorithm concerning an increase in input dimension, similar to the continuous case, we examine the Merton model jump diffusion process driven by a multi-dimensional compound Poisson process. Specifically, we compare the outcomes with a one-dimensional version guided by a modified compensated Poisson process using mixed distributions. We make use of the following well-known result.

Proposition 3.2

Let $X_1(t) = \sum _{i=1}^{N_1(t)} Y^1_i$ and $X_2(t) = \sum _{i=1}^{N_2(t)} Y^2_i$ be two compound Poisson processes where $N_1(t)$ and $N_2(t)$ are independent homogenous Poisson processes with intensities $\lambda _1$ and $\lambda _2$, respectively. Furthermore, jumps $Y_i^1$ and $Y_i^2$ are independent, coming from possibly different distributions. Consider now N(t), a homogenous Poisson process with intensity $\lambda = \lambda _1 + \lambda _2$ and random variables

$$\begin{aligned} Y_i \sim \begin{pmatrix} &{}Y_i^1 \qquad &{}Y_i^2 \\ &{}\frac{\lambda _1}{\lambda _1 + \lambda _2} \qquad &{}\frac{\lambda _2}{\lambda _1 + \lambda _2} \end{pmatrix}. \end{aligned}$$

Then, processes $X(t) = \sum _{i=1}^{N(t)} Y_i$ and $X_1(t) + X_2(t)$ have the same distribution.

This result easily extends to the sum of an arbitrary number of compensated Poisson processes. For simulation purposes, we select a three-dimensional compound Poisson process with intensities [3, 5, 2]. The log-normal jumps have means [0.1, 0.1, 0.05] and standard deviations [0.05, 0.02, 0.01]. The obtained results are presented in Table 4. Once again, the similarity in the results indicates that our algorithm scales effectively even in cases involving discontinuous multi-dimensional input.

Table 4 Comparison of theoretical and numerical results in Merton model

3.3.4 Kou market model

Here, we present numerical results for a market model introduced in Kou (2002). Kou proposed a model where the stock’s behavior is governed by a jump diffusion process where the jumps have a double exponential distribution. This means that we can use the same type of discretization as for the Merton case described in Eqs. (3.1) and (), where the jump variables $Y_i^l$ now follow a double exponential distribution:

$$\begin{aligned} Y_i^l \sim \begin{pmatrix} &{}\text {Exp}(\eta ^l_1) \qquad &{} -\text {Exp}(\eta ^l_2) \\ &{}p^l \qquad &{}1-p^l \end{pmatrix}, \end{aligned}$$

where $p^l \in [0,1]$ represents the probability of exponentially distributed jump being either upward or downward. To ensure the existence of moments, we need additional conditions on intensities of the positive jump part, and hence, $\eta ^l_1 >1$, while $\eta _2^l > 0$. The compensator of the drift in Eq. (3.1) changes accordingly and has components

$$\begin{aligned} k^l = p^l \frac{\eta ^l_1}{\eta ^l_1 - 1} + (1-p^l) \frac{\eta _2^l}{\eta _2^l + 1} -1. \end{aligned}$$

Unfortunately, the property of jumps being both positive and negative and having heavier tails makes the Kou model impractical when one wants to obtain option price through equivalent martingale measures and Monte Carlo approach as described in Sect. 2.5. The reason is that the condition $G(e^{Y_i^l}-1) >-1$, for G as in Eq. (2.27), is not satisfied for general choice of parameters $\eta _1^l$, $\eta _2^l$, and $p^l$.

Nonetheless, the option price can still be obtained through the use of the deep learning algorithm. Again, to avoid negative wealth and stock values, we select $R=150.$ Due to the heaviness of the tails in jump distribution, one needs to be careful when choosing parameters. In particular, $\eta _2$ should not be too small. Here, we choose $s_0 = 1, K=0.5,$ $\alpha _0 = 0.15, \sigma _0 = 0.2, \gamma _0 = 1, \lambda =10, \eta _1 = 50, \eta _2 = 25$, and $p=0.3$. According to Kou (2002), these parameters should reflect the ones observed on the US stock market. Graphs of the loss and initial value convergence and a graph of one market realization can be found in Fig. 9. The minimal obtained loss is 1.54e$-$5, lower than the losses recorded for the Merton model due to the choice of less noisy parameters. The algorithm predicts the initial wealth value $x_0 = 0.4987$. We know that the true option price should be higher than the BS price of 0.5 but not by much due to more conservative jump parameters. Hence, the predicted result does not seem too far off. The reason for the undershoot in the predicted initial value is the inclusion of the positive jumps in the Kou model.

Fig. 9

Convergence of loss and initial values and one market realization for the Kou model

A possible additional direction for advancing the current study is to explore the utilization of deep learning algorithms in pricing American and path-dependent options within the context of the double exponential jump diffusion model, drawing inspiration from the research conducted in Kou and Wang (2004).

3.3.5 Scalability in temporal dimension

In this section, we explore how the algorithm’s performance is influenced by variations in the temporal dimension. Specifically, we consider different time maturities T and varying numbers of timesteps R.

We examined the algorithm’s performance within the context of both the complete BS market model and the incomplete Merton market model. Various combinations of parameters T and R were scrutinized. The financial model parameters remain consistent with those outlined in Sects. 3.3.1 and 3.3.3.

Concerning machine learning parameters, we maintained a batch size of 256, a hidden dimension of 512, and a learning rate of 0.0005. For practical considerations, we conducted the learning process for a fixed 3000 epochs in each studied case. In both market models, the algorithm’s performance was evaluated by comparing the loss and the absolute error of predicted option prices. For the BS model, the estimated expected $L^2$ loss defined in Eq. (3.4) was also included in the assessment.

Results are presented in Tables 5 and 6 for the BS and Merton models, respectively.

Table 5 Comparison of algorithm performance for different choices of timesteps R and maturities T-BS model

It should be stated that due to the random nature of both inputs and the algorithm presented results are noisy in nature as well.

Nonetheless, we may with large certainty conclude that the algorithm’s performance decreases with increasing maturity. This is particularly evident in the absolute error of option prices (Table 5b) and the expected $L^2$ distance (Table 5c). The use of discrete Euler–Maruyama approximation to the continuous solution likely contributes to this trend, where errors accumulate over time. We believe that enhanced computing power may contribute to improved performance through finer discretization, extended training time, and higher hidden dimensions.

In examining performance concerning the discretization parameter R, it is harder to draw strong conclusions, since the difference in results is less significant. It seems that finer discretization positively impacts the algorithm’s performance in terms of loss and absolute error in option prices. Conversely, an inverse trend is observed in the expected $L^2$ distance. This discrepancy may arise from increased variation in the discrete theoretical portfolio as the number of timesteps grows. Nevertheless, focusing on loss and option price, which are the key outputs of our algorithm, we find a positive response to an increased number of discretization points. As discussed earlier, this may prove beneficial when considering longer maturities.

Table 6 Comparison of algorithm performance for different choices of timesteps R and maturities T-Merton model

Before presenting the results for the Merton case, we must first address the problem regarding the use of discretizations with a small number of timesteps, which was already mentioned in Sect. 3.3.3. To circumvent the problem of negative wealth and stock values, we present an alternative discretization approach. Instead of directly working with the discrete wealth process x given by the update rule in Eq. (3.1), we take its logarithm. Using Itô’s formula and Euler–Maruyama scheme, we obtain its discrete version through an update rule

$$\begin{aligned} {y_{i+1} = y_i + \left[ (\alpha _0 - \lambda ^\top k) \pi _t - \frac{\pi _t^2 \sigma _0^\top \sigma _0 }{2}\right] \Delta _t + \pi _t \sqrt{\Delta _t} B_i \sigma _0+ \log \left( \gamma _0 \pi _t J_i +1\right) ,} \end{aligned}$$

where $y_0 = \log (x_0)$ and then put $x_i = \exp (y_i)$. The same is done for the discrete stock process s where we additionally put $\pi = 1$.

Let us now present the results regarding the Merton case. In Tables 6a, b, we see that the algorithm responds to changes in maturity and the number of timesteps similarly as in the BS case. The algorithm’s worse performance is due to the increased randomness in the model, as it was explained in Sect. 3.3.3. Additionally, it must be mentioned that the algorithm’s performance slightly decreases when the logarithmic approach outlined above is used. This decline could be attributed to the non-linear dependence of the process y on the control variable $\pi$. Hence, for the jump diffusion models, we advise the use of the original update rule with the number of timesteps at least 150.