U-statistics Based Tests for Marginal Hazard Rate Orderings of Two Dependent Variables

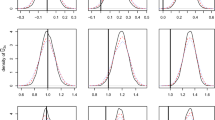
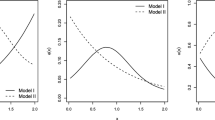
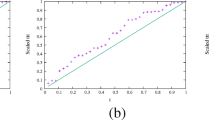
Abstract

We aim to compare marginal distributions of a bivariate random vector (X, Y) with reference to their hazard rates, $(h_F(t), h_G(t))$. In many applications, it is likely that the marginal hazard rates are ordered, e.g., $h_F(t) \le h_G(t)$. We consider two U-statistics based tests for testing equality of the marginal hazards against the alternative that they are ordered. Further, we compare these tests with the existing W and S tests when X and Y are assumed to be independent. The two proposed statistics are also extended to cover situations when the pair (X, Y) is subjected to independent univariate censoring. We provide extensive simulation studies based on copulae where the power performance of these tests is assessed. The marginal distributions considered are Weibull, linear failure rate, Gompertz and three other families of distributions based on copulae. We apply the tests to two real data examples.

Appendices

Symmetric Kernel and Asymptotic Distribution of $U_{fc}$ (10)

The symmetric version of the kernel (9) is obtained by averaging over 6 combinations, as defined below.

$$\begin{aligned} \phi _{fc}(\widetilde{Z}_1, \widetilde{Z}_2, \widetilde{Z}_3) = \left\{ \begin{array}{ l l } 1/6, &{} (\delta _1^x = 1, \delta _1^y = 1, U_1< T_1, U_1< U_2, T_1< T_3) \\ \\ &{} \text {or} \; (\delta _1^x = 1, \delta _1^y = 1, U_1< T_1, U_1< U_3, T_1< T_2) \\ \\ &{} \text {or} \; (\delta _2^x = 1, \delta _2^y = 1, U_2< T_2, U_2< U_1, T_2< T_3) \\ \\ &{} \text {or} \; (\delta _2^x = 1, \delta _2^y = 1, U_2< T_2, U_2< U_3, T_2< T_1) \\ \\ &{} \text {or} \; (\delta _3^x = 1, \delta _3^y = 1, U_3< T_3, U_3< U_1, T_3< T_2) \\ \\ &{} \text {or} \; (\delta _3^x = 1, \delta _3^y = 1, U_3< T_3, U_3< U_2, T_3< T_1) \\ \\ -1/6, &{} (\delta _1^x = 1, \delta _1^y = 1, U_1< T_1, U_1< T_3, T_1< U_2) \\ \\ &{} \text {or} \; (\delta _1^x = 1, \delta _1^y = 1, U_1< T_1, U_1< T_2, T_1< U_3) \\ \\ &{} \text {or} \; (\delta _2^x = 1, \delta _2^y = 1, U_2< T_2, U_2< T_1, T_2< U_3) \\ \\ &{} \text {or} \; (\delta _2^x = 1, \delta _2^y = 1, U_2< T_2, U_2< T_3, T_2< U_1) \\ \\ &{} \text {or} \; (\delta _3^x = 1, \delta _3^y = 1, U_3< T_3, U_3< T_1, T_3< U_2) \\ \\ &{} \text {or} \; (\delta _3^x = 1, \delta _3^y = 1, U_3< T_3, U_3< T_2, T_3< U_1) \\ \\ 0, &{}{} \; \text {otherwise}.\\ \\ \end{array} \right. \end{aligned}$$

(18)

In order to obtain the asymptotic variance of $U_{fc}$, we first define and derive $\psi _{fc}(z_i)$ as follows.

$$\begin{aligned} \psi _{fc}(z_i)=E[\phi _{fc}(\widetilde{Z}_i,\widetilde{Z}_j, \widetilde{Z}_k)| \widetilde{Z}_i = z_i] \end{aligned}$$

Then

$$\begin{aligned} E(\psi _{fc}(Z_i)) = E(U_{fc}), \end{aligned}$$

and

$$\begin{aligned} \sigma _{1c}^2 = Var(\psi _{fc}(Z_i)) = E[\psi _{fc}(Z_i)]^2 - E^2[\psi _{fc}(Z_i)] \end{aligned}$$

If $E[\psi _{fc}(Z_i)]^2 < \infty$ and $\sigma _{1c}^2>0,$ then $\sqrt{n} (U_{fc}-E(U_{fc})) \xrightarrow {d} N(0, 9\sigma _{1c}^2) \ as \ n \rightarrow \infty .$ Under the null hypothesis, $E(U_{fc}) = 0.$

Fig. 1

Otitis media data. Ratio of the Kaplan-Meier estimates of the survival functions of survival times of the surgically inserted ventilating tubes in the left ear (X) to that in the right ear (Y). Black and red colour show the estimated ratios for the control and the treatment groups, respectively

Fig. 2

Insurance data. Ratio of estimates of survival functions of ages of a couple at contract initiation for the entire data (ALL) and a randomly selected sample of size 500 (Sample), for $20\%$ censoring imposed on the complete data and on the selected sample (ALL 20% and Sample 20%)

Theorem 2

When $\sigma _{1c}^2 = Var[\Psi _{fc}(Z_i)] >0$, $\sqrt{n}(U_{fc} - E(U_{fc})) \xrightarrow {d} N(0,9\sigma _{1c}^2) \ as \ n \rightarrow \infty$. Also, $E(U_{fc}) = 0$ under $H_{0f}.$

W and S Tests

We review tests W and S (Kochar [13, 14]), and provide computational details here. Let $X_1, X_2,...X_n$ and $Y_1, Y_2,..., Y_m$ be independent random samples from the two distributions F and, G respectively. Let $X_{(1)}, X_{(2)},...,X_{(n)}$ be the order statistics of the X-sample and $Y_{(1)}, Y_{(2)},...,Y_{(m)}$ be the order statistics of the Y-sample. The U-statistic W in terms of rank representation, is defined as

$$\begin{aligned} W ={} & {} \sum _{i=1}^{n} (n-i) {{R_{(i)}-i}\atopwithdelims (){2}} - \sum _{j=1}^{m} (m-j) {{S_{(j)}-j}\atopwithdelims (){2}} + \\{} & {} \sum _{j=1}^{m} (s-S_{(j)}+j) (j-1) (S_{(j)}-j) - \sum _{i=1}^{n} (R_{(i)}-i) (m-R_{(i)}+i) (n-i), \end{aligned}$$

where $R_{(i)}, i= 1,2,...,n$ and $S_{(j)},j=1,2,...,m$ are the ranks of $X_{(i)}$ and $Y_{(j)},$ respectively, in the combined sample of X and Y observations. Detailed proof of the above representation is available in Kochar [12].

To compare the performance of the proposed tests with the W test, we take $n=m.$ Hence, under $H_0, E(W)=0,$ and

$$\begin{aligned} V(W)= \frac{1}{210 \left( {\begin{array}{c}n\\ 2\end{array}}\right) ^2} \Big [32 n^3-28n^2-6n+8\Big ]. \end{aligned}$$

Asymptotically as $n \rightarrow \infty$, $\sqrt{2n} ~ W \sim N(0, 128/105).$

Let $Y_{(1)}, Y_{(2)},...,Y_{(m)}$ be the order statistics of the Y-sample, and let $\tilde{S}_{(j)}$ denote the rank of the $Y_{(j)}$ in the combined increasing arrangement of $X's$ and $Y's$. Then the S-statistic can be expressed as

$$\begin{aligned} S=\frac{1}{nm} \Big (\sum _{j=1}^{m}a_j \tilde{S}_{(j)}- \sum _{j=1}^{m} j a_j \Big ), \end{aligned}$$

where $a_j = \frac{1}{2}+log\{1-j/(m+1)\}.$ Under $H_0$ and when $n=m$,

$$\begin{aligned} E(S) = \frac{1}{n(n+1)}\sum _{j=1}^{n} j a_j, \;\; V(S) = \frac{(2n+1)}{n^3(n+2)(n+1)^2} ~ a' ~ \Omega ~ a, \end{aligned}$$

where the matrix $\Omega =((w_{ij})) (i,j = 1,2,...,n),$ has $w_{ij}=i(m+1-j)=w_{ji}$ for $i\le j$ and $a' = (a_1, a_2,...,a_n).$ Then, asymptotically, as $n \rightarrow \infty$, $(S-E(S))/\sqrt{V(S)} \sim N(0,1).$