Using Weighted Differences in Hazards as Effect Sizes for Survival Data

Abstract

Sensitive to the change in sample sizes, traditional measures such as values of test statistics or p values can fail to quantify the difference in survival between populations for time-to-event data. We thereby propose to use effect sizes defined as the weighted differences in hazards to evaluate the survival difference between two groups. On the basis of the logrank test statistic, Gehan–Wilcoxon test statistic and Prentice–Wilcoxon test statistic, we developed three effect sizes that compare the survival experiences over the time period of investigation. Estimates of these three effect sizes were provided and their large sample behaviors were studied. In light of the Mann–Whitney parameter, we presented an effect size that compares the survival experiences over the entire possible/hypothetical time period. Two estimates of this effect size were constructed. We compared the proposed effect sizes and illuminated their use by theoretical studies, simulations and real cancer data. The effect sizes proposed in this article can help understand the survival difference in populations and are expected to have promising applications in the field of survival analysis.

1 Introduction

To report the difference (with respect to some characteristics, e.g., weight, blood pressure value) between two groups (populations), there is nothing more common than to conduct a hypothesis test and check the “statistical significance.” However, along with a series of criticism [2, 44], the conventional, dichotomous way of using the p value (e.g., $\le 0.05$ and $> 0.05$) has faced an unprecedented debate for its abuse and misuse. To that end, there is a need to find surrogate measures that can genuinely present findings from different studies in the hope of drawing better inferences.

It seems that the p value, even without being dichotomized, could not serve as such a measure of the difference between groups. This is mainly because the p value is influenced by the change in sample sizes and there is no simple relationship between the sample size and the p value that can be used to adjust the result. What measures would better describe the difference between groups?

A recommended alternative would be the effect size [2, 44]. An effect size is a quantitative measure of the magnitude of a phenomenon and is unaffected by the change in sample sizes. When analyzing or mining data, effect sizes allow researchers to ensure that statistically significant effects inferred from a sample are substantial enough to be considered practically meaningful [27]. Certain effect sizes have been proposed for data types other than time-to-event, e.g., correlation coefficient, relative risk, Cohen’s d [11], etc. For time-to-event data with censoring involved, there does not seem to have much research focusing on effect sizes that can be used to assess the difference in survival between groups.

An obvious effect size for time-to-event data is the hazard ratio from the Cox model [12]. However, it has long been known that the hazard ratio is a valid measure only under the proportional hazards (PH) assumption. Applying PH analysis to studies where PH does not hold can lead to misleading conclusions [37]. Even worse is that the PH assumption is rarely checked formally. The commonly used tests for examining the PH assumption, such as Grambsch–Therneau test, may not capture non-PH in studies with small sample sizes, but always lead to a rejection when sample sizes are large [42]. Alternatively, the PH assumption can be examined by using residual plots (e.g., plotting martingale or Schoenfeld residuals against time), by checking the predictor–time interaction effect, or by visually looking at the survival curves. Note that these methods usually provide a subjective assessment. Therefore, it is important to find an informative estimate of the difference between two survival curves regardless of the PH assumption. In the current literature, there are two types of estimates toward this goal: the average hazard ratio (AHR) proposed by [38] and the restricted mean survival time (RMST) proposed by [37]. However, the interpretation of AHR can be difficult and misleading due to its complex definition [37]. And because it is difficult to select an appropriate period of time to compute RMST, the use of RMST seems to have been limited.

In this paper, we propose to use the weighted differences in hazards as effect sizes for studying the survival difference between two groups. The use of these proposed effect sizes do not impose any particular assumptions about the distributions of the failure time. They can be applied with or without the PH assumption. We will show that the commonly used logrank test statistic [30], Gehan–Wilcoxon test statistic [18], Prentice–Wilcoxon test statistic [35], as well as the well known Mann–Whitney parameter [29] can be exploited to develop such effect sizes.

This paper is organized in the following way. Section 2 introduces three test statistics-based effect sizes, estimates of the effect sizes and their large sample results. Section 3 introduces the Mann–Whitney parameter-based effect size and two estimates of the effect size. Section 4 presents a comparison among the proposed effect sizes. Section 5 partitions values of effect sizes to facilitate applications. Section 6 illustrates various aspects, including applications, of the proposed effect sizes by simulations and real cancer data. We conclude in Sect. 7.

2 Effect Sizes Based on Test Statistics

The logrank test is one of the most popular methods for testing the null hypothesis $H_0$ that there is no difference in the survival between two groups. The test is asymptotically fully efficient for testing equality of survival distributions in a proportional hazard family when no censoring is present or when the censoring distributions are the same for compared groups [28]. The original logrank test assigns an equal weight to each failure time. Gehan [18], Peto and Peto [34], Tharone and Ware [41], Prentice [35], Andersen [3] and Fleming and Harrington [17] modified the logrank test by assigning a different weight at each failure time so that the tests can be more sensitive to the difference in survival distributions in a particular time interval. Assigning varying weights over time to the logrank test produces weighted logrank tests that have been proven to be more efficient when hazards are non-proportional [16].

Suppose that two samples of survival data containing a total of n subjects are available, with sample i coming from group i. Let $t_1,\dots ,t_J$ be the distinct failure times in increasing order from the pooled sample. Let $D_{ij}$ and $Y_{ij}$ be, respectively, the number of subjects who failed and were at risk at $t_j$ in sample i $(i=1, 2 ; j=1, 2,\dots ,J )$. Also let $D_{j}$ and $Y_{j}$ be, respectively, the total number of subjects who failed and were at risk at $t_j$ in both samples. Then, the general form of the weighted logrank test statistic, denoted by $L_w$, is

$$\begin{aligned} L_w=\frac{\sum _{j=1}^{J}w_j\left( D_{1j}-D_j\frac{Y_{1j}}{Y_j}\right) }{\left( \sum _{j=1}^{J}w_j^2D_j\frac{Y_{1j}}{Y_j}\frac{Y_{2j}}{Y_j}\frac{Y_j-D_j}{Y_j-1}\right) ^{\frac{1}{2}}}, \end{aligned}$$

(1)

where the weight $w_j=w_n(t_j)$ for a positive weight function $w_n(\cdot )$. $L_w$ includes as special cases many well-known test statistics, such as the logrank test statistic (weights $w_j=1$), Gehan–Wilcoxon test statistic (weights $w_j=Y_j/n$) and Prentice–Wilcoxon test statistic (weights $w_j=\widehat{S}(t_j-)=\prod _{k: k < j}\left( 1-{D_k}/{Y_k}\right)$) [16].

It is known that $L_w$ is close to zero when two survival functions are almost identical to each other and has a large absolute value when two survival functions are far apart. Therefore, $L_w$ could serve as a measure of the difference in survival between two groups. However, the absolute value of $L_w$ tends to increase (without bound) as the sample size increases. Consequently, when the data size increases, the p value will decrease to 0, indicating that with a large data size the p value can be non-informative in quantifying differences. Therefore, none of $L_w$, $|L_w|$, and the p value, computed using big samples, can provide an appropriate measure of the difference in survival. It is then of interest to find a statistic that can measure the survival difference and at the same time is “unaffected” by changes in sample sizes. Such a statistic is an estimate of an effect size and can be derived in light of the numerator of $L_w,$ as shown in this paper. The denominator, an estimate of the standard deviation of the numerator under the null hypothesis $H_0$, will not be utilized in constructing estimates of effect sizes.

Along with our development, we will use several notations associated with the groups and samples. Let T denote the random variable of the actual failure time, C the random variable of the censoring time, X the minimum of T and C and Z the indicator of the group number with $Z=i$ indicating group i $(i=1, 2)$. Suppose that in the study, the assignment of a subject to group i has a probability $P_i$. For group i, let $\lambda _i(t)$, $f_i(t)$, $S_i(t)$ and $S^*_i(t)$ denote, respectively, the hazard function, density function of the failure time, survival function of the failure time and censoring survival function (i.e., the survival function of the censoring time). We assume that in each group the censoring distribution and the survival distribution are continuous and independent of each other. The above quantities can be combined into $\pi (t)=P(X\ge t)=\pi _1(t)P_1+\pi _2(t)P_2$ with $\pi _i(t)=P(X\ge t|Z=i)=S_i(t)S^*_i(t)$. The quantity $\pi _i(t)$ is the probability of being at risk (at time t) for subjects in group i. The following notations are needed for survival data. For sample i, let $n_i$ denote the total number of subjects under study, and $Q_i(t)$, $N_i(t)$ and $Y_i(t)$ represent, respectively, the number of subjects with observed or unobserved failure times larger than or equal to t, number of observed failures after time 0 up through and including time t and number of subjects at risk at time t. Note that $Q_i(t)$, $N_i(t)$ and $Y_i(t)$ depend on the sample size. To facilitate the calculation, we will use the convention 0/0 = 0.

Let U denote the numerator of $L_w$ in Eq. (1). We have

$$\begin{aligned} \frac{n}{n_1 n_2}U =\frac{n}{n_1 n_2}\sum _{j=1}^{J}w_j\left( \frac{D_{1j}Y_{2j}}{Y_j}-\frac{D_{2j}Y_{1j}}{Y_j}\right) =\sum _{j=1}^{J}w_j \frac{\frac{Y_{1j}}{n_1}\frac{Y_{2j}}{n_2}}{\frac{Y_j}{n}} \left( \frac{D_{1j}}{Y_{1j}}- \frac{D_{2j}}{Y_{2j}} \right) . \end{aligned}$$

Clearly, $\frac{Y_{1j}}{n_1}$, $\frac{Y_{2j}}{n_2}$, $\frac{Y_j}{n}$, $\frac{D_{1j}}{Y_{1j}}$, $\frac{D_{2j}}{Y_{2j}}$ are the estimates, respectively, of $\pi _1(t_j)$, $\pi _2(t_j)$, $\pi (t_j)$, $\lambda _1(t_j)\varDelta t$, $\lambda _2(t_j) \varDelta t$, where $\varDelta t$ is the length of an infinitesimal interval of the time. Below we will show that the limit of $\frac{n}{n_1 n_2}U$ ($n\rightarrow \infty$) is a weighted difference (via integration) between two hazard functions of the two groups. This indicates $\frac{n}{n_1 n_2}U$ could be used to estimate the effect size that measures the difference in survival experiences between group 1 and group 2.

Theorem 1

Suppose that $w_n(t)$ is a predictable process such that $0 \le |w_n(t)| \le 1$ for all $t \in [0, \infty ]$. Also suppose that for almost all t, $w_n(t)$ converges in probability to a deterministic function $\omega (t)$. Then

$$\begin{aligned} \frac{n}{n_1 n_2}U\overset{P}{\rightarrow }\int _0^\infty \frac{\pi _1(t)\pi _2(t)}{\pi (t)}\omega (t)(\lambda _1(t)-\lambda _2(t)) \mathrm{d}t, \end{aligned}$$

provided that the integrand is absolutely integrable.

Proof

See “Appendix 1”.

The expression of $\int _0^\infty \frac{\pi _1(t)\pi _2(t)}{\pi (t)}\omega (t)(\lambda _1(t)-\lambda _2(t))\mathrm{d}t$ in Theorem 1 is a weighted difference in hazards with weight at time t equal to $\frac{\pi _1(t)\pi _2(t)}{\pi (t)}\omega (t)$ and does not depend on the sample size. Therefore, it can serve as an effect size measuring the survival difference between two groups. In general, this effect size is unknown. Theorem 1 shows that an estimate of the effect size, i.e., $\frac{{n}}{{n_1n_2}}U$, can be computed using the data at hand.

In many cases, it is straightforward to verify the conditions in Theorem 1. Let $\widehat{ES}_L,$ $\widehat{ES}_G,$ and $\widehat{ES}_P$ denote $\frac{{n}}{{n_1n_2}}U$ corresponding to the weight selection for the logrank, Gehan–Wilcoxon and Prentice–Wilcoxon test statistic, respectively. That is,

$$\begin{aligned}&\widehat{ES}_L \equiv \frac{n}{n_1 n_2}\sum _{j=1}^{J}\left( \frac{D_{1j}Y_{2j}}{Y_j}-\frac{D_{2j}Y_{1j}}{Y_j}\right) , \end{aligned}$$

(2)

$$\begin{aligned}&\widehat{ES}_G \equiv \frac{n}{n_1 n_2}\sum _{j=1}^{J}\frac{Y_j}{n}\left( \frac{D_{1j}Y_{2j}}{Y_j}-\frac{D_{2j}Y_{1j}}{Y_j}\right) ,\end{aligned}$$

(3)

$$\begin{aligned}&\widehat{ES}_P \equiv \frac{n}{n_1 n_2}\sum _{j=1}^{J}\prod _{k: k < j}\left( 1-\frac{D_k}{Y_k}\right) \left( \frac{D_{1j}Y_{2j}}{Y_j}-\frac{D_{2j}Y_{1j}}{Y_j}\right) . \end{aligned}$$

(4)

Then it follows from Theorem 1 that the following results hold true.

Corollary 1

(a) If $E_i[\lambda _{3-i}(t)/\lambda _{i}(t)] <\infty$ ($i=1,2$), where the expectation is taken with respect to the failure time in group i, then $\widehat{ES}_L \overset{P}{\rightarrow }\int _0^\infty \frac{\pi _1(t)\pi _2(t)}{\pi (t)}(\lambda _1(t)-\lambda _2(t)) \mathrm{d}t,$ where the integrand is absolutely integrable.

(b) $\widehat{ES}_G \overset{P}{\rightarrow } \int _0^\infty \pi _1(t)\pi _2(t)(\lambda _1(t)-\lambda _2(t))\mathrm{d}t,$ where the integrand is absolutely integrable.

(c) If $S^*_1(t)=S^*_2(t)=S^*(t)$, then $\widehat{ES}_P \overset{P}{\rightarrow } \int _0^\infty S^*(t)S_1(t)S_2(t)(\lambda _1(t)-\lambda _2(t))\mathrm{d}t =\int _0^\infty \frac{\pi _1(t)\pi _2(t)}{S^*(t)}(\lambda _1(t)-\lambda _2(t))\mathrm{d}t$, where the integrand is absolutely integrable.

Proof

See “Appendix 2”.

The Corollary indicates that $\widehat{ES}_L,$ $\widehat{ES}_G,$ and $\widehat{ES}_P$ estimates, respectively, the following three effect sizes:

$$\begin{aligned}&{ES}_{L}{\mathop {=}\limits ^{\text { def }}} \int _0^\infty \frac{\pi _1(t)\pi _2(t)}{\pi (t)}(\lambda _1(t)-\lambda _2(t)) \mathrm{d}t, \end{aligned}$$

(5)

$$\begin{aligned}&ES_{G}{\mathop {=}\limits ^{\text { def }}} \int _0^\infty \pi _1(t)\pi _2(t)(\lambda _1(t)-\lambda _2(t))\mathrm{d}t, \end{aligned}$$

(6)

and

$$\begin{aligned} ES_{P}{\mathop {=}\limits ^{\text { def }}} \int _0^\infty \frac{\pi _1(t)\pi _2(t)}{ S^*(t)}(\lambda _1(t)-\lambda _2(t)) \mathrm{d}t. \end{aligned}$$

(7)

Clearly, all three integrals depend on the censoring distribution. The proof of the corollary shows that both $ES_G$ and $ES_P$ belong to the interval $[-2, 2]$. Actually, Sect. 4.2 will show $ES_G$ is a difference between two probabilities and thus lies inside the interval $[-1, 1]$. In comparison, there are no constants a and b such that any $ES_L$ lies inside the interval [a, b]. Note that $ES_L$, $ES_G$ and $ES_P$ from the formulas can be negative and their magnitudes (i.e., the absolute values) are often the main interest in practical use. It follows from their definition that a positive (negative) effect size means a positive (negative) weighted difference in hazards between the two groups, which implies a “higher” (“lower”) hazard in group 1 than in group 2. This information can be useful when comparing two groups. For instance, if group 1 represents the treatment and group 2 represents the control, then a positive $ES_L$ implies an adverse effect from the treatment.

3 Effect Sizes Based on the Mann–Whitney Parameter

The Mann–Whitney parameter $P(T_1>T_2)$ assesses the stochastic ordering between the distributions of two variables $T_1$ and $T_2$. In this paper, $T_i$ is the variable of actual failure time in group i for $i=1,2$. If $P(T_1>T_2)=0.5$, then $T_1$ and $T_2$ are “statistically indifferent” to each other; if $P(T_1>T_2)>0.5$, then $T_1$ is “statistically preferred” to $T_2$ [33]. Therefore, $P(T_1>T_2)$ can serve as a measure of the difference between two distributions of $T_1$ and $T_2$. Based on $P(T_1>T_2),$ we define

$$\begin{aligned} ES_{\mathrm{MW}}=1- 2P(T_1>T_2) \end{aligned}$$

(8)

as an effect size of the difference between two distributions. Note that $ES_{\mathrm{MW}}$ ranges from $-1$ to 1, with its minimum $-1$ and maximum 1 corresponding to $P(T_1>T_2)=1 \text{ and } 0$, respectively. As in the test statistic-based effect sizes, often the magnitude of $ES_{\mathrm{MW}}$ is of interest for comparisons.

In order to estimate $ES_{\mathrm{MW}}$, it suffices to estimate $P(T_1 > T_2)$. When data are free of censoring, $P(T_1>T_2)$ can be estimated by the Mann–Whitney test statistic [29]. If censoring exists, $P(T_1>T_2)$ cannot be estimated by the Mann–Whitney test statistic since some actual failure times are unknown. In this case, an alternative way to estimate $P(T_1>T_2)$ is needed. Note that

$$\begin{aligned} P(T_1> T_2) =\int ^\infty _{t=0}\int ^\infty _{s=t}f_1(s)f_2(t)\mathrm{d}s\mathrm{d}t =-\int ^\infty _{0}S_1(t)dS_2(t), \end{aligned}$$

(9)

where $S_i$ and $f_i$ are, respectively, the survival function and density function for $T_i$ $(i=1, 2)$. Let $\widehat{S}_1$ and $\widehat{S}_2$ be the Kaplan–Meier estimates of $S_1$ and $S_2$, respectively. Efron proposed to use $\widehat{D}=-\int ^\infty _{0}\widehat{S}_1(t)d\widehat{S}_2(t)$ to estimate the right side of (9), assuming that the largest observation of each group is uncensored [15]. However, in practice it is very common that this assumption is not met. Without this assumption, using $\widehat{D}$ to estimate $P(T_1>T_2)$ may cause trouble since the Kaplan–Meier estimates could be undefined for the potentially important tail of a survival function. Below we present two remedies, which overcome the drawback of $\widehat{D}$, to estimate the Mann–Whitney parameter. One approach is based on completing the estimated survival functions using exponential tails, and the other on the conditional estimation.

3.1 Estimating $ES_{\mathrm{MW}}$ by Adding Exponential Tails

There are several methods to complete estimated survival functions by adding tails. Let $\widehat{S}(t)$ be the Kaplan–Meier estimate of the survival function S(t). Efron suggested estimating $\widehat{S}(t)$ by 0 beyond the largest observed study time $t_{\mathrm{max}}$ [15]. Gill recommended estimating $\widehat{S}(t)$ by $\widehat{S}(t_{\mathrm{max}})$ beyond $t_{\mathrm{max}}$ [20]. Moeschberger and Klein proposed estimating $\widehat{S}(t)$ by a restricted Weibull survival curve that goes through two points (0, 1) and $(t_{\mathrm{max}}$, $\widehat{S}(t_{\mathrm{max}}))$ beyond $t_{\mathrm{max}}$ [32]. Brown, Hollander and Kowar suggested estimating $\widehat{S}(t)$ by an exponential curve going through (0, 1) and $(t_{\mathrm{max}}$, $\widehat{S}(t_{\mathrm{max}}))$ beyond $t_{\mathrm{max}}$ [7]. We note that both methods from Efron and Gill are sensitive to heavy or administrative censoring. Adding Weibull tails could lead to crossing survival functions for some populations where survival functions are not supposed to cross each other. Adding exponential tails does not suffer from these drawbacks and hence is a preferred choice. We start this discussion by replacing the tail of a survival function with an exponential function.

Let $\tau _i$ be a time point such that for $t>\tau _i$, $S_i(t)$ is replaced by an exponential function determined by the exponential curve going through two points (0, 1) and $(\tau _i$, $S_i(\tau _i))$ $(i=1, 2)$. That is, ${S}_i(t)=e^{-{\lambda }_it}$ for $t > \tau _i$ with ${\lambda }_i=-\log ({S}_i(\tau _i))/\tau _i$. Then the Mann–Whitney parameter is approximated by $D_e(\tau _1, \tau _2) = A+B+C$ with $A= -\int _{0}^{\text {min}(\tau _1, \tau _2)}{S}_1(t)d{S}_2(t)$; $B = -\int _{\tau _1}^{\tau _2}e^{-{\lambda }_1t}d{S}_2(t)$ if $\tau _1 < \tau _2,$ 0 if $\tau _1 = \tau _2,$ $\int _{\tau _2}^{\tau _1}S_1(t)\lambda _2e^{-{\lambda }_2t}\mathrm{d}t$ if $\tau _1 > \tau _2$; and $C=\frac{{\lambda }_2}{{\lambda }_1+{\lambda }_2}e^{-({\lambda }_1+{\lambda }_2){\mathrm{max}}(\tau _1, \tau _2)}$. Consequently, $ES_{\mathrm{MW}}$ can be approximated by

$$\begin{aligned} ES_{\mathrm{MWE}}(\tau _1, \tau _2)=1-2D_e(\tau _1, \tau _2). \end{aligned}$$

(10)

It is worth noting that an exponential tail leads to a constant hazard beyond $\tau _i$ and two exponential tails do not intersect unless they coincide exactly.

When survival data are available, we can use the Kaplan–Meier estimates $S_i(\cdot )$ and Lebesgue–Stieltjes integration in the calculation of A, B, and C to obtain $\widehat{A}$, $\widehat{B}$, and $\widehat{C}$. Set $\widehat{D}_e( \tau _1, \tau _2) =\widehat{A} +\widehat{B} +\widehat{C}$. Then we can estimate $ES_{\mathrm{MW}}$ by using $1-2\widehat{D}_e( \tau _1, \tau _2)$. In reality, tied failure times occur due to rounding or common data collection practice/logistics (e.g., failure times are measured in months). As a result, it follows from the law of total probability that $\widehat{D}_e( \tau _1, \tau _2)$ and $\widehat{D}_e( \tau _2, \tau _1)$ based on a real dataset usually slightly underestimate $P(T_1 > T_2)$ and $P(T_2 > T_1)$, respectively. To make the adjustment, we add $\frac{1}{2}\left( 1-\widehat{D}_{e}(\tau _2,\tau _1)-\widehat{D}_{e}(\tau _1,\tau _2)\right)$ to the term $\widehat{D}_{e}(\tau _1,\tau _2)$ in $1-2\widehat{D}_e( \tau _1, \tau _2)$ to obtain an estimate of $ES_{\mathrm{MW}}$, i.e.,

$$\begin{aligned} \widehat{ES}_{\mathrm{MWE}}(\tau _1, \tau _2)=\widehat{D}_e( \tau _2, \tau _1)-\widehat{D}_e( \tau _1, \tau _2). \end{aligned}$$

(11)

Equation (11) should be used when tied failure times are possible. To be safe, it is recommended that Eq. (11) be used always in practice.

3.2 Estimating $ES_{\mathrm{MW}}$ Through Conditioning

Let $\tau$ be a preset time point before which we have the knowledge about $S_1$ and $S_2$. Then we may approximate the Mann–Whitney parameter $P(T_1>T_2)$ by the conditional probability $P(T_1>T_2|T_1\le \tau \text { or }T_2 \le \tau ),$ denoted by ${D}_c(\tau )$, which can be shown to be equal to $\frac{-\int ^\tau _{t=0}S_1(t)dS_2(t)}{1-S_1(\tau )S_2(\tau )}.$ Consequently, $ES_{\mathrm{MW}}$ can be approximated by

$$\begin{aligned} ES_{\mathrm{MWC}}(\tau )=1-2D_c(\tau ). \end{aligned}$$

(12)

When survival data are available, we can estimate ${D}_c(\tau )$ by $\widehat{D}_c(\tau )=\frac{-\int ^\tau _{t=0}\widehat{S}_1(t)d\widehat{S}_2(t)}{1-\widehat{S}_1(\tau )\widehat{S}_2(\tau )}$ using the Kaplan–Meier estimates $\widehat{S}_1(\cdot )$ and $\widehat{S}_2(\cdot )$. Similar to (11), we can obtain another estimate of ${ES_{\mathrm{MW}}}$ with adjustment for ties:

$$\begin{aligned} \widehat{ES}_{\mathrm{MWC}}(\tau ) =\frac{-\int ^\tau _{t=0}\widehat{S}_2(t)d\widehat{S}_1(t)}{1-\widehat{S}_2(\tau )\widehat{S}_1(\tau )}-\frac{-\int ^\tau _{t=0}\widehat{S}_1(t)d\widehat{S}_2(t)}{1-\widehat{S}_1(\tau )\widehat{S}_2(\tau )}. \end{aligned}$$

(13)

3.3 Selection of $\tau _1$, $\tau _2$ and $\tau$

We can determine $\tau _1$, $\tau _2$ for $ES_{\mathrm{MWE}}(\tau _1,\tau _2)$ and $\tau$ for $ES_{\mathrm{MWC}}(\tau )$ by using the data. Let $t_{\mathrm{max}_i}$ be the largest observed time (either censoring or failure time) from group i $(i=1, 2)$. We can set $\tau _1=\tau _2=\tau =\tau ^*$, where $\tau ^*$ is less than or equal to $\text {min}(t_{\mathrm{max}_1},t_{\mathrm{max}_2})$. The time point $\tau ^*$ should be selected to avoid the unstable end (if any) of the Kaplan–Meier curves and, at the same time, as close as possible to $\text {min}(t_{\mathrm{max}_1},t_{\mathrm{max}_2})$ to make as much use as possible of the information from the Kaplan–Meier estimates. Such a setting of $\tau _1$, $\tau _2$, and $\tau$ will allow $\widehat{ES}_{\mathrm{MWE}}(\tau _1, \tau _2)$ and $\widehat{ES}_{\mathrm{MWC}}(\tau )$ to produce reasonably good estimates of $ES_{\mathrm{MW}}$ if the assumption of proportional hazards holds true. This is seen in the following theorem:

Theorem 2

Let $\lambda _1(t)$ and $\lambda _2(t)$ be the hazard functions for $T_1$ and $T_2$, respectively. If there exists a constant r such that $r=\frac{\lambda _1(t)}{\lambda _2(t)}$ for any $t>0$, then for any $\tau ^*>0$, we have

$$\begin{aligned} ES_{\mathrm{MW}}=ES_{\mathrm{MWE}}(\tau _1=\tau ^*, \tau _2=\tau ^*) =ES_{\mathrm{MWC}}(\tau =\tau ^*)=\frac{r-1}{r +1}, \end{aligned}$$

where $ES_{\mathrm{MW}}$, $ES_{\mathrm{MWE}}(\tau _1, \tau _2)$ and $ES_{\mathrm{MWC}}(\tau )$ are defined by Eqs. (8), (10) and (12), respectively.

Proof

See “Appendix 3”.

Fig. 1

The survival functions of the censoring time (gray) and the failure time in group 1 (red) and group 2 (blue)

Note that in many situations, survival functions can be modeled by distributions with proportional hazards. For example, if $T_1\sim \text {Weibull}(\alpha ,\beta _1)$ and $T_2\sim \text {Weibull}(\alpha ,\beta _2)$, then it is easy to show the ratio of two hazard functions is a constant equal to $r= \frac{{\beta _2}^{\alpha }}{{\beta _1}^{\alpha }}$. (Recall that the survival function of a Weibull($\alpha ,\beta$) distribution has the expression $S(t)=e^{-(t/\beta )^\alpha }$.) By Theorem 2, we have $ES_{\mathrm{MW}} =ES_{\mathrm{MWE}}(\tau _1=\tau ^*, \tau _2=\tau ^*) =ES_{\mathrm{MWC}}(\tau =\tau ^*) =\frac{{\beta _2}^{\alpha }-{\beta _1}^{\alpha }}{{\beta _1}^{\alpha }+{\beta _2}^{\alpha }}$.

Also note that the conclusion of the theorem may not hold if the assumption of proportional hazards is violated, as shown below. Let $T_1\sim \text {Weibull}(2.5,0.5)$ and $T_2\sim \text {Weibull}(5,0.5)$ denote variables of failure times in group 1 and group 2, respectively. The ratio of the two hazard functions $(=0.5^{3.5}t^{-2.5})$ is not a constant. Assume that in each group, the only censoring is an administrative censoring uniformly distributed between 0 and $\tilde{t}=0.3$. The survival functions of the failure time and censoring time distributions are shown in Fig. 1. Straightforward computation shows ${ES}_{\mathrm{MW}}=0.091$, ${ES}_{\mathrm{MWE}}(\tau _1=0.3,\tau _2=0.3)=0.570$, and ${ES}_{\mathrm{MWC}}(\tau =0.3)=0.584$. Therefore, both ${ES}_{\mathrm{MWE}}$ and ${ES}_{\mathrm{MWC}}$ are far away from ${ES}_{\mathrm{MW}}$.

In light of Theorem 2, $\widehat{ES}_{\mathrm{MWE}}(\tau _1=\tau ^*, \tau _2=\tau ^*)$ and $\widehat{ES}_{\mathrm{MWC}}(\tau =\tau ^*)$ can estimate $ES_{\mathrm{MW}}$ very well when the proportional hazards assumption holds true. It turns out they can also estimate $ES_{\mathrm{MW}}$ well under the condition that $\widehat{S_1}(\tau ^*)$ and $\widehat{S_2}(\tau ^*)$ are close to 0. This is seen in the following theorem.

Theorem 3

If $S_1(\tau ^*)\le \epsilon _1$ and $S_2(\tau ^*)\le \epsilon _2$, then $|ES_{\mathrm{MWE}}(\tau _1=\tau ^*,\tau _2=\tau ^*)-ES_{\mathrm{MW}}|\le 2\epsilon _1\epsilon _2$ and $|ES_{\mathrm{MWC}}(\tau =\tau ^*)-ES_{\mathrm{MW}}|\le 2\epsilon _1\epsilon _2.$

Proof

See “Appendix 4”.

Theorem 3 tells us that if the values of survival functions in the two groups are close to 0 at time $t=\tau ^*$, then the biases of $ES_{\mathrm{MWE}}(\tau _1=\tau ^*,\tau _2=\tau ^*)$ and $ES_{\mathrm{MWC}}(\tau =\tau ^*)$ will be small. Therefore, we can expect $\widehat{ES}_{\mathrm{MWE}}(\tau _1=\tau ^*,\tau _2=\tau ^*)$ and $\widehat{ES}_{\mathrm{MWC}}(\tau =\tau ^*)$ to perform well if $\widehat{S}_1(\tau ^*)$ and $\widehat{S}_2(\tau ^*)$ are close to 0.

4 Comparing Effect Sizes

Two types of effect sizes have been developed: the effect sizes $ES_L$, $ES_G$ and $ES_P$ based on test statistics, and the effect sizes $ES_{\mathrm{MW}}$ based on the Mann–Whitney parameter. Various comparisons among these effect sizes are available.

4.1 Effect Sizes as Weighted Differences in Hazards

All four effect sizes represent a weighted difference between two hazard functions and share the same format of definition:

$$\begin{aligned} \int _0^\infty \xi (t)(\lambda _1(t)-\lambda _2(t))\mathrm{d}t. \end{aligned}$$

(14)

It follows from (5), (6) and (7) that $ES_L$, $ES_G$ and $ES_P$ (assuming $S_1^{*}(t)= S_2^{*}(t)=S^{*}(t)$) correspond to, respectively,

$$\begin{aligned}&\xi _L(t)=\frac{\pi _1(t)\pi _2(t)}{\pi (t)} =\left( \frac{1}{\pi _1(t)}P_2+\frac{1}{\pi _2(t)}P_1 \right) ^{-1} =\frac{S_1^{*}(t)S_2^{*}(t)S_1(t)S_2(t)}{S_1(t)S_1^{*}(t)P_1+S_2(t)S_2^{*}(t)P_2}, \\&\xi _G(t)=\pi _1(t)\pi _2(t)=S_1^{*}(t)S_2^{*}(t)S_1(t)S_2(t), \end{aligned}$$

and

$$\begin{aligned} \xi _P(t)=\frac{\pi _1(t)\pi _2(t)}{S^*(t)}=S^*(t)S_1(t)S_2(t). \end{aligned}$$

The effect size $ES_{\mathrm{MW}}$ corresponds to

$$\begin{aligned} \xi _{\mathrm{MW}}(t)=S_1(t)S_2(t), \end{aligned}$$

since

$$\begin{aligned} ES_{{\mathrm{MW}}} =&\int ^\infty _{0}S_2(t)f_1(t)\mathrm{d}t-\int ^\infty _{0}S_1(t)f_2(t)\mathrm{d}t\\ =&\int ^\infty _{0}S_1(t)S_2(t)\left( \lambda _1(t)-\lambda _2(t)\right) \mathrm{d}t. \end{aligned}$$

Formula (14) represents a weighted difference between two hazard functions with the weight at time t equal to $\xi (t)$. The interpretation of the weight for each effect size is clear. For $ES_{\mathrm{MW}}$, the weight $\xi _{\mathrm{MW}}(t)$ is the probability that the failure times of both groups are beyond t. For $ES_{G}$, the weight $\xi _{G}(t)$ is the probability that the observed times (either failure time or censoring time) of both groups are beyond t. For $ES_{L}$, the weight $\xi _{L}(t)$ is the ratio of the probability that the observed times of both groups are beyond t to the probability that the observed time of the combined group is beyond t. Note that $\xi _{L}(t)$ is essentially the weighted harmonic mean of $\pi _1(t)$ and $\pi _2(t)$. For $ES_{P}$ where $S_1^{*}(t)= S_2^{*}(t)=S^*(t)$, the weight $\xi _{P}(t)$ is the ratio of the probability that the observed times of both groups are beyond t to the probability that the censoring time is beyond t. Note that $\xi _{P}(t)$ is in fact the geometric mean of $\xi _{\mathrm{MW}}(t)$ and $\xi _{G}(t)$.

Weights can be compared under various conditions. For any censoring distributions, we have $0 \le \xi _G(t) \le \xi _L(t)$ and $0 \le \xi _G(t)\le \xi _{\mathrm{MW}}(t)$. Assuming the same censoring distribution for both groups, i.e., $S_1^*(t)=S_2^*(t)=S^*(t)$, we obtain $0 \le \xi _G(t) \le \xi _P(t) \le \xi _L(t)$ and $0 \le \xi _G(t)\le \xi _P(t) \le \xi _{\mathrm{MW}}$. Furthermore, if assuming the same light censoring distribution for both groups, we see that the weights $\xi _G$, $\xi _P$ and $\xi _{\mathrm{MW}}$ are usually close to each other; if assuming the same heavy censoring distribution for both groups, the weights $\xi _G$, $\xi _P$ and $\xi _L$ are usually much smaller than the weight $\xi _{\mathrm{MW}}$.

4.2 What Do $ES_L$, $ES_G$ and $ES_P$ Actually Measure?

The test statistic-based effect sizes $ES_L$, $ES_G$ and $ES_P$ depend on censoring through the supports and sizes of the censoring survival functions. Supports of the censoring survival functions determine where to compute the weighted differences in hazards. Clearly, the formula (14) shows that these effect sizes are the weighted difference in hazard functions over the time period where censoring is possible. This indicates that these effect sizes capture the difference in hazards during the time period of study which is designed to compare the two groups. Sizes of censoring survival functions impact the magnitudes of the effect sizes. From (14), it is seen that small magnitudes of the effect sizes are produced if either $S_1^*$ or $S_2^*$ or both are small.

To illustrate the above points, consider the scenario where an administrative censoring occurs at time $\tilde{t}$, i.e., the study is terminated at time $\tilde{t}$. We have $ES_{G} =\int _0^{\infty } \pi _{1}(t)\pi _2(t) (\lambda _1(t)-\lambda _2(t))\mathrm{d}t =\int _0^{\tilde{t}} \pi _{1}(t)\pi _2(t) (\lambda _1(t)-\lambda _2(t))\mathrm{d}t$. It is seen that $ES_{G}$ computes the weighted difference in hazard functions before time $\tilde{t}$ and thus $ES_{G}$ only compares the two groups before time $\tilde{t}$. When $\tilde{t}$ is smaller and thus censoring is heavier, $ES_{G}$ becomes smaller (assuming $\lambda _1(t)\ge \lambda _2(t)$). As $\tilde{t}$ approaches 0, $ES_{G}$ goes to 0.

In practice, there are no special restrictions on the use of $\widehat{ES}_G$. Attentions should be paid when using $\widehat{ES}_L$ and $\widehat{ES}_P$. $\widehat{ES}_L$ is sensitive to the change in sample proportions and the use of $\widehat{ES}_P$ requires the equality of two censoring distributions.

To conclude, we note that $ES_G$ is a difference between two special probabilities. Let $T_i$, $C_i$ and $X_i$ denote, respectively, the variable of failure time, the variable of censoring time and the minimum of $T_i$ and $C_i$ in group i ($i=1, 2$). Then it is easy to show $ES_{G}=A-B,$ where $A =\int _0^\infty S_2(t)S_1^*(t)S_2^*(t)f_1(t)\mathrm{d}t = P(X_2>X_1,X_1=T_1)$, $B =\int _0^\infty S_1(t)S_1^*(t)S_2^*(t)f_2(t)\mathrm{d}t =P(X_1>X_2,X_2=T_2).$ Clearly A is the probability that the observed time of a randomly selected subject from group 2 is longer than that of a randomly selected subject from group 1 who met the event, i.e., the probability that a randomly selected subject from group 2 can be observed to live longer than a randomly selected subject from group 1. A similar statement can be made for B. Therefore, $ES_G$ simply compares the failure times between groups through comparing observed times. In contrast, $ES_{\mathrm{MW}}=P(T_2>T_1)-P(T_1>T_2)$ compares the underlying failure times directly.

4.3 Practical Issues in Estimating $ES_{\mathrm{MW}}$

$ES_{\mathrm{MW}}=1- 2P(T_1>T_2)$, defined as a simple linear transformation of $P(T_1>T_2)$, has a clear interpretation. That is, any value of $ES_{\mathrm{MW}}$ will immediately translate to the Mann–Whitney parameter $P(T_1>T_2)$. However, estimating $ES_{\mathrm{MW}}$ can be problematic in practice. There may not be enough information to support estimating $ES_{\mathrm{MW}}$. Again consider the scenario where an administrative censoring presents so that the study terminates at time $t=\tilde{t}$. As a result, estimating $ES_{\mathrm{MW}}$ could become impossible without additional information on $T_1$ and $T_2$. This is illustrated in the following example. Consider two cases. For case 1 (Fig. 2a), $S_1(t)=(1-t)\mathbb {1}_{[0,1]}$ and $S_2(t)=(1-4t^3)\mathbb {1}_{[0, 0.25^{1/3}]}$, so that $ES_{\mathrm{MW}}=1-2P(T_1>T_2)=-0.055$. And for case 2 (Fig. 2b), $S_1(t)=(1-t)\mathbb {1}_{[0,1]}$ and $S_2(t)=(1-4t^3)\mathbb {1}_{[0,0.25]}+(9/8-3t/4)\mathbb {1}_{[0.25, 1.5]}$, so that $ES_{\mathrm{MW}}=1-2P(T_1>T_2)=0.477$. Here $\mathbb {1}_{[a, b]}$ equals 1 if t is inside the interval [a, b] and 0 otherwise. Assume that in both cases, the only censoring is the administrative censoring uniformly distributed between 0 and $\tilde{t}=0.25.$ Then in either case, we will only be able to observe the survivals $S_1(t)$ and $S_2(t)$ up to time $\tilde{t}$, which are identical for both cases. Therefore, estimating $ES_{\mathrm{MW}}$ using only the observed data in either case becomes problematic. In another word, if we use $\widehat{ES}_{\mathrm{MWE}}(\tau _1,\tau _2)$ or $\widehat{ES}_{\mathrm{MWC}}(\tau )$ to estimate $ES_{\mathrm{MW}}$, a big error could occur. In general, when estimating $ES_{\mathrm{MW}}$ by $\widehat{ES}_{\mathrm{MWE}}(\tau _1,\tau _2)$ or $\widehat{ES}_{\mathrm{MWC}}(\tau )$, the bias can be quite large if a large portion of the survival function(s) is not observed and we have to choose $\tau _i$ or $\tau$ such that $\widehat{S}(\tau _i)$ or $\widehat{S}(\tau )$ is much greater than 0.

Fig. 2

The survival functions of the censoring time (gray) and the failure time in group 1 (red) and group 2 (blue)

On the other hand, $ES_{\mathrm{MW}}$ can be estimated for several general situations. If the largest observation from each group is a failure time (i.e., the Kaplan–Meier curve drops to 0 at the end), $ES_{\mathrm{MW}}$ can be estimated by $1-2\widehat{D}$, where $\widehat{D}=-\int ^\infty _{0}\widehat{S}_1(t)d\widehat{S}_2(t)$ is proposed by Efron [15]. If none of the two Kaplan–Meier curves drop to 0 at the end, $ES_{\mathrm{MW}}$ can be estimated by both $\widehat{ES}_{\mathrm{MWE}}(\tau _1=\tau ^*,\tau _2=\tau ^*)$ and $\widehat{ES}_{\mathrm{MWC}}(\tau =\tau ^*)$ when the proportional hazards assumption holds true (Theorem 2) or when $\widehat{S}_1(\tau ^*)$ and $\widehat{S}_2(\tau ^*)$ are close to 0 (Theorem 3).

If the Kaplan–Meier curve on $S_1$ drops to 0 at time $t_a$, the other curve on $S_2$ stops at time $t_b \ge t_a$ but does not drop to 0, then it is easy to show $ES_{\mathrm{MW}}$ can be estimated by $1+2\int _0^{t_a}\widehat{S}_1(t)d\widehat{S}_2(t)$. If the Kaplan–Meier curve on $S_1$ drops to 0 at time $t_a$, the other curve on $S_2$ stops at time $t_b<t_a$ but does not drop to 0, then $ES_{\mathrm{MW}}$ can again be estimated by $\widehat{ES}_{\mathrm{MWE}}(\tau _1=\tau ^*,\tau _2=\tau ^*)$ and $\widehat{ES}_{\mathrm{MWC}}(\tau =\tau ^*)$ when the proportional hazards assumption holds true or when $\widehat{S}_1(\tau ^*)$ and $\widehat{S}_2(\tau ^*)$ are close to 0.

We note that $ES_{\mathrm{MW}}$ may have no clinical meaning at all in some situations. For instance, consider two survival functions $S_1$ and $S_2$ whose Kaplan–Meier estimates $\widehat{S}_1$ and $\widehat{S}_2$ are close to 1 over a long study time. Then clinically, the difference between $S_1$ and $S_2$ could be ignored. However, $ES_{{\mathrm{MW}}}$ between $S_1$ and $S_2$ can be large, say, close to 1, since $ES_{{\mathrm{MW}}} =\int ^\infty _{0}S_2(t)S_1(t)\left( \lambda _1(t)-\lambda _2(t)\right) \mathrm{d}t$ compares the difference in hazards over entire supports of survival functions. As such, a large $ES_{\mathrm{MW}}$ could be clinically meaningless. This problem can occur with diseases that have a very optimistic survival, such as thyroid cancer. To resolve, test statistic-based effect sizes should be applied since they only compare the difference over the period of study time.

4.4 Relationship Among $ES_L$, $ES_G$, $ES_P$, $ES_{\mathrm{MW}}$ and Hazard Ratio

Examining the functions $\xi (t)$ in (14) leads to the following straightforward comparisons among the values of $ES_L$, $ES_G$, $ES_P$, $ES_{\mathrm{MW}}$ and the hazard ratio.

• Assuming $\lambda _1(t)\ge \lambda _2(t)$ for all $t \in [0,\infty ]$, we have $0 \le ES_{G} \le ES_{L}$ and $0\le ES_{G}\le ES_{\mathrm{MW}}\le 1$.

• Assuming $\lambda _1(t)\ge \lambda _2(t)$ for all $t \in [0,\infty ]$ and assuming the same censoring distribution for both groups, we have $0\le ES_{G}\le ES_{P}\le ES_{L}$ and $0\le ES_{G}\le ES_{P}\le ES_{\mathrm{MW}}\le 1$.

• In the absence of censoring, $ES_G$ and $ES_P$ reduce to $ES_{\mathrm{MW}}$. If censoring is light, then the censoring survival is close to 1 so that $ES_G$ and $ES_P$ are close to $ES_{\mathrm{MW}}$.

• The value of $ES_L$ is influenced by the probabilities by which subjects are assigned to groups. For instance, if $\pi _1(t) \le \pi _2(t)$ and $\lambda _1(t)\ge \lambda _2(t)$ for all $t \in [0,\infty ]$, then $ES_L$ increases as $P_1$ increases.

• There is a relationship between $ES_{\mathrm{MW}}$ and the hazard ratio, a widely used effect size in survival analysis. Assume a constant hazard ratio $r=\frac{\lambda _1(t)}{\lambda _2(t)}$. Then from Theorem 2, we have $ES_{\mathrm{MW}}=1-2P(T_1>T_2)=\frac{r-1}{r+1}.$ In particular, $ES_{\mathrm{MW}}=0$ if $r=1$ and $ES_{\mathrm{MW}}\rightarrow 1\ (-1)$ as $r\rightarrow \infty \ (0 )$. In addition, by Taylor expansion, $ES_{\mathrm{MW}}\approx \frac{\theta }{2}$ for $\theta$ close to 0, where $\theta =\log r$.

5 Partition of Values of Effect Sizes

The proposed effect sizes can quantify the difference between two populations of time-to-event data. In many cases, one has to assess if an effect size is sufficiently large to be (practically) meaningful. For instance, in a clinical setting, one may need to evaluate the clinical meaningfulness of an effect size. As such, certain rules are needed in order to determine if an estimate of an effect size is small, medium or large. This involves partitioning the values of effect sizes. For demonstration, below we will develop such rules for effect sizes $ES_{\mathrm{MW}}$ and $ES_G$.

The rule for $ES_{\mathrm{MW}}$ can be derived in light of the widely used rule of thumb on the magnitude of Cohen’s d. The natural log of the exponentially distributed survival time was considered because the transformed time has the same variance for all exponentially distributed times and thus Cohen’s d has a clear interpretation [5]. Under the assumption that the failure time is exponentially distributed in each group, Cohen’s d can be written as a function of the hazard ratio $d =-\frac{\log (r)\sqrt{6}}{\pi }$ (“Appendix 5”), and hence small, medium and large hazard ratios correspond to values of 1.29, 1.90 and 2.79, respectively [5]. According to $ES_{\mathrm{MW}}=\frac{r-1}{r+1}$, the relationship between the hazard ratio and effect size $ES_{\mathrm{MW}}$ stated in Sect. 4.4, we see that the small, medium and large effect sizes $ES_{\mathrm{MW}}$ correspond to its values of 0.13, 0.31 and 0.47, respectively. Specifically, using the midpoint 0.22 of 0.13 and 0.31 and midpoint 0.39 of 0.31 and 0.47, we have the following rule of thumb: the effect size $ES_{\mathrm{MW}}$ is small if $|ES_{\mathrm{MW}}| \in [0, 0.22)$, medium if $|ES_{\mathrm{MW}}| \in [0.22, 0.39)$ and large if $|ES_{\mathrm{MW}}| \in [0.39, 1]$.

The same idea can be used to derive a rule for $ES_G$. In addition to the assumption that failure times in the two groups are exponentially distributed, we assume censoring times in the two groups are exponentially distributed. Then $ES_G$ can be written as (see “Appendix 5” for a proof.)

$$\begin{aligned} ES_{G}= \frac{e^{-\pi d/\sqrt{6}}-1}{e^{-\pi d/\sqrt{6}}+1+e^{-\pi d/\sqrt{6}}\frac{CR_1}{1-CR_1}+\frac{CR_2}{1-CR_2}}, \end{aligned}$$

(15)

where d is Cohen’s d and $CR_i=P(T_i>C_i)$. Note that $CR_i$ is the censoring rate in group i, which can be estimated by the observed censoring rate $\widehat{CR}_i$. Using the above formula, we can obtain a rule of thumb regarding when the effect size $ES_{G}$ is small, medium and large. Specifically, for any fixed $CR_i$, the small, medium and large effect sizes $ES_{G}$ are computed by using the corresponding values of Cohen’s d (small, 0.2; medium, 0.5; large, 0.8). Table 1 shows a list of small, medium and large effect sizes $ES_{G}$ for selected $CR_i$. Using the midpoints of numbers in any triplet in the table, intervals for small, medium and large effect sizes can be easily obtained. For instance, for $CR_1=CR_2=10\%$, the triplet consists of 0.11, 0.28, 0.43. Using the midpoint 0.20 of 0.11 and 0.28 and midpoint 0.36 of 0.28 and 0.43, we have the following rule of thumb: with $CR_1=CR_2=10\%$, the effect size $ES_{G}$ is small if $|ES_{G}| \in [0, 0.20)$, medium if $|ES_{G}| \in [0.20, 0.36)$ and large if $|ES_{G}| \in [0.36, 1]$.

Table 1 Small, medium and large effect sizes $ES_G$. The censoring rate in group i is denoted by $CR_i$ ($i=1,2$)

The above rules for $ES_{\mathrm{MW}}$ and $ES_G$ are developed under the assumption that actual failure/censoring times follow an exponential distribution. In cases where this assumption does not hold, the rules provide a simple and useful reference.

6 Experiments

6.1 Example 1: Simulations

This example presents a simulation study on five effect size estimates: $\widehat{ES}_L$, $\widehat{ES}_G$, $\widehat{ES}_P$, $\widehat{ES}_{\mathrm{MWE}}$ and $\widehat{ES}_{\mathrm{MWC}}$, defined in (2), (3), (4), (11) and (13), respectively. It illustrates various elements developed in previous sections and shows that with large samples, differences in survival between groups can be appropriately described by effect sizes.

The experiment is outlined as follows. First, we chose the two-parameter Weibull distributions as the underlying distributions for the failure and censoring times in groups 1, 2 and 3. We used $T_1\sim \text {Weibull}(2.5,0.4)$, $T_2\sim \text {Weibull}(2.5,0.5)$ and $T_3\sim \text {Weibull}(2.5,0.6)$ for the failure time in group 1, group 2 and group 3, respectively. Then the proportional hazards assumption holds between groups 1 and 2 and between groups 1 and 3, since $\frac{\lambda _1(t)}{\lambda _2(t)}\equiv 1.75$ and $\frac{\lambda _1(t)}{\lambda _3(t)}\equiv 2.76$, where $\lambda _1$, $\lambda _2$ and $\lambda _3$ are hazard functions in groups 1, 2 and 3, respectively. The censoring times in all three groups were chosen to follow a $\text {Weibull}(10,0.6)$ distribution. The survival functions of the failure and censoring times are shown in Fig. 3. (Note that the censoring survival function has a value smaller than $1\times 10^{-4}$ at time $t=0.75$, so roughly the study was terminated at $t=0.75$.) Second, survival data were generated, with sample i corresponding to group i $(i=1, 2, 3)$. And we increased the sample size for samples 1 and 2, denoted by $n_1$ and $n_2$, respectively, from 1000 to 20,000 at the same rate, while fixing the sample size for sample 3, denoted by $n_3$, at 2000.

Fig. 3

Survival functions of the failure time and censoring time in Example 1

Our goal was to compare the survival differences between group 1 and group 2 and between group 1 and group 3. We recorded the values of $\widehat{ES}_L$ , $\widehat{ES}_G$ , $\widehat{ES}_P$ , $\widehat{ES}_{\mathrm{MWE}}$ and $\widehat{ES}_{\mathrm{MWC}}$ when evaluating the survival difference between group 1 and group 2 and between group 1 and group 3. Here for $\widehat{ES}_{\mathrm{MWE}}(\tau _1, \tau _2)$ in (11) and $\widehat{ES}_{\mathrm{MWC}}(\tau )$ in (13), we chose $\tau _1=\tau _2=\tau$ to be 0.6, since all Kaplan–Meier curves are stable before time $t=0.6$. The simulation results are summarized in Table 2.

Table 2 Estimates of effect sizes in Example 1

Computation through Eq. (14) shows that values of ${ES}_L$, ${ES}_G$, ${ES}_P$ and $ES_{\mathrm{MW}}$ between group 1 and 2 are 0.44, 0.26, 0.26 and 0.27, respectively, and that values of ${ES}_G$, ${ES}_P$, and $ES_{\mathrm{MW}}$ between group 1 and 3 are 0.43, 0.44 and 0.47, respectively. (Note that $ES_{\mathrm{MW}}=\frac{r-1}{r+1}$, the relationship between $ES_{\mathrm{MW}}$ and the hazard ratio r stated in Sect. 4.4, can be easily verified between group 1 and group 2 and between group 1 and group 3.) Here in computing ${ES}_L$, we used the proportion of subjects in the sample to approximate the probability of assignment of subjects to the corresponding group. ${ES}_L$ between group 1 and group 3 could not be computed due to the change in sample proportions. The censoring rates in groups 1, 2 and 3 are 11%, 26% and 42%, respectively. Table 2 shows that except for the $\widehat{ES}_L$ column between groups 1 and 3, values of $\widehat{ES}_L$, $\widehat{ES}_G$, $\widehat{ES}_P$, $\widehat{ES}_{\mathrm{MWE}}$ and $\widehat{ES}_{\mathrm{MWC}}$ are, respectively, close to the values of $ES_L$, $ES_G$, $ES_P$, $ES_{\mathrm{MW}}$ and $ES_{\mathrm{MW}}$. This illustrates how estimates of effect sizes developed in Sects. 2 and 3 approximate their corresponding effect sizes. Note that estimates of effect sizes are not much influenced by the change in sample sizes, except for $\widehat{ES}_L$ evaluated between groups 1 and 3.

Table 2 also shows that for each of $\widehat{ES}_L$, $\widehat{ES}_G$, $\widehat{ES}_P$, $\widehat{ES}_{\mathrm{MWE}}$, and $\widehat{ES}_{\mathrm{MWC}}$, the value obtained between groups 1 and 2 is smaller than that between groups 1 and 3. In particular, all of the values of $\widehat{ES}_{\mathrm{MWE}}$, $\widehat{ES}_{\mathrm{MWC}}$ and $\widehat{ES}_G$ indicate a medium effect between group 1 and group 2 but a large effect between group 1 and group 3. Therefore, all five types of effect size estimates support the fact that the survival difference between groups 1 and 2 is smaller than the difference between groups 1 and 3 (Fig. 3). These results are consistent with the results of the modified Cohen’s d. The modified Cohen’s d applies to cases of unequal variances and is defined as the ratio of the difference in means to the square root of the mean of the two variances [11]. Both Cohen’s d and modified Cohen’s d use the same conventional definition of small, medium and large values of d. The modified Cohen’s d for the survival times in this example is $-0.516$ (medium) between Group 1 and Group 2, and is $-0.917$ (large) between Group 1 and Group 3.

To conclude this example, we make the following remark. One may wish to employ statistical tests to detect significant differences between groups. When doing this by simulations, we note that as $n_1$ and $n_2$ are large (say, above 15,000), p values of tests of logrank, Gehan–Wilcoxon and Prentice–Wilcoxon between group 1 and group 2 will be smaller than those between group 1 and group 3, indicating that the difference between group 1 and group 2 is more significant than the difference between group 1 and group 3. This is contrary to the conclusion from the proposed effect sizes and clearly against the truth shown in Fig. 3. Therefore, reporting only p values, which depend on sample sizes, may not be sufficient when differentiating differences between populations.

6.2 Example 2: Gastric Carcinoma Data

The proposed effect sizes can be applied no matter if hazards are proportional. Here we present one example with non-proportional hazards, in which our proposed effect sizes can be used to detect and quantify the difference between two groups, while the approach of the hazard ratio from the Cox regression fails to do so.

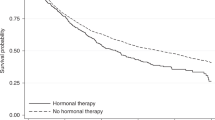
The Gastrointestinal Tumor Study Group studied survival of 90 patients with locally advanced, non-resectable gastric carcinoma by comparing two treatments: chemotherapy and radiation, and chemotherapy alone [39]. The aim was to determine if radiation was beneficial to the patients under chemotherapy. 45 and 45 patients were randomly assigned to the groups with and without radiation, respectively. The survival data are publicly available [39]. The Kaplan–Meier curves of the two groups are shown in Fig. 4, which indicates an overall negative impact of radiation on the survival of patients. Note that the observed censoring rates for both groups are low: 18% observed in each group. For convenience, the groups with and without radiation will be referenced as group 1 and group 2, respectively.

Fig. 4

Kaplan–Meier curves of failure times based on the gastric carcinoma data

The Grambsch–Therneau test for examining the proportional hazard assumption gives a significant p value of 0.0033, suggesting that the hazard ratio would not be an appropriate effect size for analyzing this problem. In fact, the estimate of the hazard ratio (group 1 over group 2) from the Cox regression gives a value of 1.30 with a wide confidence interval (CI) (95% CI: 0.83 to 2.06). These estimates are not very informative when assessing if radiation improves survival.

In comparison, our proposed effect sizes can capture the adverse effect of radiation. Between the groups with and without radiation, $\widehat{ES}_{L}$, $\widehat{ES}_{G}$, $\widehat{ES}_{P}$, $\widehat{ES}_{\mathrm{MWE}}$, and $\widehat{ES}_{\mathrm{MWC}}$, are, respectively, 0.22 (95% CI, -0.16 to 0.59), 0.27 (95% CI, 0.04 to 0.51), 0.26 (95% CI, 0.03 to 0.50), 0.26 (95% CI, 0.03 to 0.51) and 0.26 (95% CI, 0.03 to 0.51). (Hereafter, the CIs of the effect sizes are the bootstrap confidence intervals [14], based on 100,000 bootstrap samples.) Note that in computing $\widehat{ES}_{\mathrm{MWE}}$ and $\widehat{ES}_{\mathrm{MWC}}$ we used $\tau _1=\tau _2=\tau =\tau ^*=\text {min}(t_{\mathrm{max}_1},t_{\mathrm{max}_2})=1472$, since the Kaplan–Meier curves are relatively stable for the entire study period. These two estimates can be used for the example (with non-proportional hazards) since $2\widehat{S}_1(\tau ^*) \times \widehat{S}_2(\tau ^*) =2 \times 0.133 \times 0.125 \approx 0.03,$ which is small (Theorem 3). From the above estimates, several notes follow below. First, except for $\widehat{ES}_{L}$, all other four effect sizes and their CIs show that radiation decreases the survival, which is consistent with the observation in Fig. 4. Second, estimates of $ES_{\mathrm{MW}}$ and $ES_G$ suggest a medium effect size (Sect. 5). Third, because of the relatively low censoring rate (18% observed in each group), the estimates of effect sizes based on the test statistics and the Mann–Whitney parameter are close to each other except for $\widehat{ES}_{L}$ (Sect. 4.4).

6.3 Example 3: SEER Thyroid Cancer Data

The tumor, nodal involvement, metastasis (TNM) staging model provides the worldwide standard for cancer prognosis and treatment recommendations [1]. Due to the accumulation of time-to-event data with current advances in cancer research, periodic updates of the TNM are necessary for the improvement of the delivery of patient care. However, such updates often involve expert panels and can be cumbersome when one has to deal with big data. The Ensemble Algorithm for Clustering Cancer Data (EACCD) [8, 25] is a machine learning procedure designed specifically to “automatically” update the TNM or its expanded models that involve additional factor(s). This algorithm computes survival differences between groups of patients and utilizes these differences to stratify patients. Below we demonstrate an application of EACCD, integrated with effect sizes, to update and improve the current thyroid cancer staging modeling.

51,291 patients of papillary and follicular thyroid cancer were selected from the SEER 18 databases [40]. Each patient was diagnosed sometime between 2004 and 2010 and was followed up until the year 2015. Cause-specific deaths and survival times (in months) were recorded. In addition, each patient provided information for the following four variables: tumor size (T), regional lymph nodes (N), status of distant metastasis (M) and age (A). All four variables are categorical with 7 levels for T: T0, T1, T2, T2, T3, T4a, T4b; 3 levels for N: N0, N1a, N1b; 2 levels for M: M0 M1; and 2 levels for A: A1 (age < 55), A2 (age $\ge$ 55). Clinically, it is useful to consider combinations of patients. A combination is defined as a subset of the data corresponding to one level of each factor and is conveniently written using levels of factors (e.g., T2N0M0A2 denotes a subset of patients with T=T2, N=N0, M=M0, A=A2). (Note that the notation of a combination implicitly represents the corresponding underlying population/group.) The dataset contains 39 combinations each including at least 25 patients. Refer to the study by Yang et al for specific data management [46].

The goal of applying EACCD is to partition these 39 combinations into g clinically meaningful clusters such that 1) patients from the same cluster have a clinically similar survival while patients from two distinct clusters have clinically different survivals; and 2) g is as small as possible while the set of g clusters can provide the maximum possible accuracy in survival prediction. After such g clusters are obtained, one can study the survival of patients in each cluster and predict the survival for new patients by using survivals from clusters. The merit of applying EACCD is that a large number of original combinations (as often it is) is aggregated into a small number of more manageable clusters that have approximately the same survival prediction accuracy as the original set of combinations [25].

EACCD consists of 3 main steps. Step 1 defines the initial dissimilarity between survival functions of any two groups associated with two combinations. Step 2 computes learned dissimilarities by using initial dissimilarities. Step 3 clusters the combinations by the learned dissimilarities and a linkage method. The clustering result is summarized into a dendrogram which will then be cut to obtain g clusters. Algorithm 1 is one version of the algorithm that utilizes the two-phase Partitioning Around Medoids algorithm (PAM) [26].

Critical to the application of EACCD is the definition of initial dissimilarities, which can largely affect the output of EACCD [43]. To find an appropriate measure of the initial dissimilarity between two groups associated with two combinations of the thyroid cancer data, we first note that the sample sizes of combinations vary a lot. For instance, T1N0M0A1 has 17,747 cases while T4bN1bM1A2 has only 40 cases. As shown in Example 1, an effect size should serve as a good choice of the initial dissimilarity. In addition, thyroid cancer has a very good prognosis and there are many combinations that have similar and very optimistic survivals before the time of administrative censoring (12 years). According to Sect. 4.3, the test statistic-based effect sizes would serve as better initial dissimilarities than the Mann–Whitney-based effect size.

When applying EACCD to the thyroid dataset (the number of combinations $m=39$), the equal weights $w_1=\dots =w_m=1/m$ and the absolute values of 5 estimates ($\widehat{ES}_{L}$, $\widehat{ES}_{G}$, $\widehat{ES}_{P}$, $\widehat{ES}_{\mathrm{MWE}}$ and $\widehat{ES}_{\mathrm{MWC}}$) as initial dissimilarities were used in step 1 and the complete linkage [23] was employed in step 3. To compute the Mann–Whitney-based effect sizes, we first note that all Kaplan–Meier curves are stable before $\underset{1 \le k\le m}{\text {min}} \{ t_{\mathrm{max}_k} \}$, where $t_{\mathrm{max}_k}$ is the largest time at which the Kaplan–Meier estimator is defined in $\text{ Com}_k$, and therefore, for simplicity, we set $\tau _1=\tau _2=\tau =\tau ^*=\underset{1 \le k\le m}{\text {min}} \{ t_{\mathrm{max}_k} \}$ for comparing any two combinations.

Figures 5 and 6 show the results based on the test statistic and Mann–Whitney effect sizes, respectively. The left columns of both figures list dendrograms. Each red box represents cutting the dendrogram that corresponds to the optimal C-index [22, 25]. Note that g, the number of clusters from cutting, can change when different effect sizes are used. The right columns show the thyroid cancer-specific survival using the Kaplan–Meier estimates. These survival curves allow us to visually evaluate the clusters. Figure 6b and d, based on the effect size $ES_{\mathrm{MW}}$, shows that several high curves have a similar survival, indicating the clusters are not well separated and thus form a poor partition of the patients. As explained in Sect. 4.3, $ES_{\mathrm{MW}}$ tends to assign a big value of effect size to the difference between two groups (combinations) that share similar and optimistic survival experiences during the time of follow-up, because it compares not only the hazard difference over the period of study time but also the difference after the study. This tendency causes EACCD to partition combinations with similar and high survivals into different clusters, which actually do not have clinically meaningful differences in survival as their survival curves are very similar to each other. By contrast, Fig. 5b, d, and f suggests all $ES_L$, $ES_G$, and $ES_P$ lead to a meaningful partition of data.

Fig. 5

Dendrograms and survival curves of clusters from EACCD and the test statistic-based effect sizes. A 5-year disease-specific survival rate in percentage is given beneath each combination (leaf of the dendrogram)

Fig. 6

Dendrograms and survival curves of clusters from EACCD and the Mann–Whitney-based effect size. A 5-year disease-specific survival rate in percentage is given beneath each combination (leaf of the dendrogram)

The above example shows an application of the effect sizes in upgrading the staging system for thyroid cancer. There exist related works in the literature. The hazard ratio-based effect size and Mann–Whitney parameter-based effect size have been applied to expand the staging system for breast cancer and colorectal cancer [24, 25].

7 Conclusion

This paper investigates effect sizes that are used to assess the difference in survival between two groups. It studies three test statistic-based effect sizes $ES_L$, $ES_G$ and $ES_P$ and one Mann–Whitney-based effect size $ES_{\mathrm{MW}}$, all defined as weighted differences in hazards. The effect sizes $ES_L$, $ES_G$ and $ES_P$ compare the survival experiences between two groups over the time period of investigation, while $ES_{\mathrm{MW}}$ compares the survival experiences over the entire possible time period. Effect sizes $ES_L$ and $ES_G$, estimated by $\widehat{ES}_L$ and $\widehat{ES}_G$, can be applied to any data, while the use of $ES_P$, estimated by $\widehat{ES}_P$, assumes equal censoring distributions. Although $ES_{\mathrm{MW}}$ has a clear interpretation, it may not be estimable or clinically meaningful. If the Kaplan–Meier curve that stops first drops to 0, $ES_{\mathrm{MW}}$ can be estimated directly using the Kaplan–Meier estimates of the survival functions of the two groups. If the Kaplan–Meier curve that stops first does not drop to 0, $ES_{\mathrm{MW}}$ can be estimated using both $\widehat{ES}_{\mathrm{MWE}}$ and $\widehat{ES}_{\mathrm{MWC}}$ under the assumption of proportional hazards between the two groups or under the condition that both curves are low for time close to when they stop.

Effect sizes proposed in this paper have direct applications to big survival data. An estimate of an effect size, computed using two large samples, quantifies the difference between two underlying populations. This is in contrast to checking the p value from a statistical test, which may not provide any insight about the size of the survival difference and could cause misunderstanding.

Effect sizes are particularly useful when repeated comparisons of survival differences are required in a study. For instance, when updating or expanding the TNM staging system for a cancer, assessing the survival difference is needed for many pairs of groups [1]. In this case, effect sizes can be used to differentiate the survival between two groups, so that two groups can be merged if the associated effect size is small. Survival tree modeling [6] represents another scenario that requires a sequential comparison of survival for various pairs of groups. The key element in survival trees is their splitting rules, which can be determined by measuring the dissimilarities between possible nodes and finding the separation that leads to most dissimilar nodes. The largest significant value from test statistics (e.g., logrank, Gehan–Wilcoxon) is often used to suggest the “best” separation, based on the idea that the more extreme the statistic, the more dissimilar the two nodes [9, 10]. As seen in previous sections of this article, effect sizes seem to be better choices for measuring dissimilarities between nodes and their use is expected to improve the performance of survival trees.

Hazard ratio, the traditionally used effect size, requires the assumption of proportional hazards. With non-proportional hazards, hazard ratios can fail to detect and quantify the difference between two groups. However, the proposed effect sizes in this paper can be applied no matter if hazards are proportional. This is important in the settings of clinical trials. At the design and planning stages of a study, there is usually no information about whether or not two groups have proportional hazards, so that the assumption of proportional hazards should not be made. The proposed effect sizes, defined as the weighted differences in hazards, would be more reasonable to be used along with the survival time end point for the study than the hazard ratio.

We have defined the effect sizes and studied their estimates for comparing the survival difference between groups. The use of these estimates is straightforward for problems where variable adjustment is not needed. For situations where adjustment needs to be made with important variables, we propose to test the existing adjustment methods, such as matching, stratification and inverse probability weighting [45]. This constitutes an interesting future study. We have not discussed potential analytical formulas for the variances of the proposed estimators. With availability of these formulas, one can investigate not only interval estimation of effect sizes but also the minimum sample sizes required for using the estimators. Finding theoretical formulas for the variances is of interest and deserves further research.

Appendices

Appendix 1

1.1 Proof of Theorem 1

Before we prove Theorem 1, we need three propositions.

Proposition 1

(Gill’s condition) [4, 21] Suppose that for some sequence of process $X_n(t)$ we have

$$\begin{aligned} X_n(t)\overset{P}{\rightarrow }X(t)\ \ \text {as}\ n\rightarrow \infty \end{aligned}$$

for almost all $t\in [0,\tau ]$ with $0< \tau \le \infty$, and the deterministic function X satisfies

$$\begin{aligned} \int _0^\tau |X(t)|\mathrm{d}t <\infty . \end{aligned}$$

Also suppose that for all $\delta >0$, there exists $k_\delta$ with $\int _0^\tau k_\delta (t)\mathrm{d}t<\infty$ such that

$$\begin{aligned} \underset{n\rightarrow \infty }{\text {lim inf}}\ P(|X_n(t)|\le k_\delta (t)\ \text {for all t }\in [0,\tau ])\ge 1-\delta . \end{aligned}$$

Then

$$\begin{aligned} \underset{t\in [0,\tau ]}{\text {sup }}\left| \int _0^t X_n(s)\mathrm{d}s-\int _0^t X(s)\mathrm{d}s\right| \overset{P}{\rightarrow }0. \end{aligned}$$

Proposition 2

(Daniels’ “in probability linear bound”) [4, 13] Let $K_n$ be the empirical distribution function based on a random sample of size n from the continuous (cumulative) distribution function K. Then, for any $\delta \in (0,1)$,

$$\begin{aligned} P(1 - K_n(t-)\le \delta ^{-1} (1 - K(t)) \text { for all } t\in [0,\infty ]) = 1 - \delta . \end{aligned}$$

Proposition 3

(Lenglart–Rebolledo inequality) [4, 36] Let N be a counting process, and $M = N -A$ the corresponding local square integrable martingale. Suppose H is a predictable and locally bounded process. Then for any stopping time $T (\le \infty )$ and any $\epsilon , \eta > 0$,

$$\begin{aligned} P\left\{ \underset{t \le T}{\text {sup}}\left\{ \int _0^t H(s)dM(s)\right\} ^2> \epsilon \right\} \le \frac{\eta }{\epsilon }+P \left\{ \int _0^T H^2(t)d\langle M ,M\rangle (t) > \eta \right\} , \end{aligned}$$

where $\langle M ,M\rangle$ is the compensator for $M^2$.

With these propositions, we can prove Theorem 1. Rewrite

$$\begin{aligned} U =&\sum _{j=1}^{J} w_j\left( \frac{Y_{2j}}{Y_{1j}+Y_{2j}}D_{1j}-\frac{Y_{1j}}{Y_{1j}+Y_{2j}}D_{2j}\right) \\ =&\int _{0}^{\infty }\frac{Y_{2}(t)w_n(t)}{Y_{1}(t)+Y_{2}(t)}d N_{1}(t)-\int _{0}^{\infty }\frac{Y_{1}(t)w_n(t)}{Y_{1}(t)+Y_{2}(t)}d N_{2}(t), \end{aligned}$$

where the last equation is an application of the Lebesgue–Stieltjes integration. Letting

$$\begin{aligned} H_i(t)=\frac{n}{n_1n_2}\frac{Y_{3-i}(t)}{Y_{1}(t)+Y_{2}(t)}, \end{aligned}$$

(16)

we have $\frac{n}{n_1n_2}U =\int _{0}^{\infty }w_n(t)H_1(t)d N_{1}(t)-\int _{0}^{\infty }w_n(t)H_2(t)d N_{2}(t)$. According to Doob–Meyer decomposition theorem [31], $N_i(t)$ can be decomposed into a martingale $M_i(t)$ and a compensator $A_i(t)=\int _0^t\lambda _i (s)Y_i(s)\mathrm{d}s$, $i=1, 2$. Therefore,

$$\begin{aligned} \frac{n}{n_1n_2}U=\Gamma _n+\Psi _n, \end{aligned}$$

(17)

where

$$\begin{aligned} \Gamma _n=\int _{0}^{\infty }w_n(t)H_1(t)d M_{1}(t)-\int _{0}^{\infty }w_n(t)H_2(t)d M_{2}(t) \end{aligned}$$

and

$$\begin{aligned} \Psi _n =\int _{0}^{\infty }w_n(t)H_1(t)d A_{1}(t)-\int _{0}^{\infty }w_n(t)H_2(t)d A_{2}(t). \end{aligned}$$

The proof of the theorem consists of two steps.

Step 1 We show $\Gamma _n\overset{P}{\rightarrow }0$ as $n \rightarrow \infty$. We begin with the integral

$$\begin{aligned} \begin{aligned} \int _{0}^{\infty }H_i(t)^2d A_{i}(t) =&\int _{0}^{\infty }H_i(t)^2\lambda _i(t)Y_i(t)\mathrm{d}t \\ =&\int _{0}^{\infty }\left( \frac{n}{n_{3-i}}\frac{Y_{3-i}(t)}{Y_{1}(t)+Y_{2}(t)}\right) ^2\frac{\lambda _i(t)}{n_i}\frac{Y_i(t)}{n_i}\mathrm{d}t \end{aligned} \end{aligned}$$

(18)

and will use Proposition 1 to show

$$\begin{aligned} \int _{0}^{\infty }H_i(t)^2d A_{i}(t)\overset{P}{\rightarrow }0. \end{aligned}$$

(19)

First, by the fact that $\frac{n}{n_{3-i}}\overset{P}{\rightarrow }\frac{1}{P_{3-i}}$, $\frac{Y_{3-i}(t)}{Y_1(t)+Y_2(t)}\le 1$ and $\frac{Y_i(t)}{n_i}\le 1$, we have, for any $0 \le t < \infty ,$

$$\begin{aligned} \left( \frac{n}{n_{3-i}}\frac{Y_{3-i}(t)}{Y_{1}(t)+Y_{2}(t)}\right) ^2\frac{\lambda _i(t)}{n_i}\frac{Y_i(t)}{n_i}=(O_p(1))^2*o_p(1)*O_p(1)=o_p(1), \end{aligned}$$

i.e.,

$$\begin{aligned} \left( \frac{n}{n_{3-i}}\frac{Y_{3-i}(t)}{Y_{1}(t)+Y_{2}(t)}\right) ^2\frac{\lambda _i(t)}{n_i}\frac{Y_i(t)}{n_i} \overset{P}{\rightarrow }0. \end{aligned}$$

(20)

Second, we note that $(n_i-Q_i(t))/n_i$ is the value, at time $t-$ (time just before t), of the empirical distribution function from the cumulative distribution function of the failure time in group i. According to Proposition 2, for any $\delta \in (0, 1)$, we have,

$$\begin{aligned} P\left( 1-(n_i-Q_i(t))/n_i\le \delta ^{-1} S_i(t) \text { for all } t\in [0,\infty ]\right) = 1 - \delta . \end{aligned}$$

Thus, since $Y_i(t)\le Q_i(t),$ we have

$$\begin{aligned} P\left( \frac{Y_i(t)}{n_i}\le \delta ^{-1}S_i(t) \text { for all } t\in [0,\infty ]\right) \ge 1-\delta . \end{aligned}$$

(21)

Third, by Bonferroni inequality, we see

$$\begin{aligned}&P\left( \frac{n^2}{n^2_{3-i}}\frac{Y_i(t)}{n_i}\le \left( \frac{1}{P^2_{3-i}}+\delta \right) \delta ^{-1}S_i(t) \text { for all } t\in [0,\infty ]\right) \\&\quad \ge P\left( \frac{n^2}{n^2_{3-i}}\le \frac{1}{P^2_{3-i}}+\delta \right) +P\left( \frac{Y_i(t)}{n_i}\le \delta ^{-1}S_i(t) \text { for all } t\in [0,\infty ]\right) -1. \end{aligned}$$

Then, from $\frac{n^2}{n^2_{3-i}}\overset{P}{\rightarrow }\frac{1}{P^2_{3-i}}$ and Eq. (21), we have

$$\begin{aligned}&\underset{n\rightarrow \infty }{\text {lim inf}}\ P\left( \frac{n^2}{n^2_{3-i}}\frac{Y_i(t)}{n_i}\le \left( \frac{1}{P^2_{3-i}}+\delta \right) \delta ^{-1}S_i(t) \text { for all } t\in [0,\infty ]\right) \\&\quad \ge \underset{n\rightarrow \infty }{\text {lim inf}}\ P\left( \frac{n^2}{n^2_{3-i}}\le \frac{1}{P^2_{3-i}}+\delta \right) \\&\qquad + \underset{n\rightarrow \infty }{\text {lim inf}}\ P\left( \frac{Y_i(t)}{n_i}\le \delta ^{-1}S_i(t) \text { for all } t\in [0,\infty ]\right) -1\\&\quad \ge 1-\delta , \end{aligned}$$

and correspondingly

$$\begin{aligned} \underset{n\rightarrow \infty }{\text {lim inf}}\ P\left( \frac{n^2}{n^2_{3-i}}\frac{Y_i(t)}{n_i}\lambda _i(t) \le \left( \frac{1}{P^2_{3-i}}+\delta \right) \delta ^{-1}f_i(t) \text { for all } t\in [0,\infty ]\right) \ge 1-\delta . \end{aligned}$$

Hence, from

$$\begin{aligned} \left( \frac{n}{n_{3-i}}\frac{Y_{3-i}(t)}{Y_{1}(t)+Y_{2}(t)}\right) ^2 \frac{\lambda _i(t)}{n_i} \frac{Y_i(t)}{n_i}\le \left( \frac{n}{n_{3-i}}\right) ^2\frac{Y_i(t)}{n_i}\lambda _i(t), \end{aligned}$$

we obtain

$$\begin{aligned} \begin{aligned}&\underset{n\rightarrow \infty }{\text {lim inf}}\ P\left( \left( \frac{n}{n_{3-i}}\frac{Y_{3-i}(t)}{Y_{1}(t)+Y_{2}(t)}\right) ^2\frac{\lambda _i(t)}{n_i}\frac{Y_i(t)}{n_i} \le k_\delta (t) \text { for all } t\in [0,\infty ]\right) \\&\quad \ge 1 - \delta , \end{aligned} \end{aligned}$$

(22)

where $k_\delta (t)=\left( \frac{1}{P^2_{3-i}}+\delta \right) \delta ^{-1}f_i(t)$ with $\int _0^\infty k_\delta (t)\mathrm{d}t =\frac{1}{P^2_{3-i}}\delta ^{-1}+1 <\infty$ for all $\delta >0$. By Eqs. (18), (20), (22) and Proposition 1, we see (19) is established.

We are now in a position to show $\Gamma _n\overset{P}{\rightarrow }0$. In fact, from Eq. (19) and the fact that $|w_n(t)|\le 1$ and thus $\int _{0}^{\infty }\left( w_n(t)H_i(t)\right) ^2d A_{i}(t) \le \int _{0}^{\infty }H_i^2(t)d A_{i}(t),$ we see $\int _{0}^{\infty }\left( w_n(t)H_i(t)\right) ^2d A_{i}(t)\overset{P}{\rightarrow }0$. Since $A_i(t)$ is the compensator of the counting process $N_i(t)$ with $A_i(0)=0$ a.s. and $A_i(t) < \infty$ a.s. for any t, $M_i=N_i-A_i$ is a local square integrable martingale [16]. In addition, since $H_i(t)$ is a left-continuous process and $w_n(t)H_i(t) =\left( \frac{1}{n_1}+\frac{1}{n_2}\right) \frac{w_n(t)Y_{3-i}(t)}{Y_{1}(t)+Y_{2}(t)}\le 2$, $w_n(t)H_i(t)$ is a predictable and bounded process [16]. Moreover, $\langle M_i ,M_i\rangle (t)=A_i(t)$ since $A_i(t)$ is continuous [16]. Using Proposition 3, we have, for any $\epsilon , \eta > 0$,

$$\begin{aligned}&P\left\{ \underset{t \le \infty }{\text {sup}}\left\{ \int _0^t w_n(s)H_i(s)dM_i(s)\right\} ^2> \epsilon \right\} \\&\quad \le \frac{\eta }{\epsilon } +P \left\{ \int _0^\infty (w_n(t)H_i(t))^2dA_i(t)> \eta \right\} . \end{aligned}$$

Therefore, $\int _{0}^{\infty }w_n(t)H_i(t)d M_{i}(t)\overset{P}{\rightarrow }0.$ Thus, $\Gamma _n=\int _{0}^{\infty }w_n(t)H_1(t)d M_{1}(t)-\int _{0}^{\infty }w_n(t)H_2(t)d M_{2}(t) \overset{P}{\rightarrow }0$.

Step 2 We show $\Psi _n \overset{P}{\rightarrow } \int _0^\infty \frac{\pi _1(t)\pi _2(t)}{\pi (t)}\omega (t)(\lambda _1(t)-\lambda _2(t)) \mathrm{d}t$. Again the proof is done by taking advantage of Proposition 1. Rewrite $\Psi _n$ as

$$\begin{aligned} \begin{aligned} \Psi _n =&\int _{0}^{\infty }\frac{n}{n_1n_2}\frac{Y_{2}(t)}{Y_{1}(t)+Y_{2}(t)}w_n(t)\lambda _1(t)Y_1(t)\mathrm{d}t\\&-\int _{0}^{\infty }\frac{n}{n_1n_2}\frac{Y_{1}(t)}{Y_{1}(t)+Y_{2}(t)}w_n(t)\lambda _2(t)Y_2(t)\mathrm{d}t\\ =&\int _{0}^{\infty }\frac{(Y_1(t)/n_1)(Y_{2}(t)/n_2)}{(Y_{1}(t)+Y_{2}(t))/n}w_n(t)(\lambda _1(t)-\lambda _2(t))\mathrm{d}t. \end{aligned} \end{aligned}$$

By the law of large numbers, we have $\frac{Y_1(t)}{n_1}\overset{p}{\rightarrow } P(X\ge t|Z=1) =\pi _1(t),$ $\frac{Y_2(t)}{n_2}\overset{p}{\rightarrow } P(X\ge t|Z=2) =\pi _2(t),$ $\frac{Y_1(t)+Y_2(t)}{n}\overset{p}{\rightarrow } P(X\ge t) =\pi (t),$ and hence, due to the assumption $w_n(t) \overset{P}{\rightarrow } \omega (t)$, the integrand in $\Psi _n$ has the following probability limit:

$$\begin{aligned} \frac{(Y_1(t)/n_1)(Y_{2}(t)/n_2)}{(Y_{1}(t)+Y_{2}(t))/n}w_n(t)(\lambda _1(t)-\lambda _2(t)) \overset{P}{\rightarrow }\frac{\pi _1(t)\pi _2(t)}{\pi (t)}\omega (t)(\lambda _1(t)-\lambda _2(t)).\nonumber \\ \end{aligned}$$

(23)

To obtain the lower bound of $\underset{n\rightarrow \infty }{\text {lim inf}},$ we first observe

$$\begin{aligned} \left| \frac{(Y_1(t)/n_1)(Y_{2}(t)/n_2)}{(Y_{1}(t)+Y_{2}(t))/n}w_n(t)(\lambda _1(t)-\lambda _2(t))\right| \le \frac{n}{n_2}\frac{Y_{1}(t)}{n_1}\lambda _1(t)+ \frac{n}{n_1}\frac{Y_{2}(t)}{n_2}\lambda _2(t).\nonumber \\ \end{aligned}$$

(24)

As before, using Bonferroni inequality, $\frac{n}{n_{3-i}}\overset{P}{\rightarrow }\frac{1}{P_{3-i}},$ and Eq. (21), we see

$$\begin{aligned}&\underset{n\rightarrow \infty }{\text {lim inf}}\ P\left( \frac{n}{n_{3-i}}\frac{Y_i(t)}{n_i}\le \left( \frac{1}{P_{3-i}}+\frac{\delta }{2}\right) 2\delta ^{-1}S_i(t) \text { for all } t\in [0,\infty ]\right) \\&\quad \ge \underset{n\rightarrow \infty }{\text {lim inf}}\ P\left( \frac{n}{n_{3-i}}\le \frac{1}{P_{3-i}}+\frac{\delta }{2}\right) \\&\qquad + \underset{n\rightarrow \infty }{\text {lim inf}}\ P\left( \frac{Y_i(t)}{n_i}\le 2\delta ^{-1}S_i(t) \text { for all } t\in [0,\infty ]\right) -1\\&\quad =\underset{n\rightarrow \infty }{\text {lim inf}}\ P\left( \frac{Y_i(t)}{n_i}\le 2\delta ^{-1}S_i(t) \text { for all } t\in [0,\infty ]\right) \\&\quad \ge 1-\frac{\delta }{2}, \end{aligned}$$

and correspondingly

$$\begin{aligned} \underset{n\rightarrow \infty }{\text {lim inf}}\ P\left( \frac{n}{n_{3-i}}\frac{Y_i(t)}{n_i}\lambda _i(t) \le \left( \frac{1}{P_{3-i}}+\frac{\delta }{2}\right) 2\delta ^{-1}f_i(t) \text { for all } t\in [0,\infty ]\right) \ge 1-\frac{\delta }{2}. \end{aligned}$$

Then, using Bonferroni inequality one more time, we obtain

$$\begin{aligned} \underset{n\rightarrow \infty }{\text {lim inf}}\ P\left( \frac{n}{n_2}\frac{Y_1(t)}{n_1}\lambda _1(t) +\frac{n}{n_1}\frac{Y_2(t)}{n_2}\lambda _2(t) \le k_\delta (t) \text { for all } t\in [0,\infty ]\right) \ge 1-\delta , \end{aligned}$$

where $k_\delta (t)=\left( \frac{1}{P_2}+\frac{\delta }{2}\right) 2\delta ^{-1}f_1(t) + \left( \frac{1}{P_1}+\frac{\delta }{2}\right) 2\delta ^{-1}f_2(t)$ with $\int _0^\infty k_\delta (t)\mathrm{d}t =\frac{2}{P_2}\delta ^{-1}+1 +\frac{2}{P_1}\delta ^{-1}+1 <\infty$. And hence, according to (24),

$$\begin{aligned} \begin{aligned}&\underset{n\rightarrow \infty }{\text {lim inf}}\ P\left( \left| \frac{\frac{Y_1(t)}{n_1}\frac{Y_2(t)}{n_2}}{\frac{Y_{1}(t)+Y_{2}(t)}{n}}w_n(t)(\lambda _1(t)-\lambda _2(t))\right| \le k_\delta (t) \text { for all } t\in [0,\infty ]\right) \\&\quad \ge 1-\delta . \end{aligned} \end{aligned}$$

(25)

Finally, by (23), (25), the assumption $\int _0^\infty \big | \frac{\pi _1(t)\pi _2(t)}{\pi (t)}\omega (t)(\lambda _1(t)-\lambda _2(t)) \big | \mathrm{d}t < \infty ,$ and Proposition 1, we have

$$\begin{aligned} \Psi _n \overset{p}{\rightarrow } \int _0^\infty \frac{\pi _1(t)\pi _2(t)}{\pi (t)}\omega (t)(\lambda _1(t)-\lambda _2(t))\mathrm{d}t. \end{aligned}$$

Combining results in steps 1 and 2, we see that $\frac{{n}}{{n_1n_2}}U$ converges in probability to $\int _0^\infty \frac{\pi _1(t)\pi _2(t)}{\pi (t)}\omega (t)(\lambda _1(t)-\lambda _2(t))\mathrm{d}t$. $\square$

Appendix 2

1.1 Proof of Corollary 1

• (a) If $w_j=1$, then $\omega (t)=1$. Note the following:

  $$\begin{aligned} \begin{aligned}&\int _0^\infty \left| \frac{\pi _1(t)\pi _2(t)}{\pi (t)}(\lambda _1(t)-\lambda _2(t))\right| \mathrm{d}t\\&\quad \le \int _0^\infty \frac{1}{4}\left( \frac{S_2(t)S^*_2(t)}{P_1}+\frac{S_1(t)S^*_1(t)}{P_2}\right) |\lambda _1(t)-\lambda _2(t)|\mathrm{d}t\\&\quad \le \int _0^\infty \frac{S_2(t)S^*_2(t)}{4P_1}(\lambda _1(t)+\lambda _2(t))\mathrm{d}t +\int _0^\infty \frac{S_1(t)S^*_1(t)}{4P_2}(\lambda _1(t)+\lambda _2(t))\mathrm{d}t\\&\quad =E_2\left[ \frac{\left( \frac{\lambda _1(t)}{\lambda _2(t)}+1 \right) S^*_2(t)}{4P_1}\right] +E_1\left[ \frac{\left( \frac{\lambda _2(t)}{\lambda _1(t)}+1 \right) S^*_1(t)}{4P_2}\right] \\&\quad <\infty , \end{aligned} \end{aligned}$$

  where the last inequality is obtained by using the assumption $E_{i}[\lambda _{3-i}(t)/\lambda _{i}(t)] <\infty$. Then the result follows immediately from Theorem 1.

• (b) If $w_j=Y_j/n,$ then $\omega (t)=\pi (t)$. Since

  $$\begin{aligned} \int _0^\infty \left| \frac{\pi _1(t)\pi _2(t)}{\pi (t)}\omega (t)(\lambda _1(t)-\lambda _2(t))\right| \mathrm{d}t =&\int _0^\infty \left| \pi _1(t)\pi _2(t)(\lambda _1(t)-\lambda _2(t))\right| \mathrm{d}t\\ \le&\int _0^\infty \left| S_1(t)S_2(t)(\lambda _1(t)-\lambda _2(t))\right| \mathrm{d}t\\ \le&\int _0^\infty \left( S_2(t)f_1(t)+S_1(t)f_2(t) \right) \mathrm{d}t\\ \le&2, \end{aligned}$$

  the result follows immediately from Theorem 1.

• (c) Here we have $w_n(t)=\prod _{k: t_{k} < t}\left( 1-\frac{D_k}{Y_k}\right) =\widehat{S}(t-),$ which is the left-continuous version of the Kaplan–Meier estimator. Let $\Upsilon$ denote the support of $S(t)S^*(t)$, i.e., the set of t such that $S(t)S^*(t)>0$. We can show that for any $t\in \Upsilon$, $w_n(t)\overset{p}{\rightarrow }S(t)=S_1(t)P_1+S_2(t)P_2.$ First, for the pooled population, T is independent of C when $S^*_1(t)=S^*_2(t)=S^*(t)$. This is because $P(T\le t)P(C\le t')=P(T\le t,C\le t')$, which can be easily seen by conditioning and using the assumption of independence between T and C in each group. Second, for any $\epsilon >0$ and $\epsilon _1 >0,$

  $$\begin{aligned} P\left( \left| \widehat{S}(t-)-S(t)\right|>\epsilon \right) \le&P\left( \left| \widehat{S}(t-\epsilon _1)-{S}(t-\epsilon _1)\right|>\epsilon /6\right) \\&+P\left( \left| \widehat{S}(t)-S(t)\right|>\epsilon /6\right) \\&+P\left( \left| {S}(t-\epsilon _1)-{S}(t)\right|>\epsilon /6\right) \\&+P\left( \left| \widehat{S}(t)-S(t)\right| >\epsilon /2\right) . \end{aligned}$$

  Then from the continuity of S(t), the independence between T and C, and the consistence of $\widehat{S}(t)$ [19], we see that for $t\in \Upsilon$,

  $$\begin{aligned} \underset{n\rightarrow \infty }{\text {lim}}\ P\left( \left| \widehat{S}(t-)-S(t)\right| >\epsilon \right) =0, \end{aligned}$$

  showing $w_n(t)\overset{p}{\rightarrow }S(t)=S_1(t)P_1+S_2(t)P_2$ for $t\in \Upsilon$. Therefore,

  $$\begin{aligned} \frac{\widehat{S}(t-)(Y_1(t)/n_1)(Y_{2}(t)/n_2)}{(Y_{1}(t)+Y_{2}(t))/n}(\lambda _1(t)-\lambda _2(t)) \overset{P}{\rightarrow }&\frac{S(t)\pi _1(t)\pi _2(t)}{\pi (t)}(\lambda _1(t)-\lambda _2(t)) \\ =&S^*(t)S_1(t)S_2(t){(\lambda _1(t)-\lambda _2(t))} \end{aligned}$$

  holds for $t\in \Upsilon$. Clearly this limit also holds true for any $t \notin \Upsilon$, since $Y_1(t)$, $Y_2(t)$ and $S^*(t)S_1(t)S_2(t)$ all are 0 for $t\notin \Upsilon$. Hence, Eq. (23) holds. Now the result is obtained by following exactly the proof of Theorem 1 and observing $\int _0^\infty \left| S^*(t)S_1(t)S_2(t){(\lambda _1(t)-\lambda _2(t))}\right| \mathrm{d}t \le \int _0^\infty \left( S_2(t)f_1(t)+S_1(t)f_2(t) \right) \mathrm{d}t \le 2$. $\square$

Appendix 3

1.1 Proof of Theorem 2

From $\lambda _1(t)=r\lambda _2(t)$, we have $S_1(t)=\left( S_2(t)\right) ^r$. Then we have the following: $P(T_1>T_2) =\int _0^\infty S_1(t)f_2(t)\mathrm{d}t =\int _{0}^\infty \left( S_2(t)\right) ^r f_2(t)\mathrm{d}t =\frac{1}{r+1},$ so that $ES_{\mathrm{MW}}=1-2P(T_1>T_2) =\frac{r-1}{r +1}$.

Let $\lambda _1^*=-log(S_1(\tau ^*))/\tau ^*$ and $\lambda _2^*=-log(S_2(\tau ^*))/\tau ^*$. Then it follows from $S_1(t)=\left( S_2(t)\right) ^r$ that we have $\lambda _1^*=r\lambda _2^*$. In light of $D_e(\tau _1=\tau ^*,\tau _2=\tau ^*)=A+B+C$, where $A=\int _0^{\tau ^*} S_1(t)f_2(t)\mathrm{d}t =\int _0^{\tau ^*}\left( S_2(t)\right) ^r f_2(t)\mathrm{d}t =\frac{1}{r+1}\left( 1-(S_2(\tau ^*))^{r+1}\right) ,$ $B=0$ and $C= \frac{\lambda _2^*}{\lambda _1^*+\lambda _2^*} e^{-\left( \lambda _1^*+\lambda _2^*\right) {\tau ^*}} =\frac{1}{r+1}(S_2(\tau ^*))^{r+1},$ we see $D_e(\tau _1=\tau ^*,\tau _2=\tau ^*) =\frac{1}{r+1}$ so that $ES_{\mathrm{MWE}}(\tau _1=\tau ^*, \tau _2=\tau ^*)=1-2D_e(\tau _1=\tau ^*,\tau _2=\tau ^*) =\frac{r-1}{r +1}$.

Finally, we have $ES_{\mathrm{MWC}}(\tau =\tau ^*)=1-2D_c(\tau =\tau ^*) =\frac{r-1}{r +1}$, since ${D}_c(\tau =\tau ^*) =\frac{1}{1-S_1(\tau ^*)S_2(\tau ^*)}\int _0^{\tau ^*} S_1(t)f_2(t)\mathrm{d}t =\frac{1}{1-(S_2(\tau ^*))^{r+1}}\int _0^{\tau ^*}\left( S_2(t)\right) ^r f_2(t)\mathrm{d}t =\frac{1}{1-(S_2(\tau ^*))^{r+1}}\frac{1}{r+1}\left( 1-(S_2(\tau ^*))^{r+1}\right) =\frac{1}{r+1}$. $\square$

Appendix 4

1.1 Proof of Theorem 3

To prove the first inequality, recall (Sect. 3.1) $D_e(\tau _1=\tau ^*, \tau _2=\tau ^*) = -\int _{0}^{\tau ^*}{S}_1(t)d{S}_2(t) +\frac{{\lambda }_2^*}{{\lambda }_1^*+{\lambda }_2^*}e^{-({\lambda }_1^*+{\lambda }_2^*)\tau ^*}$ with $\lambda _i^*=-\log (S_i(\tau ^*))/\tau ^*$ for $i=1,2$ and $P(T_1>T_2) = -\int _{0}^{\tau ^*}{S}_1(t)d{S}_2(t) -\int _{\tau ^*}^{\infty }{S}_1(t)d{S}_2(t).$ Therefore, we have

$$\begin{aligned}&\left| D_e(\tau _1=\tau ^*, \tau _2=\tau ^*)-P(T_1>T_2)\right| \\&\quad \le \max \left( \left| \frac{{\lambda }_2^*}{{\lambda }_1^*+{\lambda }_2^*}e^{-({\lambda }_1^*+{\lambda }_2^*)\tau ^*}\right| , \left| \int _{\tau ^*}^{\infty }{S}_1(t)f_2(t)\mathrm{d}t\right| \right) \\&\quad \le \max \left( \frac{{\lambda }_2^*}{{\lambda }_1^*+{\lambda }_2^*}e^{-{\lambda }_1^*\tau ^*}e^{-{\lambda }_2^*\tau ^*} , \int _{\tau ^*}^{\infty }{S}_1(\tau ^*)f_2(t)\mathrm{d}t \right) \\&\quad = \max \left( \frac{{\lambda }_2^*}{{\lambda }_1^*+{\lambda }_2^*}{S}_1(\tau ^*){S}_2(\tau ^*) , {S}_1(\tau ^*){S}_2(\tau ^*) \right) \\&\quad \le \epsilon _1\epsilon _2. \end{aligned}$$

Hence, $|ES_{\mathrm{MWE}}(\tau _1=\tau ^*,\tau _2=\tau ^*)-ES_{\mathrm{MW}}| =2\left| D_e(\tau _1, \tau _2)-P(T_1>T_2)\right| \le 2\epsilon _1\epsilon _2.$

For the second inequality, recall (Sect. 3.2) $D_c(\tau =\tau ^*) = \frac{-\int _{0}^{\tau ^*}{S}_1(t)d{S}_2(t)}{1-S_1(\tau ^*)S_2(\tau ^*)}.$ Therefore,

$$\begin{aligned}&\left| D_c(\tau =\tau ^*)-P(T_1>T_2)\right| \\&\quad = \left| \left( \frac{1}{{1-S_1(\tau ^*)S_2(\tau ^*)}}-1 \right) \int _{0}^{\tau ^*}{S}_1(t)f_2(t)\mathrm{d}t-\int _{\tau ^*}^{\infty }{S}_1(t)f_2(t)\mathrm{d}t\right| \\&\quad \le \max \left( \frac{S_1(\tau ^*)S_2(\tau ^*)}{{1-S_1(\tau ^*)S_2(\tau ^*)}} \int _{0}^{\tau ^*}{S}_1(t)f_2(t)\mathrm{d}t, \int _{\tau ^*}^{\infty }{S}_1(t)f_2(t)\mathrm{d}t \right) \\&\quad \le \max \left( \frac{S_1(\tau ^*)S_2(\tau ^*)}{{1-S_1(\tau ^*)S_2(\tau ^*)}} \left( 1-S_2(\tau ^*)\right) , \int _{\tau ^*}^{\infty }{S}_1(t)f_2(t) \mathrm{d}t \right) \\&\quad \le \max \left( \frac{S_1(\tau ^*)S_2(\tau ^*)}{{1-S_1(\tau ^*)S_2(\tau ^*)}} \left( 1-S_1(\tau ^*)S_2(\tau ^*)\right) , \int _{\tau ^*}^{\infty }{S}_1(\tau ^*)f_2(t) \mathrm{d}t \right) \\&\quad = \max \left( S_1(\tau ^*)S_2(\tau ^*) , S_1(\tau ^*)S_2(\tau ^*) \right) \\&\quad \le \epsilon _1\epsilon _2. \end{aligned}$$

Hence,

$$\begin{aligned} |ES_{\mathrm{MWC}}(\tau =\tau ^*)-ES_{\mathrm{MW}}| =2\left| D_c(\tau )-P(T_1>T_2)\right| \le 2\epsilon _1\epsilon _2. \end{aligned}$$

$\square$

Appendix 5

1.1 Proof of (15)

Assume $S_1(t)$, $S_2(t)$, $S_1^*(t)$ and $S_2^*(t)$ are all exponentially distributed with $S_1(t)=e^{-\lambda _1t}$, $S_1^*(t)=e^{-\lambda ^*_1t}$, $S_2(t)=e^{-\lambda _2t}$, $S_2^*(t)=e^{-\lambda ^*_2t}$ and $\lambda _1=r\lambda _2$ (i.e., hazard ratio is r). Since $CR_1 =1-P(C_1>T_1) =1-\int _0^\infty S^*_1(t)f_1(t)\mathrm{d}t =\frac{\lambda _1^*}{\lambda _1+\lambda _1^*},$ we have $\lambda _1^*=\frac{\lambda _1CR_1}{1-CR_1}.$ Similarly, $\lambda _2^*=\frac{\lambda _2CR_2}{1-CR_2}.$ Then we have $ES_{G} = \int _0^\infty e^{-\lambda _1t}e^{-\lambda _2t}e^{-\lambda ^*_1t}e^{-\lambda ^*_2t}(\lambda _1-\lambda _2)\mathrm{d}t = \frac{\lambda _1-\lambda _2}{\lambda _1+\lambda _2+\lambda _1^*+\lambda _2^*} = \frac{r-1}{r+1+r\frac{CR_1}{1-CR_1}+\frac{CR_2}{1-CR_2}}.$

In addition, it is known that the natural log of the exponentially distributed survival time has mean $-\log (\lambda _i)-\gamma$ ($\gamma$ is the Euler–Mascheroni constant) and variance $\pi ^2/6$ [5]. Therefore, the Cohen’s d based on the differences of the log failure times between the two groups is

$$\begin{aligned} d=\frac{(-\log (\lambda _1)-\gamma )-(-\log (\lambda _2)-\gamma )}{\sqrt{\pi ^2/6}} =-\frac{\log (r)\sqrt{6}}{\pi }, \end{aligned}$$

which is a function of r. Using this relationship between r and d, we see that $ES_G$ can be represented as a function of Cohen’s d and censoring rates $CR_i$, as shown in formula (15). $\square$