1 Introduction

Quadrotors that belong to the wide class of Unmanned Aerial Vehicles (UAVs) have been undergoing surprising adaptations and improvements, mainly due to their exceptional maneuverability and robust hovering ability. For the past couple of decades, quadrotors have been extensively employed in many application areas, including but not limited to construction [1], cargo [2], agriculture [3], rescue operations [4], crowd monitoring [5], and surveillance [6]. Recent advancements in techniques and control architectures have significantly bolstered UAVs, furnishing them with a robust foundation for expansion [7]. The strides made in sensor technology and other critical domains of artificial intelligence serve as a catalyst for amplifying their autonomy [8]. To elaborate, the concept of autonomy implies that quadrotors can perform key operations such as flying, hovering, and landing on their own. Among these, autonomous landing is considered the most challenging flight task, mainly due to the environmental conditions and nonlinear dynamics of quadrotors [9, 10].

The major challenges faced in autonomous landing are: accurate localization of the landing platform as well as the quadrotor; state estimation of the platform; and safe landing on a stationary or dynamic platform. A large portion of the existing literature considers the platform to be stationary, whose position can be known or unknown [11,12,13]. The indoor localization is achieved mainly using computer vision [13, 14], ultra-wideband [15], IMU [16], multimodal sensor fusion [17, 18], wireless sensor networks [19], and motion capture systems [20,21,22]. To identify the platform using computer vision, certain patterns or markers are placed on the top of the platform [14, 23,24,25]. The MCSs, independent of such requirements, have proved to be more robust and accurate than other existing approaches [22, 26]. In this work, we assume no communication or perception exists between the quadrotor and the platform; i.e., the environment is non-cooperative. Our study endeavors to demonstrate the autonomous landing proficiency of a quadrotor, leveraging OptiTrack cameras within a complex, dynamic, and unfamiliar setting.

Motion capture systems were initially developed for gait analysis in health care, but are now used in various other fields, such as biomechanics, robotics, sports, virtual reality, and entertainment, among others. Depending upon the nature of the application, the number of cameras can be increased to enhance the captured volume, thus making the system much more expensive. The notable manufacturers producing MCSs are Nokov [27], Vicon [28], Qualisys [29], and OptiTrack [30]. Motion capture is a means to record the movements of specific objects or individual by determining their pose in the physical space. MCSs are mainly classified into four categories based upon the sensor measurements: optical-passive, optical-active, video, and inertial [31]. Among these, optical-passive MCSs have gained recognition for robotics applications in an indoor laboratory setting due to their significant practical value. The author in [22] used the OptiTrack system to localize a mobile robot and compared the results with odometry and kinematic localization. The results demonstrated that higher accuracy was obtained through MCS. In [26], the authors investigated the performance and accuracy of a Vicon motion capture device to record and assess the static and dynamic movements of a mobile robot.

Before the advent of MCS, computer vision and pattern matching were used as the main tools to assist in the autonomous landing of UAVs. Many vision-based algorithms have been developed for this purpose which can be broadly classified into position-based visual servoing [32, 33] and image-based visual servoing [34, 35]. Usually, these algorithms require certain patterns and markers to be affixed to the landing site. In [36], the authors presented a real-time algorithm that identifies an H-shaped landing target using invariant moments. A similar work was proposed by [37], which used a single cross at the center of a circle as a landing pattern. Niu et al. [38] proposed the usage of multiple-scale QR codes for different altitudes. For localization, the empirical formulation is defined which corresponds to the pixel size and UAV’s altitude. The authors in [39] also utilized a QR code-based visual positioning system to localize the target object - in this case, a flying drone. In [25], the authors developed a vision-based system capable of detecting fiducial ArUcO markers placed on the landing platform through a monocular camera attached to the quadrotor. The authors in [32] combined large- and small-sized fiducial AprilTag markers to locate the target object with high precision.

Once the localization of the quadrotor and the landing platform is achieved, the motion control of the quadrotor is the next big challenge. The under-actuated nature of the quadrotor makes the takeoff, hovering, tracking, and landing much more difficult. The overall control scheme is usually implemented through a multi-loop to control the position and attitude independently [33]. In a cascaded control designed by [40], MPC was used to plan the landing trajectory; whereas to track the planned trajectory, Incremental Nonlinear Dynamic Inversion (INDI) was employed. The authors of [41] performed the trajectory tracking using linear MPC, and the method was validated in the simulated environment. The MPC-based approach was also utilized by [37] to perform autonomous tracking and landing on a moving car.

The present work proposes a complete autonomous vision-based navigation and control system to perform the autonomous tracking of a stationary or moving platform and the landing of a quadrotor on it. A real-time optical MCS is utilized to track and calculate the poses of both the quadrotor and the landing platform. In this way, using MCS, the necessary condition to keep the target object’s geometric properties constantly visible to the quadrotor is eliminated. The developed control architecture guides the quadrotor to the platform by estimating the future movements of the platform. This work proposes a cascaded control scheme, in which MPC is used to perform position tracking while PID is used to control the attitude. This approach follows the fact that, nowadays, a majority of commercially available flight controllers are pre-equipped with attitude controllers. The experimental results show that the proposed approach can effectively work for both stationary and moving landing platforms and can follow a ground vehicle with a linear velocity of 0.8 m/s. The novelty of this approach is in the introduction of the state-of-the-art MCS to accomplish the challenging quadrotor landing problem in real-world experimental conditions.

The valuable contributions of this work are as follows:

  1. 1.

    An autonomous vision-based navigation, tracking, and control system is proposed that enables the localization, estimation, tracking, and landing of a quadrotor on a stationary or moving platform by employing a real-time MCS.

  2. 2.

    In contrast to the vision-based system described in [25], which relies on the quadrotor initiating tracking and detection from a hovering state with the landing platform in its field of view, necessitating constant visual monitoring to keep the platform within sight, this paper introduces a more holistic approach. Our proposed solution elevates the necessity to maintain continuous observation of the target throughout all stages of operation, encompassing rest, take-off, hovering, and landing. Moreover, the quadrotor can be initially placed anywhere in the workspace.

  3. 3.

    While significant strides have been taken in the pursuit of reference tracking for mobile robots, the prevailing literature frequently confines performance evaluation to metrics such as reference tracking error and motion smoothness [14]. This narrow focus imposes limitations on the robustness and overall performance of the system. In this article, we introduce an optimal model-based controller designed to address these shortcomings. Our approach not only minimizes energy consumption but also prioritizes smooth motion and closed-loop stability, effectively managing induced efforts to enhance overall system performance. Additionally, the closed-loop stability of the system is rigorously ensured through Lyapunov Stability analysis, further bolstering its reliability and robustness.

2 Problem description

The overall problem can be classified into three parts: localization of the quadrotor and the landing platform, tracking and estimation of the landing platform, and safe landing of the quadrotor on a stationary or moving platform. The 3D reference coordinate frames are attached to the centers of gravity of the quadrotor and the landing platform as \(X_Q=\begin{bmatrix} x_q&\quad y_q&\quad z_q \end{bmatrix}^{T}\) and \(X_P=\begin{bmatrix} x_p&\quad y_p&\quad z_p \end{bmatrix}^{T}\), respectively. The mobile platform’s frame of reference is positioned with an offset of 9 cm off the ground. The overall operation is considered successful when the quadrotor manages to land on the target platform. The three problems introduced earlier are defined as follows:

Problem 1

Localization of the quadrotor and the landing platform

Build up a framework consisting of a quadrotor, platform, and four OptiTrack cameras to localize the ground vehicle and aerial vehicle to obtain \(X_Q\) and \(X_P\) in real-time.

Problem 2

Tracking and estimation of the landing platform

The quadrotor tracks the landing platform in the horizontal plane (x, y) and initiates the landing process if

$$\begin{aligned} \begin{aligned} e_x&:= \left\| x_q - x_p \right\| \le \sigma _x\\ e_y&:= \left\| y_q - y_p \right\| \le \sigma _y \end{aligned} \end{aligned}$$
(1)

where \(\sigma _x, \sigma _y \in \mathbb {R}^{+}\) are defined as the tolerance for the position errors of the landing area.

Design an optimal MPC utilizing the estimated position and velocity of the platform obtained through KF and the actual position and velocity of the quadrotor.

$$\begin{aligned} u_{x,y}:= f_1(x_q,y_q,{\dot{x}}_q,{\dot{y}}_q,\tilde{x}_p,\tilde{y}_p,\dot{\tilde{x}}_p,\dot{\tilde{y}}_p) \end{aligned}$$

Problem 3

Landing of the quadrotor on the platform

The landing state is triggered once the quadrotor and the landing platform are aligned in the \(x-y\) plane by fulfilling the conditions in Eq. (1). The adjustment in the quadrotor’s height continues until

$$\begin{aligned} e_z:= \left\| z_q - z_p \right\| \approx 0 \end{aligned}$$
(2)

Design a PID

$$\begin{aligned} u_{z}:= f_2(z_q,{\dot{z}}_q,z_p,0) \end{aligned}$$

to achieve the vertical regulation of the quadrotor. The height of the platform is a constant, hence velocity would be zero. It is noted that both controllers for horizontal and vertical regulation are combined to generate a unified model-based predictive controller.

3 System overview

3.1 Quadrotor and landing platform

The DJI Tello EDU, a programmable quadrotor, is used in this study. With the help of SDK, it can be interfaced with many tools and programming languages, such as Python, Scratch, Swift, and MATLAB. It is very light-weight (87 g) and has the dimensions of 9.8 cm × 9.25 cm × 4.1 cm. Tello EDU has a speed limit of 8 m/s, a maximum flight time of 13 min, and a maximum flight height of 3000 cm. The landing platform having the dimensions of 30 cm × 30 cm is placed on top of a differential drive robot. Therefore, its position and velocity can be defined based on the movements of the robot, whose maximum velocity is defined as 0.8 m/s.

3.2 Motion capture system (MCS)

MCS, a very sophisticated system, comprises several components: hardware, software, and acquisition methods.

3.2.1 OptiTrack cameras

Four OptiTrack \(\hbox {Prime}^{\textsf{x}} 13\)’s \({2.7}''\) square signatures are considered for this study. They are capable of tracking active and passive markers with the positional and rotational accuracies of \(\pm 0.20\) mm and 0.5 deg, respectively. The detailed camera specifications are provided in Table 1.

Table 1 \(\hbox {Prime}^{\textsf{x}} 13\) camera specifications
Full size table

3.2.2 System architecture

Four lightweight OptiTrack cameras are connected to the host computer using an Ethernet PoE/PoE+ switch through LAN. A special software tool, known as Motive, running on a PC is responsible for the calibration and acquisition of the 3D data. The software can stream live data to other applications using a plugin or SDK. NAT-NET SDK is employed to build client/server applications and to interface Motive with MATLAB. Using this interface, client applications can run on the same PC as the tracking software (Motive). The host PC is carefully chosen to have an i5-9400F processor with six cores to satisfy the required minimum specifications and run the operations smoothly.

3.2.3 Motion capture workspace

Similar to other measurement systems, calibration is also considered critical for optical MCSs. Using the OptiTrack calibration wand, the pose of each camera is computed along with the amount of distortion in the captured images. This information is later used to define a 3D capture volume based on 2D images from multiple synchronized cameras through a process known as triangulation. The cameras should be positioned at a certain vantage point to maximize the target capture area. For our case, four cameras are positioned perpendicular to each other to define a workspace volume of 300 cm × 300 cm (Fig. 1). After the calibration is performed and the volume is defined, retro-reflective markers are carefully installed on the objects of interest. For this study, four markers are placed on both the quadrotor and the platform in a configuration where they are always observable. During the operation, Motive can record the movements of each marker or live stream them to other pipelines.

Fig. 1
figure 1

Workspace volume defined using MCS

Full size image

4 System dynamics and modeling

In this section, the kinematic and dynamic model of the quadrotor is presented.

Assumption 1

The origin and the axes of the body frame coincide with the body center of the quadrotor and the principal axes.

Assumption 2

The quadrotor is a rigid body and is perfectly balanced.

Assumption 3

The maximum velocity of the quadrotor is considered greater than the landing platform that is placed on a differential drive robot.

The linear velocity of the quadrotor in the body-fixed frame is defined using \({\textbf {v}}_{\textbf {B}}=\begin{bmatrix} u&\quad v&\quad w \end{bmatrix}^{T} \in \mathbb {R}^{3}\), whereas \({\textbf {v}}=\begin{bmatrix} {\dot{x}}_q&\quad {\dot{y}}_q&\quad {\dot{z}}_q \end{bmatrix}^{T} \in \mathbb {R}^{3}\) is used to represent its velocity in the inertial frame, which is placed globally. The linear velocities are related by the rotation matrix \({\textbf {R}}(\phi , \theta , \psi ) \in\) \(\textrm{SO}(3)\) as:

$$\begin{aligned} {\textbf {v}}={\textbf {R}}{} {\textbf {v}}_{\textbf {B}} \end{aligned}$$
(3)

Using the Euler angles, rotation matrix \({\textbf {R}}\) is determined as:

$$\begin{aligned} {\textbf {R}} = \begin{bmatrix} c\psi c\theta &{}\quad c\theta s\psi &{}\quad -s\theta \\ c\psi s\phi s\theta -c\phi s\psi &{}\quad c\phi c\psi + s\phi s\psi s\theta &{}\quad c\theta s\phi \\ s\phi s\psi + c\phi c\psi s\theta &{}\quad c\phi s\psi s\theta - c\psi s\phi &{}\quad c\phi c\theta \end{bmatrix} \end{aligned}$$
(4)

where c and s are abbreviations for the cosine and sine functions, respectively. The angular velocity vector of the quadrotor in the body-fixed frame is defined using \({\varvec{\omega }}_{\textbf {B}}=\begin{bmatrix} p&\quad q&\quad r \end{bmatrix}^{T} \in \mathbb {R}^{3}\), whereas \({\varvec{\omega }}=\begin{bmatrix} {\dot{\phi }}&\quad {\dot{\theta }}&\quad {\dot{\psi }} \end{bmatrix}^{T} \in \mathbb {R}^{3}\) is used to represent its angular velocity in the inertial frame. Therefore, the relationship between the angular velocities can be defined by:

$$\begin{aligned} {\varvec{\omega }} = {\textbf {T}} {\varvec{\omega _B}} \end{aligned}$$
(5)

Transformation matrix \({\textbf {T}} \in\) \(\textrm{SO}(3)\) is used to transform the angular velocity from the body frame to the inertial frame:

$$\begin{aligned} {\textbf {T}} = \begin{bmatrix} 1 &{}\quad s\phi t\theta &{}\quad c\phi t\theta \\ 0 &{}\quad c\phi &{}\quad -s\phi \\ 0 &{}\quad \frac{s\phi }{c\theta } &{}\quad \frac{c\phi }{c\theta } \end{bmatrix} \end{aligned}$$
(6)

where t represents the tangent function. The equations of motion are derived using the Netwon-Euler method to describe the dynamics of the quadrotor.

$$\begin{aligned} m({\varvec{\omega _B}} \times {\textbf {v}}_{\textbf {B}} + \dot{{\textbf {{v}}}}_{\textbf {B}}) = {\textbf {f}}_{\textbf {B}} \end{aligned}$$
(7)

where m is the mass of the quadrotor and \({\textbf {f}}_{\textbf {B}}=\begin{bmatrix} f_x&\quad f_y&\quad f_z \end{bmatrix}^{T} \in \mathbb {R}^{3}\) is the total force. The total torque required for the quadrotor is calculated using the Newton-Euler method:

$$\begin{aligned} {\textbf {I}} \dot{{\varvec{\omega }}}_{\textbf {B}} + {\varvec{\omega }}_{\textbf {B}} \times ({\textbf {I}} {\varvec{\omega }}_{\textbf {B}}) = {\textbf {m}}_{\textbf {B}} \end{aligned}$$
(8)

where \({\textbf {m}}_{\textbf {B}}=\begin{bmatrix} m_x&\quad m_y&\quad m_z \end{bmatrix}^{T} \in \mathbb {R}^{3}\) is the total torque and \({\textbf {I}}\in \mathbb {R}^{3\times 3}\) is the diagonal inertia matrix that contains \(\{I_{xx},I_{yy},I_{zz}\}\). The dynamic model for the quadrotor defined in Eqs. (7) and (8) remains valid as long as Assumption 1 remains intact. The consideration of the effect of the external forces \({\textbf {f}}_{\textbf {B}}\) on the quadrotor is combined with Eq. (6) as:

$$\begin{aligned} {\textbf {f}}_{\textbf {B}} = mg {\textbf {R}}^{T} \hat{{\textbf {e}}}_{\textbf {z}} - f_t \hat{{\textbf {e}}}_{\textbf {3}} \end{aligned}$$
(9)

where \(\hat{{\textbf {e}}}_{\textbf {z}}\) and \(\hat{{\textbf {e}}}_{\textbf {3}}\) are the unit vectors along the inertial and the body-fixed z axes.

The weight mg introduces the effect of the gravitational force, where \(f_t\) as a total thrust is generated by the rotors. The external moments in the body-fixed frame result in a more detailed version of Eq. (8) as:

$$\begin{aligned} {\textbf {m}}_{\textbf {B}} = {\varvec{\tau }}_{\textbf {B}} - {\textbf {m}}_{\textbf {g}} \end{aligned}$$
(10)

where \({\varvec{\tau }}_{\textbf {B}}=\begin{bmatrix} {\tau }_x&\quad {\tau }_y&\quad {\tau }_z \end{bmatrix}^{T} \in \mathbb {R}^{3}\) is the control input torque generated due to the difference in the angular velocities of the rotors. The term \({\textbf {m}}_{\textbf {g}}\), known as gyroscopic moment, is included to introduce the combined effect of the rotation of four rotors and the vehicle body, represented as:

$$\begin{aligned} {\textbf {m}}_{\textbf {g}} = \sum _{i=1}^{4}J_p ({\varvec{\omega }}_{\textbf {B}}\times \hat{{\textbf {e}}}_{\textbf {3}})(-1)^{i+1} \Omega _i \end{aligned}$$
(11)

where \(\Omega _i\) is the angular speed of the ith rotor and \(J_p\) is the motor’s inertia. According to [42], this inertia is found to be small; hence, the effect of gyroscopic moment is ignored in the controller formulation.

The control input \(u_1\) provides the thrust in a vertical axis and is defined as:

$$\begin{aligned} f_t =u_1= k_{t}\sum _{i=1}^{4} \Omega _i^{2} \end{aligned}$$
(12)

where \(k_t\) is the thrust coefficient. The other three control inputs (\(u_2,u_3,u_4)\), dependent on the angular speeds of the rotors, are represented as:

$$\begin{aligned} \begin{aligned} \left\{ \begin{array}{cl} \tau _x &{} = u_2 = k_{t} l(\Omega ^2_{3}-\Omega ^2_{1}) \\ \tau _y &{} = u_3 = k_{t} l(\Omega ^2_{4}-\Omega ^2_{2}) \\ \tau _z &{} = u_4 = k_{d}(\Omega ^2_{2}+\Omega ^2_{4}-\Omega ^2_{1}-\Omega ^2_{3}) \end{array} \right. \end{aligned} \end{aligned}$$
(13)

where l is the distance from the center of the quadrotor to any rotor, as the quadrotor is symmetrical according to Assumption 2. The drag coefficient is introduced using the term \(k_d\). The complete dynamic model of the quadrotor can be obtained by substituting the control inputs from Eqs. (12) and (13) to Eqs. (9) and (10).

5 Detection, tracking, and estimation

In this section, the problem of detection and tracking of the landing platform is investigated. The information is later used to determine the relative pose between the quadrotor and the platform and to guide the quadrotor towards the platform.

5.1 Target detection

The target landing platform is detected by the OptiTrack cameras using the four retro-reflective markers placed on the corners of the platform. It is assumed that there is no transfer of information between the quadrotor and the platform.

5.2 Kalman filter-based pose estimation of landing platform

The linear Kalman filter serves two purposes: tracking and estimation of the mobile platform’s position and velocity. Assuming that the mobile platform can only move in a 2D plane, its motion can be defined using translation along the x-axis and y-axis. To track the mobile platform, the position information \(\{x_p, y_p\}\) must be known at every instant. The KF mathematical model for the mobile platform’s tracking is defined as follows:

$$\begin{aligned} {\textbf {x}}({k+1})={\textbf {A}} {\textbf {x}}(k)+{\textbf {B}} {\textbf {u}}(k) \end{aligned}$$
(14)

where \({\textbf {x}}{(k)}=\begin{bmatrix} x_p{\left( k\right) }&\quad y_p{\left( k\right) }&\quad {\dot{x}}_p\left( k\right)&\quad {\dot{y}}_p\left( k\right)&\end{bmatrix}^{T}\) is defined as the state vector based upon displacements and velocities, and \({\textbf {u}}(k)=\begin{bmatrix} \ddot{x}_p{(k)}&\ddot{y}_p{(k)}\end{bmatrix}^{T}\) applies the acceleration as the control input at instance k. The state-space model presented in Eq. (14) has a state-transition matrix \({\textbf {A}}\) and input matrix \({\textbf {B}}\), defined as follows:

$$\begin{aligned} {\textbf {A}}&=\begin{bmatrix} 1 &{}\quad 0 &{}\quad T_s &{}\quad 0\\ 0 &{}\quad 1 &{}\quad 0 &{}\quad T_s\\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1\\ \end{bmatrix}&{\textbf {B}}&=\begin{bmatrix} \frac{T_{s}^{2}}{2} &{}\quad 0\\ 0 &{}\quad \frac{T_{s}^{2}}{2}\\ T_s &{}\quad 0\\ 0 &{}\quad T_s\\ \end{bmatrix} \end{aligned}$$

where \(T_s\) is the control time step.

To account for the uncertainty due to the inaccuracy of the model and/or the inputs (acceleration), a white-noise term is introduced to the model in Eq. (14) as:

$$\begin{aligned} {\textbf {x}}({k+1})={\textbf {A}} {\textbf {x}}(k)+{\textbf {B}}{} {\textbf {u}}(k) + {\textbf {w}}(k) \end{aligned}$$
(15)

It is assumed that \({\textbf {w}}\) is a Gaussian distribution noise with a mean of 0 and a variance \({\textbf {B}}{} {\textbf {Q}}_b {\textbf {B}}^T\), where \({\textbf {Q}}_b\) is a diagonal matrix whose diagonal values are chosen based upon the laboratory tests as 2. The off-diagonal elements of \({\textbf {Q}}_b\) are zeros; this is due to the assumption that the motions along x and y axes are uncorrelated.

The measurement vector \({\textbf {z}}\) is defined as:

$$\begin{aligned} {\textbf {z}}(k) = {\textbf {H}} {\textbf {x}}(k) + {\textbf {v}}(k) \end{aligned}$$
(16)

where \({\textbf {H}}\) is the output matrix that maps the state vector into the measurement domain and \({\textbf {v}}\) is the measurement noise. The output matrix \({\textbf {H}}\) is chosen as:

$$\begin{aligned} {\textbf {H}} = \begin{bmatrix} 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \\ 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad \\ \end{bmatrix} \end{aligned}$$

The measurement noise \({\textbf {v}}\) is assumed to be Gaussian distributed with a mean of 0 and a variance \({\textbf {H}} {\textbf {R}}_b {\textbf {H}}^T\), where the diagonal values of \({\textbf {R}}_b\) are chosen as 2.1 through trial and error.

5.3 Velocity estimation of quadrotor

Only the position and attitude of the quadrotor are available through Motive and are either streamed to the ground control station or recorded as logged data. Therefore, the linear and angular velocity of the quadrotor must be estimated. The linear velocity at the inertial frame (I) using raw position data (\(x_{raw}\)) is determined as follows:

$$\begin{aligned} v_{raw}[N] \approx (x_{raw}[N] - x_{raw}[N-1])/dt \end{aligned}$$
(17)

where dt is the step size between two successive data elements. The raw velocity information is then processed through a sliding window filter to obtain smoother data over a finite duration.

$$\begin{aligned} v[N] = \sum _{i=0}^{m-1} \mu _i v_{raw}[N-i]; \sum _{i=0}^{m-1}\mu _i = 1 \end{aligned}$$
(18)

The angular velocity of a quadrotor is estimated using the Lie algebra of the rotation matrix as:

$$\begin{aligned} w_{raw}[N] \approx -(\mathfrak {R}[N] \mathfrak {R}[N-1]/dt)^{\vee } \end{aligned}$$
(19)

where \(\vee\) is denoted as the inverse of the Lie map and the rotation matrix \(\mathfrak {R}\) between the inertial frame and body-fixed reference frame is defined as:

$$\begin{aligned} \mathfrak {R}[N] = \mathcal {R}(q[N]) \mathcal {L}(q[N])^T \end{aligned}$$
(20)

where the auxiliary matrices \(\mathcal {R}\) and \(\mathcal {L}\) are defined using quaternion \(q[N]=\begin{bmatrix} q_0&\quad q_1&\quad q_2&\quad q_3 \end{bmatrix}^{T}\) obtained from the rotation matrix \({\textbf {R}}\) defined in (4).

$$\begin{aligned} \mathcal {R}(q)= & {} \begin{bmatrix} -q_1 &{}\quad q_0 &{}\quad -q_3 &{}\quad q_2 \\ -q_2 &{}\quad q_3 &{}\quad q_0 &{}\quad -q_1 \\ -q_3 &{}\quad -q_2 &{}\quad q_1 &{}\quad q_0 \end{bmatrix}; \\ \mathcal {L}(q)= & {} \begin{bmatrix} -q_1 &{}\quad q_0 &{}\quad q_3 &{}\quad -q_2 \\ -q_2 &{}\quad -q_3 &{}\quad q_0 &{}\quad q_1 \\ -q_3 &{}\quad q_2 &{}\quad -q_1 &{}\quad q_0 \end{bmatrix} \end{aligned}$$

The filtered angular velocity estimate of angular velocity is obtained using a sliding window as follows:

$$\begin{aligned} w[N] = \sum _{i=0}^{m-1} \mu _i w_{raw}[N-i]; \sum _{i=0}^{m-1}\mu _i = 1 \end{aligned}$$
(21)

As the position and attitude data of the quadrotor are expected to vary at a much faster rate, a smaller window length of 4 is chosen based on the experimental tests.

6 Model predictive control of quadrotor

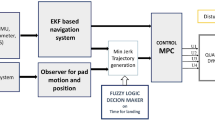
The model predictive controller is responsible for determining the desired control inputs to reduce the error between the trajectories of the quadrotor and the platform. This process is performed by solving the constrained tracking problem and minimizing the performance index of the optimization problem. The manipulated variable is computed using the Quadratic Programming (QP) optimization. The quadrotor UAV’s control system embodies a bifurcated architecture, delineated in Fig. 2, encompassing a positional regulator and an attitude regulator. Each regulator orchestrates feedback acquisition acquired via MCS, with the positional regulator managing position feedback and the attitude regulator honing in on attitude feedback. Notably, the platform’s movements remain pre-established and autonomous from the quadrotor’s actions. The linear Kalman Filter (KF) serves as a powerful tool for noise reduction and prediction within the system. By effectively filtering out white noise originating from sensor measurements, it ensures a smoother, more accurate estimate of the platform’s position. Additionally, the KF integrates a dynamic model of the landing platform’s motion, utilizing both its current state and previous observations to predict future states. This predictive capability not only aids in compensating latency but also enhances the overall responsiveness of the tracking system. The resulting position estimate is then seamlessly integrated into the MPC block, acting as the desired trajectory for precise tracking.

Fig. 2
figure 2

Vision-based navigation, tracking, and control system

Full size image

6.1 Design of the multi-objective optimization function

The optimization functions for the MPC are designed based on the following discrete form of the system

$$\begin{aligned} \begin{aligned} x ( k+1 )&= f ( x(k), U(k)) \\ y(k)&= C x(k) \end{aligned} \end{aligned}$$
(22)

where x is a state vector that holds the position and velocity information of the quadrotor, f represents the continuously differentiable function concerning its arguments, and \(f(0,0)=0\). The position and velocity of the quadrotor obtained as the output are compared with the reference information from the platform.

For the system given in (22), the multi-objective optimization problem solved using QP is defined as:

$$\begin{aligned} \underset{x,u}{\text {min}}~J(x (k), u(k))= & {} \left\| y(k) - r(k) \right\| _{Q}^{2} + \left\| u(k) \right\| _{R}^{2}\nonumber \\{} & {} \quad + \left\| \Delta u(k) \right\| _{S}^{2} + \left\| x (k) \right\| _{P}^{2} \end{aligned}$$
(23)

where Q is a positive diagonal matrix that is employed for adjusting the tracking performance; R is a positive diagonal matrix to adjust the gain for the control input; S is a positive diagonal matrix to adjust the weights for the change in control actions; and P is a symmetric positive-definite matrix that is used to tune penalties.

6.2 MPC formulation

Given an auxiliary control law

$$\begin{aligned} u = \kappa _a(x) \end{aligned}$$
(24)

and a positive invariant set \(X_f \subset X\) containing the origin \(x=0\). Thus for the closed-loop system

$$\begin{aligned} x(k+1) = f \left( x(k), \kappa _{a}(x(k)) \right) \end{aligned}$$
(25)

and for any \(\chi (\bar{k}) \in X_f\), the states and control inputs are defined as

$$\begin{aligned} \begin{array}{ll} x(k) \in X_f, &{}\quad k \ge \bar{k}\\ u(k) = \kappa _a(x(k)) \in U, &{}\quad k \ge \bar{k} \end{array} \end{aligned}$$
(26)

The Receding Horizon (RH) method is applied for prediction horizon N to determine the optimized input sequence [43]

$$\begin{aligned} u(k),u(k+1),\ldots ,u(k+N-1) \end{aligned}$$

by minimizing the cost function

$$\begin{aligned} \begin{aligned} \underset{x,u}{\text {min}}~J(x(k),u(\cdot ),N)&= \text {min} \{\sum _{i=0}^{N-1} \left\| e(k+i) \right\| _{Q}^{2} + \left\| u(k+i) \right\| _{R}^{2} \\&\quad + \left\| \Delta u(k+i) \right\| _{S}^{2} + \left\| x(k+i) \right\| _{P}^2 \}\\&\quad + V_f(x(k+N)) \end{aligned} \end{aligned}$$
(27)

s.t.:    \(x(k+1)=f(x(k),U(k))\)

\(u_{min}\le u(k) \le u_{max}, k=0,\ldots ,N-1\)

\(\Delta u_{min} \le \Delta u(k) \le \Delta u_{max}, k=0,\ldots ,N-1\)

\(e_{min} \le e(k) \le e_{max}, k=1,\ldots ,N\)

The RH solution implicitly defines the MPC time-invariant control law as

$$\begin{aligned} u = \kappa _{RH}(x) \end{aligned}$$
(28)

Theorem 1

Let \(X^{RH}(N)\) be the set of states that provides the optimal solution. If, for any \(x\in X_f\) and auxiliary control law \(\kappa _a\), the condition

$$\begin{aligned}{} & {} V_f(x(k),\kappa _a(x(k))) - V_f(x(k)) + \left( \left\| e(k) \right\| _{Q}^{2}\right. \nonumber \\{} & {} \quad \left. + \left\| \kappa _a(x(k)) \right\| _{R}^{2} + \left\| \Delta \kappa _a(x(k)) \right\| _{S}^{2} + \left\| x(k) \right\| _{P}^2 \right) \le 0 \end{aligned}$$
(29)

is fulfilled and

$$\begin{aligned} V_f(x) \le \alpha _f\left( \left\| x \right\| \right) \end{aligned}$$
(30)

where \(\alpha _f\left( \left\| x \right\| \right)\) is a class K function, then the origin of the closed-loop system with the MPC-RH control law is an asymptotically stable equilibrium point with the region of attraction \(X^{RH}(N)\). Moreover, if \(\alpha _f\left( \left\| x \right\| \right) = b \left\| x \right\| ^2\) and \(X_f = X^{RH}(N)\), then the origin defined by \(x=0\) and \(u=0\) is exponentially stable in \(X^{RH}(N)\).

Proof

Let \(x^{*}(k)\in X^{RH}(N)\) and \(U^{*}(k,N)\) be the optimal solution at k with prediction horizon N. Then, at time \(k+1\)

$$\begin{aligned} {\tilde{U}}(k+1,N)= & {} \left[ u_k^*(k+1), u_k^*(k+N-2),\right. \nonumber \\{} & {} \left. \quad \ldots ,u_k^*(k+N-1),\kappa _a(x(k+N)) \right] \end{aligned}$$
(31)

is a feasible solution, so that \(x(k+1)\in X^{RH}(N)\). Hence, the following condition is satisfied in \(X^{RH}(N)\).

$$\begin{aligned} V(x,N):= J(x,k_{RH}(x),N)\ge \left\| e \right\| _{Q}^2 + \left\| x \right\| _{P}^2 \end{aligned}$$
(32)

At time k, the sequence

$$\begin{aligned} {\tilde{U}}(k+1,N)=\left[ U^*(k,N), \kappa _a(x(k+N)) \right] \end{aligned}$$
(33)

is feasible for the MPC problem with horizon \(N+1\) and

$$\begin{aligned} \begin{aligned}&J(x,{\tilde{U}}(k,N+1),N+1) \\&\quad = V(x,N) - V_f(x(k+N))+V_f(x(k+N+1))\\&\quad + \left\| e(k+N) \right\| _{Q}^{2} + \left\| \kappa _a(x(k+N)) \right\| _{R}^{2} \\&\quad + \left\| \Delta \kappa _a(x(k+N)) \right\| _{S}^{2} + \left\| x(k+N) \right\| _{P}^2 \le V(x,N) \end{aligned} \end{aligned}$$
(34)

so that we have the monotonicity property (concerning N)

$$\begin{aligned} V(x,N+1) \le V(x,N), \forall x \in X^{RH}(N) \end{aligned}$$
(35)

with \(V(x,0) = V_f(x), \forall x \in X_f\). Then

$$\begin{aligned} V(x,N+1) \le V(x,N) \le V_f(x) \le \alpha _f(\left\| x(k)\right\| ), \forall x \in X_f \end{aligned}$$
(36)

and the condition \(V(x,N)\le \psi (\left\| x \right\| ), \forall x \in X_f\) is satisfied. Finally

$$\begin{aligned} \begin{aligned} V(x,N)&=\left\| e \right\| _Q^2 + \left\| \kappa _{RH} \right\| _R^2 + \left\| \Delta \kappa _{RH} \right\| _S^2 + \left\| x \right\| _P^2 \\&\quad + J(f(x,\kappa _{RH}(x)),u^{*}(k+1,N-1),N-1)\\&= \left\| e \right\| _Q^2 + \left\| \kappa _{RH} \right\| _R^2+ \left\| \Delta \kappa _{RH} \right\| _S^2 + \left\| x \right\| _P^2 \\&\quad + V(f(x,\kappa _{RH}(x)),N-1)\\&\ge \left\| e \right\| _Q^2 + \left\| \kappa _{RH} \right\| _R^2 + \left\| \Delta \kappa _{RH} \right\| _S^2 + \left\| x \right\| _P^2 \\&\quad + V(f(x,\kappa _{RH}(x)),N)\\&\ge \left\| e \right\| _Q^2 + \left\| x \right\| _P^2 \\&\quad + V(f(x,\kappa _{RH}(x)),N-1), \forall x\in X^{RH}(N) \end{aligned} \end{aligned}$$
(37)

and also the condition \(\Delta V(x) \le -r(\left\| x \right\| ),\forall x \in X^{RH}(N)\) is satisfied. So, V(x, N) is a Lyapunov function, and we conclude by Lyapunov’s stability theorem that the equilibrium \(x=0, u=0\) is exponentially stable if \(\alpha _f(\left\| x \right\| )=b\left\| x \right\| ^2, X_f=X^{RH}(N)\).

6.3 Hard constraints

Due to the physical saturation of the motor torque input, the hard constraints are introduced to the induced efforts as follows;

$$\begin{aligned}{} & {} 0 \le f_t(k+j|k) \le 4 k_t \Omega _{max}^{2} \end{aligned}$$
(38a)
$$\begin{aligned}{} & {} -l k_t \Omega _{max}^{2} \le \tau _i(k+j|k) \le l k_t \Omega _{max}^{2} \end{aligned}$$
(38b)
$$\begin{aligned}{} & {} -2k_d \Omega _{max}^{2} \le \tau _z(k+j|k) \le 2k_d \Omega _{max}^{2} \end{aligned}$$
(38c)

where \(i = x, y\) and    \(j=1,2,\ldots m-1\). The maximum speed, \(\Omega _{max}\), is the same for all rotors as the motors are identical and the quadrotor is balanced according to Assumption 2.

The inherent nature of MPC assists in predicting future trajectories, thus making it useful for the tracking of moving targets. The predictive model and the MPC optimization problem are solved using the MPC designer toolbox provided by MATLAB. The state-space information is provided to the designer and later used to tune the controller, prediction horizon, and control horizon. The prediction and control horizon are configured as 9 and 3, respectively.

7 Experimental results and discussion

Before initiating the experiments, calibration is performed for the MCS by tracing the motion sensor markers using the Motive. During the operation, the NAT-NET SDK is used by MATLAB to receive the data stream from the Motive. The next step is to build a WiFi communication link between MATLAB and the quadrotor. The mobile platform is set up by uploading the intended trajectory to the open-source hardware (Arduino) using the IDE software. These experimental procedures are repeated for each scenario to ensure consistency and reliable performance. Figure 3 highlights the communication chain concerning the systems and the information flow.

Fig. 3
figure 3

Communication link among all the systems

Full size image

To evaluate the performance of the proposed vision-based system, a series of three different experiments, each including 20 trials, is performed. It is observed that the success of the experiments is reduced when the marker(s) are occluded or the WiFi connection between the PC and the quadrotor is unstable, or the platform travels out of the defined workspace. The overall efficiency of the experiments carried out in this study, though, is recorded as exceeding \(90\%\), thus implying the successful landing of the quadrotor on the stationary/moving platform. Another critical factor influencing landing precision is the resolution of the estimated position of the quadrotor which can fluctuate depending on its distance and angle from the camera or the MCS. This variation in resolution is primarily a result of the principles of triangulation, which are commonly used in the MCS to estimate the position of objects. When the platform is closer to the camera, the MCS can provide higher-resolution data, leading to more accurate position estimates. This can improve the quadrotor’s ability to land precisely. Conversely, as the quadrotor moves farther away, the resolution decreases, potentially leading to less precise position estimates.

7.1 Stationary target

Initially, the most basic scenario of a stationary landing platform is considered to test the performance of the proposed strategy. From several trials carried out in this way, the results from one such trial are recorded where the relative distance between the quadrotor and the platform is defined as 214 cm. As the process is initiated, the quadrotor takes off, corrects its heading, and then starts moving towards the target by taking a step of 35 cm. This process continues until the pose error defined between the platform and the quadrotor is not acceptable. Figure 4a–d shows the complete sequence of events from the initial position to taking off, maneuvering, and finally landing.

Fig. 4
figure 4

Sequence of events concerning the quadrotor and the platform in the static scenario

Full size image
Fig. 5
figure 5

Trajectories of the quadrotor and the platform in the static scenario

Full size image
Fig. 6
figure 6

Actual and predicted position of the landing platform in the static scenario. a x-axis b y-axis c Combined error along x and y axes

Full size image
Fig. 7
figure 7

Position measurement of the platform and the quadrotor in the static scenario. a x-axis b y-axis c z-axis

Full size image

Figure 5 illustrates the initial position of the quadrotor, the stationary platform, and the trajectory of the quadrotor. The sequence begins with the quadrotor taking off; then, it ascends to an appropriate altitude before commencing its approach towards the target. As the pose error along the x and y axes falls within the acceptable range, the descent phase begins. Upon reaching a minimal height difference between the quadrotor and the platform, the entire process concludes successfully. Figure 6a, b shows the actual position of the landing platform and its estimation obtained using the KF in a 2D plane. The error norm between the actual and estimated positions for both x and y axes is plotted in Fig. 6c. It is evident from the figures that the future prediction of the platform has zero error since it is stationary.

Figure 7a, b illustrates the (x, y) trajectories of the mobile platform and the quadrotor. Once the estimation information is available, the quadrotor starts moving towards the platform, which is observable at \(t=14~\)s. In the last few seconds of the experiment, the quadrotor maintains its position in the \(x-y\) plane and starts to descend. The changes in the height of the quadrotor due to its movements are recorded and displayed in Fig. 7c. It can be observed that the quadrotor goes through the phases of take-off and hovering before commencing the descent at about \(t=23~\)s. As the pose error between the quadrotor and the platform is minimal, the experiment is concluded successfully.

7.2 Dynamic target

7.2.1 Square-shaped trajectory

For this experiment, the straight-line distance between the landing platform and the quadrotor is defined as 71 cm. Figure 8a–d shows the complete sequence of events: from the rest position to taking off, tracking, and finally landing. In this scenario, the target platform maneuvers on a pre-defined trajectory, shown in Fig. 9. The movement of the platform is triggered at \(t+2\) s. The quadrotor takes off and waits for the first prediction to become available. After each prediction, the quadrotor corrects its heading towards the predicted target and moves closer. The target is assumed to be moving at a constant speed. On the corners, some irregular movements are recorded that are mainly due to the estimation. It can be observed that the MPC thoroughly tracks the reference trajectory with minimum error due to its ability to generate an optimal output at each time step during the navigation.

Fig. 8
figure 8

Sequence of events concerning the quadrotor and the platform in the square-shaped scenario

Full size image
Fig. 9
figure 9

Trajectories of the quadrotor and the platform for the square-shaped scenario

Full size image
Fig. 10
figure 10

Actual and predicted position of the landing platform in the square-shaped scenario. a x-axis b y-axis c Combined error along x and y axes

Full size image
Fig. 11
figure 11

Position measurement of the platform and the quadrotor in the square-shaped scenario. a x-axis b y-axis c z-axis

Full size image

Figure 10a, b shows the actual and the predicted positions of the landing platform along the x and y axes, whereas the combined error norm is plotted in Fig. 10c. It can be observed that the estimation obtained through the KF is very much closer to the actual measurement. Small spikes in the prediction error are observed due to the platform being in a dynamic state. The maximum predicted error is recorded as 10 cm, which is considered acceptable.

The position of the quadrotor and the landing platform in the \(x-y\) plane is depicted in Fig. 11a, b. At \(t=28\) s and \(t=35\) s, the trajectories of the platform and the quadrotor appear to make close contact; yet, to initiate the landing process, the error along both x and y should be within an acceptable range. Figure 11c shows the elevation of the quadrotor and the platform. Though the platform maneuvers on the ground, a small variation of \(\pm 2.5\) cm is recorded in its height by the MCS. The quadrotor initiates its movements - i.e., take-off at \(t=15\) s and attaining the height of 90 cm. The MPC computes the sequence of events to optimally steer the quadrotor towards the platform and reduce the tracking error. At \(t=58\) s, the quadrotor makes a successful landing on the moving platform.

7.2.2 Circular-shaped trajectory

The mobile platform, initially placed at a straight line distance of 114 cm from the quadrotor, is programmed to maneuver in a circular-shaped trajectory of a 100 cm diameter. After taking off and stabilizing itself, the quadrotor starts moving towards the predicted location of the platform. Figure 12a–d shows four snapshots to depict each event, while Fig. 13 shows the traveling trajectories of the quadrotor and the mobile platform making a circular motion. After take-off, the quadrotor waits for the prediction concerning the position of the platform to become available. Once done, the quadrotor starts traveling towards the predicted target with a step size of 35 cm. After some maneuvers, the quadrotor successfully performs the landing operation on the moving platform. Though the estimation is performed with high frequency, the time required by the Tello EDU quadrotor to process the command from the navigation and control system somehow limits the overall performance. In this way, the test scenario exposes the technical limitation of the Tello EDU quadrotor.

Fig. 12
figure 12

Sequence of events concerning the quadrotor and the platform in the circular-shaped scenario

Full size image
Fig. 13
figure 13

Trajectories of the quadrotor and the platform in the circular-shaped scenario

Full size image
Fig. 14
figure 14

Actual and predicted position of the landing platform in the circular-shaped scenario. a x-axis b y-axis c Combined error along x and y axes

Full size image
Fig. 15
figure 15

Position measurement of the platform and the quadrotor in the circular-shaped scenario. a x-axis b y-axis c z-axis

Full size image

To overcome this limitation, a TCP server/client program is developed that runs on a separate MATLAB session. The TCP server queues up the commands from the main navigation MATLAB program necessary to control the quadrotor. The server continuously monitors the quadrotor status and only sends a command when the quadrotor is available. This solution improves the delay time caused by the quadrotor SDK.

Figure 14a, b plots the actual location of the landing platform and its estimation through KF for the x and y axes. The combined error depicting the difference between the actual and estimated data is shown in Fig. 14c. Due to the continuous change in the pose of the platform, small variations appear in the error plot; however, more importantly, the obtained steady-state error is bounded and within an acceptable range.

Figure 15a, b shows the movements of the platform and the quadrotor along the x and y axes. Before landing, the quadrotor performs a number of attempts to approach the target; yet, due to the continuously changing conditions, it cannot initiate the landing operation. The landing performance of the quadrotor in terms of the displacement along the z-axis is depicted in Fig. 15c. It is observed that after take-off, the quadrotor stabilizes itself and starts maneuvering towards the target. The landing is initiated when the platform and the quadrotor are aligned within an acceptable range. Around \(t=60\)s, the error along both the x and y axes converges towards zero and enters the acceptable range. However, only after a few seconds, the trajectory along the y-axis appears to deviate from its reference. This causes the quadrotor to terminate the landing operation and re-adjust its height, prolonging the entire operation but still landing in a successful second attempt at almost 90 s. This scenario is considered more challenging due to the continuous change in the heading of the platform and the velocities along both axes, which was not the case in any previous scenarios.

8 Conclusion

In the present study, a quadrotor (Tello EDU), a Kalman filter, a model predictive controller, and a motion capture system (OptiTrack) are used to design a vision-based system, whose role is to achieve an autonomous landing of the quadrotor on a moving platform. The tracking and landing on the platform is devised as a constrained tracking problem. An optimal model-based predictive controller is designed to ensure minimum energy consumption, smooth motion, and closed-loop stability while limiting the induced efforts. To provide smooth and noise-free information to the MPC algorithm, a KF is employed to estimate the position and velocity of the platform. This not only helps to accurately predict the future position of the mobile platform, but it also reduces the time required for landing. Several experiments are conducted to test the proposed vision-based system. The experiments involve different movements of the mobile platform, such as square, circular, and stationary. The performance tests reveal that the quadrotor is able to track various types of trajectories and, subsequently, land safely on the moving or stationary platform.

Future work can focus on the improvement of the MPC by introducing different noises and disturbance models. In the presence of such constraints, noises, and disturbances, an NMPC based on Adaptive Dynamic Programming (ADP) can be utilized to achieve fast response and strong robustness. Another potential area for upcoming attempts is to evaluate the performance of the proposed system by utilizing different estimation algorithms, such as an Extended Kalman Filter (EKF), an Unscented Kalman Filter (UKF), and a Particle Filter (PF).