1 Introduction

The occurrence of extreme climatic events has emerged as a mounting concern within both society and the scientific community. The frequency and repercussions of such events, including economic and societal damages, have garnered attention due to the adversities stemming from natural disasters [1]. These disasters are typically triggered by severe climatic factors, with intense rainfall being recognized as one of the primary causes.

The impacts caused by extreme weather events affect not only the occurrence of natural disasters, but also agricultural and livestock activities. During periods of heavy rains, the planting of crops with more fragile structures may be affected due to the decrease in soil oxygen quantity, which affects nutrient absorption [2]. In addition, heavy rainfall can result in adverse effects on public health, since exposure to flood and flood-prone areas can increase the risk of infectious diseases, such as leptospirosis, transmitted by contact with water or mud contaminated by animal urine, mainly rodents [3].

The study of the behavior of extreme variables, such as maximum rainfall, is conducted through approaches from the Extreme Values Theory. This theory was propelled by the work of [4], which described the three types of asymptotic extreme values distributions (Types I, II, and III). In this theory, the analysis of datasets with small sample sizes is common due to the nature of extreme variables. In this scenario, using Bayesian Inference for fitting extreme value models emerges as an effective approach for analyses, as it enables the incorporation of prior information, which can reduce uncertainties surrounding the parameters under study [5].

Based on point predictions obtained through Bayesian inference for different locations and return periods in a given region, it becomes possible to analyze the variable from a spatial perspective. In this study, various spatial statistical techniques were applied to investigate the spatial behavior of extreme rainfall in the southern and southwestern regions of Minas Gerais. These techniques focus on modeling variables that exhibit spatial structure, enabling inferences and predictions of attributes for unsampled locations within the spatial domain.

Spatial statistics use interpolation methods, which rely on known point values to estimate values at unsampled points [6]. Different spatial interpolation methods can be classified into two categories: Deterministic and Stochastic (e.g., Geostatistical). The Geostatistical approach is particularly appealing as it allows for the incorporation of complementary information from spatial covariates using multivariate methods [7]. In this study, both Deterministic and Geostatistical interpolation methods were employed, specifically the Inverse Distance Weighting (IDW), the Ordinary Kriging (OK) and Log-Normal Kriging (LK) methods.

Due to the extreme nature of the phenomenon under study, in addition to the Kriging and IDW methods, methodologies specific to the analysis of spatial extreme variables were employed, such as max-stable processes and the spatial Generalized Extreme Value (GEV) distribution. Through max-stable processes and the spatial GEV model, it is possible to integrate geographic and climatic covariates into trend surfaces, allowing for the spatial variation of extreme model parameters in the analyzed region and the spatial prediction of the attribute [8].

Regarding the spatial analysis of rainfall in the region of Minas Gerais, few studies in the literature have applied Geostatistical methods for interpolating the variable, only the studies by [9, 10] were found. However, distinguishing itself from the present study, these works focused on assessing the spatial distribution of the observed variable or the mean rainfall, without addressing predictions for specific return periods. It is worth noting that this region is considered the second largest mesoregion in the state of Minas Gerais, with 2.7 million inhabitants [11], an approximate size of the population of a country, such as, for example, Uruguay, which, according to the last census of 2011 [12], it is 3.39 million inhabitants. Furthermore, the majority of the state’s coffee production is located in this region, with production of 13,684 thousand bags, which corresponds to approximately 51% of the State’s total production [11].

Due to the possible consequences of intense rainfall and its influence on different socioeconomic and environmental aspects, it becomes necessary to study and understand this phenomenon through a spatial approach. Therefore, this study aimed to spatially model the maximum rainfall in the southern and southwestern region of Minas Gerais using different spatial methodologies applied from point rainfall predictions for different return periods obtained throught both Bayesian inference and max-stable methods.

2 Materials and methods

2.1 Dataset description and region of study

The southern and southwestern region of Minas Gerais is one of the 12 mesoregions of the state and has an area of 49,524 \(\hbox {km}^2\). According to [13], the climates present in the region, according to the Köppen classification, are Aw, Cwa, and Cwb. The first one is characterized by a winter with low rainfall and a rainy summer. Cwa and Cwb climates have milder temperatures compared to the Aw climate and are influenced by the high altitudes of the southern region of Minas Gerais. The Aw climate is mainly found in the northern portion of the region, while the Cwa climate is present in areas with higher altitudes, such as the Serra da Mantiqueira and nearby regions, and the Cwb climate is observed in the southern portion of the region, near the border with São Paulo, according to [14].

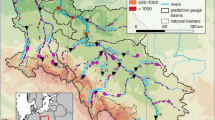
In this study, daily rainfall data, expressed in water depth (mm), were used for 29 cities in the southern and southwestern region of Minas Gerais, as highlighted in Fig. 1.

Fig. 1
figure 1

Location of the meteorological stations of the 29 cities in southern and southwestern Minas Gerais analyzed in the study numbered in alphabetical order

Full size image

Daily records were obtained through the National Water Agency (ANA) and National Institute of Meteorology (INMET). The rainfall data refers to the years from 1980 to 2021. The daily rainfall data for each city were grouped into annual series, and from these series the corresponding maximum values for each year were selected. Thus, 29 maximum value series were obtained, each containing 42 data points, representing the maximum annual daily rainfall values for each city under study.

In order to evaluate the models used in this study, the maximum value series were separated into two distinct blocks. The first block, consisting of data from 1980 to 2011, was used for fitting the models. That is, the GEV distribution was fitted throught Bayesian Inference and rainfall predictions were obtained for return periods of 2, 5, and 10 years for each city. Spatial modeling was then performed throught IDW and Kriging from these predictions, obtaining spatial predictions.

The second block, with records from the period of 2012 to 2021, was used to evaluate the effectiveness of each model. For this, cross-validation methods and calculation of the mean prediction error (MPE) were used for locations not used in the model fitting.

Table 1 presents data from the meteorological stations used in the study. It is important to note that some of the stations had gaps in their records, which led to the use of data from other stations located in the same city, in order to complete the series. The cities where gaps were identified in the stations and the alternative stations used to supplement the series are: Machado (2145002-ANA, 2145033-ANA, and 83683-INMET), Poços de Caldas (2146048-ANA, 2146074-ANA, and 83681-INMET), Pouso Alto (2244071-ANA and 2244063-ANA), São Lourenço (83736-INMET, 2245081-ANA, and 2245107-ANA), Silvianópolis (2245085-ANA and 2245075-ANA).

Table 1 Data from meteorological stations of the 29 cities in southern and southwestern Minas Gerais analyzed, with their respective percentage of failures (PF)
Full size table

Due to the failures in the records of some datasets obtained from INMET and ANA, even with the combination of data from different stations, some gaps persisted. To address this issue, the k-Nearest Neighbors imputation method was applied, which involves filling in the missing values from the weighted average of the k-nearest neighbors of that missing value [15]. In this way, complete datasets were obtained for all the studied locations.

In order to perform a descriptive analysis of the maximum rainfall data for each of the 29 study locations, the position measures of the series (mean, median, maximum and the coefficient of variation) were estimated.

2.2 Bayesian approach to maximum rainfall analysis

To verify the assumption of independence of the constructed maximum series and the presence of trend, the Ljung-Box test [16] and Mann-Kendall test [17, 18] were used, respectively, at a 5% significance level. Kolmogorov-Smirnov test was used for evaluate the goodness of fitting GEV distributions at a 5% significance level.

For each of the 29 maximum rainfall series from cities in the south and southwest of Minas Gerais, GEV distribution adjustments were performed in order to model the distribution of annual maximum rainfall. The GEV distribution has parameters \(\mu\), \(\sigma\), and \(\xi\), which are, respectively, the position, scale, and shape parameters, and its probability density function is given by:

$$\begin{aligned} f(x)=\dfrac{1}{\sigma }\left[ 1+\xi \left( \dfrac{x-\mu }{\sigma }\right) \right] ^{-\left( \frac{1+\xi }{\xi }\right) } \exp \left\{ -\left[ 1+\xi \left( \dfrac{x-\mu }{\sigma }\right) \right] ^{-\frac{1}{\xi }}\right\} , \end{aligned}$$
(1)

where, \(1+\xi \left( \dfrac{x-\mu }{\sigma }\right) >0\), \(\mu \in {\mathbb {R}}\), \(\sigma >0\), and \(\xi \in {\mathbb {R}}^*\). The form of the GEV distribution varies according to the value of the parameter \(\xi\). For \(\xi <0\), the function is defined for \(-\infty<x<\mu -\frac{\sigma }{\xi }\). For \(\xi >0\), the function is defined for \(\mu -\frac{\sigma }{\xi }<x<\infty\). When \(\xi\) equals zero, the function is defined for \(x \in {\mathbb {R}}\).

Several methods can be used to estimate the parameters of the GEV distribution, including Bayesian Inference. The Bayesian approach incorporates prior information about the phenomenon of interest and the data information to obtain the posterior density of the parameters. The prior information is represented by a prior distribution of the parameters, which reflects prior knowledge about them before obtaining or collecting the data. The information from the data is represented by the likelihood function. Thus, the posterior distribution contains all available parameter information, rendering it information-rich [19].

By using the prior distribution, \(p(\varvec{\theta })\), and the likelihood function, \(L(\varvec{\theta }|\varvec{x})\), it is possible to obtain the posterior distribution of \(\theta\), \(p(\varvec{\theta } |\varvec{x})\):

$$\begin{aligned} p(\varvec{\theta }|\varvec{x})\propto L(\varvec{\theta }|\varvec{x}) p(\varvec{\theta } ), \end{aligned}$$
(2)

where, \(\propto\) represents proportionality and \(\varvec{x} = \{ {x_1},\,{x_2},\,\ldots ,\,{x_n}\}\) is the data sample. The likelihood function of the GEV distribution is given by:

$$\begin{aligned}{} & {} L(\varvec{\theta }|\varvec{x})=\dfrac{1}{\sigma ^n}\prod _{i=1}^n\left\{ \left[ 1+\xi \left( \dfrac{x_i-\mu }{\sigma }\right) \right] ^{-\left( \frac{1+\xi }{\xi }\right) } \right\} \nonumber \\{} & {} \exp \left\{ \sum \limits _{i=1}^{n}\left\{ -\left[ 1+\xi \left( \dfrac{x_i -\mu }{\sigma }\right) \right] ^{-\left( \frac{1}{\xi }\right) }\right\} \right\} , \end{aligned}$$
(3)

where, \(\varvec{\theta } = (\mu , \sigma , \xi )\) and n is the sample size.

The prior distribution can be categorized into two distinct types based on the degree of prior knowledge available about the parameters \(\varvec{\theta }\). These types include the informative prior distribution and the non-informative prior distribution. When experts have prior information and prefer a specific range of one or more parameter values in a parameter space, the prior distribution is considered informative. On the other hand, when the researcher does not prefer any parameter value in a parameter space, the prior distribution is defined as non-informative.

[20] formulated a prior distribution for the three parameters of the GEV distribution with the aim of improving the estimation of these parameters, proposing that they follow a Trivariate Normal distribution, given by:

$$\begin{aligned} p(\varvec{\theta } )= { (2\pi ) }^{ 1/2 }{ \left| \varvec{\Sigma }_0 \right| }^{ 1/2 }\exp \left\{ -\frac{ 1 }{ 2 } { (\varvec{\theta } -\varvec{\Phi }_0 ) }^{ t }{ \varvec{\Sigma }_0 }^{ -1 }(\varvec{\theta } -\varvec{\Phi }_0 ) \right\} , \end{aligned}$$
(4)

where, \(\varvec{\theta } = (\mu ; log(\sigma ); \xi )\) is the parameter vector, \(\varvec{\Phi }_0\) is the hyperparameter means vector, and \(\varvec{\Sigma }_0\) is the hyperparameter variance-covariance matrix.

The information for the hyperparameters of the informative prior distribution for each analyzed location, that is, for the informative priors of each city, was obtained by fitting the GEV distribution to the data from the nearest municipality among the 28 available. For the non-informative prior, the respective values of the hyperparameters were adopted: \(\varvec{\Phi }_{0}=(0; 0; 0)\) and \(\varvec{\Sigma }_{0}= (10,000; 10,000; 100)\).

According to [21], the marginal distributions of the GEV parameters cannot be obtained analytically, necessitating the use of simulation techniques based on probability distributions. One such technique is Markov Chain Monte Carlo (MCMC) simulation, which utilizes iterative algorithms such as Metropolis-Hastings and Gibbs Sampler to generate variables from unknown density functions. This method aims to construct a density for each parameter, however, it is crucial to verify the convergence of the generated chains.

These algorithms can obtain samples from the posterior distribution by running a constructed Markov Chain, and the algorithm simulates Markov chains within a Monte Carlo integration to generate a set of points whose distribution converges to the posterior distribution [22].

The joint posterior distributions for the GEV distribution were obtained numerically using the Markov Chain Monte Carlo method. In this method, for each prior structure used, simulations with 120,000 iterations were performed, burning the first 20,000 iterations and adopting a thinning of every 20 iterations.

Several criteria have been proposed to assess the convergence of the posterior chains of the parameters. Among these methods, [23] recommends the application of the Raftery-Lewis [24], Geweke [25], and Heidelberg-Welch criteria [26]. Therefore, in this study, these criteria were employed to evaluate the convergence of the obtained chains.

In order to assess the performance of the different prior distributions, the return levels were analyzed for return periods of 2, 5, and 10 years. In this study, the return levels correspond to the predictions of maximum rainfall and are calculated as follows:

$$\begin{aligned} {\widehat{x}}(T)={\widehat{\mu }} -\frac{ {\widehat{\sigma }} }{ {\widehat{\xi }} } \left\{ 1-{ \left[ -\ln { \left( 1-\frac{ 1 }{ T } \right) } \right] }^{ -{\widehat{\xi }} } \right\} . \end{aligned}$$
(5)

where, \({\widehat{x}}(T)\) represents the return level for a return period T, and \(\mu\), \(\sigma\), and \(\xi\) are the posterior means of each parameter, obtained through Bayesian Inference

To evaluate the performance of the models using different priors, the results of the mean prediction error were used, given by:

$$\begin{aligned} MPE=\frac{ 1 }{ m } \sum \limits _{ i}^{ m }{ \left| \frac{ (o_{ i }-{ {\widehat{o}} }_{ i }) }{ o_{ i } } \right| } \times 100, \end{aligned}$$
(6)

where, \({{\widehat{o}}}_{ i }\) is the estimated maximum rainfall for the i-th return period, \(o_i\) is the observed maximum rainfall from the historical series, and m is the number of predictions.

The predictions of rainfall for the 29 locations were obtained for the return periods of 2, 5, 10, and also for 50 and 100 years, and for these last two, the most suitable interpolation method among those tested was applied to obtain the prediction maps.

2.3 Spatial analysis from bayesian predictions

Through obtaining the predicted rainfall values and their corresponding coordinates for each meteorological station, the analysis can be extended from a spatial perspective. For this study, the classical IDW method and the Geostatistical methods were employed. For an unobserved location, the prediction of the attribute using IDW is given by:

$$\begin{aligned} {\widehat{z}}(u_j)=\frac{\sum \limits _{i=1}^{n}\frac{1}{d_{ij}^{p}}z(u_{i})}{\sum \limits _{i=1}^{n}\frac{1}{d_{ij}^{p}}}, \end{aligned}$$
(7)

where, \({\widehat{z}}(u_j)\) is the estimate of the attribute for a non-sampled location \(u_j\), \(z(u_i)\) is the observed value of maximum rainfall for an observed point, \(d_{ij}\) is the Euclidean distance between the i-th neighbor and point \(u_j\), p is the power parameter, and n is the number of sampled points used for estimation.

The interpolation of values is performed through a weighted average of the observed values within a certain distance, where the closest observed values have greater weight (\(1/d_{ij}^{p}\)) in the weighted average. In this work, a value of \(p=2\) was used as the power parameter for the calculation of the weighted average. The IDW interpolator is widely employed in the analysis of geospatial data due to its simplicity and reliance solely on observed values and distances between points. Given its ease of understanding and application, IDW is often used for spatialization of variables at unsampled locations, making it one of the most commonly utilized methods alongside Kriging [27].

In contrast to IDW, Kriging methods are based on Geostatistical models that take into account the spatial correlation structure of the data. It is based on the assumptions of unbiasedness in estimation and minimum variance of estimates, and employs semivariogram functions to detect the spatial variability structure of the variable of interest [28,29,30].

Regarding semivariogram estimators, the classical estimator of Matheron is the most commonly used [31]. However, this estimator is sensitive to the presence of outliers and asymmetry of the random variable. Therefore, as an alternative estimator for problems where the data deviate from normality, the robust estimator of Cressie-Hawkins is presented, since, according to [32], it is not sensitive to the presence of outliers. The Cressie-Hawkins robust estimator [33] is given by:

$$\begin{aligned} {\widehat{\gamma }}(\varvec{h})=\frac{1}{2 N(\varvec{h})} \sum \limits _{i=1}^{N(\varvec{h})}\left\{ \left[ z\left( \varvec{u}_i\right) -z\left( \varvec{u}_i+\varvec{h}\right) \right] ^{\frac{1}{2}}\right\} ^4 /\left[ 0,914+\frac{0,988}{N(\varvec{h})}\right] \end{aligned}$$
(8)

where, \({{\textbf {h}}}\) is the vector distance between pairs of observations, \(N({{\textbf {h}}})\) is the number of ordered pairs, and \(z(u_i)\) and \(z(u_i + {{\textbf {h}}})\) are observed values at their respective locations. The fitting of theoretical semivariogram models was achieved using the Weighted Least Squares (WLS) method, which, according to [34], has the advantage of being able to handle small datasets.

In this work, the Gaussian, Spherical, Exponential, and Wave semivariogram models were used to evaluate which model provides the best spatial prediction results. According to [35] and [36], the models are expressed as:

$$\begin{aligned}{} & {} \gamma _{\text {gaus}}(\varvec{h})= C_0+C_1\left[ 1-\exp \left( -\left( \frac{|\varvec{h}|}{a}\right) ^2\right) \right] , |\varvec{h}|<a, \end{aligned}$$
(9)
$$\begin{aligned}{} & {} \gamma _{\text {exp}}(\varvec{h})= C_0+C_1\left[ 1-\exp \left( -\frac{|\varvec{h}|}{a}\right) \right] , |\varvec{h}|<a, \end{aligned}$$
(10)
$$\begin{aligned}{} & {} \gamma _{\text {sph}}(\varvec{h})= {\left\{ \begin{array}{ll} C_0+C_1\left[ \frac{3}{2}\left( \frac{|\varvec{h}|}{a}\right) -\frac{1}{2}\left( \frac{|\varvec{h}|}{a}\right) ^3\right] , |\varvec{h}|<a \\ C_0+C_1, |\varvec{h}| \ge a \end{array}\right. }, \end{aligned}$$
(11)
$$\begin{aligned}{} & {} \gamma _{\text{ wave } }(\varvec{h})=\left\{ C_0+C_1\left[ 1 - \frac{\sin \left( \pi \frac{\varvec{h}}{a}\right) }{\pi \frac{\varvec{h}}{a}}\right] ,\right. \end{aligned}$$
(12)

where, \(C_0\) is the nugget effect and \(C_1\) is the contribution [37]. The range a specifies the distance up to which samples are spatially correlated, and h is the vector distance between pairs of observations.

In this study, both OK and LK methods were employed. LK is variation from Ordinary Kriging, however, with the transformation of the scale of the variable under analysis. The OK estimator for unsampled point is given by:

$$\begin{aligned} {\widehat{z}}(u_i)=\sum \limits _{i=1}^{n}\lambda ^{OK} z(u_i), \end{aligned}$$
(13)

where, \({\widehat{z}}(u_i)\) represents the calculated value for location \(u_i\), \(z(u_i)\) denotes the observed value, and \(\lambda ^{OK}\) corresponds to the weights computed based on n data points.

The LK method is based on transforming the data to the logarithmic scale in order to achieve a symmetric distribution of the data [38]. The transformed data are then used to calculate the semivariogram, and subsequently, OK is employed for interpolating. The obtained values are in the logarithmic domain, necessitating a transformation back to the original scale

$$\begin{aligned} {\widehat{z}}_{LK}\left( u_i\right) =exp \left[ {\frac{{\widehat{y}}_{LK}\left( u_i\right) +\sigma _{LK}^2\left( u_i\right) }{2-\mu \left( u_i\right) }}\right] , \end{aligned}$$
(14)

where, \({\widehat{z}}_{LK}\left( u_i\right)\) represents the estimates in the original scale, \({\widehat{y}}_{LK}\left( u_i\right)\) represents the estimates in the logarithmic scale, \(\sigma _{LK}^2\) is the variance of LK, and \(\mu\) is the Lagrange parameter [39].

In order to assess the degree of spatial dependence among maximum rainfall values, the Cambardella criterion (CC) was employed [40], which quantifies the level of spatial dependence. The CC is given by:

$$\begin{aligned} CC=\frac{C_0}{C_0+C_1}\times 100, \end{aligned}$$
(15)

where, \(C_0\) and \(C_1\) are as explained before. The CC is evaluated as follows: when \(CC > 75\%\), it can be stated that the variable exhibits weak spatial dependence, for \(25\% < CC \le 75\%\), it is considered to have moderate spatial dependence, and for \(CC \le 25\%\), the variable is deemed to have strong spatial dependence.

In order to evaluate the spatial interpolators of IDW and Kriging, Cross-Validation methods were employed. Three Cross-Validation metrics were used to evaluate the models: Mean Squared Error (MSE), Root Mean Squared Error (RMSE), and Cross-Validation Mean Prediction Error (CV-MPE). The metrics are defined by the following expressions:

$$\begin{aligned}{} & {} MSE=\frac{\sum \limits _{i=1}^{n}{(z(u_i)-{\widehat{z}}(u_i))}^2}{n}, \end{aligned}$$
(16)
$$\begin{aligned}{} & {} RMSE=\sqrt{\frac{\sum \limits _{i=1}^{n}{(z(u_i)-{\widehat{z}}(u_i))}^2}{n},} \end{aligned}$$
(17)
$$\begin{aligned}{} & {} \mathrm {CV-MPE}=\frac{1}{n} \sum \limits _{t=1}^n\left| \frac{z\left( u_i\right) -{\widehat{z}}\left( u_i\right) }{z\left( u_i\right) }\right| \times 100. \end{aligned}$$
(18)

In addition to the Cross-Validation metrics, the MPE, as presented in Eq. 6, was also used for evaluating the spatial models. For this particular scenario, MPE was calculated based on the observed and predicted values of maximum rainfall from six locations that were not used for model fitting. The cities in question, along with the station codes, are: Andrelândia (02144019), Bom Jesus da Penha (02146078), Carmo da Cachoeira (02145044), Extrema (02246167), Maria da Fé (02245088) and Santa Rita de Caldas (02246047). An effort was made to select cities where complete sets of daily rainfall data were available for the years 2012 to 2021 since the aim is to compare observed and predicted rainfall for return periods of 2, 5, and 10 years.

2.4 Max-stable processes for analysis of spatial extremes

Considering that the data to be analyzed in this study are extremes, specialized methodologies were employed for the spatial analysis of these variables, namely max-stable processes and the spatial GEV model.

The max-stable process is a class of random fields of significant interest in Extreme Value Theory, as it is suitable for extreme variables [41]. A max-stable process, denoted as \(Z(\cdot )\), is the limiting process of maxima of independently and identically distributed random fields with an index set S in the spatial domain, \({{Y_i(x)}}_{x\in S}\) with \(i = 1, \ldots , n\), repetitions of a continuous random process. For two suitable sequences of numbers \(a_n(x)>0\) and \(b_n(x) \in {\mathbb {R}}\), we have that:

$$\begin{aligned} Z(x)=\lim _{n \rightarrow +\infty } \frac{\max _{i=1}^{n} Y_{i}(x)-b_{n}(x)}{a_{n}(x)}, \quad x \in S. \end{aligned}$$
(19)

There are different characterizations of max-stable process models for the analysis of extreme spatial events, such as the Smith model and the Schlatter model. The Smith model for the process Z(x) at locations \(x_1\) and \(x_2\) is given by the bivariate cumulative distribution function [42]:

$$\begin{aligned}{} & {} {\text {Pr}}\left[ Z\left( x_{1}\right) \le z_{1}, Z\left( x_{2}\right) \le z_{2}\right] =\exp \left[ -\frac{1}{z_{1}} \Phi \left( \frac{a}{2}+\frac{1}{a} \log \frac{z_{2}}{z_{1}}\right) \right. \nonumber \\{} & {} \quad \left. -\frac{1}{z_{2}} \Phi \left( \frac{a}{2}+\frac{1}{a} \log \frac{z_{1}}{z_{2}}\right) \right] , \end{aligned}$$
(20)

where \({\text {Pr}}\left[ Z\left( x_{1}\right) \le z_{1}, Z\left( x_{2}\right) \le z_{2}\right]\) is the bivariate cumulative distribution function, \(\Phi\) is the standard normal cumulative distribution function defined as \(\Phi (u)=(2 \pi )^{-1 / 2} \int _{-\infty }^u \exp \left( -x^2 / 2\right) d x\), and a represents the Mahalanobis distance, defined as \(a=\sqrt{\left( x_{1}-x_{2}\right) ^T \Sigma ^{-1}\left( x_{1}-x_{2}\right) }\), where \(\Sigma\) is the covariance matrix.

For the Schlather model, the bivariate cumulative distribution function for locations \(x_1\) and \(x_2\) is given by:

$$\begin{aligned} {\text {Pr}}\left[ Z\left( x_{1}\right) \le z_{1}, Z\left( x_{2}\right) \le z_{2}\right] =\exp \left[ -\frac{1}{2}\left( \frac{1}{z_{1}}+\frac{1}{z_{2}}\right) \left( 1+\sqrt{\left. 1-2(\rho (\varvec{h})+1) \frac{z_{1} z_{2}}{\left( z_{1}+z_{2}\right) ^{2}}\right) }\right] \right. , \end{aligned}$$
(21)

where, \(\varvec{h} \in {\mathbb {R}}^{+}\) is the vector of Euclidean distances between two locations.

There are different correlation functions, including Whittle-Matérn, Cauchy, Powered Exponential, and Bessel, given by:

$$\begin{aligned} \begin{array}{llll} \text {Whittle-Mat}\acute{\textrm{e}}\text {rn } &{} \rho (\varvec{h})=\frac{2^{1-\nu }}{\Gamma (\nu )} \left( \frac{\varvec{h}}{c_{2}}\right) ^{\nu } K_{\nu }\left( \frac{\varvec{h}}{c_{2}}\right) , &{} c_{2}>0, &{} \nu>0, \\ \text{ Cauchy } &{} \rho (\varvec{h})=\left[ 1+\left( \frac{\varvec{h}}{c_{2}}\right) ^{2} \right] ^{-\nu }, &{} c_{2}>0, &{} \nu>0, \\ \text{ Powered } \text{ Exponential } &{} \rho (\varvec{h})=\exp \left[ -\left( \frac{\varvec{h}}{c_{2}}\right) ^{\nu }\right] , &{} c_{2}>0, &{} 0<\nu \le 2, \\ \text{ Bessel } &{} \rho (\varvec{h})=\left( \frac{2 c_{2}}{\varvec{h}}\right) ^{\nu } \Gamma (\nu +1) J_{\nu }\left( \frac{\varvec{h}}{c_{2}}\right) , &{} c_{2}>0, &{} \nu \ge \frac{d-2}{2}, \end{array} \end{aligned}$$
(22)

where, \(c_2\) and \(\nu\) are the range and smoothing parameter, \(J_\nu\) and \(K_\nu\) are the Bessel function and the modified Bessel function of the third kind with order \(\nu\), and d is the dimension of the random fields.

For a spatial analysis of extremes, it is useful to have knowledge of measures of spatial dependence. One way to assess the degree of spatial dependence is through variograms, however, these may not exist when used for extreme data [43]. Therefore, approaches focused on extremes, such as the Extremal Coefficient and F-madogram, have been proposed as alternatives to overcome this limitation.

The Extremal Coefficient function, aims to assess extreme dependence in max-stable processes by quantifying the dependence between pairs of locations separated by a distance h [44]. The Extremal Coefficient functions \(\theta (x_1, x_2)\) for the Smith and Schlather models are given by:

$$\begin{aligned}{} & {} \text{ Smith: } \theta (x_1,x_2) = 2\Phi (a/2), \end{aligned}$$
(23)
$$\begin{aligned}{} & {} \text{ Schlather: } \theta (x_1,x_2) = 1+\sqrt{\frac{1-\rho (\left\| x_1-x_2 \right\| )}{2}}, \end{aligned}$$
(24)

where, \(1\le \theta (x_1,x_2)\le 2\) with \(\theta (x_1,x_2)=1\) indicating complete dependence between two observations and \(\theta (x_1,x_2)=2\) indicating complete independence.

For a location x with available observations, the GEV distribution can be fitted to the data, and parameter estimates for the distribution can be obtained. However, for a location x without observations, the parameters must be inferred from data at nearby locations. This can be achieved by modeling the spatial evolution of the parameters based on trend surfaces [45].

Trend surfaces can be directly incorporated into the max-stable process by adding extra terms that represent the spatial evolution of GEV parameters. The addition of these terms occurs during model fitting.The trend surfaces adopted for each parameter are:

$$\begin{aligned} \begin{aligned}&\mu (x)=\beta _{0, \mu }+\beta _{1, \mu } {\text {lon}}(x)+\beta _{2, \mu } {\text {lat}}(x)+\beta _{3, \mu } {\text {lon}}(x) {\text {lat}}(x) \\&\sigma (x)=\beta _{0, \sigma } +\beta _{1, \sigma } {\text {lon}}(x) +\beta _{2, \sigma } {\text {lat}}(x)+\beta _{3, \sigma } {\text {lon}}(x) {\text {lat}}(x)\\&\xi (x)=\beta _{0, \xi } \end{aligned}, \end{aligned}$$
(25)

where, lon(x) and lat(x) represent the longitude and latitude of the locations, and \(\beta _{i,\mu }\), \(\beta _{i,\sigma }\), and \(\beta _{1,\xi }\) are the coefficients of the trend surfaces, with \(i=0, 1, 2, 3\).

The model fitting was performed using the Pairwise Likelihood Maximization method, given by:

$$\begin{aligned}{} & {} l_p(z|\varvec{\psi } )=\sum _{k=1}^K \sum _{j=1}^{d-1} \sum _{s=j+1}^d \log f_{j, s}\left( t(z_{k, j}), t(z_{k, s}) | \varvec{\psi }\right) \nonumber \\{} & {} \qquad \qquad + \log \left| J\left( z_{k, j} \right) +J\left( z_{k, s} \right) \right| , \end{aligned}$$
(26)

where, \(\varvec{\psi }\) is the parameter vector of the model, \(f_{j, s}\left( t(z_{k, j}), t(z_{k, s}) | \varvec{\psi }\right)\) is the bivariate density function of the max-stable process, \(t(z_{k, j})\) and \(t(z_{k, s})\) are the k-th annual maximum observations transformed to Fréchet units for stations j and s, respectively, and \(J\left( z_{k,j} \right)\) and \(J\left( z_{k, s} \right)\) are the Jacobian terms given by: \(J\left( z_{k,j} \right) =\frac{1}{\sigma _{(x)}}\left( 1+ \xi (x)\frac{z_{k,j}-\mu (x)}{\sigma (x)} \right) ^\frac{1}{\xi (x)}\).

According to [43], since trend surfaces are used, it is more convenient to omit spatial dependence for calculating the return level prediction for an unobserved location. In this way, it is assumed that the meteorological stations are mutually independent.

Despite the fact that this strategy does not take into account all the uncertainties of the max-stable process parameters, it is expected to be effective, as spatial dependence parameters and trend surface parameters are approximately orthogonal [46].

In addition to the max-stable models, the spatial GEV model was used for the analysis. In this model, it is assumed that observations at different locations are mutually independent [47]. Therefore, the spatial GEV model is given by:

$$\begin{aligned} Z(x)\sim GEV(\mu (x), \sigma (x),\xi (x)), \end{aligned}$$
(27)

where, \(\mu (x)\), \(\sigma (x)\), and \(\xi (x)\) are trend surfaces of the form presented in Eq. 25.

The estimation of the parameters of the spatial GEV model can be performed using the Maximum Likelihood Estimation (MLE) technique. According to [46], the log-likelihood of the spatial GEV model is given by:

$$\begin{aligned} \begin{aligned} l(z_j(x_i);\varvec{\beta }) =&\sum _{i=1}^{m}\sum _{j=1}^{n}\left\{ -\log \left( \sigma (x_i) \right) \right. \\&-\left( 1+ \xi (x_i)\frac{z_j(x_i)- \mu (x_i)}{\sigma (x_i)} \right) ^{-\frac{1}{\xi (x_i)}} - \\&\left. \left( 1+\frac{1}{\xi (x_i)}\right) \log \left( 1+\xi (x_i)\frac{z_j(x_i)-\mu (x_i)}{\sigma (x_i)} \right) \right\} , \end{aligned} \end{aligned}$$
(28)

where, \(\varvec{\beta }\), \(\mu (x_i)\), \(\sigma (x_i)\), and \(\xi (x_i)\) are the parameters of the spatial GEV model, with \(x_i\) representing the i-th location for \(i=\) 1, 2,..., m, and \(z_j(x_i)\) representing the j-th observation for the i-th location, with \(j=\) 1, 2,..., n.

According to Gaume [45], based on the fitting of the max-stable process and the spatial GEV model, the return level (\(z_T(x)\)) can be calculated for an unsampled location x and a return period T using the expression:

$$\begin{aligned} z_T(x)= {\hat{\mu }}(x) -\frac{ {\hat{\sigma }}(x) }{ {\hat{\xi }}(x) } \left\{ 1-{ \left[ -\ln { \left( 1-\frac{ 1 }{ T } \right) } \right] }^{ - {\hat{\xi }}(x) } \right\} , \end{aligned}$$
(29)

where, the estimates of the trend surfaces \({\hat{\mu }}(x)\), \({\hat{\sigma }}(x)\), and \({\hat{\xi }}(x)\) for the location x are inserted.

For the evaluation of max-stable models fit, the Takeuchi’s Information Criteria (TIC), proposed by [48], was used, which is a generalization of Akaike’s information criterion. According to this criterion, the best-fitting model is considered to be the one that yields the lowest TIC value.

According to [49], the TIC function is given by:

$$\begin{aligned} {\text {TIC}}=-2l_p(\varvec{{\hat{\psi }}} )+2tr\left\{ H(\varvec{{\hat{\psi }}})^{-1}J(\varvec{{\hat{\psi }}}) \right\} , \end{aligned}$$
(30)

where, \(\varvec{{\hat{\psi }}}\) is the vector of parameters of the fitted model being evaluated.

After selecting the most suitable models based on the TIC results, the spatial predictions of these models were evaluated by calculating the MPE (6) of maximum rainfall for the locations of meteorological stations in the municipalities of Andrelândia, Bom Jesus da Penha, Carmo da Cachoeira, Extrema, Maria da Fé, and Santa Rita de Caldas, for return periods of 2, 5, and 10 years.

Therefore, after obtaining the most suitable spatial extreme model for assessing maximum rainfall in the region, the model was fitted to complete series of extremes with the goal of performing spatial prediction for return periods of 50 and 100 years in the southern and southwestern regions of Minas Gerais. The same procedure was applied to the IDW and Kriging models.

All statistical analyses were conducted using the R software [50].

3 Results and discussion

3.1 Analysing spatial maximum rainfall data through Bayesian-Geostatistical method

The descriptive statistics of the maximum rainfall data, covering the years 1980 to 2021, for the 29 cities in the south and southwest of Minas Gerais analyzed in this study, are presented in Table 2. The results showed that the city of Silvianópolis recorded the highest maximum rainfall, with a value of 226.3 mm. The municipality of Caxambu exhibited the highest variability in the data, with a coefficient of variation equal to 48.23

Table 2 Descriptive statistics of annual maximum rainfall(mm) that occurred from 1980 to 2021 in each locality
Full size table

In Bocaina de Minas, the maximum rainfall data exhibited the highest means and medians, with values of 87.6 mm and 83.5 mm, respectively. These values contrast with those observed in Pouso Alegre, which recorded the lowest means (66.6 mm) and medians (62.1 mm) of maximum rainfall.

Regarding the values of the means and medians of maximum rainfall, it can be observed that for all locations, the average value of rainfall was higher than the median, suggesting that the empirical distributions of the dataset for all municipalities are right-skewed. It can be observed that the Ljung-Box test results for independence indicate that all maximum series are independent at the 5% significance level, as the p-values for all cases were greater than the adopted significance level. Analyzing the Mann-Kendall test results, there is no evidence of trends in the series at the 5% significance level. According to the Kolmogorov-Smirnov test results, the GEV distribution fits the maximum rainfall data of the analyzed cities (Table 3).

Table 3 Results of tests (p-value), Ljung-Box (L-B), Mann-Kendall (M-K), and Kolmogorov-Smirnov (K-S) at a significance level of 5%, regarding annual maximum rainfall data (mm)
Full size table

Once the assumptions that the maximum series of the analyzed locations are independent and that there is no evidence of trends are met, it is possible to fit the GEV distribution throught Bayesian Inference to the maximum rainfall data of each municipality.

In order to verify the convergence of the posterior chains of the GEV distribution parameters, the Geweke, Raftert-Lewis and Heidelberger-Welch criteria were used. The results obtained showed that for all prior structures and all parameters (\(\mu\), \(\sigma\), \(\xi\)), there is no evidence of non-convergence of the posterior chains, since, by analyzing the dependence factor of the Raftery-Lewis criterion, it was verified that the values are close to 1, which indicates independence between the iterations. Using the Geweke criterion, it was found that the absolute values obtained were less than 1.96, indicating that there is no evidence of lack of convergence. By means of the Heidelberger and Welch criterion, it was found that their p-values were higher than the significance level (5%), therefore, it can be stated that the chains were stationary.

The results of the convergence criteria of the posterior chains are not presented in the text due to the large amount of information that would be necessary to present, since each of the three tests were applied to the chains of the three GEV parameters, and two models (non-informative and informative) were used for each of the 29 locations.

Once it was verified that there is no evidence of non-convergence of the posterior chains, it was possible to calculate the levels of maximum rainfallreturn for the 29 locations and for return periods of 2, 5, and 10 years throught Bayesian Inference. By obtaining the rainfallestimates, it was possible to evaluate the best prior structure for each city through the calculation of the MPE (Table 4).

Table 4 Mean Prediction Error (MPE %) results for annual maximum rainfall (mm) predicted for return periods of 2, 5, and 10 years, for each location, through Bayesian Inference using non-informative prior (NIP) and informative prior (IP)
Full size table

It is observed in Table 4 that among all presented values of MPE, the lowest was obtained for the estimates of maximum rainfallin the city of Poço Fundo, with an MPE of 4.20%. This MPE value is considered low when compared to other works that evaluated rainfallestimates for different return periods. For example, [51] analyzed the annual maximum daily rainfallin the city of Silvianópolis-MG using the GEV distribution fitted by Bayesian Inference with different prior structures and throught maximum likelihood, and obtained a minimum MPE of 21.53%. Meanwhile, [52] found the lowest MPE of maximum rainfall for dry and rainy periods equal to 16.44%, when analyzing the rainfallof the cities of Machado, São Lourenço, and Juiz de Fora-MG using the GEV, Gumbel and Log-Normal distributions.

Based on the MPE results presented in Table 4, it is possible to observe that by using informative priors based on data from the nearest neighboring city of each locality, better estimates of maximum rainfall were obtained in 12 of the 29 cities. On the other hand, by using non-informative prior information, better estimates were obtained in 17 cities. Thus, the maximum rainfall estimates for the 2, 5, and 10-year return periods obtained throught Bayesian Inference using the most suitable prior structure for each locality were used.

With possession of the predicted rainfall values, as well as the geographic coordinates of each meteorological station, it is possible to spatialize the attribute of interest over the study area, in this case, the southern and southwestern regions of Minas Gerais. For spatialization throught IDW, only the predicted rainfalls and their respective locations are necessary. However, for interpolation throught Kriging, it is necessary to fit the semivariograms.

For the calculation and fit of the empirical semivariogram, the robust Cressie-Hawkins semivariogram was used, and the adjustment was performed throught the weighted least squares method.

It should be highlighted that in this study, 24 different Kriging methods were used, as two Kriging methods (OK and LK) were associated with four semivariogram models (Gaussian, Exponential, Spherical, and Wave), fitted to the predictions obtained throught Bayesian Inference for three return periods. Thus, only the methods that presented the best results for each return period were presented in this section.

Table 5 Estimation of the best semivariogram models for each return period (RP) with their respective Cambardella criterion (CC) values and a comparison between the Inverse Distance Weighting (IDW) method using Cross-Validation results: Mean Squared Error (MSE), Root Mean Squared Error (RMSE), and Cross-Validation Mean Prediction Error (CV-MPE), as well as Mean Prediction Error (MPE) of the six locations not used for model fitting
Full size table

The results of the best fits of the Kriging methods associated with their respective best semivariograms, along with the results obtained throught IDW, for each return period can be found in Table 5 and Fig. 2. The models evaluation was performed through cross-validation and the calculation of the MPE.

The Kriging method that provided the best spatial predictions for the 2-year return period was the LK with a Gaussian semivariogram model. For the 5- and 10-year return periods, OK was the most suitable for adjustment, using the respective semivariogram models: Spherical and Wave. Analyzing the results of the degree of spatial dependence, it is observed that the Gaussian (RP=2) and Spherical (RP=5) semivariograms showed strong spatial dependence, since the CC results are below 25%. On the other hand, the Wave semivariogram for the 10-year return period showed moderate spatial dependence (\(25\% < CC \le 75\%\)).

The cross-validation and MPE results calculated from the IDW interpolation were inferior to the Kriging methods for the three return periods analyzed (Table 5). This result is consistent with that obtained by [53], who found that Geostatistical methods performed better compared to IDW for analyzing monthly and annual rainfallin northeast of Iran. However, it should be noted that except for the mean square error related to the 10-year return period data, all other evaluation criteria presented relatively close results. This low difference between comparisons of interpolation methods was also observed by [54], who analyzed rainfallin the Federal District of Brazil using different interpolation methods, including OK and IDW.

Fig. 2
figure 2

Graphs of the semivariograms adjusted throught weighted least squares method to the empirical semivariograms referring to maximum rainfall data for the return periods of 2, 5, and 10 years, respectively

Full size image

Based on the results, we noticed to perform spatial interpolation of the Bayesian predictions for the 50- and 100-year return periods using OK with the Wave semivariogram model. Thus, the Wave semivariograms were fitted to the maximum rainfall predictions for each location for the return periods of 50 and 100 years obtained through Bayesian Inference. The results of the fitting process are presented in Table 6 and Fig. 3. The prediction maps for the respectively return periods are presented in Fig. 4.

Table 6 Estimation of the parameters of Wave semivariograms for rainfall predictions obtained through Bayesian Inference for return periods (RP) of 50 and 100 years
Full size table
Fig. 3
figure 3

Wave semivariogram plots for the empirical semivariograms of rainfall predictions obtained through Bayesian Inference for 50 and 100 years return periods

Full size image

In the prediction map for the 100-year return period, it is observed that more intense rainfall is expected in the extreme north, center, and southeast of the study region. Additionally, higher rainfall is expected in the vicinity of the city of Poços de Caldas.

In the prediction map for the 50-year return period, minimum values of expected maximum rainfall are observed near 118 mm, while the highest values on the map are around 163 mm. As for the prediction map for the 100-year return period, the lowest values of expected maximum rainfall are near 120 mm, and the highest values are around 180 mm.

Fig. 4
figure 4

Maps of predictions of maximum annual rainfall (mm) for the return periods of 50 and 100 years, obtained throught Ordinary Kriging with the Wave semivariogram model

Full size image

Although Kriging techniques are often recommended for spatial interpolation, it is important to highlight that they do not always yield the best results [55]. In fact, comparative studies that have employed different interpolation methods, including Kriging, for the analysis of spatial rainfall have shown different models to be more suitable for different study areas. In a study by [56], which compared the performance of seven interpolation models in the analysis of annual mean rainfall in Portugal, it was found that the Empirical Bayesian Kriging with Regression model proved to be the most appropriate for the analysis. The other models used in the study included Local Polynomial Interpolation, Global Polynomial Interpolation, Radial Basis Function, IDW, Ordinary Cokriging, and Universal Cokriging. In the study conducted by [57], six interpolation models were evaluated for the analysis of annual mean rainfall in Ontario, Canada. The analyzed methods included IDW, Global Polynomial Interpolation, Local Polynomial Interpolation, Radial Basis Function, OK, and Universal Kriging. The results indicated that the most suitable model for the analysis of mean rainfall in the region was Local Polynomial Interpolation. Reference[58] investigated the annual maximum rainfall in the Haihe River basin, located in northern China, using different interpolation methods to assess their performance. The methods employed for the analysis included IDW, OK, External Drift Kriging with different covariates, and Empirical Bayesian Kriging. The results showed that the External Drift Kriging method, incorporating the annual mean rainfall as a covariate, yielded the best results among the evaluated interpolation methods.

3.2 Max-stable process and spatial GEV

Unlike the approach through Kriging and IDW employed in this study, which use only one observation for each location for spatial interpolation, in the spatial analysis of extremes using max-stable processes and spatial GEV, each location in the region is associated with a series of annual maximum rainfall values.

To fit the max-stable models via Pairwise Likelihood Maximization and assess spatial dependence, the first step is to transform the data from the maximum series to Fréchet units. To achieve this, the GEV distribution was fitted to the rainfall data from each location using the Maximum Likelihood method, aiming to obtain estimates for each parameter and thus transform the data to the new scale.

Thus, it was possible to fit the max-stable models, obtaining estimates of the dependency parameters for the Smith and Schlather models. The model fit was also assessed using the TIC. In our study, the best results were found across the Smith model and Schlather model with Bessel correlation, and the spatial GEV model.

Through the fitting of max-stable models, it is possible to obtain estimates of the dependency parameters as well as to estimate the coefficients \(\varvec{\beta }\) of the trend surfaces. As for the spatial GEV model, from its fitting, it is possible to obtain estimates of its parameters, which include \(\varvec{\beta }\) and the trend surfaces (Table 7).

Table 7 Estimation of the coefficients of the trend surfaces (t.s.) for the parameters of the GEV distribution
Full size table

To assess the spatial dependence structure of extremes using the max-stable models, the Extremal Coefficient was used. The evaluation of spatial dependence in extremes is done visually through a graph of the Extremal Coefficient as a function of the distance between pairs of observations. The Extremal Coefficient graph for the Smith and Schlather (Bessel) max-stable models in relation to pairs of meteorological stations is presented in Fig. 5.

Fig. 5
figure 5

Extremal coefficient for the Smith and Schlather max-stable models with Bessel correlation function, related to the maximum rainfall data from 1980 to 2011

Full size image

Analyzing the Extremal Coefficient graphs presented in Fig. 5, it can be observed that for the Smith model, spatial dependence decreases as the distance between stations increases. This occurs because the closer \(\theta (h)\) is to 2, the weaker the dependence between locations. In addition, for both models, the Extremal Coefficient presents values greater than 1.4 regardless of the distance h. According to [59], who obtained similar results in the analysis of spatial dependence, an Extremal Coefficient value greater than 1.4 suggests that the dependence between pairs of observations is low, indicating low evidence of dependence for the annual maximum rainfall data.

According to [59], one way to improve the assessment of spatial dependence would be to use the approach of selecting extremes above a threshold. This approach would allow for better utilization of available data, thereby increasing the amount of data to be used for model fitting.

Based on the results regarding the spatial dependence of extremes, omitting the dependence for spatial prediction calculations for different return periods, as previously discussed, becomes a plausible strategy. In this way, spatial rainfall predictions were calculated for return periods of 2, 5, and 10 years for the southern and southwestern regions of Minas Gerais.

By the fitted models, spatial predictions can be calculated, which allowed for model evaluation through the calculation of the MPE for rainfall at the six locations that were not used in model fitting. The results of the MPE are presented in Table 8.

Table 8 Results of the Mean Prediction Error (MPE), given in percentage, for predictions at the six locations that were not used in model fitting, obtained from the Smith and Schlather max-stable models with Bessel correlation, in addition to the spatial GEV model
Full size table

It is possible to observe that the three models demonstrated similar performances in spatial predictions for return periods of 2 and 5 years, with subtle differences in the MPE values (Table 8). Despite the proximity of the results, it was found that using the Smith model yielded the lowest MPE values for all the considered return periods. Therefore, it was resolved to make spatial predictions for return periods of 50 and 100 years in the southern and southwestern regions of Minas Gerais using the Smith max-stable model. The results of fitting the Smith model, now considering the complete maximum rainfall series from 1980 to 2021, is presented in Table 9.

Table 9 Results of fitting the Smith max-stable model to the maximum rainfall data for the period from 1980 to 2021
Full size table

Through fitting the Smith max-stable model and subsequently obtaining the coefficients of the trend surfaces, spatial predictions were calculated, and maps of maximum rainfall prediction for the southern and southwestern regions of Minas Gerais for return periods of 50 and 100 years were obtained. These maps are presented in Fig. 6.

Fig. 6
figure 6

Maps of maximum rainfall prediction (mm) for return periods of 50 and 100 years, obtained using the Smith max-stable model

Full size image

When analyzing the prediction maps for return periods of 50 and 100 years, it can be observed that more intense rainfall events are expected in the eastern portion of the analyzed region, while areas located to the north are expected to have lower volumes of daily maximum rainfall.

However, it is noted that the spatial distribution of the expected maximum rainfall for the two return periods is similar, with significant differences primarily in the scale of expected rainfall. Furthermore, the maps show that the spatial distribution of rainfall occurs continuously and smoothly in the region, without the formation of isolated contours.

This characteristic was also observed in the work of [60], who analyzed maximum rainfall in Switzerland using Copula models and max-stable processes. According to the authors, a disadvantage of max-stable processes is the difficulty in finding suitable trend surfaces, which can result in unrealistically smooth prediction maps.

4 Conclusion

The maximum rainfall series from the 29 analyzed cities are independent and show no evidence of trend. The Generalized Extreme Value distribution provided a good fit to the maximum series of the 29 locations.

The results of the Mean Prediction Error for maximum rainfall obtained through Bayesian Inference showed that the use of non-informative priors led to better prediction results for 17 municipalities. On the other hand, the use of informative priors based on data from the nearest location yielded better results for 12 locations.

The Gaussian and Spherical semivariograms exhibited a strong degree of spatial dependence for the data corresponding to return periods of 2 and 5 years, respectively. Meanwhile, the Wave semivariogram, fitted to the rainfall data for a return period of 10 years, showed a moderate spatial dependence.

The models that provided the best spatial predictions for return periods of 2, 5, and 10 years, among the Kriging and Inverse Distance Weighting methods, were the Log-Normal Kriging with a Gaussian semivariogram model, Ordinary Kriging with a Spherical semivariogram model, and Ordinary Kriging with a Wave semivariogram model, respectively.

For the 50-year return period, it is expected that more intense rainfall will occur in the center and surrounding areas of the city of Poços de Caldas. As for the 100-year return period, higher daily rainfall volumes are expected in the extreme north, center, and southeast of the region, as well as in Poços de Caldas neighborhood.

For the evaluation of spatial extremes models, it was found that the Smith and Schlather max-stable models with Bessel correlation outperform. Through the Mean Prediction Error calculation, it was observed that the models showed similar results, however, the Smith model proved to be more suitable for the analysis of maximum rainfall in the southern and southwestern regions of Minas Gerais.

The fitted Extremal Coefficient for the Smith and Schlather max-stable models with Bessel correlation showed low evidence of spatial dependence in the maximum rainfall data.

The prediction maps for return periods of 50 and 100 years obtained from the Smith max-stable model exhibited a similar spatial variability structure for rainfall. Furthermore, the spatial variation occurred continuously and smoothly throughout the analyzed region.

It is worth noting that both methodologies used in this study constitute viable analysis alternatives. Using the method discussed in section 3.1, it was found that the best geostatistical approach using Bayesian predictions presented mean average prediction error similar to that found with spatial gev. Therefore, when it comes to using a certain methodology, time and expertise can be taken into consideration to obtain spatial predictions, that is, in the Bayesian approach, convergence of the Markov chains must be proceded for each municipality evaluated, and, in the max-stable approach, one must proceed with the most appropriate model.