1 Introduction

In the last years, adhesive bonding technology has gained the attention in transport industries such as aerospace/aeronautics [1], automotive [2], railways [3] and shipping [4]. Bonding materials together using adhesives is also an attractive technique in other sectors such as construction [5], electronics [6], sports [7], and others. Compared to bolting, riveting or welding, traditional joining methods, the method adhesive bonding excels in more uniform stress distribution, less weight increase, possibility of joining different materials and with complex shapes, good vibration damping, greater resistance to fatigue, lower manufacturing costs, among others [8, 9]. However, adhesive bonding also presents some limitations, such as the frequent need for surface treatment to improve adhesion, depending on the adhesive it may be necessary to perform curing under pressure and temperature, loss of properties when exposed to adverse environmental conditions (humidity and temperature), limited resistance to peel loads, among others [8]. The single-lap joint is the most frequently used geometry due to its relative simplicity of manufacturing [10, 11]. Nevertheless, when subjected to a tensile load, the asymmetry of load transfer induces bending, leading to considerable peeling stresses (σy) at the overlap edges of the adhesive layer, which are detrimental to the joint performance [12]. Another drawback of this type of joint is the fact that the differential deformation effect of the adherends creates high shear stress (τxy) gradients [13]. Several joint geometries were developed aiming to minimise the described disadvantages. Configurations of adhesive joints such as the double-lap, joggle lap, bevelled lap, scarf, stepped, among others, have emerged to overcome the shortcomings of the single-lap joint [14, 15]. The stepped-lap joint presents several advantages when compared to the single-lap joint regarding the reduction of σy and τxy peak stresses, and improved aesthetics. On the other hand, the manufacture of the stepped-lap joint is more complex and involves machining operations that require more time and money to produce. Another alternative to reduce stress gradients is the use of the mixed adhesive technique, in which the bond line is formed by two adhesives, ideally a stiffer one in the middle of the adhesive layer and a more flexible one at its edges [16]. This technique has been widely used in the single-lap joint geometry and, for it to perform better when compared to a single-adhesive, the load transmitted by the brittle adhesive must be higher than that of the ductile one [17].

There are several methods to perform strength prediction of adhesive joints. Some are analytical, as the pioneer formulations of Volkersen [18], and others are numerical, as is the case of Finite Element Method (FEM) based approaches [19, 20]. Volkersen's formulation [18] was developed in the 1930s and is a closed-form model that considers fully elastic materials, and the adhesive deformation only takes place under shear [21]. The continuum mechanics approach was in the early design stages used to predict the strength of bonded joints, requiring the prior assumption of a failure criterion and knowledge of the stress distribution [22]. Fracture mechanics concepts combined with FEM analyses can also be used to perform strength prediction of adhesive joints, through the implementation of the virtual crack closure technique (VCCT) or stress intensity factors [23]. The main disadvantage of fracture mechanics in general lies in its high computational effort and complexity, since it requires the creation of a new mesh each time crack propagation takes place [24]. Currently, one of the most accepted and used method is Cohesive Zone Modelling (CZM) which, in combination with FEM and employing fracture mechanics approach, enables accurate strength prediction of adhesive joints. In CZM, cohesive elements are considered to simulate crack growth along specific planes, and solid FEM elements are used in the regions where the damage is not considered [25]. CZM uses one or more crack growth interfaces/regions that can be inserted artificially into structures or components, thus allowing damage propagation. The CZM method has been widely used to mimic crack initiation and propagation in the delamination of composites or in the analysis of cohesive and interfacial failures [26]. Recent developments like the eXtended Finite Element Method (XFEM) can also be used to model crack propagation. XFEM uses functions that account for a continuous field of displacements. This technique has demonstrated promising results in predicting the strength of bonded joints, but also presents some limitations [27].

Numerous works have been presented regarding the bi-adhesive joint (BAJ) technique applied to single-lap joints [28]. This methodology was presented for the first time in 1966 by Raphael [29]. By adopting this technique, it is possible to increase the joint's strength and also to design safe multi-stage joints for specific operating conditions. In the work of da Silva and Adams [16], the BAJ concept was experimentally analysed under high and low temperatures. The authors considered adhesive joints composed with the same adherend (titanium alloy) and different adherends (titanium and composite). The results showed that the BAJ, in comparison to single-adhesive joints (SAJ) suitable for high temperature, provides a stronger joint from the range of low to high temperatures. The authors stated that for adhesive joints composed of adherends of dissimilar materials, BAJ promotes higher load-bearing capacity over the temperature range analysed, than a high-temperature adhesive SAJ. The authors also demonstrated that BAJ can be used at low temperatures after a high-temperature phase, and in the reversed temperature variation is also applicable. Regarding dissimilar adherend joints (titanium/composite), the authors concluded that BAJ joints show higher strength, especially if materials with high thermal expansion coefficient are employed. In the work of Jairaja and Naik [30], an experimental and numerical study was performed on the strength of SAJ of dissimilar adherends and with single or dual adhesive. For the SAJ, the authors evaluated carbon fibre reinforced polymer (CFRP) and aluminium adherends, bonded with the Araldite® AV138 and 2015 adhesives. For the BAJ, the adhesive AV138 was placed at the middle and the 2015 at the edges of the adhesive layer. Digital Image Correlation (DIC) was used to determine the relative displacements between the adherends, and the σy and τxy stress distributions were estimated by the FEM software Abaqus®. The researchers' conclusion was that, for the SAJ, the 2015 adhesive outperformed the AV138 in terms of joint strength. For the BAJ, the authors observed a significant improvement in performance when compared to SAJ, specifically for small portions of the brittle adhesive located at the centre of the adhesive layer. Ferreira et al. [31] experimentally and numerically addressed the performance of stepped-lap BAJ between aluminium adherends. Three adhesives were considered: Araldite® AV138 (brittle), Araldite® 2015 (moderately ductile) and Sikaforce® 7752 (ductile). The authors also analysed different overlap lengths (LO) and compared the results of BAJ with SAJ. Overall, it was concluded that no significant strength increase was obtained for the BAJ, although a significant increase of the dissipated energy was found.

There are numerous studies involving the analyses of stepped-lap adhesive joints [32,33,34]. Sawa et al. [35] experimentally and numerically studied the stress distribution in step joints with dissimilar adherends under bending. The authors considered aluminium and steel adherends bonded with a structural epoxy adhesive. Stresses concentrated at the edge of the adherend interface with higher Youngs’ modulus. On the other hand, the decrease in the Young’s modulus ratio between the two adherends, as well as in the adhesive thickness (tA), leads to a decrease in the maximum stress. Increasing the step number also results in a decrease in the maximum stress. Overall, joints of dissimilar adherends showed lower resistance than joints of similar adherends. Bayramoglu et al. [36] compared an SLJ with interior step joints of varying dimensions, consisting of aluminium adherends and a structural ductile epoxy adhesive. In its ideal configuration, the interior step joint improved the SLJ strength by 60%. It was also concluded that the maximum tensile stresses occur at the LO ends, while at the beginning of the inner step the adhesive is under compression loading. The numerical predictions of the failure by CZM agreed with the experiments. The work of Brito et al. [37] numerically and experimentally addresses the influence of LO on the strength of a ductile adhesive step joint. A triangular CZM was used to study the step joints between CFRP adherends. It was found that the joint strength increased linearly with LO. However, this increase may trigger delamination of the adherends if higher LO were used. When compared to SLJ, step joints allow a decrease of the stress state along LO. In the end, it was possible to obtain a satisfactory relation between experimental and numerical results.

In this work, the strength of single-step single-adhesive joints and BAJ manufactured with AW 6082-T651 aluminium adherends is experimentally and numerically studied for different LO. Three commercial adhesives were studied, from brittle to ductile, along with different adhesive combinations in the BAJ technique. The experimental work was mainly used for numerical model validation. The numerical analysis took advantage of triangular CZM and included the study of peel and shear stresses, strength, and energy to failure. It was possible to validate the CZM accuracy by comparison with the experimental data.

2 Experimental materials and methods

2.1 Material characterisation

The high strength aluminium alloy AW6082 T651 was selected to be the material for the adherends. According to the manufacturer datasheet, this alloy presents a tensile strength of approximately 340 MPa. The stress–strain (σ−ε) curves of this aluminium alloy, which served as input properties in the numerical models were determined following the specifications of the ASTM-E8M-04 standard [38]. In Table 1 are listed the main mechanical properties of the aluminium alloy AW6082 T651.

Table 1 Mechanical properties of the aluminium alloy AW6082 T651 [39]
Full size table

The adhesives used in this work are the Araldite® AV138 (epoxy-based), which presents brittle behaviour, the Araldite® 2015 (also epoxy-based), which is considered a moderately ductile adhesive, and the Sikaforce® 7752 (polyurethane-based), showing a markedly ductile behaviour. The main mechanical and fracture properties required for the CZM simulations were obtained experimentally and are listed in Table 2 [39,40,41]. To obtain the tensile mechanical properties of the adhesive, such as E, σe, σf and εf, bulk dogbone specimens were tested. The shear data of the adhesive were acquired using Thick Adherend Shear Tests (TAST). Due to the knowledge of the Youngs’ modulus (E) and Poisson’s coefficient (v), it was possible to estimate the shear modulus (G). The tensile yield stress (σe) and shear yield stress (τe) evaluation involved plotting a parallel line in the elastic region and offsetting the strain by 0.2%, whose intersection gave the respective values. Pure mode I fracture energy or tensile toughness (GIC) was determined using the Double-Cantilever Beam (DCB) test, while the fracture energy in pure mode II or shear toughness (GIIC) was obtained using the End-Notched Flexure (ENF) test.

Table 2 Mechanical and fracture properties of the Araldite® AV138, Araldite® 2015 and Sikaforce® 7752 [39,40,41]
Full size table

2.2 Geometry and experimental details

This subsection describes the details of the specimens, and both boundary and loading conditions applied to the experimental tests. Figure 1 is a schematic representation of the stepped-lap joint geometry, boundary and loading conditions, and relevant geometrical parameters. The specimens were clamped at one of the edges, and in the other one a horizontal tensile displacement was applied jointly with vertical restriction of movement. The main dimensions of the joint, such as LO, adherends’ thickness (tP), adhesive thickness (tA), step transitions’ adhesive thickness (tA1), joint total length (LT) and width (B) are presented in Table 3.

Fig. 1
figure 1

Geometry of the stepped-lap joint

Full size image
Table 3 Dimensions of the stepped-lap joint
Full size table

The adhesive joint under analysis, as already mentioned, has a step geometry. In combination with this geometry, the BAJ concept is also studied. This concept consists of using two adhesives in the same joint aiming to reduce the stress concentrations, since the adhesive with a more ductile behaviour is usually applied at the LO edges [30]. In terms of the experimental tests, only the single-adhesive joints composed of the Araldite® 2015 and Sikaforce® 7752 were tested, while numerically the Araldite® AV138 was also considered. Moreover, experimentally, the BAJ concept was tested in the Sikaforce® 7752-Araldite® 2015-Sikaforce® 7752 and Sikaforce® 7752-Araldite® AV138-Sikaforce® 7752 configurations, always with the adhesive ratio of 25/50/25 (percentile lengths of LO). Numerically, apart from these conditions, the Araldite® 2015-Araldite® AV138-Araldite® 2015 BAJ configuration was added to the analysis, and two additional adhesive ratios were also analysed for all BAJ configurations: 12.5/75/12.5 and 33/34/33. Figure 2 and Table 4 schematise and summarise the dimensions considered for the experimental BAJ ratio evaluated, as an example.

Fig. 2
figure 2

Considered geometry in the bonding area

Full size image
Table 4 Values considered in the geometry of bonding area by adhesive ratio
Full size table

The first stage for the stepped-lap adhesive joint manufacturing was the cutting of the supplied plate into adherends’ with the desired width (B), followed by the machining of the steps that was performed in a milling machine. To achieve the maximum joint strength, it is necessary to undertake a proper surface treatment before bonding. In this case, preparation consisted of sand blasting the adherends with corundum sand, to remove the oxide layer and contaminants, followed by surface degreasing and cleaning with acetone, which was adequate to assure cohesive failures of the adhesive layer. Application of the adhesive to the adherends was particularly relevant for the BAJ. In these joints, thin indentations were induced at the side edges and bond surface of the adherends with a sharp razor blade to stipulate the transition between adhesives along LO. The adhesives were subsequently applied in sequence respecting these boundaries and the joints carefully assembled. The required longitudinal alignment of the adherends and tA were achieved by assembling the adhesive joint on a steel jig. Adhesive curing was performed at room temperature, for a period never lower than 48 h, and pressure was applied with plastic spring clamps to the adherends at both sides of the bonding regions during the entire curing cycle. The applied pressure over a flat surface was enough to ensure the adherends collinearity during the process and the stipulated tA, which was naturally enforced by the adherends’ geometry. Excess of adhesive on the overlap edges was trimmed off by milling. The mechanical tests were performed on a universal testing machine, Shimadzu AG-X 100, which was equipped with a 100 kN load cell. The tests were carried out in displacement control with speed of 1 mm/min and at room temperature. For each adhesive joint type that was tested, at least three valid results were obtained.

2.3 Numerical modelling

The Finite Element Method software Abaqus®, from Dassault Systèmes, was used to perform the numerical work. In the numerical models, a two-dimensional implicit analysis with plane strain elements and a non-linear geometric formulation was considered [42]. Two modelling approaches were considered for the studies: elastic stress analysis and failure analysis. Although elasto-plastic plane-strain solid elements with four nodes (CPE4) were used for the adherends in both approaches, the adhesive layer was modelled differently between approaches. For the elastic stress analyses, the adhesive layer elements were considered as plane-strain solid elements, identically to the elements used for the adherends, and the stress profiles were taken at the adhesive layer mid-thickness. For the failure analyses, four-node CZM elements (COH2D4) were selected to promote damage onset and propagation or crack growth for strength prediction analyses. In this case, a continuous modelling approach was adopted to model the adhesive layer by CZM, which translates into the implementation of a single row of cohesive elements throughout the entire layer. To avoid distortion of the CZM elements caused by the inability to model the corners between the adhesive segments of the step transition, between the vertical and horizontal branch, material discontinuities were considered. Figure 3 presents an example of modelled adhesive layer discontinuity for a stepped-lap joint with LO = 12.5 mm (example of failure analysis modelling).

Fig. 3
figure 3

Mesh detail and geometrical parameters (LO = 12.5 mm)

Full size image

A mesh convergence analysis was performed for the failure analysis modelling approach, and it was found that the 0.2 × 0.2 mm2 element size of the adhesive layer showed stabilised results. In a previous work [43], it was proven that this modelling technique, in which the length of the CZM element is taken to be equal to tA, ensures the accuracy of the results. It is worth noting that no bias effect was used in the numerical models analysed in this work. The meshes used for the elastic stress analyses were significantly more refined to obtain more accurate results and minimise noise in the curves. In fact, along the thickness of the adhesive layer ten solid elements were considered. The boundary and loading conditions imposed on the models involved clamping one edge of the joint, while the other edge was subjected to a tensile displacement at the same time as the transverse constraint was also applied, aiming to replicate the experimental tests (Fig. 1).

2.4 Cohesive zone model

CZM laws can be established in pure and mixed-mode and give the possibility to reproduce the materials’ behaviour till failure, including elastic loading, damage, and failure [44]. In this work, the adhesive layer was simulated by means of a triangular CZM for pure and mixed-mode loadings. It is recognised that more refined shapes are also available, although in the present case, the trilinear or trapezoidal law could provide a better approximation for the Sikaforce® 7752 adhesive because of its ductile behaviour. The suitability of the mixed-mode triangular shape CZM law, which is available in commercial software, was validated for different types of adhesives. For this law, the damage onset for pure mode loading takes place when the cohesive strengths in tension (tn0) or shear (ts0) are attained [45]. Moreover, when the values of the current tensile (tn) or shear (ts) cohesive stresses reach zero, the crack will propagate to the next pair of neighbouring nodes. In mixed-mode loading, which accommodates almost all real scenarios, specific criteria (stress or energy-based) result in a mixed-mode law that combines the pure-mode laws’ effect. In this case, damage onset initiates when the mixed-mode cohesive strength (tm0) is achieved [46]. The numerical work carried out in this study was based on the quadratic nominal stress criterion for damage onset and on a linear power law fracture criterion for damage propagation. More details about this model can be found in the study of Rocha and Campilho [43]. The adhesives’ properties that were used as input values in the Abaqus® software simulations are listed in Table 2, considering that tn0 is equal to the tensile strength (σf) and the ts0 is equal to the shear strength (τf). The initial stiffness of the CZM laws in tension and shear are given by the E/tA and G/tA ratios, respectively.

3 Results

3.1 Numerical model validation

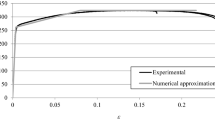
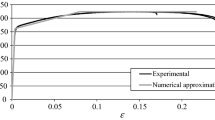
The numerical model is initially validated by verifying the agreement between numerically and experimentally obtained data, for selected joint geometries. In the following subsections, the analysis will be fully numerical and focus on the parametric study with different geometries and adhesives. Figure 4 compares the experimental and numerical maximum load (Pm) data for the single-adhesive joints (SAJ) bonded with the 2015 (a) and 7752 (b). For the 2015 SAJ joints, the experimental results were similar to those obtained numerically. For LO = 37.5 mm, the Pm variation was less than 1%, while for the remaining LO the difference was around 3%. Numerically, it was also possible to capture the phenomenon of adherend plasticisation for higher LO. Oppositely, for the 7752 SAJ, bigger differences were found in the Pm values, always with smaller numerical Pm. The relative differences were 9.8%, 18.5%, 13.9% and 1.5% for increasing LO between 12.5 and 50 mm. Up to LO = 37.5 mm, this difference is due to modelling a ductile adhesive layer with a triangular CZM [40], while for LO = 50 mm this effect is nullified due to the change in the failure mode, for adherend failure.

Fig. 4
figure 4

Experimental and numerical Pm data for the SAJ bonded with the a 2015 and b 7752

Full size image

Figure 5 compares the experimental and numerical Pm data for the 25/50/25 BAJ bonded with the 7752-2015-7752 (a) and 7752-AV-7752 (b) configurations. In the 7752-2015-7752 configuration, for LO = 12.5 mm the Pm difference is only 1%, increasing to 7% for LO = 25 mm. For the bigger LO, which suffered adherend plasticisation, the variation was around 3%. The 7752-AV-7752 BAJ configuration kept the same tendency, with a Pm difference of 9% for LO = 12.5 mm and stabilisation at around 4% for the remaining LO. Moreover, for LO = 37.5 and 50 mm, it was possible to capture the premature adherend failure, which was observed in the experimental tests. In view of the obtained results, the FEM-CZM approach and material models are considered validation, and the numerical parametric study on the BAJ solution follows.

Fig. 5
figure 5

Experimental and numerical Pm data for the BAJ bonded with the a 7752-2015-7752 and b 7752-AV-7752 configurations

Full size image

3.2 Failure modes

Contrarily to experimental methods, in which failure occurs abruptly, static numerical analyses offer the possibility of monitoring damage propagation during the entire loading process. This analysis can be put into practice using the stiffness degradation (SDEG) variable, which allows visualising the degradation of the adhesive from tm0 to failure. Table 5 labels, identifies, and characterises the types of failure occurring in the numerical simulations.

Table 5 Identification of failure modes for the SAJ and BAJ
Full size table

Table 6 summarises the failure modes for all numerical configurations, now including the three adhesive ratios and BAJ configurations described in Sect. 2.2. The predominant failure mode in SAJ was A, except for 7752/LO = 50 mm, leading to type D. The difference for this particular joint arises from the significant loads attained for this LO, associated to the high ductility of the adhesive, which prevents failure of the adhesive layer during extensive adherend deformations. The following conclusions were drawn from the BAJ configurations:

  • 12.5/75/12.5 BAJ—Configuration 2015-AV-2015 showed failure A for all LO. Configuration 7752-2015-7752 revealed either failure A (LO = 12.5 and 25 mm) or failure D (LO = 37.5 and 50 mm). The configuration 7752-AV-7752 presented three different failures depending on LO: failure B for LO = 12.5 mm, failure C for LO = 25 mm, and failure D for bigger LO. In the 7752-2015-7752 and 7752-AV-7752 configurations, failure B for the bigger LO took place due to reaching the tensile limit of the adherend. In the configuration 7752-AV-7752 and LO = 12.5 and 25 mm, premature failure in the central adhesive layer of AV138 can be justified by the significant difference in allowable deformation to the outer (7752) adhesive.

  • 33/34/33 BAJ—Configuration 2015-AV-2015 once again showed failure A for all LO. In configuration 7752-2015-7752, failure A took place up to LO = 37.5, and failure D for LO = 50 mm. Configuration 7752-AV-7752 exhibited all failure modes depending on LO, namely failures B, C, A, and D for increasing LO up to 50 mm. Failure D for LO = 50 mm and two configurations was found to take place due to the placement of 7752 at the edges. Actually, the high ductility of this adhesive prevents failure of the adhesive layer at the necking initiation of the adherends. On the other hand, failures B and C for the 7752/AV138/7752 configuration arises from the large stiffness/ductility difference between these two adhesives.

  • 25/50/25 BAJ—As with the other proportions, the 2015-AV-2015 configuration shows failure A for all LO. Configuration 7752-2015-7752 switches from failure A (LO = 12.5 and 25 mm) to failure D for bigger LO, due to the higher loads. In configuration 7752-AV-7752, the smaller LO up to 25 mm revealed failure B, while the bigger LO showed failure A (LO = 37.5 mm) or D (LO = 50 mm). Detailed analysis of the numerical results revealed identical justifications for these changes, compared to the 33/34/33 BAJ discussion.

Table 6 Failure modes identified for the different joint configurations
Full size table

3.3 Peel and shear stresses

Σy and τxy stresses are analysed during the elastic loading stage for the different SAJ and BAJ configurations. Although failure is a post-elastic event, especially for adhesives showing a ductility, elastic stresses serve to provide an indication of stress gradients and peaks stresses, which result in failure onset sites and can be indicators of the different failure behaviours encountered between tested geometrical configurations and adhesives. Only the 33/34/33 adhesive ratio BAJ is addressed due to similarities between conditions. Both stress components are normalised by dividing the absolute stresses by the average τxy (τavg) for a given LO. Moreover, the adhesive layer’s length coordinate (x) was equally subjected to a normalisation process, (x/LO) to achieve 0 ≤ x/LO ≤ 1 in all models and ease the comparison between curves. The LO comparison is performed between LO = 12.5 and 50 mm, since the variation of peak stresses is proportional to LO.

Figure 6 presents σy/τavg stress distributions in the adhesive layer for LO = 12.5 (a) and 50 mm (b). σy stresses are symmetrical and peak at both adhesive ends (x/LO = 0 and 1). Minor compressive σy peak stresses also appear at the vicinity. The overall shape of these curves arises due to the load asymmetry leading to adherend bending at the overlap [47]. In relation to LO, the larger its value, the higher are σy peak stresses, while concurrently σy compressive peak stresses move towards the bond edges. The AV138 presents the highest peak stresses, due to having the highest stiffness between the three adhesives (σy/τavg = 4.31 and 8.42 for LO = 12.5 and 50 mm, respectively). On the other hand, the 7752, as the most flexible adhesive, shows a reduction of 65% and 35% with respect to these values, with peak σy/τavg of 1.49 and 5.45 for LO = 12.5 and 50 mm, respectively.

Fig. 6
figure 6

Elastic σy/τavg stress distributions in the adhesive layer for the SAJ with a LO = 12.5 and b 50 mm

Full size image

Figure 7 reports σy/τavg stress distributions in the adhesive layer for the 25/50/25 BAJ (used as representative example), considering LO = 12.5 (a) and 50 mm (b). Symmetry can again be found in all σy stress curves, equally to compressive stresses at the transition zones between adhesives (x/LO≈0.1 and x/LO≈0.9). For LO = 12.5 mm, the 2015-AV-2015 BAJ shows the highest tensile σy peak stresses, while the lowest σy peak stresses relate to the 7752-AV-7752 BAJ. For larger LO (i.e., 50 mm), while the highest tensile σy peak stresses also take place for the 2015-AV-2015 BAJ, it equally has the highest compressive peaks. Nonetheless, the 2015-AV-2015 BAJ σy stresses exceed those of the other two BAJ configurations by a similar amount (approximately 36.3%). Between LO, σy peak stresses tend to increase with LO, and this increase is consistent across all three BAJ configurations. Moreover, larger LO provide a central region with nearly nil σy stresses. These conclusions are qualitatively similar comparing with the other adhesive ratios, including the tensile σy peak stresses values at the overlap ends. However, minor increase of these peaks values was detected for higher percentage of adhesive at the bondline edges (33/34/33 ratio BAJ).

Fig. 7
figure 7

Elastic σy/τavg stress distributions in the adhesive layer for the 25/50/25 BAJ with a LO = 12.5 and b 50 mm

Full size image

Figure 8 shows τxy/τavg stress distributions in the adhesive layer for LO = 12.5 (a) and 50 mm (b). Symmetry is also present in these plots and τxy stresses concentrate at the overlap ends (x/LO = 0 and x/LO = 1). τxy stresses at the central zone of the joint are close to zero. This gradient is caused by the shear-lag effect of the adherends, according to which the longitudinal deformation is zero at the free end of the adherends and increases gradually to the opposite overlap end. By overlapping both adherends, shear peak strains are observed at the two overlap ends, while this effect is cancelled in the intermediate zone of the bond. The shear-lag effect increases with LO. Similarly to σy stresses, the joints bonded with the AV138 lead to the highest τxy peak stresses, showing τxy/τavg of 4.65 for LO = 12.5 mm and 18.08 for LO = 50 mm. The 2015 and 7752 showed lower peak values by about 44% and 61%, respectively, as they have increased flexibility compared to the AV138, and this difference remained consistent in the remaining LO.

Fig. 8
figure 8

Elastic τxy/τavg stress distributions in the adhesive layer for the SAJ with a LO = 12.5 (a) and b 50 mm

Full size image

Figure 9 depicts τxy/τavg stresses in the adhesive layer considering the same 25/50/25 BAJ, for LO = 12.5 (a) and 50 mm (b). The curves are perfectly symmetric with respect to the mid-length of adhesive, and the transition between adhesives is clearly noticed by abrupt stress variations. Considering the BAJ with LO = 12.5 mm, the highest peak values of τxy stresses relate to the 2015-AV-2015 BAJ, in opposition to the 7752-AV-7752 BAJ, holding the smallest gradients. There is a significant difference for LO = 50 mm, namely in the magnitude of peak τxy/τavg, and also gradients towards the overlap edges. Nonetheless, the 2015-AV-2015 BAJ still presents the highest peak stresses, with a significant difference to the other two BAJ configurations, which almost overlap. The relative difference between the 2015-AV-2015 BAJ and the other configurations is nearly 84%. The LO effect is visible in the significant increase of τxy/τavg with this parameter, which applies to all three BAJ configurations tested in this work. Equally to the σy stress plots, for bigger LO a central unloaded region reduces the efficiency of load transfer. All these conclusions can be extended to the other two BAJ configurations. Nonetheless, equally to the discussion on σy stresses, bigger ductile adhesive lengths at the overlap edges (i.e., 33/34/33 ratio BAJ) are responsible for increased peak stresses, in this case τxy/τavg.

Fig. 9
figure 9

Elastic τxy/τavg stress distributions in the adhesive layer for the 25/50/25 BAJ with a LO = 12.5 and b 50 mm

Full size image

3.4 Joint strength

In this section, the results of the numerical study on the joints’ strength under analysis are listed, for the SAJ bonded with each adhesive, and the BAJ with the three configurations depicted in Sect. 2.2. For discussion purposes, a percentile different comparison of the Pm increment of each joint configuration is made in relation to the SAJ with the AV138, which is considered the baseline configuration. Figure 10 shows the numerically obtained Pm for the SAJ and either the 12.5/75/12.5 (a), 25/50/25 (b) or 33/34/33 (c) BAJ configurations. Table 7 compiles, for the same SAJ and BAJ configurations, the Pm values and presents the percentile differences over the baseline configuration (∆Pm).

Fig. 10
figure 10

Numerical Pm for the SAJ and either the a 12.5/75/12.5, b 25/50/25 or c 33/34/33 BAJ configurations

Full size image
Table 7 Pm and ∆Pm for the different joint configurations
Full size table

The analysis that follows is divided into the three BAJ configurations and final overview:

  • For the 12.5/75/12.5 BAJ configuration (Fig. 10a), the best performing configuration is the 7752-2015-7752 BAJ for LO = 12.5 and 25 mm, and both this configuration and the 7752-AV-7752 BAJ for LO = 37.5 and 50 mm. Due to the brittleness of the AV138, the SAJ bonded with this adhesive presents the lowest Pm for all LO. Between all configurations, BAJ always show the highest Pm. For LO = 12.5 and 25 mm, this fact is visible by comparing the best SAJ (2015 for LO = 12.5 to 37.5 mm, and 7752 otherwise) with the two-adhesive counterpart (7752-2015-7752), leading to differences of 14.4% and 22.9%, respectively. However, for higher LO, the difference reduces to 4.0% (LO = 37.5 mm) and 0.4% (LO = 50 mm), due to plasticisation of the adherends, which for this adherend material, can make the SAJ more advantageous by simplifying its manufacturing process. ∆Pm often surpass 100%, with the exception being joints with LO = 12.5 mm.

  • For the 25/50/25 BAJ configuration (Fig. 10b), the highest Pm correspond to the 7752-AV-7752 BAJ (LO = 12.5 mm), 2015-AV-2015 BAJ (LO = 25 mm), or both 7752-2015-7752 BAJ and 7752-AV-7752 BAJ (LO = 37.5 and 50 mm). Equal to the former analysis, the AV138 SAJ data is the lowest between configurations. Irrespectively of LO, BAJ is always recommended over SAJ. on account of Pm performance. Over the best SAJ (2015 for LO = 12.5 to 37.5 mm, and 7752 otherwise), the percentile improvement of the best configuration overall were 5.6% (LO = 12.5 mm), 10.6% (LO = 25 mm), 3.6% (LO = 37.5 mm), and 0.4% due to adherend plasticisation (LO = 50 mm). The ∆Pm values, equally to the former analysis, excel 100% apart from the joint configuration with LO = 12.5 mm, further emphasising the BAJ advantage.

  • For the 33/34/33 BAJ configuration (Fig. 10c), BAJ give the best Pm solutions for all LO: 2015-AV-2015 BAJ (LO = 12.5 and 25 mm), or equally 7752-2015-7752 BAJ and 7752-AV-7752 BAJ (LO = 37.5 and 50 mm). The AV138 SAJ is the worst-case scenario by a large margin for all LO, while on the other hand BAJ achieve major Pm improvements. Comparing with the best performing SAJ (2015 for LO = 12.5 to 37.5 mm, and 7752 otherwise), the relative Pm improvement of the best BAJ was 14.0% (LO = 12.5 mm and 2015-AV-2015 BAJ), 11.9% (LO = 25 mm and 2015-AV-2015 BAJ), 4.0% (LO = 37.5 mm and 7752-2015-7752 BAJ), and 0.4% corresponding to failure by adherend plasticisation (LO = 50 mm and 7752-AV-7752 BAJ). ∆Pm resemble the former BAJ configurations, as well as the relative improvements, thus showing the advantage in this technique.

  • Between all BAJ configurations, clear differences are found up to LO = 25 mm, at which point adherend plasticisation assumes the failure process, while over LO the differences are negligible. The 12.5/75/12.5 BAJ provides the highest Pm for both LO = 12.5 and 25 mm and the 33/34/33 BAJ the lowest. The minimum Pm difference to the other configurations is 9.9% for LO = 25 mm, while it is minimal for LO = 12.5 mm.

3.5 Failure energy

The numerically obtained failure energy (U) values, estimated by the area beneath the load–displacement (P-δ) curves to failure of each specimen, are presented and discussed. To aid the comparison between configurations, the percentile U variations (∆U) in relation to the AV138 SAJ (baseline configuration) are also assessed. The acquired U data is gathered in Fig. 11 for both SAJ and the 12.5/75/12.5 (a), 25/50/25 (b) or 33/34/33 (c) BAJ configurations. Table 8 summarises the U and ∆U data for the same SAJ and BAJ configurations.

Fig. 11
figure 11

Numerical U for the SAJ and either the a 12.5/75/12.5, b 25/50/25 or c 33/34/33 BAJ configurations

Full size image
Table 8 U and ∆U for the different joint configurations
Full size table

The discussion on U effects is split into BAJ configurations and respective comparison:

  • For the 12.5/75/12.5 BAJ configuration (Fig. 11a), the highest U were found for the 7752 SAJ (LO = 12.5 mm), 7752-2015-7752 BAJ (LO = 25 mm), and 7752-AV138-7752 (LO = 37.5 and 50 mm). The AV138 BAJ presents the most modest results due to its brittleness, equally to the other BAJ configurations. Although for LO = 12.5 mm the best result relates to a SAJ, it only provides a 5.7% improvement over the 7752-2015-7752 BAJ. All other LO benefit for the BAJ concept, with emphasis to the 7752-AV138-7752 BAJ for the bigger LO. A particularly significant difference between the best BAJ (7752-AV138-7752) and best SAJ (2015) exists for LO = 37.5 mm, reaching in this case a 178.8% improvement.

  • For the 25/50/25 BAJ configuration (Fig. 11b), the best U results relate to the 7752 SAJ (LO = 12.5 mm), 7752-2015-7752 BAJ (LO = 25 and 37.5 mm), and 7752-AV138-7752 (LO = 50 mm), which is an almost identical result to the former BAJ configuration, qualitatively speaking. Despite these recommended configurations, the BAJ proposals are always the best or proximal solution. Actually, the 7752-2015-7752 BAJ with LO = 12.5 mm is only 4.3% below the optimal SAJ solution. The largest BAJ/SAJ difference takes place for LO = 37.5 mm, with a 140.0% variation. The best U takes a significant change between the LO = 37.5 and 50 mm conditions, which is not visible for the other BAJ configurations.

  • For the 33/34/33 BAJ configuration (Fig. 11c), the same SAJ (7752) gives the best U predictions. For the other LO, the best U were the 7752-2015-7752 BAJ (LO = 25 and 37.5 mm) and 2015-AV-2015 BAJ (LO = 50 mm), thus constituting a slight modification of the previous pattern. Moreover, there is noticeably a convergence of U values between all BAJ, resulting in no particular configuration to be recommended. Nonetheless, the relative advantage over the best BAJ is generally small (up to 30.2% for LO = 37.5 mm), which means that the BAJ with this adhesive ratio has no great advantage.

  • A comparison between the three BAJ configurations shows that some differences exist between the 33/34/33 BAJ and the other two BAJ ratios, which are clearly largest for LO = 37.5 mm. The justification lies in the absence of adherend plasticisation for the former configuration, as shown in Table 6. For the other LO, the differences are relatively small.

4 Conclusions

The present work consisted of an experimental and numerical study of step adhesive joints with aluminium adherends using the BAJ concept. Therefore, three commercial adhesives were studied: from brittle (AV138) to ductile (2015 and 7752). A numerical study was then carried out using Abaqus® modelling software. The main conclusions are as follows:

  • Numerical model validation: Pm comparison on the SAJ showed relative differences up to approximately 3% for the 2015 and up to 18.5% for the 7752. On the BAJ, between the tested conditions, the maximum difference was approximately 9%, for the 7752-AV-7752 BAJ with LO = 12.5 mm. The FEM-CZM approach was thus considered validated, with enabled the exhaustive numerical analysis that followed.

  • Failure modes: The analysis was based on the SDEG evaluation, and four failures were identified. Failure took place mostly by cohesive failure of the adhesive layer followed by propagation in the adhesive layer. Larger LO induced failure in the adherends before the adhesive strength was attained. Few joint conditions exhibited failure onset either at the transition between adhesives, or in the middle adhesive.

  • Peel and shear stresses: In the SAJ, both σy and τxy peak stresses were highest for the AV138 and lowest for the 7752, as a reflect of the stiffness differential between adhesives. In all cases, peak stresses increase with LO, leading to a reduction of load transfer efficiency. The BAJ configurations managed to reduce both σy and τxy peak stresses, but with higher preponderance for τxy stresses, in which case the relative reductions were between approximately 30% (LO = 12.5 mm) and 50% (LO = 50 mm).

  • Joint strength: The BAJ technique revealed improvements over the base SAJ conditions, and the recommended configuration for each LO was always a BAJ solutions, although the difference to the best performing SAJ could not be significant. Moreover, for bigger LO, the adherend failure could nullify the Pm difference. The highest difference between the recommended solutions and the best SAJ was 22.9%.

  • Failure energy: The BAJ/SAJ differences were higher for the 12.5/75/12.5 and 25/50/25 configurations. However, in few configurations, namely with smaller LO, SAJ could even provide higher U than all BAJ concepts. Nonetheless, for bigger LO, the BAJ technique was in some cases best by a margin up to 178.8% for the 12.5/75/12.5 BAJ and LO = 37.5 mm (7752-AV138-7752 BAJ over 2015 SAJ case).