1 Introduction

In modern times, we now understand that arteries can become blocked due to lifestyle factors, such as smoking, high cholesterol levels in the blood, and occasionally genetic conditions. The narrowing and stiffening of blood vessel walls are widely recognized afflictions in the arterial system, known as arterial stenosis in the medical field. Arterial stenosis occurs when the inner layer of an artery is compressed or narrowed, resulting in reduced blood flow to tissues and organs. The relationship between the mechanical properties of blood vessel walls and the flow characteristics of blood is a topic of ongoing debate in relation to the underlying causes of various cardiovascular ailments. As microorganisms produce biosurfactants and surface-active chemicals, their importance in industrial microbiology is growing. Biosurfactants are utilized in incremental oil recovery and numerous environmental bioremediation applications. The combined impact of microorganisms and nanofluids has numerous industrial applications, including microfluidic devices such as micro-channels and micro-reactors. Nanofluids are highly beneficial for researchers due to their rapid heat transfer rate, which can be applied in various industrial processes.

The circulatory system, which includes the heart and blood vessels, transports nutrition and oxygen to all cells in the body. The arteries are in charge of transporting blood away from the heart, while the veins are in charge of returning it to the heart. The left ventricle pumps oxygen-rich blood into the main artery (aorta) during systemic circulation. The blood travels from the main artery to peripheral arteries and into the capillary network where the oxygen and nutrients are delivered to various organs and tissues. Biological fluids play a crucial role in the diagnosis, monitoring, and treatment of a variety of disorders. Examples of biological fluids contain blood, lymph, vitreous fluid in the eye, synovial fluid in joints, and lymph, which is formed when blood plasma is filtered across tissues. Among these biofluids, blood is of utmost importance. Red blood cells (RBCs), white blood cells (WBCs), and platelets are all found in the bloodstream, according to scientific research. Blood is considered non-Newtonian when the flow shear rate is low, as is the case in smaller arteries, downstream of stenosis, veins. Conversely, in wider arteries with substantial flow shear rate, blood behaves in a Newtonian manner. Hussain et al. [1] examined a study on the thermal radiative properties of an electrically conducting viscous fluids thru a permeable medium. Tanveer et al. [2], on the other hand, investigated electro-osmotic blood flow induced by an electrostatic potential in a microchannel using a non-Newtonian Bingham nanofluid from a theoretical standpoint. Considering the claims regarding stenoses, Lubna and Hussain [3] examined the behavior of human blood flow, considering it as a viscous fluid.

The field of blood-mediated nanoparticle delivery has recently expanded and become significant in diagnostics and therapeutics. Nanoparticles can be tailored in terms of surface chemistry, size, and shape to improve their performance in biological systems. These modifications enhance their ability to distribute contents within tissues or cells, improve blood detoxification, alter interactions with the immune system, and facilitate targeted cell delivery. Fluids such as blood, engine oil, ethylene glycol, water, and polymer solutions have lower heat conduction properties compared to solids. However, by incorporating solid particles with higher thermal conductivity into these fluids, their overall thermal conductivity can be increased. Many nanoparticles have been developed for biomedical applications, showing promise in disease imaging and treatment. Bhatti [4] extensively investigated magnetized gold (Au) nanomaterial suspensions. Afridi et al. [5] investigated the effect of entropy production and thermal dissipation on hybrid nanofluid (HNF) flow over a curved sheet in another study.

Furthermore, where manufactured magnetic bacteria swim within real cells, the use of a twisted spreading surface for interstitial nanoparticle movement is feasible. To investigate peristaltic blood flow, Bhatti et al. [6] employed endoscopic techniques using a tube containing Sisko fluid with titanium magneto-nanoparticles. Ebrahimpour and Mohsin [7] investigated the use of nanoparticles to augment the radiative capacity of a linear Fresnel solar system. Ijaz and Nadeem [8] explored the effects of copper nanoparticles in a composite stenosed artery using a catheter and concluded that nanoparticles can be utilized as drug carriers. They provided a theoretical review of catheter injection and its impact on permeability in vertically stenosed arteries, highlighting the effectiveness of copper nanoparticles in treating composite stenosis.

Blood is considered a magnetohydrodynamic (MHD) fluid, and a sufficiently strong magnetic field can be employed to alleviate travel sickness, joint pain, and headaches. Kolins [9] first introduced the usage of electromagnetic fields in biomathematics. Tzirtzilakis [10] conducted a study on the mathematical modeling of blood flow in the presence of a magnetic field. In alignment with the principles of magnetohydrodynamics and ferrohydrodynamics, and by considering the electrical conductivity, Mekheimer [11] scrutinized the impression of a uniform magnetic field on a peristaltic blood flow model. The impact of MHD on power law flow through an angled artery was examined by Akbar et al. [12]. Eldesoky et al. [13] studied the peristaltic heat transfer and MHD flow of a suspended viscous fluid in a channel subjected to pressure change and an external magnetic field.

Bioconvection is a term used to designate the enhanced swimming ability of microorganisms resulting from macroscopic fluid movement caused by spatial density fluctuations in an area. When self-propelled motile bacteria direct the base fluid in a specific direction, a bio-convective stream is generated. Three groups of moving microorganisms are recognized: oxytactic or chemotactic microorganisms, gyrotactic microorganisms, and undesirable gravitaxis bacteria. In contrast to motile microorganisms, nanoscale particles do not possess self-directed motion. Their movement is influenced by Brownian motion and Thermal-migration. In nanoscale fluids, the transport of microorganisms is expected to be possible if the nanoparticle saturation is low, but it is unlikely to significantly upsurge the viscosity of the base fluid. Kuznetsov and Avramenko [14, 15] were the first to investigate bioconvection in the presence of nanoparticles. Subsequently, Kuznetsov [16] employed Buongiorno's theory to study the interaction of nanoparticles with gyrotactic microorganisms. Bég et al. [17] conducted numerical modeling to explore the bioconvection flow of nanofluids through a permeable medium. Akbar [18] proposed a bionano-engineering model assuming consistent channel flow with nanoparticles, considering the occurrence of bioconvection. Bhatti et al. [19] utilized the Jeffrey fluid model incorporating microorganisms and nanoparticles to examine the performance of a fluctuating magnetic field and the clot blood model. Ahmed et al. [20] investigated the magnetized laminar flow of gyrotactic microorganisms and nanofluids in a non-Darcy permeable channel. Chakraborty et al. [21] studied the combined effects of magnetic field stimulation and bioconvective flow with nanofluids.

In the majority of experiments on blood flow in the catheterized arterial system, a Newtonian fluid was utilized. However, the viscosity of blood can change under specific physiological circumstances, such as low shear levels, smaller arteries, or pathological diseases like atherosclerosis or hypertension. Consequently, blood exhibits non-Newtonian characteristics. The Carreau fluid model has been suggested as an appropriate approach for modeling blood flow in arteries with varying diameters, as it accounts for alterations in blood viscosity across a broad range of shear rates. This concept was introduced by Carreau [22], who based it on his ideas about molecular networks. Subsequently, Siska et al. [23] proposed the use of the Carreau fluid model to measure the terminal velocity of non-spherical particles in areas of transient flow, which are associated with the development of stenosis in arteries and the resulting symptoms of cardiovascular dysfunction, such as nausea, back pain, and stenosis that can lead to stroke. As a result, the study of blood vessels, particularly stenotic arteries, has become a prominent focus in the field of fluid dynamics [24]. The Carreau fluid model has been shown to effectively describe the shear-thickening and shear-thinning mechanisms of the fluid [25, 26]. This model combines elements of the power-law model and the Newtonian fluid model. Chhabra and Uhlherr [27] studied the Carreau viscosity equations for shear-thinning elastic liquids. Bush and Phan-Thein [28] investigated the theoretical evaluation of the Carreau fluid model. Lee [29] discussed the application of the Carreau extrapolated Newtonian model for fault classification. Tabakova et al. [30] employed the Carreau model to investigate the flow dynamics in blood vessels, studying both steady-state and oscillatory flows and obtaining numerical solutions. Liu and Liu [31] experimentally examined blood flow in tapering stenosed arteries, focusing on the effects of heat and mass transport caused by the fluid. Liu et al. [32] explored the consequences of stenosis and taper on blood flow.

The current study focuses on exploring non-Newtonian blood flow in narrow arteries by modeling blood as a Carreau fluid. The momentum equations are considered, taking into account MHD and Darcy-Forchheimer porous media. The study also investigates heat transfer properties, including thermal radiation, joule dissipation, and bio-convective microorganisms. The gold nanoparticles (NPs) employed in the study were combined with blood as the base fluid. ANOVA, also known as Analysis of Variance, is a solid statistical approach used to evaluate regression models and execute numerous statistical analyses. These evaluations include errors, total error computations, F-values, p-values, and adequacy of fitting for Nusselt number simulation outcomes. The study compares the physical implications of flow limitations with fictitious fluid flow, utilizing physical interpretations. Furthermore, the study explores interpretations of blood flow based on heat transfer and drag force.

2 Mathematical formulation

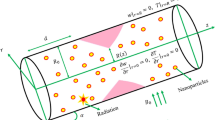
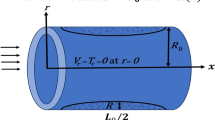
For the present scenario, we assumed that blood flows through arterial stenosis of a particular length \(\frac{{L}_{0}}{2 }\) as a steady, incompressible non-Newtonian Carreau fluid. The coordinate axes is designated so that blood flow is parallel to the \(x-axis\) and perpendicular to the \(r-axis\). In the problem's graphical representation, blood flows over a vein with a cosine shape compression with a width of possible section \(2{R}_{0}, R(x)\) is the radius of the artery, and \(\lambda \) is the extreme height of the stenosis (Fig. 1). The stenosed section's profile is picked as:

Fig. 1
figure 1

Sketch of the fluid flow in stenosed artery

Full size image
$$R\left(x\right)={R}_{0}-\frac{\lambda }{2}\left(1+Cos\left(\frac{4\pi x}{{L}_{0}}\right)\right), -\frac{{L}_{0}}{4}<x<\frac{{L}_{0}}{4}={R}_{0} Otherwise$$
(1)

Under specific assumptions, the steady boundary layer equations for MHD non-Newtonian Carreau nanofluid flow, accounting for Darcy–Forchheimer effects, heat transfer, and bio-convective microorganisms, can be expressed as follows [19, 25].

$$\frac{\partial \left(ru\right)}{\partial x}+\frac{\partial \left(rv\right)}{\partial r}=0$$
(2)
$$\begin{array}{c}{\rho }_{nf}\left(u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial r}\right)={\mu }_{nf}\left(\frac{{\partial }^{2}u}{{\partial r}^{2}}+\frac{1}{r}\frac{\partial u}{\partial r}+\frac{3{\Gamma }^{2}\left(n-1\right)}{2} {\left(\frac{\partial u}{\partial r}\right)}^{2}\frac{{\partial }^{2}u}{\partial {r}^{2}}+\frac{{\Gamma }^{2}\left(n-1\right)}{2r}{\left(\frac{\partial u}{\partial r}\right)}^{3}\right)-\\ {\sigma }_{nf}{B}_{0}^{2}u-\frac{{\mu }_{nf}}{{k}_{2}}u-F{u}^{2}\end{array}$$
(3)
$${\left(\rho {C}_{p}\right)}_{nf}\left(u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial r}\right)={k}_{nf}\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial T}{\partial r}\right)-\frac{\partial {q}_{r}}{\partial r}+{\sigma }_{nf}{B}_{0}^{2}{u}^{2}$$
(4)
$$u\frac{\partial N}{\partial x}+v\frac{\partial N}{\partial r}={D}_{n}\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial N}{\partial r}\right)$$
(5)

as well as boundary constraints [3]

$$\begin{array}{c}u={u}_{0}, v=0, T={T}_{w} ,N={N}_{w} at r=R\\ u\to 0, T\to {T}_{\infty } ,N\to {N}_{\infty } at r\to \infty \end{array}$$
(6)

Considering the following transformation [3]

$$u=\frac{{u}_{0}x}{{L}_{0}}{f}{^\prime}\left(\eta \right), v=-\frac{R}{r}\sqrt{\frac{{u}_{0}{\upsilon }_{f}}{{L}_{0}}}f\left(\eta \right), \theta \left(\eta \right)=\frac{T-{T}_{\infty }}{{T}_{w}-{T}_{\infty }},L\left(\eta \right)=\frac{N-{N}_{\infty }}{{N}_{w}-{N}_{\infty }}, \eta =\frac{{r}^{2}-{R}^{2}}{2R}\sqrt{\frac{{u}_{0}}{{\upsilon }_{f}{L}_{0}}}$$
(7)
$$\begin{array}{c}\frac{{\mu }_{nf}}{{\mu }_{f}}\left(\begin{array}{c}\left(1+2\eta \gamma \right){f}^{\prime\prime\prime}+2\gamma {f}^{\prime\prime}+\frac{\left(n-1\right)}{2}W{e}^{2}\left(1+2\eta \gamma \right)\gamma {{f}^{\prime\prime}}^{3}\\ +\frac{3\left(n-1\right)}{2}W{e}^{2}{\left(1+2\eta \gamma \right)}^{2}{{f}^{\prime\prime}}^{2}\left({f}^{\prime\prime\prime}+\frac{\gamma }{\left(1+2\eta \gamma \right)}{f}^{\prime\prime}\right)\end{array}\right)\\ +\frac{{\rho }_{nf}}{{\rho }_{f}}\left(f{f}^{\prime\prime}-{{f}^{\prime}}^{2}\right)-\frac{{\sigma }_{nf}}{{\sigma }_{f}}M{f}^{\prime}-\frac{{\mu }_{nf}}{{\mu }_{f}}{\beta }_{0}{f}^{\prime}-{F}_{r}{{f}^{\prime}}^{2}=0\end{array}$$
(8)
$$\begin{array}{c}\frac{{k}_{nf}}{{k}_{f}}\left(\left(1+2\eta \gamma \right){\theta }^{{^\prime}{^\prime}}+2\gamma {\theta }{^\prime}\right)+\frac{4}{3}Rd\left(\left(1+2\eta \gamma \right){\theta }^{{^\prime}{^\prime}}+\gamma {\theta }{^\prime}\right)+\\ \frac{{\left(\rho {C}_{p}\right)}_{nf}}{{\left(\rho {C}_{p}\right)}_{f}}Prf{\theta }{^\prime}+\frac{{\sigma }_{nf}}{{\sigma }_{f}}MEc{{f}{^\prime}}^{2}=0\end{array}$$
(9)
$$\left(1+2\eta \gamma \right){L}^{{^\prime}{^\prime}}+2\gamma {L}{^\prime}+Scf{L}{^\prime}=0$$
(10)

The non-dimensional boundary conditions are specified as:

$$\begin{array}{c}F\left(0\right)=0, {F}{^\prime}\left(0\right)=1, \theta \left(0\right)=1, L\left(0\right)=1\\ {F}{^\prime}\left(\eta \right)\to 0, \theta \left(\eta \right)\to 0, L\left(\eta \right)\to 0 as \eta \to \infty \end{array}$$
(11)

In eqs. (8–9), the dimensionless parameters are

$$We=\Gamma x\sqrt{\frac{{u}_{0}^{3}}{{L}_{0}^{3}{\nu }_{f}}}, \gamma =\sqrt{\frac{{\upsilon }_{f}{L}_{0}}{{u}_{0}{R}^{2}}}, M=\frac{{\sigma }_{f}{B}_{0}^{2}{L}_{0}}{{\rho }_{f}{u}_{0}}, {\beta }_{0}=\frac{{\mu }_{f}{L}_{0}}{{\rho }_{f}{u}_{0}{k}_{2}}, F=\frac{{c}_{b}}{\sqrt{{k}_{2}}}, {F}_{r}=\frac{Fx}{{\rho }_{f}}, Pr=\frac{{\left(\rho {C}_{p}\right)}_{f}{\upsilon }_{f}}{{k}_{f}}, Ec=\frac{{{u}_{0}}^{2}{x}^{2}}{{C}_{p}\left({T}_{w}-{T}_{\infty }\right){{L}_{0}}^{2}}, Sc=\frac{{\nu }_{f}}{{D}_{n}}$$

where \({\mu }_{nf}, {\rho }_{nf}, {\left(\rho {C}_{p}\right)}_{nf}, and {k}_{nf}\) are demonstrated as [3], Physical properties are of nanofluid are shown in Table.1.

Table 1 Nanoparticles investigational values with base fluid (blood) [3]
Full size table
$$\left.\begin{array}{c}\begin{array}{c}{\mu }_{nf}={\mu }_{f}{\left(1-\phi \right)}^{-2.5}\\ {\rho }_{nf}={\rho }_{f}\left(1-\phi \right)+\phi {\rho }_{s}\\ {\left(\rho {c}_{p}\right)}_{nf}={\left(\rho {c}_{p}\right)}_{f}\left(1-\phi \right)+\phi {\left(\rho {c}_{p}\right)}_{s}\end{array}\\ {k}_{nf}={k}_{f}\left[\frac{{k}_{s}+2{k}_{f}-2\phi \left({k}_{f}-{k}_{s}\right)}{{k}_{s}+2{k}_{f}+2\phi \left({k}_{f}-{k}_{s}\right)}\right]\end{array}\right\}$$
(12)

3 Skin friction and Nusslet number

Skin friction and Nusslet number are defined as

$$\begin{array}{c}{C}_{f}=\frac{2{\tau }_{w}}{{\rho }_{f}{{u}_{w}}^{2}}\\ Nu=\frac{{xq}_{w}}{{k}_{f}\left({T}_{w}-{T}_{\infty }\right)}\end{array}$$
(13)

where \({\tau }_{w}\) is shear stress and \({q}_{w}\) heat flux.

The non—dimensional form of Eq. (13) are:

$$\begin{array}{c}{{Re}_{x}}^{1/2}{C}_{f}=\frac{{\mu }_{nf}}{{\mu }_{f}}\left({f}^{{^\prime}{^\prime}}\left(0\right)+\frac{n-1}{2}W{e}^{2}{\left({f}^{{^\prime}{^\prime}}\left(0\right)\right)}^{3}\right)\\ {{Re}_{x}}^{-1/2}{Nu}_{x}=-\frac{{k}_{nf}}{{k}_{f}}\left(1+\frac{4}{3}Rd\right){\theta }{^\prime}\left(0\right)\end{array}$$
(14)

4 Methodology and validations

In this section, we delve into a comprehensive analysis of the various constraints that are considered in this study. The primary focus is on investigating the flow, heat transfer, and microorganism transmission characteristics of stenotic arteries using a base fluid consisting of gold (Au) nanoparticles and blood. To make the analysis easier, the governing nonlinear partial differential equations (PDEs) are converted into nonlinear ordinary differential equations (ODEs). The homotopy analysis method (HAM) is used to find solutions to these nonlinear ODEs. This method enables the determination of accurate numerical solutions and allows for a thorough examination of the physical behavior and visualization of the impact of flow restrictions on the temperature and velocity fields.

4.1 Validation

The focus of this section is to validate the obtained results. In Fig. 2a–c, numerical results are compared to HAM results for velocity, temperature and microorganism profiles. Tables 2, 3 and 4 show a numerical and HAM comparison for velocity, temperature, and microorganism profiles. We can see from the tables and figures that there is a high degree of agreement between the two results.

Fig. 2
figure 2

a–c Comparison of numerical outcomes for velocity, temperature and microorganism profiles with HAM outcomes

Full size image
Table 2 Shows a numerical comparison of and HAM outcomes for \({f}{^\prime}(\eta )\)
Full size table
Table 3 Shows a numerical comparison of and HAM outcomes for \(\theta (\eta )\)
Full size table
Table 4 Shows a numerical comparison of and HAM outcomes for \(L(\eta )\)
Full size table

5 Results and discussions

To facilitate a comprehensive understanding of the system's behavior, Figs. 3–11 are presented, showcasing the results obtained from the analysis. These figures provide visual representations and insights into how various parameters and constraints influence the temperature, velocity, drag force, and heat transfer rates in the system. The findings from this analysis shed light on the intricate interplay between fluid dynamics, heat transfer, and microorganism transmission in stenotic arteries.

Fig. 3
figure 3

Modification of \({f}{^\prime}(\eta )\) for numerous values of \(\phi \)

Full size image

The impacts of the volume fraction of nanofluid on the radial velocity are portrayed in Fig. 3, showcasing different parameter values. The findings clearly indicate that the velocity of the nanofluid strengthens as the volume fraction parameter values are adjusted. This phenomenon can be attributed to the reduction in blood flow resistance resulting from an increase in the volumetric friction parameter, consequently leading to an upsurge in fluid velocity. These findings provide valuable insights for understanding non-spherical particle behavior in areas of transient flow and their implications for cardiovascular dysfunction, such as arterial stenosis.

The effects of fluid radial velocity were analyzed in Fig. 4, considering different magnetic parameter values. The investigation focused on the interaction between magnetic fields and magnetic nanoparticles in blood, particularly in the occurrence of gold nanoparticles. These nanoparticles were functionalized with magnetic elements and introduced into the bloodstream for magnetic particle imaging (MPI) purposes. The experimental findings indicated that the radial velocity of blood containing gold nanoparticles could be diminished by increasing the magnetic field strength. This outcome can be attributed to the interplay between the magnetic fields and the magnetic nanoparticles. When a magnetic field is generated, the magnetic nanoparticles experience a force that is proportional to the gradient of the magnetic field. Consequently, they tend to migrate radially towards the center of a blood artery, altering the blood flow dynamics. By observing the changes in fluid velocity, this study sheds light on the impression of magnetic fields on blood flow behavior when magnetic nanoparticles are present. The ability to control and manipulate the radial velocity of blood has significant implications for applications such as magnetic particle imaging. It enables researchers to precisely guide the movement of magnetic nanoparticles within blood vessels, facilitating targeted imaging and diagnostic procedures.

Fig. 4
figure 4

Modification of \({f}{^\prime}(\eta )\) for numerous values of \(M\)

Full size image

The inspiration of the porosity parameter \({\upbeta }_{0}\) on fluid velocity is demonstrated in Fig. 5. The study findings designate that the fluid velocity experiences enhancement as a outcome of varying the porosity parameter \({\upbeta }_{0}\). It is observed that increasing the permeability of the porous material reduces drag force, hence speeding the fluid's velocity profile. The reduction in drag force observed with increasing permeability is a key factor contributing to the acceleration of the fluid's velocity profile. The drag force refers to the resistance encountered by the fluid as it flows through the porous medium. As the permeability rises, the fluid encounters less resistance, enabling it to move more rapidly through the medium.

Fig. 5
figure 5

Modification of \({f}{^\prime}(\eta )\) for numerous values of \({\beta }_{0}\)

Full size image

The impression of the curvature parameter on velocity \(\mathrm{f{^\prime}} (\upeta )\) is depicted in Fig. 6, revealing an increase in velocity as the curvature parameter is elevated. The graph clearly demonstrates this relationship. The observed phenomenon can be attributed to the reduction in the radius of curvature as the curvature parameter increases. When the curvature parameter is raised, the touch region between the fluid and the cylinder decreases due to the diminishing radius of curvature. This reduction in contact area leads to an enhancement in the velocity field. As a result, there is less opposition to fluid motion on the surface of the cylinder.

Fig. 6
figure 6

Modification of \({f}{^\prime}(\eta )\) for numerous values of \(\gamma \)

Full size image

Figure 7 depicts the implications of the fluid's temperature profile when different values of the volume fraction parameter are used. The results offer insights into the phenomenon behind the temperature drop in the liquid as the volume fraction parameter varies. This can be attributed to the relationship between the volume fraction parameter, blood flow resistance, and the release of frictional energy. When the volume fraction parameter increases, it implies a higher concentration of non-spherical particles within the fluid. As a result, the opposition to blood flow decreases due to reduced viscosity and increased fluidity. This reduction in resistance allows for the release of frictional energy, leading to a concomitant drop in blood temperature. The findings from this study provide a plausible explanation for the observed temperature variations in the liquid as the volume fraction parameter changes. Understanding the relationship between the volume fraction parameter and temperature is crucial in fields such as biomedicine and thermodynamics, as it contributes to the comprehension of heat transfer processes in fluid flow.

Fig.7
figure 7

Modification of \(\theta (\eta )\) for numerous values of \(\phi \)

Full size image

The consequences of the fluid's temperature profile are depicted in Fig. 8, considering different magnetic parameter values. The study explores the impact of hyperthermia on the blood content of gold nanoparticles as the magnetic parameter increases. This phenomenon is associated with the absorption of energy from an alternating magnetic field by the magnetic nanoparticles present in the blood, which subsequently transforms into heat. The outcomes propose that an upsurge in the magnetic parameter leads to a rise in the blood content of gold nanoparticles. This effect can be attributed to the process of hyperthermia, wherein the magnetic nanoparticles present in the blood absorb energy from the alternating magnetic field. As a result, this absorbed energy is converted into heat, thereby increasing the temperature of the fluid. Understanding the relationship between magnetic parameters, the presence of magnetic nanoparticles, and temperature variations in the fluid is crucial in the field of magnetic hyperthermia. Hyperthermia is a therapeutic approach that utilizes heat to treat certain medical conditions, such as cancer. By selectively targeting and heating the areas with accumulated magnetic nanoparticles, it is possible to achieve localized hyperthermia and effectively destroy cancerous cells.

Fig.8
figure 8

Modification of \(\theta (\eta )\) for numerous values of \(M\)

Full size image

The study's findings contribute to the understanding of how magnetic parameters influence temperature changes in fluid containing magnetic nanoparticles, specifically gold nanoparticles in this case. This knowledge has implications for the development and optimization of hyperthermia-based treatments, as well as the design of magnetic particle imaging techniques.

The effect of the curvature parameter \(\upgamma \) on temperature distribution is illustrated in Fig. 9, revealing a significant relationship between \(\upgamma \) and temperature. The findings demonstrate a pronounced trend wherein temperature exhibits an increasing pattern with respect to \(\upgamma \). This phenomenon can be attributed to the reduced surface contact area between the fluid particles and the curved surface as the curvature parameter \(\upgamma \) increases. Consequently, there is less resistance to fluid flow, leading to an increase in velocity. As per the principles of thermodynamics, an increase in average kinetic energy characterizes an increase in Kelvin temperature. Therefore, the observed rise in velocity results in an elevation of the temperature.

Fig. 9
figure 9

Modification of \(\theta (\eta )\) for numerous values of \(\gamma \)

Full size image

The consequences of the fluid's temperature profile are illustrated in Fig. 10, considering different values of the Eckert number. The Eckert number is a dimensionless parameter that determines the onset of turbulence in fluid flow and is defined as the ratio of buoyant forces to inertial forces within the fluid. The exact mechanisms of heat transfer operating in the system influence how temperature affects the Eckert number. The relationship between temperature and the fluid's Eckert number is influenced by the heat transfer mechanisms present in the system. Changes in temperature can affect the thermal diffusion time scale, which, in turn, can impact the significance of the Eckert number. The Eckert number becomes more or less relevant depending on how temperature influences the field's thermal diffusion behavior.

Fig. 10
figure 10

Modification of \(\theta (\eta )\) for numerous values of \(Ec\)

Full size image

The consequences of the microorganism profile are illustrated in Fig. 11, considering different Smidth number \((\mathrm{Sc})\) values. The Smidth number is a dimensionless parameter that characterizes bio-convection and relates the effects of mass transfer and fluid flow. The results show that the bio-convection Schmidt number has a considerable impact on the thickness of the boundary layer. The thickness of the boundary layer tends to decrease as the bio-convection Schmidt number (\(Sc\)) increases. The bio-convection Schmidt number is the kinematic viscosity to mass diffusivity ratio. Therefore, a higher \(\mathrm{Sc}\) value indicates a significant reduction in mass diffusivity. The non-dimensional motile microorganism density is inversely affected by the bio-convection Schmidt number. As the \(\mathrm{Sc}\) value increases, there is a corresponding decrease in the non-dimensional motile microorganism density. This reduction in density is primarily a consequence of the diminished mass diffusivity associated with higher \(\mathrm{Sc}\) values, resulting in lower microorganism concentrations.

Fig. 11
figure 11

Modification of \(L(\eta )\) for numerous values of \(Sc\)

Full size image

6 Physical quantities

Tables 5 and 6 provide insights into the changes in drag force and heat transfer rate across different physical parameters. Table 5 presents the physical behavior of the system in terms of the drag force. It reveals that the skin friction coefficient, which represents the drag force experienced by the fluid, intensifications with an upsurge in the magnetic parameter \((\mathrm{M})\). This suggests that the occurrence of a magnetic field enhances the drag force on the fluid. Conversely, the skin friction coefficient decreases with an intensification in the volume fraction parameter \((\upphi )\), porosity parameter \(({\upbeta }_{0})\), and Weissenberg number \(({\mathrm{We}}^{2})\). This indicates that higher volume fractions, greater porosity, and increased polymer elasticity contribute to reduced drag forces in the fluid flow. In Table 6, the physical behavior of the system is examined in terms of the heat transfer rate, signified by the Nusselt number. The results show that an upsurge in the volume fraction parameter \((\upphi )\) leads to a rise in the Nusselt number. This suggests that higher volume fractions of particles or additives in the fluid enhance heat transfer by promoting convective heat exchange. On the other hand, an upsurge in the magnetic curvature parameter \((\upgamma )\), parameter \((\mathrm{M})\), and Eckert number \((\mathrm{Ec})\) results in a diminution in the Nusselt number. This suggests that larger magnetic fields, greater curvature, and more fluid flow energy tend to lower the system's rate of heat transfer. Table 7 delivers association of the skin friction results with those reported in the literature, allowing for a validation or comparison of the obtained findings with existing research.

Table 5 Signifies the modification of skin friction for numerous parameters
Full size table
Table 6 Signifies the modification of Nusselt number for numerous parameters
Full size table
Table 7 Comparison of numerical results with literature
Full size table

7 Optimization analysis: RSM

A newly established statistical technique known as Response Surface Methodology (RSM) is used to determine the ideal response of heat transmission rate and mass flow for the efficacy of specific components and other parameter. The simulation procedure is carried out within the permissible range of these parameters, and these considerations are taken into account when finding the rate of heat transfer as \(0.010 \le \phi \le 0.040\), \(0.100 \le \gamma \le 0.500\) & \(0.100 \le Rd \le 0.300\) and for friction factor as \(0.200 \le We \le 0.600\), \(0.100 \le M \le 0.300\), \(0.100 \le \gamma \le 0.500\). To implement the proposed 2nd order model, we applied the CCD's in-built rectilinear, quadratic, and interface terms with squat medium and higher numbers, as recommended by the face-centered scheme. The ranges with their consistent levels for the parameters \(\left( {\phi ,\gamma ,Rd} \right)\) & \(\left( {We,M,\gamma } \right)\) with coded symbols (A, B, C) applied for the reaction of the \(\left( {Nu} \right)\) and \(\left( {C_{f} } \right)\) are displayed in Table 8 correspondingly. Table 9 depicts the distribution of related responses obtained from 20 individual runs for independent parameters. The multivariate models for the response function in terms of the related components for \(Nu_{r}\) is

$$ \begin{gathered} Nu_{r} = 2.57498 \, + \, 0.077731 \times \phi \, + \, 0.071390 \times \gamma \, + \, 0.228817 \times Rd \, + \, 0.000213 \times \phi^{2} \, - \, 0.000212 \times \gamma^{2} \hfill \\ - \, 0.004027 \times Rd^{2} \, + \, 0.005619 \times \phi \times \gamma \, + \, 0.006786 \times \phi \times Rd \, + \, 0.006989 \times \gamma \times Rd \hfill \\ \end{gathered} $$
$$ \begin{gathered} Cf_{r} = - 2.49514 \, - \, 0.231368 \times We \, - \, 0.035407 \times M \, - \, 0.160747 \times \gamma \, + \, 0.05283 \times We^{2} \, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \, 0.00023 \times M^{2} - \, 0.00426 \, \times \gamma^{2} - \, 0.007043 \, \times We \times M \, - \, 0.041515 \times We \times \gamma \, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \, 0.001640 \times M \times \gamma \hfill \\ \end{gathered} $$
Table 8 Range of independent factors and their levels to assess Nusselt number and Skin friction respectively
Full size table
Table 9 Experimentation design for the \(\left( {Nu} \right)\) & \(\left( {C_{f} } \right)\)
Full size table

With eliminating the insignificant components we reach to the following response functions

$$ \begin{gathered} Nu_{r} = 2.57498 \, + \, 0.077731 \times \phi \, + \, 0.071390 \times \, \gamma \, + \, 0.228817 \, \times Rd - \, 0.004027 \, \times Rd^{2} \hfill \\ \,\,\,\,\,\,\,\,\,\,\, + \, 0.005619 \times \, \phi \times \gamma \, + \, 0.006786 \, \times \phi \times Rd \, + \, 0.006989 \times \, \gamma \times Rd \hfill \\ \end{gathered} $$
$$ \begin{gathered} Cf_{r} = \, - 2.49514 \, - \, 0.231368 \times \, We \, - \, 0.035407 \, \times M \, - \, 0.160747 \times \, \gamma \, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \, 0.05283 \times We^{2} - 0.00426 \times \gamma^{2} - 0.007043 \times We \times M - 0.041515 \times \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,We \times \gamma \, \, - \, 0.001640 \times M \times \gamma \hfill \\ \end{gathered} $$

7.1 Validity of the model

In Tables 7 and 8, investigation of Variance (ANOVA) was used to examine regression models and perform a variety of statistical analyses. These evaluations include the study of errors, total errors, F-values, p-values, and the assessment of fitting adequacy for the Nusselt number simulation findings. The findings of these statistical trials, which were performed on the provided dataset, were aimed at obtaining a 95% confidence level. Tables 7 and 8 reveal that components of the proposed Nusselt number and Skin friction regression models with p-values greater than 0.05 were eliminated. This procedure resulted in the formulation described in the text. With a high level of confidence in its ability to forecast and optimise, the resulting expression is regarded as the best appropriate framework for interpreting the results. The calculated values support this confidence, demonstrating a 100% adjustment for heat transfer rate and a 99.99% adjustment for friction factor. The model summary shown in Tables 10 and 11 respectively corroborates the following:

Table 10 Analysis of Variance for Nusselt Number
Full size table
Table 11 Analysis of Variance for Skin Friction
Full size table

Figures 12 and 13 illustrate the data distributions for the \({N}_{u}\) and \({C}_{f}\) responses, as well as the fitted values. The linear model provides an excellent fit for these data points, as indicated by the residuals in the histogram and data arrangement inside the plot closely agreeing with the straight line. This verifies the model's outstanding suitability for the presented dataset.

Fig. 12.
figure 12

Residual plots for \(Nu\)

Full size image
Fig. 13.
figure 13

Residual plots for \(C_{f}\)

Full size image

Figure 14a–f depicts the outline and surface graphs for the interface of two autonomous parameters \(\left( {\phi ,\gamma ,Rd} \right)\) by sustaining one of it as the third factor at the central level on the response of the \(Nu\). Figures (a, c, and e) and (b, d, and f) serve as examples of \(Nu\) for numerous possible collaborative factors. The contour lines and reflections of the surface in Fig. 14a, b correspondingly demonstration while thermal radiation is at the middle level, the boosted volume fraction and curvature parameter \(\left( {\phi \& \gamma } \right)\) rise in the response function. Figure 14c, d explains the effect of the interaction factors \(\left( \phi \right)\) and \(\left( {Rd} \right)\) on the \(Nu\) whenever \(\left( \gamma \right)\) sustained at the medium level. The consequence displays that \(\left( \phi \right)\) and \(\left( {Rd} \right)\) changing from low to higher level values, a significant improvement in the response function is witnessed. Figure 14e, f portrays the role of the factors \(\left( \gamma \right)\) and \(\left( {Rd} \right)\) for the variation of the Nusselt number at a medium level of thermal radiation \(\left( \phi \right)\). The obtainable consequence reveals that the growing \(\left( \gamma \right)\) and \(\left( {Rd} \right)\) have a substantial role to enhance the heat transfer rate.

Fig. 14.
figure 14

(\(a,c,and e\)) Contour and (\(b, d,and f\)) Surface plots for \(Nu\)

Full size image

Furthermore, Fig. 15a–f illustrates the interface impacts of the autonomous parameters \(\left( {We,M,\gamma } \right)\) on the deviation of the \(Cf\) asuuming one of them at the middle level. The responses are represented by contour plots (a, c, e) and surface plots (b, d, f) on dissimilar interacting factors.

Fig. 15.
figure 15

(\(a,c,and e\)) Contour and \((b, d, and f)\) surface plots for \(C_{f}\)

Full size image

It is perceived from Figs. 15a, b that at the lower level values of \(\left( M \right)\), the significant reduction in the \(Cf\) is marked when \(\left( {We} \right)\) changing from low to higher values. Figure 15c, d show that at the lower level values of \(\left( \gamma \right)\), the substantial augmentation in the \(Cf\) is marked when \(\left( {We} \right)\) changing from higher level to lower level values. Figures 15e, f depicts that at the lower level values of \(\left( {We} \right)\), the substantial augmentation in the \(Cf\) is marked when \(\left( M \right)\) changing from lower level to higher level values.

7.2 Sensitivity analysis of response functions

The primary goal of this research is to investigate the effect of modest parameter changes on heat transfer rates and friction factor. The purpose of this study is to look deeper into the ramifications of making minor changes to one or more variables and how these changes may impact the overall effectiveness of surface friction and the broader domain of thermal energy transfer. The study uses sensitivity analysis as a crucial tool to do this. The use of sensitivity analysis provides a helpful insight on how even little parameter changes can have a significant impact on the efficiency of thermal energy conveyance and the ability to regulate fluid flow. This analytical method not only increases our understanding of these complex dynamics, but it also lays a solid platform for future research devoted to system design optimisation. The assessment of Nusselt number and skin friction sensitivity, often known as their derivatives, in particular, provides vital insights into how parameter alterations might cause fluctuations in the response functions. These results have the potential to be used to develop more efficient systems and improve existing ones. Furthermore, by using simulation and modelling approaches for the proposed design, we can gain a better grasp of the issue. This allows us to make precise predictions about the rates of heat exchange and surface friction, making it easier to develop methods to ensure optimal efficiency in thermal operations. By employing pertinent effective parameters, the calculation of the partial derivative proceeds as follows:

$$ \begin{aligned} \frac{{\partial Nu_{r} }}{\partial \phi } = 0.077731 \, + \, 0.005619 \times \, \gamma \, + \, 0.006786 \times \, Rd \hfill \\ \frac{{\partial Nu_{r} }}{\partial \gamma } = 0.071390 \, + \, 0.005619 \times \, \phi \, + \, 0.006989 \, \times Rd \hfill \\ \frac{{\partial Nu_{r} }}{\partial Rd} = 0.228817 \, - \, 0.008054 \, \times Rd \, + \, 0.006786 \times \, \phi \, + \, 0.006989 \times \, \gamma \hfill \\ \end{aligned} $$
$$ \begin{gathered} \frac{{\partial Cf_{r} }}{\partial We} = - \, 0.231368 \, + \, 0.10566 \times We \, - \, 0.007043 \times M \, - \, 0.041515 \times \gamma \, \hfill \\ \frac{{\partial Cf_{r} }}{\partial M} = - \, 0.035407 \, - \, 0.007043 \times We \, - \, 0.001640 \times \gamma \hfill \\ \frac{{\partial Cf_{r} }}{\partial \gamma } = - \, 0.160747 \, - \, 0.00852 \times \gamma \, - \, 0.041515 \times We \, - \, 0.001640 \times M \hfill \\ \end{gathered} $$

The graphs in 16(a), 16 (b), and 16 (c) respectively display the impact of heat transfer on the \(\phi ,M\) and \(Rd\) parameters and it sensitivity. Similarly, the graphs 16(d), 16(e), and 16(f) indicate the rate of sensitive friction factor with \(\phi ,M\) and \(Rd\) respectively. The bars with –ve and + ve values present, respectively, how the surface rate of heat transmission and friction factor rate has decreased and increased.

From Figs. 16a–c, it is known that towards factors \(\phi ,M\) and \(Rd\), heat transfer has the highest sensitivity value (0.243657) near the \((Rd)\) (see Fig. 16c) at the internal level of curvature parameter \(\left( {\gamma = 0.30} \right)\). Also, the lowermost sensitivity value (0.058782) in the direction of the \(\left( \gamma \right)\) (see Fig. 16a) of heat is at the coded values of \(\,(A = - 1,B = 0,C = - 1)\) \(\phi = 0.01,\gamma = 0.30,Rd = 0.1\) respectively. The sensitivity towards volume fraction \(\left( {\frac{\partial Nu}{{\partial \phi }}} \right)\) is reduced when \((Rd)\) is varying from higher to lower level values, while \(\left( {\frac{\partial Nu}{{\partial \phi }}} \right)\) remains unchanged when the volume fraction \((\phi )\) variations from low to higher level values. Moreover, the sensitivity is observed declines which is (0.070945) towards \((\phi )\) (see Fig. 16a) when \(\phi = 0.01,\gamma = 0.30,Rd = 0.1\) and increased (− 0.084517) towards \((\phi )\) (see Fig. 16a) at the same values \(\phi = 0.01,\gamma = 0.30,Rd = 0.1\). The sensitivity towards the curvature parameter \(\left( {\frac{\partial Nu}{{\partial \gamma }}} \right)\) is augmented when the volume fraction \((\phi )\) and curvature parameter \(\left( \gamma \right)\) is increased. Furthermore, the sensitivity is reduced (0.058782) towards thermal radiation (see Fig. 16a) with \(\phi = 0.01,\gamma = 0.30,Rd = 0.1\) augmented (0.083998) towards \(\left( {We} \right)\) (see Fig. 16c). The sensitivity towards thermal radiation \(\left( {\frac{\partial Nu}{{\partial Rd}}} \right)\) is falling when radiative heat flux \(Rd\) is inceasing while \(\left( {\frac{\partial Nu}{{\partial Rd}}} \right)\) enhancing as change \((\phi )\). Moreover, the lowest value (0.213977) of sensitivity is observed towards \((Rd)\) (see Fig. 16a) at the levels of \(\phi = 0.01,\gamma = 0.30,Rd = 0.3\) and the highest sensitivity value (0.243657) towards \((Rd)\) (see Fig. 16c).

Fig. 16
figure 16

(a-f). Sensitivity investigation of the \({\text{Nu }}(a,b,c)\) where \(\gamma = 0\) and for \({\text{Cf }}(d,e,f)\) when \(M = 0\)

Full size image

From Fig. 16d–f, it is observed that the friction factor rate has the uppermost sensitivity value (− 0.026724) towards the \((M)\)(see Fig. 16d) at the center-level values of \((M = 0.2)\). Similarly, the lowest sensitivity value (− 0.378543) towards the Weissenberg number \((We)\) (see Fig. 16e) of friction factor rate is at the coded values of \(\,(A = - 1,B = 0,C = - 1)\) \(We = 0.20,M = 0.2,\gamma = 0.5\) respectively. The sensitivity towards the Weissenberg number \(\left( {\frac{{\partial C_{f} }}{\partial We}} \right)\) is diminished when the curvature parameter \((\gamma )\) and Weissenberg number \((We)\) is changing, Furthermore, the smallest value (− 0.378543) of sensitivity is observed towards \((We)\) (see Fig. 16d) at the levels of \(We = 0.20,M = 0.2,\gamma = 0.5\) and the highest sensitivity value (− 0.084193) towards \((We)\) (see Fig. 16f) of friction factor rate is identified at \(We = 0.6,M = 0.2,\gamma = 0.1\). The sensitivity towards the magnetic field parameter \(\left( {\frac{{\partial C_{f} }}{\partial M}} \right)\) is diminished when the curvature parameter \((\gamma )\) and Weissenberg number \((We)\) is changing from low to higher level values. Furthermore, the lowest value (− 0.044090) of sensitivity is observed towards \((M)\) (see Fig. 16f) at the levels of \(We = 0.6,M = 0.2,\gamma = 0.5\) and the maximum sensitivity value (− 0.026724) towards \((M)\) (see Fig. 16d) of friction factor rate is obtained at \(We = 0.2,M = 0.2,\gamma = 0.1\). The sensitivity towards the curvature parameter \(\left( {\frac{{\partial C_{f} }}{\partial \gamma }} \right)\) is reduced when the \((\gamma )\) and Weissenberg number \((We)\) is changing.

8 Conclusions

This paper aims to examine how MHD and Darcy–Forchheimer porous media influence the flow of Carreau nanoliquid containing gold (Au) nanoparticles in stenosed arteries. The study is exploring the heat transference characteristics involving thermal radiation, joule dissipation, and bio-convective microorganisms. The following are the study's main findings:

  • The fluid velocity upsurges for growing values of \(\phi \), \({\beta }_{0}\), and \(\gamma \), while for rising values of \(M\) the velocity declined.

  • The temperature of the fluid declined for rising values of \(\phi \) whereas; for rising values of \(\gamma \), \(M\), and \(Ec\), the temperature rises.

  • As the bio convection Schmidt number rises, the density of non-dimensional motile microorganisms decreases.

  • When \(M\) increases, the skin friction coefficient increased, while the skin friction declined when \(\phi \), \({\beta }_{0}\), and \(W{e}^{2}\) increases.

  • Nusselt number rises when \(\phi \) increases whereas; for increasing values of \(M\), \(\gamma \), and \(Ec\) the Nusselt number declined.

  • The enhanced volume fraction and curvature parameter \(\left( {\phi \& \gamma } \right)\) cause the rise in the response function \(\left( {Nu} \right)\) when thermal radiation is at the middle level.

  • The substantial augmentation in the \(Cf\) is marked when \(\left( M \right)\) changing from lower level to higher level values while \(\left( {We} \right)\) at the lower level.

  • The transmission of heat has the maximum sensitivity value (0.243657) towards the thermal radiation \((Rd)\) for all three independent components, it has been determined at the middle level of levels of curvature parameter \(\left( {\gamma = 0.30} \right)\).

  • The friction factor rate has the greatest sensitivity value towards all three independent components, as can be seen (− 0.026724) towards the magnetic parameter \((M)\) at the middle-level values of \((M = 0.2)\).

  • The uncoded values \(\phi = 0.01,\gamma = 0.30,Rd = 0.1\) have the lowest sensitivity (0.058782) to the curvature parameter \(\left( \gamma \right)\) of heat transmission.

  • The uncoded values \(We = 0.20,M = 0.2,\gamma = 0.5\) have the lowest sensitivity (− 0.378543) to the friction factor rate parameter associated with the \((We)\) Weissenberg number.