1 Introduction

Heat transport is widely used and its heat loss is inevitable, sometimes this loss is very large. For instance, during heat transport in the district heating systems, Wojdyga et al. [1] presented that, in Poland, the heat losses stay at 10–20% in annual average, and sometimes it is more than 50% when the systems operate only to satisfy the domestic hot water goals in the summer. Abugabbara et al. [2] said that the heat losses are nearly between 10 and 30%. Werner [3] showed that the annual averaged heat losses were 12% in Sweden. Flores et al. [4] considered that the relative heat loss is 34.22% for heat-only boiler. Buffa et al. [5] believed that the heat losses, of the usual networks running only for the domestic hot water goals in summer season, may rise up to 30% of the heat fed into the networks. Also, the energy consumption in the district heating systems shares very large portion of all the energy consumed, for example, nearly 40% in Europe [5, 6]. The heat transport pipeline length of many heating systems is very long, e.g., its length is 18.3 km of a system in Jinan, 25 km of a system in Lanzhou, 40.8 km of a system in Hohhot. Even more, in a heating system to be built in Urumqi with the initial temperature 125 °C and the pipeline diametre DN1400, its heat transport pipeline length is 57 km. The heat transport pipeline length has an increasing trend in the newly built heating systems, and as the pipeline length increases, its heat loss increases.

Therefore, how to control this heat loss is becoming more and more important. Increasing the heat transfer coefficient of heat exchanger is one method to reduce the heat loss indirectly, for more heat is shifted to the target medium. There are many ways to enhance heat transfer, for instance, Ajeel et al. [7] employed nanofluids to enhance the heat exchanger efficiency. Biswas et al. [8] used a free aspiration technique to enhance heat transport and its augmentation is seven times more than that in non-aspiration cases. The methods, by which directly cut down heat loss of the pipeline, are also be applied in the engineering. For example, Mu et al. [9] applied pipe insulation to reduce the heat loss from the pipeline buried in the ground.

Here, we will take the heat transport pipeline as an example, of water-based heat system within which the heat carrier is hot water, to derive the formulas to calculate the relative heat loss and temperature drop along or across the pipeline. subsequently, the change of heat loss with pipeline diametre, water initial temperature, flow velocity, surrounding temperature, insulation thickness and its thermal conductivity, are calculated and discussed in detail. And then, according to acquired results, the methods to reduce the heat loss are achieved.

In the next section, we consider the material and methods, covering derivation of formulas, relevant parametres and Calculation. Section 3 shows the results, in which there are thermal resistance, temperature drop along the pipeline, relative heat loss across the pipeline, feasible insulation thickness and thermal conductivity. In Sect. 4, we present the discussion corresponding to the results in Sect. 3, and the case discussion is also presented. Finally, the conclusion is given in Sect. 5.

2 Material and methods

First of all, the formulas are derived, by which the temperature drop, relative heat loss, feasible insulation thickness and thermal conductivity are calculated and discussed. Sequentially, with all the obtained results, we will look for the methods to control the heat loss. Finally, in Sect. 4.6, two engineering applications are used to verify that our results are validated and our methods are practicable.

2.1 Derivation of formulas

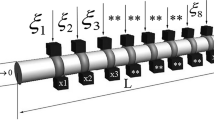
The heat transport pipeline with insulation is schematically shown in Fig. 1. Its heat loss comes from the hot water, goes through the pipeline wall and insulation successively, and finally releases into its surrounding as heat emission. Here, everything outside of the insulation is termed the surrounding, whose temperature is called as surrounding temperature. During the heat loss, there are convective thermal resistances of the pipeline inner surface and the insulation outer surface, and conductivity thermal resistances of the pipeline wall and the insulation layer. Comparing to the insulation layer conductivity thermal resistance (hereafter referred to as insulation thermal resistance), the others are so small that they can be ignored, e.g., the minimum insulation thermal resistance, among those for all cases in the paper, is nearly 0.111 m2 K W−1, and the maximum water convective one is about 0.000455 m2 K W−1. And then, according to Yang [10], the pipeline thermal resistance on a per unit length basis, or being called as the thermal resistance per metre, can be expressed as

$$R=\frac{ln\left[\left(D+\delta \right)/D\right]}{2\pi \lambda }$$
(1)

where δ is the pipeline insulation thickness, D the pipeline outer diametre, λ the insulation thermal conductivity and π a constant with a value of 3.14. Across a differential length dL, the thermal resistance of the heat transport pipeline is

$${R}_{dL}=\frac{ln\left[\left(D+\delta \right)/D\right]}{2\pi \lambda dL}=\frac{R}{dL}$$
(2)

Then the heat loss across the differential amount length dL, which comes from the hot water within the pipeline and releases into the surrounding, can be determined from

$$dQ=\frac{T-{T}_{s}}{{R}_{dL}}=\frac{T-{T}_{s}}{R}dL$$
(3)

where T is the temperature of the hot water and Ts its surrounding temperature. Also, we can determine this dQ shown in Eq. (3) from another perspective. When the hot water is running within the pipeline, the heat loss, which caused by the hot water temperature drop across the same differential amount length dL as above, can be written as

$$dQ=-{c}_{p}GdT$$
(4)

where G is the mass flow rate of the hot water, cp its specific heat at constant pressure, dT the temperature increment across the differential amount length dL of the pipeline, the minus sign means that the dQ is positive and the dT is negative across this pipeline length dL. Both the dQs in Eqs. (3) and (4) are the same, resolving these two equations, leads to obtaining

Fig. 1
figure 1

Heat transport pipeline diagram

Full size image
$$\frac{1}{T-{T}_{s}}dT=-\frac{1}{{c}_{p}GR}dL$$
(5)

Integrates Eq. (5) with respect to dT and dL, i.e.,

$${\int }_{{T}_{i}}^{T}\frac{1}{T-{T}_{s}}dT={\int }_{0}^{L}-\frac{1}{{c}_{p}GR}dL$$
(6)

and hence

$$T=\left({T}_{i}-{T}_{s}\right)exp\left(-\frac{L}{{c}_{p}GR}\right)+{T}_{s}$$
(7)

where L is the pipeline length, Ti the initial temperature of the hot water, T its local temperature. And then, the temperature drop across the pipeline is

$$\Delta T={T}_{i}-T=\left({T}_{i}-{T}_{s}\right)\left[1-\mathrm{exp}\left(-\frac{L}{{c}_{p}GR}\right)\right]$$
(8)

Substituting Eq. (7) into Eq. (3), obtains

$$dQ=\frac{{T}_{i}-{T}_{s}}{R}exp\left(-\frac{L}{{c}_{p}GR}\right)dL$$
(9)

Integrates Eq. (9) with respect to dQ and dL, i.e.,

$${\int }_{0}^{Q}dQ={\int }_{0}^{L}\frac{{T}_{i}-{T}_{s}}{R}exp\left(-\frac{L}{{c}_{p}GR}\right)dL$$
(10)

And then, the heat loss Q, of the hot water which runs across the pipeline length L with the initial temperature Ti and the surrounding temperature Ts, can be given by

$$Q={c}_{p}G\left({T}_{i}-{T}_{s}\right)\left[1-\mathit{exp}\left(-\frac{L}{{c}_{p}GR}\right)\right]$$
(11)

In order to obtain the relative heat loss, the available thermal energy is introduced as

$${Q}_{a}={c}_{p}G\left({T}_{i}-{T}_{ex}\right)$$
(12)

where Tex is exhaust temperature, i.e., the temperature of the hot water whose carrying heat has just been used. And then, the relative heat loss Rhl can be calculated by

$${R}_{hl}=\frac{Q}{{Q}_{a}}=\frac{{T}_{i}-{T}_{s}}{{T}_{i}-{T}_{ex}}\left[1-\mathit{exp}\left(-\frac{L}{{c}_{p}GR}\right)\right]$$
(13)

In Eqs. (4) - (13), the mass flow rate G of the hot water within the pipeline is determined by

$$G=\frac{\pi {d}^{2}}{4}\rho v$$
(14)

where d is the inner diametre of the pipeline, ρ the density of the hot water, and v its flow velocity. Because the mass flow rate G stays the same along the pipeline, we can determine it by simultaneously using the density and flow velocity at the initial state, where the temperature is the initial temperature.

2.2 Relevant parametres

During the heat transport, the initial temperatures of hot water are approximately 70–120 °C in most heating systems [11, 12]. And, the higher initial temperatures are adopted in the heating systems too, for example, the temperatures of 140 °C are adopted in Germany [13], and the ones of 150 °C are adopted in Poland [1]. And then, the initial temperatures, ranging from 70 °C to 150 °C, are used in calculation, as shown in Table 1. In many heating systems, the diametres of heat transport pipeline are very large, some with hundreds millimetre [1, 14], some with more than one thousand millimetres (for instance, DN1400, as described in Sect. 1). Accordingly, the pipeline diametres (nominal diametres), ranging from 0.4 m to 2.0, are used in calculation, as shown in Table 1. In Table 1, DN is the nominal diametre of the heat transport pipeline, D its outer diametre, d its inner diametre; Ti is the initial temperature of the hot water, ρ its density and v its flow velocity at the initial state; Ts is the surrounding temperature. And, the outer diametre D and inner diametre d of the pipeline are corresponding to its nominal diametre DN within the same column; the density ρ, whose value is adopted according to [15], is corresponding to its initial temperature within the same column.

Table 1 Relative main parametres selected
Full size table

In the following, one of the methods applied to reduce the heat loss, is to increase the insulation thickness of the heat transport pipeline. However, if the pipeline outer diametre D is less than the critical insulation diametre Dcr, the heat loss will increase with the increase in the insulation thickness. This scenario will be discussed now. According to Yang [10], Dcr = 2λ / h, here λ is thermal conductivity of the insulation, h convective transfer rate of the surrounding air to the insulation outer surface, whose value ranges from 5 W m−2 K−1 to 25 W m−2 K−1 for free convection and from 20 W m−2 K−1 to 100 W m−2 K−1 for forced convection [16]. In our study, the maximum critical insulation diametre is 0.072 m at the case of h = 5 W m−2 K−1 and λ = 0.18 W m−1 K−1. The minimum pipeline outer diameter, with the value of 0.42 m in our study, is larger than this maximum critical insulation diametre. Therefore, increasing insulation thickness to decrease the heat loss is feasible.

In Eqs. (4)–(12), the specific heat cp is likely to change with the temperature and pressure, we will calculate its average ones to see whether they can be taken as a constant value. According to Zeng [15], the average specific heat at constant pressure can be defined as

$${c}_{pa}=\frac{\Delta h}{\Delta T}$$
(15)

where ΔT is the temperature increment, and Δh its enthalpy increase generated by ΔT. According to the thermal properties of unsaturated water [15], by using Eq. (15), all the average specific heat, with temperatures from 0 °C to 160 °C at different absolute pressures of 0.1 MPa, 0.5 MPa, 1.0 MPa and 5.0 MPa, are calculated, respectively. Moreover, all the temperatures and pressures, applied to water-based heating systems, are covered by this range as above.

The average specific heats obtained are shown in Table 2, the maximum is 4.31 kJ kg−1 K−1, and the minimum 4.17 kJ kg−1 K−1, their relative error is 0.032. Therefore, the average specific heat cpa, in the range of temperature and pressure above, can be regarded as the specific heat cp. We take the average of all the values shown in Table 2 as the specific heat, that is, cp = 4.20 kJ kg−1 K−1.

Table 2 Average specific heat at constant pressure
Full size table

The exhaust temperature of the hot water is the return temperature in water-based heating systems. Gadd et al. [17] displayed that the annual averaged return ones are about 40—50 °C, we will take the Tex of 50 °C to calculate all the available thermal energy Qa in Eq. (12).

2.3 Calculation

By using Eq. (1), we can get the pipeline thermal resistance, and get the temperature, the temperature drop, the heat loss and the relative heat loss along or across the pipeline by using Eqs. (7), (8), (10) and (12), respectively. The temperature drop is better than the temperature to show the change along or across the pipeline; and the relative heat loss is mutually corresponding to the heat loss, the former has more practical significances. So, we will calculate and discuss the pipeline thermal resistance, the temperature drop and not the temperature, the relative heat loss and not the heat loss, and the results are shown in Figs. 2, 3, 4, respectively.

Fig. 2
figure 2

Heat transport pipeline thermal resistances

Full size image
Fig. 3
figure 3

Temperature drop along the pipeline

Full size image
Fig. 4
figure 4

Relative heat loss across the pipeline

Full size image

In reverse, by using Eqs. (8) or (13) and (1), we can determine the feasible thermal insulation, including insulation thickness and its thermal conductivity. However, along or across the pipeline, the G stays the same, the cp is the constant, and the relative heat loss can be rewritten as

$${R}_{hl}=\frac{Q}{{Q}_{a}}=\frac{{c}_{p}G\left({T}_{i}-T\right)}{{c}_{p}G\left({T}_{i}-{T}_{ex}\right)}=\frac{{T}_{i}-T}{{T}_{i}-{T}_{ex}}$$
(16)

and hence, the temperature drop is

$$\Delta T={T}_{i}-T={R}_{hl}\left({T}_{i}-{T}_{ex}\right)$$
(17)

For a running pipeline, the initial temperature Ti and exhaust temperature Tex are ascertained, according to Eq. (17), it doesn’t matter whether by using the temperature drop or by the relative heat loss to calculate the insulation thickness and its thermal conductivity. Also, the relative heat loss has more practical significances. Therefore, we will calculate the insulation thickness and its thermal conductivity by using Eqs. (13) and (1), and the results are shown in Figs. 5, 6, respectively.

Fig. 5
figure 5

Feasible insulation thickness for the pipeline

Full size image
Fig. 6
figure 6

Feasible thermal conductivity of the insulation

Full size image

3 Results

3.1 Thermal resistance

The pipeline thermal resistances per metre (hereinafter referred to as thermal resistance) Rs, which change with the pipeline diametre DN, insulation thickness δ and thermal conductivity λ, are shown in Fig. 2a–c, respectively. Taking the δ = 0.050 m and the λ = 0.10 W m−1 K−1 as constants, as shown in Fig. 2a, the R drops from 0.179 K m W−1 down to 0.039 K m W−1 with the rise in the DN from 0.4 m up to 2.0 m, and the R drops less and less. When the DN = 1.0 m and the λ = 0.10 W m−1 K−1 are kept unchanged, the R rises up with the δ almost linearly, from 0.031 K m W−1 at δ = 0.020 m up to 0.358 K m W−1 at δ = 0.260 m, as shown in Fig. 2b. Figure 2c exhibits that, the R drops less and less with the λ, from 0.377 K m W−1 at λ = 0.02 W m−1 K−1 down to 0.042 K m W−1 at λ = 0.18 W m−1 K−1, at the case of the DN = 1.0 m and the δ = 0.050 m.

3.2 Temperature drop along the pipeline

Along the heat transport pipeline, its temperature drops ΔTs are shown in Fig. 3. Here, we take the pipeline diametre DN = 1.0 m, initial temperature Ti = 100 °C, flow velocity v = 2.5 m s−1, surrounding temperature Ts = 0 °C, insulation thickness δ = 0.050 m and its thermal conductivity λ = 0.10 W m−1 K−1. And then, across the same pipeline length, the temperature drops, for the DN = 1.0 m in Fig. 3a, for the Ti = 100 °C in Fig. 3b, for the v = 2.5 m s−1 in Fig. 3c, and for the Ts = 0 °C in Fig. 3d, are the same. In addition, we present the data not only for the DN = 1.0 m but also for the DN = 0.4 m and 2.0 m in Fig. 3a; not merely the data of the Ti = 100 °C is shown in Fig. 3b, but also the data of the Ti = 70 °C and 150 °C; Fig. 3c exhibits not only the data of the v = 2.5 m s−1, but also the data of the v = 1.0 m s−1 and 5.0 m s−1; and we also provide the data of the Ts = -40 °C and 40 °C besides the Ts = 0 °C in Fig. 3d.

All the temperature drops ΔTs increase with the increase in the pipeline length L from 10 to 50 km, and all the increases of ΔTs are nearly linearly, as shown in Fig. 3a–d. From Fig. 3a, it can be seen that, the ΔT increases between 4.31 K and 19.76 K when the DN is 0.4 m, increases in the range of 1.66 K to 8.02 K while keeping the DN being 1.0 m, and increases from 0.81 K up to 4.01 K at the case of the DN = 2.0 m. It is exhibited in Fig. 3b that, the ΔT increases from 1.14 K up to 5.52 K when the Ti being 70 °C, increases between 1.66 K and 8.02 K while remaining the Ti being 100 °C, and increases in the range of 2.60 K to 12.58 K whilst the Ti being 150 °C. The ΔT rises up in the range of 4.09–18.86 K at the case of the v = 1.0 m s−1, rises up from 1.66 to 8.02 K while the v = 2.5 m s−1, and rises up between 0.83 K and 4.09 K when the v = 5.0 m s−1, as shown in Fig. 3c. Figure 3d shows that, the ΔT rises up between 2.32 K and 11.23 K at the case of the Ts is -40 °C, rises up from 1.66 to 8.02 K when the Ts is 0 °C, and rises up in the range of 0.99 K to 4.81 K while the Ts is 40 °C. The largest temperature drop is 19.96 K in this study. Furthermore, the temperature drop, across the same pipeline length, is more with the higher initial temperature, and is less with the greater pipeline diametre, larger velocity or higher surrounding temperature, as shown in Fig. 3a–d, respectively.

3.3 Relative heat loss across the pipeline

Across a certain pipeline length, the relative heat losses Rhls are shown in Fig. 4. Here, the constants, including the pipeline diametre DN = 1.0 m, initial temperature Ti = 100 °C, flow velocity v = 2.5 m s−1, surrounding temperature Ts = 0 °C, insulation thickness δ = 0.050 m and its thermal conductivity λ = 0.10 W m−1 K−1, and pipeline length L = 50.0 km, are kept the same; except the DN is taken as the variable in Fig. 4a, and so does the Ti in Fig. 4b as well as v in Fig. 4c and Ts in Fig. 4d.

With the rise in the pipeline diametre DN, initial temperature Ti, flow velocity v, or surrounding temperature Ts, the relative heat loss Rhl drops down, as shown in Fig. 4a–d respectively. We can see that from Fig. 4a, the Rhl decreases with the DN, and decreases less and less, from 39.52% at DN = 0.4 m down to 8.02% at DN = 2.0 m. The Rhl drops down less and less ranging from 27.61% to 12.58%, when the Ti rises up from 70  to 150 °C, as exhibited in Fig. 4b. Figure 4c shows that, the Rhl decreases with the v, from 37.71% at v = 1.0 m s−1 down to 8.19% at v = 5.0 m s−1, and the Rhl decreases less and less. The Rhl drops down in the range of 22.45% to 9.62% with the increase in the Ts from − 40 °C up to 40 °C, and its drop is almost linearly, as displayed in Fig. 4d.

3.4 Feasible insulation thickness

In order to control the relative heat loss within an ascertained range, we can use a feasible insulation thickness, as shown in Fig. 5. Here, the constants, including the DN = 1.0 m, Ti = 100 °C, v = 2.5 m s−1, Ts = 0 °C, λ = 0.10 W m−1 K−1, Rhl = 10% and L = 50 km, are kept unchanged; except the DN in Fig. 5(a) as well as Ti in Fig. 5b and v in Fig. 5c and Ts in Fig. 5d are taken as the variables.

It is described in Fig. 5 the change of the feasible insulation thickness δ with the DN, Ti, v or Ts. Figure 5a displays that, the δ drops from 0.261 m at DN = 0.4 m down to 0.040 m at DN = 2.0 m, and drops less and less. The δ decreases between 0.148 m and 0.064 m with the increase in the Ti from 70 °C up to 150 °C, and decreases less and less, as exhibited in Fig. 5b. From Fig. 5c, it can be seen that, the δ drops down in the range of 0.219 m to 0.041 m, and drops less and less, when the v speeds up from 1.0 m s−1 to 5.0 m s−1. The δ decreases from 0.119 m at Ts =  − 40 °C down to 0.048 m at Ts = 40 °C, and decreases close to linearly, as shown in Fig. 5(d).

3.5 Feasible thermal conductivity

In addition to changing the insulation thickness to control the relative heat loss, we can also use a feasible insulation thermal conductivity to control it, as shown in Fig. 6. The constants, including the DN = 1.0 m, Ti = 100 °C, v = 2.5 m s−1, Ts = 0 °C, δ = 0.050 m, Rhl = 10% and L = 50 km are kept unchanged here, except the variables of DN in Fig. 6a, Ti in 6(b), v in 6(c), and Ts in 6(d) are taken, respectively.

Figure 6a shows that, while the DN increases from 0.4 m up to 2.0 m, the λ close to linearly increases within the range of 0.023 W m−1 K−1 to 0.125 W m−1 K−1. In Fig. 6b, the λ rises up with the Ti, from 0.035 W m−1 K−1 at Ti = 70 °C up to 0.079 W m−1 K−1 at Ti = 150 °C, and the rise is less and less. From Fig. 6c, it can be seen that, the λ increases close to linearly between 0.025 W m−1 K−1 and 0.123 W m−1 K−1, when the v speeds up from 1.0 m s−1 to 5.0 m s−1. The λ increases with the Ts, from 0.044 W m−1 K−1 at Ts = -−40 °C up to 0.104 W m−1 K−1 at Ts = 40 °C, and the increase is more and more, as shown in Fig. 6d.

4 Discussion

It can be seen that, the temperature change (shown in Eq. (7) or (8)) and relative heat loss (shown in Eq. (13)) vary with the initial temperature, surrounding temperature, pipeline length, mass flow rate and thermal resistance. The mass flow rate is related to pipeline diametre, water density and flow velocity, as shown in Eq. (14). Due to the mass flow rate keeping the same along the pipeline, we can determine it by the paremetres at the initial state; the initial water density is corresponded to its initial temperature, as shown in Table 2; and then, according to Eq. (14), it can be regarded that the mass flow rate is related to the pipeline diametre, initial temperature and water flow velocity. The thermal resistance is related to the pipeline diametre, insulation thickness and its thermal conductivity, as shown in Eq. (1). Therefore, in a word, the temperature change and relative heat loss vary with the initial temperature, surrounding temperature, pipeline length and diametre, water flow velocity, insulation thickness and its thermal conductivity. Leitner et al. [18] noted that, the heat loss and temperature change, of the heat carrier flowing along the heat transport pipeline, rely merely upon the pipeline insulation, the surrounding temperature, the initial temperature of the heat carrier and the time it takes to flow across the pipeline. Ours result is consistent with theirs.

According to the results above, we will discuss the pipeline thermal resistance, temperature drop and relative heat loss along or across the pipeline, and thermal insulation for the pipeline.

4.1 Thermal resistance

Comparing to the heat transport pipeline diametre, its wall thickness is very small, as shown in Table 1. Then we can get that, D ≈ d ≈ DN. And because the insulation thickness δ is much less than the pipeline outer diametre D, the Eq. (1) can be simplified as

$$R=A\frac{\delta }{DN\cdot \lambda }$$
(18)

where A is a positive constant. So, according to Eq. (18), when only R and DN or λ are variables, they are inversely proportional to one another. And then, we can interpret that, the R drops with the DN or with the λ, and drops less and less, from 0.179 K m W−1 down to 0.039 K m W−1 shown in Fig. 2a or from 0.377 K m W−1 down to 0.042 K m W−1 shown in Fig. 2c, respectively; when only R and δ are variables, they are proportional to one another, and then the R rises with the δ, and rises almost linearly, from 0.031 K m W−1 up to 0.358 K m W−1 shown in Fig. 2b.

The thermal resistances above are those per metre of the pipeline. Among the thermal resistance per square metre for all cases in the paper, the minimum insulation thermal one is nearly 0.111 m2 K W−1, and other thermal resistances are very small and can be ignored, for instance, the maximum water convective one is about 0.000455 m2 K W−1. Therefore, during the derivation of the formulas, it is practicable to ignore the other thermal resistances but except insulation one.

4.2 Temperature drop along the pipeline

Here, we will discuss the temperature drop ΔT changes with the pipeline length L. From Eq. (8), we can get that

$$\mathrm{exp}\left(-\frac{L}{{c}_{p}GR}\right)=1-\frac{\Delta T}{{T}_{i}-{T}_{s}}$$
(19)

In Eq. (19), the value of the second term on the right side is positive and much less than 1, and then,

$$-\frac{L}{{c}_{p}GR}=ln\left(1-\frac{\Delta T}{{T}_{i}-{T}_{s}}\right)\approx -\frac{\Delta T}{{T}_{i}-{T}_{s}}$$
(20)

In Fig. 3, including (a)—(d), only the temperature drop ΔT and pipeline length L are variables, and then, Eq. (20) becomes

$$\Delta T\approx A\bullet L$$
(21)

where A is a positive constant. So, according to Eq. (21), we can interpret that, as the pipeline length L increases, all the temperature drops ΔTs along the pipeline increase nearly linearly, as shown in Fig. 3. For instance, the ΔT increases with the L almost linearly, from 4.31 °C at L = 10 km up to 19.76 °C at L = 50 km, when the DN is 0.4 m, as shown in Fig. 3a.

Similarly, when only the relative heat loss Rhl and pipeline length L are variables, according to Eqs. (17) and (21), we can also know that,

$${R}_{hl}\approx A\bullet L$$
(22)

where A is a positive constant. According to Eq. (22), we can also know that, the relative heat loss Rhl along the pipeline increases with the pipeline length L, and increases nearly linearly too.

As well, comparing Eq. (8) with Eq. (11), we can get that, Q = cp G ΔT. Namely, the temperature drop ΔT is consistent with the heat loss Q. Therefore, it is rational to calculate the insulation thickness and its thermal conductivity by using Eqs. (13) and (1), as described in Sect. 1.3. calculation.

4.3 Relative heat loss across the pipeline

Now, we will discuss how the relative heat loss Rhl changes with the pipeline diametre DN, initial temperature Ti, flow velocity v, and surrounding temperature Ts, respectively.

Here, we will discuss the relative heat loss Rhl changing with the pipeline diametre DN, and only the Rhl and DN are variables. Because the insulation thickness δ is much less than the pipeline outer diametre D, then D ≈ d ≈ DN, according to Eq. (1) we can obtain that, R ≈ A δ / DN = B / DN, here A, B and δ are positive constants. And then, according to Eqs. (13), (14), we can obtain that,

$$\mathrm{exp}\left(-\frac{C}{{DN}^{2}\bullet B/DN}\right)=1-{R}_{hl}\frac{{T}_{i}-{T}_{ex}}{{T}_{i}-{T}_{s}}$$
(23)

where C is a positive constant. In Eq. (23), the value of the second term on the right side is positive and much less than 1, we can get that,

$$-\frac{C}{B\bullet DN}=ln\left(1-{R}_{hl}\frac{{T}_{i}-{T}_{ex}}{{T}_{i}-{T}_{s}}\right)\approx -{R}_{hl}\frac{{T}_{i}-{T}_{ex}}{{T}_{i}-{T}_{s}}$$
(24)

And then, because only the Rhl and DN are variables here, we can obtain

$${R}_{hl}\approx \frac{E}{DN}$$
(25)

where E is a positive constant. Therefore, according to Eq. (25), it can be interpreted that, the relative heat loss Rhl decreases with the pipeline diametre DN, and decreases less and less, from 39.52% down to 8.02%, across the heat transport pipeline, as shown in Fig. 4a. Zhang et al. [14] provided that, as the pipeline diametre increases, the energy saving increases too, our results coincide with theirs.

When only the Rhl and Ti are variables, according to Eq. (13), we can obtain

$${R}_{hl}=A+\frac{B}{{T}_{i}-C}$$
(26)

where A, B and C are positive constants, due to the Ti > Tex > Ts. And then, according to Eq. (26), it can be interpreted that, the relative heat loss Rhl drops with the initial temperature Ti, and drops less and less, from 27.61% down to 12.58%, across the heat transport pipeline, as shown in Fig. 4(b). Moreover, although the temperature drop (as well as the heat loss) is more with the higher initial temperature shown in Fig. 3(b), its relative heat loss may be less owing to its available thermal energy being much more according to Eq. (12), and in fact, it is true according to Eq. (26).

Similarly, when only the Rhl and v are variables, according to Eqs. (13), (14), and D ≈ d ≈ DN, we can obtain that,

$${R}_{hl}\approx \frac{A}{v}$$
(27)

where A is a positive constant. And then, according to Eq. (27), it can be interpreted that, the relative heat loss Rhl decreases with the flow velocity v, and decreases less and less, across the heat transport pipeline, from 37.71% down to 8.19%, as shown in Fig. 4(c).

When only the Rhl and Ts are variables, according to Eq. (13), we can obtain

$${R}_{hl}=A-B\bullet {T}_{s}$$
(28)

where A, and B are positive constants, due to the Ti > Tex > Ts. And then, according to Eq. (28), it can be interpreted that, the relative heat loss Rhl drops with the temperature Ts, and drops almost linearly, from 22.45% down to 9.62%, across the heat transport pipeline, as shown in Fig. 4(d).

4.4 Feasible insulation thickness

Thermal insulation includes insulation thickness and its thermal conductivity, we will discuss them respectively. The first one discussed is the change of the insulation thickness δ with the pipeline diametre DN, only the δ and DN are variables here. We can get that, G R = A according to Eq. (13), and R ≈ B δ / DN according to Eq. (1), here A and B are positive constants, resolving them and Eq. (14), leads to

$$\delta \approx \frac{C}{DN}$$
(29)

where C is a positive constant. And then, according to Eq. (29), it can be interpreted that, across the heat transport pipeline with an ascertained relative heat loss, the insulation thickness δ drops down with the pipeline diametre DN, and drops less and less, from 0.261 m down to 0.040 m, as shown in Fig. 5(a).

When only the δ and Ti are variables, Eq. (1) becomes R ≈ A δ / DN = B δ, here A, B and DN are positive constants. Substitute this relation for R into Eq. (13), we can obtain

$$-\frac{C}{\delta }=ln\left(1-{R}_{hl}\frac{{T}_{i}-{T}_{ex}}{{T}_{i}-{T}_{s}}\right)\approx -{R}_{hl}\frac{{T}_{i}-{T}_{ex}}{{T}_{i}-{T}_{s}}$$
(30)

where C is a positive constant. And then,

$$\delta \approx E+\frac{F}{{T}_{i}-I}$$
(31)

where E, F and I are positive constants, due to the Ti > Tex > Ts. And then, according to Eq. (31), it can be interpreted that, across the heat transport pipeline with an ascertained relative heat loss, the insulation thickness δ decreases with initial temperature Ti, and decreases less and less, from 0.148 m down to 0.064 mm, as shown in Fig. 5b.

Similarly, when only the δ and v are variables, we can obtain

$$\delta \approx \frac{A}{v}$$
(32)

where A is a positive constant. And then, according to Eq. (32), it can be interpreted that, across the heat transport pipeline with an ascertained relative heat loss, the insulation thickness δ drops down with the flow velocity v, and drops less and less, from 0.219 m down to 0.041 m, as shown in Fig. 5c.

When only the δ and Ts are variables, according to Eq. (31), we can get that,

$$\delta \approx A-B\bullet {T}_{s}$$
(33)

where A and B are positive constants. And then, according to Eq. (33), it can be interpreted that, across the heat transport pipeline with an ascertained relative heat loss, the insulation thickness δ decreases with the surrounding temperature Ts, and decreases close to linearly, from 0.119 m down to 0.048 m, as shown in Fig. 5d.

4.5 Feasible thermal conductivity

Now, we will discuss how the thermal conductivity λ varies with the pipeline diametre DN, initial temperature Ti, flow velocity v, surrounding temperature Ts, if the hot water flows across the heat transport pipeline with an ascertained relative heat loss. When only the λ and DN are variables, we can get that, G R = A according to Eq. (13), R ≈ B δ / (DN λ) according to Eq. (1), here A and B are positive constants, resolving them and Eq. (14), leads to

$$\lambda \approx C\bullet DN$$
(34)

where C is a positive constant. And then, according to Eq. (34), it can be interpreted that, across the heat transport pipeline with an ascertained relative heat loss, the thermal conductivity λ increases with the pipeline diametre DN, and increases close to linearly, from 0.023 W m−1 K−1 up to 0.125 W m−1 K−1, as shown in Fig. 6(a).

When only the λ and Ti are variables, Eq. (1) becomes R = A / λ, here A is a positive constant. Substitute this relation for R into Eq. (13), we can obtain

$$-B\lambda =ln\left(1-{R}_{hl}\frac{{T}_{i}-{T}_{ex}}{{T}_{i}-{T}_{s}}\right)\approx -{R}_{hl}\frac{{T}_{i}-{T}_{ex}}{{T}_{i}-{T}_{s}}$$
(35)

where B is a positive constant. Due to the Ti > Tex > Ts, and then,

$$\lambda \approx C-\frac{E}{{T}_{i}-F}$$
(36)

where C, E and F are positive constants. Consequently, according to Eq. (36), it can be interpreted that, across the heat transport pipeline with an ascertained relative heat loss, the thermal conductivity λ rises up with the initial temperature Ti, and rises less and less, from 0.035 W m−1 K−1 up to 0.079 W m−1 K−1, as shown in Fig. 6(b).

Similarly, when only the λ and v are variables, we can obtain

$$\lambda \approx A\bullet v$$
(37)

where A is a positive constant. And then, according to Eq. (37), it can be interpreted that, across the heat transport pipeline with an ascertained relative heat loss, the thermal conductivity λ increases with the flow velocity v, and increases close to linearly, from 0.025 W m−1 K−1 up to 0.123 W m−1 K−1, as shown in Fig. 6(c).

when only the λ and Ts are variables, according to Eq. (35), we can get that,

$$\lambda \approx \frac{C}{E-{T}_{s}}$$
(38)

where C and E are positive constants. And then, according to Eq. (38), it can be interpreted that, across the heat transport pipeline with an ascertained relative heat loss, the thermal conductivity λ increases with the surrounding temperature Ts, and increases more and more, from 0.044 W m−1 K−1 up to 0.104 W m−1 K−1, as shown in Fig. 6d.

In addition, we will discuss the change of the relative heat loss Rhl with the insulation thickness δ and its thermal conductivity λ. Namely, only the Rhl, δ and λ are variables here. According to Eqs. (1) and (13), we can obtain that,

$$\mathit{exp}\left(-A\bullet \frac{\lambda }{\delta }\right)=1-B\bullet {R}_{hl}$$
(39)

where A and B are positive constants. In Eq. (39), the value of the second term on the right side is positive and much less than 1, we can get that,

$$-A\bullet \frac{\lambda }{\delta }=ln\left(1-B\bullet {R}_{hl}\right)\approx -B\bullet {R}_{hl}$$
(40)

and then

$${R}_{hl}\approx C\bullet \frac{\lambda }{\delta }$$
(41)

where C is a positive constant. We can know that from Eq. (41), the relative heat loss Rhl is nearly proportional to the thermal conductivity λ and is inversely proportional to the insulation thickness δ. In other words, the relative heat loss decreases with the insulation thickness and increases with the thermal conductivity. Liu et al. [19] indicated that the Annual energy consumption decreases with the insulation thickness, Batiha et al. [20] presented that the energy saving increases with the insulation thickness, Zhang et al. [14] offered that the annual fuel cost decreases with the insulation thickness, and Nematchoua et al. [21] exhibited that the cooling transmission load decreases with the insulation thickness. Our results coincide with theirs.

Among the data in this study, when the hot water flows across 50 km long pipeline, the largest relative heat loss is 39.52%, and the smallest one 8.02%; and the thinnest feasible insulation thickness is 0.040 m while the thickest one 0.261 m, the maximum feasible thermal conductivity is 0.125 W m−1 K−1 while the minimum 0.023 W m−1 K−1, at the condition of the relative heat loss of 10%. Namely, the minimum relative heat loss is 20.3 percent of the maximum one across 50 km long pipeline. And the thinnest feasible insulation thickness is 15.3 percent of the thickest one, the largest feasible thermal conductivity 5.43 times the smallest one, across 50 km long pipeline with the relative heat loss of 10%.

According to the results above, the methods to control the heat loss can be obtained. For instance, when the relative heat loss of the heat transport pipeline is too much, we can increase the pipeline diametre, initial temperature, flow velocity or surrounding temperature to reduce it, as shown in Fig. 3 and 4. The pipeline diametre, initial temperature and flow velocity, can be artificially chosen. The surrounding temperature can be changed by the pipeline laying method. There are roughly three types of the pipeline laying method, i.e., directly buried, ground-based, and in district heating channels. The surrounding temperature of ground-based type is greatly affected by the local atmospheric temperature. According to [1], about 54% of the heating system pipelines are in district heating channels, 40% are directly buried, and 6% are ground-based in Poland. When the pipeline diametre, initial temperature, flow velocity and surrounding temperature are keeping the same respectively, we can take the thicker insulation thickness and (or) the smaller thermal conductivity to reduce the relative heat loss, because the relative heat loss is nearly proportional to the thermal conductivity and inversely proportional to the insulation thickness, as shown as Eq. (41). On the other hand, according to the pipeline length and diametre, initial temperature, flow velocity and surrounding temperature, we can choose the feasible thermal insulation, include insulation thickness and its thermal conductivity, to ensure the relative heat loss within the determined range, as shown in Fig. 5 and 6, respectively.

Especially, some thermal problems of the pipeline can be easily handled, because both the temperature drop and relative heat loss along the pipeline increase close to linearly, as shown as Eqs. (21) and (22), and because the relative heat loss is nearly proportional to the thermal conductivity and is inversely proportional to the insulation thickness, as shown as Eq. (41). Reducing the heat loss of the pipeline by 50%, for example, can be achieved by doubling the insulation thickness or by cutting down the thermal conductivity by half.

4.6 Case discussion

Li et al. [22] reported that, the heat transport pipeline with the outer diametre of 0.53 m, covered by using the new thermal insulation material with thickness 0.070 m and thermal conductivity 0.021 W m−1 K−1 replacing the old with thickness 0.170 m and thermal conductivity 0.062 W m−1 K−1, may reduce the relative heat loss by nearly 20%. According to our method, we can calculate the relative heat loss by Eq. (41), i.e., Rhl2 / Rhl1 = 0.170 / 0.070 \(\bullet \) 0.021 / 0.062 = 0.82. The relative heat loss is reduced by 18% by using new insulation material, this calculated result agrees with that reported by Li et al. [22]. In another instance, when the water flow velocity is 2.8 m s−1, the hot water temperature drop is about 5 °C across a nearly 2.5 km pipeline length in a certain heating system. When the velocity is cut down to 1.4 m s−1, its temperature drop becomes around 10 °C, this result is consistent with Eq. (27). In return, these two engineering applications can also verify that our results are validated and our methods are practicable.

5 Conclusion

In the current paper, we take the heat transport pipeline, of water-based heat system in which hot water is the heat carrier, as an example, to derive the formulas to calculate the temperature drop and relative heat loss along or across the heat transport pipeline. The pipeline diametre, initial temperature, flow velocity, surrounding temperature, insulation thickness and its thermal conductivity on the temperature drop and the heat loss are studied. We find that, the temperature drop is consistent with the heat loss; the relative heat loss increases almost linearly with the pipeline length; the relative heat loss is nearly in proportion to the thermal conductivity and is close to inversely proportional to the insulation thickness; the relative heat loss decreases with the pipeline diametre, initial temperature, flow velocity, surrounding temperature. As well, the causations of all the results are exhibited in detail.

Therefore, the methods to reduce the heat loss are obtained. We can employ the larger pipeline diametre, higher initial temperature, larger flow velocity, higher surrounding temperature, thicker insulation thickness and/or smaller insulation thermal conductivity to reduce the heat loss, and control it within an ascertained range, even less than 10%. In particular, some thermal problems can be resolved easily, decreasing the heat loss by 50% , for instance, can be achieved by doubling the insulation thickness or by halving the thermal conductivity.

This work will be conducive to the heat transport field, especially in the project designing or overhauling stages, to control its heat transporting loss within the determined range.

The limitations of our study are that, our method is not widely applied to real-world now, and our research only focus on the heat loss not on the pressure loss although the heat transportation is usually accompanied by both those two losses.

In the future, we hope to study the suitable values, of the flow velocity, pipeline diametre, surrounding temperature, initial temperature, insulation thickness and its thermal conductivity, by which the life cycle cost of the heating projects will be reduced to the minimum one.