Dimensional crossovers in the Gaussian critical fluctuations above T_c of two-layer and three-layer superconductors

Abstract

By using a Ginzburg–Landau functional in the Gaussian approximation, we calculate the energy of superconducting fluctuations above the transition, at zero external magnetic field, of a system composed by a small number N of parallel two-dimensional superconducting planes, each of them Josephson coupled to its first neighbour, with special focus in the N = 2 and 3 cases. This allows us to obtain expressions for the critical contributions to various observables (fluctuation specific heat and magnetic susceptibility and Aslamazov–Larkin paraconductivity). Our results suggest that these systems may display deviations from pure 2D behaviour and interesting crossover effects, with both similitudes and differences to those known to occur in infinite-layers superconductors. Some challenges for future related research are also outlined.

Article Highlights

• We study superconductors composed of a few parallel layers, in the Gaussian-Ginzburg-Landau approach above their critical temperature.

• We calculate the heat capacity, susceptibility and conductivity induced by critical thermal fluctuations, mainly for bi- and tri-layers.

• We obtain dimensional crossovers in the critical behaviors and compare them with the ones in infinite-layers superconductors.

1 Introduction

The different interplays between reduced dimensionality and superconducting properties is a research subject of increasing activity, fostered by the novel posibilities for fabricating nanosized and/or nanostructured superconductors [1,2,3,4]. Also by the fact that both Cu- and Fe-based high-temperature superconductors are layered materials that may be modelled as stacks of parallel 2D layers [5, 6]. One of the notable effects of low dimensionality is the enhancement of the critical fluctuations near the superconducting transition temperature $T_c$ [6, 7]. For instance, it is well known that in 2D films the superconducting fluctuation-induced contributions to various experimental observables above but near $T_c$ are well larger than in 3D bulks. Not only the amplitude, but also the critical exponent is affected [6, 7]. For instance, in low-$T_c$ superconductors the fluctuation contribution above $T_c$ to the heat capacity, $c_\mathrm{\, fl}$, has in 3D bulks critical exponent $x=1/2$ [i.e., ${c_\mathrm{\, fl}}\propto \varepsilon ^{-1/2}$ with $\varepsilon =\ln (T/T_c)$] and in most cases unobservable amplitude [6, 7], while in 2D films the amplitude is well measurable and the critical exponent is $x=1$ [6, 7]. (For $T<T_c$, fluctuations are also observable in 2D but display the more complex vortex-antivortex phenomenology famously predicted by Kosterlitz and Thouless [8, 9]). Reduced dimensionality also changes the fluctuation contributions to other observables such as magnetic susceptibility, electrical conductivity, etc. [6].

Some of the richer phenomenologies for the interrelations between low dimensionality and critical fluctuations are provided by layered superconductors. These may be modelled using the Lawrence–Doniach (LD) functional [10], i.e., the Ginzburg–Landau (GL) free energy for a superconductor composed of an infinite (macroscopic) number of parallel planes, each of them Josephson-coupled with its adjacent neighbour. Panel (a) of Fig. 1 schematizes such superconductors. By introducing small (Gaussian) excitations, it is possible to calculate expressions for the critical fluctuations above $T_c$ [10] that are in good agreement with measurements in various macroscopic layered materials, including for instance the Cu-and Fe-based high-$T_c$ superconductors [11,12,13]. The basic prediction of this LD modelization for the fluctuation-induced heat capacity above $T_c$ under zero external magnetic field $c_\mathrm{\, fl}$ may be written as [6, 10, 14, 15]:

$$\begin{aligned} {c_\mathrm{\, fl}}=\frac{A_\mathrm{TF}}{\varepsilon }\left( 1+\frac{B_\mathrm{LD}}{\varepsilon }\right) ^{-1/2}, \end{aligned}$$

(1)

where $A_\mathrm{TF}=k_\mathrm{B}/[4\pi \xi _{ab}^2(0)s]$ is the Thouless-Ferrell amplitude [16, 17], $B_\mathrm{LD}=[2\xi _{c}(0)/s]^2$ is the LD parameter [6, 10, 14, 15], s is the inter-layer distance and $\xi _{ab}(0)$ and $\xi _{c}(0)$ are the GL amplitudes of the coherence length in the in-plane and out-of-plane directions. The latter is given in terms of the Josephson coupling constant between adjacent planes, $\gamma$, as $\xi _{c}(0)=s\sqrt{\gamma }$ [6, 10]. A representation of the resulting $c_\mathrm{\, fl}$ is given in Fig. 2. We also plot, in Fig. 3, the corresponding critical exponent (calculated from the log-log slope of the $c_\mathrm{\, fl}$-vs-$\varepsilon$ curve) showing that it crosses over the 2D ($x=1$) and 3D ($x=1/2$) values as $\varepsilon$ decreases and $T_c$ is approached [and as the inter-plane correlation grows by $\xi _c(\varepsilon )=\xi _c(0)\varepsilon ^{-1/2}$; note that the crossover is located at around $\varepsilon _\mathrm{crossover}\simeq B_\mathrm{LD}=4\gamma$.]

Fig. 1

Panel a Schematic representation of a Lawrence–Doniach (LD) or infinite-layer ($N\rightarrow \infty$) superconductor, with single interlayer distances and Josephson couplings between adjacent layers. Panel b Schematic representation of a two-layer superconductor ($N=2$, see Sects. 2.2 and 4). Panel c Schematic representation of a three-layer superconductor ($N=3$; see Sect. 2.3, and also Sect. 5 for the $\gamma _1=\gamma _2$ case or Sect. 6 for $\gamma _1>\gamma _2$). In (b, c), each layer j may have a different $T_{cj}$ or a common one; our discussions in Sect.s 4–6 focus in the latter case

Fig. 2

Fluctuation specific heat $c_\mathrm{\, fl}$ from the well-known GGL-LD predictions for superconductors composed of an infinite number of parallel 2D planes, as a function of the reduced temperature $\varepsilon$ and for different values of the Josephson-coupling constant $\gamma$ between adjacent layers. (As a reference, for optimally-doped cuprates of the YBaCuO family values $\gamma \simeq 0.001\sim 0.1$ are usually proposed [11,12,13]). The $c_\mathrm{\, fl}$ is given in arbitrary units, and is proportional to the also observables $-{\chi _\mathrm{\, fl}}/T$ and $\sigma _\mathrm{\, fl AL}$ (see main text for details). The figure illustrates that when $\varepsilon \ll \gamma$ the $c_\mathrm{\, fl}$ behaves as in a 3D system (somewhat decreased amplitude and log-log slope $-\,1/2$) while if $\varepsilon \gg \gamma$ it displays a 2D behaviour (log-log slope $-\,1$). See also Fig. 3

Fig. 3

Critical exponent x of $c_\mathrm{\, fl}$ (and of $-{\chi _\mathrm{\, fl}}/T$ and ${\sigma _\mathrm{\, fl AL}}$) resulting from the GGL-LD calculations for infinite-layers superconductors, as a function of the reduced temperature $\varepsilon$ for different values of the Josephson coupling $\gamma$. The figure illustrates the crossover from the 3D value ($x=1/2$) to the 2D one ($x=1$) as $\varepsilon$ evolves from $\varepsilon \ll \gamma$ to $\varepsilon \gg \gamma$, ant that the dimensional corossover occurrs around $\varepsilon _\mathrm{crossover}\simeq 4\gamma$

The LD calculations have been generalized by various authors to a number of different cases, including for instance non-Gaussian fluctuations [18, 19], inclusion of high-temperature effects [19,20,21,22], or also considering an infinite amount of layers but with two alternating interlayer Josephson couplings $\gamma _1$ and $\gamma _2$ [6, 23, 24].

However, to our knowledge the critical fluctuations in superconductors composed of only a few layers [see Fig. 1b, c] have not been calculated yet, even in the relatively simple Gaussian–Ginzburg–Landau (GGL) approximation above $T_c$. This will be the main purpose of the present work, with a focus on identifying possible dimensional crossover effects due to the Josephson couplings.

Let us note that a topic with some mathematical resemblance may be multi-band superconductors (with each band corresponding to the gap in different sheets of the Fermi surface) when Josephson-like expresions are chosen for the interband coupling. This case was considered in terms of fluctuations, e.g., in  [25]. However, this is a different physical problem in various respects, the main ones being that such couplings do not introduce dimensional crossovers [25] (consequently with the fact that they do not correspond to spatial variations of the gaps) and that the interband interactions change $T_c$ differently to the few-layer case [26,27,28].

In the present Topical Collection Article, we consider a GL functional of such a few-layer system and calculate the effects of critical fluctuations near but above the critical temperature, in the GGL approximation, for some of the main observables in the zero-external magnetic field limit (fluctuation heat capacity, magnetic suscetibility and electrical conductivity). We find explicit expression for various cases, and physically discuss the dimensional crossover effects induced by the inter-layer Josephson couplings in such geometries, focusing mainly in the two-layer and three-layer cases. Our results suggest that the finite-layer superconductors have the capability to display dimensional crossover effects quite comparable, in the variety of its phenomenology, to those in the LD model for infinite-layers superconductors. This includes, for instance, deviations from the 2D values of the critical exponents or crossovers of the amplitudes of the fluctuations when $\varepsilon$, and hence $T/T_c$, varies.

We organize this Topical Collection Article as follows: In Sect. 2 we write our basic equations and calculate the GGL fluctuation spectra. In Sect. 3 we write the resulting fluctuation contributions to three observables (the fluctuation specific heat, $c_\mathrm{\, fl}$, the fluctuation-induced magnetic susceptibility, $\chi _\mathrm{\, fl}$, and the Aslamazov–Larkin electrical paraconductivity ${\sigma _\mathrm{\, fl AL}}$); we also write expressions for their corresponding critical exponents, x, and amplitudes, the latter through a so-called effective number of independent fluctuating planes $N_e$ that will be helpful for the interpretation of the results. In Sect. 4 we discuss these results for two-layer superconductors in terms of their x and $N_e$ crossovers as $\varepsilon$ varies, for different Josephson couplings. In Sects. 5 and 6 we discuss the three-layer superconductors, for different values of the Josephson couplings and their ratio. In Sect. 7 we summarize our conclusions and briefly comment on some of the difficulties and challenges for further reseach in this topic.

2 Basic expressions for the Gaussian–Ginzburg–Landau fluctuations above $T_c$ in two-layer and three-layer superconductors

2.1 GL functional

As starting point, let us model a superconductor composed by a (small) number N of parallel superconducting planes, each of them Josephson-coupled to its adjacent neighbour, by writing its Ginzburg–Landau (GL) functional as composed of the sum of free energies intrinsic to each $j =1, \dots N$ plane, plus interactions between each j and $j+1$ planes:

$$\begin{aligned} {\Delta F}= \sum _{j=1}^{N} { {\Delta F}_j^\mathrm{intr} +\sum _{j=1}^{N-1}{{\Delta F}_{j,j+1}^\mathrm{inter} }}, \end{aligned}$$

(2)

with

$$\begin{aligned} {\Delta F}_j^{\mathrm{intr}} = a_0\; \int \text{ d}^2 \text{ r }\; \left\{ \varepsilon _j |\psi _j|^2 + \frac{b}{2a_0} |\psi _j|^4 + \xi ^2_{ab}(0) |\nabla _{xy} \psi _j |^2 \right\} , \end{aligned}$$

(3)

where $\psi _j$ are the GL wavefunctions of each plane, $\text{ r }=(x,y)$ are the in-plane coordinates, and $a_0$, b and $\xi _{ab}(0)$ are the GL constants and the in-plane coherence length amplitude. Also, $\varepsilon _j$ is the reduced temperature of each plane:

$$\begin{aligned} \varepsilon _j = \ln \left( {T}/{T_{cj}} \right) \simeq (T-T_{cj})/T_{cj}, \end{aligned}$$

(4)

where $T_{cj}$ is its intrinsic critical temperature. In these initial equations we consider the general case in which $T_{cj}$ and $\varepsilon _{j}$ may be different in each plane, but let us note already here that many of our discussions in the present Topical Collection Article will focus, for concreteness, in the case in which all critical temperatures coincide ($T_{cj}=T_{c}$, and hence also $\varepsilon _{j}=\varepsilon$, for all j). We also emphasize that we used the same $\xi _{ab}(0)$ for all the planes, which is probably a fair approximation if all of them are of the same material. Let us note that for most superconductors eventual variations of $\xi _{ab}(0)$ are linked to variations of $T_c$ of greater extent, so that we expect that any eventual effects due to $\xi _{ab}(0)$ variations between layers are expected to be smaller than the corresponding effects due to different $T_{cj}.$

For the inter-plane interaction term between planes j and $j+1$ we employ (as is also done by the usual LD functional for infinite-layers superconductors):

$$\begin{aligned} {\Delta F}_{j,j+1}^\mathrm{inter} = a_0 \int \text{ d}^2 \text{ r } \;\left\{ \; \gamma _j \,|\psi _j - \psi _{j+1} |^2\;\right\} , \end{aligned}$$

(5)

where $\gamma _j$ is a Josephson coupling constant between the planes j and $j+1$. Note that in the limit $N\rightarrow \infty$ our functional given by Eqs. 2 to 5 simply recovers the usual LD functional for infinite-layers superconductors [10, 29]. Note also that we assumed, in Eqs. 3 and 5, zero external magnetic field and negligible effects of the potential vector gauge field (the latter would be important for the Kosterlitz-Thouless fluctuations below $T_c$). This is because we focus in this paper on $H=0$ and for temperatures sufficiently above $T_c$ as to be in the Gaussian–Ginzburg–Landau (GGL) region of the fluctuations. In that region, the $|\psi |^4$ term in Eq. 3 may be neglected and independent fluctuation modes, and their corresponding free energy, are searched. In the rest of this Topical Collection Article we proceed with that program for $N=2$ and 3, and discuss the results.

2.2 GGL fluctuation modes for $N=2$

In the $N=2$ case, we have two (potentially different) intrinsic $T_c$’s, and hence two reduced temperatures $\varepsilon _1$ and $\varepsilon _2$, and only one interlayer Josephson coupling constant $\gamma _1 = \gamma$. When considering this $N=2$ case, the Eqs. 2 to 5 in the GGL approximation above $T_c$ may be rewritten in explicit matrix form as:

$$\begin{aligned} {\Omega }(\psi _1,\psi _2)= \left( \begin{array}{cc} \psi _1^*&\psi _2^* \end{array} \right) \left( \begin{array}{cc} \varepsilon _1 + \gamma &{} -\gamma \\ -\gamma &{} \varepsilon _2+\gamma \end{array} \right) \left( \begin{array}{c} \psi _1 \\ \psi _2 \end{array} \right) , \end{aligned}$$

(6)

where ${\Omega }$ is an interlayer contribution so that the total GL functional is:

$$\begin{aligned} {\Delta F}= a_0 \sum _{\alpha =Re,Im}\int \text{ d}^2 \text{ r } \left\{ \xi ^2_{ab}(0) \sum _{j=1,2} |\nabla _{xy} \psi _j^{\alpha } |^2 + {\Omega }(\psi _1^{\alpha },\psi _2^{\alpha })\right\} . \end{aligned}$$

(7)

In this expression it has been convenient to separate the wavefunctions into their real and imaginary parts, labeled by the index $\alpha$. Note that Eq. 7 can be also written in $k_{xy}$-Fourier space as:

$$\begin{aligned} {\Delta F}\propto \sum _{\alpha =Re,Im}\int \text{ d }k_x \text{ d }k_y \left\{ \xi ^2_{ab}(0) k_{xy}^2\sum _{j=1,2}\left| \psi _{jk_{xy}}^{\alpha }\right| ^2 + {\Omega }(\psi _{1k_{xy}}^{\alpha },\psi _{2k_{xy}}^{\alpha }) \right\} . \end{aligned}$$

(8)

We now diagonalize the $2 \times 2$ matrix in Eq. 6. This leads to

$$\begin{aligned} {\Omega }(\psi _1,\psi _2)= \left( \begin{array}{cc} f_1^*&f_2^* \end{array} \right) \left( \begin{array}{cc} \omega _1 &{} 0 \\ 0 &{} \omega _2 \end{array} \right) \left( \begin{array}{c} f_1 \\ f_2 \end{array} \right) , \end{aligned}$$

(9)

with

$$\begin{aligned}&\omega _1= \frac{1}{2} \left[ \varepsilon _1 + \varepsilon _2 + 2\gamma - \sqrt{(\varepsilon _1-\varepsilon _2)^2 + 4 \gamma ^2} \right] , \end{aligned}$$

(10)

$$\begin{aligned}&\omega _2= \frac{1}{2} \left[ \varepsilon _1 + \varepsilon _2 + 2\gamma + \sqrt{(\varepsilon _1-\varepsilon _2)^2 + 4 \gamma ^2} \right] . \end{aligned}$$

(11)

The $f_{1,2}$ themselves are linear combinations of $\psi _{1,2}$ that in this small-N case may be expressed in a relatively compact form:

$$\begin{aligned}&f_1 = \frac{\left( \omega _2-\varepsilon _1-\gamma \right) \psi _1 +\gamma \psi _2}{ \sqrt{\left( \omega _2-\varepsilon _1-\gamma \right) ^2+\gamma ^2}}, \end{aligned}$$

(12)

$$\begin{aligned}&f_2 = \frac{\left( \omega _1-\varepsilon _1-\gamma \right) \psi _1 +\gamma \psi _2}{ \sqrt{\left( \omega _1-\varepsilon _1-\gamma \right) ^2+\gamma ^2}}, \end{aligned}$$

(13)

Note that in the limit of zero Josephson interplane coupling these quotients become simpler: In particular, for $\gamma \rightarrow 0$ it is $f_1\rightarrow \psi _1$ and $f_2 \rightarrow \psi _2$ when $\varepsilon _2>\varepsilon _1$, or $f_1 \rightarrow \psi _2$ and $f_2 \rightarrow -\psi _1$ when $\varepsilon _1>\varepsilon _2$ (see next paragraph for the case $\varepsilon _1=\varepsilon _2$; we used l’Hôpital’s rule for the simultaneous zeroes in the numerator and denominator of Eqs. 12 and 13).

2.2.1 The case $N=2$ with $T_{c1}=T_{c2}\; (=T_c)$

Let us here consider $N=2$ but with all the planes having the same critical temperature, and hence also $\varepsilon _1=\varepsilon _2=\varepsilon$. In that case, the inter-layer GGL energy eigenvalues $\omega _1$ and $\omega _2$ become:

$$\begin{aligned}&\omega _1 = \varepsilon , \end{aligned}$$

(14)

$$\begin{aligned}&\omega _2 = \varepsilon + 2\gamma , \end{aligned}$$

(15)

and the $f_1$, $f_2$ eigenwavefunctions are:

$$\begin{aligned}&f_1 = (\psi _1 + \psi _2)/\sqrt{2},\end{aligned}$$

(16)

$$\begin{aligned}&f_2 = (\psi _2 - \psi _1)/\sqrt{2}. \end{aligned}$$

(17)

2.3 GGL fluctuation modes for $N=3$

For $N=3$, the matrix form of $\Omega$ becomes:

$$\begin{aligned} {\Omega }(\psi _1,\psi _2,\psi _3)= \left( \begin{array}{ccc} \psi _1^*&\psi _2^*&\psi _3^* \end{array} \right) \left( \begin{array}{ccc} \varepsilon _1 + \gamma _1 &{} -\gamma _1 &{} 0 \\ -\gamma _1 &{} \varepsilon _2+\gamma _1 +\gamma _2 &{} - \gamma _2 \\ 0 &{} -\gamma _2 &{} \varepsilon _3 + \gamma _2 \end{array} \right) \left( \begin{array}{c} \psi _1 \\ \psi _2 \\ \psi _3 \end{array} \right) . \end{aligned}$$

(18)

Diagonalizing this matrix is possible with the use of Cardano’s formulas for the roots of third order polynomials. The expression of the corresponding eigenvalues $\omega _1$ to $\omega _3$ are considerably long and therefore we devote Appendix 1 to write them. In the next subsection, we consider a more manegeable case.

2.3.1 The case $N=3$ with $T_{c1}=T_{c2}=T_{c3}\; (=T_c)$

Fortunately, the cumbersome general $N=3$ expressions for $\omega _{1,2,3}$ dramatically collapse in size when considering the case in which all the planes share the same critical temperature. In this case, the inter-layer GGL energy eigenvalues simply become:

$$\begin{aligned}&\omega _1 = \varepsilon , \end{aligned}$$

(19)

$$\begin{aligned}&\omega _2 = \varepsilon + \gamma _1+\gamma _2-\sqrt{\gamma _1^2-\gamma _1\gamma _2+\gamma _2^2}, \end{aligned}$$

(20)

$$\begin{aligned}&\omega _3 = \varepsilon + \gamma _1+\gamma _2+\sqrt{\gamma _1^2-\gamma _1\gamma _2+\gamma _2^2}, \end{aligned}$$

(21)

where again $\varepsilon =\varepsilon _1=\varepsilon _2=\varepsilon _3$.

2.4 The quantity $\sum _{j=1}^N \omega _j^{-1}$

From such $\omega$ eigenvalues of the GGL functional, in principle most fluctuation-induced observables quantities may be obtained. In this regard, of particular significance will be the quantity $\sum \omega _j^{-1}$ because it will be proportional, in the GGL approach above $T_c$, to the fluctuation-induced heat capacity $c_\mathrm{\, fl}$ (see next Section; it will be also proportional to $-{\chi _\mathrm{\, fl}}/T$ and ${\sigma _\mathrm{\, fl AL}}$) [6, 23].

In the $N=2$ case with a single $T_c$, this quantity becomes:

$$\begin{aligned} \sum _{j=1}^2 \omega _j^{-1} = \frac{1}{\varepsilon }\; \frac{2\varepsilon +2\gamma }{\varepsilon +2\gamma }. \end{aligned}$$

(22)

In the $N=3$ case with a single $T_c$, it becomes:

$$\begin{aligned} \sum _{j=1}^3 \omega _j^{-1} = \frac{1}{\varepsilon }\; \frac{3\varepsilon ^2+3\gamma _1\gamma _2+4\varepsilon (\gamma _1+\gamma _2)}{\varepsilon ^2+3\gamma _1\gamma _2+2\varepsilon (\gamma _1+\gamma _2)}. \end{aligned}$$

(23)

3 Fluctuation-induced heat capacity, magnetic susceptibility and AL paraconductivity

3.1 Expressions for $c_\mathrm{\, fl}$, $\chi _\mathrm{\, fl}$ and $\sigma _\mathrm{\, fl AL}$

From the GGL free energy written in terms of independent modes, it is possible to calculate its thermal statistical averages and then the fluctuation-induced contributions to various observables. In particular, for the basic averages of the independent modes, as expected it is $\langle |f_{jkxy}^{\alpha}|^2\rangle \propto k_\mathrm{B} T/[\xi _{ab}^2(0)k_{xy}^2+\omega _{j}]$, where not only the inter-plane contribution appears but also the in-plane kinetic energy term.¹ This is very similar to the case in the LD model, except for the substitution of the LD spectrum $\omega _{k_z}^\mathrm{LD}=2\gamma (1-\cos k_z s)$ by our $\omega _j$. Therefore it is easy to adapt to our case well-known LD calculations for the superconducting fluctuation contributions to various observables. In particular, for the following ones (always considered above $T_c$ and in the limit of zero external magnetic field):

For the fluctuation-induced specific heat, $c_\mathrm{\, fl}$ (see, e.g., [6, 23] for a parallel calculation in the LD case):

$$\begin{aligned} {c_\mathrm{\, fl}}=\frac{k_\mathrm{B}}{4\pi \xi _{ab}^2(0)L_z} \;\sum _{j=1}^{N}\omega _j^{-1}, \end{aligned}$$

(24)

where $L_z$ is the thickness of the N-layer system.

For the fluctuation-induced magnetic susceptibility, $\chi _\mathrm{\, fl}$, with the magnetic field perpendicular to the layers and always in the weak magnetic field limit (see, e.g., [6] for a similar calculations in the LD case):

$$\begin{aligned} \frac{-{\chi _\mathrm{\, fl}}}{T}=\frac{\mu _0\pi k_\mathrm{B}\xi _{ab}^2(0)}{3\phi _0^2L_z} \;\sum _{j=1}^{N}\omega _j^{-1}. \end{aligned}$$

(25)

For the in-plane electrical conductivity, we also calculated (adapting the procedures of [6, 7, 23]) the direct fluctuation contribution (also known as Aslamazov–Larkin paraconductivity ${\sigma _\mathrm{\, fl AL}}$ ), that is the dominant contribution to the experimental $\sigma _\mathrm{fl}$ at least in high-temperature cuprates [11,12,13]:²

$$\begin{aligned} {\sigma _\mathrm{\, fl AL}}=\frac{e^2}{16\hbar L_z} \;\sum _{j=1}^{N}\omega _j^{-1}. \end{aligned}$$

(26)

When combined with our explicit formulae for the quantity $\sum \omega _j^{-1}$ for $N=2$ and $N=3$ (Eqs. 22 and 23), the above expressions for $c_\mathrm{\, fl}$, $\chi _\mathrm{\, fl}$ and $\sigma _\mathrm{\, fl AL}$ become also explicit.

3.2 Critical exponents

In order to physically discuss the above results for $c_\mathrm{\, fl}$, $\chi _\mathrm{\, fl}$ and $\sigma _\mathrm{\, fl AL}$, a first quantity of interest will be the critical exponent, defined from the log-log slope of the plot of the fluctuation heat capacity versus reduced-temperature:

$$\begin{aligned} x= -\frac{\partial \ln {c_\mathrm{\, fl}}}{\partial \ln \varepsilon }. \end{aligned}$$

(27)

Note that the same critical exponent is going to be shared with $-{\chi _\mathrm{\, fl}}/T$ and ${\sigma _\mathrm{\, fl AL}}$. Note also that in the 2D limit it is ${c_\mathrm{\, fl}}\propto \varepsilon ^{-1}$ and therefore $x=1$ (while for 3D bulks it is $x=1/2$).

When applied to the Eqs. 22 to  24 obtained in the previous sections, Eq. 27 leads to the following result for the $N=2$ case:

$$\begin{aligned} x= \frac{\varepsilon ^2+2\gamma \varepsilon +2\gamma ^2}{ \left( \varepsilon + \gamma \right) \;\left( \varepsilon + 2 \gamma \right) }, \end{aligned}$$

(28)

and for the $N=3$ case:

$$\begin{aligned} x= \frac{ 3 \varepsilon ^4 +8 (\gamma _1+\gamma _2)\varepsilon ^3 +8 (\gamma _1+\gamma _2)^2\varepsilon ^2 +12 \gamma _1 \gamma _2 (\gamma _1+\gamma _2)\varepsilon +9 \gamma _1^2 \gamma _2^2 }{\left[ \varepsilon ^2+3 \gamma _1 \gamma _2+2 \varepsilon (\gamma _1+\gamma _2) \right] \;\left[ 3 \varepsilon ^2+3 \gamma _1 \gamma _2+4 \varepsilon (\gamma _1+\gamma _2) \right] }. \end{aligned}$$

(29)

Both of these expressions saturate to the pure 2D value $x=1$ in the limit of zero Josephson coupling between planes ($\gamma _j\rightarrow 0$), as it could be expected.

3.3 Effective number of independently fluctuating planes

We also introduce now a second relevant quantity, informing about the amplitude of the fluctuactions. We shall call this the “effective number of independently fluctuating superconducting planes”, $N_e$, and we define it as

$$\begin{aligned} N_e= \frac{{c_\mathrm{\, fl}}}{{c_\mathrm{\, fl}}^{N=1}} = \frac{\chi _\mathrm{fl}}{\chi _\mathrm{fl}^{N=1}} = \frac{\sigma _\mathrm{flAL}}{\sigma _\mathrm{flAL}^{N=1}}. \end{aligned}$$

(30)

In other words, this quantity is the increment of the fluctuactions with respect to the value expected for a $N=1$ 2D layer (with the same $L_z$). A value $N_e=1$ would indicate all of the N planes are fluctuating together as a single plane, and is expected to correspond at least to the limit $\gamma \rightarrow \infty$ (strong inter-plane correlation). In contrast, a value $N_e =N$ is expected to be recovered at least in the limit $\gamma \rightarrow 0$ (no inter-plane correlations, each plane fluctuates independently of the other).

4 Discussion of the results for two-layer superconductors

Let us now present a more physical discussion of the consequences of the expressions obtained up to now, starting here with the simpler $N=2$ case (we defer $N=3$ to the Sects. 5 and 6).

We first note that in this $N=2$ case the interlayer fluctuation energy is split into two contributions, the ones of Eqs. 14 and 15, what may be understood as one half of the fluctuation modes having the same energy as in a regular 2D layer, and the other half having the fluctuation energy of a 2D layer but with an “effective” reduced temperature $\varepsilon + 2\gamma$ [or with effective critical temperature $T_c/\exp {(2\gamma )}$]. Logically, the total fluctuation superfluid density accumulates both contributions, and so does ${c_\mathrm{\, fl}}^{N=2}$ (via the quantity $\sum \omega _j^{-1}$).

In the case $\gamma = 0$ (no interlayer interactions) both independent modes behave with the same effective critical temperature. In that case, as it could be expected the critical exponent is the 2D value, $x=1$, and the effective number of independently fluctuating planes becomes $N_e=2$:

$$\begin{aligned}&N_e (\gamma = 0) \;=\; 2, \end{aligned}$$

(31)

$$\begin{aligned}&x(\gamma = 0) \;=\; 1. \end{aligned}$$

(32)

In the case with $\gamma \rightarrow \infty$ we expect however the two planes acting as a single one, and in fact in that limit we get:

$$\begin{aligned}&N_e (\gamma \rightarrow \infty ) \;=\; 1, \end{aligned}$$

(33)

$$\begin{aligned}&x (\gamma \rightarrow \infty ) \;=\; 1. \end{aligned}$$

(34)

Note that the limit $\gamma \rightarrow \infty$ has the physical meaning that any variation of the superconducting wave function between adjacent layers would be energetically prohibitive, so that the only physically relevant situation in the statistical averages would be having the two layers acting as a single one - what directly should imply $x=1$ and $N_e=1$, as the above equations confirm. (These equations can be also understood by considering that if $\gamma \rightarrow \infty$ the $f_2$ fluctuating mode becomes too difficult to excite and does not contribute to $c_\mathrm{\, fl}$).

Between these two pure 2D limits ($x=1$ with either $N_e = 1$ or 2) intermediate cases must appear, in which the inter-plane correlations will result in deviations of the critical exponent from the 2D value, $x\ne 1$. Also, $N_e$ must undergo a crossover between $N_e = 2$ and $N_e = 1$ as $\gamma$ evolves from 0 to $\infty$. This is represented in Figs. 4, 5 and 6. In particular, Fig. 6 plots $N_e ^{N=2}$ versus $\varepsilon$ for different values of the inter-layer coupling $\gamma$. For $\gamma \rightarrow \infty$ and $\gamma = 0$, the limiting values 1 and 2 are obtained, as commented before. For intermediate $\gamma$ values, also $N_e \rightarrow 1$ if $\varepsilon \rightarrow 0$. This agrees with the fact that when $\varepsilon \rightarrow 0$ both planes are expected to be strongly correlated due to the growth (and divergence at $T=T_c$) of the coherence length between them (that may be estimated as $\xi _c(\varepsilon ) = \xi _c(0) / \sqrt{\varepsilon }$ with $\xi _c(0)=L_z/\sqrt{\gamma }$, in analogy to the usual LD model for infinite-layers superconductors). In contrast, as $\varepsilon \rightarrow \infty$ and $\xi _c(\varepsilon ) \rightarrow 0$ both planes will become progressively independent and $N_e=N$ ($=2$ in this case), as confirmed by Fig. 6. A rough estimate of the midpoint of this $N_e$ crossover may be obtained from $\xi _c(\varepsilon ) \sim L_z$, again in analogy to what occurs in the LD model. This leads to $\varepsilon _\mathrm{crossover} \sim \gamma$, in good agreement with Fig. 5.

Fig. 4

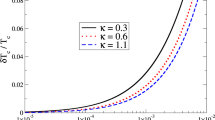
Fluctuation specific heat $c_\mathrm{\, fl}$ from our expressions for two-layer superconductors, as a function of the reduced temperature $\varepsilon$ and for different values of the Josephson coupling $\gamma$. The $c_\mathrm{\, fl}$ is given in arbitrary units (and is proportional to the also observables $-{\chi _\mathrm{\, fl}}/T$ and $\sigma _\mathrm{\, fl AL}$). See also Figs. 5 and 6 for an interpretation of the results

Fig. 5

Critical exponent x of $c_\mathrm{\, fl}$ (and of $-{\chi _\mathrm{\, fl}}/T$ and ${\sigma _\mathrm{\, fl AL}}$) for two-layer superconductors, as a function of $\varepsilon$ and for different $\gamma$. The figure illustrates deviations from the 2D value ($x=1$) when $\varepsilon$ and $\gamma$ take comparable values, which may be further understood when contrasted with the $N_e$ evolution in Fig. 6

Fig. 6

Effective number of independent fluctuating planes, $N_e$, for two-layer superconductors, as a function of $\varepsilon$ and for different $\gamma$. The figure illustrates crossovers between the $N_e=1$ and 2 values as $\varepsilon$ and $\gamma$ vary, and with them the corresponding inter-plane correlations. These crossovers may be correlated with the evolutions of the critical exponent x in Fig. 5

In Fig. 5, it may be observed a phenomenology for the critical exponent x that is consequent with the above considerations. In particular, for both $\gamma = 0$ and $\gamma \rightarrow \infty$ a pure 2D value $x = 1$ is obtained (irrespectively of $N_e=1$ or 2 the system behaves as a planar one). This pure 2D exponent is also obtained for intermediate values of $\gamma$ when either $\varepsilon \rightarrow 0$ or $\varepsilon \rightarrow \infty$, corresponding to the fact that also $N_e \rightarrow 1$ or 2. But when both $\gamma$ and $\varepsilon$ have intermediate values, a deviation from the pure 2D behaviour appears, indicating precursor correlations in the third dimension. Then, x becomes intermediate between the 2D and 3D values ($x=1$ and 1/2). In fact, the minimum of $x(\varepsilon )$, calculable by $\partial x / \partial \varepsilon = 0$, just happens at $\varepsilon _\mathrm{crossover} = \sqrt{2} \,\gamma$, corresponding to $x \approx 0.83$, which is similar to what was estimated above for the $N_e$ crossover. Therefore, we conclude that this $N=2$ finite layer case has a capability of displaying intermediate-dimensionality crossover not very far from what happens in the infinite-layers case, although without the capability of reaching the 3D limit.

5 Discussion of the results for three-layer superconductors with $\gamma _1 = \gamma _2 \;(=\gamma )$

We now explore the physical consequences of the expressions obtained for the $N = 3$ case. For concreteness, we first consider the case in which $\gamma _1$ and $\gamma _2$ take a common value $\gamma$ (in the Sect. 6 we shall consider the $\gamma _1\ne \gamma _2$ case). As in the $N = 2$ case, the relevant quantities will be ${c_\mathrm{\, fl}}$, $N_e$ and x.

First of all, note that when $\gamma = 0$ we obtain the expected 2D result ($x=1$), with $N_e = 3$ as also expected (each plane behaves independently and acts twodimensionally):

$$\begin{aligned}&N_e (\gamma _1 = \gamma _2 = 0) \;=\; 3, \end{aligned}$$

(35)

$$\begin{aligned}&x (\gamma _1 = \gamma _2 = 0) \;=\; 1. \end{aligned}$$

(36)

The equations also reproduce the expected result for the opposite limit $\gamma \rightarrow \infty$, in which the three planes should act as a single one. In that case, the equations produce $x=1$ and $N_e=1$ as it corresponds to that physical situation:

$$\begin{aligned}&N_e (\gamma _1 = \gamma _2 \rightarrow \infty ) \;=\; 1, \end{aligned}$$

(37)

$$\begin{aligned}&x (\gamma _1 = \gamma _2 \rightarrow \infty ) \;=\; 1. \end{aligned}$$

(38)

Between these two pure 2D limits, intermediate-dimensionality cases must appear for intermediate values of $\gamma$. This is represented in Figs. 7, 8 and 9. In Fig. 9, $N_e$ is plotted versus $\varepsilon$ for different values of $\gamma$. As expected, there is a crossover as $\varepsilon$ increases from $N_e = 1$ up to $N_e = 3$. The crossover temperature increases as $\gamma$ decreases (and for $\gamma = 0$ or $\gamma \rightarrow \infty$ the crossover is outside of the experimental window). In Fig. 8 the critical exponent x is plotted versus reduced temperature. Again, the $x(\varepsilon )$ behaviour is correlated with the evolution of $N_e$: When $N_e = 1$ or 3, x takes the 2D value $x=1$, and when $N_e$ is crossing over those values the system develops a non-2D critical exponent (becoming closer to the 3D value the further away $N_e$ is from its limiting values 1 or 3).

Fig. 7

Fluctuation specific heat $c_\mathrm{\, fl}$ from our expressions for three-layer superconductors with a single Josephson coupling, $\gamma =\gamma _1=\gamma _2$, as a function of the reduced temperature $\varepsilon$ and for different $\gamma$. The $c_\mathrm{\, fl}$ is given in arbitrary units (and is proportional to the also observables $-{\chi _\mathrm{\, fl}}/T$ and $\sigma _\mathrm{\, fl AL}$). See also Figs. 8 and 9 for an interpretation of the results

Fig. 8

Critical exponent x of $c_\mathrm{\, fl}$ (and of $-{\chi _\mathrm{\, fl}}/T$ and ${\sigma _\mathrm{\, fl AL}}$) for three-layer superconductors with a single Josephson coupling, $\gamma =\gamma _1=\gamma _2$, as a function of $\varepsilon$ and for different $\gamma$. The figure illustrates deviations from the 2D value ($x=1$) when $\varepsilon$ and $\gamma$ take comparable values, which may be further understood when contrasted with the $N_e$ evolution in Fig. 9

Fig. 9

Effective number of independent fluctuating planes, $N_e$, for three-layer superconductors with a single Josephson coupling, $\gamma =\gamma _1=\gamma _2$, as a function of $\varepsilon$ and for different $\gamma$. The figure illustrates crossovers between the $N_e=1$ and 3 values (with no plateau at $N_e\simeq 2$) as $\varepsilon$ and $\gamma$ vary (and with them the corresponding inter-plane correlations) correlated with the evolutions of the critical exponent x in Fig. 8

6 Discussion of the results for three-layer superconductors with $\gamma _1 > \gamma _2$

We now explore the case $N=3$ with significantly different interlayer Josephson couplings $\gamma _1$ and $\gamma _2$. For concreteness, we take $\gamma _1/\gamma _2 >1$ (but note that the equations are symmetrical to interchanges of $\gamma _1$ and $\gamma _2$).

Figures 10, 11 and 12 [panels (a) for $\gamma _1/\gamma _2 = 100$ and panels (b) for $\gamma _1/\gamma _2 = 1000$] display the ${c_\mathrm{\, fl}}$, x and $N_e$ versus reduced temperature obtained for $N = 3$ and different values of $\gamma _2$.

Fig. 10

Panel a Fluctuation specific heat $c_\mathrm{\, fl}$ from our expressions for three-layer superconductors with different Josephson couplings $\gamma _1/\gamma _2=100$, as a function of the reduced temperature $\varepsilon$ and for different values of $\gamma _2$. Panel b Same for an increased $\gamma _1/\gamma _2=1000$. See also Figs. 11 and 12 for an interpretation of the results

Fig. 11

Panel a Critical exponent x of $c_\mathrm{\, fl}$ for three-layer superconductors with $\gamma _1/\gamma _2=100$, as a function of $\varepsilon$ and for different $\gamma _2$. The figure hints at double-featured deviations from the 2D value ($x=1$) which may be correlated with the $N_e$ changes (and plateaus) in Fig. 12 (see also main text). Panel b Same for an increased $\gamma _1/\gamma _2=1000$, illustrating a softening (rather than a displacement) of the $x\ne 1$ features

Fig. 12

Panel a Effective number of independent fluctuating planes, $N_e$, for three-layer superconductors with $\gamma _1/\gamma _2=100$, as a function of $\varepsilon$ and for different $\gamma _2$. The figure illustrates not only a crossover between $N_e=1$ and 3, but also a small plateau around $N_e\simeq 2$. Panel b Same for $\gamma _1/\gamma _2=1000$, demonstrating an enlargement of the plateau around $N_e\simeq 2$ (correlated to the softening of the $x\ne 1$ features in Fig. 11)

As it happened in the previous Section, for $\gamma _2 = 0$ and $\gamma _2 \rightarrow \infty$ two different 2D limit cases are obtained, with $x=1$ and $N_e = N = 3$ for $\gamma _2 = 0$, and with $x=1$ and $N_e = 1$ for $\gamma _1 \rightarrow \infty$.

Intermediate dimensionality behaviour appears for intermediate values of $\gamma _2$ (and hence $\gamma _1$), in which x may develop deviations from the 2D value simultaneously to deviations of $N_e$ from its saturation values 1 or 3. But an interesting additional feature may appear at certain reduced temperatures, in which $N_e$ plateaus at $N_e = 2$. This must correspond to the case in which two of the layers have already saturated their mutual correlation, while the third still develops fluctuations not locked to the ones of the other layers. This feature may be seen in our Figs. 10, 11 and 12, mainly in those corresponding to $\gamma _1/\gamma _2 = 1000$ [i.e., panels (b)], while for the lower $\gamma _1/\gamma _2 = 100$ the $N_e$ plateau is well smaller. The resulting evolution of $x(\varepsilon )$ becomes then of non-trivial aspect (also for $\gamma _1/\gamma _2 = 100$), though it may be understood as a double valey of deepness tracking the slope of $N_e(\varepsilon )$. We conclude therefore that this $N = 3$ case not only is able to display intermediate dimensionality behaviour in comparable significance to the infinite-layers case, but also that this case is to some extent able to display richer phenomenology (multiple crossovers) in spite of never reaching true 3D ($x=1/2$) behaviour.

7 Conclusions and some remaining challenges

In conclusion, we have considered a GL functional of a few-layer superconductor (mainly two- and tree-layer) and calculated the effects of critical fluctuations above the critical temperature, in the GGL approximation, for some of the main observables in the zero-external magnetic field limit (fluctuation heat capacity, magnetic suscetibility and electrical conductivity). The resulting expressions suggest the capability of these systems to display crossover effects on the critical exponents and amplitudes, with similitudes and differences with respect to those predicted by the Lawrence–Doniach (LD) model for infinite-layers superconductors. For instance, in the bi-layer ($N=2$) case the critical exponent develops deviations from the pure 2D value as the temperature approaches $T_c$ (as in the LD model) but, instead of crossing over from the 2D to the 3D values (see Fig. 3), it undergoes a different evolution (see Fig. 5) of critical spatial dimensionality (2D - intermediate dimensionality - 2D), including two 2D regimes with different effective number of independently fluctuating planes (see Fig. 6). Also, for $N=3$ the evolution of the critical exponent displays a similar frustrated change of dimensionality plus an evolution of the number of independent layers from $N_e=1$ to $N_e=3$.

Let us finally briefly comment on some of the expected challenges and difficulties on further studying these potentially interesting superconducting fluctuations of few-layer systems. First, in spite of sample availability now being far easier than in the past [1,2,3,4], the specimens are bound to be small in volume; this could make measurements of the heat capacity challenging, probably favouring magnetic screening or electrical measurements (and hence $\chi$ and/or $\sigma$). Smallness also makes boundary conditions more important, and while for negligible external magnetic fields and above the transition (the case studied in this Topical Collection Article) a change in the value of $T_c$ may be expected to roughly summarize most of these boundary effects, for other situations involving well-developed vortices (sizeable magnetic fields, temperatures below the transtion, etc.) the constraints imposed by the substrate of the sample will have to be taken into account, both experimentally and theoretically. Also, because of these substrate effects and other issues, it could be important to further extend our calculations to the case with different $T_c$ for each plane, only hinted at in the present article. Probably more challenging may be to extend them to the case with larger number of planes, as the difficulty of the matrix diagonalization increases considerably with N, what could constraint calculations to be only numerical instead of analytical.

Appendices

Appendix 1: Full expression for $\omega _j$ in the $N=3$ case

The following are the complete expressions for the fluctuation energy spectrum for $N=3$ and arbitrary $\varepsilon _1$, $\varepsilon _2$, $\varepsilon _3$, $\gamma _1$ and $\gamma _2$:

$$\omega _1 = 1/3 (\varepsilon _1 + \varepsilon _2 + \varepsilon _3 + 2 \gamma _1 + 2 \gamma _2) - (2^{ 1/3} (-(-\varepsilon _1 - \varepsilon _2 - \varepsilon _3 - 2 \gamma _1 - 2 \gamma _2)^2 + 3 (\varepsilon _1 \varepsilon _2 + \varepsilon _1 \varepsilon _3 + \varepsilon _2 \varepsilon _3 + \varepsilon _1 \gamma _1 + \varepsilon _2 \gamma _1 + 2 \varepsilon _3 \gamma _1 + 2 \varepsilon _1 \gamma _2 + \varepsilon _2 \gamma _2 + \varepsilon _3 \gamma _2 + 3 \gamma _1 \gamma _2)))/(3 (2 \varepsilon _1^3 - 3 \varepsilon _1^2 \varepsilon _2 - 3 \varepsilon _1 \varepsilon _2^2 + 2 \varepsilon _2^3 - 3 \varepsilon _1^2 \varepsilon _3 + 12 \varepsilon _1 \varepsilon _2 \varepsilon _3 - 3 \varepsilon _2^2 \varepsilon _3 - 3 \varepsilon _1 \varepsilon _3^2 - 3 \varepsilon _2 \varepsilon _3^2 + 2 \varepsilon _3^3 + 3 \varepsilon _1^2 \gamma _1 - 12 \varepsilon _1 \varepsilon _2 \gamma _1 + 3 \varepsilon _2^2 \gamma _1 + 6 \varepsilon _1 \varepsilon _3 \gamma _1 + 6 \varepsilon _2 \varepsilon _3 \gamma _1 - 6 \varepsilon _3^2 \gamma _1 + 6 \varepsilon _1 \gamma _1^2+ 6 \varepsilon _2 \gamma _1^2 - 12 \varepsilon _3 \gamma _1^2 + 16 \gamma _1^3 - 6 \varepsilon _1^2 \gamma _2 + 6 \varepsilon _1 \varepsilon _2 \gamma _2 + 3 \varepsilon _2^2 \gamma _2 + 6 \varepsilon _1 \varepsilon _3 \gamma _2 - 12 \varepsilon _2 \varepsilon _3 \gamma _2 + 3 \varepsilon _3^2 \gamma _2 - 6 \varepsilon _1 \gamma _1 \gamma _2 + 12 \varepsilon _2 \gamma _1 \gamma _2 - 6 \varepsilon _3 \gamma _1 \gamma _2 - 6 \gamma _1^2 \gamma _2 - 12 \varepsilon _1 \gamma _2^2 + 6 \varepsilon _2 \gamma _2^2 + 6 \varepsilon _3 \gamma _2^2 - 6 \gamma _1 \gamma _2^2 + 16 \gamma _2^3 + ((2 \varepsilon _1^3 - 3 \varepsilon _1^2 \varepsilon _2 - 3 \varepsilon _1 \varepsilon _2^2 + 2 \varepsilon _2^3 - 3 \varepsilon _1^2 \varepsilon _3 + 12 \varepsilon _1 \varepsilon _2 \varepsilon _3 - 3 \varepsilon _2^2 \varepsilon _3 - 3 \varepsilon _1 \varepsilon _3^2 - 3 \varepsilon _2 \varepsilon _3^2 + 2 \varepsilon _3^3 + 3 \varepsilon _1^2 \gamma _1 - 12 \varepsilon _1 \varepsilon _2 \gamma _1 + 3 \varepsilon _2^2 \gamma _1 + 6 \varepsilon _1 \varepsilon _3 \gamma _1 + 6 \varepsilon _2 \varepsilon _3 \gamma _1 - 6 \varepsilon _3^2 \gamma _1 + 6 \varepsilon _1 \gamma _1^2 + 6 \varepsilon _2 \gamma _1^2 - 12 \varepsilon _3 \gamma _1^2 + 16 \gamma _1^3 - 6 \varepsilon _1^2 \gamma _2 + 6 \varepsilon _1 \varepsilon _2 \gamma _2 + 3 \varepsilon _2^2 \gamma _2 + 6 \varepsilon _1 \varepsilon _3 \gamma _2 - 12 \varepsilon _2 \varepsilon _3 \gamma _2 + 3 \varepsilon _3^2 \gamma _2 - 6 \varepsilon _1 \gamma _1 \gamma _2 + 12 \varepsilon _2 \gamma _1 \gamma _2 - 6 \varepsilon _3 \gamma _1 \gamma _2 - 6 \gamma _1^2 \gamma _2 - 12 \varepsilon _1 \gamma _2^2 + 6 \varepsilon _2 \gamma _2^2 + 6 \varepsilon _3 \gamma _2^2 - 6 \gamma _1 \gamma _2^2 + 16 \gamma _2^3)^2 + 4 (-(-\varepsilon _1 - \varepsilon _2 - \varepsilon _3 - 2 \gamma _1 - 2 \gamma _2)^2 + 3 (\varepsilon _1 \varepsilon _2 + \varepsilon _1 \varepsilon _3 + \varepsilon _2 \varepsilon _3 + \varepsilon _1 \gamma _1 + \varepsilon _2 \gamma _1 + 2 \varepsilon _3 \gamma _1 + 2 \varepsilon _1 \gamma _2 + \varepsilon _2 \gamma _2 + \varepsilon _3 \gamma _2 + 3 \gamma _1 \gamma _2))^3)^{1/2})^{1/3}) + (1/( 3 2^{1/3}))((2 \varepsilon _1^3 - 3 \varepsilon _1^2 \varepsilon _2 - 3 \varepsilon _1 \varepsilon _2^2 + 2 \varepsilon _2^3 - 3 \varepsilon _1^2 \varepsilon _3 + 12 \varepsilon _1 \varepsilon _2 \varepsilon _3 - 3 \varepsilon _2^2 \varepsilon _3 - 3 \varepsilon _1 \varepsilon _3^2 - 3 \varepsilon _2 \varepsilon _3^2 + 2 \varepsilon _3^3 + 3 \varepsilon _1^2 \gamma _1 - 12 \varepsilon _1 \varepsilon _2 \gamma _1 + 3 \varepsilon _2^2 \gamma _1 + 6 \varepsilon _1 \varepsilon _3 \gamma _1 + 6 \varepsilon _2 \varepsilon _3 \gamma _1 - 6 \varepsilon _3^2 \gamma _1 + 6 \varepsilon _1 \gamma _1^2 + 6 \varepsilon _2 \gamma _1^2 - 12 \varepsilon _3 \gamma _1^2 + 16 \gamma _1^3 - 6 \varepsilon _1^2 \gamma _2 + 6 \varepsilon _1 \varepsilon _2 \gamma _2 + 3 \varepsilon _2^2 \gamma _2 + 6 \varepsilon _1 \varepsilon _3 \gamma _2 - 12 \varepsilon _2 \varepsilon _3 \gamma _2 + 3 \varepsilon _3^2 \gamma _2 - 6 \varepsilon _1 \gamma _1 \gamma _2 + 12 \varepsilon _2 \gamma _1 \gamma _2 - 6 \varepsilon _3 \gamma _1 \gamma _2 - 6 \gamma _1^2 \gamma _2 - 12 \varepsilon _1 \gamma _2^2 + 6 \varepsilon _2 \gamma _2^2 + 6 \varepsilon _3 \gamma _2^2 - 6 \gamma _1 \gamma _2^2 + 16 \gamma _2^3 + ((2 \varepsilon _1^3 - 3 \varepsilon _1^2 \varepsilon _2 - 3 \varepsilon _1 \varepsilon _2^2 + 2 \varepsilon _2^3 - 3 \varepsilon _1^2 \varepsilon _3 + 12 \varepsilon _1 \varepsilon _2 \varepsilon _3 - 3 \varepsilon _2^2 \varepsilon _3 - 3 \varepsilon _1 \varepsilon _3^2 - 3 \varepsilon _2 \varepsilon _3^2 + 2 \varepsilon _3^3 + 3 \varepsilon _1^2 \gamma _1 - 12 \varepsilon _1 \varepsilon _2 \gamma _1 + 3 \varepsilon _2^2 \gamma _1 + 6 \varepsilon _1 \varepsilon _3 \gamma _1 + 6 \varepsilon _2 \varepsilon _3 \gamma _1 - 6 \varepsilon _3^2 \gamma _1 + 6 \varepsilon _1 \gamma _1^2 + 6 \varepsilon _2 \gamma _1^2 - 12 \varepsilon _3 \gamma _1^2 + 16 \gamma _1^3 - 6 \varepsilon _1^2 \gamma _2 + 6 \varepsilon _1 \varepsilon _2 \gamma _2 + 3 \varepsilon _2^2 \gamma _2 + 6 \varepsilon _1 \varepsilon _3 \gamma _2 - 12 \varepsilon _2 \varepsilon _3 \gamma _2 + 3 \varepsilon _3^2 \gamma _2 - 6 \varepsilon _1 \gamma _1 \gamma _2 + 12 \varepsilon _2 \gamma _1 \gamma _2 - 6 \varepsilon _3 \gamma _1 \gamma _2 - 6 \gamma _1^2 \gamma _2 - 12 \varepsilon _1 \gamma _2^2 + 6 \varepsilon _2 \gamma _2^2 + 6 \varepsilon _3 \gamma _2^2 - 6 \gamma _1 \gamma _2^2 + 16 \gamma _2^3)^2 + 4 (-(-\varepsilon _1 - \varepsilon _2 - \varepsilon _3 - 2 \gamma _1 - 2 \gamma _2)^2 + 3 (\varepsilon _1 \varepsilon _2 + \varepsilon _1 \varepsilon _3 + \varepsilon _2 \varepsilon _3 + \varepsilon _1 \gamma _1 + \varepsilon _2 \gamma _1 + 2 \varepsilon _3 \gamma _1 + 2 \varepsilon _1 \gamma _2 + \varepsilon _2 \gamma _2 + \varepsilon _3 \gamma _2 + 3 \gamma _1 \gamma _2))^3)^{1/2} )^{1/3})$$

$$\omega _2 = 1/3 (\varepsilon _1 + \varepsilon _2 + \varepsilon _3 + 2 \gamma _1 + 2 \gamma _2) + ((1 + i \sqrt{3}) (-(-\varepsilon _1 - \varepsilon _2 - \varepsilon _3 - 2 \gamma _1 - 2 \gamma _2)^2 + 3 (\varepsilon _1 \varepsilon _2 + \varepsilon _1 \varepsilon _3 + \varepsilon _2 \varepsilon _3 + \varepsilon _1 \gamma _1 + \varepsilon _2 \gamma _1 + 2 \varepsilon _3 \gamma _1 + 2 \varepsilon _1 \gamma _2 + \varepsilon _2 \gamma _2 + \varepsilon _3 \gamma _2 + 3 \gamma _1 \gamma _2)))/(3 2^{ 2/3} (2 \varepsilon _1^3 - 3 \varepsilon _1^2 \varepsilon _2 - 3 \varepsilon _1 \varepsilon _2^2 + 2 \varepsilon _2^3 - 3 \varepsilon _1^2 \varepsilon _3 + 12 \varepsilon _1 \varepsilon _2 \varepsilon _3 - 3 \varepsilon _2^2 \varepsilon _3 - 3 \varepsilon _1 \varepsilon _3^2 - 3 \varepsilon _2 \varepsilon _3^2 + 2 \varepsilon _3^3 + 3 \varepsilon _1^2 \gamma _1 - 12 \varepsilon _1 \varepsilon _2 \gamma _1 + 3 \varepsilon _2^2 \gamma _1 + 6 \varepsilon _1 \varepsilon _3 \gamma _1 + 6 \varepsilon _2 \varepsilon _3 \gamma _1 - 6 \varepsilon _3^2 \gamma _1 + 6 \varepsilon _1 \gamma _1^2 + 6 \varepsilon _2 \gamma _1^2 - 12 \varepsilon _3 \gamma _1^2 + 16 \gamma _1^3 - 6 \varepsilon _1^2 \gamma _2 + 6 \varepsilon _1 \varepsilon _2 \gamma _2 + 3 \varepsilon _2^2 \gamma _2 + 6 \varepsilon _1 \varepsilon _3 \gamma _2 - 12 \varepsilon _2 \varepsilon _3 \gamma _2 + 3 \varepsilon _3^2 \gamma _2 - 6 \varepsilon _1 \gamma _1 \gamma _2 + 12 \varepsilon _2 \gamma _1 \gamma _2 - 6 \varepsilon _3 \gamma _1 \gamma _2 -6 \gamma _1^2 \gamma _2 - 12 \varepsilon _1 \gamma _2^2 + 6 \varepsilon _2 \gamma _2^2 + 6 \varepsilon _3 \gamma _2^2 - 6 \gamma _1 \gamma _2^2 + 16 \gamma _2^3 + ((2 \varepsilon _1^3 - 3 \varepsilon _1^2 \varepsilon _2 - 3 \varepsilon _1 \varepsilon _2^2 + 2 \varepsilon _2^3 - 3 \varepsilon _1^2 \varepsilon _3 + 12 \varepsilon _1 \varepsilon _2 \varepsilon _3 - 3 \varepsilon _2^2 \varepsilon _3 -3 \varepsilon _1 \varepsilon _3^2- 3 \varepsilon _2 \varepsilon _3^2 + 2 \varepsilon _3^3 + 3 \varepsilon _1^2 \gamma _1 - 12 \varepsilon _1 \varepsilon _2 \gamma _1 + 3 \varepsilon _2^2 \gamma _1 + 6 \varepsilon _1 \varepsilon _3 \gamma _1 + 6 \varepsilon _2 \varepsilon _3 \gamma _1 - 6 \varepsilon _3^2 \gamma _1 + 6 \varepsilon _1 \gamma _1^2 + 6 \varepsilon _2 \gamma _1^2 - 12 \varepsilon _3 \gamma _1^2 + 16 \gamma _1^3 - 6 \varepsilon _1^2 \gamma _2 + 6 \varepsilon _1 \varepsilon _2 \gamma _2 + 3 \varepsilon _2^2 \gamma _2 + 6 \varepsilon _1 \varepsilon _3 \gamma _2 - 12 \varepsilon _2 \varepsilon _3 \gamma _2 + 3 \varepsilon _3^2 \gamma _2 - 6 \varepsilon _1 \gamma _1 \gamma _2 + 12 \varepsilon _2 \gamma _1 \gamma _2 - 6 \varepsilon _3 \gamma _1 \gamma _2 - 6 \gamma _1^2 \gamma _2 - 12 \varepsilon _1 \gamma _2^2 + 6 \varepsilon _2 \gamma _2^2 + 6 \varepsilon _3 \gamma _2^2 - 6 \gamma _1 \gamma _2^2 + 16 \gamma _2^3)^2 + 4 (-(-\varepsilon _1 - \varepsilon _2 - \varepsilon _3 - 2 \gamma _1 - 2 \gamma _2)^2 + 3 (\varepsilon _1 \varepsilon _2 + \varepsilon _1 \varepsilon _3 + \varepsilon _2 \varepsilon _3 + \varepsilon _1 \gamma _1 + \varepsilon _2 \gamma _1 + 2 \varepsilon _3 \gamma _1 + 2 \varepsilon _1 \gamma _2 + \varepsilon _2 \gamma _2 + \varepsilon _3 \gamma _2 + 3 \gamma _1 \gamma _2))^3)^{1/2})^{1/3}) - (1/( 6\cdot 2^{1/3}))(1 - i \sqrt{3}) (2 \varepsilon _1^3 - 3 \varepsilon _1^2 \varepsilon _2 - 3 \varepsilon _1 \varepsilon _2^2 + 2 \varepsilon _2^3 - 3 \varepsilon _1^2 \varepsilon _3 + 12 \varepsilon _1 \varepsilon _2 \varepsilon _3 - 3 \varepsilon _2^2 \varepsilon _3 - 3 \varepsilon _1 \varepsilon _3^2 - 3 \varepsilon _2 \varepsilon _3^2 + 2 \varepsilon _3^3 + 3 \varepsilon _1^2 \gamma _1 - 12 \varepsilon _1 \varepsilon _2 \gamma _1 + 3 \varepsilon _2^2 \gamma _1 + 6 \varepsilon _1 \varepsilon _3 \gamma _1 + 6 \varepsilon _2 \varepsilon _3 \gamma _1 - 6 \varepsilon _3^2 \gamma _1 + 6 \varepsilon _1 \gamma _1^2 + 6 \varepsilon _2 \gamma _1^2 - 12 \varepsilon _3 \gamma _1^2 + 16 \gamma _1^3 - 6 \varepsilon _1^2 \gamma _2 + 6 \varepsilon _1 \varepsilon _2 \gamma _2 + 3 \varepsilon _2^2 \gamma _2 + 6 \varepsilon _1 \varepsilon _3 \gamma _2 - 12 \varepsilon _2 \varepsilon _3 \gamma _2 + 3 \varepsilon _3^2 \gamma _2 - 6 \varepsilon _1 \gamma _1 \gamma _2 + 12 \varepsilon _2 \gamma _1 \gamma _2 - 6 \varepsilon _3 \gamma _1 \gamma _2 - 6 \gamma _1^2 \gamma _2 - 12 \varepsilon _1 \gamma _2^2 + 6 \varepsilon _2 \gamma _2^2 + 6 \varepsilon _3 \gamma _2^2 - 6 \gamma _1 \gamma _2^2 + 16 \gamma _2^3 + ((2 \varepsilon _1^3 - 3 \varepsilon _1^2 \varepsilon _2 - 3 \varepsilon _1 \varepsilon _2^2 + 2 \varepsilon _2^3 - 3 \varepsilon _1^2 \varepsilon _3 + 12 \varepsilon _1 \varepsilon _2 \varepsilon _3 - 3 \varepsilon _2^2 \varepsilon _3 - 3 \varepsilon _1 \varepsilon _3^2 - 3 \varepsilon _2 \varepsilon _3^2 + 2 \varepsilon _3^3 + 3 \varepsilon _1^2 \gamma _1 - 12 \varepsilon _1 \varepsilon _2 \gamma _1 + 3 \varepsilon _2^2 \gamma _1 + 6 \varepsilon _1 \varepsilon _3 \gamma _1 + 6 \varepsilon _2 \varepsilon _3 \gamma _1 - 6 \varepsilon _3^2 \gamma _1 + 6 \varepsilon _1 \gamma _1^2 + 6 \varepsilon _2 \gamma _1^2 - 12 \varepsilon _3 \gamma _1^2 + 16 \gamma _1^3 - 6 \varepsilon _1^2 \gamma _2 + 6 \varepsilon _1 \varepsilon _2 \gamma _2 + 3 \varepsilon _2^2 \gamma _2 + 6 \varepsilon _1 \varepsilon _3 \gamma _2 - 12 \varepsilon _2 \varepsilon _3 \gamma _2 + 3 \varepsilon _3^2 \gamma _2 - 6 \varepsilon _1 \gamma _1 \gamma _2 + 12 \varepsilon _2 \gamma _1 \gamma _2 - 6 \varepsilon _3 \gamma _1 \gamma _2 - 6 \gamma _1^2 \gamma _2 - 12 \varepsilon _1 \gamma _2^2 + 6 \varepsilon _2 \gamma _2^2 + 6 \varepsilon _3 \gamma _2^2 - 6 \gamma _1 \gamma _2^2 + 16 \gamma _2^3)^2 + 4 (-(-\varepsilon _1 - \varepsilon _2 - \varepsilon _3 - 2 \gamma _1 - 2 \gamma _2)^2 + 3 (\varepsilon _1 \varepsilon _2 + \varepsilon _1 \varepsilon _3 + \varepsilon _2 \varepsilon _3 + \varepsilon _1 \gamma _1 + \varepsilon _2 \gamma _1 + 2 \varepsilon _3 \gamma _1 + 2 \varepsilon _1 \gamma _2 + \varepsilon _2 \gamma _2 + \varepsilon _3 \gamma _2 + 3 \gamma _1 \gamma _2))^3)^{1/2})^{1/3}$$

$$\omega _3 = 1/3 (\varepsilon _1 + \varepsilon _2 + \varepsilon _3 + 2 \gamma _1 + 2 \gamma _2) + ((1 - i \sqrt{3}) (-(-\varepsilon _1 - \varepsilon _2 - \varepsilon _3 - 2 \gamma _1 - 2 \gamma _2)^2 + 3 (\varepsilon _1 \varepsilon _2 + \varepsilon _1 \varepsilon _3 + \varepsilon _2 \varepsilon _3 + \varepsilon _1 \gamma _1 + \varepsilon _2 \gamma _1 + 2 \varepsilon _3 \gamma _1 + 2 \varepsilon _1 \gamma _2 + \varepsilon _2 \gamma _2 + \varepsilon _3 \gamma _2 + 3 \gamma _1 \gamma _2)))/(3\cdot 2^{ 2/3} (2 \varepsilon _1^3 - 3 \varepsilon _1^2 \varepsilon _2 - 3 \varepsilon _1 \varepsilon _2^2 + 2 \varepsilon _2^3 - 3 \varepsilon _1^2 \varepsilon _3 + 12 \varepsilon _1 \varepsilon _2 \varepsilon _3 - 3 \varepsilon _2^2 \varepsilon _3 - 3 \varepsilon _1 \varepsilon _3^2 - 3 \varepsilon _2 \varepsilon _3^2 + 2 \varepsilon _3^3 + 3 \varepsilon _1^2 \gamma _1 - 12 \varepsilon _1 \varepsilon _2 \gamma _1 + 3 \varepsilon _2^2 \gamma _1 + 6 \varepsilon _1 \varepsilon _3 \gamma _1 + 6 \varepsilon _2 \varepsilon _3 \gamma _1 - 6 \varepsilon _3^2 \gamma _1 + 6 \varepsilon _1 \gamma _1^2 + 6 \varepsilon _2 \gamma _1^2 - 12 \varepsilon _3 \gamma _1^2 + 16 \gamma _1^3 - 6 \varepsilon _1^2 \gamma _2 + 6 \varepsilon _1 \varepsilon _2 \gamma _2 + 3 \varepsilon _2^2 \gamma _2 + 6 \varepsilon _1 \varepsilon _3 \gamma _2 - 12 \varepsilon _2 \varepsilon _3 \gamma _2 + 3 \varepsilon _3^2 \gamma _2 - 6 \varepsilon _1 \gamma _1 \gamma _2 + 12 \varepsilon _2 \gamma _1 \gamma _2 - 6 \varepsilon _3 \gamma _1 \gamma _2 - 6 \gamma _1^2 \gamma _2 - 12 \varepsilon _1 \gamma _2^2 + 6 \varepsilon _2 \gamma _2^2 + 6 \varepsilon _3 \gamma _2^2 - 6 \gamma _1 \gamma _2^2 + 16 \gamma _2^3 + ((2 \varepsilon _1^3 - 3 \varepsilon _1^2 \varepsilon _2 - 3 \varepsilon _1 \varepsilon _2^2 + 2 \varepsilon _2^3 - 3 \varepsilon _1^2 \varepsilon _3 + 12 \varepsilon _1 \varepsilon _2 \varepsilon _3 - 3 \varepsilon _2^2 \varepsilon _3 - 3 \varepsilon _1 \varepsilon _3^2 -3 \varepsilon _2 \varepsilon _3^2 + 2 \varepsilon _3^3 + 3 \varepsilon _1^2 \gamma _1 - 12 \varepsilon _1 \varepsilon _2 \gamma _1 + 3 \varepsilon _2^2 \gamma _1 + 6 \varepsilon _1 \varepsilon _3 \gamma _1 + 6 \varepsilon _2 \varepsilon _3 \gamma _1 - 6 \varepsilon _3^2 \gamma _1 + 6 \varepsilon _1 \gamma _1^2 + 6 \varepsilon _2 \gamma _1^2 - 12 \varepsilon _3 \gamma _1^2 + 16 \gamma _1^3 - 6 \varepsilon _1^2 \gamma _2 + 6 \varepsilon _1 \varepsilon _2 \gamma _2 + 3 \varepsilon _2^2 \gamma _2 + 6 \varepsilon _1 \varepsilon _3 \gamma _2 - 12 \varepsilon _2 \varepsilon _3 \gamma _2 + 3 \varepsilon _3^2 \gamma _2 - 6 \varepsilon _1 \gamma _1 \gamma _2 + 12 \varepsilon _2 \gamma _1 \gamma _2 - 6 \varepsilon _3 \gamma _1 \gamma _2 - 6 \gamma _1^2 \gamma _2 - 12 \varepsilon _1 \gamma _2^2 + 6 \varepsilon _2 \gamma _2^2 + 6 \varepsilon _3 \gamma _2^2 - 6 \gamma _1 \gamma _2^2 + 16 \gamma _2^3)^2 + 4 (-(-\varepsilon _1 - \varepsilon _2 - \varepsilon _3 - 2 \gamma _1 - 2 \gamma _2)^2 + 3 (\varepsilon _1 \varepsilon _2 + \varepsilon _1 \varepsilon _3 + \varepsilon _2 \varepsilon _3 + \varepsilon _1 \gamma _1 + \varepsilon _2 \gamma _1 + 2 \varepsilon _3 \gamma _1 + 2 \varepsilon _1 \gamma _2 + \varepsilon _2 \gamma _2 + \varepsilon _3 \gamma _2 + 3 \gamma _1 \gamma _2))^3)^{1/2})^{1/3}) - (1/( 6\cdot 2^{1/3}))(1 + I \sqrt{3}) (2 \varepsilon _1^3 - 3 \varepsilon _1^2 \varepsilon _2 - 3 \varepsilon _1 \varepsilon _2^2 + 2 \varepsilon _2^3 - 3 \varepsilon _1^2 \varepsilon _3 + 12 \varepsilon _1 \varepsilon _2 \varepsilon _3 - 3 \varepsilon _2^2 \varepsilon _3 - 3 \varepsilon _1 \varepsilon _3^2 - 3 \varepsilon _2 \varepsilon _3^2 + 2 \varepsilon _3^3 + 3 \varepsilon _1^2 \gamma _1 - 12 \varepsilon _1 \varepsilon _2 \gamma _1 + 3 \varepsilon _2^2 \gamma _1 + 6 \varepsilon _1 \varepsilon _3 \gamma _1 + 6 \varepsilon _2 \varepsilon _3 \gamma _1 - 6 \varepsilon _3^2 \gamma _1 + 6 \varepsilon _1 \gamma _1^2 + 6 \varepsilon _2 \gamma _1^2 - 12 \varepsilon _3 \gamma _1^2 + 16 \gamma _1^3 - 6 \varepsilon _1^2 \gamma _2 + 6 \varepsilon _1 \varepsilon _2 \gamma _2 + 3 \varepsilon _2^2 \gamma _2 + 6 \varepsilon _1 \varepsilon _3 \gamma _2 - 12 \varepsilon _2 \varepsilon _3 \gamma _2 + 3 \varepsilon _3^2 \gamma _2 - 6 \varepsilon _1 \gamma _1 \gamma _2 + 12 \varepsilon _2 \gamma _1 \gamma _2 - 6 \varepsilon _3 \gamma _1 \gamma _2 - 6 \gamma _1^2 \gamma _2 - 12 \varepsilon _1 \gamma _2^2 + 6 \varepsilon _2 \gamma _2^2 + 6 \varepsilon _3 \gamma _2^2 - 6 \gamma _1 \gamma _2^2 + 16 \gamma _2^3 + ((2 \varepsilon _1^3 - 3 \varepsilon _1^2 \varepsilon _2 - 3 \varepsilon _1 \varepsilon _2^2 + 2 \varepsilon _2^3 - 3 \varepsilon _1^2 \varepsilon _3 + 12 \varepsilon _1 \varepsilon _2 \varepsilon _3 - 3 \varepsilon _2^2 \varepsilon _3 - 3 \varepsilon _1 \varepsilon _3^2 - 3 \varepsilon _2 \varepsilon _3^2 + 2 \varepsilon _3^3 + 3 \varepsilon _1^2 \gamma _1 - 12 \varepsilon _1 \varepsilon _2 \gamma _1 + 3 \varepsilon _2^2 \gamma _1 + 6 \varepsilon _1 \varepsilon _3 \gamma _1 + 6 \varepsilon _2 \varepsilon _3 \gamma _1 - 6 \varepsilon _3^2 \gamma _1 + 6 \varepsilon _1 \gamma _1^2 + 6 \varepsilon _2 \gamma _1^2 - 12 \varepsilon _3 \gamma _1^2 + 16 \gamma _1^3 - 6 \varepsilon _1^2 \gamma _2 + 6 \varepsilon _1 \varepsilon _2 \gamma _2 + 3 \varepsilon _2^2 \gamma _2 + 6 \varepsilon _1 \varepsilon _3 \gamma _2 - 12 \varepsilon _2 \varepsilon _3 \gamma _2 + 3 \varepsilon _3^2 \gamma _2 - 6 \varepsilon _1 \gamma _1 \gamma _2 + 12 \varepsilon _2 \gamma _1 \gamma _2 - 6 \varepsilon _3 \gamma _1 \gamma _2 - 6 \gamma _1^2 \gamma _2 - 12 \varepsilon _1 \gamma _2^2 + 6 \varepsilon _2 \gamma _2^2 + 6 \varepsilon _3 \gamma _2^2 - 6 \gamma _1 \gamma _2^2 + 16 \gamma _2^3)^2 + 4 (-(-\varepsilon _1 - \varepsilon _2 - \varepsilon _3 - 2 \gamma _1 - 2 \gamma _2)^2 + 3 (\varepsilon _1 \varepsilon _2 + \varepsilon _1 \varepsilon _3 + \varepsilon _2 \varepsilon _3 + \varepsilon _1 \gamma _1 + \varepsilon _2 \gamma _1 + 2 \varepsilon _3 \gamma _1 + 2 \varepsilon _1 \gamma _2 + \varepsilon _2 \gamma _2 + \varepsilon _3 \gamma _2 + 3 \gamma _1 \gamma _2))^3)^{1/2})^{1/3}$$

Appendix 2: Expressions for $\omega _j$ in the $N=4$, $N=5$ and $N=6$ cases, with a single $T_c$ and Josephson coupling

In the main text of this Topical Collection Article we have focused on the $N=2$ and $N=3$ cases, because they are analytically solvable and relatively maneagable. Here, let us brielfy comment on the $N>3$ cases. Their main difficulty is to solve the eigenvalue problem of the corresponding $N\times N$ matrix, and associated $N^\mathrm{th}$ order polynomical equation. In general this is not feasible for $N>3$. However, we found that in the case $\varepsilon _1=\varepsilon _2=\dots \varepsilon _N$ and $\gamma _1=\gamma _2=\dots \gamma _{N-1}$ (i.e., a single $T_c$ and Josephson coupling) it is possible to rewrite the $N=4, 5$ and 6 polynomials in a solvable form (we were unable to solve the $N=7$ case). We provide those solutions in this Appendix.

For $N=4$ and $\varepsilon _1=\varepsilon _2=\varepsilon _3=\varepsilon _4 (=\varepsilon )$ and $\gamma _1=\gamma _2=\gamma _3=\gamma _4 (=\gamma )$, we found:

$$\begin{aligned}&\omega _1 = \varepsilon \end{aligned}$$

(39)

$$\begin{aligned}&\omega _2 = \varepsilon + 2\gamma \end{aligned}$$

(40)

$$\begin{aligned}&\omega _3 = \varepsilon + 2\gamma -\sqrt{2}\gamma \end{aligned}$$

(41)

$$\begin{aligned}&\omega _4 = \varepsilon + 2\gamma +\sqrt{2}\gamma \end{aligned}$$

(42)

For $N=5$ and $\varepsilon _1=\varepsilon _2=\dots \varepsilon _5 (=\varepsilon )$ and $\gamma _1=\gamma _2=\dots \gamma _5 (=\gamma )$, we found:

$$\begin{aligned}&\omega _1 = \varepsilon \end{aligned}$$

(43)

$$\begin{aligned}&\omega _2 = \frac{1}{2} ( 2\varepsilon + 3\gamma -\sqrt{5}\gamma ) \end{aligned}$$

(44)

$$\begin{aligned}&\omega _3 = \frac{1}{2} ( 2\varepsilon + 5\gamma -\sqrt{5}\gamma ) \end{aligned}$$

(45)

$$\begin{aligned}&\omega _4 = \frac{1}{2} ( 2\varepsilon + 3\gamma +\sqrt{5}\gamma ) \end{aligned}$$

(46)

$$\begin{aligned}&\omega _5 = \frac{1}{2} ( 2\varepsilon + 5\gamma +\sqrt{5}\gamma ) \end{aligned}$$

(47)

For $N=6$ and $\varepsilon _1=\varepsilon _2=\dots \varepsilon _6 (=\varepsilon )$ and $\gamma _1=\gamma _2=\dots \gamma _6 (=\gamma )$, we found:

$$\begin{aligned}&\omega _1 = \varepsilon \end{aligned}$$

(48)

$$\begin{aligned}&\omega _2 = \varepsilon + \gamma \end{aligned}$$

(49)

$$\begin{aligned}&\omega _3 = \varepsilon + 2\gamma \end{aligned}$$

(50)

$$\begin{aligned}&\omega _4 = \varepsilon + 3\gamma \end{aligned}$$

(51)

$$\begin{aligned}&\omega _5 = \varepsilon + 2\gamma - \sqrt{3}\gamma \end{aligned}$$

(52)

$$\begin{aligned}&\omega _6 = \varepsilon + 2\gamma + \sqrt{3}\gamma \end{aligned}$$

(53)