Reversal modeling and optimal design of hyper-elastic diaphragm in space fuel tanks

Abstract

Diaphragm tanks are a common type of pressurized tanks in which the diaphragm is used to separate the fuel part from the high-pressure part, compress the fuel in the tank, and reduce free space to avoid liquid fuel sloshing. The main purpose of the application of the diaphragm tanks is to ensure the continuous flow of pure fuel without the gas bubble into the spacecraft engine. In space mission, diaphragm tanks will experience a wide range of acceleration at different levels of filling. These conditions change the state of equilibrium between the volume of the gas and the fluid and move the diaphragm toward the discharge portion of the tank. As a result of this movement, the diaphragm curvature is changed and the structure collapses at rest, which is called folding. When large nonlinear folding occurs, there is potential for diaphragm damage through wear, rubbing, and excessive stress. Predicting diaphragm behavior in order to calculate a diaphragm’s susceptibility to corrosion, rupture, and surface strain is one of the major design challenges. In this study, new method is provided to analyze deformation of diaphragm tanks by using numerical techniques. Also, the investigation method is verified by using experimental methods. In this process, first a 3D numerical model is developed to investigate the inverse behavior of a hyper-elastic diaphragm by using ANSYS software and the results of the simulations are compared with the results of experimental tests in the same situation. After validation, a second case study is performed to survey the effect of reducing diaphragm thickness according to the strain energy and natural frequency behavior of the diaphragm in different fill levels. The results of this study showed that numerical simulations are capable of reconstructing diaphragm inversion properties with good accuracy. In addition, the numerical model can detect the proper thickness for the diaphragm. In the last section, algorithm and software for optimal automatic modeling of diaphragm tanks are proposed.

1 Introduction

The sloshing and distribution of liquid fuel are an important topic in aerospace research such as the launch vehicle and spacecraft. Fuel behavior during orbital changes and during the discharge process greatly affects the dynamics of the spacecraft. Slosh control systems are used to reduce this concerns. One of the common turbulence control systems is the use of elastomeric diaphragms in liquid fuel tanks. In these types of tanks, the elastomeric diaphragm is used to separate the fuel part from the pressure part, control the fuel slosh, and transfer the fuel to the engine. The biggest advantage of the diaphragm than the other slosh control systems is its superior advantage in fluid damping and slosh control. In this method, by controlling the pressure on the diaphragm control the outflow of fuel under different acceleration of the mission path is possible (Chiba et al. [1]; Radtke [2]; Ballinger et al. [3]). Due to its reliable performance and ease of operation, the same diaphragm materials are also applied in the nuclear power industry, chemical engineering and other fields (Ganesan and Kadoli [4]; Faltinsen [5]; Vincent et al. [6]). Figure 1 shows the components of a diaphragm tank.

Usually, the diaphragm is made of flexible soft materials such as hyper-elastic rubber (Benton and Debreceni [7]; Gupta et al. [8]). A different acceleration along the path of the space mission changes the equilibrium between the volume of the pressurized gas and the fluid and moves the diaphragm toward the fuel discharge portion of the tank. As a result of this movement, the diaphragm curvature is altered and the structure folding. In fact, folding is formed when the material under stress has a low bending strength and the hardness of the plate interacting with it is high. At the tank filling level of 50%, the potential of folding increases. Examples of this type of folding are shown in Figs. 1, 2.

Fig. 1

The components of a diaphragm tank [3]

Fig. 2

Diaphragm folding shape in a 40-inch tank, (a) 50% fill fraction, (b) 75% fill fraction (Levine [22])

As shown in Fig. 2, when large irregular folds happen, there is potential for diaphragm damage through rub, wearing and excessive stress. The maximum folding stress occurred when two complete folds form in an elastomeric sheet. However, the maximum strain resulting from complete folding is not sufficient for tearing. But over time, the rupture caused by rubbing in this type of corrosion is a serious concern. Given that existing hyper-elastic diaphragms are highly susceptible to wear and nonlinear folding, prediction of diaphragm behavior is essential under compressive and sloshing loads to calculate rupture potential, surface strain, folding prevention and accurate failure evaluation. The models must predict the behavior of the hyper-elastic diaphragm against the pressure. The oldest and most commonly numerical methods used to approximate and model large deformation of hyper-elastic materials are finite element analysis (FEA) and structural finite element method (FEM). The finite element analysis method is by far the oldest and most commonly used industry standard method for structural analysis. Mazuch [9] studied the modes of oscillation and natural frequencies for a vertical cylindrical shell by adding the fill fractions of the liquid. He applied both the experimental and the finite element (FE) technical modal calculation. Finite Fourier transformed and Fourier's series expansions were applied by Kyeong and Seong [10] to expand a theoretical approach for the approximation of the natural frequencies of a circular cylindrical shell partly filled with liquid fluid. Tran et al. [11] investigated the liquid–solid coupling, in special the change in natural frequencies and relating mode shapes of an uncovered cylindrical tank, including fluid for the different volume of fluid by experimental and finite element's modal analysis. Zhang Liang et al. [12] used the numerical expansion of asymmetric cylindrical shells, including the sloshing liquid. They applied the finite element's simulation for the oscillation analysis of cylindrical shells. Regarding the free oscillation of fuel, Bauer and Chiba in a cylindrical tank covered with a membrane developed frequency analyses of viscid liquid (Bauer and Chiba [13, 14]). Adam Wisniewski and Robert Kucharski [15] numerically studied the eigenresponse of heavy fluid and gas reservoir rectangular tanks. An extensive literature survey on the challenge of FSI particularly the sloshing phenomenon for partly loaded fluid tanks was created by Ribouillat and Liksonov [16]. Sances [17] developed a numerical model analysis for diaphragm spherical tank. The simulation, however, indicates the ability to interact with the liquid–solid couplings, but the liquid response when limited by a diaphragm is realized to be more influenced by the viscoelastic behavior of the diaphragm and the influence of increased stiffness on the fluid–diaphragm coupling. These excesses the usual sloshing frequency of the interacted structure. Curadelli [18] offered a finite element simulation considering the interacting between liquid and solid for calculating the vibration characteristics of raised spherical tanks exposed to horizontal support movement, and the finite element responses were verified versus the experimental ones. Lou and Chen [19] studied the wave elevation on the free surface with a horizontal excited acceleration and a vertical excited acceleration and give the wave elevation errors. They depicted the sloshing modes for standing waves with different frequencies and time. Guan [20] presented new approach of study in sloshing field of research by using optimization method to provide optimal control in the design of the board shape. Hassan Jalali and Fardin Parvizi [21] expanded a numerical simulation to investigate the modal specifications of a cylindrical reservoir tank and pipe. In this model, the influences of fluid on the modal specifications of fluid-comprising systems are studied in an experimental and numeric manner. Levin [22] compares numerical soft body deformation simulations to experimentally results gained from 3D scans of an elastomer diaphragm. Tao et al. [23] for proving SMP diaphragm (shape memory polymer) capabilities analyzed the diaphragm inversion and recovery behavior by using a nonlinear finite element method and investigated the influence of structural and temperature parameters on the diaphragm inversion process and optimal diaphragm design. Sabaghzadeh et al. [29] investigated the excitation specifications of the diaphragm tank under vertical vibration, by numerical method, and verified the results with experimental tests.

A review of past studies shows that research on elastomeric diaphragm modeling is very restricted. In fact, while there are multitude models for fluid–structure interaction (FSI), studies in which a detailed numerical model is developed to investigate elastomeric diaphragm behavior are very limited. Linear and at different filling volume ratios and acceleration situations can cause large deformations resulting in folding and bending patterns. This complicates the subject and makes it difficult for researchers to perform. Numerical methods available to calculate large deformations under large time steps are highly sensitive to numerical divergence, making these methods often costly. Therefore, there is sufficient incentive to model diaphragm behavior to improve the status quo. On the other hand, manufacturing companies are now because of corrosion concerns, optimum performance in slosh control and reduced production costs use diaphragms with constants thickness [about 0.06 inches (1.52 mm)] that are not the same size as the tank. Because of the growing concern about the weight of structural components in spacecrafts, diaphragm weight loss is desirable. For current medium size tanks, the diaphragm weight is approximately 4.5 lbf, which is clearly much heavier than other slosh control devices. This weight can be substantially reduced. Experimental studies have shown diaphragm deformations in 16-inch tanks to be almost non-fold but less stable in 40-inch tanks. Both of these situations mean that the damping system with significant and the damping system prone to folding, rubbing, and ultimately failing are not desirable. Currently, there is no optimized diaphragm. The optimized diaphragm thickness tank can be used in tanks of similar size and shape, thus optimizing the diaphragm thickness, reducing weight, manufacturing and launch costs, and increase the reliability of the diaphragm. Therefore, reducing the diaphragm mass is an important goal. In this study, new method is provided to analyze deformation of diaphragm tanks by using numerical techniques. Also, the investigation method is verified by using experimental methods. The main purpose of this study is to provide modeling method for industrial diaphragm to predict the nonlinear behavior of hyper-elastic diaphragms as well as the occurrence of folding and tearing due to slosh conditions. For this purpose, first large deflection bending plate theory is reviewed, and then, a numerical study is performed to investigate the motion of the diaphragm in a 16.5-inch diameter (200.5 mm) spherical tank. The spherical diaphragm of the AF-E-332 hyper-elastic with a thickness of 0.07 inch (1.8 mm) is used as the test diaphragm. In this process, the geometrical shape of the structure is first designed in the Solid Works software, and then, ANSYS Workbench software was used for numerical analysis. Next, numerical dynamical models built in ANSYS software are validated with experimental results. For this purpose, the results of three-dimensional scanning experiments of a 16.5-inch similar tank with an elastomeric membrane of AF-E-332 with a thickness of 0.07 inches were used at the University of Florida (Levine [22]). After validation and reliability of the numerical models, the second case study is done to determine the possibility of reducing the elastomeric diaphragm thickness according to the strain energy variation and natural frequency of the diaphragm. In the next section, algorithm and software for optimal automatic modeling of diaphragm tanks are proposed. In the final section, conclusions and discussion are summarized.

2 Introducing of hyper-elastic materials

Generally, the behavior is beyond the tensile behavior of custom engineering materials that the material in accepting large deformations of matter does not undergo elastic deformation called hyper-elastic behavior. Rubbers and polymers have the nearest tensile behavior to an ideal hyper-elastic material. In hyper-elastic materials, the stress–strain relationship in the elastic region is nonlinear. Hyper-elastic materials can retain their elastic properties against large strains. Hyper-elastic behavior is very close to ideal rubber behavior. That is, when deformed at a constant temperature, stress is only a function of current strain and independent with history of loading rates. Their bulk modulus is competitive with metals but is very weak against shear stresses, and its shear modulus is negligible compared to most of the metals. In hyper-elastic materials, the shear modulus is dependent on temperature, and with increasing temperature, they become more resistant to shear. The hyper-elastic materials are isotropic, and their stress–strain relations are independent of the coordinate system. Apart from industrial applications in biomechanics, where the construction of artificial heart valves, artificial cartilage, and even artificial skin and gingiva uses hyper-elastic materials, the use of hyper-elastic materials in aerospace science is also very important. Figure 3 shows the difference between the behavior of the elastic and the hyper-elastic material.

Fig. 3

The difference between the behavior of the elastic and the hyper-elastic material

Because large deformations in elastomeric materials cause large strains (approximately 100% or more) under small loading conditions, Hook's law predicts only linear strains for less than 5 to 10%. Therefore, predicting the behavior of elastomeric diaphragm under large deformation by linear elastic theories is not accurate. As a result, the stretch of the diaphragm material is classified as nonlinear and must be simulated as hyper-elastic material, known as a Green elastic material Beer [24]. Various models have been proposed to describe the behavior of hyper-elastic diaphragm at different periods, each of which has its own characteristic and most utilizes potential strain energy to calculate the material's behavior. The hyper-elastic diaphragm is a subset of Cauchy elastic materials, meaning that the stress is a function of its displacement value and initial position, but unlike Cauchy elastic materials, it retains the value of work done by the stress. The hyper-elastic diaphragm is completely or almost incompressible and can completely recover its deformation. In the hyper-elastic diaphragm, the force–deformation manner of a given function (the function between two physical values) every time follows the strain energy density function. The general form of the strain energy function is obtained by experimental tests. The strain density function is defined by the strain potential energy W, and C_i is related to the three strain constants of the tensile ratio (and sometimes the volume ratio J). Also, N is the number of order in model of strain energy density function. In the relation (1), the energy function is shown.

$$W=\sum_{i=1}^{N}{c}_{i0}({{I}_{1} - 3)}^{i}+\sum_{k=1}^{N}\frac{1}{{d}_{k}}({J - 1)}^{2k}$$

(1)

The strain constants are calculated by strain ratios. The strain ratio, λ, is the ratio of the current length (deformed length) of the element L to the non-deformable length (initial length) L₀. The strain ratio λ is a function of the engineering strain ε_E, shown in relationship (2)

$$\lambda = = \frac{l}{{L_{0} }} = 1 + \varepsilon_{E}$$

(2)

There are three strain ratios in the three main directions. The ratios λ₁ and λ₂ describe the deformation inside the plane that are perpendicular to each other parallel to the plane, and λ₃ describes the deformation in the normal direction perpendicular to the surface of an element (thickness). Strain ratios are extracted from experimental test data. The experimental tests used to derive the tensile ratios are in four types: uniaxial strain, biaxial strain, shear, and three-axis strain (volumetric). Uniaxial strain to collect deformation data in a main axis, two axis deals with the deformation in the two main axes inside the plane perpendicular to each other, the volumetric deformation to deform in volume deformation (in 3 main directions). The volume ratio J is the ratio of the deformed volume V to the unformed volume V₀ shown in relation (3).

$$J = \lambda_{1} \lambda_{2} \lambda_{3} = \frac{V}{{V_{0} }}$$

(3)

Strain energy function formulas always include strain constants that can be adjusted for a specific material. Strain constants can be calculated using the values of strain ratios. The strain constants are the left constants of the Cauchy–Green displacement tensor. The three strain constants I₁, I₂, and I₃ are shown in relation to 4–6 in three terms.

$${I}_{1}={\lambda }_{1}^{2}+{\lambda }_{2}^{2}+{\lambda }_{3}^{2}$$

(4)

$${I}_{2}={\lambda }_{1}^{2}{\lambda }_{2}^{2}+{\lambda }_{2}^{2}{\lambda }_{3}^{2}+{\lambda }_{3}^{2}{\lambda }_{1}^{2}$$

(5)

$${I}_{3}={\lambda }_{1}^{2}{\lambda }_{2}^{2}{\lambda }_{3}^{2}$$

(6)

The general form of the strain energy function is obtained by experimental tests, and strain energy formulas always contain constants that can be adjusted for a particular material. The use of empirical, statistical (mechanical), or hybrid models is classified. Choosing the best model from the simulated methods depends on several factors. The compatibility of the model with the type of simulation material, the existence and quality of experimental curves (uniaxial, two-axis, shear, and volume) to accurately determine the model parameters, and finally the simplicity of the model and computational cost are the most important factors in determining the model type for simulating hyper-elastic diaphragm. One of the most well-known empirical models for the classification of hyper-elastic materials is the Yeoh model Bridson (Bridson et al. [25]).The Yeoh hyper-elastic material model [26] is a phenomenological simulation for the displacement of nonlinear elastic and approximately incompressible materials such as plastic and rubber. The simulation is formed on Ronald Rivlin's perception that the hyper-elastic attributes of plastic may be explained applying a strain energy density function that is a power series in the I₁, I₂, and I₃ of the Cauchy–Green displacement tensors (Rivlin [27] The Yeoh simulation for incompressible plastic is a dependent only of I₁. For compressible plastics, a function on I₃ is added on. Since a polynomial form of the strain energy density function is applied but all the three invariants of the left Cauchy–Green displacement tensor are not, the Yeoh simulation is also named the reduced polynomial simulation. The main simulation suggested by Yeoh had a cubic shape with only I₁ function and is proper to merely incompressible materials. The strain energy density for this model is written as:

$$W=\sum_{i=1}^{3}{c}_{i}({{I}_{1} - 3)}^{i}$$

(7)

Tc_i are material constants. The value 2c₁ can be explicated as the primary shear modulus. Generalized version of the Yeoh simulation is applied by Selvadurai [28]. This model is expressed as follows:

$$W=\sum_{i=1}^{n}{c}_{i}({{I}_{1} - 3)}^{i}$$

(8)

At n = 1, the Yeoh model reduces to the neo-Hookean model for incompressible materials. For consistency with linear elasticity, the Yeoh model has to satisfy the condition. To calculate the stress in the Yeoh model, it must be derived from the Yen strain energy function relative to the only available strain constant.

$$2\frac{\partial w}{ \partial {I}_{1}}(3)=\mu (i\ne j)$$

(9)

where μ is the shear modulus of the material. When I₁ = 3(λ_i = λ_j = 1)

$$\frac{\partial w}{ \partial {I}_{1}}={C}_{1}$$

(10)

To model hyper-elastic materials using strain energy functions, it is necessary to enter the constants of material Ci in the potential energy function. The constants of the energy function for the material are homogeneous and according to the experimental data extracted from three uniaxial, biaxial, and shear tensile tests, as well as the stress–tension theory relations governing a homogeneous hyper-elastic body under these loads and using how to minimize squares errors are obtained. These constants are related to the shear modulus of the material with a series of specific relationships. These constants are directly related to the shear modulus of the material, and as they increase and decrease, the material becomes harder or softer. Thus, the stability situation for the Yeoh model is 2C₁ = μ and the Cauchy stress for the incompressible Yeoh model is expressed by:

$$s = - P1 + 2\frac{\partial w}{{ \partial I_{1} }}B; \frac{\partial w}{{ \partial I_{1} }} = \mathop \sum \limits_{i = 1}^{n} i C_{i} (I_{1} {-} 3)^{i - 1}$$

(11)

For uniaxial extension in the n1-direction, the principal stretches are λ₁ = λ, λ₂ = λ₃. From in compressibility λ₁λ₂λ_3, we have

$$\lambda_{2}^{2} = \lambda_{3}^{2} = \frac{1}{\lambda }$$

(12)

Thus,

$${I}_{1}={\lambda }_{1}^{2}+{\lambda }_{2}^{2}+{\lambda }_{3}^{2}={\lambda }^{2}+\frac{2}{ \lambda }$$

(13)

The left Cauchy–Green displacement tensor can then be written as:

$$B={\lambda }^{2}{n}_{1}\times {n}_{1}+\frac{1}{ \lambda }({n}_{2}\times {n}_{2}+{n}_{3}{\times n}_{3})$$

(14)

If the directions of the principal stretches are oriented with the coordinate basis vectors, then

$$\sigma_{11} = - P + 2\lambda^{2} \frac{\partial w}{{ \partial I_{1} }} ; \sigma_{22} = - P + \frac{2}{ \lambda }\frac{\partial w}{{ \partial I_{1} }} = \sigma_{33}$$

(15)

Since s₂₂ = s₃₃ = 0, then

$$P = \frac{2}{ \lambda }\frac{\partial w}{{ \partial I_{1} }}$$

(16)

Thus,

$$\sigma_{11} = 2\left( {\lambda^{2} - \frac{1}{ \lambda }} \right)\frac{\partial w}{{ \partial I_{1} }}$$

(17)

The engineering strain is λ-1

$$T_{11} = \frac{{\sigma_{11} }}{ \lambda } = 2\left( {\lambda - \frac{1}{{\lambda^{2} }}} \right)\frac{\partial w}{{ \partial I_{1} }}$$

(18)

Using these definitions and numerical experiments performed in ANSYS software, the Yeoh experimental modeling method was used as the modeling method used for modeling the hyper-elastic diaphragm material due to its stability under pressure-driven conditions.

3 Numerical simulation of spherical diaphragm tank

In this section, the methods for determining the deformation of space spherical diaphragm tank model in the commercial ANSYS workbench 19.2 software will be outlined in detail. This part concentrates on the procedure of simulation development. The modal transient structure capability of ANSYS workbench has enough ability to obtain the deformation characteristics of diaphragm spherical fuel tank.

The transient structural solver needs a geometry file and a material model. The geometry of the diaphragm tank is designed in Solid Works and then imported to ANSYS as a step file. One of the most important aspects of numerical simulation is the precise definition of material's properties in software, especially a thin silicon sheet diaphragm. If hyper-elastic properties of diaphragm material are improperly defined, its capability of large deformations is mostly computationally unstable and causes numerically divergent behavior. A block schematic for the entire ANSYS transient structural simulation is indicated in Fig. 4.

Fig. 4

Block schematic of ANSYS transient structural model

The first step of the numerical transient structural simulation is to construct the diaphragm tank geometry. The geometry and boundary conditions of the spherical tank used for this model according to the actual experimental test tank as mentioned before are generated in Solid Works software and imported into the ANSYS geometry construction tool as STEP file. Figure 5 shows the Solid Works model of the sample diaphragm tank.

Fig. 5

Solid Works model of the sample diaphragm tank

A spherical hyper-elastic diaphragm of 419.21 mm diameter (16.5 inch) is defined as the numerical modeling diaphragm. The diaphragm of semi-spherical shape made of AF-E-332 with 1.77 mm (0.07 inch) thickness is defined to match the thickness used at real space diaphragms tank. The properties of diaphragm of the model tank are listed in Table 1.

Table 1 Specification of diaphragm

The diaphragm height is 155. 7 mm. The image of geometric model of the diaphragm is shown in Fig. 6.

Fig. 6

Geometric model images of elastomer diaphragm

3.1 Transient structure setting for elastomer diaphragm tank

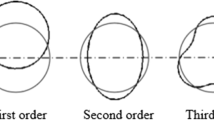
This part explains the development of the elastomer diaphragm simulation in ANSYS Workbench 19.2 for the displacement analysis. Particularly, the simulation is intended for the modeling of the behavior of the semi-spherical diaphragm. The transient structure simulation needs geometry and material model file. One of the most important aspects of numerical simulation is the precise definition of the model materials especially a thin hyper-elastic elastomer diaphragm. Hyper-elastic materials subjected to large displacements are sometimes computationally unstable, if their hyper-elastic model is improperly constructed led to numerically divergent behavior. Material modeling is the most important part of the elastomeric diaphragm simulation. Since the materials are highly deformable, if the diaphragm flexibility property is incorrectly defined, it is prone to divergent behavior in the numerical computation process, and hence, models with large deformations are often needed to reduce time steps in order converged solution. The first part of the Transient Structural Solver input is the material modeling section. The elastomeric diaphragm material model must include a density parameter equal to 1070 kg/m3 for the AF-E-332 material. To solve the hyper-elastic manner of the diaphragm material, the stress–strain curves of the experimental data must be entered into the software. If the experimental data are not available, hyper-elastic models with a simple modulus of elasticity initial tensile test provide acceptable simulation. If experimental data are available, the ANSYS hyper-elastic models require the data of one-way, two-way tensile and shear experimental data. Also, if non-shell elements are applied to create the diaphragm membrane geometry, volumetric data entry is also become essential. When the experimental data are entered into the ANSYS material section, these data can be converted to a specific hyper-elastic model with a suitable curve. Most hyper-elastic models by default in ANSYS, such as the Ogden, Mooney–Rivlin, polynomial, and neo-Hookean, are capable of predicting large transient displacements and are relatively well suited to simulate their regimes effectively. Based on experiments, the proven Yeoh hyper-elastic model has the least instability (divergence) and can be used in shell elements, which has a higher convergence percentage than other models under pressure simulations. Because of these reasons, the Yeoh hyper-elastic simulation was elected to be applied in this study for its stability in pressure-driven situations. The simulation uses the material experimental data from the “Elastomer Sample (Yeoh)” for the material model curve fitting, and this instance data is contained by default in ANSYS 19.2's material library. Due to the ability of the Yeoh model to model hyper-elastic materials under pressurized conditions, these models are still highly unstable. However, in the case of a reversing diaphragm, the deformation is completely pressurized. As previously mentioned, the recommended Yeoh hyper-elastic model, especially the 2nd or 3rd order, should be used. The selected order depends on the quality of the curve fitted to the experimental data. Better curve fitting will improve the results. Model order is effective in fitting a high degree of fit to the curve. Therefore, the order 3 curves are used in this study. To use the Yeoh hyper-elastic model, one must first extract the material constant (s) by fitting the experimental data material data. The number of constants describing the fit of the strain stress data curve is completely dependent on the order and type of the hyper-elastic model. ANSYS software performs this extraction automatically when the experimental data are entered into the model, and the conformity curve is figure out. Using model material data from the “Elastomer Sample (Yeoh)” to fit the material model curve, sample data are included by default in the ANSYS 19.2 material library. When model constancy is estimated, material modeling is perfected. For more information on material modeling and curve fitting in ANSYS, see Material Modeling Reference Manual. Figure 7 shows how to model and derive engineering constant from the Yeoh Model of Level 3.

Fig. 7

The software Yeoh 3rd-order automatic curves fitting from the experimental data

The material model for elastomer AF-E-332 diaphragm should include material parameters, all of which are shown in Table 2. Once the materials' properties are imported in the model, the materials module is completed.

Table 2 Mechanical properties of hyper-elastic diaphragm

Because of alone diaphragm, contact regions are not defined, and then, the geometry should be meshed. In order to increase the mesh quality, the normal curvature angle should be chosen to a maximum of 4.0 degrees, or a smaller angle will result in a smoother grid. The resulting mesh for elastomer diaphragm can be seen in Fig. 8. According to the mesh statistics for this model, totally 101,929 nodes and 50,599 elements are used to mesh the model.

Fig. 8

ANSYS simulation mesh model for elastomer diaphragm

When the mesh grid is created, the transient structural properties are conducted. Moving to the Analysis Settings options, the step end time is defined 3e-2 s and time step is 1e-4 s; auto-time stepping is off and also time integration is on. In the solver controls menu, the solver type should be chosen to “program controlled” by default, large deflection is on and weak springs should be turned off. In nonlinear controls line search is off and stabilization is constant and method is energy activation for first is no. All additional settings are kept by default. The loads and limitations on the simulation should be implemented at this section. A fixed support should be added to surfaces of spherical ring part of the diaphragm to fix it. Fluid–solid interface is added in interior part of diaphragm, and pressure must add to outer surface of the diaphragm. Figure 9 shows the model setting of the semi-spherical diaphragm includes supports, the fluid–solid interface area, and the pressure on the surface.

Fig. 9

Model setting of elastomer diaphragm tank

3.2 Numerical result for elastomer diaphragm tank

The results of deformation of elastomer diaphragm tank in 50% to 100% fill levels of liquid investigated by finite element transient structural analysis capability of ANSYS software are outlined in this part. It is discovered that the volume ratios of fuel affected the folding behavior of elastomer diaphragm tank. Figure 10 shows the deformation of elastomer diaphragm in relating the 100% to 50% fill level of liquid in the tank.

Fig. 10

Deformation of elastomer diaphragm from 50 to 100% (a) 100%, (b) 90%, (c) 80, (d) 70%, (e) 60%, (f) 50%

Six shape modes and amount of deformation elastomer diaphragm tank with liquid level of 100% to 50 are shown in Table 3.

Table 3 Six observed shape modes and amount of deformation diaphragm elastomer tank, η = 80%

4 Experimental method for verification

In order to determine the accuracy of the numerical method, an experimental test was performed with a 3D scan of the AF-E-332 elastomeric diaphragm with a 16.5-inch diameter of 0.07 inches’ thickness. This experimental test was performed by using 3D scanning equipment at the Florida Tech's Institute of Technology (Levine [22]). The experimental tank includes a gas outlet, a liquid inlet, a thick Lexan plastic glass, and an aluminum retaining ring. The retaining platform is made of aluminum 80–20 and can measure up to twice the height to measure the center of gravity. A tank with four springs is mounted on each corner on the platform. Displacement sensors LVDT are located at the corners of the tank to calculate displacements according to changes in the center of gravity. The experimental platform that holds the diaphragm tank is shown in Fig. 11.

Fig. 11

Experimental 3D scanning of 16.5-inch diaphragm tank at 70% fills level (a) gas port, (b) block support for 3D sensors, (c) tank, (d) diaphragm, (e) support frame

The scanning equipment consists of six Xbox 360 Kinect infrared sensors. Each sensor uses a small electric motor that vibrates the sensor and reduces interference with other sensors. Figure 12 shows the three-dimensional scan test image, with 6 Xbox Kinects sensors mounted on the cement blocks and the computer used for 3D scanning.

Fig. 12

Overview of 3D scan test (a) 3D sensors, (b) workstation, (c) block support for sensors, (d) diaphragm tank

The 3D scans are exactly 1 mm wide and cannot capture sharp slits near the diaphragm edge. These difficult topologies at lower levels of liquid filling show greater. Because this decrease in scanning quality is very pronounced at low liquid filling levels, three-dimensional scanning is only performed for filling levels between 50 and 100%. Increase in liquid filling level at each step is 10%. The scanned images were processed by applying the “Kscan3D” software and then imported into MATLAB software. Figure 13 shows an example of a three-dimensional diaphragm scan at 70% fill volume ratio and the same fill volume numerical result.

Fig. 13

Three-dimensional scan image of diaphragm 70% fill volume and the same numerical result

4.1 Comparing results

The results of numerical modeling were compared with experimental results with filling level from 100 to 50% and step increment of 10%. To compare the results of 3D scans obtained from the experimental test and the numerical model, an error function is defined. This function assumes that if the curve of two same levels are perfectly integrated and the space between them is zero, then the amount of error is zero. These suppositions let the percentage of error rates to be defined as the difference area between the two numerical and experimental diaphragm curves divided by the total area under the experimental curve. This equation is shown below.

$${\text{Error}} = \frac{{{\text{offset}}\;{\text{surface}}}}{{{\text{Total}}\;{\text{surface}}}}$$

(19)

Due to too much noise, sharp and deep folds in the diaphragm edges, 3D scanning equipment is not possible because the diaphragm edges cannot be properly scanned at sharp angles, and thus, the edges obtained at different levels of experimental filling are inaccurate. Hence, only 80% of the diaphragm surface center is measured in error calculation and 20% of the edges are ignored. However, all parts of the cross sections are shown in the comparison. Table 4 shows the cross section mode shapes of numerical results in different fill levels.

Table 4 The cross section mode shapes of numerical results in different fill levels

In Fig. 14, the comparison between the numerical simulation and the experimental scanned topology for the 100% fill volume is shown. The measured error between these two levels is 5%.

Fig. 14

Comparison between numerical simulation results and experimental scans of diaphragm at 100% volume ratio

In Fig. 15, the comparison between simulated topologies and experimental scans for 90% fill level is shown.

Fig. 15

Comparison between numerical simulation results and experimental scans of diaphragm at 90% volume ratio

In Fig. 16, the comparison between simulated topologies and experimental scans for 80% fill level is shown.

Fig. 16

Comparison between numerical simulation results and experimental scans of diaphragm at 80% volume ratio

In Fig. 17, the comparison between simulated topologies and experimental scans for 70% fill level is shown.

Fig. 17

Comparison between numerical simulation results and experimental scans of diaphragm at 70% volume ratio

In Fig. 18, the comparison between simulated topologies and experimental scans for 60% fill level is shown.

Fig. 18

Comparison between numerical simulation results and experimental scans of diaphragm at 60% fill volume

Figure 18 shows the difference movement behavior between the two diaphragms is obvious. Numerical topology is not uniform, and cavity appears in center of numerical diaphragm. In Fig. 19, the comparison between simulated topologies and experimental scans for 50% fill level is shown.

Fig. 19

Comparison between numerical simulation results and experimental scans of diaphragm at 50% fill volume

A prominent representation of this difference is shown in Fig. 19 at 50% fill volume, where the experimental diaphragm contains a large narrow deformation and this is very effective in not reversing the numerical diaphragm center shown in Fig. 19. It can be seen that the numerical models predict that the middle part of the diaphragm will be reversed downward and around the center appears the cavity, while experimental data show that the diaphragm remains at this level filling as dome. This difference is probably due to the difference in local resting stiffness between the actual diaphragm and the numerical diaphragm. These differences in local hardness can be due to the production process, the installation process, and the utilizable behavior. Table 5 shows the amount of difference between numerical and experimental results. As shown in Fig. 19 for 50% full filling volume in numerical simulation a slope moves downward while in the experimental scan remaining as dome. For this full filling volume, where there is deep corrosion, there is intense noise at the edge of the tank. This feature can be observed in all different fill volumes. This has an important reason: It simulates numerically a semicircular geometry with constant thickness, while the actual diaphragm surface has varied thicknesses and these differences in geometry changes surface stiffness and affects the behavior of deformation. This property cause to bending in the center area of numerical diaphragm and explains the differences between numerical simulation and experimental data.

Table 5 The amount of difference between numerical and experimental results

Further research by authors has shown that the main reason for this behavioral difference between the results of numerical analysis and experiments at low fill volume ratio is the emergence of a tensile force in the diaphragm body. This force does not appear at the beginning of fluid exit, but gradually with the increase in fluid exit and also increase in gas pressure at body of the diaphragm, this tensile force increases. In order to consider the effect of this tensile force and its effect on the diaphragm behavior, this force was added as a time function just in the center of the diaphragm with a filling volume ratio of 50%, which had the biggest error between experimental and numerical results. Figure 20 shows the time function entered the center of the diaphragm at 50% filling volume.

Fig. 20

The time function entered the center of the diaphragm at 50% filling volume

Figure 21 shows the results of numerical analysis in the diaphragm tank with a filling volume of 50% taking into account the tensile force in the center of the diaphragm.

Fig. 21

The results of numerical analysis in volume of 50% taking into account the tensile force

Figure 22 shows the comparison of the results of numerical and experimental analysis in the volume of 50% filling considering the tensile force in the center of the diaphragm. The new results clearly show that the hole in the center of the diaphragm has disappeared and the numerical results are closer to the experimental results. However, the presence of tensile force in the body in addition to the center of the diaphragm is evident.

Fig. 22

The comparison of the results of numerical and experimental analysis considering the tensile force

Figure 23 shows the comparison between the numerical and experimental results of the diaphragm deformation at a filling volume of 50%, by considering the tensile force at the center of the diaphragm. Although the results show that the error rate between the experimental and numerical results in the filling volume ratio of 50% is reduced and the results of numerical analysis be closer to the experimental results, the presence of tensile force in the body of the diaphragm is evident. Obviously, determining the exact amount and distribution of this tensile force requires a comprehensive study in this regard, and this issue will be considered in future investigations by researchers.

Fig. 23

The comparison between numerical and experimental results of diaphragm deformation at 50% filling volume (a considering tensile force) b not considering tensile force

5 A second case study investigating the reduction of diaphragm thickness

Manufacturing companies are currently using diaphragms with a fixed thickness (about 0.07 inches). Using diaphragm with constant thickness due to concerns about corrosion, performance in controlling turbulence and lower production costs and also increasing weight of structural components in space mission is not proper and decreasing diaphragm mass is desirable. For current medium size tanks, the diaphragm weight is approximately 4.5 lbf, which is clearly much heavier than other propellant management devices (PMD). However, if the diaphragm thickness is appropriate to the tank scale, this weight can be substantially reduced. Diaphragm thickness should be a function of tank size. Experimental studies have shown that diaphragm deformation in 16.5-inch tanks is almost stable, but 40-inch tanks are unstable. Both of these conditions, overweight PMD and PMD prone to folding and instability, are not desirable. Currently, there is no optimized slosh diaphragm. The optimized diaphragm thickness can be used in tanks with a similar size and shape, thus optimizing the design of diaphragm thickness and weight, decrease tanks weight, manufacturing and launch costs, and also increase flight reliability. Therefore, diaphragm mass optimization is an important goal and achieving predictable diaphragm manner while decreasing its mass is important for competitive design especially when the diaphragm structure is applied in space missions.

5.1 Study method

To optimize the diaphragm weight, the strain energy variation diagrams at different fill levels based on different diaphragm thicknesses are used. For this purpose, the initial 16.5-inch diaphragm thickness ranges from 1.778 mm to 1.3 inches reduced and strain energy variations in different filling volumes are calculated in ANSYS software. Figure 24 shows the variation of strain energy at different filling levels at different thicknesses of the diaphragm.

Fig. 24

The variation of strain energy at different filling levels at different thicknesses of the diaphragm

The results of the diagram show that the 16.5-inch diaphragm thickness can be reduced from the initial value of 1.778 to 1.3 mm. Further reduction results in a sharp decrease in strain energy, so the diaphragm thickness can be reduced to 1.3 mm which decreases the weight of the diaphragm and manufacturing costs and, on the other hand, ensures reliable operation during space missions. The effect of thickness on absorbed strain energy was investigated. The study was carried out in the thickness range of 1.3–1.8 mm. It can be seen that as the filling ratio decreases, the adsorbed strain energy increases and more strain energy is absorbed by increasing shell thickness. Therefore, the results of modeling in the studied area are relatively stable and have a reasonable trend. It is noteworthy that in small deformations, the increase in thickness has negligible effect. It has a large amount of energy absorbed, but in large deformations the shell thickness has noticeable effect on the amount of energy absorbed. Figure 25 shows the variation of strain energy at different thickness.

Fig. 25

The variation of strain energy at different thickness

The result from this study shows that in the small deformation range of 80 fill level with an increase of about 1.5 times of the diaphragm thickness, the absorption of strain energy is less than 10%, but the increase in absorbance of strain energy in the large deformation range of 50% fill level is about 80%.

5.2 Natural frequency analysis

In different parts of the space mission, the elastomeric diaphragm tank can be positioned vertically or horizontally and apply a heavy fluid weight to the diaphragm in the case of natural frequencies, and the tensile forces are sufficient to pull the diaphragm out or rub the diaphragm on it selves or against the tank wall, that may weaken or rupture the diaphragm, which may eventually lead to the failure of the space mission. Therefore, it is very important for designers that diaphragm tanks do not reach their natural frequencies. Numerically modeled vibration modes can also predict diaphragm rupture and friction at the normal frequencies of the diaphragm tank. The numerical model designed for the tank was able to model the fluid effect, diaphragm thickness change, and other dynamic properties of the structure and thus could reduce the costly costs of experimental tests [29]. In order to ensure the reduction of the diaphragm thickness on the diaphragm tank frequencies, the diaphragm thickness in a tank with 100% filling volume was reduced from 1.8 to 1.3 at a rate of 0.1 mm and the natural frequencies and mode shapes of the diaphragm tank were calculated. In this process, the Modal acoustics property of ANSYS workbench software was used. This model is specifically designed to simulate the mode shapes and determine the natural frequencies of the diaphragm tank. The Modal acoustics solver calculates the natural frequencies and mode shapes of the diaphragm tank by accurately modeling the materials and geometry of the components of the diaphragm tanks in the fluid–structure interaction environment [29]. Figure 26 shows the geometry of diaphragm tank in 100% volume ratio in ANSYS workbench software.

Fig. 26

The geometry of diaphragm tank in 100% volume ratio in ANSYS workbench

Modeling block of Modal acoustics property in ANSYS workbench software is shown in Fig. 27.

Fig. 27

Modal acoustics model in ANSYS workbench software [29]

In the first step, the mechanical properties of the hyper-elastic diaphragm and other components of the tank must be entered into the software. The mechanical properties of the hyper-elastic diaphragm and other components of the spherical tank are shown in Tables 2 and 6.

Table 6 Mechanical properties of diaphragm tank components [29]

Water has a density and properties similar to hydrazine, which makes it a suitable replacement. The speed of sound in water is 1486 m per second, which is equivalent to bulk modulus of 2.2 GPa. The value of 5-e 8.9 is also used as the viscosity of water. The results of the mode shapes and natural frequencies related to the diaphragm tank with a thickness of 1.8 mm and volume ratio of 100% are given in this section. Figure 28 and Table 7 show the first four modes and the corresponding natural frequencies.

Fig. 28

First four mode shapes of diaphragm tank (a) first mode (b) second mode (c) third mode (d) fourth mode

Table 7 Frequency analysis result of diaphragm tank with 100% filling ratio and 1.8 mm thickness

To optimize the diaphragm weight, the natural frequency diagrams at different modes at 100% fill levels based on different diaphragm thicknesses are used. For this purpose, the initial 16.5-inch diaphragm thickness ranges from 1.8 mm to 1.3 inches reduced and natural frequency in different modes are calculated in ANSYS software. Figure 29 shows the variation of natural frequency at different modes at different thicknesses of the diaphragm.

Fig. 29

The variation of natural frequency at different modes and different thicknesses of the diaphragm

The results of Fig. 29 show that as the diaphragm thickness in the tank decreases, the natural frequencies also decrease in different modes. So that diaphragm thickness can be reduced from the initial value of 1.8 to 1.3 mm. Decreases the weight of the diaphragm, cause to reduce the manufacturing costs and, on the other hand, ensure reliable operation during space missions. The presented results show that modal numerical analysis can be used as an efficient tool to investigate the frequency properties of a diaphragm tank in any ratio of liquid filling volume. This study understands the effect of diaphragm thickness and liquid filling levels on the fuel tank dynamic properties in the design process of fuel tank and prevents resonance in all operational conditions of space missions.

6 Diaphragm tank design algorithm and software based on inversion criterion

As mentioned before, achieving predictable diaphragm behavior while minimizing its natural frequencies and weight is essential for competitive design, especially when used in space missions. In this section, in order to improve the automatic concept design and modeling process of diaphragm tanks, by investigating the numerical and experimental results, the effective parameters in inversion of the hyper-elastic diaphragm were determined. Totally, the diaphragm structure was designed to have minimum weight and natural frequencies under different loading conditions in addition to having maximum resistance to destruction. Based on this, the parameters of diaphragm thickness and height are determined as design parameters and the parameters of radius, pressure, tensile force, and diaphragm material are determined as fixed parameters. In general, the choice of fixed and variable parameters depends on the designer's opinion. Also, the values of weight, strain energy, natural frequencies, displacement, and stress can be determined as objective functions in multi-objective optimization challenge of diaphragm tank design. Also, the parameters of maximum displacement and maximum allowable stress are determined as a constraint of this challenge. The optimal diaphragm is determined using a combination of a multi-objective algorithm with geometry design and analytical software in an integrated environment. Figure 30 shows the algorithm, and Fig. 31 shows the block diagram of the concept of automatic software for designing the diaphragm tanks based on the inversion criterion in the integrated environment of Modefrontier software.

Fig. 30

Algorithm for optimal design of diaphragm tank

Fig. 31

Diagram block of automatic software for designing diaphragm tanks based on inversion criteria

According to Fig. 30 in the design algorithm of diaphragm tanks, thickness and height parameters defined as design parameters and parameters such as radius, diaphragm material, tensile force, and pressure are determined as fixed parameters. After determining the fixed and variable parameters, the multi-objective optimization algorithm is determined; then, based on the specified parameters the geometry of diaphragm created and numerical inverse calculations are performed, and then, the allowable stress values and displacement are controlled; then, the objective functions are calculated, and this process continues until the best design with the lowest value of the objective functions is selected.

According to Fig. 31, thickness and height parameters are defined as design parameters as well as radius, pressure, material, and tensile force characteristics as fixed parameters are entered by the user in Excel software. Also, multi-objective optimization algorithm NSGA-II is defined as multi-objective optimization algorithm in the integrated environment of Modefrontier software. Each time the program is run, the values of design parameters are determined by multi-objective optimization algorithm, and then, both of these design parameter values and fixed parameter values from Excel are entered to MATLAB software. MATLAB software controls the allowable range of these parameters and then transmits the geometric parameters to SolidWorks software and the structural parameters of material, pressure, and tensile force into ANSYS Workbench software. After drawing the geometry, SolidWorks transfers the geometry of diaphragm tank to the ANSYS software. ANSYS software by using the entered geometry and the structural parameters performed inverse calculations and natural frequencies and computed the output results. The multi-objective optimization algorithm controls the defined constraints of deformation and maximum stress and optimizes the objective functions of minimum deformation, minimum weight, minimum strain energy, and minimum natural frequency, and this process continues until the best answer is selected.

7 Consequences

Acquiring science of predicting diaphragm deformation under loading situations is important for lifetime assessment. Existing computational models are only used for simple cases of spherical diaphragms tanks to apply problem simplification assumptions and focus on general-purpose modeling methods. Therefore, these models need to analyze the large deformations caused by the pressure of the hyper-elastic materials. Computational modeling, such as finite element deformation model, relieves these limitations for external use. Using the finite element diaphragm model is a new and advanced method and significantly speeds up computational calculations. In addition, the use of these simple techniques in deformation modeling techniques has accelerated the speed of modeling process and improved accuracy, allowing for rapid simulation of diaphragm status in fluid sloshing. On the issue of increasing accuracy, the method of calculating the bending forces resulting from finite element deformation, performing experiments with different systems for considering bending forces, increases the predicting capability of nonlinear bending behavior; as a result, the numerical displacement simulation is able to predict the displacement with much less error. The improvement of displacement method is very valuable for the analysis of slosh diaphragm, and its most important applications are realistic computation of stiffness of diaphragm. On the other hand, the case study two shows that reducing diaphragm thickness is possible and reducing weight and manufacturing cost of the diaphragm tanks. According to this case study in the small deformation range of fill level with an increase of the diaphragm thickness, the absorption of strain energy is negligible, but the increase in absorbance of strain energy in the large deformation range of fill level is very noticeable. Also, by decreasing diaphragm thickness the natural frequency of diaphragm tank is reduced. Also, the development of algorithms and software introduced for automatic optimal design of diaphragm tanks based on numerical methods performed in this manuscript has improved the modeling process of these kinds of tanks and is an effective step in the performance of diaphragm tank design.