1 Introduction

The idea of artificial freezing originates from seasonal ground freezing under natural conditions. Artificial frozen soil has high bearing capacity and strong water sealing capacity, which fully meets the requirements of temporary ground support in underground structure construction. Therefore, artificial ground freezing technology has been rapidly adopted by many countries and applied to the construction of coal mine shaft [1]. Meanwhile, with the acceleration of urbanization, in order to alleviate the pressure of land traffic, people gradually turn their attention to the development of urban underground space. In the 1990s, artificial horizontal freezing reinforcement technology was successfully applied in many tunnel construction sections of Shanghai Metro line 1, line 2 and Beijing Metro “Fu-Ba” line [2]. In the past 20 years, China’s coastal cities such as Guangzhou, Shenzhen, Nanjing, Suzhou and Nantong have constantly broken the record of artificial horizontal freezing length, making China’s artificial freezing technology leap to the world’s leading level [3]. However, the thawing settlement caused by the melting of horizontal frozen wall in the subway tunnel construction has always been the focus of the engineering research.

During the natural thawing of horizontal frozen wall, the temperature of frozen soil rises continuously, the ice crystals in frozen soil gradually thaw, and its volume reduces. At the same time, under the joint action of overlying soil and surface surcharge, the soil consolidates and compresses. The resulting comprehensive effect is thawing settlement [4]. Research shows that the volume expansion of soil during freezing is about 9% [5]. Therefore, the thawing settlement of frozen soil during natural thawing of freezing wall is considered as the reverse process of soil volume expansion, which is generally characterized by thawing settlement coefficient [6]. At present, in the study of consolidation and compaction settlement of thawed soil, the laboratory test only uses the compaction coefficient [7] to characterize the macro-phenomenon and does not consider the water migration in the thawed soil. In 1925, Terzaghi put forward the principle of effective stress, established Terzaghi’s theory of saturated soil consolidation and quantified the calculation method of soil consolidation settlement. He thinks that the soil can be compressed and deformed in one direction, and the water in the soil flows in one direction according to Darcy’s law. Then, Nixon [8] applied the theory to the thawing compression test of artificial frozen soil, combined with the power function of thawing front changing with time, established the time-dependent function of effective stress in thawed soil and calculated the consolidation settlement displacement of thawed soil. The thawing of artificial horizontal frozen wall can be considered as a two-dimensional problem [9], as shown in Fig. 1, so the soil consolidation theory still has a certain applicability in the study of this problem.

Fig. 1
figure 1

Simplification of thawing model

Full size image

In addition, there are many methods predicting the ground surface settlement, such as artificial neural network method [10], artificial bee colony algorithm [11], Peck method [12] and stochastic medium theory [13]. Artificial neural network method and artificial bee colony algorithm are more inclined to evaluate the risk of ground surface collapse, while Peck method is put forward based on the concept of soil loss. Obviously, stochastic medium theory is more suitable for the prediction of ground surface thawing settlement because the thawing settlement process of artificial horizontal freezing wall is regarded as a random process. Yang et al. [14] analyzed the surface movement and deformation caused by several tunnel construction methods, such as precipitation method, freezing method, extrusion shield method, compressed air method, and proposed a feasible prediction method of surface settlement based on the stochastic medium theory. Ning [15] predicted the ground thawing settlement caused by freezing construction of a side passage of Shanghai Metro pearl line, and compared it with the measured deformation data. The predicted vertical surface deformation curve is consistent with the measured data curve, which fully proves the practicability of the stochastic medium theory ground thawing settlement prediction model. Liu et al. [16] combined the soil pressure and thawing settlement coefficient with the stochastic medium theory to predict the surface settlement caused by the freezing method construction of a subway tunnel side passage, and drew a conclusion with reliable engineering application value. Shi et al. [17] used stochastic medium theory and soil consolidation compaction theory to analyze the settlement and deformation of the stratum in the dewatering stage of dewatering well before tunnel construction, and concluded that the closer the dewatering well is to the tunnel, the greater the settlement value of the stratum. Furthermore, Shi et al. [18] used the same analysis method to predict the settlement, inclination and deformation of soil in the disturbed area of tunnel pipe jacking construction, which provided guarantee for the formulation of effective settlement control measures at the construction site. Cai et al. [9, 19,20,21,22,23] introduced the power function of thawing front changing with time in the study of thawing process of horizontal frozen wall, assumed that the natural thawing transient temperature field of frozen wall conforms to the plate thawing theory, and the forced thawing conforms to the single tube thawing theory, and improved the calculation method of average temperature of frozen wall under forced thawing. Taking the stable settlement of one-dimensional frozen soil melting as the upper and lower limits of double integral of stochastic medium theory, a diachronic prediction model of surface settlement is established. The model has good response to the thickness of frozen wall, tangent value of soil main influence angle, tunnel depth, melting and compaction coefficient, and can reflect the real process of surface settlement more accurately. Wu [24] thinks that the displacement of the bottom soil is not zero in the convergence process of the tunnel excavation section, and verifies it by using the stochastic medium theory. It is found that the convergence law of the tunnel excavation section obtained by this convergence model is more practical than that obtained by the uniform convergence model. Li et al. [25] assumed that the soil loss at the variable cross section of the tunnel is linear, and established the calculation model of the surface settlement and horizontal displacement at the variable cross section of the tunnel through the stochastic medium theory. The calculation results show that the slope of the surface settlement curve at the variable cross section increases with the increase in the ratio of the tangent of the main influence angle of the stratum to the buried depth of the tunnel, and the application scope of stochastic medium theory in tunnel engineering is further expanded.

In the process of predicting the surface deformation of tunnel construction, the above stochastic medium theory has drawn some meaningful conclusions, but it has not analyzed the consolidation of thawed soil due to the self-weight stress of overlying soil layer and surface surcharge during the thawing period of tunnel horizontal frozen wall. In view of this, this paper further optimizes the ground surface settlement diachronic prediction model proposed by Cai et al. [9], aiming to solve the problem of conservative prediction of the original model. Besides, different from the modeling ideas of Cai et al., this model focuses on reflecting the phenomena of the thawing of frozen soil and consolidation of thawed soil during the melting of horizontal frozen wall.

Specifically, before the theoretical derivation, the thawing model is simplified, as shown in Fig. 1. This paper takes a two-dimensional section of horizontal frozen wall to study the ground surface settlement caused by the thawing of frozen soil and the consolidation of thawed soil. It combines the unidirectional consolidation theory of thawing soil with stochastic medium theory, so as to obtain the ground surface thawing settlement law more in line with the engineering practice. It will provide a theoretical calculation model for the ground surface thawing settlement during the tunnel construction using artificial ground freezing technology (AGF).

2 Consolidation theory of soil

2.1 Average degree of consolidation

Terzaghi studied the variation law of excess pore water pressure with time by exerting full pressure on saturated clay layer, established the basic differential equation of one-way consolidation and obtained the analytical solution under certain initial and boundary conditions, which has been used up to now. It is assumed that only one-dimensional vertical consolidation occurs in the soil in the melting zone. After the beginning of drainage consolidation, the pore water pressure at the same point at different times is different, and at the same time, the pore water pressure at different positions of the stratum is also different. Therefore, the pore water pressure (u) is a function of time (t) and coordinate (Z), namely \(u = u(Z,t)\).

The basic differential equation of one-way consolidation established by Terzaghi is as follows:

$$\frac{\partial u}{{\partial t}} = C_{v} \frac{{\partial^{2} u}}{{\partial z^{2} }}$$
$$C_{v} = \frac{k}{{\gamma_{w} }}\frac{1 + e}{{\alpha_{v} }}$$
(2)
$$\alpha_{v} = \frac{{e_{1} - e_{2} }}{{p_{1} - p_{2} }} = \frac{\Delta e}{{\Delta p}}$$
(3)

where Cv is the consolidation coefficient of soil layer; k is the permeability coefficient of soil layer; γw is the volumetric weight of pore water; αv is the compressibility of soil layer; e is the void ratio of the micro unit; e1 is the void ratio under the condition of stress p1 on the compression curve; e2 is the void ratio under the condition of stress p2 on the compression curve; Δe is the change of soil void ratio; and Δp is the change of soil stress.

Combining initial condition with boundary condition (\(u(Z,0) = u_{0}\),\(u(0,t) = 0\),\({{\partial u} \mathord{\left/ {\vphantom {{\partial u} {\partial t}}} \right. \kern-\nulldelimiterspace} {\partial t}}(H,t) = 0\)), Eq. (1) can be solved by the variable separation method; then, the particular solution is obtained by substituting the initial value condition (\(u_{0} = \gamma_{w} Z\)).

$$u\left( {Z,t} \right) = \sum\limits_{m = 1}^{\infty } {\frac{{8\gamma_{w} h_{0} }}{{m^{2} \pi^{2} }}} \exp \left( { - m^{2} \frac{{\pi^{2} }}{4} \cdot \frac{{C_{v} t}}{{h_{0}^{2} }}} \right)\sin \left( {\frac{m\pi }{{2h_{0} }}Z} \right)$$
(4)

where m is an odd positive integer (1, 3, 5 ·······); u0 is the initial pore water pressure; and h0 is the depth of precipitation. The meaning of other symbols is the same as before.

The stress of each point in the soil layer caused by drainage consolidation is not the same, and the consolidation degree of each point is also different. In practical application, the average degree of consolidation (Ut) can be used to calculate.

$$U_{t} = \frac{{U_{0} - U(Z,t)}}{{U_{0} }} = 1 - \frac{{U_{0} }}{U(Z,t)} = 1 - \frac{{\int_{0}^{{h_{0} }} {u(Z,t)dZ} }}{{\int_{0}^{{h_{0} }} {u_{0} dZ} }} = 1 - \frac{32}{{\pi^{3} }}\exp \left( { - \frac{{\pi^{2} }}{4} \cdot \frac{{C_{v} t}}{{h_{0}^{2} }}} \right)$$
(5)

2.2 Consolidation compaction function

Figure 2a shows the one-dimensional drainage-consolidation model, which only reflects the change of the vertical water level and displacement; however, the two-dimensional drainage-consolidation model is considered for the thawing settlement during the thawing of tunnel horizontal frozen wall, as is shown in Fig. 2b. Through coordinate system transformation, the precipitation depth (h0) and initial water level depth (H0) can be transformed into:

$$h_{0} = \left( {R_{1} - R_{0} } \right)\sin \theta$$
(6)
$$H_{0} = h - R_{1} \sin \theta$$
(7)
Fig. 2
figure 2

Drainage-consolidation model: a one-dimensional; b two-dimensional

Full size image

The consolidation displacement component (ds(η1,t)) generated by the drainage consolidation of micro unit soil (dεdη) at time t is shown as follows:

$$ds(\eta_{1} ,t) = \frac{{\alpha_{v} \Delta p}}{{1 + e_{0} }}d\eta_{1}$$
(8)
$$\Delta p = U_{t} \gamma_{w} (\eta_{1} - H_{0} )$$
(9)

where e0 is the initial void ratio before consolidation and η1 is the depth from the center of micro unit to the ground surface.

Then, the unit consolidation compaction function G(η1, t) of the thawed soil is shown as follows:

$$G(\eta_{1} ,t) = \frac{{ds\left( {\eta_{1} ,t} \right)}}{{d\eta_{1} }} = \frac{{\alpha_{v} U_{t} \gamma_{w} (\eta_{1} { - }H_{0} )}}{{1{ + }e_{0} }}$$
(10)

It can be considered that the micro unit soil has no lateral deformation after drainage consolidation, and the volume compression caused by drainage consolidation of the micro unit soil at the depth of η1 is G(η1, t)dη1.

3 Diachronic prediction model of thawing settlement

Before the horizontal frozen wall thaws naturally, the circular cylindrical frozen wall with outer radius of R1 has been formed around the tunnel. In the general horizontal freezing project of tunnel, the soil temperature at the excavation boundary is negative. Therefore, the inside radius of frozen wall can be considered as R0 (the outside radius of tunnel lining), and the effective thickness of the frozen wall is R1-R0. The inner edge radius of the frozen wall changes with the increase in thawing time (t) due to the heat exchange between the frozen wall and the tunnel lining. Specifically, the radius of the thawing inner front is R1(t), the inner edge of the frozen wall gradually thaws from R0 to Ra(t), and then consolidation to Rb(t). The inner thawing shrinkage region is Δa(t), and the inner consolidation region is Δb(t), as shown in Fig. 3a. The outer edge radius of the frozen wall changes with the increase in thawing time (t) due to the heat exchange between the frozen wall and the external stratum. Specifically, the radius of the thawing outer front is R2(t), the outer edge of the frozen wall gradually thaws from R1 to Rc(t), and then consolidation to Rd(t). The outer thawing shrinkage region is Δc(t), and the outer consolidation region is Δd(t), as shown in Fig. 3b. In all, the accumulated thawing displacement and consolidation displacement of the stratum together reflect the thawing settlement of ground surface.

Fig. 3
figure 3

Coordinate system transformation of frozen wall: a inner edge frozen wall; b outer edge frozen wall

Full size image

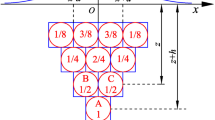
As can be seen from Fig. 4, when the ball A is removed, ball B or C will fill its space with a certain probability. Correspondingly, the upper balls will fill the empty space downward in turn; therefore, the behavior can be described by the following probability expression.

$$\frac{1}{2}P(x - a,z) + \frac{1}{2}P(x + a,z) = P(x,z + h)$$
(11)
Fig. 4
figure 4

Stochastic medium model

Full size image

Transforming the above equation by Lagrange mean value theorem, when a and h infinitely tend to zero, we can obtain the following differential equation.

$$\frac{1}{2}\frac{{\partial^{2} P(x,z)}}{{\partial x^{2} }} = \frac{\partial P(x,z)}{{\partial z}}$$
(12)

Giving Eq. (12) practical engineering meaning,

$$B(z) \cdot \frac{{\partial^{2} S(x,z)}}{{\partial x^{2} }} = \frac{\partial S(x,z)}{{\partial z}}$$
(13)

where B(z) is the coefficient of soil heterogeneity and S(x, z) is the vertical displacement.

According to the actual working conditions, the boundary condition can be expressed as:

$$S(x,0) = \delta (x)$$
(14)

where δ(x) is the subsidence function of ground surface, which approximates a Gaussian curve.

Thus, the special solution of Eq. (13) is as follows.

$$S_{e} (x,z) = \frac{1}{r(z)}\exp \left[ { - \frac{\pi }{{r^{2} (z)}}x^{2} } \right]$$
(15)
$$r(z) = \frac{\eta - z}{{\tan \beta }}$$
(16)

where Se(x, z) is the vertical settlement of micro unit with the coordinate of (x, z), r(z) is the radius of the vertical settlement, η is the depth from the center of the micro unit to the ground surface, and β is the main influence angle of soil layer.

The main influence angle (β) is related to the cohesion and the internal friction angle of soil layer. According to Terzaghi’s loose earth pressure theory, the shear plane with the angle of (45°-φ/2) along the horizontal direction is formed in the process of stress transfer of soil particles through mutual friction and sliding. Shi et al. [26] optimized the calculation method of the main influence angle combining with the retaining wall theory.

$$\beta = 90^\circ - \arctan \left[ {\tan \left( {45^\circ + \frac{\varphi }{2}} \right) + \frac{2c}{{\gamma H}}} \right]$$
(17)

where φ is the internal friction angle of soil; c is the cohesion of soil; γ is the volumetric weight of soil; and H is the buried depth of the soil above the tunnel. For the sandy soil or saturated soft clay with very poor cohesion, that is c = 0 kPa, the main influence angle of the stratum degenerates to β = 45°-φ/2.

Therefore, when z = 0, the ground surface settlement caused by the thawing shrinkage and consolidation compaction of each micro unit in the thawing shrinkage region and consolidation region is S1(x) and S2(x), respectively, based on the stochastic medium theory, during the natural thawing process of horizontal frozen wall.

$$S_{1} \left( x \right) = \frac{\tan \beta }{\eta }\exp \left[ { - \frac{{\pi \tan^{2} \beta }}{\eta }x^{2} } \right]d\varepsilon d\eta$$
(18)
$$S_{2} \left( x \right) = \frac{\tan \beta }{\eta }\exp \left[ { - \frac{{\pi \tan^{2} \beta }}{\eta }x^{2} } \right]G\left( {\eta_{1} ,t} \right)d\varepsilon d\eta$$
(19)

where x is the abscissa of each point on the ground surface in the rectangular coordinate system (εoη (xoz)); dε and dη are the length and width of micro unit.

For the plane problem, the calculation equation of the accumulated thawing settlement displacement caused by the natural thawing of the frozen wall during the horizontal freezing construction of the tunnel is as follows:

$$S\left( x \right) = S_{1} (x) + S_{2} (x)$$
(20)

Taking the rectangular coordinate system εoη (xoz) to the polar coordinate system ro1θ, the conversion equation is as follows:

$$\varepsilon = r\cos \theta$$
(21)
$$\eta = h - r\sin \theta$$
(22)

For the thawing of the inner edge of the horizontal frozen wall, the depth (η1) from the center of the micro unit to the ground surface at the consolidated front is as follows:

$$\eta_{1} = h - R_{b} (t)\sin \theta$$
(23)

For the thawing of the outer edge of the horizontal frozen wall, the depth (η1) from the center of the micro unit to the ground surface at the consolidated front is as follows:

$$\eta_{1} = h - R_{d} (t)\sin \theta$$
(24)

where h is the distance between the tunnel center and the ground surface; r and θ are the polar diameter and polar angle in the polar coordinate system (ro1θ).

The inner radius of the thawing shrinkage region (Δa(t)) of inner edge of frozen wall is Ra(t), and the outer radius is R1(t). The inner radius of the consolidation region (Δb(t)) is Rb(t), and the outer radius is Ra(t). The inner radius of the thawing shrinkage region (Δc(t)) of outer edge of frozen wall is Rc(t), and the outer radius is R1. The inner radius of the consolidation region (Δd(t)) is Rd(t), and the outer radius is Rc(t). According to the exchange equation of double integral, the expressions of thawing displacement and consolidation displacement caused by natural thawing of frozen wall at time (t) are as follows:

$$\begin{gathered} S_{1} (x) = \iint\limits_{{\Delta_{a} (t) + \Delta_{c} (t)}} {\frac{\tan \beta }{{h - r\sin \theta }}}\exp \left\{ { - \frac{{\pi \tan^{2} \beta }}{{(h - r\sin \theta )^{2} }}\left[ {x - r\cos \theta } \right]^{2} } \right\}rdrd\theta \hfill \\ = \int_{{R_{a} (t)}}^{{R_{1} (t)}} {\int_{0}^{2\pi } {\frac{\tan \beta }{{h - r\sin \theta }}} } \exp \left\{ { - \frac{{\pi \tan^{2} \beta }}{{(h - r\sin \theta )^{2} }}\left[ {x - r\cos \theta } \right]^{2} } \right\}rdrd\theta \hfill \\ + \int_{{R_{c} (t)}}^{{R_{1} }} {\int_{0}^{2\pi } {\frac{\tan \beta }{{h - r\sin \theta }}} } \exp \left\{ { - \frac{{\pi \tan^{2} \beta }}{{(h - r\sin \theta )^{2} }}\left[ {x - r\cos \theta } \right]^{2} } \right\}rdrd\theta \hfill \\ \end{gathered}$$
(25)
$$\begin{gathered} S_{2} (x) = \iint\limits_{{\Delta_{b} (t) + \Delta_{d} (t)}} {\frac{\tan \beta }{{h - r\sin \theta }}}\exp \left\{ { - \frac{{\pi \tan^{2} \beta }}{{(h - r\sin \theta )^{2} }}\left[ {x - r\cos \theta } \right]^{2} } \right\}G(\eta_{1} ,t)rdrd\theta \hfill \\ = \int_{{R_{b} (t)}}^{{R_{a} (t)}} {\int_{0}^{2\pi } {\frac{\tan \beta }{{h - r\sin \theta }}} } \exp \left\{ { - \frac{{\pi \tan^{2} \beta }}{{(h - r\sin \theta )^{2} }}\left[ {x - r\cos \theta } \right]^{2} } \right\}G(h - R_{b} (t)\sin \theta ,t)rdrd\theta \hfill \\ + \int_{{R_{d} (t)}}^{{R_{c} (t)}} {\int_{0}^{2\pi } {\frac{\tan \beta }{{h - r\sin \theta }}} } \exp \left\{ { - \frac{{\pi \tan^{2} \beta }}{{(h - r\sin \theta )^{2} }}\left[ {x - r\cos \theta } \right]^{2} } \right\}G(h - R_{d} (t)\sin \theta ,t)rdrd\theta \hfill \\ \end{gathered}$$
(26)

4 Determination of thawing front radius

The solution of the inner and outer front radius (R1(t) and R2(t)) is the key to establish the prediction model of thawing settlement under natural thawing of horizontal frozen wall. Cai et al. [9] solved the transient temperature field of horizontal frozen wall approximately using plate thawing theory, and then obtained the calculation equations of the inner and outer front radius during thawing.

As shown in Fig. 5, assuming the thickness of the frozen wall is infinite, the tunnel lining and the unfrozen soil are thin plates, whose surface have the constant positive temperature (Tb); correspondingly, the soil temperature in the inner and outer thawing regions is Tu, soil temperature in the frozen region is Tf, and all the temperatures are only related to time (t) and coordinate (x). The thawing front is a moving phase transition boundary, its distance from the inner or outer edge of the initial frozen wall is X(t), and the temperature (Tr) at the thawing front is 0℃ during the process of frozen wall thawing from outside to inside.

Fig. 5
figure 5

Schematic diagram of plate thawing theory

Full size image

The differential equations of heat conduction in thawing region and frozen region are as follows:

$$\frac{{\partial T_{{\text{u}}} }}{\partial t} = \alpha_{{\text{u}}} \frac{{\partial^{2} T_{{\text{u}}} }}{{\partial x^{2} }},\begin{array}{*{20}c} {} & {(0 \le x \le X\left( t \right))} \\ \end{array}$$
(27)
$$\frac{{\partial T_{{\text{f}}} }}{\partial t} = \alpha_{{\text{f}}} \frac{{\partial^{2} T_{{\text{f}}} }}{{\partial x^{2} }},\begin{array}{*{20}c} {} & {(X\left( t \right) \le x \le \infty )} \\ \end{array}$$
(28)

where αf and αu are the thermal diffusivity of frozen soil and thawed soil.

$$\alpha_{f} = \frac{{k_{f} }}{{c_{f} \rho_{f} }},\;\alpha_{u} = \frac{{k_{u} }}{{c_{u} \rho_{u} }}$$
(29)

where kf and ku are the thermal conductivity of frozen soil and thawed soil, respectively; cf and cu are the specific heat of frozen soil and thawed soil, respectively; and ρf, and ρu are the saturated density of frozen soil and thawed soil.

The initial uniform temperature of the frozen wall is equal to the average temperature of the frozen wall (Tv) without considering the temperature gradient in the frozen wall; thus, the initial condition of the differential equation is as follows:

$$T_{f} = T_{u} = T_{v} ,\;(t = 0)$$
(30)

The boundary condition of the differential equation is as follows:

$$\left\{ \begin{gathered} T_{u} = T_{b} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(x = 0) \hfill \\ T_{f} = T_{u} = T_{r} = 0\;\;\;\;\;\;\;\;\;(x = X(t)) \hfill \\ T_{f} = T_{v} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(x = \infty ) \hfill \\ \end{gathered} \right.$$
(31)

The heat balance equation at the inner and outer thawing front (X(t)) is as follows:

$$(k_{f} \frac{{\partial T_{f} }}{\partial x} - k_{u} \frac{{\partial T_{u} }}{\partial x})_{x = X(t)} = L\frac{dX(t)}{{dt}}$$
(32)

where L is the latent heat of phase change per unit volume of soil.

Therefore, the temperature distributions in the inner and outer thawing region and frozen region are as follows:

$$T_{u} = T_{b} \left[ {1 - \frac{{\Phi (\frac{x}{{2\sqrt {\alpha_{u} t} }})}}{{\Phi (\frac{B}{{2\sqrt {\alpha_{u} } }})}}} \right]\;\;\;\;\;(0 \le x \le X(t))$$
(33)
$$T_{f} = T_{v} \left[ {1 - \frac{{\Phi (\frac{x}{{2\sqrt {\alpha_{f} t} }})}}{{\Phi (\frac{B}{{2\sqrt {\alpha_{f} } }})}}} \right]\;\;\;\;(X(t) \le x \le \infty )$$
(34)

where Φ(y) is a Gaussian error function, and it can be shown as follows:

$$\Phi (y) = \frac{2}{\sqrt \pi }\int_{0}^{y} {e^{{ - \eta^{2} }} } d\eta$$
(35)

When x = X(t), Tf = Tu = Tr = 0, it can be found that the thawing front (X(t)) is proportional to the square root of thawing time, namely:

$$X(t) = B\sqrt t$$
(36)

where B is the undetermined constant, satisfying the following equation:

$$\frac{{k_{u} T_{b} e^{{ - \frac{{B^{2} }}{{4\alpha_{u} }}}} }}{{\sqrt {\alpha_{u} } \Phi (\frac{B}{{2\sqrt {\alpha_{u} } }})}} + \frac{{k_{f} T_{v} e^{{ - \frac{{B^{2} }}{{4\alpha_{f} }}}} }}{{\sqrt {\alpha_{f} } \left[ {1 - \Phi (\frac{B}{{2\sqrt {\alpha_{f} } }})} \right]}} = LB\frac{\sqrt \pi }{2}$$
(37)

The thawing front (X(t)) can be calculated by Eq. (37) after determining the thermal conductivity, specific heat and density of frozen soil and thawed soil. The initial outer radius of frozen wall is R1, and the initial inner radius is R0; correspondingly, the radius of the inner and outer thawing front of frozen wall can be obtained as follows:

$$R_{1} (t) = R_{0} + B\sqrt t$$
(38)
$$R_{2} (t) = R_{1} - B\sqrt t$$
(39)

It should be noted that the thawing speed of the inner and outer edges of the frozen wall is different, and the thawing speed of the inner edge of the frozen wall is greater than that of the outer edge [27, 28] under natural thawing conditions in actual engineering. There are many factors affecting the thawing speed of frozen soil, such as the heat exchange capacity [29] and the unfrozen water content [30] of frozen soil, ambient temperature [31] and ventilation [32]. For the tunnel construction using artificial ground freezing technique, the ambient temperature and ventilation around the excavation surface are the main reasons for the different thawing speeds of the inner and outer edges of the frozen wall. In this paper, it is considered to be synchronous due to the lack of quantitative research.

5 Determination of inner radius of thawing shrinkage region and consolidation region

Цытoвич [4] proposed the calculation equation of stable settlement of frozen soil thawing based on the indoor compression test of natural frozen soil:

$$S = \varepsilon_{th} h_{r} + \varepsilon_{a} ph_{r}$$
(40)

where S is the stable settlement of the thawed soil; hr is the thickness of thawed soil; p is the external load of thawed soil; εth is the thawing settlement coefficient of frozen soil; and εa is the compaction coefficient of thawed soil.

The external load (p) is approximately considered as the self-weight of the overlying soil of the tunnel without considering the ground surface overload.

$$p = \gamma h$$
(41)

where γ is the average volumetric weight of each soil layer over the tunnel; h is the distance between the tunnel center and the ground surface.

The vertical settlement of soil can be considered as the sum of the settlement of all micro units in the region, so the inner radius of thawing shrinkage region of the inner edge of frozen wall is:

$$R_{a} (t) = R_{1} (t) - \int_{{R_{0} }}^{{R_{1} (t)}} {\varepsilon_{th} } dr$$
(42)

The inner radius of consolidation region of the inner edge of frozen wall is:

$$R_{b} (t) = R_{a} (t) - \int_{{R_{0} }}^{{R_{a} (t)}} {\varepsilon_{{\text{a}}} \gamma h} dr$$
(43)

The inner radius of thawing shrinkage region of the outer edge of frozen wall is:

$$R_{c} (t) = R_{1} - \int_{{R_{2} (t)}}^{{R_{1} }} {\varepsilon_{th} } dr$$
(44)

The inner radius of consolidation region of the outer edge of frozen wall is:

$$R_{d} (t) = R_{c} (t) - \int_{{R_{2} (t)}}^{{R_{c} (t)}} {\varepsilon_{a} \gamma h} dr$$
(45)

6 Case analysis

Figure 6 shows a full section tunnel construction project using artificial ground freezing technology (AGF) [33,34,35]. The geological survey report shows that the soil property of the tunnel construction stratum is sandy clay, its cohesion (c) is 0 kPa, and internal friction angle is 12.68°. According to Eq. (17), the main influence angle (β) is 38.66°; correspondingly, the tangent value of main influence angle is approximately 0.8. In addition, the structural dimension parameters of tunnel are shown in Table 1, the physical structural parameters of soil are shown in Table 2, and the thermophysical parameters of thawed and frozen soil are shown in Table 3.

Fig. 6
figure 6

Case calculation model diagram

Full size image
Table 1 Structural dimension parameters of tunnel
Full size table
Table 2 Physical structural parameters of soil
Full size table
Table 3 Thermophysical parameters of soil
Full size table

Besides, the ground surface monitoring distance is approximately set as 20 m on the left and right bounded by the tunnel centerline, whose computing method comes from the equation of D = h/tanβ, and this distance also be used as the calculation range of theoretical prediction model. A total of nine ground surface displacement monitoring points (S1 ~ S9) are set in this case, and the space between adjacent two points is 5 m.

The thawing front (X(t)) can be obtained by substituting “Tb = 15℃,” “Tv = -− 10℃,” and the thermophysical parameters into Eqs.(36) and (37):

$$X(t) = 127.8\sqrt t \;mm$$
(46)

The time (tj) of the horizontal frozen wall completed natural thawing is as follows:

$$t_{j} = \left( {\frac{2350}{{2 \times 127.8}}} \right)^{2} = 85d$$
(47)

The inner thawing front radius of frozen wall is as follows according to Eq. (38):

$$R_{1} (t) = 3000 + 127.8\sqrt t \;mm$$
(48)

The inner radius of thawing shrinkage region of the inner edge of frozen wall is as follows according to Eq. (42):

$$R_{a} (t) = 3000 + 0.99 \times 127.8\sqrt t \;mm$$
(49)

The inner radius of consolidation region of the inner edge of frozen wall is as follows according to Eq. (43):

$$R_{b} (t) = 3000 + 0.9603 \times 127.8\sqrt t \;mm$$
(50)

The outer thawing front radius of frozen wall is as follows according to Eq. (39):

$$R_{2} (t) = 5350 - 127.8\sqrt t \;mm$$
(51)

The inner radius of thawing shrinkage region of the outer edge of frozen wall is as follows according to Eq. (44):

$$R_{c} (t) = 5350 - 0.01 \times 127.8\sqrt t \;mm$$
(52)

The inner radius of consolidation region of the outer edge of frozen wall is as follows according to Eq. (43):

$$R_{d} (t) = 5350 - 0.0397 \times 127.8\sqrt t \;mm$$
(53)

The calculation program of thawing settlement under natural thawing condition is compiled by Maple software according to Eq. (20). The law of the ground surface thawing settlement is shown in Fig. 7 during the natural thawing period of horizontal frozen wall as the calculation range is taken as -20 m ≤ x ≤ 20 m.

Fig. 7
figure 7

Predictive curve of the ground surface thawing settlement

Full size image

Figure 7 shows that the accumulated thawing settlement displacement of the ground surface gradually decreases with the increase in the horizontal distance from tunnel center during the natural thawing period. The accumulated thawing settlement displacement of ground surface at tunnel center axis is -22.737 mm, -32.022 mm, -38.977 mm, -44.679 mm, -49.552 mm, -53.815 mm, -57.599 mm, -60.991 mm and -62.561 mm after thawing for 10d, 20d, 30d, 40d, 50d, 60d, 70d, 80d and 85d, respectively, while it is only -2.305 mm at ± 20 m away from tunnel centerline after thawing for 85d, which indicates that the influence distance of the ground surface thawing settlement is less than ± 6.7 R0 when the horizontal frozen wall completely natural thaws.

Cai et al. [9] also predicted the thawing settlement displacement of the same project, but there was no obvious distinction between the thawing stage and the consolidation stage in their prediction model. In order to reflect the optimization degree of this model in these two stages, the ground surface settlement law of these two models is shown in Fig. 8.

Fig. 8
figure 8

Predictive curve of ground surface settlement: a comparison of Cai’s model and this model; b comparison of thawing displacement and consolidation displacement

Full size image

Figure 8a shows that the variation trend of the ground surface thawing settlement in this model is as same as Cai’s model [9], but the predicted value of this model is generally larger than that of Cai’s model. Compared with the field measured data, the predicted value of Cai’s model is conservative, while the predicted value of this model is closer to the measured data. Specifically, the accumulated thawing settlement displacement in this model is -62.561 mm at the tunnel centerline, while it is -40.700 mm in Cai’s model; subtracting from the field measured value, it is with the difference of 7.610 mm and 14.700 mm, respectively. It also shows that the displacement caused by the consolidation of thawed soil cannot be ignored, and this model has the advantage to describe this stage. In addition, Fig. 8b shows that the displacement generated by the consolidation of thawed soil is less than that generated by the thawing of frozen soil in this model, and the consolidation of thawed soil has hysteresis and timeliness. Specifically, the consolidation displacement is -27.084 mm at the tunnel centerline, while the thawing displacement is -35.476 mm, with the difference of 7.392 mm. The thawing displacement is dominant in the early stage of thawing, while the consolidation displacement begins to generate after the thawed soil existence, which reflects the non-simultaneity of these two displacements. Besides, the consolidation of soil will continue to develop with time after the horizontal frozen wall completely thawing, which is consistent with the conclusion of Wang et al. [36].

The accumulated thawing settlement displacement of tunnel horizontal frozen wall during thawing period is the key factor to judge whether the project site needs to adopt compaction grouting reinforcement, and the ground surface thawing settlement velocity is the key parameter to determine the grouting reinforcement time. Figure 9 reflects the diachronic change law of the ground surface thawing settlement.

Fig. 9
figure 9

Diachronic change curve of the ground surface thawing settlement

Full size image

Figure 9 shows that the thawing settlement velocity of each point of the ground surface is first fast and then slow during the natural thawing period of horizontal freezing wall. For example, the thawing settlement velocity of the ground surface is 2.274 mm/d, 0.928 mm/d, 0.696 mm/d, 0.570 mm/d, 0.487 mm/d, 0.426 mm/d, 0.378 mm/d, 0.339 mm/d and 0.157 mm/d after thawing for 10d, 20d, 30d, 40d, 50d, 60d, 70d, 80d and 85d, respectively. The ground surface has experienced a certain degree of frost heaving deformation in the positive freezing period, so the ground surface has a rapid thawing settlement deformation after thawing for 10 d, which is theoretically considered to be the process of surface displacement clearing, and this stage is considered as the safety period of engineering protection. Besides, the thawing settlement velocity of each point of the ground surface gradually tends to be stable after thawing for 30 d. Therefore, in view of the large deformation of the ground surface during the natural thawing period in the project, it is theoretically considered that thawing for 20 ~ 30 d is the best grouting time.

According to the distribution of ground surface frost heaving, the location of grouting holes shall be reasonably arranged. Besides, it is required to closely monitor the temperature change of temperature measuring holes, and adopt the interval grouting method to ensure the unity of grouting amount and thawing settlement. The grouting pressure is generally set as 2 to 2.5 times of the hydrostatic pressure, and the grouting volume is usually 1.15 times [37] that of frozen soil.

In order to further explain the influence of the thawing of frozen soil and the consolidation of thawed soil on the speed of ground surface settlement, the comparison of the diachronic thawing settlement of ground surface at the tunnel centerline is shown in Fig. 10.

Fig. 10
figure 10

Diachronic change curve of ground surface settlement: a comparison of Cai’s model and this model; b comparison of thawing displacement and consolidation displacement

Full size image

Figure 10a shows that the thawing settlement velocity of this model is significantly higher than that of Cai’s model [9] at the tunnel centerline. For example, the thawing settlement velocity of this model is 2.274 mm/d after natural thawing for 10 d, while it is 1.390 mm/d of Cai’s model. There is a certain gap between them and the velocity of the field measured data (2.05 mm/d), but the velocity is closer to this model. In addition, Fig. 10b shows that the curvature of thawing displacement and consolidation displacement is almost the same within 20 days of natural thawing at the tunnel centerline. Besides, the consolidation displacement is obviously smaller than the thawing displacement after natural thawing for 20 d, and the change rate of consolidation displacement is slow, with an average value of 0.173 mm/d, while the change rate of thawing displacement is fast, with an average value of 0.298 mm/d. The thawing displacement will finish with the horizontal frozen wall completely thawing, while the consolidation displacement will continue at a lower settlement rate for a long time (Table 4). Therefore, the accumulated thawing settlement displacement of the stratum is further increased after considering the consolidation of the thawed soil, which is helpful for the project site to predict in advance and take the compaction grouting measures to control the thawing settlement.

Table 4 Gauss–Legendre integral point
Full size table

7 Conclusion

Based on the research results of Cai et al., a diachronic prediction model of ground surface thawing settlement is established by combining consolidation compaction function with stochastic medium theory considering the thawing of frozen soil and the consolidation of thawed soil during the thawing period of tunnel horizontal frozen wall. Specifically, based on the plate freezing theory, the calculation equations of the inner and outer radius of thawing shrinkage region and consolidation region are established considering the thawing settlement coefficient and compaction coefficient.

(1) The case analysis results show that, firstly, the accumulated thawing settlement gradually decreases with the horizontal distance from the tunnel center gradually increasing during the natural thawing period. The accumulated thawing settlement increases rapidly at the initial stage of thawing, while the accumulated thawing settlement decreases gradually with the extension of thawing time. Secondly, the comparison curve of the thawing displacement and consolidation displacement shows that the thawing displacement of ground surface is greater than the consolidation displacement. The thawing displacement will finish with the horizontal frozen wall completely thawing, while the consolidation displacement will continue at a lower settlement rate for a long time. Finally, the thawing settlement predicted in this paper is larger than that of Cai et al., which indicates that the consolidation settlement in natural thawing period cannot be ignored.

(2) It is suggested that this diachronic prediction method should be adopted in advance to predict the thawing settlement of the ground surface during the natural thawing period of horizontal frozen wall in the design stage of tunnel freezing engineering, and then taking the appropriate compaction grouting measures to reduce the impact of ground surface thawing settlement on the surrounding environment.

8 Data Availability and material

The datasets generated and analyzed during the current study are available from the corresponding author upon reasonable request.