1 Introduction

River floods are one of the most serious disasters worldwide. Amongst the natural catastrophes, floods cause about half of all deaths [44] and a third of all economic losses [3]. The global losses due to river floods are estimated at US$104 billion and are expected to increase with economic growth, urbanization and climatic change [5].

Moreover, floods cause not only short-term consequences such as deaths and economical and material losses, but also long-term diseases, disability and poverty-related diseases [60]. These latter effects may be even more important than other illnesses or injuries because the psychological problems may continue for long after the water has receded [44].

Differently from other hazards, natural flooding is spread around the world and in most of the cases total protection is impossible. Even in developed countries such as France or England, river floods are responsible for dramatic losses (e.g. [6] and [50]. Taking this context into consideration, flood management plays a rather important role in urban planning and the correct modelling of inundation characteristics is of paramount importance. Flood management programs must be defined according to several concepts such as weather forecasts, flood damages, land use, floodplain characteristics and flood control structures. Amongst whole concepts needed to conduct a successful program, the delimitation of the affected area is the most prominent. In most cases, due to the extent of the river to be modelled, 1D simulations are chosen and accordingly conservation laws must be used.

For these reasons, floods have been a concern since ancient times. Earlier civilizations were challenged to deal with flood control [19]. Hydraulic engineers must handle with the above-mentioned issues and they have to take reasonable steps to ensure the success of flood management. At the same time, engineers must promote a form of river training works progressively more sensitive to the environment [23].

The destructive damages of floods were the main reason for extensive research on this theme in the last century.

In the European context, the European Union Floods Directive (Directive 2007/60/EC) reflects the concern of the member states to handle with floods. Each state is required to assess which watercourses are at risk from flooding and to map the inundation extent. They also must take adequate and coordinate measures to reduce the flood risk.

The extent of inundation due to natural floods depends on two main factors: the hydrological regime and the river configuration. The first controls the flow discharge that drains into a certain river reach and can be evaluated from statistical models based on historical data or on the description of the processes associated with the transformation of the precipitation in runoff (e.g. [35]). The main issue of the present work is related to the second factor, namely, the influence of the cross-sectional configuration on the flow structure and therefore on the channel conveyance.

Taking as reference the extended research conducted in compound channels, i.e. when the floodplains are inundated and a complex flow structure is generated, this paper aims at reviewing the main flow mechanisms of overbank flows and consequences in terms of modelling. Moreover, following the work started in Fernandes [18], the paper presents a method to incorporate the concept of apparent shear stress (developed in the interface between the main channel and the floodplains) in the Manning roughness coefficient. In the current state, most of the used hydraulic models worldwide such as HEC-RAS or MIKE 11 do not account for this extra shear stress. With the proposed adaptation of the Manning roughness coefficient, it is expected to improve the discharge prediction of overbank flows. The calibration and validation of the proposed method are conducted taking advantage of a large dataset of experimental data obtained in compound channels.

2 Overview of the mechanisms of overbank flows

It is widely recognized that, when overbank flow occurs, the flow structure becomes much more complex than in a single channel [53]. The interaction between faster main channel flow and slower floodplain flow generates a shear layer in a region near the interface of these two subsections [61] and [10]. In that shear layer, the lateral momentum exchange between the main channel and the floodplains [56] and the secondary currents due to the non-isotropic turbulence [40] lead to a 3D flow structure. The momentum transfer due to the interaction between the two flows was quantified by Myers [37] who showed the importance of such phenomenon for the conveyance of compound channels.

For its wide scope, the UK project, developed in the late 1980s, with the participation of several universities and the H.R. Wallingford, financially supported by the Science and Engineering Research Council (SERC), should be mentioned. This project supported the construction, amongst others, of the Flood Channel Facility (FCF-SERC), a 10-m wide and 50-m-long compound channel [30].

Figure 1 presents the main flow mechanisms that occur in compound channels.

Fig. 1
figure 1

adapted from [56]

Turbulent flow structure in compound channel (

Full size image

The flow structure in straight compound channels was experimentally and numerically studied in the last decades (e.g. [42] and [9]. Much of the research on compound channel flows has been devoted to floodplains with smooth bed (e.g. Knight and Shiono 1991 and [27]. However, as compared to the main channel, floodplains usually present a rougher bottom. They are often covered with vegetation, easily submerged during floods. The effect of submerged vegetation has been extensively studied in single channels (e.g. [32] and [41]. In compound channels, it was experimentally observed that the vegetation in the floodplains strongly affects the compound channel flow (e.g. [66]. In many studies the roughness of the floodplains does not mimic the natural environment. For instance, triangular metal meshes and submerged rods were used in the floodplain by Tang and Knight [59] and by Sun and Shiono [57], respectively. The specific influence in compound channel flows of submerged floodplain vegetation closer to what can be observed in the nature (e.g. grass) was experimentally studied by Pasche and Rouvé [45] and by Yang et al. [66].

Recently, Pradhan and Khatua [47] evaluated the momentum transfer coefficients of compound channels with various roughness which was able to establish a new method to compute the discharge distribution in compound channels. Due to the complexity of the flow mechanisms in compound channels, the flow discharge in these cases at a given flow depth is not as easily predicted as for single channels.

The river system cannot be perceived as limited to the watercourse. A more comprehensive concept of river may also include, for instance, riparian vegetation, wetlands, banks and ponds [39]. For hydraulic engineers, as for the society in general, the ecological protection is an increasing concern. In this framework, the ecological role and the preservation of the riparian vegetation are very much recognized as a crucial issue. As the ecological strata require diversity, a better understanding of hydrodynamics of channels with vegetation is needed. The influence of vegetation corridors on compound channel flows has been studied by Sun and Shiono [57] and by Sanjou and Nezu [51]. These studies deal with the effect of rigid rods in the floodplain edge, at the interface with the main channel, and no considerations on the influence of foliage were made. From studies in a single channel, it is well known that the contribution of vegetation to flow resistance depends strongly on the type and combination of vegetation and exhibits considerable variation in time and space (e.g. [25] and [65]. Despite that, the compound channel experiments with vegetation elements with foliage are still rare in the literature.

Due to the non-prismatic nature of rivers, non-uniform flow in compound channels is the most common situation in nature. In the last decades, several geometries were investigated including skewed compound channels, converging or diverging floodplains (Bousmar et al. 2004 and [12] and meandering channels [46]. In prismatic geometries, the non-uniform flow may be a consequence of: (i) a backwater effect caused by the downstream boundary condition, under subcritical flow, (ii) a change in the water depth caused by the rising or declining phases of a hydrogram, or (iii) a disequilibrium in the upstream velocity distribution between the main channel and the floodplains. Non-uniform flow in compound channels induces the mass transfer between main channel and floodplains. Comparing to uniform flow, it was observed that boundary shear stress, turbulence and secondary flows are strongly affected by the non-uniformity [62].

3 Computation of compound channel conveyance

3.1 Traditional method

The traditional procedure to compute the flow discharge in straight compound channels is the divided channel method (DCM). It proposes the conceptual division of the compound channel following vertical, horizontal or diagonal lines dividing main channel and lateral floodplains. Most hydraulic models (such as HEC-RAS and MIKE 11) use vertical dividing lines. The total discharge, Q, is then evaluated by the sum of the subsection discharges. Using Manning–Strickler equation, this method is described by:

$$Q={\sum }_{i}{Q}_{i}={\sum }_{i}\frac{{A}_{i}{R}_{i}^{2/3}}{{n}_{i}}{s}_{0}^{1/2}$$
(1)

where A is the area, R is the hydraulic radius, n is the Manning roughness coefficient for each subsection, i (i.e. main channel and floodplain) and so is the streamwise slope.

For the DCM, the diagonal division of the compound channel is preferred for the total discharge evaluation, whereas no division gave accurate results for the subsection discharges (e.g. [29] and [1]. The vertical division tends to under predict the floodplain discharge and to over predict the main channel and the total discharges. This inaccuracy is increased for wider and rougher floodplains [63].

Bhowmik and Demissie [4] carried out field measurements in American rivers with a compound section configuration. They separated the effects of the interaction between the main channel and the floodplain flows according to the relative depth (relation of the floodplain and main channel flow depths). For small relative depths, due to the vegetation in the floodplains, in some cases the discharge in the floodplains is extremely low and they can be considered as a storage area. For higher relative depths, the floodplains contribute effectively for the total discharge.

Seckin [52] applied four prediction methods to laboratory experimental data with fixed and mobile beds in the main channel. As two methods included the effects of the interaction between the main channel and the floodplain flows, they gave better results than the traditional methods. Despite that, absolute error between the calculated and the observed discharge of approximately 10% was found. With a mobile bed in the main channel, all the methods failed to accurately predict flow discharge.

Hin et al. [20] presented a field study including the stage–discharge relation and bed roughness for three Malaysian rivers with overbank flow. The apparent shear between flows in the main channel and in the floodplains was quantified in terms of an apparent friction factor that was found to be many times greater than the averaged friction factor associated with boundary shear stress. For the three rivers, the DCM with vertical division lines between the subsections led to an averaged over estimation of the total discharge of about 20%.

In a fluvial restoration project, MacWilliams et al. [34] evaluated the effects of a constructed compound channel in the velocity and in the boundary shear stress. Analysing post-project surveys, the authors made clear that the compound channel design reduced the channel incision while achieving the specific geomorphic, ecological and flood conveyance objectives of the restoration project. The authors found that the use of 1D model HEC-RAS (i.e. DCM with vertical divisions) was of very limited value in assessing changes in channel shear stress, resulting from the construction of a compound channel on an incised stream.

3.2 Apparent shear stress

To account for the additional head loss generated by the interactions between the flows in the main channel and in the floodplains, the apparent shear stress method, ASSM [36] and [8], proposes the inclusion of an additional shear stress, \({\tau }_{a}\), acting on the vertical interface between the main channel and the floodplains. The total discharge may be calculated by the sum of the subsections discharges assuming this additional shear stress:

$$Q={Q}_{mc}+{Q}_{fp}={A}_{mc}\frac{{{R}_{mc}}^{2/3}}{{n}_{mc}}{S}_{0}^{1/2}\sqrt{1-\left(\frac{{N}_{fp}{\tau }_{a}{h}_{fp}}{\rho g{A}_{mc}{S}_{0}}\right)}+{A}_{fp}\frac{{{R}_{fp}}^{2/3}}{{n}_{fp}}{S}_{0}^{1/2}\sqrt{1+\left(\frac{{\tau }_{a}{h}_{fp}}{\rho g{A}_{fp}{S}_{0}}\right)}$$
(2)

where h is the flow depth, Nfp the number of floodplains (1 or 2), \(\rho \) is the fluid density, g is the gravity acceleration and subscripts fp and mc stand for floodplain and main channel, respectively. When compared to the results of DCM, the flow discharge of the floodplains is increased because of the influence of the faster flow of the main channel. In the opposite way, the main channel flow discharge is reduced. Globally, the inclusion of the apparent shear stress leads to a decrease of the flow discharge in the whole compound cross section.

This apparent shear stress, \({\tau }_{a}\), may be obtained by the integration, over the floodplain or the main channel widths, of the depth-averaged momentum equation in the streamwise direction for uniform flow. Under uniform flow, neglecting the dispersion term and the lateral variation of the water depth (see e.g. [56]:

$$-\frac{1}{H}\left(\rho gh{s}_{0}-{\tau }_{0}\right)=\frac{\partial {\tau }_{xy}^{d}}{\partial y}-\rho \frac{\partial VU}{\partial y}$$
(3)

where superscript d means a depth-averaged value and \({\tau }_{xy}\) is the Reynolds shear stress.

Integrating this equation over the floodplain width, from lateral position Bmc to B (see Fig. 2 for geometrical parameters):

Fig. 2
figure 2

Schematic cross section of a a symmetric and b asymmetric compound channel

Full size image
$${\int }_{{B}_{mc}}^{B}\left[-\frac{1}{H}\left(\rho gH{s}_{0}-{\tau }_{0}\right)\right]dy={\int }_{{B}_{mc}}^{B}\left[\frac{\partial {\tau }_{xy}^{d}}{\partial y}\right]dy-{\int }_{{B}_{mc}}^{B}\left[\rho \frac{\partial VU}{\partial y}\right]dy$$
(4)

The right-hand side of Eq. (4) is denominated apparent shear stress. In the vertical interface between the main channel and the floodplain it takes the following value:

$${\left.{\tau }_{a}=-{\left.{\tau }_{xy}^{d}\right|}_{{B}_{mc}}+\rho UV\right|}_{{B}_{mc}}$$
(5)

Equation (5) shows that the apparent shear stress has two distinct components: one arising from turbulence and the other from secondary currents [56]. The ASSM assumes that \({\tau }_{a}\) can be modelled as a function of the channel characteristics (such as geometrical parameters or roughness parameters).

Taking into account a momentum balance in each subsection and the boundary shear stress measurements under uniform flow, Myers [37] quantified the apparent shear stress in the vertical interface of the subsections. Since then several researchers tried to model it, following a similar empirical procedure. Based on the Prandtl’s mixing length theory, Ervine and Baird [14] suggested the dependency of the apparent shear stress on the square of the velocity gradient between the flows in each subsection. Prinos and Townsend [48] obtained a solution for the apparent shear stress using a multiple linear regression to their experimental data in symmetric compound channel. Using the data of FCF-SERC, Wormleaton and Merret [63] proposed an empirical formula to estimate the apparent shear stress in straight compound channels. Christodoulou [11] proposed a simple and dimensionally sound formula that suggests that the apparent shear stress that depends on the ratio between the floodplain and the main channel widths. Huthoff et al. [22] developed a new equation for the apparent shear stress in the interface based on the difference between the squared average velocities in the main channel and in the floodplain.

For its wide range of geometries, geometrical scales and roughness distributions, it is important to highlight the equation from Moreta and Martin-Vide [36]. These authors propose two equations, separating the prediction of the apparent shear stress into small- and large-scale channels. Fernandes et al. [15] validated this equation with experimental data and the authors proposed the consideration of the equation for large-scale channels for whole conditions. The need to divide the data into two sub-data was assigned to establishment of uniform flow conditions in small-scale channels with single water supply for both main channel and floodplain.

It is quite common to consider that although the empirical equations for the apparent shear stress fit quite well to the data series for which they are developed, a more general implementation should be carefully regarded [28].

4 Proposed method

The proposed method aims at using an extensive compound channel flows data to evaluate the correction of the Manning roughness coefficient in the main channel and in the floodplains to account for the apparent shear stress generated in the interface of these two subsections.

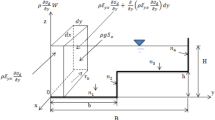
The dataset used to calibrate and validate the proposed method was gathered in Fernandes et al. [17]. The schematic representations of symmetrical and asymmetrical compound channels with vertical and inclined main channel sidewalls and the main cross-sectional geometrical parameters are presented in Fig. 2.

The experimental data are presented in Table 1, where they are split into four groups depending on the geometry and on the roughness of the floodplains. All experiments were conducted under uniform flow.

Table 1 Summary of the experimental data
Full size table

Data comprise relatively small laboratory compound channels as well as data from the large-scale FCF-SERC. Different combinations of symmetry and inclination, such as symmetrical channel with vertical walls, are covered. Some of the data from FCF-SERC were recovered from the large database published on the website of the University of Birmingham (identified as flow database FCF-SERC). In Table 1, N stands for the number of experiments, hr is the relative flow depth, i.e. the relation between the floodplain and the main channel flow depths, and sy and syfp stand for the transverse slopes of the main channel and the floodplain(s) banks (1: sy and1: syfp, vertical: horizontal).

This relative depth is rather important when referring compound channel as it gives a clue to the interaction of the flows. For low relative depths, typically hr < 0.3, this interaction can be rather important and for higher relative depths, the compound channel effects vanish, and flow mechanisms are close to what can be observed in a single channel.

In the total of 710 flow cases used in this study, there is a preponderance of experiments that were performed in symmetric compound channels (284 with smooth floodplains and 181 with rough floodplains). The remaining 245 flow cases refer to asymmetric channels: 164 with rough floodplains and 81 with smooth floodplains.

Besides these laboratory data, field data were collected from Singh and Tang [54, 55] and associated supplementary data. These river datasets refer to rivers Batu, Severn and Main and were used only in the validation process.

It is rather important to point out that the value of the Manning roughness coefficient is available for all experiments. The experimental data comprise the stage–discharge relation for whole flow cases and the subsection discharge (main channel and floodplain) was available for approximately 1/3 of the flow cases. In some cases, this coefficient is different for main channel and floodplains as different bed materials were used. With these data, the calculation of the flow discharge in each subsection with DCM is quite straightforward (cf. Equation 1).

Depending on the availability of the subsection discharge, the complete database was divided into:

  • Dataset A (used for calibration) data with experimental measurement of the flow discharge in the main channel and floodplain and

  • Dataset B (used for validation) Experimental data with measurement of only total discharge.

Note that experimental data from Dataset A was not included in Dataset B, i.e. these two groups do not intersect. For each reference, last column of Table 1 presents the corresponding dataset.

The proposed method aims at easily accounting for the effects of the apparent shear stress in the interface of main channel and floodplain flows is based on the experimental observation that this shear stress leads to an increase of the flow discharge in the floodplains and reduces the main channel and total flow discharge. Therefore, even if the bed material corresponds to a certain Manning roughness coefficient, when overbank flow occurs, the method proposes to affect this coefficient by different factors, \(\varphi \), to account for this effect.

The proposed method was calibrated and validated according to the following steps:

  1. (i)

    Evaluation of the flow discharge in the main channel and floodplain by the divided channel method (Eq. 1) using the experiments of Dataset A (those with complete discharge data for each subsection), with vertical division lines and the Manning roughness coefficient corresponding to the channel bed material;

  2. (ii)

    Calculation, for each flow case of Dataset A, of the correction factors associated with Manning roughness coefficients for the main channel, \({\varphi }_{mc}\), and for the floodplain, \({\varphi }_{fp}\), using the following equations:

$${Q}_{mc}={A}_{mc}\frac{{{R}_{mc}}^{2/3}}{{\varphi }_{mc}{n}_{mc}}{s}_{0}^{1/2}$$
(9)
$${Q}_{fp}={A}_{fp}\frac{{{R}_{fp}}^{2/3}}{{\varphi }_{fp}{n}_{fp}}{s}_{0}^{1/2}$$
(10)

and using the experimentally measured flow discharges in the main channel and in the floodplains, Qmc and Qfp.

  1. (iii)

    Validation of the method by comparing the experimental flow discharges of flow cases from Dataset B with the flow discharges calculated assuming the average correction coefficients for each subsection calculated in (ii) and the total flow discharge by the sum of the subsection discharges.

The Dataset A was used to calibrate the correction factors for the Manning roughness coefficient in the floodplain and in the main channel. A total of 184 experiments collected from the literature were included in this dataset.

Figure 3 presents the results for the correction factors compared to the relative depth of each experiment.

Fig. 3
figure 3

Correction factors for the Manning roughness coefficients for main channel and floodplain

Full size image

Despite the stronger shear layer generated by lower relative depths, it was not observed a strong correlation between this depth and the correction coefficients. The same type of correlation was tried for the relationship between the correction factors with other characteristics of the compound channel like the geometrical dimensions or the aspect ratio or cross-section shape. As the results did not reveal strong correlations with any compound channel characteristic, it was decided to assume constant correction coefficients. Their values, obtained by averaging all values, were \({\varphi }_{mc}=\) 1.15 and \({\varphi }_{fp}=\) 0.91.

The validation Dataset B was then used to check the advantage of considering these coefficients in comparison with the results of DCM and of method developed by Moreta and Vide [36]. The results are presented in Fig. 4 for the laboratory experiments of Dataset B.

Fig. 4
figure 4

Results of the three methods for laboratory experiments of Dataset B

Full size image

The deviation,\(\Delta \), between each pair of calculated and measured discharge was calculated for both methods using the following equation:

$$\Delta =100\times \left({Q}_{c}-{Q}_{m}\right)/{Q}_{m}$$
(8)

where subscripts m and c stand for, respectively, the measured and the calculated flow discharge.

In Fig. 4, dashed lines correspond to a band ± 20% deviation.

The results of the deviations obtained with Dataset B are presented in Table 2.

Table 2 Deviations obtained by the three methods
Full size table

The results show that a global improvement in the flow discharge prediction was achieved by the simple change of the Manning roughness coefficients, i.e. by following the proposed method. By analysing the deviations per type of channel, it becomes clear that this improvement is much more evident in smooth floodplains. This result is linked with the number of experiments considered for the calibration of the correction factors (see column Dataset in Table 1).

5 Concluding remarks

In terms of natural hazards, floods are one of the most problematic tragedies generating high number of deaths and economic losses on both short and long terms. In natural rivers and particularly in the alluvial downstream reaches, compound channels configurations are rather common. In these cases, complex flow structure is observed and important interactions between main channel and lateral floodplains flows must be accounted for when dealing with modelling inundated areas.

Under these conditions the subsection and the total flow discharge are not as easily predicted as for single channels. To overcome with this difficulty, a new and simple method was proposed to evaluate this flow discharge in compound channels by including the concept of apparent shear stress as a correction of the Manning roughness coefficients. A considerable improvement in the traditional method was obtained with the use of simple average correction factors for the Manning coefficients in the main channel and floodplains for smooth floodplains. Following these promising results, further research will be conducted to understand the influence of the characteristics of the compound channel in the correction factors.