Abstract
This work proposes a series of quantum experiments that can, at least in principle, allow for examining microscopic mechanisms associated with decoherence. These experiments can be interpreted as a quantum-mechanical version of non-equilibrium mixing between two volumes separated by a thin interface. One of the principal goals of such experiments is in identifying non-equilibrium conditions when time-symmetric laws give way to time-directional, irreversible processes, which are represented by decoherence at the quantum level. The rate of decoherence is suggested to be examined indirectly, with minimal intrusions—this can be achieved by measuring tunnelling rates that, in turn, are affected by decoherence. Decoherence is understood here as a general process that does not involve any significant exchanges of energy and governed by a particular class of the Kraus operators. The present work analyses different regimes of tunnelling in the presence of decoherence and obtains formulae that link the corresponding rates of tunnelling and decoherence under different conditions. It is shown that the effects on tunnelling of intrinsic decoherence and of decoherence due to unitary interactions with the environment are similar but not the same and can be distinguished in experiments.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The goal of this work is to consider experiments that can, at least in principle, examine time-directional quantum effects in an effectively isolated system. Such experiments need to be conducted somewhere at the notional boundary between the microscopic quantum and macroscopic thermodynamic worlds, that is we need to deal with quantum systems that can exhibit some degree of thermodynamic behaviour. At the quantum level, this corresponds to persisting decoherence, which is, perhaps, the most fundamental irreversible process that we are aware of—it takes place at the smallest scales, increases entropy [1] and, expectedly, induces various macroscopic effects associated with the thermodynamic arrow of time [2]. A large volume of literature is dedicated to decoherence, which may involve both intrinsic [3,4,5,6] and environmental [6,7,8,9,10,11,12,13] mechanisms.
The present work examines a problem that, at least conceptually, can become an experiment probing the direction of time. This problem represents a quantum-mechanical version of non-equilibrium mixing between two volumes separated by a thin interface. In this quantum version of the classical problem, particles tunnel through the interface and, at the same time, are subject to the omnipresent influence of quantum decoherence, which, presumably, is the fundamental mechanism enacting non-equilibrium, time-directional effects in the macroscopic world [14].
In quantum experiments, one has to face another fundamental difficulty—interferences from the environment and measurements. Environmental interferences can overwhelm intrinsic mechanisms of decoherence, while quantum measurements routinely cause decoherences and collapses (which are interpreted here as defined in the Appendix of Ref. [15]) instead of observing these decoherences and collapses without interfering. It appears, however, that, under the conditions examined in this work, decoherence affects the rate of quantum tunnelling and, therefore, can be characterised by the tunnelling rates without measuring decoherence directly. Among many formulations of tunnelling problems [16,17,18,19,20,21,22], we select one that has a transparent and, at the same time, sufficiently general solution. For this formulation involving quantum tunnelling through a high potential barrier under non-equilibrium conditions, we examine mechanisms that may be ultimately responsible for the direction of time. Conducting such experiments is not easy but seems possible even under the current level of technology. Conceptually and technically similar experiments have been performed in the past [18, 20, 22,23,24]. These experiments investigated mesoscopic decoherence in context of the Aharonov-Bohm effect [23], proton tunnelling under thermal bath conditions [18], the effect of invasive frequent measurements on quantum tunnelling [20] (i.e. the quantum Zeno effect [25]). Our main interest is in examining decoherence by using tunnelling but, unlike in the previous of experiments, under conditions that avoid direct interferences from the environment and measurements, and screen the experiment from a supposed direct influence of the temporal boundary conditions imposed on the universe.
This manuscript is organised as follows. Section 2 briefly reviews the interpretation of the arrow of time from a philosophical perspective pointing to the ideas of Hans Reichenbach as a source of critical thinking about the time that is relevant to the present work. The readers, who are interested in quantum mechanics and non-equilibrium dynamics more than in philosophical issues, can omit this section at first reading. Section 3 introduces the tunnelling problem and, in the context of this problem, discusses emergence of the arrow of time. Section 4 reviews different time-asymmetric and time-symmetric interpretations of quantum mechanics, in particular the two-state vector formalism [26,27,28]. Section 5 examines tunnelling in absence of decoherence, while Sect. 6 investigates the influence of decoherence on the tunnelling rates. Section 7 discusses conduct of experiments based on the results of this work. Section 8 summarises our conclusions. More extensive derivations of asymptotic tunnelling rates are presented in Appendix A and a brief consideration of the problem from the perspective of the theory of environmental decoherence [7] is given in Appendix B.
2 Discrimination of the past and the future from a philosophical perspective
It is well known that the most important physical laws—those of classical, relativistic and quantum mechanics—are time-symmetric, but our experience of physical reality strongly discriminates the past and the future. The observed arrow of time is reflected in the second law of thermodynamics, which permits entropy increases but bans reduction of entropy in isolated thermodynamic systems. While the Boltzmann time hypothesis, which suggests that the perceived arrow of time and the direction of entropy increase must be the same (i.e. connected at some fundamental level), may be striking at first, but after some thinking over the issue, most people tend to arrive at the same conclusion. Since Ludwig Boltzmann [15, 29], the overall conditions prevailing in the universe (or its observable part) have been thought to be responsible for this temporal asymmetry. In modern physics, the increasing trend for entropy is commonly explained by the asymmetry of temporal boundary conditions imposed on the universe, i.e. by low-entropy conditions at the time of Big Bang [30]. This explanation is called the past hypothesis by Albert [31] and in other publications. There are no doubts that the past conditions existing in the universe are very important. The pertinent question, however, is not whether these conditions are important, but whether the direct influence of the initial conditions imposed on the universe is sufficient to explain all time-directional phenomena observed in experiments. A number of publications seem to be content with the sufficiency of the special initial conditions in the early universe to explain all entropy increases in thermodynamically isolated systems, even if it is presumed that all laws of physics are time-symmetric [31, 32].
The alternative view is that the past hypothesis is important but, on its own, is insufficient to fully explain entropy increases required by the second law. This view can be traced to the principle of parallelism of entropy increase, which was introduced by Hans Reichenbach [33], and further explained, evaluated and extended by Davies [34], Sklar [35] and Winsberg [36, 37]. The Reichenbach principle concurs that initial conditions imposed on the universe can explain many effects associated with entropy increase; nor does it deny that entropy can fluctuate. The initial conditions imposed on the universe may explain why entropy tends to increase more often than to decrease in semi-isolated thermodynamic subsystems (branches) but, assuming that all governing physical laws are time-symmetric, these initial conditions do not explain the persistence and consistency of this increase (this, of course, does not exclude the existence of fluctuations of entropy but indicates that, according to the fluctuation theorem, entropy increases over a given time interval are consistently more likely than entropy decreases [38]). Consider a system that is isolated from the rest of the universe without reaching internal equilibrium: would such a system demonstrate conventional thermodynamic behaviour, or would its entropy increase terminate under these conditions? Reichenbach [33] conjectured that such an isolated system would still display conventional thermodynamic properties, and we do not have any experimental evidence to the contrary. The principle of parallelism of entropy increase is useful not only as a thought experiment. When applied at a physical level, Reichenbach’s ideas lead us to the existence of a time priming mechanism that continues to exert its influence even in isolated conditions [2, 15, 39]. Implications of the directionality of time in quantum mechanics [1] and chemical kinetics [40] are further discussed in special issue [41].
Huw Price [42] pointed out that our temporal (antecedent) intuition often results in implicit discrimination of the directions of time in physical theories—this tends to introduce conceptual biases that may be difficult to identify due to the all-encompassing strength of our intuitive perception of time. These biases conventionally involve assumptions associated with the conceptualisation of antecedent causality, such as imposing initial (and not final) conditions or presuming stochastic independence before (and not after) interactions. These assumptions are very reasonable and supported by our real-world experience, but may form a logical circle: effectively, we often presume antecedent causality in order to explain entropy increase forwards in time, which, in turn, is used to explain and justify antecedent causality [2]. Here, we recognise that the laws of classical and quantum mechanics are time-symmetric, and will endeavour to avoid implicit discrimination of the directions of time [15]. When reading this article, the reader, who is accustomed to thinking in terms of antecedent causality, might feel that something is strange or missing. The concept of time priming used here is aimed at avoiding intuitive assumptions introducing directionality of time by implying antecedent causality in one form or another—time priming does not seem relevant whenever antecedent causality is presumed. Since the directions of time are, obviously, not equivalent, there must be a physical mechanism that is responsible for this and, at least in principle, testable in experiments. One of such possible mechanisms, pointing to interactions of quantum effects and gravity, has been suggested by Penrose [43]. Another possibility is that this mechanism is related to the temporal asymmetry of matter and antimatter [14, 39, 44, 45]. In the present work, however, we do not presume any specific form of the mechanism and use this special term, the time primer, as a place holder for possible physical explanations. Detecting the time primer in experiments is most likely to be difficult due to the expected smallness of its magnitude.
The Reichenbach parallelism principle is not a trivial statement or tautology: one can imagine a state of affairs in which this principle has only limited validity. A thermodynamic system, placed in isolation and screened by equilibrium states from the initial and final conditions imposed on the universe, might, at least in principle, cease to exhibit thermodynamic, entropy-increasing behaviour even if non-equilibrium conditions are created within a selected time interval. Reichenbach’s conjecture tells us that this should not happen: such an isolated system would still tend to increase its entropy similarly to and in parallel with entropy increases of various thermodynamic systems scattered in the rest of the universe. While general implications of the Reichenbach principles are discussed in Ref. [2], our broad goal is to consider specific experiments where these principles can be examined directly or indirectly but, desirably, examined in a way that can give some indications of the underlying mechanisms responsible for decoherence and, ideally, for the direction of time. While the experiments suggested in the present work are related to modern quantum mechanics more than to Reichenbach’s branch model, one needs to acknowledge that these experiments are following the direction of his thinking.
3 Quantum mixing in a branch system
This section introduces a detailed description of the problem, which, as noted above, represents a quantum-mechanical version of mixing across an interface that is deemed to be branched and isolated from the rest of the universe.
3.1 Formulation of the problem
We consider a number (say, \(N_{0}\)) of quantum particles placed in a rectangular box AB, which is partitioned into two sections A and B. The quantum levels in the system are sparsely populated so that the rules of the Maxwell-Boltzmann statistics apply. The tunnelling particles are initially located in section A of the box AB, as shown in Fig. 1. The value of the potential V is prohibitively high in section B to permit any significant presence of the particles in this section. Section A also contains a number \(N_{1}\) of inert, non-tunnelling particles, and this number is sufficiently large so that the system of particles can be expected to behave thermodynamically (\(N_{1}\gg N_{0}\)). We expect that all of the particles achieve thermodynamic equilibrium during the passive stages of the experiment (the particles interact with each other but these interactions are deemed to be weak). The particles in the box are trapped by a potential field and completely isolated from the environment (which is also deemed to be in an equilibrium state) during the duration of the experiment \(-t_{b}<t<+t_{b}\). In a more simple experimental set-up, the tunnelling particles can be brought into thermodynamic equilibrium with their container box. Using inert particles, however, allows us to control the statistical scale of the experiment.
System, which is isolated from the environment and screened from the temporal boundary conditions imposed on the universe by equilibrium states, involves quantum tunnelling from section A to section B and back in response to the time-symmetric disturbance of the potential \(V_{\text {B}}\). Here, \(N_{ \text {B}}\) is expected number of particles in section B: 1 - under equilibrium, 2 - as predicted by master equations with dominant decoherence and by thermodynamic considerations; 3 - possible quantum solution without decoherence
The equilibrium state is maintained for a long time \(\sim t_{b}\) prior to (and after) the active phase of the experiment—this time is much larger than the characteristic thermalisation time \(\tau _{t}\) for this system \( t_{b}\gg \tau _{t}\). Thermalisation implies achieving thermodynamic equilibrium between all particles under consideration while, in the present context, equilibration implies reaching steady-state concentrations of the tunnelling particles. Depending on conditions, equilibration may or may not require thermalisation. During the passive stages of the experiment, equilibration requires energy exchanges between different modes and, therefore, presumes thermalisation. In the active stage of the experiment, however, the system may reach equilibrium values of \(N_{\text {A}}\) and \(N_{\text {B}}\) without reaching (or without significantly disturbing) thermodynamic equilibrium. Thermalisation and equilibration are generally not synonymous [13]. Thermalisation requires a substantial energy exchange between different modes to reach the equilibrium thermodynamic distributions, while this is not necessarily the case for equilibration.
The active phase of the experiment \(-t_{s}\le t\le +t_{s}\) is short \( t_{s}\ll t_{b}\). At time \(t=-t_{s},\) the particle access to section B of the box is opened by rapid lowering of the potential \(V({{\mathbf {r}}},t)\) in this section to the same level as in section A, so that the tunnelling particles can now tunnel through the barrier that separates sections A and B, while the inert particles remain in section A. The rate of change of the potential is fast compared to the characteristic tunnelling time so that the concentrations of the particles in sections A and B deviate from their equilibrium values. Particles tunnel from A to B and back through a potential barrier separating the sections until the process is terminated at \(t=t_{s}\) in a time-symmetric manner by increasing potential in section B to its original value. The experiment is expected to follow by a long-lasting equilibrium state, where particles are again in a thermodynamic equilibrium (this implies that their location is in section A). It is also worthwhile to consider the temporal symmetry in the experiment of lowering and rising the potential \(V({{\mathbf {r}}},t)\) in a piston-like manner (e.g. as discussed in Refs. [2, 46]), although the present work is primarily focused on examining the effects of decoherence on tunnelling.
3.2 Expected emergence of temporal asymmetry
Would the concentration of particles in section B behave in a thermodynamics manner with time-delayed relaxations towards its equilibrium value as illustrated by curve 2 in Fig. 1? The Reichenbach conjecture states that it would: despite being completely isolated from the environment and fully screened by the equilibrium states from the initial and final conditions imposed on the universe, the system is still expected to display time-directional thermodynamic behaviour (this, of course, needs to be confirmed by actual experiments, but, for the sake of the argument, we assume at this point that the Reichenbach conjecture is correct). If the laws of the universe are time-symmetric, the initial and final conditions are similar, and interactions of the system and the universe take place only through strictly time-symmetric disturbance of the potential \(V({\mathbf {r}} ,t)=V({\mathbf {r}},-t)\), why the response of the system to time-symmetric inputs is evidently time-asymmetric?
3.3 Environmental interferences
While we have declared complete isolation of the system, controlling and eliminating environmental interferences for a particle or a system of particles may, in real-world experiments, be quite difficult. According to thinking common among many physicists, any quantum system is always subject to influences of the environment; environmental interactions, no doubts, can cause and do cause decoherences as indicated in many theories and experiments [6, 7, 9,10,11,12,13, 47] . The interferences that involve a measurable, specific influence of environment on the system (such as the direct effect of cosmic radiation on superconducting qubits measured in Ref. [47]) can be evaluated and, at least in principle, protected from in these experiments. Bell entanglement of two elementary particles can be protected from environmental interferences and preserved for a very long time. However, the presumed omnipresent environmental interference that induces decoherence but does not have any specific measurable mechanism and any specific physical particles or surrounding objects casing it (e.g. interference involving a special quantum field that is like, say, the Higgs field present everywhere), is, conceptually, no different from intrinsic decoherence. While the distinction between the intrinsic and environmental mechanisms of decoherence is blurred and depends on exact definitions, the principal difference between various theories of decoherence and thermalisation is in relying or not relying on time-symmetric scientific frameworks (such as unitary evolutions in quantum mechanics). We therefore distinguish intrinsic or effectively intrinsic mechanisms of decoherence from unitary interferences with the environment.
Unitary environmental interferences do not, by themselves, discriminate the directions of time: all theories of environmental decoherence based on time-symmetric physical laws (e.g. unitary evolutions of quantum mechanics) must involve another principal element—an assumption that violates the equivalence of the directions of time. The effect of the environment on decoherence becomes clear only if we presume antecedent causality (although causality is something that we have vowed to avoid in the present work). Indeed, in the absence of directionality of time required by antecedent causality, environmental interactions can induce recoherences in the same way as they induce decoherences. The time-directional effect of random interventions produced by the environment is determined by imposing initial (as opposite to final) conditions on the system (individual realisations of a random process with independent increments are not time-directional [2]). Note that the immediate environment can be in a thermal equilibrium state and experience only time-symmetric fluctuations or, even better, be kept at (nearly) absolute zero temperature (while radiation that can transmit interactions over long distances is expected to be decoherence-neutral by itself [45]). In the casual model, the final state depends on random interventions but the initial state does not, because the initial state is fixed but the final state is not. The interventions are deemed to cause the final state but not the initial state. If we fix the final state instead of fixing the initial state, then the effect of environmental interferences would be recohering. By themselves, the environmental interferences only introduce some effective randomness into the system. Presuming antecedent causality is the central element of the major theories of environmental interference—it is causality and not the interference that breaks the symmetry of the directions of time.
3.4 Initial and final conditions imposed on the universe
One, of course, may abandon antecedent causality and, instead, invoke low-entropy initial conditions imposed on the universe. While these conditions must be very important, the main question concerning our experiment remains: how can these conditions influence the stochastic state of the system after a long period of equilibrium? We may assume that \( N_{0}\sim 1\) so that the system of \(N_{1}\) inert particles under consideration is small (while \(t_{b}\) is extremely long, much longer than \(t_{s}\)) and repeatedly experiences very substantial fluctuations around equilibrium during the passive phases of the experiment. Due to these fluctuations, we may, in principle, select the time moments \(t=\pm t_{b}\) when the final state at \(t=+t_{b}\) has lower entropy than the initial state at \(t=-t_{b}\)—does this mean that the arrow of time should be reversed during the active phase of the experiment and the changes in \(N_{\text {B}}\)—the number of particles in section B – would tend to preempt the changes of the potential \(V({\mathbf {r}},t)\) rather than to follow them? While the negative answer to this question is expected, the physical mechanism that can allow the temporal boundary conditions imposed on the universe to affect the active phase of our experiment is not obvious. Or, alternatively, should the arrow of time disappear and the directions of time become equivalent under these conditions? According to the Reichenbach conjecture, we tend to believe that the arrow of time should persist.
In the suggested experiment, the system cannot preserve any statistical information about the conditions that preceded the experiment or follow the experiment—equilibrium states achieve maximal entropy and necessarily destroy all such information. Yet, there must be a physical mechanism that discriminates the directions of time in lieu of the direct action of the temporal boundary conditions imposed on the universe if the Reichenbach conjecture is correct. This mechanism is called here the time primer. Conceptually, the time primer does not replace global temporal boundary conditions imposed on the universe but reflects the local action of these global conditions.
The time primer may act predominantly on a larger system and propagate to a semi-localised subsystem through time-priming interference, which (the subsystem) in this case can behave similarly to the effect of intrinsic time priming but without any intrinsic time priming on its own. One may invoke time priming in larger and larger environments but this interpretation neither gives a complete explanation (now we need to explain time priming in the environment, which may well be in its equilibrium state) nor helps the experiments (instead of confining and measuring the effect of interest, we disperse it over the environment in a way that it is likely to become experimentally untraceable). Therefore, environmental interactions should be avoided as much as possible or, at least, they need to be measured and quantified. The boundary conditions imposed on the universe may indeed determine the direction of decoherence in a tiny experiment with quantum mixing, but this influence must have a specific physical mechanism and should be measurable and quantifiable.
3.5 Conditions of the experiment
By changing the parameters of the experiment, we can observe different physical conditions. The system of particles may consist of one or more particles, which do not strongly interact between themselves and may or may not interact with a thermodynamic (or statistical microscopic) object (e.g. a system of inert particles), while the particles and the object remain fully isolated from the environment. The characteristic tunnelling time can also be changed by varying the shape of the potential. If the active phase of the experiment is sufficiently short \(t_{s}\ll \tau _{t}\), then there is no substantial exchange of energy taking place within the system during the active phase. This, however, does not imply that quantum particles evolve unitarily since they may still be affected by decoherence. Since the equilibrated system should be, from the quantum perspective, in or close to its maximally mixed state under specified conditions (or in the effectively maximally mixed state specified by canonical typicality [11, 12]), thermalisation necessarily implies decoherence, and, therefore, the characteristic decoherence time cannot be longer than the characteristic thermalisation time. In fact, one may expect the decoherence time \(\tau _{d}\) to be significantly shorter than the thermalisation time \( \tau _{t}\) (at least for sufficiently large systems) so that characteristic time \(\tau _{d}\) can be shorter or comparable to \(t_{s},\) even if \(t_{s}\) is much smaller than \(\tau _{t}.\) In the case of \(\tau _{d}\ll t_{s},\) decoherence must have a strong influence on the experiment. If however, the active phase of the experiment is much shorter than the characteristic decoherence time \(t_{s}\ll \tau _{d}\), then decoherence has little effect on the quantum system of particles, which is now expected to evolve unitarily and be governed by the Schrödinger equation during the active phase.
4 Time-directional and time-symmetric interpretations of quantum mechanics
This section discusses time-asymmetric and time-symmetric interpretations of quantum mechanics. The former tends to imply antecedent causality, while the latter can be used to avoid implicit discrimination of the directions of time.
4.1 Schrödinger equation and its solution
As we have to deal with quantum mixtures, different particles generally do not form coherent superpositions, and quantum wave functions and density matrices are more useful tools than quantum fields under these conditions. Hence, we focus first our attention on behaviour of a single quantum particle but remember that interactions between particles within the system are conducive to decoherence. According to the conventional interpretation of the problem, evolution of the wave function is governed by the Schrödinger equation in the position representation
with the Dirichlet (zero) boundary conditions
since the potential V is assumed to be very high at and beyond the boundaries. Here, \(\psi \) is the wave function, t is time, \({\mathbb {H}}\) is the Hamiltonian, \(\hbar \) is the Planck constant and m is the particle mass. Relations (4.1) and (4.2) apply to all wave functions that correspond to different particles, assuming that interactions between particles can be neglected. The sections A and B are separated by a thin high-energy barrier located near \(x=0.\) The probability of tunnelling is relatively small but essential; tunnelling may or may not be affected by decoherence as discussed in the rest of this paper.
According to the formulation of the problem presented above, the potential V is assumed to be time-independent \(V({\mathbf {r}},t)=V({\mathbf {r}})\) within the time interval \(-t_{s}<t<+t_{s}\), which is of interest in the present work. Since the Hamiltonian is Hermitian \(\left\langle \phi \Big |\mathbb {H }\psi \right\rangle =\left\langle {\mathbb {H}}\phi \Big |\psi \right\rangle \) , the solution of the problem is based on the Hilbert–Schmidt theorem
where
\(\psi _{0}=\left. \psi \right| _{t=t_{0}}\) specifies the initial conditions, \(t^{\circ }=t-t_{0},\) and the energy eigenstates \(\Psi _{j}( {\mathbf {r}})\) satisfy the same boundary conditions as \(\psi \). The initial (or final) conditions can be set at \(t_{0}=-t_{s}\) or at \(t_{0}=+t_{s}\). The jumps of the potential at \(t=\pm t_{s}\) are assumed to be so rapid that the wave function does not have time to adjust and \(\left. \psi \right| _{t=t_{0}+0}=\left. \psi \right| _{t=t_{0}-0}\). The bra/ket product notation \(\left\langle \phi \Big |\psi \right\rangle \) implies integration of the product \(\phi ^{*}\psi \) over the interior of box AB. For the potential \(V({\mathbf {r}})=V(x),\) which depends only on x but not on y and z (these are the Cartesian components of the physical coordinate \({\mathbf {r}}\)), the eigenstate variables are separated \(\Psi _{j}={\tilde{\Psi }} _{j}(x)\sin (k_{y}y)\sin (k_{z}z)\) so that
4.2 On time-symmetric formulations of quantum mechanics
The conventional formulation of quantum mechanics implies that the solution \( \psi \) of the Schrödinger equation (4.1) can have only one temporal boundary condition \(\left. \psi \right| _{t=t_{0}}=\psi _{0},\) requiring us to set either the initial condition at \(t_{0}=-\zeta t_{s}\) or the final condition at \(t_{0}=+\zeta t_{s},\) where \(\zeta \ge 1\). Despite the unitarity and reversibility of quantum evolutions governed by (4.1 ), this violates the symmetry of time and forces us to make a time-asymmetric choice between the initial and final conditions. Selection of initial or final conditions is explicitly discriminating in case of random or diffusional systems [2], but one may note that any given solution \(\psi =\psi _{S}(t)\) of the Schrödinger equation (4.1) allows for two conditions \(\left. \psi \right| _{t=-t_{s}}=\psi _{S}(-\zeta t_{s})\) and \(\left. \psi \right| _{t=+t_{s}}=\psi _{S}(+\zeta t_{s})\), which correspond to the same \(\psi _{S}(t)\). Our temporal, causality-based intuition, however, forces us to select specific types of conditions that are associated with antecedent causality and, quite often, are time-asymmetric. For example, one can choose 1) \(\psi =0\) in section B at \(t=-t_{s}\) or 2) \(\psi =0\) in section B at \(t=+t_{s}\)—these conditions are generally not equivalent and, therefore, choosing between conditions 1 and 2 is time-asymmetric. The fundamental dilemma of selecting between initial and final conditions is commonly resolved by invoking antecedent causality and choosing initial conditions over final conditions—this is practically correct but tends to hide the inequivalence of the directions of time, especially when some degree of uncertainty is introduced into the system.
Several interpretation of quantum mechanics permit time-symmetric formulation of temporal boundary conditions [26, 28, 48]. Time reversal is naturally present in relativistic quantum mechanics due to its Lorentz invariance. For example, the Klein–Gordon (Klein–Gordon–Fock) equation [49]
is of the second order in time, is invariant with respect to the reversal of time \(t\rightarrow -t\) and therefore necessarily involves at least two waves propagating forwards and backwards in time. Note that only free spinless particles satisfy equation (4.6): interactions of the particle spin with electromagnetic fields require more elaborate treatment—the Dirac equation [50])—which generally is invariant only under charge-parity-time (CPT) conjugation and not under mere reversals of time. Interactions of the thermodynamic, time-directional effects with CPT-invariance have been extensively discussed elsewhere [14, 39, 44, 45, 51, 52] and are not specifically considered here. The Klein–Gordon equation is used here only to illustrate the effects of Lorentz invariance. The non-relativistic limit of the Klein–Gordon equation is obtained by substituting \(\psi =e^{-i\omega _{0}t}\varphi \) and \(\psi =e^{+i\omega _{0}t}\phi \) to offset the domination of the \(mc^{2}\) term by selecting \( \omega _{0}=mc^{2}/\hbar \). This yields the two corresponding equations
where the second equation is the time-reversal \(t\rightarrow -t\) of the first. Conventional non-relativistic quantum mechanics admits only equation ( 4.7a), while quantum field theory interprets (4.7b) as corresponding to antiparticles that nominally move backwards in time. The transactional interpretation of quantum mechanics [48] argues that both of these equations play a role: the first corresponds to waves propagating forwards in time and the second corresponds to waves propagating backwards in time and both of these waves are physically significant.
Another interpretation is given by the so-called two-state vector formalism [26,27,28], where each quantum system is characterised by two vectors, which are usually written as bra and ket: \( \left\langle \phi \right| \) and \(\left| \varphi \right\rangle .\) These vectors satisfy the Schrödinger equation
Equation (4.8b) can be obtained as the Hermitian (conjugate) transpose of (4.8a), although the Hermitian transpose \(\varphi ^{\dagger }\)of the state \(\varphi \) is not necessarily the same as \(\phi ,\) since, as discussed below, \(\left\langle \phi \right| \) and \(\left| \varphi \right\rangle \) are generally constrained by different initial and final conditions: the initial conditions are imposed on \(\left| \varphi \right\rangle ,\) while \(\left\langle \phi \right| \) satisfies the final conditions. Equations (4.8b) and (4.7b) may look similar but, in fact, these equations are generally different (unless, as in equation ( 4.1), the Hamiltonian \({\mathbb {H}}\) is strictly invariant with respect to the reversal of time), as are the corresponding conceptual interpretations. The two-state formalism is conventionally interpreted along time-asymmetric, casual lines: the state of the system \(\left| \varphi \right\rangle \) is determined by its past, while \(\left\langle \phi \right| \) specifies how the system will affect measuring devices in the future, reflecting postselection. According to this casual perspective, \( \left| \varphi \right\rangle \) is a genuine characteristic of the system at a given moment, while \(\left\langle \phi \right| \) is not but can be treated as such for the sake of convenience [28]. There is also an implied time-symmetric interpretation of the two-state formalism, where both states \(\left\langle \phi \right| \) and \(\left| \varphi \right\rangle \) are considered to be intrinsic physical characteristics of the system at a given time moment.
Finally, the two-state vector formalism requires that the Born rule for the probability density of particle location \(P({\mathbf {r}})\), which is conventionally given by
should be replaced by the time-symmetric Aharonov, Bergman and Lebowitz (ABL) rule [26]
where \({\mathbb {P}}_{\text {J}},\) J = A,B is projector in the wave function into either section A or section B and
The ABL rule is similar to the interpretation of quantum mechanics called consistent histories [53, 54]. In this context, we stress that the location operators in (4.10) form a consistent set of projectors since \({\mathbb {P}}_{\text {A}}{\mathbb {P}}_{\text {B}}=0\). The approach of consistent histories also has time-symmetric and time-asymmetric, casual versions of the approach [52].
4.3 The initial and final conditions
Leaving aside philosophical aspects of quantum mechanics, we focus on the initial and final conditions. As specified above, the problem shown in Fig. 1 does not have any explicitly measured initial and final conditions. Such measurements can be performed at \(t=-\zeta t_{s}\) and \( t=+\zeta t_{s}\) with \(\zeta >1\) and \(\zeta t_{s}\ll t_{b}\), so that the evolution of the system is not disturbed by these measurements during the active phase of the experiment. The case of a single particle is discussed here for the sake of simplicity. The measurements attempt to detect the presence of particles in section A. If the particle is not detected either at \(t=-\zeta t_{s}\) or at \(t=+\zeta t_{s}\) then this realisation is discarded (i.e. both pre-selection and post-selection apply). The two-state formalism seems to be the most suitable time-symmetric framework available for this case. According to this formalism, the state \(\left| \varphi \right\rangle \) is deemed to propagate forwards in time and, therefore, is subject to the initial conditions, while \(\left\langle \phi \right| \) is deemed to propagate backwards in time and, therefore, is subject to the final conditions:
Assuming that the initial and final conditions are the same or similar, so should be \(\varphi _{1}\) and \(\phi _{2}\). In conventional quantum mechanics, we invoke antecedent causality to justify our preference for initial conditions over final conditions and impose only the initial condition (4.12a).
While we can set the initial and final conditions at \(t=\pm \zeta t_{s}\), the corresponding solutions of equations (4.8) remain undisturbed until the moments of the potential jumps \(t=\pm t_{s}\) are reached. Hence, from the mathematical perspective, we can put \(\zeta =1\) in (4.12), and set these undisturbed conditions at \(t=t_{0}=\pm t_{s}\) so that the equations (4.8) are to be solved only within the time interval \( -t_{s}<t<+t_{s}\). Note that, according to the two-state vector formalism, changes in probabilities may precede the relevant changes of the potential. The jumps of the potential V in box B at \(t_{0}=\pm t_{s}\) are presumed to be rapid so that the wave functions do not have time to change substantially and remain practically the same at \(t_{0}-0\) and at \(t_{0}+0.\) Therefore, we do not need to specify whether the initial and final conditions are applied before or after the jumps of the potential. If the final conditions are not set, the ABL rule (4.10) reverts to the Born rule (4.9).
If the thermalisation time \(\tau _{t}\) is smaller than or comparable to \( \zeta t_{s}\) then, post-selection should have little effect—the experiment is effectively screened from the final conditions. If the characteristic time associated with decoherence \(\tau _{d}\) is smaller than or comparable to \(\zeta t_{s}\) (but \(\tau _{t}\gg \zeta t_{s}\)), then decoherence can affect the active phase of the experiment by screening it from the final conditions (in this context decoherence can be seen as an intermediate projective measurement that remains unknown, i.e. a latent collapse [15]). If the basis of the measurement and decoherence are consistent (while accounting for unitary evolution of the system between the time moments of decoherence and measurement), decoherence should not have any effects on the measurement. In the opposite case, \(\tau _{d}\gg \zeta t_{s}\), decoherence does not have much influence on the experiment.
4.4 Non-intrusive measurements
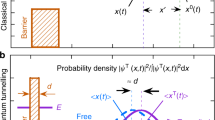
If the system under consideration involves a sufficiently large, statistically significant number of particles \(N_{0}\), measurements conducted over one or few particles should have a minimal effect on the system. In more accurate terms, this implies that the projection operator \( {\mathbb {P}}\) associated with this measurement projects the overall large Hilbert space into its subspace that has only a slightly smaller dimension than the original space (i.e. mostly preserving the complexity of the original state). Measuring interventions, however, involve decoherences and collapses, and, as demonstrated in experiments [20], this can affect the rate of tunnelling. It is preferable to avoid any irreversible measurements, at least during the active phase of the experiment. This goal can be achieved by resorting to generalised or weak measurements [28, 54,55,56], which use an ancilla system.
The ancilla system is created well before \(t=-\zeta t_{s}\) with a few quantum particles in a specific coherent state, (say, spin down). At some time moment \(t_{m}\), during the active phase \(-t_{s}\le t_{m}\le +t_{s}\), an interaction window is created \(t_{m}-\Delta t/2\le t\le t_{m}+\Delta t/2\) as shown in Fig. 2. During this window, unitary interactions are allowed between the ancilla and tunnelling particles in section B. If interactions take place, the state of the ancilla particles changes (there also must be at least some minor change in the state of a particle, say, alteration of its spin). The state of the ancilla is measured only after \( t=+\zeta t_{s}\) and alterations of the original ancilla state are indicative of the presence of tunnelling particles in section B. These type measurements allow us to detect the presence of tunnelling particles in section B without causing any decoherence or collapses during the active phase of the experiment.
5 Tunnelling without decoherence
While many tunnelling problems can be solved analytically [16, 17] , our goal is in obtaining sufficiently general but relatively simple and transparent solutions, which are suitable for further analysis involving decoherence. The initial conditions correspond to all particles located in section A, presumably in a maximally mixed state although, in this section, we neglect interactions between the particles and focus on the interaction of the relevant pure states with the barrier. During the active stage of the experiment \(-t_{s}<t<+t_{s}\), particles tunnel to section B. In this section, the evolution of quantum particles is examined without the influence of decoherence so that a coherent wave function remains coherent during the active phase. For a potential barrier specified by the delta function \(V(x)=s\delta (x),\) we can easily evaluate the energy eigenfunctions. The probability of tunnelling is presumed to be small \(\sim {\hat{s}}^{-2}\ll 1\), \({\hat{s}}=sm/k_{0}\hbar ^{2}.\) The problem under consideration involves many possible quantum states but can be effectively reduced to a two-state dynamic by introducing the partition states. The resonant, intermediate and non-resonant cases need to be considered separately. The details of the solutions are elaborated in Appendix A.
5.1 Evolution of the partition states
As demonstrated in Appendix A(g), resonant \(\eta \rightarrow 0,\) near-resonant \(\left| \eta \right| \sim 1\) and intermediate \(1\ll \left| \eta \right| \ll {\hat{s}}\) modes form pairs – the “plus” mode \(\psi _{+}\) and the “minus” mode \(\psi _{+}\) with very close energies and wave numbers. Here, \(\eta =2{\hat{s}}\theta \) and \(\theta \) is the phase of the deviation from resonant conditions, i.e. \(\theta =0\) corresponds to the exact resonance (see (A.19) for details). These modes are energy eigenstates and, according to (4.3), evolve as
The conventional normalisation
is conveniently expressed in terms of the volume-adjusted amplitudes \(\tilde{ A}\) and \({\tilde{B}},\) which satisfy
according to (A.25).
The stationary orthogonal (unitary) transformation of the basis
converts the “plus” \(\left| +\right\rangle \) and “minus” \(\left| -\right\rangle \) eigenstates, into states |A\(\rangle \) and |B\(\rangle \). Unlike the states \(\left| +\right\rangle \) and \(\left| -\right\rangle ,\) the states |A\(\rangle \) and |B\(\rangle \) are not energy eigenstates. Here, we denote
where the function \(F_{+}\) is defined by (A.23) and \(\sigma =\pm 1\) as specified in (A.21). The states |A\(\rangle \) and |B\(\rangle \) are referred to as the “partition states”: to the leading order of our analysis, the state |A\(\rangle \) implies exclusive localisation in section A of the box, while the state |B\(\rangle \) corresponds to exclusive localisation in section B. Indeed, with the definition of \(\xi \) given by ( 5.6) and the use of equations (A.11), (A.19)-(A.25) the partition states are approximated by
since \(k_{+}=\Delta k_{+}+k_{0}\approx k_{-}=\Delta k_{-}+k_{0}\approx k_{0}\) at the leading order and we select \(A_{+}>0\) and \(A_{-}>0\) to remove freedom in choosing signs.
It is clear that the normalised amplitudes of the wave functions that correspond to states |A\(\rangle \) and |B\(\rangle \) are given by \(\tilde{ A}\) and \({\tilde{B}}\). Since the states |A\(\rangle \) and |B\(\rangle \) are not energy eigenstates, their amplitudes \({\tilde{A}}\) and \({\tilde{B}}\) change in time as determined by the equation
where the Hamiltonian in the new basis is given by
Here, \(\left\langle +\right| {\mathbb {H}}\left| +\right\rangle =E_{+}\) , \(\left\langle -\right| {\mathbb {H}}\left| -\right\rangle =E_{-}\) and \(\left\langle +\right| {\mathbb {H}}\left| -\right\rangle =\left\langle -\right| {\mathbb {H}}\left| +\right\rangle =0\) since the states \( \left| +\right\rangle \) and \(\left| -\right\rangle \) are energy eigenstates. According to (4.3), this equation is solved by the following unitary evolution matrix
where we denote
and D is specified in (A.24). With the initial conditions
which correspond to particle location in section A at \(t=t_{0}\), the amplitudes of the partition states depend on time \(t^{\circ }=t-t_{0}\) and evolve as
assuming that all particles are initially present only in the section A. Note that the evolution preserves normalisation \(|{\tilde{A}}|^{2}+|{\tilde{B}} |^{2}=1,\) where the amplitudes \(|{\tilde{A}}|^{2}\) and \(|{\tilde{B}}|^{2}\) are conventionally interpreted as probabilities of localisation P(A\()=|\tilde{A }|^{2}\) and P(B\()=|{\tilde{B}}|^{2}\) associated with this resonant pair. The extent of tunnelling (i.e. a quantity constraining \(|{\tilde{B}}|\) and P(B) for any \(t^{\circ }\)), which is determined by \(\varsigma =\left| \xi \right| /(1+\xi ^{2})\), remains small when \(\left| \xi \right| \ll 1\) or \( \left| \xi \right| \gg 1\).
5.2 Tunnelling by resonant and near-resonant modes
The resonant modes (\(\eta \rightarrow 0\)) are energy eigenstates that are energy eigenstates in all sections of the box, that is resonant modes are resonant in both sections A and B. The near-resonant modes are (\(\left| \eta \right| \sim 1\)) close to the resonant conditions in A and B. For these modes, the characteristic transmission frequency \({\hat{\omega }}_{\text {r}}\) and the characteristic transmission time \({\hat{\tau }}_{\text {r}}=1/\hat{ \omega }_{\text {r}}\) are evaluated from equations (5.6), (5.12) and (5.13)
where \(F_{+}\) and D depend on \(\eta =2{\hat{s}}\theta ,\) \(x_{{\mathrm{A}} }\) and \(x_{{\mathrm{B}}}\) as specified in (A.22)–(A.24). For the resonance modes \(\eta \rightarrow 0,\) these equations simplify according to (A.27) and (A.28):
Here, we also introduce useful parameters
where \(\tau _{0}\) is the characteristic fly time defined in terms of the characteristic length of the box section \(x_{0}\) and the characteristic velocity \(u_{0},\) which can be estimated using thermodynamic quantities \( mu_{0}^{2}=2{\tilde{E}}\approx k_{B}T\).
If \(x_{{\mathrm{B}}}=x_{{\mathrm{A}}}=x_{0},\) then all modes are resonant, while the “minus” mode becomes symmetric and the “plus” mode antisymmetric—this case is referred to as the resonance case (see Appendix A(e)). In the resonance case, the evolution of the partition states simplifies into
5.3 Tunnelling by intermediate and non-resonant modes
We now examine the limit \(\eta \rightarrow \pm \infty \) and turn to consideration of the intermediate (\(1\ll \left| \eta \right| \ll {\hat{s}}\)) and non-resonant modes (\(\left| \eta \right| \sim {\hat{s}}\) ), which as shown in Appendix A(f) must be either A-resonant or B-resonant, assuming that \({\hat{s}}\gg 1\). Generally, links between the plus and minus modes are preserved for the intermediate modes but weaken for non-resonant modes, which do not necessarily form pairs. Appendix A(f) indicates that \(\left| B/A\right| \sim 1/\left| \eta \right| \ll 1\) for A-resonant modes and \(\left| B/A\right| \sim \left| \eta \right| \gg 1\) for B-resonant modes. Since the initial wave function \(\psi _{0}=\left. \psi \right| _{t=t_{0}}\) is localised exclusively in section A, the A-resonant modes dominate the expansion in energy eigenstates (4.3)-(4.4). The components with different values of k and \(\omega \) quickly lose phase correlation and we focus on modes that have close k and \(\omega \). If \(\eta \rightarrow +\infty ,\) the “plus” branch corresponds to A-resonant modes and the “minus” branch corresponds to B-resonant modes. Equations (5.4), ( 5.5) and (5.15) are still valid for intermediate modes, but the solution parameters are evaluated differently
from equations (5.12), (5.13), (A.29) and (A.30) assuming \(\eta =2{\hat{s}}\theta \rightarrow \pm \infty \). For the non-resonant modes, we can use the same estimates but put \(\left| \theta \right| \approx 1\), \(\left| \eta \right| \sim {\hat{s}}\) and estimate
The modes away from the resonance conditions are characterised by relatively small extent of tunnelling determined by \(\varsigma \approx \xi \). The probability of localisation in section B delivered by the intermediate modes evolves periodically
and becomes small \(\sim 1/{\hat{s}}^{2}\) for non-resonant modes (despite progressing faster in time than the resonant modes \(\left| t-t_{0}\right| \sim {\hat{\tau }}_{\text {n}}\sim \tau _{0}\ll {\hat{\tau }}_{ \text {r}}\)). Note that the resonant modes also achieve probability P(B\( ,t)\sim 1/{\hat{s}}^{2}\) over time \(t\sim \tau _{0}\) but, unlike the non-resonant modes, they proceed further to deliver P(B\(,t)\sim 1\) when \( t\sim {\hat{\tau }}_{\text {r}}\sim \tau _{0}{\hat{s}}\gg \tau _{0}\).
The estimates of (5.21) and (5.22) remain the same even if a non-resonant mode (say, A-resonant but not B-resonant) is not explicitly coupled with any B-resonant mode. Indeed, over time \(t\sim \tau _{n}\sim \tau _{0},\) this mode would lose correlations with the other modes and according to (A.17) can contribute to particles appearing in section B only a small probability \(\sim 1/{\hat{s}}^{2}\) at any time \( t\gtrsim {\hat{\tau }}_{\text {n}}\). Without a sufficiently large fraction of the resonant modes, the probability of finding tunnelling particles in section B remains small indefinitely. While tunnelling is contributed less by non-resonant modes, these modes are often more numerous than the resonant and intermediate modes.
The fraction of resonant modes is determined by geometry, i.e. by \(x_{{\mathrm{A}}}\) and \(x_{{\mathrm{B}}}\). For example, if \(x_{{\mathrm{A}} }=2x_{{\mathrm{B}}},\) then each second A-resonant mode is also B-resonant. Note that under conditions of \(x_{{\mathrm{A}}}\sim x_{{\mathrm{B}}}\) the fraction of resonant and near-resonant modes cannot fall below \(\sim 1/{\hat{s}}\). First, let us assume \(x_{{\mathrm{A}}}\ge x_{ {\mathrm{B}}}\) or, otherwise, swap A and B. Appendix A(g ) indicates that \(\theta \sim 1/{\hat{s}}\) to achieve near-resonance conditions. Equations (A.19) result in \(j_{{\mathrm{B}} }=\gamma j_{{\mathrm{A}}}-\theta ^{\prime }\) where \(j_{{\mathrm{B}}}\) and \(j_{{\mathrm{A}}}\) are integers, \(\gamma =\) \(x_{{\mathrm{B}}}/x_{ {\mathrm{A}}}\le 1\), and \(\theta ^{\prime }=\theta (1+x_{{\mathrm{B} }}/x_{{\mathrm{A}}})/\pi \sim 1/{\hat{s}}\) is small. Assuming that \(j_{ {\mathrm{B}}}\) can reach 1 for typical energies, the overall fraction of resonant and near-resonant modes \(\left| j_{{\mathrm{B}}}-\gamma j_{{\mathrm{A}}}\right| \lesssim 1/{\hat{s}}\) of all modes \(j_{{\mathrm{A}}}=1,2,3,...\) and \(j_{{\mathrm{B}}}=1,2,3,...\), cannot be smaller than \(\sim 1/{\hat{s}}\). Therefore, despite being relatively small in the numbers of modes, these numbers are sufficient for the resonant and near-resonant modes to dominate tunnelling.
6 Effect of decoherence on tunnelling
This section examines the effects of decoherence on tunnelling, which appear to be substantial and, therefore, detectable in experiments. We begin with a general consideration of decoherence leading to a specific form of the Lindblad equation [57] that corresponds to our understanding of decoherence. The exact physical mechanism responsible for decoherence remains unknown and referred to here as time priming; while the main parameter that quantifies decoherence is its characteristic frequency \( \omega _{d}\). Decoherence is expected to result in loss of coherent interferences without any substantial unitary interactions with the environment [18, 23], measurements [20], or any other effects that may cause a significant redistribution of energy. With exception of the last subsection, we consider effects that are intrinsic or effectively intrinsic. While decoherence triggers equilibration and thermalisation, the latter does involve a redistribution of energy and should not be confused with decoherence, which is deemed to have negligible energy effects. The obtained form of the Lindblad equation is converted into a Pauli master equation [58] for state probabilities, which is subsequently used for determining the effect of decoherence on the tunnelling rates in the resonant and non-resonant cases.
6.1 Decoherence in the context of time priming.
While unitary evolution of a quantum system is fully specified by the Schrödinger equation, our knowledge of decoherence and collapses is much more limited. Let us illustrate this point by a simple example: consider two states of a quantum system
that are expressed in terms the energy eigenstates \(\left| E_{1}\right\rangle \) and \(\left| E_{2}\right\rangle \). The superposition state \(\psi =(\psi _{+}+\psi _{-})/2^{1/2}=\left| E_{1}\right\rangle \) would have its energy measured as \(E_{1}\). Assume that \(\psi \) decoheres into a mixture of \(\psi _{+}\) and \(\psi _{-}\) with equal probabilities. Measuring energy for each of these functions \(\psi _{+}\) and \(\psi _{-}\) would produce either \(E_{1}\) or \(E_{2}\) with equal probability. The choice of \(\psi _{+}\) and \(\psi _{-}\) as the decoherence basis that does not coincide with energy eigenstates results in substantial energy change in the system. In the context of the direction of time, however, decoherence is commonly understood as loss of interference between the components with minimal energy interactions. This, of course, does not exclude other forms of decoherence with stronger interactions and significant energy exchanges and these other forms may be important under some conditions. In the present work, however, we restrict our attention to less energetic forms of decoherence that can be associated with the time primer.
Still, choosing exact energy eigenstates as the basis for decoherence does not solve the problem—these eigenstates continue to exist without interacting with each other and this is not a particularly interesting case. Analysis of decoherence becomes most meaningful when decoherence basis is selected along with eigenstates of the principal part \({\mathbb {H}}_{0}\) of the Hamiltonian \(\mathbb {H=H}_{0}+{\mathbb {H}}^{\prime }\) but there is also a smaller interference component \({\mathbb {H}}^{\prime }\) that acts along with decoherence. It is clear that splitting the Hamiltonian in two parts requires some physical grounds for doing this. For example \({\mathbb {H}}_{0}\) may be Hamiltonian that is intrinsically associated with a system, while \( {\mathbb {H}}^{\prime }\) corresponds to external influence or some other form of interference. In context of particle physics, \({\mathbb {H}}_{0}\) is conventionally related to strong interactions, while \({\mathbb {H}}^{\prime }\) pertains to weak interactions that are known to break the symmetry of the directions of time in CP violations (which seems to be consistent with time-directional character of decoherence). In any case, the decoherence basis that is associated with eigenstates of some Hamiltonian \({\mathbb {H}} _{0} \) must be orthogonal (and is conventionally selected orthonormal). The wave functions undergo unitary transformations \(\left| \psi \right\rangle _{t^{\prime }}={\mathbb {V}}(t^{\prime }-t)\left| \psi \right\rangle _{t}\) but may also experience decoherence events, where the projections \(\left| d_{j}\right\rangle \left\langle d_{j}\right| \left| \psi \right\rangle \) of every wave function \(\psi \) onto the decoherence basis \(\left| d_{1}\right\rangle ,...,\left| d_{n}\right\rangle \) lose their coherence (completely or partially). As considered above, \(\left\langle d_{i}\right| \left| d_{j}\right\rangle =\delta _{ij}\) since \(\left| d_{j}\right\rangle \) satisfies \({\mathbb {H}}_{0}\left| d_{j}\right\rangle =E_{j}^{\circ }\left| d_{j}\right\rangle \).
Consider the density matrix \({\varvec{\rho }}\), which generally evolves by unitary transformations \({\varvec{\rho }}^{\prime }={\mathbb {U}}{\varvec{\rho }} {\mathbb {U}}^{\dagger }\) but also experiences decoherence events, where it is transformed by the Kraus operators \({\mathbb {K}}_{j}\)
Note that equation (6.2) represents a specific form of the Kraus transformation
that corresponds to specific action of decoherence that is discussed above (assuming \(0\le \lambda \le 1\)) and, at least in principle, can be associated with the time primer. The last constraint in (6.2) is satisfied since, obviously, \(\Sigma _{j}\left| d_{j}\right\rangle \left\langle d_{j}\right| ={\mathbb {I}}\) . If \(\lambda =0\), transformation (6.2) is identical \({\varvec{\rho }} ^{\prime }={\mathbb {I}}{\varvec{\rho }}\) and no decoherence occurs. If \( \lambda =1\), the projections on the decoherence basis becomes fully independent. The transformation (6.2) with \(\lambda ^{\prime }=1-(1-\lambda )^{-1}\) reverses (6.2) with \(\lambda \) and, therefore, represents recoherence. While Kraus operators are convenient to characterise discrete decoherence events that interrupt unitary evolution, continuous decoherence can be conventionally described by the Lindblad operators \({\mathbb {L}}_{j}={\mathbb {K}}_{j}/\sqrt{\lambda }\) so that
Assuming that \(\lambda =\Delta t/\tau _{d}\), we obtain
where the Hamiltonian term reflects a time differential of the unitary transformation \({\varvec{\rho }}^{\prime }={\mathbb {U}}{\varvec{\rho }}{\mathbb {U}} ^{\dagger }.\) Dividing this equation by \(\Delta t\) and taking the limit \( \Delta t\rightarrow 0\) leads to a specific, simple form of the Lindblad equation
The simplification of the Lindblad equation is due to the relation \(\sum _{j} {\mathbb {L}}_{j}^{\dagger }{\mathbb {L}}_{j}={\mathbb {I}}\), which is valid here but not satisfied in the general case. The value \(\tau _{d}\) represents the characteristic decoherence time. Since \({\mathbb {L}}_{j}\) are Hermitian and \( \tau _{d}>0\) in this form of the Lindblad equation, the evolution governed by (6.6) does not decrease entropy [59].
While the physical implications of discrete and continuous decoherence should be similar, we, for the sake of transparency, consider discrete decoherence events specified by (6.2) with \(\lambda =1\) and spaced by the characteristic decoherence time \(\tau _{d}\). The decoherence events suppress all non-diagonal elements of the density matrix, while the unitary evolution \({\varvec{\rho }}^{\prime }={\mathbb {U}}{\varvec{\rho }}\mathbb { U}^{\dagger }\) persists between the decoherence events [14]. Hence, the density matrix is transformed by the unitary evolution and a subsequent decoherence event as
over each of the intervals \([t,t^{\prime }],\) where \(t^{\prime }=t+\tau _{d}\) . Here, \(U_{kj}\) represent the components of the unitary evolution operator \( {\mathbb {U}}(t^{\prime }-t)\). Considering long times \(t>\tau _{d}\), we conclude that the probabilities \(P_{j}=\rho _{jj}\) are transformed according to
which, essentially, is a Pauli master equation describing evolution of a Markov chain with transitional probabilities given by deviations of \( \left| U_{kj}\right| ^{2}\) from the unity matrix.
Despite the existence of many theories [9, 60, 61], there is no certainty about the exact effect of decoherence on wave functions distributed in space. We, however, expect loss of coherence between energy eigenstates with substantially different energies, as well as expect and are primarily interested in losses of coherence between the branches of the wave functions located in sections A and B, which converts coherent waves into a mixture of probabilities for particle presence in these sections. In any case, decoherence can be characterised by its principal parameter—the characteristic frequency of decoherence \(\omega _{d}\) or the characteristic decoherence time \(\tau _{d}=1/\omega _{d}\), which is featured in equation ( 6.7).
6.2 Effect on the resonant and near-resonant modes
If the characteristic time of decoherence is longer than the resonance tunnelling time \(\tau _{d}>{\hat{\tau }}_{\text {r}}\approx \tau _{0}{\hat{s}},\) decoherence has little effect on the tunnelling rate but even infrequent decoherence changes the character of the solution—it relaxes towards stationary distributions instead of oscillating indefinitely. When, however, the decoherence time becomes short \(\tau _{d}<{\hat{\tau }}_{\text {r}}\) (but not too short \(\tau _{d}>\tau _{0}\)) it converts the unitary evolution of the resonance modes, which is specified by (5.9)-(5.11) and (5.15) in the basis of the partition states, into a Markov process, which according to (6.7) is given by
where \({\tilde{\tau }}_{\text {r}}=W/\tau _{d},\) \(W=\left| U_{{\mathrm{AB }}}\right| ^{2}\) and \(\left| U_{{\mathrm{AB}}}\right| \sim 2\varsigma \sin \left( \Delta \omega \tau _{d}/2\right) ,\ \ \varsigma =\left| \xi \right| /(1+\xi ^{2})\) is the off-diagonal component of the unitary evolution matrix (5.11) and \(\Delta \omega \) is given by ( 5.16). Note that, according to (6.8), the extent of tunnelling is no longer limited by \(\varsigma \). Since \(\Delta \omega ^{-1}\sim {\hat{\tau }}_{\text {r}}>\tau _{d}\) , the sine can be expanded \(\left| U_{{\mathrm{AB}}}\right| \sim \varsigma \Delta \omega \tau _{d}\). For exact resonance, we assume \(x_{{\mathrm{B}}}\sim x_{{\mathrm{A}}}\), put \(\eta =0\), \( \varsigma \sim 1\) and obtain
This expression reflects the quantum Zeno effect, which is well-known and has been recently demonstrated in experiments [20] applying frequent measurements to quantum tunnelling. Increasing frequency of decoherence reduces the rate of tunnelling for resonant modes. Note that, even in the presence of decoherence, the resonant modes do not lead to the same density of particles in both sections (when \(x_{{\mathrm{A}}}\ne x_{{\mathrm{B}}}\)) but to the equal probabilities of being in these sections \(P_{{\mathrm{A}}},P_{{\mathrm{B}}}\rightarrow 1/2\) as \( t\rightarrow \infty \). This is consistent with general expectations of statistical quantum mechanics: the amplitudes of modes having similar energies are expected to be similar under equilibrium conditions.
6.3 Effect on the non-resonant and intermediate modes.
For non-resonant modes, we can estimate \(\Delta \omega \sim 1/\tau _{0}\) and \(\left| U_{{\mathrm{AB}}}(t)\right| \sim 1/{\hat{s}}\) for any \( t\gtrsim \tau _{0}\)—see equations (5.21) and (5.11). Hence, decoherence of a moderate intensity \(\tau _{d}>\tau _{0}\) leads to \( W=\left| U_{{\mathrm{AB}}}\right| ^{2}\sim 1/{\hat{s}}^{2}.\) The characteristic frequency \({\tilde{\omega }}\) and time \({\tilde{\tau }}\) of tunnelling associated with decoherence of non-resonant modes becomes
Decoherence promotes tunnelling carried by non-resonant modes and impedes tunnelling conducted by resonant modes. While \({\tilde{\omega }}\) specified by ( 6.10) is generally smaller than \({\tilde{\omega }}\) given by (6.9) (assuming \(\tau _{d}>\tau _{0}\)), the non-resonant modes are likely to be more numerous. The A-resonant modes are primarily responsible for tunnelling from A to B and the B-resonant modes are primarily responsible for tunnelling from B to A. The overall tunnelling rate is an aggregate of the tunnelling rates produced by each mode and estimated by ( 6.10). Note that the ratio of the number of A-resonant the number of B-resonant modes is roughly proportional to \(x_{{\mathrm{A}}}/x_{{\mathrm{B}}}\) for a given small energy interval; hence, in the equilibrium (or near-equilibrium) conditions, where modes with close energies must have similar amplitudes, the probability of finding a particle in a particular section (e.g. A or B) is proportional to the volume of this section. Note that Markov models (6.8) do not constrain the extent of tunnelling by its unitary value \(\varsigma ,\) but promote equidistribution between modes.
The estimates for the intermediate modes are similar \(\Delta \omega \sim \left| \eta \right| /({\hat{s}}\tau _{0})\) and \(\left| U_{{\mathrm{AB}}}(t)\right| \sim \left| \xi \right| \sim 1/\left| \eta \right| \) for any \(t\gtrsim \tau _{0}{\hat{s}}/\left| \eta \right| ,\) where parameter \(\eta =2{\hat{s}}\theta \) is moderately large \( 1\ll \left| \eta \right| =2{\hat{s}}\left| \theta \right| \ll {\hat{s}}\) and determines how far the mode is from the resonance and \( \left| \eta \right| \sim {\hat{s}}\) corresponds to non-resonant modes. The tunnelling rate depends on relative values of \(\Delta \omega \) and \( \omega _{d}\)
6.4 The effect of intensive decoherence
Finally as decoherence becomes more intensive and \(\tau _{d}\lesssim \tau _{0},\) the coherent solutions cannot be sustained within each section of the box—the model of standing and evolving waves gives way to quantum particles represented by wave packets. The coherent solutions stretching from one side of the section to another are meaningless if the characteristic decoherence time is shorter than the time of reflection from the walls. In these conditions, we necessarily use the transmission \( \left| q\right| ^{2}\) and reflection \(\left| r\right| ^{2}\) probabilities associated with tunnelling, which are specified by (A.7) for the case under consideration. There is no longer any difference between the resonant and non-resonant modes. The probabilities of location in section A and section B are governed by the following Markov chain
where the intensity of collisions with the barrier is evaluated to be proportional to \(u_{0}/(2x)\). Assuming \(x_{{\mathrm{A}}}\approx x_{{\mathrm{B}}}\approx x_{0}\) With \(\left| q\right| ^{2}\) given by (A.7), the transmission frequency becomes
Note the consistency of (6.13) with the previous estimates (6.9) and (6.10), which can be converted into (6.13) by substituting \(\tau _{d}=\tau _{0}\). The model (6.13) based on tunnelling probabilities should be valid for a wide range of small decoherence times \(\tau _{d}\lesssim \tau _{0},\) perhaps as long as decoherence does not interfere with the actual passage through the barrier.
6.5 Intrinsic versus environmental decoherence
The tunnelling frequencies are shown versus the decoherence frequency for different modes in Fig. 3. The tunnelling frequency of the resonant modes decreases with increasing \(\omega _{d}\) while the tunnelling frequency of the non-resonant modes increases with increasing \(\omega _{d}\) up until the both types of modes reach the common value specified by (6.13). The figure also shows an intermediate mode that displays features that are intermediate between the resonant and non-resonant modes. The effect of intrinsic decoherence is complex but can be broadly characterised by enhancing the extent of tunnelling and promoting equidistribution (and, effectively, equilibration) of the particle locations between sections A and B.
Note that the effect of intrinsic (or effectively intrinsic) decoherence on tunnelling considered here is generally different from the decoherence effect produced by unitary interactions with a larger system or with the environment. Unlike the former, the latter does not enhance the extent of tunnelling. The effect of environmental interference does not become significant until its energy of interactions becomes comparable with the energy gap \(E_{+}-E_{-}\). The effect of such significant decoherence is conventionally described by the Zurek theory [7], which indicates that the rate of tunnelling increases significantly when the energy of interactions exceeds the energy gap (see Appendix B). If some minor energy exchanges (much smaller than those required by thermalisation) are allowed in addition to the classical interpretation of decoherence, then the acceleration of tunnelling mentioned above would be supplemented by a reduction of the extent of tunnelling, which may result in the effective termination of tunnelling (see Appendix B (b)). One can see that different types of decoherence affect tunnelling differently and, therefore, can (at least in principle) be distinguished in experiments.
7 Discussion of the experiment
The Reichenbach conjecture suggests that all branch systems tend to evolve forwards in time towards equilibrated and thermalised conditions, even if they are fully isolated from the rest of the universe. Obtaining experimental confirmation or repudiation of this conjecture would be of principal importance for our understanding of the universe. Thermalisation, however, is the overall outcome of numerous microscopic processes, whose fine mechanisms are concealed by the significance and magnitude of the outcome. We, therefore, are interested in and focus on decoherence that, as one would hope, can provide more information about the actual mechanisms of time priming than thermalisation. We assume, by default, that the active phase of the experiment \(-t_{s}\le t\le +t_{s}\) is faster than the rate of thermalisation \(t_{s}\ll \tau _{t}.\) The thermalisation time \(\tau _{t}\) can be assessed during the passive phase of the experiment (e.g. by examining the system after \(t=+t_{s},\) when, as discussed in Sect. 4, thermalisation is expected to screen the active phase of the experiment from the final conditions, even if such final conditions are imposed on the system by postselection).
The present work analyses different regimes of interference between decoherence and tunnelling, producing a range of behaviours illustrated in Fig. 3 and in Appendix B. The frequency of decoherence can be estimated indirectly by measuring the tunnelling rates. Although some of these experiments might be difficult to conduct, experimental studies of decoherence [23, 24] and tunnelling [18, 20, 22] that have some parallels with the present analysis have been successfully carried out in the past. These experiments, however, need to be modified to reduce influence of the environment, avoid both thermalisation and near-zero temperatures, and satisfy a number of conditions discussed below. As described in Sect. 3, the suggested experiments involve trapping quantum particles in section A, allowing them to tunnel to another section B and measuring the tunnelling rates. This seems straightforward but the devil is always in the details.
In order to examine the effect of decoherence on tunnelling experimentally, the characteristic times of tunnelling \({\hat{\tau }}\approx {\hat{s}}\tau _{0}= {\hat{s}}x_{0}/u_{0}\) and decoherence \(\tau _{d}\) must be comparable. The key point of the experiment is selecting experimental parameters so that the transition between coherent and non-coherent regimes is observed. While the characteristic time of tunnelling \({\hat{\tau }}\) can be changed in experiments (although only within certain limits that are determined by the conditions of the experiment), \(\tau _{d}\) is expected to be very small for macroscopic objects and very large (possibly infinite) for elementary particles. Hence, the number of particles in the experiment needs to be selected so that the expected decoherence rate for this system is not too large and not too small.
This experiment is concerned with the state of the quantum system when all external interferences are (gradually) removed. As we increase the isolation of the system by encircling it with perfect insulators, mirrors and shields, screening the system from cosmic radiations and other forms of environmental interferences, the intensity of environment-induced decoherence should also reduce in proportion to the reduction of its cause. We might observe that at some stage decoherence disappears or becomes too small and infrequent to be detected—in this case, we, as discussed above, need to increase the scale of the experiment to bring the rate of decoherence into the measurable range. If decoherence does not reappear even for sufficiently large, macroscopic objects and decoherence can be reduced below any given level by increasing isolation of a system, this would demonstrate the incorrectness of the Reichenbach conjecture.
We assume, however, that the Reichenbach conjecture is correct and there is a component of decoherence that cannot be eliminated by progressive isolation of the system under any circumstances. We refer to such ineliminable component as intrinsic (or effectively intrinsic). Measuring the rate of tunnelling gives us information not only about the decoherence rate but also about its nature. The effects of intrinsic and environmental decoherences are similar in some respects but, as discussed in Sect. 6(6.5), are different in others. One of the most interesting outcomes of the experiments would be determining which of the two patterns is followed by the ineliminable component of decoherence.
Any experiments that can bring some light into this matter and demonstrate either existence of an (effectively) intrinsic component of decoherence or its absence would be of the highest importance. The arrow of time is real and so must be its time primer—an underlying physical mechanism that enacts the direction of time—but, generally, it is difficult to say whether this mechanism can be confidently detected under the current level of technology.
The tunnelling experiments can be conducted with different particles: photons, electrons, protons and, possibly, neutrons or even atomic nuclei are the most likely candidates. The best choice of particles is not clear—while tunnelling is easier to achieve with lighter particles, photons are expected to be decoherence-neutral [45] and thus are less likely to exhibit any intrinsic decoherence. Considering that the known cases of CP violations, which have been detected in hadrons [62, 63], imply violation of the symmetry of time (assuming CPT invariance) and that high-energy hadron collisions seem to lead to thermodynamic behaviour in quark-gluon plasma [64, 65], we infer that these experiments point in the direction of protons and nuclei as the most interesting particles for these experiments—these particles are most likely to possess properties associated with intrinsic decoherence, presuming that such properties exist [2]. (Note that thermodynamic interferences may become apparent as ostensible CPT violations in systems that are in fact CPT-preserving [44].) The experiment needs to be organised so that the tunnelling particles are baryons (or are in contact with baryons although jointly isolated from the environment). While cooling the surrounding to near-zero temperatures to control environmental interferences seems like a good idea, cooling the system is generally not desirable since this may dramatically reduce the magnitude of intrinsic decoherence or completely freeze it.
If time-directional behaviour associated with decoherence can be detected in the tunnelling of protons, it seems logical to conduct similar experiments with antiprotons (assuming that the substantial practical difficulties associated with such experiments can be overcome). Since conventional thermodynamics can be extended from matter to antimatter in two possible mutually exclusive ways: symmetric (i.e. CP-invariant) and antisymmetric (i.e. CPT-invariant) [14, 39, 45], decohering behaviour of antiparticles is of particular interest. The CPT-invariant version of thermodynamics expects antibaryons to predominantly recohere while the CP-invariant version of thermodynamics insists that both baryons and antibaryons must exhibit the same decohering behaviour.
8 Conclusion
The present work evaluates the effect of decoherence on the dynamic of quantum tunnelling, carried out by resonant, intermediate and non-resonant modes under generally non-equilibrium conditions that exist during the active phase of the experiments. Decoherence tends to enhance tunnelling by non-resonant modes and attenuate resonant tunnelling. The main conclusion of the present analysis is that, under conditions considered here, the rate of decoherence substantially affects the rate of tunnelling, and therefore can be determined or estimated by measuring the rate of tunnelling. This seems to be easier and less intrusive than direct testing of the coherent states. The effects noted above become clear when the quantum barrier is high (\(\hat{ s}\gg 1\)), the tunnelling transmission coefficient is low and the energy eigenstates on both sides of the barrier are weakly coupled.
The problem of interference from the environment and measurements, which inevitably cause decoherences and collapses, is especially pertinent to examining decoherence. In simple terms, quantum measurements are bound to cause the effects that they are intended to detect not create. Hence, measuring the decoherence rates indirectly, through proxies is always preferable. Examining tunnelling rates as proxies for decoherence rates and using ancillary quantum systems to avoid direct interference seem very useful in this context.
This work shows that despite a significant degree of similarity, the intrinsic (or effectively intrinsic) and unitary environmental mechanisms of decoherence, affect the tunnelling rates differently and, therefore, can be, at least in principle, experimentally distinguished from each other. In such experiments, we need to minimise environmental interferences and avoid strong interactions between different modes causing substantial energy exchanges and thermalisation.
The principal question that was formulated by Hans Reichenbach half a century ago and still remains unanswered is whether thermodynamic directionality of time would persist in fully isolated conditions. While Reichenbach’s conjecture (that it would) seems more probable, scientific questions of this kind cannot be answered without experimental evidence. If the arrow of time persists, there must be a dynamic mechanism (which we call the time primer) that is responsible for this, and this mechanism should be experimentally testable. This work suggests that these issues can be examined in experiments involving quantum tunnelling.
Data availability
Not applicable
References
Shi Z, Abe S (2020) Quantum weak invariants: Dynamical evolution of fluctuations and correlations. Entropy 22(11)
Klimenko AY (2020a) Mixing, tunnelling and the direction of time in the context of Reichenbach’s principles. In: de Gier J et al (eds) 2019-20 MATRIX Annals (MATRIX Book Series 4). pp 387–409
Zurek WH (2002) Decoherence and the transition from quantum to classical - revisited. Los Alamos Sci 27:1–26
Bassia A, Ghirardi G (2003) Dynamical reduction models. Phy Rep 379:257–426
Beretta GP (1981) On the general equation of motion of quantum thermodynamics and the distinction between quantal and nonquantal uncertainties. MIT. arXiv: quant-ph/0509116, 2005
Stamp PCE (2012) Environmental decoherence versus intrinsic decoherence. Philosophical Trans Series A Math Phy Eng Sci 370(1975):4429
Zurek WH (1982) Environment-induced superselection rules. Phys Rev Lett 26(8):1862–1888
Joos E (1984) Continuous measurement: Watchdog effect versus golden rule. Phy Rev D 29(8):1626–1633
Joos E, Kiefer C, Zeh HD (2003) Decoher Appear Classical World in Quantum Theory, 2nd edn. Springer Berlin Heidelberg, Berlin, Heidelberg
Schlosshauer M (2005) Decoherence, the measurement problem, and interpretations of quantum mechanics. Rev Mod Phys 76:1267–1305
Goldstein S, Lebowitz JL, Tumulka R, Zanghi N (2006) Canonical typicality. Phys Rev Lett 96:050403
Popescu S, Short AJ, Winter A (2006) Entanglement and the foundations of statistical mechanics. Nat Phy 2(11):754–758
Yukalov VI (2011) Equilibration and thermalization in finite quantum systems. Laser Phy Lett 8(7):485–507
Klimenko AY (2016) Symmetric and antisymmetric forms of the Pauli master equation. Sci Rep (nature.com) 6:29942
Klimenko AY (2019) The direction of time and Boltzmann’s time hypothesis. Physica Scripta 94:034002
Landau LD, Lifshits EM (1980) Course of Theor Phy vol.3: Qunatum Mech. Butterworth-Heinemann, Oxford
Razavy Mohsen (2003) Quantum Theory of Tunnel. World Scientific, Singapore
Dattagupta Sushanta, Dattagupta Sushanta, Puri Sanjay (2004) Dissipative Phenomena in Condensed Matter Some Applications / by Sushanta Dattagupta, Sanjay Puri. Springer Series in Materials Science, 71. Berlin, Heidelberg
Elçi A, Hjalmarson HP (2009) The tunneling solutions of the time-dependent schrödinger equation for a square-potential barrier. Journal of Mathematical Physics 50(10)
Patil YS, Chakram S, Vengalattore M (2015) Measurement-induced localization of an ultracold lattice gas. Phy Rev Lett 115(14):140402
Smith Kevin, Blaylock Guy (2017) Simulations in quantum tunneling. Am J Phy 85(10):763–768
Poltavsky Igor, Zheng Limin, Mortazavi Majid, Tkatchenko Alexandre (2018) Quantum tunneling of thermal protons through pristine graphene. The Journal of Chemical Physics 148(20)
Imry Yoseph (2002) Introduction to mesoscopic physics / Yoseph Imry. Mesoscopic physics and nanotechnology ; 2, 2nd edn. Oxford University Press, Oxford; New York
Deléglise S, Dotsenko I, Sayrin C, Bernu J, Brune M, Raimond J-M, Haroche S (2008) Reconstruction of non-classical cavity field states with snapshots of their decoherence. Nature 455(7212)
Misra B, Sudarshan ECG (1977) The Zeno’s paradox in quantum theory. J Math Phy 18(4):756–763
Aharonov Y, Bergmann PG, Lebowitz JL (1964) Time symmetry in the quantum process of measurement. Phys Rev B 134:1410
Aharonov Yakir, Vaidman Lev (1998) On the two-state vector reformulation of quantum mechanics. Physica scripta 1998(1):85
Aharonov Y, Vaidman L (2008) The two-state vector formalism: An updated review. Lect Notes Phys 734:399–447
Boltzmann L, Lectures on gas theory. English translation by S.G. Brush. University of California Press, Berkeley and L.A., 1964 (1895,1897)
Penrose R (2005) Road to Reality: A Complete Guide to the Laws of the Universe. A. Knopf Inc., New York
Albert David Z (2000) Time and chance. Harvard University Press, Cambridge, Mass
North J (2011) Time in thermodynamics. In: The Oxford Handbook of Philosophy of Time. Oxford University Press
Reichenbach H (1956) The direction of time. University of California Press, Berkeley. (reprinted 1971)
Davies PCW (1977) The Physics of Time Asymmetry. University of California Press, Berkeley
Sklar Lawrence (1993) Physics and chance : Philosophical issues in the foundations of statistical mechanics. Cambridge University Press, Cambridge
Winsberg Eric (2004a) Can conditioning on the “past hypothesis’’ militate against the reversibility objections? Philosophy of Sci 71(4):489–504
Winsberg Eric (2004b) Laws and statistical mechanics. Philosophy of Sci 71(5):707–718
Sevick EM, Prabhakar R (2008) Stephen R Williams, and Debra J Searles. Fluctuation Theorems 59(1):603–633
Klimenko AY, Maas U (2014) One antimatter- two possible thermodynamics. Entropy 16(3):1191–1210
Maas U (2020) Some aspects of time-reversal in chemical kinetics. Entropy 22(12):1386
Klimenko AY, Bernhardt D (2021) The second law and asymmetry of time (special issue). Entropy 22–23
Price H (1996) Time’s Arrow and Archimedes’ Point: New Directions for the Physics of Time. Oxford Univ. Press, Oxford, UK
Penrose R (1996) On gravity’s role in quantum state reduction. General Relativity and Gravit 28(5):581–600
Klimenko AY (2014) Note on invariant properties of a quantum system placed into thermodynamic environment. Physica A: Stat Mech Appl 398:65–75
Klimenko AY (2017) Kinetics of interactions of matter, antimatter and radiation consistent with antisymmetric (CPT-invariant) thermodynamics. Entropy 19:202
Klimenko AY (2020b) On quantum tunnelling with and without decoherence and the direction of time. arXiv:quant-ph/2011.12955v1
Vepsalainen Antti P, Karamlou Amir H, Orrell John L, Dogra Akshunna S, Loer Ben, Vasconcelos Francisca, Kim David K, Melville Alexander J, Niedzielski Bethany M, Yoder Jonilyn L, Gustavsson Simon, Formaggio Joseph A, VanDevender Brent A, Oliver William D (2020) Impact of ionizing radiation on superconducting qubit coherence. Nature 584(7822):551–556
Cramer JG (1986) The transactional interpretation of quantum mechanics. Rev Modern Phy 58(3):647–687
Yndurain FJ (2012) Relativistic Quantum Mechanics and Introduction to Field Theory. Theoretical and Mathematical Physics. Springer
Dirac PAM (1928) The quantum theory of the electron. Proceed Royal Soc London. Series A 117(778):610–624
Sakharov AD (1967) Violation of CP invariance, C asymmetry, and baryon asymmetry of the universe. J Exp Theor Phys 5:24–27
Gell-Mann Murray, Hartle James B (1993) Time symmetry and asymmetry in quantum mechanics and quantum cosmology. In: Halliwell J, Perez-Mercader J, Zurek W (eds) Phy Orig of Time Asym. Cambridge University Press, Cambridge
Griffiths RB (1984) Consistent histories and the interpretation of quantum mechanics. J Stat Phy 36(1–2):219–272
Griffiths RB (2019) The Consistent Histories Approach to Quantum Mechanics. In: Zalta EN (ed) The Stanford Encyclopedia of Philosophy
Aharonov Y, Vaidman L (1991) Complete description of a quantum system at a given time. J Phy A, Math General 24(10):2315–2328
Tamir Boaz, Cohen Eliahu (2013) Introduction to weak measurements and weak values. Quanta (Isperih) 2(1):7–17
Lindblad G (1976) On the generators of quantum dynamical semigroups. Commun Math Phy 48(2):119–130
Pauli W (1928) Uber das h-theorem vom anwachsen der entropie vom standpunkt der neuen quantenmechanik. In: Probleme der Modernen Physik. Arnold Sommerfeld zum 60 Geburtstage. Hirzel, Leipzig, pp 30–45
Ou C, Chamberlin RV, Abe S (2017) Lindbladian operators, von Neumann entropy and energy conservation in time-dependent quantum open systems. Physica A: Stat Mech Appl 466:450–454
Schlosshauer MA (2007) Decoherence and the quantum-to-classical transition. The frontiers collection. Springer, Berlin ; London
Zeh HD (2007) The physical basis of the direction of time, 5th edn. Springer, New York;Berlin
Beringer J et al, (Particle Data Group) (2012) The review of particle physics. Phys. Rev. D 86:010001
Lees JP et al, (BABAR Collaboration) (2016) Tests of \(cpt\) symmetry in \({B}^{0}\)-\({{\overline{b}}}^{0}\) mixing and in \({B}^{0}{\rightarrow }c{\overline{c}}{K}^{0}\) decays. Phys. Rev. D 94:011101
Braun-Munzinger P, Stachel J (2007) The quest for the quark-gluon plasma. Nature 448(7151):302–309
Andronic A, Braun-Munzinger P, Stachele J, Stöckera H (2011) Production of light nuclei, hypernuclei and their antiparticles in relativistic nuclear collisions. Phy Lett B 697:203–207
Kolmogorov AN, Fomin SV (1970) Introductory real analysis. Prentice-Hall, Englewood Cliffs, N.J
Funding
Not applicable
Author information
Authors and Affiliations
Contributions
Not applicable
Corresponding author
Ethics declarations
Conflict of interest
The author states that there is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A. Tunnelling in a box and energy eigenstates
This Appendix presents equations for particle tunnelling in a rectangular box and is subject to conditions imposed by the box boundaries—the problem is selected to allow for a complete and transparent analytical evaluation. The results are used in the main body of the paper. Various tunnelling solutions can be found in vast literature dedicated to this topic [16, 17, 19].
1.1 (a) Tunnelling through symmetric barriers
The quantum outcomes of tunnelling can be expressed by the scattering matrix \({\mathbb {S}}\), which is a unitary matrix (\({{\mathbb {S}}}{{\mathbb {S}}}^{\dag }=\mathbb {I}\)) that connects the amplitudes \(A^{-}\) and \(B^{-}\) of incoming waves \( A^{-}e^{-i(\omega t+kx)}\) and \(B^{-}e^{-i(\omega t-kx)}\) with the amplitudes \(A^{+}\) and \(B^{+}\) of the outgoing waves \(A^{+}e^{-i(\omega t-kx)}\) and \(B^{+}e^{-i(\omega t+kx)}\) (see Fig. 4) so that:
In the last expression for \({\mathbb {S}}\) in (A.1), the quantum barrier is assumed to be symmetric, which corresponds to a symmetric matrix \( {\mathbb {S}}\), which is invariant with respect swapping A and B. The first expression for \({\mathbb {S}}\) is general provided \(\left| {\tilde{q}} \right| ^{2}+\left| {\tilde{r}}\right| ^{2}=1\). The reflection r and transmission q coefficients satisfy \(\left| q\right| ^{2}+\left| r\right| ^{2}=1\) and \(\left| r^{2}-q^{2}\right| =1\) (implying that \(\chi =q^{2}/r^{2}\) is real and \(\chi \le 0\)) due to the unitary of \({\mathbb {S}}\). Hence, \(q=\pm ir(\left| r\right| ^{-2}-1)^{1/2}\) and \(r=\mp iq(\left| q\right| ^{-2}-1)^{1/2}\).
The matrix \({\mathbb {S}}\) should not be confused with the commonly used transfer matrix \({\mathbb {M}}\) that links the wave amplitudes on one side of the barrier to the wave amplitudes on the other side.
where
and \(q^{2}-r^{2}=-r^{2}/\left| r^{2}\right| =q^{2}/\left| q^{2}\right| \).
The values of r and q can be easily evaluated for a rectangular barrier of height \(V_{0}\) and width \(\Delta x\) [2, 16]. Assuming that \( V_{0}\rightarrow \infty \) and \(\Delta x\rightarrow 0\) so that \(s\ =V_{0}\Delta x\ \sim {\mathrm{const}}\) and \(V(x)\rightarrow s\delta (x),\) we obtain
where
If \(A^{+}=\left( A^{-}\right) ^{*}=A,\) then (A.2)-(A.4) yield \(B^{+}=\left( B^{-}\right) ^{*}=B=A^{*}-i{\hat{s}}(A+A^{*})\) and
With \(\left| q\right| ^{2}\) ranging from 1 to 0 and \(\left| r\right| ^{2}\) ranging from 0 to 1 as \({\hat{s}}\) increases from 0 to \( \infty \), the barrier shaped as the delta function is a basic representation for many other barriers. Generally, r and q can be jointly multiplied by any arbitrary phase \(e^{i\vartheta _{1}}\) and preserve unitarity of \(\mathbb { S}\) (if the barrier is non-symmetric, then \({\mathbb {S}}\) involves another arbitrary angle \(\vartheta _{2}\)) but, if the phase shifts are not of major concern, the delta function tends to provide a good model for interactions of a wave function of given k with the barriers.
If \({\hat{s}}\rightarrow \infty \), the transmission \(\left| q\right| ^{2}\) and reflection \(\left| r\right| ^{2}\) probabilities are given by
These equations are special cases of more general expressions for the transmission and reflection probabilities obtained by Igor Vladimirov (2008, unpublished).
1.2 (b) Energy eigenstates
The eigenstates of the Schrödinger equation (4.5)
are to be determined within the interval \(-x_{{\mathrm{B}}}\le x\le x_{ {\mathrm{A}}}\) with homogeneous boundary conditions
and singular potential \(V(x)=s\delta (x)\). The parameter s is assumed to be sufficiently large so that the probabilities of tunnelling through the barrier are low.
1.3 (c) Note on singular potentials
Consider a rectangular barrier \(V=V_{0}\) at \(-\Delta x/2\le x\le +\Delta x/2\) and \(V=0\) elsewhere. The limit \(V_{0}=V_{n}^{\circ }\rightarrow \infty , \) \(\Delta x=\Delta x_{n}\rightarrow 0\) as \(n=1,2,...\) so that \( V_{n}^{\circ }\Delta x_{n}=s\) corresponds to introducing singularity \( V(x)=V_{n}(x)\rightarrow s\delta (x)\) into the model. The presence of the delta function \(\delta (x)\) in the potential does not affect validity of the Hilbert–Schmidt theorem. With the use of the Green function \(\tilde{\mathbb { H}}G(x,x_{0})=\delta (x-x_{0})\) and \(G=0\ \)at \(x=x_{{\mathrm{A}}}\ \)and \(x=x_{{\mathrm{B}}}\), the eigenstate problem \(\tilde{{\mathbb {H}}}\tilde{ \Psi }_{j}={\tilde{E}}_{j}{\tilde{\Psi }}_{j}\) is conventionally converted into a Fredholm integral equation
where the integral operator \(\mathbb {G={\tilde{H}}}^{-1}\) is compact and Hermitian in compliance with the conditions of the Hilbert–Schmidt theorem. In three-dimensional case, the Green function defined by \({\mathbb {H}}G( {\mathbf {r}},{\mathbf {r}}_{0})=\delta ({\mathbf {r}}-{\mathbf {r}}_{0})\) and \(G=0\ \)at \({\mathbf {r}}\in \partial \)AB can be used to convert the eigenstate problem \( {\mathbb {H}}\Psi _{j}=E_{j}\Psi _{j}\) into integral equation. Since the sequence \({\mathbb {G}}_{n}\) of integral operators \({\mathbb {G}}_{1},{\mathbb {G}} _{2},...\) corresponding to \(V_{0}=V_{1}^{\circ },V_{2}^{\circ },...\) converge \({\mathbb {G}}_{n}\rightarrow {\mathbb {G}}_{\delta }\) by the operator norm when \(n\rightarrow \infty \) and \(V_{n}(x)\rightarrow s\delta (x)\), the theorem by Kolmogorov and Fomin [66] (Theorem 1, Sec. 2, Chpt. 6, Part IV ) ensures that the limiting integral operator \({\mathbb {G}} _{\delta }\) is compact and, obviously, Hermitian. Hence, solution (4.3 ) must be universally valid even for singular potentials \(V(x)=s\delta (x)\). The system of energy eigenstates is complete in Hilbert space and covers all possible evolutions of the Schrödinger equation.
1.4 (d) Eigenfunctions for a delta-function barrier
Since Hamiltonian \(\tilde{{\mathbb {H}}}\) is time-symmetric, the energy eigenstates \({\tilde{\Psi }}_{j}\) can be treated as real without loss of generality. Assuming \(V(x)=s\delta (x),\) the solution of (A.8) with boundary conditions (A.9) is given by
The amplitudes \(A_{j}\) and \(B_{j},\) which are assumed real, are constrained by (A.6) (i.e. \(2A=-iA_{j}e^{i\alpha _{j}}\) and \(2B=-iB_{j}e^{i\beta _{j}}\)), that is by continuity of the functions \(\ x=0\) and jumps of the derivatives induced by \(V=s\delta (x)\)
Dividing the second equation by the first equation and substituting \(\alpha _{j}\) and \(\beta _{j}\) from (A.11) yields the dispersion equation
that determines energy eigenvalues
in terms of \({\tilde{s}}=ms/\hbar ^{2}\). The amplitude ratio is then given by
In the rest of the analysis, we assume that \({\hat{s}}={\tilde{s}}/k\) is large for typical values of k to simplify the equations and obtain conditions that are of interest for our consideration.
1.5 (e) The resonance case
In this case, \(x_{{\mathrm{B}}}=x_{{\mathrm{A}}}=x_{0}\) and all modes are resonant. Two family of solutions are distinguished: first, antisymmetric \({\tilde{\Psi }}_{j}(-x)=-{\tilde{\Psi }}_{j}(x),\) smooth at \(x=0\) with \(k_{j}\) specified by \(\sin (k_{j}^{(\text {a})}x_{0})=0;\) and, second, symmetric \({\tilde{\Psi }}_{j}(-x)={\tilde{\Psi }}_{j}(x),\) V-shaped at \(x=0\) with \(k_{j}\) evaluated from \(\cot (k_{j}^{(\text {s})}x_{0})=-{\tilde{s}}/k_{j}^{( \text {s})}\). Note that \(\left| B_{j}\right| =\left| A_{j}\right| \) for both of the families. Assuming that \({\hat{s}}={\tilde{s}} /k_{j}\) is large, we expand \(\cot (\pi j+\alpha )=1/\alpha +...\) and obtain
where\(\ j=1,\) 2, 3, ... for both the symmetric (s) and antisymmetric (a) modes.
Existence of symmetric and antisymmetric modes is a general property of quantum equations with any symmetric potential \(V(x)=V(-x)\) (implying that \( x_{{\mathrm{B}}}=x_{{\mathrm{A}}}\)). Indeed, let \({\tilde{\Psi }}_{j}\) be a solution of (A.8) and \({\mathbb {P}}\) be the parity operator that transforms \(x\rightarrow -x\). Without loss of generality, we can assume that \( {\tilde{\Psi }}_{j}\) is real. The parity transformation preserves (A.8) for symmetric potentials V(x) and \([{\mathbb {P}},\tilde{{\mathbb {H}}}]=0.\) Hence, \({\mathbb {P}}{\tilde{\Psi }}_{j}\) is also solution of (A.8) and, provided the eigenvalue \({\tilde{E}}_{j}\) is not degenerate, we can always chose c so that \(c{\mathbb {P}}{\tilde{\Psi }}_{j}={\tilde{\Psi }}_{j}\) coincides with the original solution, where c is an unknown constant satisfying \( \left| c\right| =1\) to preserve normalisation. By applying the operator \(c{\mathbb {P}}\) twice we obtain \(x\rightarrow x\) and \(c{\mathbb {P}}c {\mathbb {P}}{\tilde{\Psi }}_{j}=c^{2}{\tilde{\Psi }}_{j}={\tilde{\Psi }}_{j}\). Hence, either \(c=+1,\) which corresponds to a symmetric mode, or \(c=-1\), which corresponds to an antisymmetric mode. Under the limit of a high, impenetrable barrier (i.e. \({\hat{s}}\rightarrow \infty \) in our terms) the wave functions in sections A and B interact less and less and, therefore, the symmetric and antisymmetric modes become very similar and merge \({\tilde{E}} _{j}^{(\text {a})}-{\tilde{E}}_{j}^{(\text {s})}\rightarrow 0\).
1.6 (f) Non-resonant modes
If \(x_{{\mathrm{B}}}\ne x_{{\mathrm{A}}}\), at least some and, typically, most modes are non-resonant. Assuming that \({\hat{s}}={\tilde{s}}/k\) is large, we identify two family of solutions among the non-resonant modes: A-resonant where \(\cot (k_{j}x_{{\mathrm{A}}})\approx -2{\tilde{s}}/k_{j}\) and B-resonant where \(\cot (k_{j}x_{{\mathrm{B}}})\approx -2{\tilde{s}} /k_{j}\). For these modes, one can easily obtain from (A.13) and (A.15) the following expansions
where \(\ j=1,\) 2, 3, ... and \(\sigma _{j}=\cos (\pi j)=(-1)^{j}\) alternates the signs. These expressions are valid unless a mode is (or is close to) A-resonant and B-resonant at the same time—these resonant, near-resonant or intermediate modes require a more careful examination and are considered below.
1.7 (g) Resonant, near-resonant and intermediate modes
Although \(x_{{\mathrm{B}}}\ne x_{{\mathrm{A}}}\) some of the modes can still be exactly resonant or close to resonant conditions simultaneously in both sections A and B:
for some real \(k_{0},\) integer \(j_{{\mathrm{A}}}\) and integer \(j_{{\mathrm{B}}},\) where \(\left| \theta \right| \sim 1/{\hat{s}}\ll 1\) is a phase shift indicating small deviations from the resonance. The condition \( \theta =0\) corresponds to exact resonance. In the rest of the Appendix the subscript “j” is omitted implying that wave vectors, energies and amplitudes considered here are related to a selected mode with some integer \( j_{{\mathrm{A}}}\) and \(j_{{\mathrm{B}}}\) in (A.19). Let \( k=k_{0}+\Delta k\) where \(\Delta k\sim 1/{\hat{s}}\) is small, then at the leading order
Equations (A.20)–(A.21) can be solved to yield:
where
Note the equality
which implies that when one branch of the solution becomes large, the other inevitably becomes small and vice versa. The superscript indices “\(+\)” and “\( -\)” are used to denote values that correspond to the “plus” and “minus” solutions of (A.20). When the sections of the box are of similar sizes \(x_{{\mathrm{B}}}\approx x_{{\mathrm{A}}}\approx x_{0}\) (although not necessarily exactly identical \(x_{{\mathrm{B}}}\ne x_{ {\mathrm{A}}}\)), equations (A.22) and (A.23) can be simplified
1.8 (h) Asymptotes for the resonant and intermediate modes
When using parameter \(\eta \), we distinguish resonant \(\eta \rightarrow 0,\) near-resonant \(\left| \eta \right| \sim 1\), intermediate \(1\ll \left| \eta \right| \ll {\hat{s}}\) and non-resonant \(\left| \eta \right| \sim {\hat{s}}\gg 1\) modes. For equations (A.22) and (A.23), the resonance limit of \(\eta =2{\hat{s}}\theta \rightarrow 0\) is given by
Comparison with the resonance case of subsection (e) indicates that, at \(\eta =0\) and \(x_{{\mathrm{B}}}=x_{{\mathrm{A}}},\) the “minus” solution represents the symmetric mode and the “plus” solution represents the antisymmetric mode.
The asymptotic representation of equations (A.22) and (A.23 ) for intermediate modes is evaluated at the non-resonant limit \(\eta \rightarrow +\infty \) yielding
The “minus” branch matches the B-resonant solution in (A.18) and the “plus” branch matches the A-resonant solution in (A.17). For example, substituting \(\pi j_{{\mathrm{B}}}=\pi j_{{\mathrm{A}}}x_{{\mathrm{B}}}/x_{{\mathrm{A}}}-\left( 1+x_{{\mathrm{B}}}/x_{{\mathrm{A}}}\right) \theta \) obtained from (A.19) into \(\sin (\pi jx_{{\mathrm{A}}}/x_{{\mathrm{B}}})\) in (A.18) (while putting \( j=j_{{\mathrm{B}}}\) and expanding \(\sin (...)\) to the leading order) results in the first equation in (A.30). Similarly, substituting the equivalent expression \(\pi j_{{\mathrm{A}}}=\pi j_{{\mathrm{B}} }x_{{\mathrm{A}}}/x_{{\mathrm{B}}}+\left( 1+x_{{\mathrm{A}}}/x_{ {\mathrm{B}}}\right) \theta \) into expansion of \(\sin (\pi jx_{{\mathrm{B}}}/x_{{\mathrm{A}}})\) in (A.17) (while putting \(j=j_{ {\mathrm{A}}}\) this time) results in the second equation in (A.30). These asymptotes, however, are swapped under the limit \(\eta \rightarrow -\infty \) that yields the following expressions:
Appendix B. Tunnelling influenced by environmental interferences
The system under consideration is placed in a contact with a larger system or the environment, which has the following energy eigenstates \(\left| l\right\rangle =\left| E_{l}\right\rangle ,\) where \(l=1,2,...,N_{e}\) and \(N_{e}\) is extremely large. The joint Hamiltonian of the system and environment is given by the usual expression
where the subscripts “s” indicates the system, “e” indicates the environment (or a larger system) and \({\mathbb {H}}_{\text {int}}\) specifies interactions between the system and the environment and acts in the system \( \otimes \) environment product space \(\left| s\right\rangle \left| l\right\rangle =\left| s\right\rangle \otimes \left| l\right\rangle \). We consider weak interactions of the eigenstates of the system Hamiltonian \({\mathbb {H}}_{s}={\mathbb {H}}_{0}+{\mathbb {H}}_{1}\), which is specified previously in (5.10), with a selected environmental energy eigenstate \(\left| l\right\rangle \). Obtaining the overall solution of the problem \(\left| \psi _{s\otimes e}\right\rangle \) is followed by tracing out the degrees of freedom associated with the environment to determine the effective density matrix of the system: \( {\varvec{\rho }}_{s}={\mathrm{tr}}_{e}(\left| \psi _{s\otimes e}\right\rangle \left\langle \psi _{s\otimes e}\right| ).\) In our analysis, we omit the environmental energy exponents \(\exp \left( -iE_{l}t^{\circ }/\hbar \right) \) since they do not affect the trace. As in other theories of environmental decoherence, we necessarily use antecedent causality in this analysis.
1.1 (a) Environmental decoherence without energy exchange
According to Zurek’s theory [7], decoherence occurs due to environmental interferences without any energy exchange between different energy modes. Hence, the interaction Hamiltonian takes a diagonal form when energy eigenstates are used so that
and all other components are zeros, for example, \(\left\langle -\right| \left\langle l\right| {\mathbb {H}}_{\text {int}}\left| +\right\rangle \left| l\right\rangle =0\) and \(\left\langle +\right| \left\langle l\right| {\mathbb {H}}_{\text {int}}\left| +\right\rangle \left| l^{\prime }\right\rangle =0\) when \(l\ne l^{\prime }\). This form of the interaction Hamiltonian \({\mathbb {H}}_{\text {int}}\) in (B.1) results in adjustments of the natural frequencies of the system (i.e. \(\omega _{+}\) and \(\omega _{-}\)). The solution of this problem is obvious and, by analogy with (5.15), is given by
where \(\Delta \omega _{_{l}}=(E_{+l}-E_{-l})/\hbar \) and \(\omega _{0l}=(E_{+l}+E_{-l})/(2\hbar ),\) while the other quantities \(\omega _{0},\) \( \Delta \omega \) and \(\xi \) are the same as defined in (5.12), (5.13) and (5.6). One can easily see that the effect of environment is negligible as long as \(\Delta \omega _{_{l}}\ll \Delta \omega \). If, however, \(\Delta \omega _{_{l}}\gg \Delta \omega ,\) then the environment would cause a rapid loss of the coherence between the “plus” \(\left| +\right\rangle \left| l\right\rangle \) and “minus” \(\left| -\right\rangle \left| l\right\rangle \) modes, resulting in the corresponding acceleration of tunnelling without any changes in the extent of tunnelling determined by \(\varsigma =\left| \xi \right| /(1+\xi ^{2}) \).
1.2 (b) Environmental decoherence with minimal energy exchanges
The analysis of the influence of decoherence on tunnelling considered in Sect. 6 uses the partition states \(\left| \text {A} \right\rangle \) and \(\left| \text {B}\right\rangle \) as the decoherence basis. We now apply a similar assumption, implying that the environmental interferences affect sections A and B autonomously. As demonstrated below, it is sufficient to assume that the environment interferes only with the state \(\left| \text {A}\right\rangle \) but not with the state \(\left| \text {B}\right\rangle \). As in Sect. 6, the energy exchanges due to these interferences are deemed to be small (i.e. weaker than those that can cause thermalisation during the active stage of the experiment). The Hamiltonian takes the following form
while the other elements of the interaction Hamiltonian are zeros. Note that simultaneous adjustment of both energies \(\left\langle \text {A}\right| \left\langle l\right| {\mathbb {H}}_{\text {int}}\left| \text {A} \right\rangle \left| l\right\rangle =E_{0l}\) and \(\left\langle \text {B} \right| \left\langle l\right| {\mathbb {H}}_{\text {int}}\left| \text {B}\right\rangle \left| l\right\rangle =E_{0l}\) corresponds to \( \left\langle +\right| \left\langle l\right| {\mathbb {H}}_{\text {int} }\left| +\right\rangle \left| l\right\rangle =E_{0l}\) and \( \left\langle -\right| \left\langle l\right| {\mathbb {H}}_{\text {int} }\left| -\right\rangle \left| l\right\rangle =E_{0l}\) and results in a mere adjustment of the principal frequency \(\omega _{0}\). Any exclusive interference of the environment with section B \(\left\langle \text {B} \right| \left\langle l\right| {\mathbb {H}}_{\text {int}}\left| \text {B}\right\rangle \left| l\right\rangle =E_{\text {B}l}\) can be considered to be a result of changes in \(E_{\text {A}l}\) and \(E_{0l}\). Hence, we need to consider only the interaction Hamiltonian specified by (B.4). The solution of the Schrödinger equation for Hamiltonian (B.1) with (5.10) and (B.4) (which can be validated by substitution) is given here without derivation
where
while the other quantities \(\omega _{0},\) \(\Delta \omega \) and \(\xi \) are the same as defined in (5.12), (5.13) and (5.6). When \(\omega _{_{l}}\ll \Delta \omega ,\) (B.5) yields (5.15) and the interferences do not exercise much influence on the system. If \(\omega _{_{l}}\gg \Delta \omega \), these influences are strong since the asymptotic limit of (B.5) is given by
As in the previous subsection, tunnelling is accelerated by the factor of \( 2\omega _{_{l}}/\Delta \omega \), but the extent of tunnelling \(\varsigma =\left| \xi \right| /(1+\xi ^{2})\) is reduced by the factor of \( \Delta \omega /\omega _{_{l}}\). At the limit of \(\Delta \omega /\omega _{l}\rightarrow 0,\) sections A and B become effectively isolated from each other. Tracing out the degrees of freedom associated with the environment suppresses the off-diagonal elements of the effective density matrix of the system \({\varvec{\rho }}_{s}\) but would not affect our conclusions limiting the amplitude of \((\rho _{s})_{\text {BB}}.\)
The extent of tunnelling can be enhanced by assuming that \(\left| E_{ \text {AB}l}\right| \ne 0,\) where \(\ E_{\text {AB}l}=\left\langle \text {A} \right| \left\langle l\right| {\mathbb {H}}_{\text {int}}\left| \text {B}\right\rangle \left| l\right\rangle .\) This assumption, however, does not seem physical, since it implies a rather strange possibility of tunnelling from A to B through the environment (even if the magnitude of the barrier \({\hat{s}}\) is prohibitively high to permit tunnelling).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Klimenko, A.Y. On the effect of decoherence on quantum tunnelling. SN Appl. Sci. 3, 710 (2021). https://doi.org/10.1007/s42452-021-04675-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s42452-021-04675-5