Optimal feeder reconfiguration in distributed generation environment under time-varying loading condition

Abstract

The development and planning of optimal network reconfiguration strategies for electrical networks is greatly improved with proper application of graph theory techniques. This paper investigates the application of Kruskal's maximal spanning tree algorithm in finding the optimal radial networks for different loading scenarios from an interconnected meshed electrical network integrated with distributed generation (DG). The work is done with an objective to assess the prowess of Kruskal's algorithm to compute, obtain or derive an optimal radial network (optimal maximal spanning tree) that gives improved voltage stability and highest loss minimization from among all the possible radial networks obtainable from the DG-integrated mesh network for different time-varying loading scenarios. The proposed technique has been demonstrated on a multiple test systems considering time-varying load levels to investigate the performance and effectiveness of the suggested method. For interconnected electrical networks with the presence of distributed generation, it was found that application of Kruskal's algorithm quickly computes optimal radial configurations that gives the least amount of power losses and better voltage stability even under varying load conditions.

Article Highlights

• Investigated network reconfiguration strategies for electrical networks with the presence of Distributed Generation for time-varying loading conditions.

• Investigated the application of graph theory techniques in electrical networks for developing and planning reconfiguration strategies.

• Applied Kruskal’s maximal spanning tree algorithm to obtain the optimal radial electrical networks for different loading scenarios from DG-integrated meshed electrical network.

1 Introduction

In the delivery and supply of electricity, the distribution stage is the final stage following the generation and transmission stages. The electrical distribution network delivers the electrical power to the consumers via its distribution feeders. Certain problems faced in lengthy distribution feeders include fall in voltage levels [1], power factor distortion, power loss, etc. In order to mitigate these problems, the authors in [2,3,4] implemented measures such as embodiment of additional hardware like tap-changing transformers, shunt capacitors, FACTs devices etc. Apart from these approaches, another important approach is by reconfiguring the network via network reconfiguration by operating the series and sectional switches [5, 6]. By means of network reconfiguration, the power lines can be restructured in such a way that an optimal radial network may be obtained thereby providing a path for optimal power to flow in the network. The authors in [7, 8] discussed that appropriate reconfiguration arrangement can contribute towards reduction in power loss in the network. In [9] the authors have used reconfiguration studies for microgrid applications, and in [10] the authors have worked on developing reconfiguration strategies for shipboard power systems considering local and global reconfiguration. The advantage of network reconfiguration technique over other methods is that just by operating the sectional and tie line switches network reconfiguration can help obtain an optimal stable network with minimized losses, with no requirement for additional equipment or supports. In [11], the authors found that application of graph theory techniques such as Edmond’s Maximal Spanning Tree Algorithm can help obtain optimal radial network configurations from an originally meshed network. It may be worth noted that in practice, radial structured networks are generally used in rural and sub-urban areas due to several advantages it offers such as lower short circuit current and less complex relay coordination. Also, sometimes during situations such as during fault or planned maintenance condition, a mesh network may be required to be reconfigured into a radial network thereby keeping the supply uninterrupted when the maintenance is being carried out. Some of the advantages of network reconfiguration were further discussed by the authors in [12] such as trimming of peak demands leading to curtailment of overburdening of network components and enhancing the system stability.

A substantial amount of time has been invested by contemporary researchers in studying the influence of network reconfiguration in achieving loss reduction [13] and voltage stability improvement [14]. It can be seen from the works presented in [15,16,17,18] that most of the strategies are focused on reducing the feeder active power losses and enhancement of voltage stability for constant loading condition. This particular aspect of considering only constant loading condition becomes a limitation since in a practical scenario the power demands in a distribution network varies with time. The demand for electricity depends on the consumers, and the requirements of power by the consumers vary throughout the day; thus in actual practice, the demand seldom remains constant instead it varies continuously with time. This varying loading scenario follows a pattern, and thus by relying on past historical data, a predictive varying load model can be generated in the form of daily load curves. By using the information from the daily load curves, network reconfiguration plans can be formulated for the different varying load scenarios. The authors in [12, 19] considered time-varying load demand in the study and by employing network reconfiguration techniques were able to obtain the best network with minimum system power loss and higher voltage stability.

Now, the demand for electricity is always on the rise, but the same cannot be said for the improvement in the transmission infrastructure. Thus, with increasing demand, the power transmission and distribution lines operate under a heavy burden and sometimes even under over loaded conditions, resulting in high transmission losses and low voltage stability. One ingenious solution to this problem is to connect certain capacity power plants or distributed generation (DG) sources directly or nearby to the load centres, thereby minimizing the burden on the transmission and distribution networks, which ultimately contributes to reduction in transmission losses and improvement in the voltage stability [20].

Apart from the potential benefits that come with the integration of distributed generation (DG) to an electrical network, another aspect of DG integration is its impact on the topology of the power system. In a traditional power system architecture or a centralized power system topology, the distribution or transfer of power is unidirectional [21] i.e., electricity is transferred from the centralized generating stations to the loads through the transmission and distribution lines, but in a power system network where small-scale DGs are connected directly to the distribution side any excess power generated by the DG can be fed back to the main grid via the feeders thereby making the flow of power in the feeder bidirectional [22]. This simple characteristic of an electrical network with and without DGs contributes to huge changes in the planning and implementation of network reconfiguration strategies of respective power system networks. Proper integration of DG offers technical benefits including power loss minimization and improvement in voltage stability, and also environmental as well as economic benefits [23,24,25]. The incorporation of DGs to supply the demand during peak load periods renders benefits in both technical as well as economical areas. DGs can also supply reactive power for improving the voltage profile to meet real power demands [26]. The technical benefits of incorporating distributed generation include voltage stability improvement, power loss minimization, distribution capacity release, improved system reliability and voltage support [27, 28]. The integration of renewable energy-based DGs also has a small likelihood of causing some disturbance in the system stability owing to its intermittent nature which is affected by natural conditions, which ultimately will have some impact on the electrical energy losses in distribution lines, voltage profile, Var Control and set of pollutants produced by the grid, etc. [29,30,31].

Now, with the presence of distributed generation in the grid, the issue of distribution feeder planning and reconfiguration becomes more complex. As discussed earlier, due to the bidirectional nature of power flow in electrical networks with DG, the reconfiguration process and strategies for an electrical network with and without DG become slightly different. It can be observed from the literature that by means of network reconfiguration an optimal radial reconfigured network with minimized line losses and improved voltage stability can be obtained. However, there still exists some issues (with regards to computation) when carrying out network reconfiguration techniques. The larger the system, the more complex it becomes to find the optimal radial configuration via manual network reconfiguration process, since if a network has ‘n’ number of switches, then there exists ‘2ⁿ’ possible switching combinations with some set of switching configurations resulting in radial network topologies. Thus, for large systems, any manual attempts to find the optimal radial network by tracking all the possible configurations becomes a tedious task involving an impractically long duration of time. The proper application of graph theory techniques in the field of network reconfiguration has been found helpful in resolving these issues.

In this paper, the application of graph theory-based Kruskal’s maximal spanning algorithm in electrical networks for developing reconfiguration and planning strategies is further investigated for a network with time-varying load model and in the presence of DG. The work is done with an objective to assess the ability of Kruskal’s maximal spanning algorithm to compute an optimal radial network (an optimal maximum spanning tree) that gives the best voltage stability and highest loss minimization from among all the possible radial configurations that can be obtained from the original DG-integrated connected mesh network for different time-varying loading scenarios. A computation is carried out on a modified IEEE 30 bus network in MATLAB to assess the performance of the suggested method.

2 Theory

2.1 Reconfiguration strategy

Consider a 4-node power distribution network consisting of one power supply bus, three load buses, and four feeders, as shown in Fig. 1. Let the reactance (in p.u.) of the feeders be X₁, X₂, X₃ and X₄, respectively, and the voltage (in p.u.) of the nodes be V₁∠δ₁, V₂∠δ₂, V₃∠δ₃, and V₄∠δ₄, respectively. From the available data, the load-carrying capabilities of the feeders 1 to 4 can be calculated as,

$$P_{1} = \left| {\left( {{\raise0.7ex\hbox{${v_{1} v_{2} }$} \!\mathord{\left/ {\vphantom {{v_{1} v_{2} } {X_{1} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${X_{1} }$}}} \right)\sin \left( {\delta_{1} - \delta_{2} } \right)} \right|$$

(1)

$$P_{2} = \left| {\left( {{\raise0.7ex\hbox{${v_{1} v_{3} }$} \!\mathord{\left/ {\vphantom {{v_{1} v_{3} } {X_{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${X_{2} }$}}} \right)\sin \left( {\delta_{1} - \delta_{3} } \right)} \right|$$

(2)

$$P_{3} = \left| {\left( {{\raise0.7ex\hbox{${v_{3} v_{4} }$} \!\mathord{\left/ {\vphantom {{v_{3} v_{4} } {X_{3} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${X_{3} }$}}} \right)\sin \left( {\delta_{3} - \delta_{4} } \right)} \right|$$

(3)

$$P_{4} = \left| {\left( {{\raise0.7ex\hbox{${v_{2} v_{4} }$} \!\mathord{\left/ {\vphantom {{v_{2} v_{4} } {X_{4} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${X_{4} }$}}} \right)\sin \left( {\delta_{2} - \delta_{4} } \right)} \right|$$

(4)

Fig. 1

A 4-node mesh network

Now, if we consider that the load carrying capabilities of the feeders are in the order P₁ > P₂ > P₃ > P₄, then reconfiguring the network by eliminating the feeder with least load-carrying capability (i.e. feeder 4), a radial network can be obtained from the originally mesh network. The feeder can be eliminated or disconnected by opening the sectionalizing switch as shown in Fig. 2. The newly obtained radial network consists of only the feeders with high load carrying capability.

Fig. 2

A 4-node reconfigured radial network

The cost matrix (weight matrix) can also be obtained from the load-carrying capability of feeders. For a system with n number of nodes, the size of the cost matrix (weight matrix) will be n × n. If ‘c’ represents the cost matrix, then its elements will be represented as c_ij, where c_ij represents the load-carrying capability (in p.u.) of the feeder connected between node i and node j. For the system shown in Fig. 1, the cost matrix will be a 4 × 4 matrix. The elements of the cost matrix can be calculated as, c₁₁ = c₂₂ = c₃₃ = c₄₄ = c₁₄ = c₄₁ = c₂₃ = c₃₂ = 0, since these are either single nodes or there are no direct connection between these nodes. As for the connected nodes, the nonzero cost matrix elements are, c₁₂ = c₂₁ = P₁, c₁₃ = c₃₁ = P₂, c₃₄ = c₄₃ = P₃, and c₂₄ = c₄₂ = P₄. The values of the cost matrix elements can be calculated using the Newton–Raphson load flow analysis. For the reconfigured radial network shown in Fig. 2, since feeder 4 is now disconnected with help from sectionalizing switch, node 4 will receive the supply from feeder 3 only, and the new cost matrix element for c₂₄ = c₄₂ = P₄ = 0.

In Kruskal’s algorithm, a radial network is extracted from a mesh network by disconnecting the feeder with lowest load-carrying capability from among all the feeders in a step-by-step manner. This results in a radial network where all the nodes are connected only by the feeders with higher load-carrying capacity. It is observed that for the reconfigured radial network obtained through Kruskal’s algorithm, the active and reactive power losses in each feeder are also minimized. By minimizing the overall power loss of the system, the voltage stability of the system is also further improved.

For a 4-node network, the number of possible network configurations would be 2^4. For a mesh network with ‘n’ number of feeders, there will be 2^n possible switch configurations. The number of possible feeder configurations increases with the increase in the number of feeders in the network, which also makes the process of finding an optimal radial network from an originally mesh network more complex. In large networks, trying to find an optimal radial network by testing every possible network configuration is a very tedious, time consuming and labor intensive process, and if a time-varying loading condition is considered, the task becomes even more difficult. In such circumstances, the Kruskal’s algorithm helps to obtain an optimal radial network in less time and makes the process easier.

Certain important criteria should be maintained during the reconfiguration process, three such important criteria are:

• i. All nodes should be in service.

• ii. The maximum power transfer capability of a feeder should not be violated during each operation.

• iii. The sectionalizing switches of the feeders with lower load-carrying capability should be opened first compared to the other lines.

The final radial network obtained using Kruskal’s maximal spanning tree normally contains the feeders with higher load-carrying capability, while the feeders with lower load-carrying capability are disconnected.

2.2 Voltage stability indicator (L-index) evaluation

For the voltage stability analysis, single feeder equivalent method of distribution network which comprises of multiple feeders [32] has been employed. The single line system is shown in Fig. 3. P = injected real power, Q = injected reactive power, R = line resistance, X = line reactance, P_L = real load, Q_L = reactive load, V = voltage.

Fig. 3

Single line system

The real power equations from Fig. 3 may be derived as

$$P = r\left( {P^{2} + Q^{2} } \right)/V^{2} + P_{{\text{L}}}$$

(5)

$${\mathbf{or}}\user2{,}\;\user2{P - P}_{\user2{L}} \user2{/r = }\left( {\user2{P}^{\user2{2}} \user2{ + Q}^{\user2{2}} } \right)\user2{/V}^{\user2{2}}$$

(6)

and the reactive power equations from Fig. 3 may be derived as

$$Q = x\left( {P^{2} + Q^{2} } \right)/V^{2} + Q_{{\text{L}}}$$

(7)

$${\mathbf{or}},\;\user2{Q} - \user2{Q}_{{\mathbf{L}}} /\user2{x} = \left( {\user2{P}^{2} + \user2{Q}^{2} } \right)/\user2{V}^{2}$$

(8)

From (6) and (8), the terms (P² + Q²)/V² can be eliminated, and by rearranging the equations we acquire

$$x\left( {P - P_{L} } \right) = r\left( {Q - Q_{L} } \right)$$

(9)

Considering sending end voltage as reference voltage (thus, V = 1), and on rearranging Eq. (9), and eliminating Q from Eq. (5), a quadratic equation in terms of P is acquired.

$$\left( {\user2{r}^{{\mathbf{2}}} + \user2{x}^{{\mathbf{2}}} } \right)\user2{P}^{{\mathbf{2}}} - \left( {{\mathbf{2}}\user2{x}^{{\mathbf{2}}} \user2{P}_{{\mathbf{L}}} - {\mathbf{2}}\user2{rxQ}_{{\mathbf{L}}} + \user2{r}} \right)\user2{P} + \left( {\user2{x}^{{\mathbf{2}}} \user2{P}_{{\mathbf{L}}}^{{\mathbf{2}}} + \user2{r}^{{\mathbf{2}}} \user2{Q}_{{\mathbf{L}}}^{{\mathbf{2}}} - {\mathbf{2}}\user2{rxP}_{{\mathbf{L}}} \user2{Q}_{{\mathbf{L}}} + \user2{rP}_{{\mathbf{L}}} } \right) = {\mathbf{0}}$$

(10)

From Eq. (10) the real power P can be derived as,

$$\begin{aligned} P = \frac{{2x^{2} P_{{\text{L}}} - 2rxQ_{{\text{L}}} + r}}{{2\left( {r^{2} + x^{2} } \right)}} \pm \frac{{\left[ {\left( {2x^{2} P_{{\text{L}}} - 2rxQ_{{\text{L}}} + r^{2} } \right) - 4\left( {r^{2} + x^{2} } \right)*\left( {x^{2} P_{{\text{L}}}^{2} + r^{2} Q_{{\text{L}}}^{2} - 2rxP_{{\text{L}}} Q_{{\text{L}}} + rP_{{\text{L}}} } \right)} \right]^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} }}{{2\left( {r^{2} + x^{2} } \right)}} \\ \end{aligned}$$

(11)

|||^rly, taking into consideration the symmetry between the real power and the reactive power in power systems, the reactive power Q can be derived as,

$$\begin{aligned} Q = \frac{{2x^{2} Q_{{\text{L}}} - 2rxP_{{\text{L}}} + x}}{{2\left( {r^{2} + x^{2} } \right)}} \pm \frac{{\left[ {\left( {2x^{2} P_{{\text{L}}} - 2rxQ_{{\text{L}}} + r^{2} } \right) - 4\left( {r^{2} + x^{2} } \right)*\left( {x^{2} P_{{\text{L}}}^{2} + r^{2} Q_{{\text{L}}}^{2} - 2rxP_{{\text{L}}} Q_{{\text{L}}} + rP_{{\text{L}}} } \right)} \right]^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} }}{{2\left( {r^{2} + x^{2} } \right)}} \\ \end{aligned}$$

(12)

Now, for P and Q of Eqs. (11) and (12) to have real roots, the determinant of the quadratic equations should be b²–4ac > 0.

Hence,

$$\left( {{\mathbf{2}}\user2{x}^{{\mathbf{2}}} \user2{P}_{{\mathbf{L}}} - {\mathbf{2}}\user2{rxQ}_{{\mathbf{L}}} + \user2{r}} \right)^{{\mathbf{2}}} - {\mathbf{4}}\left( {\user2{r}^{{\mathbf{2}}} + \user2{x}^{{\mathbf{2}}} } \right)\left( {\user2{x}^{{\mathbf{2}}} \user2{P}_{{\mathbf{L}}}^{{\mathbf{2}}} + \user2{r}^{{\mathbf{2}}} \user2{Q}_{{\mathbf{L}}}^{{\mathbf{2}}} - {\mathbf{2}}\user2{rxP}_{{\mathbf{L}}} \user2{Q}_{{\mathbf{L}}} + \user2{rP}_{{\mathbf{L}}} } \right) > {\mathbf{0}}$$

(13)

$${\mathbf{or}},\;\left[ {\left( {{\mathbf{2}}\user2{x}^{{\mathbf{2}}} \user2{P}_{{\mathbf{L}}} - {\mathbf{2}}\user2{rxQ}_{{\mathbf{L}}} + \user2{r}} \right)*\left( {{\mathbf{2}}\user2{x}^{{\mathbf{2}}} \user2{P}_{{\mathbf{L}}} - 2\user2{rxQ}_{{\mathbf{L}}} + \user2{r}} \right)} \right] - {\mathbf{4}}\left[ {\user2{r}^{{\mathbf{2}}} \left( {\user2{x}^{{\mathbf{2}}} \user2{P}_{{\mathbf{L}}}^{{\mathbf{2}}} + \user2{r}^{{\mathbf{2}}} Q_{{\mathbf{L}}}^{{\mathbf{2}}} - {\mathbf{2}}\user2{rxP}_{{\mathbf{L}}} \user2{Q}_{{\mathbf{L}}} + \user2{rP}_{{\mathbf{L}}} } \right) + \user2{x}^{{\mathbf{2}}} \left( {\user2{x}^{{\mathbf{2}}} \user2{P}_{{\mathbf{L}}}^{{\mathbf{2}}} + \user2{r}^{{\mathbf{2}}} \user2{Q}_{{\mathbf{L}}}^{{\mathbf{2}}} - {\mathbf{2}}\user2{r}x\user2{P}_{{\mathbf{L}}} \user2{Q}_{{\mathbf{L}}} + \user2{rP}_{{\mathbf{L}}} } \right)} \right] > {\mathbf{0}}$$

(14)

Which on simplification, reduces to,

$$\left( {4\left[ {\left( {xP_{{\text{L}}} - rQ_{{\text{L}}} } \right)^{2} + xQ_{{\text{L}}} + rP_{{\text{L}}} } \right] < 1} \right)$$

(15)

Based on the network loading, if the calculated value of the LHS of Eq. (15) goes beyond the critical limit i.e., 1, then the power becomes imaginary and it results in voltage collapse. The LHS of Eq. (15) is also termed as the voltage stability index and is represented by the term $L_{{{\text{index}}}}$.

Thus for a stable system, $L_{index} < 1$.

Now, considering Eq. (5) with sending ending voltage as reference voltage (thus, V = 1), the equation becomes

$$\varvec{P} =\varvec{r}\left( {\varvec{{P}^{2}} + \varvec{{Q}^{2} }} \right) + \varvec{P}_{{\textbf{L}}}$$

(16)

$${\textbf{or}},\;\varvec{P} - \varvec{P}_{{\textbf{L}}} = \varvec{r}\left( {\varvec{{P}^{2}} + \varvec{{Q}^{2}} } \right)$$

(17)

But we know that, Generation(P)–Demand ($P_{{\text{L}}}$) = Losses ($P_{{{\text{loss}}}}$).

Thus Eq. (17) becomes,

$$\user2{P}_{{{\mathbf{loss}}}} = \user2{r}\left( {\user2{P}^{{\mathbf{2}}} + \user2{Q}^{{\mathbf{2}}} } \right)$$

(18)

$${\mathbf{or}},\;\user2{r} = {{\user2{P}_{{{\mathbf{loss}}}} } \mathord{\left/ {\vphantom {{\user2{P}_{{{\mathbf{loss}}}} } {\left[ {\left( {\user2{P}_{{\mathbf{L}}} + \user2{P}_{{{\mathbf{loss}}}} } \right)^{{\mathbf{2}}} + \left( {\user2{Q}_{{\mathbf{L}}} + \user2{Q}_{{{\mathbf{loss}}}} } \right)^{{\mathbf{2}}} } \right]}}} \right. \kern-\nulldelimiterspace} {\left[ {\left( {\user2{P}_{{\mathbf{L}}} + \user2{P}_{{{\mathbf{loss}}}} } \right)^{{\mathbf{2}}} + \left( {\user2{Q}_{{\mathbf{L}}} + \user2{Q}_{{{\mathbf{loss}}}} } \right)^{{\mathbf{2}}} } \right]}}$$

(19)

|||^rly, by considering Eq. (7), we get

$$\user2{x} = {{\user2{Q}_{{{\mathbf{loss}}}} } \mathord{\left/ {\vphantom {{\user2{Q}_{{{\mathbf{loss}}}} } {\left[ {\left( {\user2{P}_{{\mathbf{L}}} + \user2{P}_{{{\mathbf{loss}}}} } \right)^{{\mathbf{2}}} + \left( {\user2{Q}_{{\mathbf{L}}} + \user2{Q}_{{{\mathbf{loss}}}} } \right)^{{\mathbf{2}}} } \right]}}} \right. \kern-\nulldelimiterspace} {\left[ {\left( {\user2{P}_{{\mathbf{L}}} + \user2{P}_{{{\mathbf{loss}}}} } \right)^{{\mathbf{2}}} + \left( {\user2{Q}_{{\mathbf{L}}} + \user2{Q}_{{{\mathbf{loss}}}} } \right)^{{\mathbf{2}}} } \right]}}$$

(20)

Now, for reduced network,

$$L_{{{\text{index}}}} = 4\left[ {\left( {x_{{{\text{eq}}}} P_{{{\text{Leq}}}} - r_{{{\text{eq}}}} Q_{{{\text{Leq}}}} } \right)^{2} + x_{{{\text{eq}}}} Q_{{{\text{Leq}}}} + r_{{{\text{eq}}}} P_{{{\text{Leq}}}} } \right]$$

(21)

Where $L_{{{\text{index}}}}$ = voltage stability index, $r_{{{\text{eq}}}}$ = equivalent resistance for single line, $x_{{{\text{eq}}}}$ = equivalent reactance for single line, $P_{{{\text{Leq}}}}$ = total real loads in the distribution network, $Q_{{{\text{Leq}}}}$ = total reactive loads in the distribution network.

And from Eqs. (19) and (20), we get,

$$r_{{{\text{eq}}}} = {{\left( {\sum P_{{{\text{loss}}}} } \right)} \mathord{\left/ {\vphantom {{\left( {\sum P_{{{\text{loss}}}} } \right)} {\left[ {\left( {P_{{{\text{Leq}}}} + \sum P_{{{\text{loss}}}} } \right)^{2} + \left( {Q_{{{\text{Leq}}}} + \sum Q_{{{\text{loss}}}} } \right)^{2} } \right]}}} \right. \kern-\nulldelimiterspace} {\left[ {\left( {P_{{{\text{Leq}}}} + \sum P_{{{\text{loss}}}} } \right)^{2} + \left( {Q_{{{\text{Leq}}}} + \sum Q_{{{\text{loss}}}} } \right)^{2} } \right]}}$$

(22)

$$x_{{{\text{eq}}}} = {{\left( {\sum Q_{{{\text{loss}}}} } \right)} \mathord{\left/ {\vphantom {{\left( {\sum Q_{{{\text{loss}}}} } \right)} {\left[ {\left( {P_{{{\text{Leq}}}} + \sum P_{{{\text{loss}}}} } \right)^{2} + \left( {Q_{{{\text{Leq}}}} + \sum Q_{{{\text{loss}}}} } \right)^{2} } \right]}}} \right. \kern-\nulldelimiterspace} {\left[ {\left( {P_{{{\text{Leq}}}} + \sum P_{{{\text{loss}}}} } \right)^{2} + \left( {Q_{{{\text{Leq}}}} + \sum Q_{{{\text{loss}}}} } \right)^{2} } \right]}}$$

(23)

where $P_{{{\text{loss}}}}$ and $Q_{{{\text{loss}}}}$ are the active and reactive power losses of the system.

The voltage stability index i.e. $L_{{{\text{index}}}}$ value varies between 0 and 1, with values nearer to 0 designating a more stable system.

2.3 Kruskal’s maximal spanning tree and its application in the present study

A graph is a set of nodes connected with edges. And, a connected graph whose edges have weights assigned to it forms a network. Figure 4(a) shows an arbitrary network G with three nodes A, B and C and three edges AB, AC and BC with weights 1, 2 and 3, respectively.

Fig. 4

A Network and its Spanning Trees

A connected sub-graph extracted from the graph G, which contains no cycles or loops in it, forms a spanning tree (T) of G. Figure 4(b), (c) and (d) is possible spanning tree of Fig. 4(a). The spanning tree with the most weight forms the maximum weight spanning tree. Kruskal’s algorithm [33] helps compute a maximal spanning tree from a given network by initially sorting the edges in order of decreasing weight then systematically constructing a maximal spanning tree by prioritizing the edges with more weights in each step of forming the spanning tree.

2.3.1 Kruskal’s maximal spanning tree algorithm

Consider, a graph G represented by,

$$G = \{ ((u,v),e_{{u,v}} ):u,v\;{\text{are}}\;{\text{nodes}},\;e_{{u,v}} \xrightarrow{{}}{\text{weight}}\;{\text{of}}\;{\text{the}}\;{\text{edge}}\;(u,v)\}$$

(24)

Then, the target spanning tree T may be represented as,

$$T = \{ ((u,v),e_{u,v} ):u,v \, \text{are} \, \text{nodes},\,e_{u,v} \, \text{is} \, \text{the} \, \text{weight} \, \text{of} \, \text{the} \, {\text{edge}} \, (u,v) \,$$

(25)

And edge,$E = \{ (u,v),e_{u,v} \}$.

To obtain a maximum spanning tree from a given network G, a simplified procedure based on Kruskal’s [34,35,36] may be summarized as:

• i. Arrange the edges of G in decreasing order of weight via sorting. And let T be the set of edges constituting the maximum spanning tree. Initially, T = $\Phi$.

• ii. Add the first edge to T.

• iii. Continue adding the remaining edges to T one edge at a time always checking that it does not form a loop in T. Exit and report G to be disconnected when no further edges can be added.

• iv. If the obtained tree (T) has n − 1 edges (n = number of nodes in G) stop and output T. Otherwise go to step 3.

The flow chart of the Kruskal’s Maximal Spanning Tree Algorithm has been shown in Fig. 5.

Fig. 5

Flowchart of Kruskal’s maximal spanning tree algorithm

3 Results and discussions

Here, for different varying loading scenarios, Kruskal’s maximal spanning tree algorithm was applied to find an optimal radial network (optimal spanning tree) from among the many possible spanning trees present in a meshed electrical network integrated with distributed generation. The proposed algorithm was tested on a modified IEEE 30 node test system integrated with distributed generation, with each feeder of the test system containing series sectionalizing switches numbered from S1 to S41. All simulations were carried out in MATLAB and MATLAB-based Power System Analysis Toolbox (PSAT). A representation of the 30-node test system is shown in Fig. 6, and the test system input data for feeder and load have been shown in Appendix Tables 12 and 13, respectively, and are also obtainable from [37]. The DG unit is modelled as a wind turbine with doubly fed induction generator (DFIG) as per [38]and its output is considered to be constant. The parameters of the DG are also given in Appendix Table 15. Initially, a load flow analysis was carried out on the original mesh network, and from the information obtained, the node with the least voltage magnitude value (in per unit value) was chosen as the location for DG installation. In the case of 30-node test system, the bus (node) with the least value of voltage magnitude was found to be bus 30. The DG was thus installed at the chosen node under the constraint that the capacity of the installed DG does not exceed the base load of that particular node. Thus, for the modified 30 node system case since the base load at bus 30 is 10.6 MW, the capacity of the DG is thus fixed at a constant output of 10.6 MW for all cases. Similar procedure was done for the cases for 3-node test system [37] and a 14-node test system [39].

Fig. 6

Modified IEEE 30-node test system considered for the study

Consumers play an important part in shaping the load demand in electrical distribution systems. Depending on several factors the demand for power may rise or fall at any given time. By collecting and accumulating information over a period of time on power consumption in an area, the load demand in that area can be predicted following the pattern of consumption. One of the most popular method of observing and planning for the variable loading condition is through the information obtained via daily load curves. Since the load demands in a distribution system vary with time, it is reasonable to predict that in accordance with the time-varying load demands the optimal radial network which yields the optimal voltage stability will also vary. Thus, there potentially exists different optimal radial configurations corresponding to the different loading scenarios. Therefore, formulating network reconfiguration strategies and plans considering different varying loading scenarios can help power system operators better understand and well equipped to handle network reconfiguration tasks whenever required to do so.

In this study, we have considered a time-varying model based on data as given in Appendix Table 14. Figure 9 characterizes a typical daily load curve (with values in p.u.) for a 24-h time interval based on the time-varying demand furnished in appendix Table 14. By applying Kruskal’s Maximal Spanning Tree algorithm, we have tried to obtain an optimally reconfigured radial network which yields lower losses and better voltage stability index value corresponding to the different loading conditions.

Initially we have considered a small network and carried out a detailed computation on a 3-node test system taken from Example 6.7 of [35], including a comparison study between all manually obtainable possible radial configurations and the radial configuration obtained via application of the Kruskal’s algorithm, followed by Kruskal’s computation of optimal radial networks for varying load scenario. The results of the computation carried out have been presented in Tables 1 and 2, respectively. It may be seen from Table 1 that the radial network computed by the Kruskal’s algorithm corresponds to the best possible radial network obtained via manual operation of the switches.

Table 1 Comparison of the radial networks obtained via manual switching and via application of Kruskal algorithm for a 3-node test system with and without DG integration

Table 2 Performance of the radial networks obtained via application of Kruskal algorithm for a 3-node test system with and without DG integration for varying loading

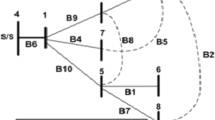
Similarly, computation was also carried out for the modified 30-node test system. For the 30-node test system, at base loading condition, the proposed technique recommends that sectionalizing switches S3,S6,S8,S12,S20,S23,S26,S28,S31,S32,S38,S40 should be open to successfully reconfigure the original network into the optimal radial network. When load flow calculation was done on the resulting radial network, we obtained a total active and reactive power losses of 25.0578 MW and 74.4049 MVAr, respectively, and a voltage stability index value of 0.5516. Unlike a small network where all its radial networks can be manually mapped, for large networks it is complex and lengthy to obtain all possible radial networks via manual operation. Thus, to validate the optimality of the radial network obtained via the proposed algorithm at base loading condition, its performance is compared with that of the performance of ten manually configured radial reconfigured networks (also at base loading condition). The ten manually reconfigured radial networks as the name implies are radial networks obtained by manually operating the switches without relying on graph theory techniques, and are just a small number of the many potential radial networks that can be obtained from the original mesh network. The performance of the ten manually reconfigured radial networks (viz. configuration number 1 to 10) with regard to active power loss, reactive power loss and voltage stability are compared to those of the optimal radial network obtained via the application of Kruskal’s algorithm at base loading scenario is shown in Table 3. It can be clearly seen from the results furnished in Table 3 that the radial network configured through the application of Kruskal’s maximal spanning tree algorithm gives better performance. Figure 7 shows the optimal radial network for base loading scenario obtained via the application of the proposed technique.

Table 3 Calculated values of L-index, P-loss, and Q-loss at base loading scenario

Fig. 7

Optimal radial network obtained by applying Kruskal’s algorithm for base loading condition and 90% base-load condition

Similar to the computation and comparison carried out for the base loading scenario for the 30-node test system, identical procedures were applied to obtain, test for and verify the optimality of the radial networks computed by the proposed technique for all the different loading scenarios considered. Further, in order to reduce confusion, the computations were done considering descending order of loading scenario. Tables 4, 5, 6, 7 and 8 represent the simulation results showing the different manual switching configurations (resulting in radial networks) and the switching configuration obtained via the proposed technique and comparing its corresponding resulting values of L-index, P-loss, and Q-loss for the loading conditions at 90%, 80%, 70%, 60% and 59% of base load conditions, respectively. For each of the different loading scenarios considered, it is clearly visible from the results that the optimal network computed via Kruskal’s algorithm results in the least amount of losses and most optimal voltage stability index value. For 90% base-load scenario the Kruskal’s algorithm computed radial network as shown in Fig. 7, and Fig. 8 depicts the optimal radial networks obtained via application of Kruskal’s maximal spanning tree algorithm at different loading scenarios of 80%, 70%, 60%, and 59% of the base load, respectively. Additionally, from Tables 3, 4, 5, 6, 7 and 8 it may also be noticed that, as the loading level is reduced from 100 to 59% of base load there is a corresponding reduction in the L-index value. Thus, for the different loading scenarios considered here, the L-index value of 0.1501 p.u. at 59% of base load is the least value.

Table 4 Calculated values of L-index, P-loss, and Q-loss at 90% of base load

Table 5 Calculated values of L-index, P-loss, and Q-loss at 80% of base load

Table 6 Calculated values of L-index, P-loss, and Q-loss at 70% of base load

Table 7 Calculated values of L-index, P-loss, and Q-loss at 60% of base load

Table 8 Calculated values of L-index, P-loss, and Q-loss at 59% of base load

Fig. 8

Optimal radial network obtained by applying Kruskal’s algorithm for the cases with 80%, 70%, 60% and 59% of base-load condition

In order to further validate the optimality of the reconfigured radial network obtained via the proposed technique for a given DG-integrated mesh network for different time-varying loading conditions, the proposed approach is compared with a similar graph theoretic approach known as Edmond’s algorithm from [11]. Since in [11], the work is primarily focused on obtaining the optimal radial network for an electrical system for constant load and without DG integration, we are unable to properly compare the performance of the algorithms against each other. Thus, in order to properly compare the performance of the algorithms under similar conditions, we have also studied Edmond’s algorithm as well and applied it to find the optimal radial network configurations of the test system for different time-varying loading conditions. The performance analysis based on the comparison of the active and reactive power loss and the voltage stability index of the respective optimal radial networks obtained via application of Kruskal’s algorithm and Edmond’s algorithm for different time-varying loading scenarios for the test system are summarily tabulated and presented in Table 9. The impact DG integration has on the network such as minimization of the active and reactive power losses and the corresponding improvement in the voltage stability index (L-index) can also be observed from Table 9. Furthermore, it can be observed from Table 9 that in the case of finding an optimal radial network for an electrical network without DG integration, similar to [11] the performance of Edmond’s algorithm outshines the performance of Kruskal’s algorithm for base-load and 90% loading conditions, but when the load is less or equal 80% of the nominal load, the Kruskal's algorithm is superior to the Edmond's algorithm. As for when DG integrated networks are considered, the performance of Kruskal’s algorithm is much better than that of Edmond’s algorithm in finding the optimal radial network for all the different varying loading scenarios considered. The results obtained clearly indicate that for a DG integrated network, the optimal radial networks computed via the application of Kruskal’s maximal spanning tree algorithm have lower losses and better L-index values for all the different time-varying loading scenarios considered.

Table 9 Comparison of the results of the network with and without DG using Kruskal’s and Edmond’s Algorithms

The application of Kruskal’s algorithm to obtain optimal radial networks from DG integrated meshed networks under time-varying load was further experimented on a robust test systems considering a modified IEEE-14 node test system. The results of the computations are furnished below in detail in tabular form in Table 10.

Table 10 Comparison of the radial networks obtained via manual switching and via application of Kruskal algorithm for a 14-node test system with and without DG integration

4 Conclusion

The process of finding the optimal spanning tree of a mesh-connected network through manual procedure involves a lot of labour and time and becomes increasing difficult for networks containing large amounts of nodes and edges. In an electrical network with distributed generation the process becomes more complicated due to the introduction of the phenomenon of bi-directional flow of power. However, unlike manual operation, the use of graph theory techniques makes it easier to compute tasks such as finding the optimal spanning tree quickly and accurately, and by making slight adjustments, the complexity in DG integrated networks is also greatly reduced. In this paper, the performance of Kruskal’s maximal spanning tree algorithm in obtaining optimal radial networks from DG integrated mesh networks was investigated. The proposed technique has been demonstrated in detail on a modified 30 node meshed distribution system integrated with DG, and multiple computations carried out for different time-varying load levels. The optimality of the radial networks obtained through the application of Kruskal’s maximal spanning tree algorithm for different loading levels was verified by comparing the power loss and L-index values with those obtained from (randomly selected) manually configured radial networks. The performance of the proposed technique was further compared with another similar graph theory technique known as Edmond’s algorithm, and it was found that the proposed technique performed better for DG integrated networks. The results of the study suggest that the proper application of Kruskal’s maximal spanning tree algorithm in distributed generation integrated electrical networks can help power system researchers and operators quickly identify and obtain the most optimal radial network that can be reconfigured from the meshed network.

Appendix

See Fig 9 is modeled as per Table 14 and Tables 11, 12, 13, 14, 15 and 16.

Fig. 9

Percentage loading versus time plot corresponding to Table 14

Table 11 The 3-node test system line data [37]

Table 12 IEEE 30 bus feeder data [37]

Table 13 IEEE 30 bus busdata [37]

Table 14 Time-varying loading considered

Table 15 Data of doubly-fed induction machine (DFIG) wind turbine [38]

Table 16 The 14-node test system line data [39]