Abstract
In this study, we present the application of two novel hybrid multiple-criteria decision-making (MCDM) techniques in the mineral potential mapping (MPM), namely FUCOM-MOORA and FUCOM-MOOSRA, as robust computational frameworks for MPM. These were applied to a set of exploration targeting criteria of skarn. The multi-objective optimization method on the basis of ratio analysis (MOORA) and the multi-objective optimization on the basis of simple ratio analysis (MOOSRA) approaches are used to prioritize and rank individual cells. What makes MOORA and MOOSRA more reliable compared to many other methods is the fact that the optimizations procedure is applied to calculate the prospectivity score of individual unit cells. This reduces the uncertainty stemming from erroneous mathematical calculations. The full consistency method (FUCOM), on the other hand, is useful for assigning weights to the spatial proxies. The FUCOM method, as a pairwise comparison method, reduces a large number of pairwise comparisons of similar and popular approaches such as analytic hierarchy process (AHP) with \(n\left( {n - 1} \right)/2\) and the best–worst method (BWM) with \(2n - 3\) number of pairwise comparisons with \(n - 1\) which leads to a less time-consuming and more consistent performance compared with AHP and BWM. These were applied to a set of exploration targeting criteria of skarn iron deposits from Central Iran. Two potential maps were retrieved from the procedures applied, the comparison of which using correct classification rates and field checks revealed the superiority of FUCOM-MOOSRA over the FUCOM-MOORA.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
A great deal of attention has been recently focused on greenfields’ mineral potential mapping (MPM), in which the intent is to reduce the search space for the possible detailed surveys (e.g., [24, 44, 79, 82, 91, 92, 96, 97, 112, 125]). In these studies, expert-based methods are applied for weighting and integrating exploration targeting criteria into potential maps. Of the various expert-based methods employed in this context, multi-criteria decision-making (MCDM) methods have gained a considerable reputation (e.g., [8, 14, 89, 95, 100, 102]). These methods are either comparison-based or matrix-based approaches [71]. The former and the latter methods are used for assigning weights to the targeting criteria and integrating the weighted criteria into potential maps, respectively.
The matrix-based MCDM methods are often too complex [26, 77, 142, 143], making it challenging decision makers to follow their mathematical procedures. The multi-objective optimization method on the basis of ratio analysis (MOORA: [21]) and the multi-objective optimization on the basis of simple ratio analysis (MOOSRA: [32]) have been proposed to provide more straightforward mathematical procedures to follow. Notwithstanding the robustness and myriad applications of these methods (e.g., MOORA: [4, 20, 22, 25, 47, 48, 70, 84, 98, 103, 137], MOOSRA: [7, 11, 33, 75, 116, 129, 137]), seldom have they been applied to the context of MPM.
The comparison-based methods and, on the other hand, a large number of pair-wise comparisons (e.g., AHP: [113], BWM: [109]) make these methods time-consuming and less consistent (e.g., [9, 42, 83, 89, 99, 100, 102, 124]). The full consistency method (FUCOM: [94]), a novel comparison-based procedure, has reduced the number of comparisons required. This method results in a higher consistency ratio by determining the deviation from utmost consistency ([12, 17, 35, 94, 105]) compared to those of similar procedures, making its outputs more reliable. Although this method has been applied in different decision-making procedures (e.g., [12, 17, 18, 35, 41, 90, 105, 127]), it is yet to be applied in MPM.
The intent of this study is to showcase the application of two novel hybrid MCDM techniques in MPM, namely FUCOM-MOORA and FUCOM-MOOSRA. The FUCOM technique was used in various scientific fields after it was published in 2018 because of two outstanding reasons: (1) this approach has reduced the number of comparisons required (which is less time-consuming) and (2) has more reliable outputs in comparison with previous approaches [17, 35, 94]; however, this method has been never used in MPM. In addition of applying the FUCOM method in MPM, we combined it to MOORA and MOOSRA to present two-step methodologies, namely FUCOM-MOORA and FUCOM-MOOSRA. MOORA and MOOSRA, like the FUCOM approach, have been never used in MPM. MOORA and MOOSRA with approximately similar and authentic mathematical backgrounds have been well validated in various scientific fields based on comparison with other methods. The superiority of MOORA and MOOSRA methods in comparison with other similar methods is related to the optimization procedure in their mathematical theory, which reduces the uncertainty stemming from erroneous mathematical calculations and causes having more reliable outputs [7, 33, 98, 129, 137]. In this paper, FUCOM-MOORA and FUCOM-MOOSRA were applied on a set of regional-scale targeting criteria of iron skarn deposits from Varan area in Central Iran to show the robustness of the proposed approaches in MPM. The intrusion of the Eocene plutonic rocks into the sediments of Qom formation, Cretaceous in age, yielded several cases of calcic skarn iron mineralization in the study area.
2 Methods
2.1 FUCOM
The full consistency method (FUCOM: [94]) is a comparison-based MCDM procedure applying the principles of pairwise comparison and deviation from maximum consistency [18, 35, 94, 136]. FUCOM requires only n − 1 pairwise comparisons for assigning weights to n mappable targeting criteria in MPM. The deviation from maximum consistency (DMC) of comparisons is used for validating the results of FUCOM [18].
FUCOM is implemented with regard to the following steps [18, 35, 94, 136]:
-
Step 1: The set of exploration targeting criteria, \(C = \left\{ {C_{1} , C_{2} , \ldots , C_{n} } \right\}\), are initially ranked according to their importance; that is, the higher the initial rank is, the more critical the criterion is to mineralization. This is shown by the following formulation:
$$C_{j\left( 1 \right)} > C_{j\left( 2 \right)} > \cdots > C_{j\left( k \right)}.$$(1) -
Step2: The ranking criteria are compared and the comparative priority (\(\varphi_{{k/\left( {k + 1} \right)}} , k = 1,2, \ldots ,n,\) in which \(k\) represents the rank of the criteria) of the criteria is determined according to Eq. (2):
$$\varphi = \left( {\varphi_{1/2} ,\varphi_{2/3} , \ldots , \varphi_{k/(k + 1} } \right).$$(2) -
Step3: Weight coefficients of the targeting criteria \(\left( {w_{1} , w_{2} , \ldots , w_{n} } \right)^{T}\) are calculated. These values should meet the following conditions:
-
1.
The weight coefficients (wk) are proportional to the comparative priorities \((\varphi_{k} ):\)
$$\frac{{w_{k} }}{{w_{k + 1} }} = \varphi_{{k/\left( {k + 1} \right)}}.$$(3) -
2.
The mathematical transitivity must be met among all the comparative priorities \((\varphi_{k} ):\)
$$\varphi_{{k/\left( {K + 1} \right)}} \times \varphi_{{\left( {K + 1} \right)/\left( {K + 2} \right)}} = \varphi_{{k/\left( {k + 2} \right)}}.$$(4)
-
1.
-
Step 4: The following optimization problem should be solved for calculating the optimal weights \(\left( {w_{1} , w_{2} , \ldots , w_{n} } \right)^{T}\) of the targeting criteria:
$$\begin{aligned} &{\text{Min}}\,X \\ & {\text{s}}.{\text{t}}{.} \\ & \left| {\frac{{w_{j\left( k \right)} }}{{w_{{j\left( {k + 1} \right)}} }} - \varphi_{k/k + 1} } \right| = X,\,\, \forall j \\ & \left| {\frac{{w_{j\left( k \right)} }}{{w_{{j\left( {k + 2} \right)}} }} - \varphi_{{k/\left( {k + 1} \right)}} \times \varphi_{{\left( {k + 1} \right)/\left( {k + 2} \right)}} } \right| = X,\,\, \forall j \\ & \mathop \sum \limits_{j = 1}^{n} w_{j} = 1 \\ & w_{j} \ge 0, \forall j. \\ \end{aligned}.$$(5)
2.2 MOORA
The multi-objective optimization method on the basis of ratio analysis (MOORA) has been proposed by Brauers and Zavadskas [21]. This method can be applied for integrating a set of weighted targeting criteria (cf. [10,25]) into maps of mineral potential. In the first step, targeting criteria are marked by positive and negative signs. The positive sign refers to the criteria in which higher values should be prioritized. Negative criteria, on the other hand, are those in which lower values are more important (cf. [25]). Next, the following matrix is developed in which m and n refer to the number of unit cells in the area and the number of targeting criteria, respectively [23]:
For individual targeting criteria, each xij in the above matrix is normalized to *xij in which the values vary in a [0, 1] range. This is implemented according to the following equation [23]:
Finally, the potential values assigned to individual unit cells, yi, are derived from the following optimization function [10, 25, 70]:
where g is the number of positive criteria [21] and wj refers to weight of jth criterion [19, 73].
3 MOOSRA
The multi-objective optimization on the basis of simple ratio analysis (MOOSRA: [32]) is a matrix-based MCDM, with its procedure bearing a striking resemblance to that of MOORA [12]. The matrix alignment and the normalization of arrays in MOORSA are identical to those of MOORA. However, the optimization procedure used for deriving the potential values assigned to individual unit cells is applied according to Eq. (9) as follows [11,32]:
where g and wj refer to the number of positive criteria and the weight assigned to the jth criterion, respectively.
4 The Varan area and input data
4.1 Geological setting and the deposit model
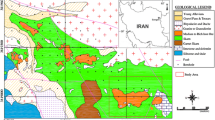
The NW–SE trending metallogenic belt of Zagros [46, 121, 123, 139], as a segment of Alpine-Himalayan orogenic system [27, 93, 110, 117, 128] in the western section of Tethyan domain [63, 67, 132, 134, 135], is developed by the collision of the Arabian and Eurasia platforms [52, 87, 108, 126, 131] (Fig. 1). The Zagros orogenic belt includes three aligned tectonic zones of (1) the Zagros fold–thrust belt, (2) the Sanandaj–Sirjan magmatic–metamorphic zone, and (3) the tertiary Urumieh–Dokhtar magmatic belt (UDMB) [5, 6, 60, 118, 122]. The Varan area is situated in the UDMB (Fig. 2) resulted from a convergent tectonic regime [2, 3, 31, 66, 141]. This Andean volcanic arc, having extended over a length of some 2000 km, hosts plutonic complexes included intrusive, extrusive, and volcano-sedimentary units post Eocene volcanic, plutonic, and volcanic–sedimentary complexes [31, 60, 61, 66, 69, 74, 115, 119, 138, 141]. The magmatism of the UDMB is associated with continual steps of the Neo-Tethys closure within Paleogene–Neogene times, started at ∼ 50 Ma [16], continued into middle Eocene, and followed by magmatic activities of Oligocene–Miocene intrusions [2, 3, 141]. The magmatism of UDMB is of calc–alkaline affinity [60, 61, 69, 138, 141]. However, Jamali et al. [65] stated alkaline rocks locally, related to younger plutonic activity in some components of the UDMB. This tectonic setting emplaced extensive magmatism constituting the trigger and heat source, and the convention forces developed a vast array of metallic ore deposits [51], especially copper [58, 104, 139, 140, 141] and Iron [42, 81, 83, 88, 138]. According to the existence of carbonate rocks, which are mostly older than plutonic complexes of the UDMB (mainly at the age of Cretaceous), there is remarkable potential for skarn mineralization in this tectonic setting.
Location of study area on the Urumieh–Dokhtar magmatic arc and the generalized geological map of the area (modified after Ghalamghash and Babakhani [49])
Skarn mineralization is genetically and temporally associated with mafic to intermediate plutons that intruded an older sedimentary basement comprising limestones and dolostones [15, 29,29,30, 34, 36,38,−38, 53, 55, 57, 86, 120]. Three consecutive steps occur are required for developing skarn mineralization: (a) contact metamorphism, (b) ascending the temperature of the plutonic body and the release of ore-bearing content, and (c) developing the ore-bearing and alteration mineral assemblages [56]. Steps b and c are associated with skarn mineralization and deposition [56]. This style of mineralization can be divided into two categories that include endoskarn or exoskarn on the basis of the host rock [34, 40,41,−38, 56, 86]. Endo- and exoskarns are the consequences of replacements of intrusive rocks within the contact zone and carbonate host rocks at or near the contact, respectively [36, 86]. Fe skarn deposits are associated with magnetite mineralization in calc–silicate contact metasomatic rocks, which can be categorized into two groups including calcic and magnesian skarn irons [28, 36, 37, 42, 81, 83, 86, 138]. The former is mostly developed by the replacement of limestone, tending to occur in convergent tectonic environments, especially in island arc settings. The latter, however, is mostly developed by the replacement of dolomite and is associated with orogenic belts along continental margins [28, 34, 36, 37, 86]. The majority of the world's economic iron skarn deposits are calcic iron, while magnesian iron skarns are less documented [38]. Calcic skarn iron deposits are large deposits averaging some 300 million tons of iron content [133]. Calcic skarn irons are characterized by less silicic intrusions compared with magnesian skarns, minor amount of alkaline rocks, somewhat great amount of endoskarn mineralization, the extensive event of Na metasomatism, in association with magnetite, pyrite, hematite, garnet, pyroxene, and calcite, with geochemical enrichments of Fe, Cu, Zn, Au, and As [28, 34, 36, 37, 42, 56, 106]. Magnesian iron skarns are characterized by more silicic intrusions compared with calcic skarns, mostly occurred in dolomitic strata, in association with magnetite, forsterite, spinel, diopside, apatite, tremolite, phlogopite, talc, amphibole, serpentine, talc, chlorite, chondrodite, magnesite, and clinohumite [36, 37, 55,56,57].
Most of the skarns are related to magmatic arcs and subduction zones, which also host porphyry copper deposits [55] such as the UDMB which has the same situation. Iron deposits of Iran, especially the ones located in the UDMB, are the consequence of magmatic activities pending Eocene to Miocene [122]. The Sarvian deposit, hosting some 2 million tons of Iron [138], is one of the calcic skarn irons of the UDMB [83], situated in the Varan area. This deposit is resulted from a quartz diorite intruding an early Permian to Tertiary limestone of Qom formation, with the temperature of 370–550 °C according to Garnet–pyroxene thermometry [138]. Mansouri et al. [83] implemented successfully the potential mapping of calcic skarn iron in the Sarvian area, which is considered in this study for the Varan area, with using intrusive rocks of tonalites and quartz diorites as the source of mineralization, a reduced-to-pole map of ground magnetic data representing a further proxy for the source, the outcropping limestones and skarn units representing the trap; uni-element geochemical signatures of ore-related elements derived from litho-geochemical samples including Fe, Cu, Zn, Au, and As; and the remotely sensed derived accumulation of minerals include magnetite, pyrite, hematite, garnet, pyroxene, and calcite. Figure 1 shows a schematic representation of the subduction-related tectonic regime and ore formation model of calcic skarn iron deposit in the Varan area (after Lowell and Guilbert 1978).
The Varan area is marked by the presence of Eocene plutonic rocks and the sediments of Qom formation, Cretaceous in age [49]. The intrusion of the former into the latter yielded several cases of calcic skarn iron mineralization in the area [42]. Figure 2 depicts a simplified geological map of the study area, thoroughly discussed in Feizi et al. [43]. In the area confined by this study, calcic skarn iron mineralization [133] occurs in the contact of basic to intermediate intrusions and crystalline limestones, sandstones, and shales of Qom formation. The Qom formation has been reported as a proper trap of Skarn deposits in the UDMB [42, 81, 83, 88, 138].
4.2 Translating the deposit model to spatial proxies with using mineral system approach
Proper insight into mineral systems leads to defining the exploration targeting criteria in regional- and district-scale exploration targeting systems [62, 80, 85] which should be translated to mappable spatial proxies with the goal of targeting undiscovered mineralization [71, 72, 78, 111]. The same suit of targeting criteria exploited in Feizi et al. [42] was employed to vector toward skarn iron mineralized zones. They used a minerals system framework [76] to translate critical processes to the formation of calcic skarn iron deposits—source, trap, and deposition—to a set of targeting criteria. This set comprises the outcropping tonalites and quartz diorites representing the source of mineralization (Fig. 3a), the outcropping limestones of the Qom formation representing the physiochemical trap (Fig. 3b), the remotely sensed derived accumulation of ore minerals as a criterion representing the deposition (Fig. 3c), uni-element geochemical signatures of ore-related elements derived from litho-geochemical samples (Fig. 3d), and a reduced-to-pole map of aeromagnetic data representing another proxy for the source (Fig. 3e) (Feizi et al. [42]). Table 1 provides a summary of these criteria. Readers are referred to Feizi et al. [42] for further details.
Targeting criteria derived from mineral systems approach: a outcropping tonalities and quartz diorites representing the source, b outcropping calcareous sediments representing the physiochemical trap, c distribution of ore-related minerals representing the depositional processes, d uni-elemental litho-geochemical anomalies representing the depositional processes, e and geophysical anomalies representing the depositional processes
5 Mineral potential mapping
5.1 Weighting spatial proxies
Spatial proxies for calcic skarn iron mineralization comprising surficial heat sources (C1), physiochemical trap (C2), mineral assemblages (C3), geochemical anomalies (C4), and subsurficial heat sources (C5) were procreated (Fig. 3). According to step 1 of FUCOM, the ranking of spatial proxies was determined as \(C_{1} > C_{2} > C_{3} > C_{4} > C_{5}\). Then, based on step 2, a comparison was applied based on the ranking criteria, determining the significance (\(\varphi_{k}\)) of the proxies, which led to computing the comparative priority of the proxies (Table 2). Step 3 was performed to calculate the final values of the weight coefficients, which satisfied two conditions of Eqs. 3 and 4. (Table 3). After that, Step 4 was accomplished with solving an optimization problem in Lingo software as follows:
Thus, the optimal weights \(\left( {w_{1} , w_{2} , \ldots , w_{n} } \right)^{T}\) acquired are given in Table 4. The spatial proxies were, therefore, ranked from the most to the least critical as heat sources (C1: \(w\) = 0.434), trap (C2: \(w\) = 0.255), mineral assemblages (C3: \(w\) = 0.128), geochemical anomalies (C4: \(w\) = 0.096), and subsurficial heat sources (C5: \(w\) = 0.087).
5.2 Prioritization and ranking of alternatives (pixels)
The targeting criteria were converted to raster maps with a cell size of 50 × 50 square meters according to the distribution of geochemical samples [59] and flight-line distancing of aeromagnetic data [64] used in this work. These criteria were converted to the matrix represented in Eq. (6). Given the weights of the FUCOM method in Table 4, Eqs. (7–10) are used for integrating the weighted criteria into maps of mineral potential (Figs. 4, 5).
5.3 Validation of the results
Natural breaks [68] were employed for the initial classification of prospectivity maps (Figs. 4, 5). Nevertheless, for a more robust delineation of exploration targets, favorability–area [9, 42] fractal modeling was employed. Figure 6 represents the favorability–area model applied to the potential maps of MOORA (Fig. 4) and MOOSRA (Fig. 5). This process retrieved two classified maps represented in Figs. 7 and 8. Also, the thresholds derived from the fractal model are illustrated in Tables 5 and 6. According to these tables and figures, each map is divided into five classes. Field surveys were carried out to ground-check the anomalies derived from the two potential maps. Evidence of skarn iron mineralization has been observed in the area as illustrated in Fig. 9. In each ground control point illustrated in Fig. 9, litho-geochemical sampling was conducted. These samples were analyzed for their iron content using XRF. We sought the opinion of many experts regarding the concentration of iron in calcic skarn iron deposits. The average opinion of experts is represented in Table 7, according to which we classified our collected samples into five classes (Table 7). Table 8 provides a comparative tool through which one can opt for the more robust potential map. According to the result of the last column in Table 8, the accuracy of the MOOSRA method is 80% (8 correct predictions of 10), but the MOORA method is 70% (7 correct predictions of 10). Based on this comparison, the method of MOOSRA outperformed MOORA in MPM.
In addition, with respect to high prospective classes retrieved from the two methods, the method of MOOSRA is superior to MOORA. This is because the former has reduced the search space to some 1.7 square kilometers, while this number is some 3.7 square kilometers for the latter (cf. [79]). An illustration of this comparison is provided in Fig. 10.
We also applied confusion matrixes [1, 71] to compare the two modeling methods using the correct classification rate (CCR) (Tables 9, 10). We qualitatively translate the values of very low, low, moderate, high, and very high derived from Table 8 into the values of 1, 2, 3, 4, and 5, respectively. The sum of values of diagonal lines in confusion matrixes is divided by the total number of control points, which is 10 in this study. The value of CCR is therefore 0.7 and 0.8 for MOORA and MOOSRA, respectively. This also implies that MOOSRA provides a more robust map of mineral potential.
6 Discussion
Several multi-criteria decision-making (MCDM) methods, which have their advantages and disadvantages [42, 71, 100,101,102], have been applied to knowledge-driven GIS-based issues, such as mineral potential mapping studies (e.g., [13, 40, 45, 50, 107, 114, 130]). These methods are used in weighting spatial proxies [9, 13, 39, 42, 71, 99, 124]. The FUCOM method, as a pairwise comparison method, reduces the large number of pairwise comparisons of similar and popular approaches such as analytic hierarchy process (AHP: [113]) with n(n − )/2 and the best–worst method (BWM: [109]) with 2n − \(3\) number of pairwise comparisons with n − \(1\) which leads to a less time-consuming and more consistent performance compared with AHP and BWM. Yet, the application of FUCOM in MPM is not without drawbacks. The subjectivity has been regarded as the most crucial flaw of FUCOM in MPM (cf. [94]). Further research should account for fuzziness and ambiguity to modulate this caveat in FUCOM-based MPM (cf. [94]). Turning to the MOORA [21] and MOOSRA [32] methods, this study demonstrated the application of these approaches in the integration of weighted evidence maps. Regional-scale maps of mineral potential are used for reducing the search space and thus the cost of exploratory surveys [79]. In this work, two multi-criteria decision-making approaches, namely MOORA [21] and MOOSRA [32], were applied in the context of knowledge-driven mineral potential mapping (MPM). Both methods successfully limited the search space for field checks and further surveys. However, MOOSRA returned a more cost-effective potential map, with its target zones occupying merely some 1.7 km2. Ground-truth analysis of the delineated target also sheds light on the superiority of the MOOSRA method. Furthermore, the statistical comparison of the two methods using correct classification rates (CCR) revealed that MOOSRA returned a more reliable map of mineral potential.
There are a whole host of different multi-criteria decision-making methods used in MPM. However, what makes MOORA and MOOSRA more reliable compared to many other methods is the fact that optimizations procedure is applied to calculate the prospectivity score of individual unit cells [4, 7, 11, 33, 70, 75, 84, 98, 116, 129, 137]. This reduces the uncertainty stemming from erroneous mathematical calculations. In addition, this study was applied on a suite of mineral systems-derived targeting criteria (e.g., [85]), modulating the errors embedded in the local-scale deposit models [80]. Therefore, the target zones retrieved from these frameworks can be assumed as confident targets, in which the risk of exploration has been reduced.
Aside from the comparison of these methods, the delineated target zones show evidence of calcic skarn mineralization. The presence of mineral assemblages critical to the exploration of this style of mineralization, such as magnetite, crystalline calcite, and pyrite, provides compelling evidence for the presence of mineralization. The delineated targets, therefore, are worthy of detailed surveys.
7 Conclusions
This study proposed the application of FUCOM method as a MCDM approach for assigning weights to the spatial proxies and two matrix-based decision-making methods of MOORA and MOOSRA for intergrading a set of targeting criteria for mineral potential mapping. These methods combined to each other to present two-step methodologies, namely FUCOM-MOORA and FUCOM-MOOSRA. The results of combined methods were interesting and accurate because FUCOM weighting method has the minimum possible number of comparisons in its theory, which lead to having more reliable outputs in comparison with previous approaches, and both MOORA and MOOSRA methods have robust mathematical theory, which reduces the uncertainty stemming from erroneous mathematical calculations and causes having more trusty results. The proposed methods FUCOM-MOORA and FUCOM-MOOSRA were utilized for intergrading a set of 2D spatial proxies representing calcic skarn mineralization in Central Iran. The latter method revealed superior results as shown by field checks and statistical analyses. Both methods successfully reduced the search space for further exploratory surveys. Moreover, a mineral system approach was applied for deriving the targeting criteria, which itself reduces the bias of fallacious assumptions in geological models. As a result, the retrieved maps of mineral potential can be assumed as a high confident map, based on which further decisions can be made. The target zones suggested in the potential maps are probably worthy of conducting further exploration surveys including litho-geochemical sampling, magnetic geophysical survey, trenching, and exploration drilling. The genetic characteristics of calcic skarn deposits and the data available were used to develop a set of 2D spatial proxies representing iron skarn mineralization. In the future, the proposed methods can be used to integrate a set of 3D spatial proxies for determining exploration drilling points in the target zones.
References
Abedi M, Torabi SA, Norouzi GH, Hamzeh M, Elyasi GR (2012) PROMETHEE II: a knowledge-driven method for copper exploration. Comput Geosci 46:255–263
Agard P, Omrani J, Jolivet L, Mouthereau F (2005) Convergence history across Zagros (Iran): constraints from collisional and earlier deformation. Int J Earth Sci 94:401–419
Agard P, Omrani J, Jolivet L, Whitechurch H, Vrielynck B, Spakman W, Monié P, Meyer B, Wortel R (2011) Zagros orogeny: a subduction-dominated process. Geol Mag 148:692–725
Akkaya G, Turanoğlu B, Öztaş S (2015) An integrated fuzzy AHP and fuzzy MOORA approach to the problem of industrial engineering sector choosing. Expert Syst Appl 42(24):9565–9573
Alavijeh BS, Rashidnejad-Omran N, Corfu F (2017) Zircon U-Pb ages and emplacement history of the Nodoushan plutonic complex in the central Urumieh-Dokhtar magmatic belt, Central Iran: product of Neotethyan subduction during the Paleogene. J Asian Earth Sci 143:283–295
Aliyari F, Rastad E, Mohajjel M (2012) Gold deposits in the Sanandaj-Sirjan zone: orogenic gold deposits or intrusion-related gold systems? Resour Geol 62(3):296–315
Anitha J, Das R (2020) Optimization of process parameters in electro discharge machine using standard deviation, MULTIMOORA and MOOSRA methods. In: Innovative product design and intelligent manufacturing systems, Springer, Singapore, pp 619–629
Arabameri A, Rezaei K, Cerda A, Lombardo L, Rodrigo-Comino J (2019) GIS-based groundwater potential mapping in Shahroud plain, Iran. A comparison among statistical (bivariate and multivariate), data mining and MCDM approaches. Sci Total Environ 658:160–177
Asadi HH, Sansoleimani A, Fatehi M, Carranza EJM (2016) An AHP–TOPSIS predictive model for district-scale mapping of porphyry Cu–Au potential: a case study from Salafchegan area (central Iran). Nat Resour Res 25(4):417–429
Attri R, Grover S (2013) Decision making over the production system life cycle: MOORA method. Int J Syst Assur Eng Manag 5:320–328
Aytac E, Işık A (2016) The multi-objective decision-making methods based on MULTIMOORA and MOOSRA for the laptop selection problem. J Ind Eng Int 13:229–237
Badi I, Abdulshahed A (2019) Ranking the Libyan airlines by using full consistency method (FUCOM) and analytical hierarchy process (AHP). Oper Res Eng Sci Theory Appl 2(1):1–14
Bahrami Y, Hassani H, Maghsoudi A (2019) BWM-ARAS: A new hybrid MCDM method for Cu prospectivity mapping in the Abhar area. NW Iran Spatial Stat 33:100382
Bakhtavar E, Lotfian R (2017) Applying an integrated fuzzy gray MCDM approach: a case study on mineral processing plant site selection. Int J Min Geo-Eng 51(2):177–183
Belousov VI, Belousova IV, Filippov Y (2012) The formation of hydrothermal-magmatic systems of skarn type. In: Proceedings, thirty-seventh workshop on geothermal reservoir engineering Stanford University, Stanford, California, January
Berberian M, King GCP (1981) Towards a paleogeography and tectonic evolution of Iran. Can J Earth Sci 18(2):210–265
Bozanic D, Tešić D, Kočić J (2019) Multi-criteria FUCOM–Fuzzy MABAC model for the selection of location for construction of single-span bailey bridge. Decis Making Appl Manag Eng 2(1):132–146
Bozanic D, Tešić D, Milić A (2020) Multicriteria decision making model with Z-numbers based on FUCOM and MABAC model. Decis Making Appl Manag Eng 3(2):19–36
Brauers W, Zavadskas E (2009) Robustness of the multi-objective MOORA method with a test for the facilities sector. Technol Econ Dev Econ 15:352–375
Brauers WKM, Ginevičius R, Podvezko V (2010) Regional development in Lithuania considering multiple objectives by the MOORA method. Technol Econ Dev Econ 16(4):613–640
Brauers WK, Zavadskas EK (2006) The MOORA method and its application to privatization in a transition economy. Control Cybern 35:445–469
Brauers W, Ginevičius R, Podvezko V (2010) Regional development in Lithuania considering multiple objectives by the MOORA method. Technol Econ Dev Econ 16:613–640
Brauers W, Zavadskas E, Peldschus F, Turskis Z (2008) Multi-objective decision-making for road design. Transport. 23:183–193
Burkin JN, Lindsay MD, Occhipinti SA, Holden EJ (2019) Incorporating conceptual and interpretation uncertainty to mineral prospectivity modelling. Geosci Front 10(4):1383–1396
Chakraborty S (2011) Applications of the MOORA method for decision making in manufacturing environment. Int J Adv Manuf Technol 54(9–12):1155–1166
Chatterjee P, Athawale VM, Chakraborty S (2011) Materials selection using complex proportional assessment and evaluation of mixed data methods. Mater Des 32(2):851–860
Collins WJ, Belousova EA, Kemp AI, Murphy JB (2011) Two contrasting Phanerozoic orogenic systems revealed by hafnium isotope data. Nat Geosci 4(5):333–337
Cox DP (1986) Descriptive model of Fe skarn deposits. Miner Depos Models US Geol Surv Bull 1693:94
Cox DP, Singer DA (1986) Mineral deposit models, vol 1693, Bulletin: US Government Printing Office
Cox DP, Theodore TG (1986) Descriptive model of Cu skarn deposits. Miner Depos Models US Geol Surv Bull 1693:86
Dargahi S, Arvin M, Pan Y, Babaei A (2010) Petrogenesis of post-collisional A-type granitoids from the Urumieh-Dokhtar magmatic assemblage, Southwestern Kerman, Iran: constraints on the Arabian-Eurasian continental collision. Lithos 115(1–4):190–204
Das MC, Sarkar B, Ray S (2012) Decision making under conflicting environment: a new MCDM method. Int J Appl Decis Sci 5(2):142–162
Dorfeshan Y, Mousavi SM, Mohagheghi V, Vahdani B (2018) Selecting project-critical path by a new interval type-2 fuzzy decision methodology based on MULTIMOORA, MOOSRA and TPOP methods. Comput Ind Eng 120:160–178
Du Bray EA (1995) Preliminary compilation of descriptive geoenvironmental mineral deposit models. US Geological Survey, Denver, CO, pp 95–831
Durmić E (2019) Evaluation of criteria for sustainable supplier selection using FUCOM method. Oper Res Eng Sci Theory Appl 2(1):91–107
Einaudi MT, Burt DM (1982) Introduction; terminology, classification, and composition of skarn deposits. Econ Geol 77(4):745–754
Einaudi MT, Meinert LD, Newberry RJ, Skinner Brian JE (1981) Skarn deposits
Elliott JE, Wallace CA, Lee GK, Antweiler JC, Lidke DJ, Rowan LC, Moll SH (1992) Mineral resource assessment map for skarn deposits of gold, silver, copper, tungsten, and iron in the Butte l 0 X2 quadrangle, Montana
Elyasi GR, Bahroudi A, Abedi M (2019) Risk-based analysis in mineral potential mapping: application of quantifier-guided ordered weighted averaging method. Nat Resour Res 28(3):931–951
Elyasi GR, Bahroudi A, Abedi M, Rahimi H (2020) Weighted photolineaments factor (WPF): an enhanced method to generate a predictive structural evidential map with low uncertainty, a case study in Chahargonbad Area, Iran. Nat Resour Res 1–33
Fazlollahtabar H, Smailbašić A, Stević Ž (2019) FUCOM method in group decision-making: Selection of forklift in a warehouse. Decis Making Appl Manag Eng 2(1):49–65
Feizi F, KarbalaeiRamezanali A, Mansouri E (2017) Calcic iron skarn prospectivity mapping based on fuzzy AHP method, a case Study in Varan area, Markazi province. Iran Geosci J 21(1):123–136
Feizi F, Karbalaei-Ramezanali A, Tusi H (2017) Mineral potential mapping via TOPSIS with hybrid AHP–Shannon entropy weighting of evidence: a case study for porphyry-cu, Farmahin area, Markazi Province. Iran Nat Resour Res 26(4):553–570
Ford A, Hart CJ (2013) Mineral potential mapping in frontier regions: a Mongolian case study. Ore Geol Rev 51:15–26
Forson ED, Menyeh A, Wemegah DD, Danuor SK, Adjovu I, Appiah I (2020) Mesothermal gold prospectivity mapping of the southern Kibi-Winneba belt of Ghana based on Fuzzy analytical hierarchy process, concentration-area (CA) fractal model and prediction-area (PA) plot. J Appl Geophys 174:103971
Förster H (1978) Mesozoic–cenozoic metallogenesis in Iran. J Geol Soc 135(4):443–455
Gadakh VS (2010) Application of MOORA method for parametric optimization of milling process. Int J Appl Eng Res 1(4):743
Gadakh VS, Shinde VB, Khemnar NS (2013) Optimization of welding process parameters using MOORA method. Int J Adv Manuf Technol 69(9–12):2031–2039
Ghalamghash J, Babakhani AR (1996) Geological map of Kahak area, scale 1: 100,000, Geol. Surv, Tehran, Iran
Gheshlaghi HA, Feizizadeh B (2017) An integrated approach of analytical network process and fuzzy based spatial decision making systems applied to landslide risk mapping. J Afr Earth Sc 133:15–24
Ghorbani M (2013) Economic geology of Iran, vol 581. Springer, Berlin
Golonka J (2004) Plate tectonic evolution of the southern margin of Eurasia in the Mesozoic and Cenozoic. Tectonophysics 381(1–4):235–273
Goryachev NA, Shpikerman VI, Church SE, Gvozdev VI (2018) Calcic skarn ore deposits of the North-East Russia. Ore Geol Rev 103:3–20
Guilbert JM, Lowell JD (1974) Variations in zoning patterns in porphyry copper deposits: Canadian Institute of Mining and Metallurgy Bulletin, vol 67
Hammarstrom JM (2002) Environmental geochemistry of skarn and polymetallic carbonate-replacement deposit models. Prog Geoenviron Models Sel Miner Depos Types 2:115
Hammarstrom JM, Kotlyar BB, Theodore TG, Elliott JE, John DA, Doebrich JL et al (1995) Cu, Au, and Zn-Pb Skarn deposits preliminary compilation of descriptive geoenvironmental mineral deposit models US Geological Survey Open-File Report 95, p 831
Hammarstrom JM, Theodore TG, Kotlyar BB, Doebrich JA, Elliott JE, Nash JT et al (2004) FE SKARN DEPOSITS (MODEL 18d; Cox, 198)
Haschke M, Ahmadian J, Murata M, McDonald I (2010) Copper mineralization prevented by arc-root delamination during Alpine-Himalayan collision in central Iran. Econ Geol 105(4):855–865
Hengl T (2006) Finding the right pixel size. Comput Geosci 32(9):1283–1298
Honarmand M, Li XH, Nabatian G, Neubauer F (2017) In-situ zircon U-Pb age and Hf-O isotopic constraints on the origin of the Hasan-Robat A-type granite from Sanandaj-Sirjan zone, Iran: implications for reworking of Cadomian arc igneous rocks. Miner Pet 111(5):659–675
Honarmand M, Omran NR, Corfu F, Emami MH, Nabatian G (2013) Geochronology and magmatic history of a calc-alkaline plutonic complex in the Urumieh-Dokhtar Magmatic Belt, Central Iran: zircon ages as evidence for two major plutonic episodes. Neues Jahrbuch für Mineralogie-Abhandlungen: J Mineral Geochem 190(1):67–77
Hronsky JM, Kreuzer OP (2019) Applying spatial prospectivity mapping to exploration targeting: fundamental practical issues and suggested solutions for the future. Ore Geology Reviews
Hutchison CS (1989) The palaeo-Tethyan realm and Indosinian orogenic system of Southeast Asia. In: Tectonic evolution of the Tethyan region, Springer, Dordrecht, pp 585–643
Isles DJ, Rankin LR (2013) Geological interpretation of aeromagnetic data. Society of Exploration Geophysicists and Australian Society of Exploration Geophysicists
Jamali H, Dilek Y, Daliran F, Yaghubpur A, Mehrabi B (2010) Metallogeny and tectonic evolution of the Cenozoic Ahar-Arasbaran volcanic belt, northern Iran. Int Geol Rev 52(4–6):608–630
Jamali H, Zohouri FS, Manesh SMT (2019) Exhalative deposits in eocene volcano-sedimentary rocks in the middle part of the Urumieh-Dokhtar magmatic belt: Detailed evidence from nabar deposit, west of Kashan, Urumieh-Dokhtar Magmatic Belt. J Afr Earth Sci 154:120–135
Janković S (1977) The copper deposits and geotectonic setting of the Thethyan Eurasian Metallogenic Belt. Miner Deposita 12(1):37–47
Jenks GF (1967) The data model concept in statistical mapping. Int Yearbook Cartogr 7:186–190
Kananian A, Sarjoughian F, Nadimi A, Ahmadian J, Ling W (2014) Geochemical characteristics of the Kuh-e Dom intrusion, Urumieh-Dokhtar Magmatic Arc (Iran): implications for source regions and magmatic evolution. J Asian Earth Sci 90:137–148
Karande P, Chakraborty S (2012) Application of multi-objective optimization on the basis of ratio analysis (MOORA) method for materials selection. Mater Des 37:317–324
Karbalaei Ramezanali A, Feizi F, Jafarirad A, Lotfi M (2020) Application of best-worst method and additive ratio assessment in mineral prospectivity mapping: a case study of vein-type copper mineralization in the Kuhsiah-e-Urmak Area. Iran Ore Geol Rev 117:103268
Karbalaei Ramezanali A, Feizi F, Jafarirad A, Lotfi M (2020) Geochemical anomaly and mineral prospectivity mapping for vein-type copper mineralization, kuhsiah-e-urmak area, Iran: application of sequential gaussian simulation and multivariate regression analysis. Nat Resour Res 29(1):41–70
Karel W, Brauers W, Zavadskas E, Turskis Z, Vilutienė T (2008) Multi-objective contractor’s ranking by applying the MOORA method. J Bus Econ Manag 9:245–255
Khodami M, Noghreyan M, Davoudian AR (2009) Pliocene-Quaternary Adakite volcanism in the Isfahan area, Central Iranian magmatic belt. Neues Jahrbuch für Mineralogie-Abhandlungen: J Mineral Geochem 186(3):235–248
Kılıç G, Organ A (2019) Comparison of private shopping sites with user data from entropy-based Moosra method. In: Multi-criteria decision-making models for website evaluation, IGI Global, pp 103–120
Knox-Robinson CM, Wyborn LAI (1997) Towards a holistic exploration strategy: using geographic information systems as a tool to enhance exploration. Aust J Earth Sci 44:453–463
Kuo MS, Liang GS (2012) A soft computing method of performance evaluation with MCDM based on interval-valued fuzzy numbers. Appl Soft Comput 12(1):476–485
Lin N, Chen Y, Lu L (2020) Mineral potential mapping using a conjugate gradient logistic regression model. Nat Resour Res 29(1):173–188
Lindsay M, Aitken A, Ford A, Dentith M, Hollis J, Tyler I (2016) Reducing subjectivity in multi-commodity mineral prospectivity analyses: Modelling the west Kimberley, Australia. Ore Geol Rev 76:395–413
Lisitsin VA, González-Álvarez I, Porwal A (2013) Regional prospectivity analysis for hydrothermal-remobilised nickel mineral systems in western Victoria, Australia. Ore Geol Rev 52:100–112
Maleki S, Alirezaei S, Corfu F (2019) Dating of Oligocene granitoids in the Khak-Sorkh area, Central Urumieh-Dokhtar arc, Iran, and a genetic linkage with the associated skarn iron deposit. J Asian Earth Sci 182:103930
Manap MA, Sulaiman WNA, Ramli MF, Pradhan B, Surip N (2013) A knowledge-driven GIS modeling technique for groundwater potential mapping at the Upper Langat Basin, Malaysia. Arab J Geosci 6:1–17
Mansouri E, Feizi F, Rad AJ, Arian M (2017) A comparative analysis of index overlay and topsis (based on AHP weight) for iron skarn mineral prospectivity mapping, a case study in Sarvian area, Markazi province. Iran Maden Tetkik ve Arama Dergisi 155:147–160
Mavi RK, Goh M, Zarbakhshnia N (2017) Sustainable third-party reverse logistic provider selection with fuzzy SWARA and fuzzy MOORA in plastic industry. Int J Adv Manuf Technol 91(5–8):2401–2418
McCuaig TC, Beresford S, Hronsky J (2010) Translating the mineral systems approach into an effective exploration targeting system. Ore Geol Rev 38(3):128–138
Meinert, L. D. (1992). Skarns and skarn deposits. Geoscience Canada, vol 19, no 4
Meulenkamp JE, Sissingh W (2003) Tertiary palaeogeography and tectonostratigraphic evolution of the Northern and Southern Peri-Tethys platforms and the intermediate domains of the African-Eurasian convergent plate boundary zone. Palaeogeogr Palaeoclimatol Palaeoecol 196(1–2):209–228
Nabatian G, Rastad E, Neubauer F, Honarmand M, Ghaderi M (2015) Iron and Fe–Mn mineralisation in Iran: implications for Tethyan metallogeny. Aust J Earth Sci 62(2):211–241
Najafi A, Karimpour MH, Ghaderi M (2014) Application of fuzzy AHP method to IOCG prospectivity mapping: A case study in Taherabad prospecting area, eastern Iran. Int J Appl Earth Obs Geoinf 33:142–154
Nunić Z (2018) Evaluation and selection of Manufacturer PVC carpentry using FUCOM-MABAC model. Oper Res Eng Sci Theory Appl 1(1):13–28
Nykänen V, Niiranen T, Molnár F, Lahti I, Korhonen K, Cook N, Skyttä P (2017) Optimizing a knowledge-driven prospectivity model for gold deposits within Peräpohja Belt, Northern Finland. Nat Resour Res 26(4):571–584
Occhipinti SA, Metelka V, Lindsay MD, Hollis JA, Aitken AR, Tyler IM et al (2016) Multicommodity mineral systems analysis highlighting mineral prospectivity in the Halls Creek Orogen. Ore Geol Rev 72:86–113
Okay AI (1989) Alpine-Himalayan blueschists. Annu Rev Earth Planet Sci 17(1):55–87
Pamucar D, Deveci M, Canıtez F, Bozanic D (2020) A fuzzy Full Consistency Method-Dombi-Bonferroni model for prioritizing transportation demand management measures. Appl Soft Comput 87:105952
Park I, Kim Y, Lee S (2014) Groundwater productivity potential mapping using evidential belief function. Groundwater 52(S1):201–207
Parsa M, Maghsoudi A, Ghezelbash R (2016) Decomposition of anomaly patterns of multi-element geochemical signatures in Ahar area, NW Iran: a comparison of U-spatial statistics and fractal models. Arab J Geosci 9(4):260
Parsa M, Maghsoudi A (2018) Controls on Mississippi valley-type Zn-Pb mineralization in Behabad district, central Iran: constraints from spatial and numerical analyses. J Afr Earth Sci 140:189–198
Patnaik PK, Swain PTR, Mishra SK, Purohit A, Biswas S (2020) Composite material selection for structural applications based on AHP-MOORA approach. Mater Today Proc 33:5659–5663
Pazand K, Hezarkhani A (2015) Porphyry Cu potential area selection using the combine AHP-TOPSIS methods: a case study in Siahrud area (NW, Iran). Earth Sci Inf 8(1):207–220
Pazand K, Hezarkhani A, Ghanbari Y (2014) Fuzzy analytical hierarchy process and GIS for predictive Cu porphyry potential mapping: a case study in Ahar-Arasbaran Zone (NW, Iran). Arab J Geosci 7:241–251
Pazand K, Hezarkhani A, Ataei M (2012) Using TOPSIS approaches for predictive porphyry Cu potential mapping: A case study in Ahar-Arasbaran area (NW, Iran). Comput Geosci 49:62–71
Pazand K, Hezarkhani A, Ataei M, Ghanbari Y (2011) Combining AHP with GIS for predictive Cu porphyry potential mapping: A case study in Ahar Area (NW, Iran). Nat Resour Res 20:251–262
Pérez-Domínguez L, Rodríguez-Picón LA, Alvarado-Iniesta A, Luviano Cruz D, Xu Z (2018) MOORA under Pythagorean fuzzy set for multiple criteria decision making. Complexity
Pour AB, Hashim M (2012) Identifying areas of high economic-potential copper mineralization using ASTER data in the Urumieh-Dokhtar Volcanic Belt. Iran Adv Space Res 49(4):753–769
Prentkovskis O, Erceg Ž, Stević Ž, Tanackov I, Vasiljević M, Gavranović M (2018) A new methodology for improving service quality measurement: Delphi-FUCOM-SERVQUAL model. Symmetry 10(12):757
Purtov VK, Kholodnov VV, Anfilogov VN, Nechkin GS (1989) The role of chlorine in the formation of magnetite skarns. Int Geol Rev 31(1):63–71
Rahimi E, Shekarian Y, Farahani S, Asgari G, Nakini A (2020) New Approach in Application of the AHP–Fuzzy TOPSIS Method in Mineral Potential Mapping of the Natural Bitumen (Gilsonite): A Case Study from the Gilan-e-Gharb Block, the Kermanshah, West of Iran. Am J Eng Appl Sci 13(1):96–110
Reilinger RE, McClusky SC, Oral MB, King RW, Toksoz MN, Barka AA et al (1997) Global Positioning System measurements of present-day crustal movements in the Arabia-Africa-Eurasia plate collision zone. J Geophys Res Solid Earth 102(B5):9983–9999
Rezaei J (2015) Best-worst multi-criteria decision-making method. Omega 53:49–57
Rosenbaum GIDEON, Lister GS (2002) Reconstruction of the evolution of the Alpine-Himalayan orogeny—an introduction. J Virtual Explor 8:1–2
Roshanravan B (2020) Translating a mineral systems model into continuous and data-driven targeting models: An example from the Dolatabad Chromite District Southeastern Iran. J Geochem Explor 215:106556
Roshanravan B, Tabatabaei SH, Kreuzer O, Moini H, Parsa M (2020) Structural and non-structural statistical methods: implications for delineating geochemical anomalies. Appl Earth Sci 129(3):111–121
Saaty TL (1980) The analytic hierarchy process: planning, priority setting, resources allocation. McGraw, New York, p 281
Sabbaghi H, Tabatabaei SH (2020) A combinative knowledge-driven integration method for integrating geophysical layers with geological and geochemical datasets. J Appl Geophys 172:103915
Sarjoughian F, Javadi S, Azizi H, Ling W, Asahara Y, Lentz D (2019) Geochemical and Sr–Nd isotopic constraints on the genesis of the Soheyle-PaKuh granitoid rocks (central Urumieh-Dokhtar magmatic belt, Iran). Int Geol Rev 62:1–27
Sarkar A, Panja SC, Das D, Sarkar B (2015) Developing an efficient decision support system for non-traditional machine selection: an application of MOORA and MOOSRA. Prod Manuf Res 3(1):324–342
Şengör AMC (1986) The dual nature of the Alpine-Himalayan system: progress, problems and prospects. Tectonophysics 127(3–4):177–195
Sepahi AA, Salami S, Lentz D, McFarlane C, Maanijou M (2018) Petrography, geochemistry, and U-Pb geochronology of pegmatites and aplites associated with the Alvand intrusive complex in the Hamedan region, Sanandaj-Sirjan zone, Zagros orogen (Iran). Int J Earth Sci 107(3):1059–1096
Sepidbar F, Ao S, Palin RM, Li QL, Zhang Z (2019) Origin, age and petrogenesis of barren (low-grade) granitoids from the Bezenjan-Bardsir magmatic complex, southeast of the Urumieh-Dokhtar magmatic belt. Iran Ore Geol Rev 104:132–147
Sepidbar F, Mirnejad H, Li JW, Ma C (2017) Mineral and stable isotope compositions, phase equilibria and 40Ar–39Ar geochronology from the iron skarn deposit in Sangan, northeastern Iran. Ore Geol Rev 91:660–681
Shahabpour J (1999) The role of deep structures in the distribution of some major ore deposits in Iran, NE of the Zagros thrust zone. J Geodyn 28(2–3):237–250
Shahabpour J (2005) Tectonic evolution of the orogenic belt in the region located between Kerman and Neyriz. J Asian Earth Sci 24(4):405–417
Shahabpour J (2007) Island-arc affinity of the Central Iranian volcanic belt. J Asian Earth Sci 30(5–6):652–665
Shahsavar S, Rad AJ, Afzal P, Nezafati N, Aghdam MA (2019) Prospecting for polymetallic mineralization using step-wise weight assessment ratio analysis (SWARA) and fractal modeling in Aghkand Area. NW Iran Arab J Geosci 12(7):248
Skirrow RG, Murr J, Schofield A, Huston DL, van der Wielen S, Czarnota K et al (2019) Mapping iron oxide Cu-Au (IOCG) mineral potential in Australia using a knowledge-driven mineral systems-based approach. Ore Geol Rev 113:103011
Sosson M, Kaymakci N, Stephenson R, Bergerat F, Starostenko V (2010) Sedimentary basin tectonics from the Black Sea and Caucasus to the Arabian Platform: introduction. Geol Soc Lond Spec Publ 340(1):1–10
Stević Ž, Brković N (2020) A novel integrated FUCOM-MARCOS model for evaluation of human resources in a transport company. Logistics 4(1):4
Storetvedt KM (1990) The Tethys Sea and the Alpine-Himalayan orogenic belt; mega-elements in a new global tectonic system. Phys Earth Planet Inter 62(1–2):141–184
Suriani S, Purnama Y, Nguyen PT (2020) Decision support system in determining smart TV using MOORA. J Crit Rev 7(1):80–85
Talkhablou M, Kianpour M, Aghda SF (2019) ArcGIS fuzzy modeling to assess the relationship between seismic wave velocity and electrical resistivity with limestone mass quality (case study: Asmari Formation, southwest Iran). Model Earth Syst Environ 5(3):1025–1035
Thomas JC, Grasso JR, Bossu R, Martinod J, Nurtaev B (1999) Recent deformation in the Turan and South Kazakh platforms, western central Asia, and its relation to Arabia-Asia and India-Asia collisions. Tectonics 18(2):201–214
Vergés J, Fernàndez M (2012) Tethys-Atlantic interaction along the Iberia-Africa plate boundary: the Betic-Rif orogenic system. Tectonophysics 579:144–172
Vidal C, C. E., Injoque-Espinoza, J., Sidder, G. B., & Mukasa, S. B. (1990) Amphibolitic Cu-Fe skarn deposits in the central coast of Peru. Econ Geol 85(7):1447–1461
Wu C, Yin A, Zuza AV, Zhang J, Liu W, Ding L (2016) Pre-Cenozoic geologic history of the central and northern Tibetan Plateau and the role of Wilson cycles in constructing the Tethyan orogenic system. Lithosphere 8(3):254–292
Yang J, Xu Z, Robinson PT, Zhang J, Zhang Z, Liu F, Wu C (2011) HP–UHP metamorphic belts in the Eastern Tethyan orogenic system in China. In: Ultrahigh-pressure metamorphism, Elsevier, pp 459–499
Zagradjanin N, Pamucar D, Jovanovic K (2019) Cloud-based multi-robot path planning in complex and crowded environment with multi-criteria decision making using full consistency method. Symmetry 11(10):1241
Zaied ANH, Ismail M, Gamal A, Mostafa N (2019) An integrated neutrosophic and MOORA for selecting machine tool. Neutrosophic Sets Syst 28(1):4
Zamanian H, Sameti M, Pazoki A, Barani N, Ahmadnejad F (2017) Thermobarometry in the Sarvian Fe-skarn deposit (Central Iran) based on garnet–pyroxene chemistry and fluid inclusion studies. Arab J Geosci 10(3):54
Zarasvandi A, Charchi A, Carranza EJM, Alizadeh B (2008) Karst bauxite deposits in the Zagros mountain belt. Iran Ore Geol Rev 34(4):521–532
Zarasvandi A, Liaghat S, Zentilli K, Porter TM (2005) Porphyry copper deposits of the Urumieh-Dokhtar magmatic arc Iran. Super Porphyry Copper Gold Depos Glob Perspect 2:441–452
Zarasvandi A, Rezaei M, Sadeghi M, Lentz D, Adelpour M, Pourkaseb H (2015) Rare earth element signatures of economic and sub-economic porphyry copper systems in Urumieh-Dokhtar Magmatic Arc (UDMA). Iran Ore Geol Rev 70:407–423
Zavadskas EK, Turskis Z, Kildienė S (2014) State of art surveys of overviews on MCDM/MADM methods. Technol Econ Dev Econ 20(1):165–179
Zolfani SH, Chen IS, Rezaeiniya N, Tamošaitienė J (2012) A hybrid MCDM model encompassing AHP and COPRAS-G methods for selecting company supplier in Iran. Technol Econ Dev Econ 18(3):529–543
Acknowledgements
The authors give thanks to Dr. Edris Mansouri for his helpful suggestions.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Feizi, F., Karbalaei-Ramezanali, A.A. & Farhadi, S. FUCOM-MOORA and FUCOM-MOOSRA: new MCDM-based knowledge-driven procedures for mineral potential mapping in greenfields. SN Appl. Sci. 3, 358 (2021). https://doi.org/10.1007/s42452-021-04342-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s42452-021-04342-9