1 Introduction

The study of viscous boundary layer fluid flow and heat transfer due to stretching surface has a significant role in manufacturing procedures and polymer production. More industrial applications are cooling of fibers, paper productions, glass blowing, continuous stretching of plastic sheets, hot rolling, synthetic filaments, bar drawing, fiberglass, aerodynamics, etc. Wang [1] was one of the first successful pioneers who analyzed the heat transfer and fluid flow outside a hollow stretching tube. He confirmed his theory with analytical data and concluded that fluid flow over stretching surface has a significant role in extrusion process. His excellent work on stretching surface pushed researchers to involve in various problems subjected to flow and heat transfer in numerous fields of engineering, manufacturing functions and medical. Later, Ishak et al. [2] in their work focused on various hydrothermal parameters such as Prandtl number, suction/blowing, Reynolds number, friction factor and heat transfer coefficient along a permeable stretching pipe. They found that suction enhances skin friction, while blowing reduces it. Also, Ishak et al. [3] conducted their study on viscous fluid stream subjected to a stretched cylinder. The influence of Lorentz force on nanofluid flow over a stretching pipe using different varieties of nanocrystals (Ag, Cu, Al2O3 and TiO2) was investigated by Ashorynejad et al. [4]. Their research indicates that metal-based nanofluids enhance the thermal performance of the fluid problem. Ahmed et al. [5] noticed this result and added different-shaped solid nanoparticles. They also derived numerical solution to discuss the source/sink factor by incorporating various models of thermal conductivity and dynamic viscosity. All the aforementioned heat transfer investigations have been examined under “no-slip boundary conditions” over stretching cylinder. The no-slip boundary condition is one of the central principles of “Navier–Stokes theory”. But, there are many conditions where this phenomenon does not work. The phenomenon “slip” may take place on the stretching boundary when the liquid is in the form of suspensions such as, nanofluid, polymer solutions and foams. The non-adherence solid–fluid interface motion, also called velocity slip, is a hydrodynamic term that has been examined under some conditions [6]. Mukhopadhyay [7] presented a numerical study of nanofluid flow in the presence of velocity slip over an elongating tube. She found that slip reduces velocity but increases the temperature profile. This priceless information leads to improvement of flow model associated with slip conditions. Later, Hayat et al. [8] used thermal slip along with velocity slip to discuss the heat and mass transfer performance over a vertical stretching tube. They observed that slip parameter has a propensity to increase the rate of heat and mass transfer. The fluid models with boundary slip have significant roles in medical and engineering applications, for instance, in the cleaning of mechanical heart valves and inner cavities. For several coated physical bodies, such as bakelite, that resist adhesion, the no-slip condition is replaced by Navier’s slip, where the slip velocity is corresponding to local shear stress. However, experimental studies indicate that slip velocity also depends on the normal stress. Recently, several fluid models (Refs. [9,10,11,12,13,14]) have been modified for explaining the influence of slip that occurs at solid hydrodynamic restrictions. The study of flow and heat transportation of moving liquid, such as nanofluid with the effect of magnetic field, has gained the attention of numerous scientists and investigators because of its vast functions in the fields of manufacturing and mechanics, for instance, liquid cooling systems for thermonuclear fusion power plants, optical gratings, mechanical flow meters, fuel and gases technologies, hydraulic pumps, etc. Such study related to mutual interaction between the magnetic flux and electricity conducting fluid is generally called magnetohydrodynamics (MHD). The magnetic field strength changes the behavior of nanofluid flow. These nanofluids under the influence of magnetic field are very helpful in the various fields of engineering and medical. One of the best examples of the use of nanofluid is in chemotherapy treatment and tumor analysis. The nanofluid is optimized to absorb extra radiation and generate a large amount of free radicals than base fluid. When these nanoparticles are carefully delivered to tumors, they damage the cellular composition of cancer cells without affecting the healthy tissue. Whereas healthy tissues obtain regular dose from radiation, tumor destroys very fast. An individual injection of nanoparticles can potentially reduce radiotherapy sessions and eventually diminishes the cancerous tumor over the time. Many researchers have used MHD flow using stretching surface to improve the thermal performance in different boundary value problems. One such instance is investigated by Nourazar et al. [15]. They analyzed nanofluid flow, where various nanoparticles were suspended into base fluid. They found increment in temperature profile when magnetic parameter enhances. Babu et al. [16] provided the insight into the nanofluid flow problem under the effect of thermal radiation where MHD flow was induced by stretching sheet. Venkateswarlu and Narayana [17] described MHD flow against a porous flat plate, and they analyzed thermo-physical characteristics of the developed model using slip effects. Recently, many analytical and numerical studies [18,19,20,21] related to MHD effect were done on different surfaces.

The factors such as viscous dissipation and Joule heating are also essential features for heat transportation past a stretching cylindrical pipe, as these effects play a significant character during thermal transportation of nanofluid over heated surfaces. Physically, viscous dissipation is a rate at which kinetic energy is converted into thermal energy in a viscous fluid per unit mass. Sheikholeslami et al. [22] reported the influences of viscous dissipation and presented the fluid problem through zigzag motion effects of nanoparticles on MHD nanofluid flow connecting two plates in a rotating system. They concluded that heat transfer rate has an opposite trend with dissipation parameter. Maleki et al. [23] discussed about the performance of pseudo-plastic nanofluid past a movable porous surface with dissipation effect. A study of nanomaterial fluid flow under the influence of viscous dissipation was done by Saleem et al. [24]. They derived an analytical solution with the help of optimal homotopy analysis technique and pointed out that dissipation parameter enhances the temperature field. On the other hand, Joule heating is a process to generate excessive heat in nanofluid either due to applied magnetic force or electric current. It plays a crucial role in food processing equipment, incandescent light bulbs, electrolysis, electric fuses and heaters, etc. Ganga et al. [25] analyzed viscous–Ohmic (Joule) heating effects on MHD nanofluid flow toward a plate by adding heat generation/absorption. Their study showed that with magnetic parameter and dissipation parameter, heat transfer rate slows down. Das et al. [26] illustrated the joined influences of Joule heating and friction heating characteristics on combined free and force convective MHD flow against an inclined surface. Hussain et al. [27] investigated cumulative influences of viscous dissipation and Ohmic heating over axially stretched pipe filled with hydromagnetic Sisko nanofluid. Abbasi et al. [28] considered Ohmic heating and Hall effect inside a symmetric conduit occupied with silver–water nanofluid. Tarakaramu and Narayana [29] conducted their investigation on heated stretching surface with Joule heating and thermal radiation effects. A list of key references in the literature concerning the impact of viscous dissipation and Ohmic heating can be found in Refs. [30,31,32,33,34,35]. The effect of heat generation (or) absorption phenomenon is related to energy has extremely important attributes in production and manufacturing procedures for example, disassociating fluids, packed bed bioreactors, dissipative storage space materials, thinning and improving the ductility of copper wire. Problem pertaining to flow of nanofluid along a wavy surface due to internal heat generation including magnetic flux was presented by Mustafa et al. [36]. Mishra and Kumar [37] used Riga plate to study magnetic hydraulic flow of nanofluid involving heat generation/absorption. References [38,39,40,41] are some recent sources of additional studies about the influence of heat generation/absorption.

All the above-mentioned studies clearly indicate that although many research works have shown the characteristics of nanofluid model, many of its applications are yet to be investigated in heat transfer problems. Therefore, our aim of current study is to bridge such gap. Literature review also suggests that no such attempt has been done to investigate the effects of slip on MHD boundary layer flow through stretching tube including viscous–Joule heating when the effects due to ambiguities of thermal conductivity and dynamic viscosity have been incorporated. The current study is the extension of previous work of Mishra et al. [10] using two physical models of thermal conductivity and dynamic viscosity. They explored the MHD nanofluid flow in the occurrence of Joule–viscous dissipation with suction/injection through a stretching cylinder adding heat generative/absorptive effect. Their investigation was concentrated only on the nanofluid flow using classic two-phase nanofluid models with various factors using RKF45 method. In general, when nanofluid flows through a medium, the production of heat is witnessed due to its higher thermal conductivity. So, we have studied heat transfer with friction heating and thermal slip effects. The current study includes the comparison of two different types of silver nanoparticles: spherical and cylindrical shape (nanotubes) under various relevant parameters. Solutions of the present problem are computed by RKF45 technique with shooting algorithm. The performances of pertinent parameters on velocity and temperature fields are showcased via graphs and tables. It is expected that the outcomes of present study will not only provide valuable information for applications, but also serve as a complement to the previous published works.

2 Formulation of mathematical problem

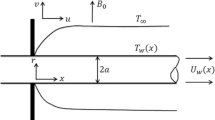
Consider an incompressible, steady, laminar two-dimensional MHD flow of water-based nanofluid inclusive of silver as nanoparticles through stretching cylinder with diameter \(2a\). The polar coordinate system \(\left( {z,r} \right)\) is considered, where \(z\)-axis toward horizontal and radial distance \(r\) is measured along vertical to the cylindrical surface (Fig. 1). \(B_{0}\) is a homogeneous magnetic field that acts toward radial direction, which is generated by a DC power source (see Ref. [15]). Furthermore, it is understood that the induced magnetic field can be omitted over applied magnetic flux due to extremely small amount of magnetic Reynolds number. Thermal radiation, Hall effect and chemical reactions are neglected. With the aforementioned assumptions, the principal nonlinear boundary layer flow and heat transfer equations for present mathematical model are developed as follows (Refs. [2] and [15]):

Fig. 1
figure 1

Physical model and coordinate system

Full size image

2.1 Momentum formulation

  • Mass conservation equation:

    $$\frac{{\partial \left( {rw} \right)}}{\partial z} + \frac{{\partial \left( {ru} \right)}}{\partial r} = 0$$
    (1)

  • Momentum equation:

    $$w\frac{\partial w}{\partial z} + u\frac{\partial w}{\partial r} = \frac{{\mu_{{\rm nf}} }}{{\rho_{{\rm nf}} }}\left( {\frac{{\partial^{2} w}}{{\partial r^{2} }} + r^{ - 1} \frac{\partial w}{\partial r}} \right) - \frac{{\sigma_{{\rm nf}} }}{{\rho_{{\rm nf}} }}B_{0}^{2} w,$$
    (2)
    $$w\frac{\partial u}{\partial z} + u\frac{\partial u}{\partial r} = - \frac{1}{{\rho_{{\rm nf}} }}\left( {\frac{\partial p}{\partial r}} \right) + \frac{{\mu_{{\rm nf}} }}{{\rho_{{\rm nf}} }}\left( {\frac{{\partial^{2} u}}{{\partial r^{2} }} + r^{ - 1} \frac{\partial u}{\partial r} - \frac{u}{{r^{2} }}} \right)$$
    (3)

The above equations are subjected to following boundary conditions [2,3,4,5]:

$$\begin{aligned} & {\text{on}}\,{\text{surface}}\,{\text{of}}\,{\text{cylinder}}\, ( {\text{at}}\,r = a ) :\;u = U_{w} ,\,w = W_{w} + l_{1} \frac{\partial w}{\partial r}, \\ & {\text{at}}\,{\text{boundary}}\,{\text{layer}}\, ( {\text{as}}\,r \to \infty ) :\;u \to 0. \\ \end{aligned}$$
(4)

where \(\left( {w,u} \right)\) is velocity constituent along \(\left( {z,r} \right)\) directions, respectively. \(\mu\) is dynamic viscosity, \(\kappa\) is dynamic viscosity, \(W_{w} = 2zc\), \(c\) is constant, and \(l_{1}\) is the slip factors for velocity. Value of \(l_{1}\) becomes zero in the absence of slip flow. The subscript \(nf\) symbolizes nanofluid.

The following transformations and dimensionless scheme (Table 2) with thermo-physical nanofluid factors are used (Table 1) [2,3,4,5]:

$$\begin{aligned} & u = - \frac{ca}{\sqrt \eta }f\left( \eta \right),\;w = 2zcf^{{\prime }} \left( \eta \right),\;\eta = \left( {\frac{r}{a}} \right)^{2} \\ & \alpha_{{\rm nf}} = \frac{{\kappa_{{\rm nf}} }}{{\left( {\rho C_{p} } \right)_{{\rm nf}} }},\sigma_{{\rm nf}} = \left( {1 - \varphi } \right)\sigma_{{\rm bf}} + \varphi \sigma_{{\rm sp}} , \\ & \rho_{{\rm nf}} = \left( {1 - \varphi } \right)\rho_{{\rm bf}} + \varphi \rho_{{\rm sp}} . \\ \end{aligned}$$
(5)

where \(\varphi\) is volume fraction of nanoparticles. The symbols \(bf\) and \(sp\) in the subscripts denote conventional fluid and Ag particles, respectively.

Table 1 Models of nanofluid based on different formulae for thermal conductivity and dynamic viscosity (see in Ref. [5])
Full size table

The continuity equation is identically satisfied, and by adopting (5) in Eqs. (2) and (3) we yield following nonlinear ODE [2,3,4,5]:

$$\frac{{\mu_{{\rm nf}} }}{{\mu_{{\rm bf}} }}\left( {\eta f^{{{\prime \prime \prime }}} + f^{{\prime \prime }} } \right) + \left( {1 - \varphi + \varphi \frac{{\rho_{{\rm sp}} }}{{\rho_{{\rm bf}} }}} \right)Re\left( {ff^{{\prime \prime }} - f^{{{\prime }2}} } \right)\, - M\left( {1 - \varphi + \varphi \frac{{\sigma_{{\rm sp}} }}{{\sigma_{{\rm bf}} }}} \right)f^{{\prime }} = 0$$
(6)

and limit conditions (4) become:

$$\begin{aligned} & f\left( {\eta_{1} } \right) = S,\;f^{{\prime }} \left( {\eta_{1} } \right) = 1 + Vsf^{{\prime \prime }} \left( {\eta_{1} } \right), \hfill \\ & f^{{\prime }} \left( \eta \right) \to 0,\;\,\,{\text{as}}\,\,\eta \to \infty \hfill \\ \end{aligned}$$
(7)

where dashes represent for derivative w.r.t. to dimensionless length \(\eta\). The non-dimensional prevailing parameters are \(f\) dimensionless velocity, \(\text{Re} \left( { = \frac{{ca^{2} }}{{2\nu_{{\rm bf}} }}} \right)\) Reynolds number, \(M\left( { = \frac{{\sigma_{{\rm bf}} B_{0}^{2} a^{2} }}{{4\rho_{{\rm bf}} \nu_{{\rm bf}} }}} \right)\) magnetic parameter, \(S = \left( { - \frac{{\sqrt \eta U_{w} }}{ca}} \right)\) suction parameter \(\left( {S > 0} \right)\) and blowing parameter \(\left( {S < 0} \right)\) and \(Vs\left( { = \frac{{2l_{1} }}{a}} \right)\) velocity slip parameter.

2.2 Temperature formulation

Energy equation:

The principal nonlinear energy equation for present mathematical model is (Refs. [2] and [15]):

$$w\frac{\partial T}{\partial z} + u\frac{\partial T}{\partial r} = \alpha_{{\rm nf}} \left( {\frac{{\partial^{2} T}}{{\partial r^{2} }} + r^{ - 1} \frac{\partial T}{\partial r}} \right) + \frac{{Q_{0} }}{{\left( {\rho C_{p} } \right)_{{\rm nf}} }}\left( {T - T_{\infty } } \right)\, + \frac{{\mu_{{\rm nf}} }}{{\left( {\rho C_{p} } \right)_{{\rm nf}} }}\left( {\frac{\partial w}{\partial r}} \right)^{2} + \frac{{\sigma_{{\rm nf}} }}{{\left( {\rho C_{p} } \right)_{{\rm nf}} }}B_{0}^{2} w^{2}$$
(8)

with compatible to boundary conditions:

$$\begin{aligned} & {\text{on}}\,{\text{surface}}\,{\text{of}}\,{\text{cylinder}}\, ( {\text{at}}\,r = a ) :\;T = T_{w} + l_{2} \frac{\partial T}{\partial r}, \\ & {\text{at}}\,{\text{boundary}}\,{\text{layer}}\, ( {\text{as}}\,r \to \infty ) :\;T \to T_{\infty } .\\ \end{aligned}$$
(9)

In the governing model, \(T\) denotes fluid temperature, \(\rho C_{p}\) is heat capacitance, \(Q_{0}\) is heat generation/absorption coefficient and \(l_{2}\) is the slip factor for temperature. Under no-slip condition, \(l_{2}\) becomes zero.

The cylinder pipe surface is also assumed to be heated at \(T_{w}\) and ambient fluid has temperature \(T_{\infty }\), where \(\left( {T_{w} - T_{\infty } } \right) > 0\).

Subsequent transformations and dimensionless scheme (Table 2) with nanofluid factors are used (Table 1):

$$\begin{aligned} & \theta \left( \eta \right) = \frac{{T - T_{\infty } }}{{T_{w} - T_{\infty } }}, \\ & \left( {\rho C_{p} } \right)_{{\rm nf}} = \left( {1 - \varphi } \right)\left( {\rho C_{p} } \right)_{{\rm bf}} + \varphi \left( {\rho C_{p} } \right)_{{\rm sp}} . \\ \end{aligned}$$
(10)
Table 2 Thermophysical properties of pure water and Ag nanoparticle (see in Ref. [37])
Full size table

Using Eq. (5) in (8), it becomes [2,3,4,5]:

$$\left[ {1 - \varphi + \varphi \frac{{\left( {\rho C_{p} } \right)_{{\rm sp}} }}{{\left( {\rho C_{p} } \right)_{{\rm bf}} }}} \right]\Pr \text{Re} f\theta^{\prime } + \frac{{\mu_{{\rm nf}} }}{{\mu_{{\rm bf}} }}\left( {\eta \Pr Ec} \right)f^{\prime \prime 2} + \frac{{\kappa_{{\rm nf}} }}{{\kappa_{{\rm bf}} }}\left( {\eta \theta^{\prime \prime } + \theta^{\prime } } \right) + Q\theta + \left( {1 - \varphi + \varphi \frac{{\sigma_{{\rm sp}} }}{{\sigma_{{\rm bf}} }}} \right)EcM\Pr f^{\prime 2} = 0$$
(11)

and limit conditions (9) become:

$$\begin{aligned} & \theta (\eta_{1} ) = 1 + Ts\theta^{{\prime }} \left( {\eta_{1} } \right) \\ & \theta \left( \eta \right) \to 0\,\,{\text{as}}\,\,\eta \to \infty \\ \end{aligned}$$
(12)

where \(\theta\) is dimensionless temperature, \(\Pr \left( { = \frac{{\nu_{{\rm bf}} }}{{\alpha_{{\rm bf}} }}} \right)\) is Prandtl number, \({\text{Ec}}\left[ { = \frac{{4\rho_{{\rm bf}} \left( {cz} \right)^{2} }}{{\left( {\rho C_{p} } \right)_{{\rm bf}} \left( {T_{w} - T_{\infty } } \right)}}} \right]\) is Eckert number, \(Q\left( { = \frac{{Q_{0} a^{2} }}{{4\kappa_{{\rm bf}} }}} \right)\) is heat generation/absorption parameter and \(Ts\left( { = \frac{{2l_{2} }}{a}} \right)\) is thermal slip parameter.

2.3 Parameter of engineering interest

The physical measures of interest, namely skin friction coefficient and heat transfer rate at stretching surface, are expressed in the following manner [14]:

$$\begin{aligned} & C_{f} = \frac{{\tau_{w} }}{{\frac{1}{2}W_{w}^{2} \rho_{{\rm bf}} }}, \\ & {\text{Nu}} = \frac{{aq_{w} }}{{\kappa_{{\rm bf}} \left( {T_{w} - T_{\infty } } \right)}} \\ \end{aligned}$$
(13)

where \(\tau_{w} \left[ { = \mu_{{\rm nf}} \left. {\left( {\frac{\partial w}{\partial r}} \right)} \right|_{r = a} } \right]\) is shear stress at the surface and \(q_{w} \left[ { = - \kappa_{{\rm nf}} \left. {\left( {\frac{\partial T}{\partial r}} \right)} \right|_{r = a} } \right]\) is surface heat flux. Now, Eq. (13) can be written as:

$$\begin{aligned} & C_{f} = \frac{{2\mu_{{\rm nf}} }}{{W_{w}^{2} \rho_{{\rm bf}} }}\left( {\frac{\partial w}{\partial r}} \right)_{r = a} , \\ & {\text{Nu}} = - \frac{{a\kappa_{{\rm nf}} }}{{\left( {T_{w} - T_{\infty } } \right)\kappa_{{\rm bf}} }}\left( {\frac{\partial T}{\partial r}} \right)_{r = a} \\ \end{aligned}$$
(14)

Now, using Eqs. (5) and (10) along with Table 1 into Eq. (14) in this manner, the skin friction coefficient and Nusselt number are transformed into such form as [14]:

$$\begin{aligned} C_{f}^{ * } & = \left( {z{{\text{Re} } \mathord{\left/ {\vphantom {{\text{Re} } a}} \right. \kern-0pt} a}} \right)C_{f} = \frac{{\left( {{\raise0.7ex\hbox{${zca^{2} }$} \!\mathord{\left/ {\vphantom {{zca^{2} } {2\nu_{{\rm bf}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${2\nu_{{\rm bf}} }$}}} \right)}}{a}\frac{{2\mu_{{\rm nf}} }}{{W_{w}^{2} \rho_{{\rm bf}} }}\left( {\frac{\partial w}{\partial r}} \right)_{r = a} = \frac{{zca^{2} }}{{2a\nu_{{\rm bf}} }}\frac{{2\mu_{{\rm nf}} }}{{\left( {2zc} \right)^{2} \rho_{{\rm bf}} }}\left( {\frac{\partial w}{\partial \eta }\frac{\partial \eta }{\partial r}} \right)_{r = a} \\ & = \frac{{zca^{2} }}{{2a\nu_{{\rm bf}} }}\frac{{2\mu_{{\rm nf}} }}{{\left( {2zc} \right)^{2} \rho_{{\rm bf}} }}\left( {\frac{2r}{{a^{2} }}} \right)_{r = a} \left[ {2zcf^{{\prime \prime }} \left( \eta \right)} \right]_{\eta = 1} = \frac{{\mu_{{\rm nf}} }}{{\nu_{{\rm bf}} \rho_{{\rm bf}} }}f^{{\prime \prime }} \left( 1 \right)\,\, = \frac{{\mu_{{\rm nf}} }}{{\mu_{{\rm bf}} }}f^{{\prime \prime }} (1), \\ {\text{Nu}}^{*} & = - \frac{{a\kappa_{{\rm nf}} }}{{\left( {T_{w} - T_{\infty } } \right)\kappa_{{\rm bf}} }}\left( {\frac{\partial T}{\partial r}} \right)_{r = a} = - \frac{{a\kappa_{{\rm nf}} }}{{\left( {T_{w} - T_{\infty } } \right)\kappa_{{\rm bf}} }}\left( {\frac{\partial T}{\partial \eta }\frac{\partial \eta }{\partial r}} \right)_{r = a} \\ & = - \frac{{a\kappa_{{\rm nf}} }}{{\left( {T_{w} - T_{\infty } } \right)\kappa_{{\rm bf}} }}\left( {\frac{2r}{{a^{2} }}} \right)_{r = a} \left[ {\left( {T_{w} - T_{\infty } } \right)\theta^{{\prime }} \left( \eta \right)} \right]_{\eta = 1} = - \frac{{2\kappa_{{\rm nf}} }}{{\kappa_{{\rm bf}} }}\theta^{{\prime }} (1). \\ \end{aligned}$$
(15)

3 Numerical method

The non-dimensional flow governing Eqs. (6) and (11) along with appropriate limit conditions (7) and (12) are explicated numerically utilizing RK Fehlberg method of fourth–fifth-order invoking shooting process [42]. The flowchart of shooting technique is presented in Fig. 2. One of the major benefits of this technique is that it consists fifth-order truncation error and computational process of solutions is very simple than other numerical techniques. Recently, this technique has been used by many researchers (see Refs. [39] and [42]). RKF scheme only deals with initial value problems (IVP); hence, leading Eqs. (6) and (11) are converted to first order. Now to convert the above-described two coupled nonlinear equations into six equivalent single-order ODEs, a new set of variables is defined such as \(y_{1} = \eta\), \(y_{2} = f\), \(y_{3} = f^{{\prime }}\), \(y_{4} = f^{{\prime \prime }}\), \(y_{5} = \theta\), \(y_{6} = \theta^{{\prime }}\) and the following system of first-order equations is formed as:

$$\begin{aligned} & y_{1}^{\prime }= 1 \\ & y_{2}^{\prime } = y_{3} \\ & y_{3}^{\prime } = y_{4} \\ & y_{4}^{\prime } = \frac{{\left( {A_{1} \text{Re} \left( {y_{3} y_{3} - y_{2} y_{4} } \right) - A_{3} y_{4} + A_{5} My_{3} } \right)}}{{\left( {A_{3} y_{1} } \right)}} \\ & y_{5}^{\prime } = y_{6} \\ & y_{6}^{\prime } = \frac{{\left( { - A_{4} y_{6} - \Pr \text{Re} A_{2} y_{2} y_{6} - Qy_{5} - {\text{Ec}}\Pr A_{3} y_{1} y_{4} y_{4} - {\text{Ec}}M\Pr A_{5} y_{3} y_{3} } \right)}}{{\left( {A_{4} y_{1} } \right)}} \\ \end{aligned}$$
(16)

Subsequently, the corresponding conditions are:

$$\begin{aligned} & y_{1} \left( 1 \right) = 0,\,y_{2} \left( 1 \right) = S, \\ & y_{3} \left( 1 \right) = 1 + t_{1} Vs,\,y_{4} \left( 1 \right) = t_{1} , \\ & y_{5} \left( 1 \right) = 1 + t_{2} Ts,\,y_{6} \left( 1 \right) = t_{2} , \\ & y_{3} \left( \infty \right) = 0,\,y_{5} \left( \infty \right) = 0. \\ \end{aligned}$$
(17)

where \(A_{1} \left[ { = \left( {1 - \varphi } \right) + \varphi \frac{{\rho_{{\rm sp}} }}{{\rho_{{\rm bf}} }}} \right]\), \(A_{2} \left[ { = \left( {1 - \varphi } \right) + \varphi \frac{{\left( {\rho C_{p} } \right)_{{\rm sp}} }}{{\left( {\rho C_{p} } \right)_{{\rm bf}} }}} \right]\), \(A_{3} \left( { = \frac{{\mu_{{\rm nf}} }}{{\mu_{{\rm bf}} }}} \right)\), \(A_{4} \left( { = \frac{{\kappa_{{\rm nf}} }}{{\kappa_{{\rm bf}} }}} \right)\) and \(A_{5} \left[ {\left( {1 - \varphi } \right) + \varphi \left( {\frac{{\sigma_{{\rm sp}} }}{{\sigma_{{\rm bf}} }}} \right)} \right]\) are dimensionless constants. For conventional fluid \(\varphi = 0\), all values of \(A_{i} \,\left( {1 \le i \le 5} \right)\) become one, i.e., \({\text{A}}_{\text{i}} = 1,\,\forall \,i \in \left[ {1,5} \right]\).

Fig. 2
figure 2

Flowchart of shooting method

Full size image

Equation (16) along with limit conditions (17) as IVP is solved by finding suitable values of missing slopes (\(t_{1}\) and \(t_{2}\)) which must satisfy the applied far-field conditions. The value of these slopes is unknown in current problem; thus, we start with initial guess value of \(t_{1}\) and \(t_{2}\) satisfying appropriate fixed length \(\eta_{\hbox{max} }\). The values of \(t_{1} = f^{{\prime \prime }} \left( 1 \right)\) and \(t_{2} = \theta '\left( 1 \right)\) are regulated iteratively by Newton’s scheme. The iteration process is stopped when \(\hbox{max} \left\{ {\left| {t_{1} \left( {\eta_{\hbox{max} } } \right) - 1} \right|,\left. {\left| {t_{1} \left( {\eta_{\hbox{max} } } \right) - 1} \right|} \right\}} \right. \le 1 \times 10^{ - 6}\). For achieving the convergence criteria of \(1 \times 10^{ - 6}\) (iteration limit) and desired accuracy, the aforesaid routine is repeated such that no numerical oscillations would occur. The step size is taken \(\Delta \eta = 0.001\). Table 3 represents the grid refinement effect on \(\theta \left( \eta \right)\) for various values of Ec. It is cleared from the table that the value of \(\theta \left( \eta \right)\) decreases with grid refinement until \(\eta \to 6\). Hence, \(\infty\) is replaced by 6 throughout the computation which follows the usual practice in boundary layer theory.

Table 3 Grid Independency on \(\theta \left( \eta \right)\) for various value of Eckert number, when \(\Pr = 6.2\), \(Vs = 0.05\), \(Ts = 0.05\)
Full size table

4 Code validation

For the verification of accuracy of present numerical method to solve flow model of nanofluid toward a stretching cylinder, a comparison is done with numerical outcomes of \(f^{{\prime \prime }} \left( 1 \right)\) and \(- \theta^{{\prime }} \left( 1 \right)\) for numerous values of Re and Pr, respectively, with the results of Refs. [1, 2, 5, 14] under some special cases. Tables 4 and 5 are constructed for comparison of the numerical outcomes of both \(f^{{\prime \prime }} \left( 1 \right)\) and \(- \theta^{{\prime }} \left( 1 \right)\) with exiting values. Also, Fig. 3 is created as a proof for the accuracy of the present numerical approach. Here, heat transfer coefficient \(- \theta^{{\prime }} \left( 1 \right)\) is compared for various value of Pr. In detail, we have considered MHD boundary layer flow of silver–water nanofluid over a stretching cylinder. In addition, under no-slip boundary condition, if we substitute \(M = Ec = Q = S = \varphi = 0\), Eqs. (6) and (11) reduce to the fluid problem considered by Wang [1]. If we consider impermeable surface along with \(M = {\text{Ec}} = Q = Vs = Ts = \varphi = 0\), Eq. (6) and Eq. (11) reduces to the flow model given by Ishak et al. [2]. In the absence of slip and magnetic field, by setting \({\text{Ec}} = Q = S = \varphi = 0\), we obtained the case (see Ref. [5]) in which base fluid flow under an impermeable flat stretching surface. One can note that if \(M = 0\) (stretching cylinder without MHD), the present problem reduces to the work of Pandey and Kumar [14]. As in the present study, numerical solution is obtained through shooting technique, our results slightly vary with the results of Wang [1], Ishak et al. [2], Ahmed et al. [5] and Pandey and Kumar [14]. In fact, such type of solution depends on the initial guess values which obviously can’t be exact. Hence, a slight difference due to tolerance error in the present data is observed in Tables 4 and 4. The present scrutiny shows excellent agreement with the results of Refs. [1, 2, 5, 14] for both physical quantities (\(f^{{\prime \prime }} \left( 1 \right)\) and \(- \theta^{{\prime }} \left( 1 \right)\)) which leads to surety of the current work (Table 5).

Table 4 Comparison of numerical values of \(f^{{\prime \prime }} \left( 1 \right)\), for regular fluid \(\left( {\varphi = 0} \right)\) with various values of Reynolds number, when \(\Pr = 0.7\)
Full size table
Table 5 Comparison of numerical values of \(- \theta '\left( 1 \right)\), for regular fluid \(\left( {\varphi = 0} \right)\) with various values of Prandtl number, when \(\text{Re} = 10\)
Full size table
Fig. 3
figure 3

Variation in the value of \(- \theta^{{\prime }} \left( 1 \right)\) due to Pr

Full size image

5 Results and discussion

This section is devoted to visualize the influence of physical parameters on velocity distribution and nanofluid temperature profile. The present investigation also deals with two models, which are denominated as Model I and Model II, where Model I and Model II correspond to spherical- and cylindrical-shaped nanoparticles, respectively. Also, they have dissimilar dynamic viscosity and thermal conductivity on the basis of their diverse physical structures of Ag nanoparticles. During this whole process of numerical computations, we have chosen H2O as base fluid; consequently, the default values are kept as \(\Pr = 6.2\) and \(\text{Re} = 5\). Also, dimensionless quantity \(\eta_{\infty } = 6\) is fixed in the entire work. The relevant physical factors such as velocity slip \(\left( {Vs} \right)\) lie in the domain of [0.2, 0.6] and thermal slip parameter \(Ts \in \left[ {0.2,\,\,0.6} \right]\). Furthermore, the mathematical measures of other important parameters are \(1 \le M \le 5\), \(- 2 \le Q \le 2\), \(0.2 \le Ec \le 1.0\) and \(- 0.1 \le S \le 0.1\). The role of volumetric fraction of silver–liquid \(\varphi\) is inspected in range \(0.05 \le \varphi \le 0.20\), where \(\varphi = 0\) is the case of base fluid. Any changes in default values are mentioned in the appropriate figures or tables. Also, in all of the graphical outlines, a solid line indicates the Model I, while dashed line represents the same for Model II. The impacts of pertinent dynamic factors on velocity profiles and temperature fields are exhibited through Figs. 4, 5, 6, 7, 8, 9, 10, 11, 12 and 13. For both models, the behavior of heat transfer rate is listed in Table 6 for assorted numeric quantities of parameters \(Vs\), \(Ts\), \(M\), \(Ec\), \(Q\), \(S\) and \(\varphi\) of nanosilver particles. From the table, when \(Vs\) and \(S\left( { > 0} \right)\) increase, we observe that the absolute value of heat transfer coefficient \(\left( { - \theta^{{\prime }} \left( 1 \right)} \right)\) increases. Moreover, the table shows that the Nusselt number of flow field decreases as the values of \(Ts\), \(M\), Ec and \(Q\) increase.

Fig. 4
figure 4

Variation in velocity profiles due to \(Vs\) for different models

Full size image
Fig. 5
figure 5

Variation in velocity profiles due to \(M\) for different models

Full size image
Fig. 6
figure 6

Variation in velocity profiles due to \(S\) for different models

Full size image
Fig. 7
figure 7

Variation in velocity profiles due to \(\varphi\) for different models

Full size image
Fig. 8
figure 8

Variation in temperature profiles due to \(Ts\) for different models

Full size image
Fig. 9
figure 9

Variation in temperature profiles due to \(M\) for different models

Full size image
Fig. 10
figure 10

Variation in temperature profiles due to Ec for different models

Full size image
Fig. 11
figure 11

Variation in temperature profiles due to \(S\) for different models

Full size image
Fig. 12
figure 12

Variation in temperature profiles due to \(Q\) for different models

Full size image
Fig. 13
figure 13

Variation in temperature profiles due to \(\varphi\) for different models

Full size image
Table 6 Several values of \(- \theta^{{\prime }} \left( 1 \right)\) for both models, when \(\Pr = 6.2\) and \(\text{Re} = 5.0\)
Full size table

5.1 Computational results for fluid flow

The graphical visualization of the behavior of velocity profiles \(f^{{\prime }} \left( \eta \right)\) due to various values of velocity slip parameter \(\left( {Vs} \right)\) is sketched out in Fig. 4. Generally, slip parameter \(\left( {Vs} \right)\) calculates the quantity of slip at the surface of cylinder. Here, we analyze that fluid velocity \(\left( {f^{{\prime }} \left( \eta \right)} \right)\) reduces as \(Vs\) rises. It is due to the fact that velocity slip mainly slows down the fluid motion which effectively confirms a reduction in net movement of fluid molecules (Ref. [8]). As a result, less molecular movement causes a reduction in velocity fields. Thus, both models show a reduction due to parameter \(Vs\). Moreover, the momentum boundary layer is found to be higher for Model II than Model I. Figure 5 confirms the comparison of velocity distribution \(f^{{\prime }} \left( \eta \right)\) versus similarly variable \(\eta\) for dissimilar numerical estimations of \(M\). Magnetic parameter is a ratio of electromagnetic force to viscous force that evaluates the strength of applied magnetic force in the medium. A rise in \(M\) accelerates the strength of activated magnetic field. It is examined that momentum distribution of nanofluid decreases as \(\eta \to \infty\) for stretching cylinder. It is due to induced Lorentz force; thus, momentum boundary layer is reduced. This is in accordance with the results obtained by Mukhopadhyay [7] that velocity profiles were decelerated with the increment in magnetic parameter. Actually, the magnetic force together with slip effects acts as retarding force which opposes the occurrence of transport. It decreases the velocity of fluid with the effect of magnetic flux by raising the value of magnetic parameter inflicting high fluid restriction. Consequently, the momentum boundary layer thickness reduces in both models. In addition, whenever a backflow in stretching cylinder occurs, then magnetic parameter can be applied to reduce the backflows. Its involvement also averts the separation. As a result, a smooth flow occurs. Figure 6 is presented to observe the behavior of velocity field for two nanofluid models with \(\eta\) for assorted values of \(S\). Suction is an effective process to avoid the boundary layer separation which also controls the velocity and heat energy. It is observed that after attaining the maximum value of suction/blowing parameter, the amounts of fluid particles are close into the wall. Hence, the outline of associated boundary layer constantly becomes thinner; thus, the velocity profiles get decelerated with increasing the strength of \(S\). According to Fig. 7, on incorporating more solid volumetric fraction of Ag nanoparticles in base fluid, the momentum profiles of Ag–water nanofluid decrease for spherical shape nanoparticles, whereas reverse tendency is observed in Model II, i.e., momentum boundary layer is increased for cylindrical-shaped nanoparticles as \(\varphi\) rises. Physically, it means that intensification in strength of volumetric fraction parameter leads higher concentration of nanoparticles in conventional fluid. Hence, more amount of nanoparticles in base fluid increases resistance to flow of nanofluid in the medium, which causes the reduction in velocity for spherical-shaped nanoparticles. In other words, spherical nanoparticles slow down the system by shrinking the thickness of boundary layer. On the other hand, width of hydrodynamic boundary layer becomes wider for Model II. Physically, viscosity of Ag nanotubes is less than spherical Ag nanoparticles which is responsible for acceleration in velocity profiles.

5.2 Computational results for heat transfer

Figure 8 is drawn to examine the characteristic of thermal distribution for both models of nanofluid with \(\eta\) for several values of slip parameter \(Ts\). It is concluded that temperature drops when nanofluid approaches to boundary layer. Physically, maximum strength of thermal slip parameter reduces the surface drag leading to a decrease in production of amount of heat; thus, the reduction is found in temperature fields. Therefore, we have also examined the joined impacts of velocity and thermal slip parameters on flow and thermal field, respectively. It is interesting to see that the influences of thermal slip parameter are quite similar to those of velocity slip parameter. It is also indicated that one can control the momentum and thermal boundary layers up to the desired estimations by regulating the velocity and thermal slip parameters. Also, results obtained by Hayat et al. [8] show the same trend on temperature profiles with the increasing values of thermal slip parameter. Hence, slip at the surface reduces temperature for any kind of fluid model. Figure 9 is sketched to discuss the response of \(M\) on \(\theta \left( \eta \right)\) with fixed values of other parameters. It is witnessed that maximum amount of magnetic parameter corresponds to an increase in \(\theta \left( \eta \right)\). An extreme heat occurs during this process which helps to enhance thermal boundary layer of both models. Moreover, this cumulating nature is slightly higher in Model II than in Model I. The analysis of temperature profile under the action of viscous dissipation parameter also known as Eckert number \(\left( {\text{Ec}} \right)\) is illustrated in Fig. 10. It is traced out from graph that higher values of Ec helps to rise in temperature field in the vicinity of boundary. Saleem et al. [24] also obtained the similar result on thermal profiles for different values of Eckert number over a stretching surface. Physically, fluid friction plays an essential part to augment the measure of heat in both nanofluid models, because heat energy is stored in the fluid during this entire process. Also, in stretched condition of cylinder, more fluid particles near to surface and high friction produce maximum amount of heat throughout this process. Consequently, cylindrical-shaped nanoparticles provide a fine enhancement on comparing with spherical one. This outcome implies that Model II is better than Model I, when the higher temperature is desired in the system. Figure 11 exhibits the temperature variation of nanofluid with varying suction/injection parameter. A drop in temperature is found, when parameter \(S\) shifts from blowing to suction domain for both nanofluids. Also, Model I provides accelerated amount of heat transfer coefficient corresponding to each value of \(S\) as compared to Model II. The temperature profile under the action of heat generation/absorption parameter \(Q\) is portrayed in Fig. 12. The positive value of \(Q\) corresponds to heat generation, whereas the negative values of \(Q\) represent heat absorption. From this figure, we analyze that larger values of parameter \(Q\) demonstrate an increase in temperature \(\left( {\theta \left( \eta \right)} \right)\). Elevated values of heat generation/absorption parameter supply more energy to functioning system that leads to an increase in thermal boundary layer width in both models. The influence of \(\varphi\) on non-dimensional outline of temperature is demonstrated in Fig. 13. As expected, the graph confirms a significant rise in temperature after adding more silver nanoparticles into water. An upsurge in thermal conductivity was found, when the amount of \(\varphi\) is varied from \(\varphi = 0.05\) to \(\varphi = 0.20\). Therefore, the width of thermal boundary layer increases extensively after some larger distance from cylindrical surface when \(\varphi\) increases. We also noticed that the temperature of spherical nanoparticles is lesser as the temperature of cylindrical nanoparticles. Generally, the thermal conductivity is stronger for cylindrical-shaped nanoparticles; hence, associated boundary layer is increased with the use of higher volumetric fraction parameter \(\varphi\) for Model II. Therefore, this result helps us to figure out that when the heating is desired, technically Model II is favorable. Also this result indicates that the choice of a suitable shape of nanoparticles is important in the heating and processes.

6 Conclusions

The numerical explanation of flow and heat transfer under the action of viscous dissipation, Ohmic (Joule) dissipation, heat generation/absorption with suction or blowing on MHD flow of nanofluid involving silver as nanoparticles past an elongating tube in the existence of slip boundary conditions is examined, and the central findings are drawn as follows:

  • An enhancement in magnetic parameter, viscous dissipation parameter and heat generation/absorption parameter yields an increasing trend for thermal field.

  • The velocity of fluid lessens for escalating values of velocity slip parameter, while temperature distribution reduces for higher thermal slip parameter.

  • The magnetic parameter leads to lessen velocity profile, while a contrary trend is examined in temperature field. It is true for both nanofluid models.

  • Velocity profile of nanoparticles accelerates with cylindrical-shaped nanoparticles, whereas it decreases for spherical-shaped nanoparticles.

  • The rate of heat transfer decreases with higher estimations of heat generation/absorption, magnetic parameter and viscous dissipation parameter, whereas it confirms opposite tendency when velocity slip and suction/blowing parameters are accelerated in both models.

  • In both nanofluid models, a rise in volume fraction parameter has a tendency to upturn the thermal profile.

Undeniably, the ambiguities related to distinct dynamic viscosity and thermal conductivity with distinct shapes of silver nanoparticles have a strong effect on the behavior of boundary layer flow and heat transfer over a stretching cylinder. The results of current investigation may be useful for exploring different physical models. Also, the obtained outcomes have huge significance in the field of fluid mechanics, where layers of the surface are being stretched.