1 Introduction

The possibility of severe earthquakes occurrence due to natural geology conditions on the one hand, and the design and construction of many RC buildings in which seismic loading criteria are not considered, or their seismic loads are underestimated because of changes in these criteria on the other hand would result in necessity of seismic evaluation and rehabilitation [6, 39, 40]. Recent earthquakes around the world have shown that non-ductile (gravity load-designed) reinforced concrete (RC) buildings are vulnerable to severe damage or complete collapse. The application of eccentrically braced frames with a vertical link in seismic rehabilitation, not only eliminates the possible buckling of braces, but also leads to large inelastic deformations reduction which is applied to RC members. Hence, this research is focused on the seismic performance reliability analysis of RC frames which is rehabilitated by eccentrically braced frame with a vertical link, which is able to dissipate the earthquake input energy without buckling of the braces and the minimum damage of RC members.

In the last decade, there are important efforts to retrofit the reinforced concrete elements. Seismic behavior of steel moment resisting frames associated with RC shear walls were investigated by Esmaeili et al. [11]. Naderpour et al. [30] predicted the FRP-confined compressive strength of concrete. Ahmadi et al. [3] presented a model for predicting the compressive strength of circular steel-confined concrete. Compressive strength of environmentally friendly concrete was investigated by Naderpour et al. [31]. Furthermore, Ahmadi et al. [4] studied the seismic failure probability and vulnerability assessment of steel–concrete composite structures. Shear failure capacity prediction of concrete beam–column joints and classification of failure modes in ductile and non-ductile concrete joints were also studied [28, 29]. Haji et al. [14] performed an experimental study on influence of proposed FRP-strengthening techniques on RC circular short columns considering different types of damage index. Finally, Moradi et al. [26] conducted an experimental approach for shear strengthening of RC beams using a proposed technique by embedded through-section FRP sheets.

The most appropriate approach for evaluating the influence of earthquake-resistant structural system becomes possible with reliability analysis, because reliability analysis can easily reflect the uncertainties which exist in seismic loading and structure capacity. Seismic performance assessment based on reliability is performed by using the information obtained from past earthquakes investigation [27, 33]. Therefore, for seismic performance reliability assessment, the full coupling between a finite element analysis and common reliability methods such as the Monte Carlo simulation method (MC) and Hasofer–Lind should be used. Reliability-based finite element method (RFEM) tends to be high computational and time-consuming for practical problems. This is because, at any iteration, the limit-state function and its derivatives are to be evaluated through finite element computations. To solve the problems associated with the finite element full coupling reliability analysis, the response surface-based method (RSM) was introduced by Khuri and Cornell [18]. This method enables us to fit the structural response such as stresses or displacements in terms of random variables for reliability analyses.

In the study of Lou et al. [19], two flat slab buildings, three and 10 stories in height, designed according to the ACI 318-56 building code, were used in the nonlinear dynamic analysis and reliability calculations. The member dimensions, material strengths, and live load were treated as random variables and the effect of model uncertainty was included in the calculations of reliability indices. The limit-state function was based on the punching failure capacity of the interior slab-column connections. Huh and Haldar [16] used a proposed algorithm for reliability assessment of a steel building under the seismic loads, this algorithm concluded response surface method, finite element method, first-order reliability method and linear interpolation. Their research by considering serviceability limit states showed that the maximum drift is more critical than the total drift of the structure under seismic excitation. Hadianfard and Razani [13] presented a study for semi-rigid connections of steel frames using the finite element analysis and reliability analysis. The loads and resistance of members were selected as the random variables. The Monte Carlo simulation technique was used to calculate the probability of failure of the steel frame. It was concluded that semi-rigid connections should be considered for steel frames for more realistic and reliable results. The goal of the research conducted by Marinilli [21] was to perform a simplified stochastic analysis of reinforced concrete frames under seismic loads. Simplified analyses were performed based on the point estimate method (PEM), considering compressive concrete strength (fc′) and reinforcement steel yield stress (fy) as independent stochastic variables. Jalayer et al. [17] examined the influence of structural modeling uncertainties on the assessment of existing RC structures through a relatively simple response spectrum based method, and verified the code-based requirements with regard to the confidence factors. Abdelouafi et al. [1] were focused on the seismic performance reliability analysis of a 5 story concrete building by regarding three random variables which are characterizing material resistance variations of concrete and reinforcement steel as well as member’s sections dimensions. In this research two limit states defined in terms of the total building roof displacement and the maximum inter-story drift were considered and for seismic performance reliability analysis two approximate methods: Monte Carlo based sampling analysis and first-order reliability method (FORM) was performed. In the study of Basaga et al. [5], the reliability analysis of the four and eight stories, consisting of a portal frame and three types of concentrically braced frames with semi-rigid connections is presented. The direct coupling method, which is a combination of the reliability method such as FORM and Monte Carlo and finite element method, is utilized to determine the reliability indexes and probabilities of failure for the structure. Results showed that X braced frames are determined as the safest structures, while the portal frames are regarded as the most unsafe structures. As the connection percentage increases, the safety of the structure increases. In the study of Celarec and Dolsek [7] the impact of modeling uncertainties on the seismic performance assessment of reinforced concrete frame buildings was investigated. In their research the effects of the epistemic uncertainty are treated by using the first-order second-moment (FOSM) method, and the Latin hypercube sampling (LHS) technique. At least, explicit consideration of epistemic uncertainties in the process of the assessment of structural performance can lead to more accurate results, and consequently also to a more reliable assessment of seismic risk.

The aim of this work is to apply the response surface-based reliability analysis methodology to evaluate the seismic performance of reinforced concrete frames rehabilitated by eccentrically bracing. The effects of variations resulting from loading will be overlooked and the focus will be towards the effects resulting from the building structure’s geometric dimensions and from durability problems that affect the mechanical properties of reinforced concrete materials, specifically the characteristic value of the concrete resistance and the nominal yielding point of steel reinforcement and profiles. A comparison between results obtained by the Monte Carlo sampling method and the Hasofer–Lind method will be performed by regarding two probability distribution Normal and Lognormal in order to model the random variables. The discussion will be carried out in order to select the appropriate method that can be used to evaluate the reliability of RC frames which is seismically rehabilitated by eccentric bracing with a vertical link.

2 RC frame with eccentric bracing with vertical link

The RC Frame with eccentric bracing with a vertical link, as shown in Fig. 1, can be applied in various configurations such as: (a) the shear link and the braces are directly connected to the RC members via steel plates, bolts and epoxy grouting (see PSRM-1), (b) the shear link is connected to a collector steel beam attached to the concrete beam and the rest of the members are connected to the RC members via steel plates, bolts and epoxy grouting (see PSRM-2) or (c) the shear link and the braces are housed in a rectangular steel frame (housing frame) where the steel frame is connected to the RC members by bolts and epoxy grouting (see PSRM-3). In this work the (a) configuration is used as a proposed seismic rehabilitation system since it is easy in construction and widespread in the executive application as well as reduces the time and cost of erecting.

Fig. 1
figure 1

Details and configurations of RC frame with eccentric bracing with vertical link

Full size image

3 Basics of reliability methods

In the reliability theory, the probability of exceeding a limit state is studied in which the limit state is defined by a mathematic function called limit state function that is based on the design parameters. The limit state function divides the data space into two regions: safe and failure regions. The safety of structures is determined by two parameters of the reliability index (β) and failure probability (Pf). So many techniques are available for performing reliability analysis in order to obtain the mentioned parameters. In the following, two common ways of expressing their basic concepts are introduced.

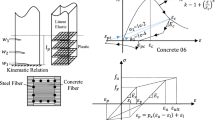
In [15], Hasofer and Lind defined the reliability index of a structure in standard Normal space as the shortest distance from the origin of the coordinate system to the failure point (design point). The Hasofer–Lind reliability analysis method is considered as the first-order approximation of the Taylor series for limit state functions. According to Fig. 2, the design point is a point on the failure surface g = 0. Since this design point is not known completely, a repeated process is used to reach the desired reliability index (β). Based on the geometry, the reliability index (shortest distance) can be introduced by \(\beta =\frac{{\mu }_{R}-{\mu }_{Q}}{\sqrt{{{\sigma }_{R}}^{2}+{{\sigma }_{Q}}^{2}}}\) in which \({\mu }_{R}\) and \({\mu }_{Q}\) represent the mean value of resistance and demand respectively and also \({\sigma }_{R}\) and \({\sigma }_{Q}\) represent the standard deviation of resistance and demand respectively. Then the probability of failure (Pf) is determined as Pf = ϕ (− β) in which ϕ is the cumulative distribution of standard Normal variable (Fig. 2).

Fig. 2
figure 2

Reliability index defined as the shortest distance from the origin of the coordinate system to the failure point [32]

Full size image

Monte Carlo simulation method, similar to a computer laboratory, simulates the test on the computer. In this method, random values would be generated for each random variable based on the distribution type and statistic parameters such as mean and standard deviation and so the limit state function associated with these values are obtained. A negative value of limit state means that the limit state is not satisfied and the failure of the system occurs. The failure probability (PF) is then calculated by dividing the number of times that the limit state is negative by a total number of simulated tests on the computer.

Expressing the limit state function as G(X), where X = (X1, X2, …, Xn) is the vector of the basic random variables, the probability of failure can be determined using the below relationship.

$${\text{PF}} = \int_{G\left( X \right) \le 0} {{\text{f}}_{{\text{x}}} \left( {\text{X}} \right){\text{dX}}}$$
(1)

where fX (X) is the joint probability and G(X) is an irregular domain with highly non-linear boundaries. Following the law of large numbers, an unbiased estimator of the probability of failure is given by

$$\overline{{{\text{PF}}}} = \frac{1}{{\text{N}}}\mathop \sum \limits_{{{\text{i}} = 1}}^{{\text{N}}} {\text{I }}\left( {{\text{X}}_{{\text{i}}} } \right)$$
(2)

where I (Xi) is an indicator defined as:

$${\text{I}}\,\left( {{\text{X}}_{{\text{i}}} } \right) = \left\{ {\begin{array}{*{20}c} 1 & {{\text{if}}\,\,{\text{G}}\left( {{\text{X}}_{{\text{i}}} } \right) \le 0} \\ 0 & {{\text{if}}\,\,{\text{G}}\left( {{\text{X}}_{{\text{i}}} } \right) > 0} \\ \end{array} } \right.$$
(3)

Accordingly, N independent random samples of a specific probability density function of the vector X are prepared and the failure function is computed for each sample Xi. If \(\mathrm{G}\left({\mathrm{X}}_{\mathrm{i}}\right)\le 0\) a successful simulation is counted. The Monte Carlo estimate of the probability of failure (Pf) can then be expressed in terms of the sample mean as

$$\overline{{{\text{PF}}}}=\frac{{\mathrm{N}}_{\mathrm{H}}}{\mathrm{N}}$$
(4)

where NH is the number of successful simulations and N is the total number of simulations [13].

Since this technique is so time to consume and expensive and also needs so much volume for performing, the approximate methods for reliability analysis like Hasofer–Lind are preferred [14].

4 Numerical study

4.1 Details of frames

Analytical models to evaluate RC frame with eccentric bracing with a vertical link, are two office non-ductile RC frames, 3 and 9 stories, that are designed based on gravity load [9] according to the ACI code [2]. The design concrete strength is 21 MPa and the design steel strength is 300 MPa and the modulus of elasticity is 200,000 MPa. The design dead load and live load for the frames are considered respectively 35 kN/m2 and 12 kN/m2. The frames mass due to the weight of all structural and nonstructural elements are equal to 945 kg/floor. The structural details of the frames are given in Table 1.

Table 1 Structural details of 3- and 9-story RC buildings
Full size table

4.2 Design

For the seismic rehabilitation design of these frames, a performance-based approach is used. The performance-based approach is based on the objective performance level in order to encounter different probabilistic earthquakes. The objective performance levels (PLs) which are used to design the proposed seismic rehabilitation system are: Life Safety (LS) building performance level for the BSE-1 earthquake hazard level (10%-in-50-year probability of exceedance or 474-year return period) and collapse prevention (CP) building performance level for the BSE-2 earthquake hazard level (2%-in-50-year probability of exceedance or 2475 year return period). In FEMA 356 [12], the acceptance criteria for the mentioned PLs are mainly defined by the plastic rotation limits of the RC members. In order to design the seismic rehabilitation details of frames, a technique based on performance is used that is mainly associated with the equal energy dissipation principle. In this method, the monotonic energy dissipation capacities of the frames in the linear elastic range based on the roof displacement obtained from response spectrum (RS) analyses and in the nonlinear inelastic range obtained from NLSP analyses for each PL are calculated and compared with each other. The difference between the areas under base shear force versus roof displacement curves in the elastic and inelastic cases is equal to the additional energy that needs to be absorbed by the RC frame with eccentric bracing with a vertical link [8]. The arrangement of the seismic rehabilitation system in the frames view is shown in Fig. 3. Also, braces and shear links details of probabilistic seismic response model (PSRM) for frames are available in Table 2.

Fig. 3
figure 3

View of RC frames rehabilitated by eccentric bracing with vertical link

Full size image
Table 2 Details of PSRM for 3 and 9 story for RC frames
Full size table

4.3 Modeling

Numerical models of frames were formed by using the 2D modeling capabilities of OpenSees [34]. Nonlinear behavior distribution along the length and cross-section of the element is modeled completely and this causes in the failure distribution. The connections of all frames members except the shear link are considered to be rigid. In order to model pinned joints for both ends of braces, a “zero Length” element with high rigidity just in the transition directions was used. In dynamic computations according to the assumption of the rigid diaphragm in roofs, stories mass in the height of stories are equally distributed between the nodes which are connected to the beam and column. The command of “Concrete01” is used to define concrete material including confined and unconfined concrete and the command of “steel 02” is used to define the steel material. In order to model beam, column, and brace elements in the OpenSees “non-linear Beam-Column” is used and is divided into five sections. All the sections are modeled by the “Fiber” model. The assigned damping to the elements and nodes is modeled by the command of “Rayleigh”. By assuming a small eccentricity, the buckling of braces is also taking into the account. Besides, P–Δ effects are considered [35].

Ramadan and Ghobarah [36] modeled the shear link as a linear element with six nonlinear rotational and translational springs at each end. So that 3 rotational bilinear springs and 3 translational bilinear springs were used to represent respectively inelastic behaviors of the flexural plastic hinge and shear of the web link at the end of the link. The selected model in this paper is the Richards model [37] that is the same model of Ramadan and Ghobarah but with different stiffness values for the shear springs. The values of My and Vy are equal to MP and 0.9VP, respectively. The relationships of flexure–rotation and shear–displacement of the shear link with their stiffness values are shown in Fig. 4. The values of \({\mathrm{K}}_{1\mathrm{M}}\) and \({\mathrm{K}}_{1\mathrm{V}}\) is equal respectively to \(\frac{3\mathrm{E}\mathrm{I}}{\mathrm{e}}\) and \(\frac{\mathrm{G}{\mathrm{A}}_{\mathrm{w}\mathrm{e}\mathrm{b}}}{\mathrm{e}}\), in which, E is Young’s modulus of steel, I is the moment of inertia of the link cross-section, G is the rigidity modulus of steel, and Aweb is the web area of the link section.

Fig. 4
figure 4

Moment–rotation and Shear force–shear deformation relationships of a steel link [37]

Full size image

4.4 Nonlinear static pushover analyses

After defining nonlinear elements of the model, the initial nonlinear analysis is performed by calculating frame base shear. According to FEMA356, frame base shear in the concerning target level is expressed by V = C1C2C3CmSaW. Seismic rehabilitated RC buildings due to changes in the lateral load resisting system (increase in the strength and stiffness), have a fundamental frequency less than the original case. Based on FEMA356, given that more than 75% of the total mass participates in the fundamental mode in the direction under consideration, the parabolic lateral load pattern can be used. Gravity loads combination defined in combination with seismic loads is equal to \({\mathrm{Q}}_{\mathrm{G}}=1.1({\mathrm{Q}}_{\mathrm{D}}+{\mathrm{Q}}_{\mathrm{L}})\),\({\mathrm{Q}}_{\mathrm{G}}=0.9{\mathrm{Q}}_{\mathrm{D}}\),where \({\mathrm{Q}}_{\mathrm{D}}\) is dead load effect, \({\mathrm{Q}}_{\mathrm{L}}\) is live load effect which is equal to 25% of the unreduced design live load but not less than the measured live load.

4.5 Reliability analysis

In this section the comparison between the seismic performance reliability analysis of original and rehabilitation frames with eccentric bracing with the vertical link by means of NLSP analysis results and the reliability methods such as Monte Carlo and Hasofer–Lind is evaluated. In Monte Carlo analysis 25, 100, 1000, 10,000 and 100,000 simulated random variables are used. The NLSP analysis is conducted by means of OpenSees software package in two PLs: life safety and collapse prevention. Concrete resistance (fc′), steel yield stress of bars and profiles (Fy), beams height (H), columns dimension (D) and bars area section (As) are considered as random variables in this article. Limit state functions that are defined as maximum roof displacement (groof) and maximum inert-story displacement (gmax) can be expressed by means of different combinations in accordance with random variables values obtained from NLSP analysis. The total number of NLSP analysis is 1944. These functions are derived by statistic software called Minitab [22]. Equations (5) and (6) clearly show those limit states.

$${\mathrm{g}}_{\mathrm{roof}}({\mathrm{f}}_{\mathrm{c}};\, {\mathrm{F}}_{\mathrm{y}};\, {\mathrm{A}}_{\mathrm{s}};\, \mathrm{H};\,\mathrm{D})= {\updelta }_{\mathrm{c},\mathrm{roof}}-{\updelta }_{\mathrm{roof}} ({\mathrm{f}}_{\mathrm{c}};\, {\mathrm{F}}_{\mathrm{y}};\, {\mathrm{A}}_{\mathrm{s}};\, \mathrm{H};\,\mathrm{D})$$
(5)
$${\mathrm{g}}_{\mathrm{max}} ({\mathrm{f}}_{\mathrm{c}};\, {\mathrm{F}}_{\mathrm{y}};\, {\mathrm{A}}_{\mathrm{s}};\, \mathrm{H};\,\mathrm{D})= {\updelta }_{\mathrm{c};\,\mathrm{max}}-{\updelta }_{\mathrm{max}} ({\mathrm{f}}_{\mathrm{c}};\, {\mathrm{F}}_{\mathrm{y}};\, {\mathrm{A}}_{\mathrm{s}};\, \mathrm{H};\, \mathrm{D})$$
(6)

where the allowable displacements according to FEMA356 in original case for (LS) PL. are δc,max = 0.02hs, δc,roof = 0.02H and for (CP) PL. are δc,roof = 0.04H, δc,max = 0.04hs. And these values in rehabilitation case for (LS) PL. are δc,max = 0.015hs, δc,roof = 0.015H and for (CP) PL. are δc,roof = 0.02H, δc,max = 0.02hs. δroof and δmax represent the demand function that express in terms of nonlinear regression of random variables. In this study two types of probability of distribution in order to model the random variables are used. The characteristic of random variables in accordance with their probability distribution is shown in Table 3.

Table 3 Characteristics of random variables [10, 20, 23,24,25, 38]
Full size table

4.6 Reliability analysis of 3 story RC frame in original case

According to Figs. 5, 6, 7 and 8, in the Monte Carlo method by increasing the number of simulated random variables into 100,000 samples, the reliability index (β) and probability of failure (PF) for the limit state of groof in (LS, CP) PLs are converged respectively in (10,000, 1000) and (100, 1000) samples with difference percentage of (1.3%, 5.2%) and (0.1%, 3.6%). And also the converging of (β) and (PF) for limit state of gmax in (LS, CP) PLs occur in (10,000, 10,000) and (1000, 1000) simulated samples with different percentage of (7%, 0.3%) and (2.9%, 2.3%). So based on the above results, more simulated samples are not needed.

Fig. 5
figure 5

Reliability analysis according to limit state (groof) in (LS) PL

Full size image
Fig. 6
figure 6

Reliability analysis according to limit state (groof) in (CP) PL

Full size image
Fig. 7
figure 7

Reliability analysis according to limit state (gmax) in (LS) PL

Full size image
Fig. 8
figure 8

Reliability analysis according to limit state (gmax) in (CP) PL

Full size image

By comparison between all of the simulated samples of Monte Carlo and Hasofer–Lind method, it is cleared that reliability index (β) and the probability of failure (PF) in the Hasofer–Lind method have respectively larger and smaller amount than simulated samples in considered limit sates and PLs. And this shows that Hasofer–Lind overestimates the reliability index (β) and underestimates the probability of failure (PF). The difference percentage of (PF) between Hasofer–Lind and the converged sample of Monte Carlo method for the limit state of groof in (LS, CP) PLs are (24.4%, 6.9%) and for the limit state of gmax are (11.1%, 15.1%).

4.7 Reliability analysis of 3 story RC frame in rehabilitation case

As it is shown in Figs. 9 and 10, the converging of β in the Monte Carlo method, for the limit states of (groof) and (gmax) in (LS, CP) PLs are in (100, 1000) and (10,000, 10,000) samples with difference percentage of (0.8%, 3.5%) and (4.8%, 4.8%).

Fig. 9
figure 9

Reliability analysis according to limit state (groof) in (LS) and (CP) PLs

Full size image
Fig. 10
figure 10

Reliability analysis according to limit state (gmax) in (LS) and (CP) PLs

Full size image

By comparison of the results in original and rehabilitation cases, it can be concluded that the failure occurred in the original case by the negative value of limit states (groof < 0) and (gmax < 0). and in the rehabilitation case safety region is concluded; (groof > 0) and (gmax > 0) so in this condition the probability of failure is approximated to zero and the effectiveness of seismic performance of RC frame with eccentric bracing with the vertical link is clearly recognized.

The results of reliability index (β) in rehabilitation case of 3 story frame for simulated samples are not in the specified range and have large amounts; on the other hand, the Hasofer–Lind reliability method is close to its upper limit and has a certain amount. Therefore, the overestimating of Hasofer–Lind still remains. While both methods result in zero value for the probability of failure (PF).

4.8 Reliability analysis of 9 story RC frame in original case

According to Figs. 11, 12, 13 and 14, in the Monte Carlo method by increasing the number of simulated random variables into 100,000 samples, (β) and (PF) for the limit state of groof in (LS, CP) PLs are converged respectively in (100,000, 1000) and (100,000, 100) samples with difference percentage of (5.8%, 3.5%) and (6.6%, 2.4%). And also the converging of (β) and (PF) for limit state of gmax in (LS, CP) PLs occur in (100,000, 10,000) and (10,000, 100) simulated samples with different percentage of (0.2%, 0.8%) and (4.7%, 1.2%). The results show that by increasing the number of stories, the required number of samples increase. It is particularly obvious that by increasing the earthquake intensity in (CP) PL. compared to (LS) PL., more simulated samples are needed.

Fig. 11
figure 11

Reliability analysis according to limit state (groof) in (LS) PL

Full size image
Fig. 12
figure 12

Reliability analysis according to limit state (groof) in (CP) PL

Full size image
Fig. 13
figure 13

Reliability analysis according to limit state (gmax) in (LS) PL

Full size image
Fig. 14
figure 14

Reliability analysis according to limit state (gmax) in (CP) PL

Full size image

In the 9 story frame similar to the 3-story frame, the Hasofer–Lind method over-estimates the reliability index (β) compared to all simulated samples of the Monte Carlo method. And in both PLs for two limit states the probability of failure (PF) is underestimated by Hasofer–Lind method so that the difference percentage of (PF) between Hasofer–Lind and the converged sample of Monte Carlo method for the limit state of groof in (LS, CP) PLs are (10.9%, 3.2%) and for the limit state of gmax is (5.4%, 14.2%). And these results show higher seismic resistance of frames expressed by Hasofer–Lind reliability analysis.

4.9 Reliability analysis of 9 story RC frame in rehabilitation case

According to Figs. 15, 16 and 17, in the Monte Carlo method by increasing the number of simulated random variables into 100,000 samples, (β) for the limit state of groof in (LS, CP) PLs are converged respectively in (10,000, 100,000) samples with different percentage of (1.7%, 2.07%). And also the converging of (β) for the limit state of gmax in LSPL. is occurred in 10,000 simulated samples with a different percentage of 1.8%, but in (CP) PL. more simulated samples are needed for attaining reasonable converge. By comparison of the results with 3 story frame, it can be concluded that by increasing the number of stories, the required number of samples increases. Similar to the previous results, also in this frame it is recognized that by increasing the earthquake intensity in (CP) PL. compared to (LS) PL., more samples should be simulated.

Fig. 15
figure 15

Reliability analysis according to limit state (groof) in (LS) and (CP) PLs

Full size image
Fig. 16
figure 16

Reliability analysis according to limit state (gmax) in (LS) and (CP) PLs

Full size image
Fig. 17
figure 17

Reliability analysis according to limit state (a): gmax and (b): groof in (CP) PL

Full size image

The probability of failure (PF) for the limit state of groof in (CP) PL. in all samples of Monte Carlo and Hasofer–Lind method results in the range of (0–2%), therefore, similar to the rehabilitated 3 story frame (PF) is approximated to zero. For the limit state of gmax in (CP) PL. the difference between the converged sample of Monte Carlo method and the Hasofer–Lind is around 20.3% and this difference shows the underestimation of (PF) in the Hasofer–Lind method and so higher resistance is concluded by this method.

As the results of the 3-story frame, it is clear that in 9 story frame the failure occurred in the original case with the condition of (groof < 0) and (gmax < 0). And safety condition is declared in rehabilitation case; (groof > 0) and (gmax > 0) so in this condition the effectiveness of seismic performance of RC frame with eccentric bracing with the vertical link is clearly recognized.

For both limit states in (CP) PL. the overestimation of (β) in Hasofer–Lind method compared to all samples of Monte Carlo is clearly expressed, and in (LS) PL. the result of (β) according to the Hasofer–Lind method is close to its upper bound so in this case the overestimation of (β) of this approximate method is observed.

5 Conclusion

In this article, the seismic performance reliability analysis of two 3 and 9 story RC frames that need rehabilitation based on the present criteria in two cases of original and rehabilitation with RC frame with eccentric bracing with the vertical link was assessed. This was presented by exact and approximate methods of reliability analysis; Monte Carlo and Hasofer–Lind based on the results of NLSP analysis. The NLSP analysis was done under the parabolic lateral load pattern in two (LS) and (CP) PLs. Two limit states of (groof) and (gmax) were defined, and five random variables represented the variation in resistance of concrete material, bars and steel profiles yield stress, beams height, columns dimension, and also bars cross-section were introduced.

According to the reliability analysis based on the exact method of Monte Carlo with 25, 100, 1000, 10,000 and 100,000 simulated samples, it was found that the volume of evaluation was increased by raising the story of the frames so that in the 9 story frame compare to 3 story frame, more simulated samples were needed.

By comparison two reliability analysis methods applied in this study, it was determined that in both PLs., the Hasofer–Lind method had a smaller amount of PF and a larger amount of β than Monte Carlo analysis. Therefore, the Monte Carlo reliability analysis method is a more conservative approach and presents a stronger seismic rehabilitation system for RC frames.

Based on the results of seismic performance reliability analysis of two 3 and 9 story RC frames in original and rehabilitation cases, it was found that the failure condition (groof < 0) and (gmax < 0) was established in the original case of these frames that showed the seismic weakness of these frames according to present criteria. Hence after adding the eccentric bracing with a vertical link to these frames in order to increase their seismic performance, the results of reliability analysis showed the safe condition (groof > 0) and (gmax > 0) of frames after seismic rehabilitation.