1 Introduction

Thermoelectricity is a phenomenon that involves the coupled interaction between heat and current. A desirable thermoelectric material is a material with high Seebeck coefficient; low resistivity; and low thermal conductivity. These combinations in properties will yield improve performances in terms of its high voltage; minimise the Joule heating losses; and maintain a significant temperature difference across the p/n legs respectively.

Thermoelectric generators (TEGs) basically, are stand-alone devices that find usefulness in very remote regions such as outer space and beneath the ocean. For example, TEGs can be used to power autonomous sensors which can be used in these remote areas, thereby replacing the use of battery cells. In general, TEGs are durable and require little or no maintenance because of their solid state property. This makes them suitable for use in remote regions that are difficult to access by humans. The best material used for building TEGs so far is the Bi2Te3/Sb2Te3 material. However, Tellurium is considered to be the 9th rarest element available, it is toxic and volatile at high temperatures. This makes them non-ideal for commercial purposes [1].

Thus, Ge/SiGe material can serve as an alternative to the Bi2Te3/Sb2Te3 material. Ge/SiGe material can operate at substantially higher temperatures (> 1000 K) than most of the other TE materials [2]. Although these materials have a poor ZT at room temperatures, they could be used for high temperatures applications such as TEGs for harnessing electrical energy from automobile exhaust. Other advantages include: non-toxicity and can be integrated with silicon platform, which is mostly used in the semiconductor industry.

In this study, the Ge/SiGe Superlattices having a total thickness of 4 µm is considered. It has a doping density of about 2.0 × 1018 cm−2. Having a low thermal conductivity is desirable for improving the ZT and hence efficiency of TEGs. One method employed in achieving a low thermal conductivity is by increasing the number of periods in the superlattice structure [3]. This effect has been demonstrated in [4,5,6] where the thermal resistance of Ge/SiGe superlattices is increased (and hence reduced thermal conductivity) for samples with a larger number of periods.

1.1 Overview

This study is organized into five key sections: The introductory section gives a brief background information about the Ge/SiGe-based TEG. The second section explains the step by step development of an FEM for Ge/SiGe-based TEG module. The third section shows the simulation of the TEG in terms of its temperature and voltage distribution. The fourth section is the result and discussion. This section discusses about the optimal design of the Ge/SiGe TEG module for improved performances. The results obtained from this investigation are intended to form a basis for fabricating a more efficient Ge/SiGe-based TEG. The fifth and final section is the conclusion of this study.

2 Finite element modelling of the Ge/SiGe TEG module

This study shows the development of FEM for the Ge/SiGe TEG module which involves (a) geometrical design of the Ge/SiGe – based TEG module, (b) defining the thermoelectric material properties (c) defining the boundary conditions (d) development of the governing equations and (e) meshing of the TEG – module.

2.1 Geometry design of Ge/SiGe-based TEG module

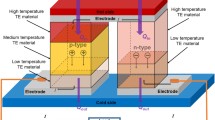
The p-type and n-type Ge/SiGe material are connected together by a connector as shown in Fig. 1(a). Figure 1(b) shows an expanded view of the different layers. The labels (a)–(f) in Fig. 1(b) represent:

  1. a.

    0.6 μm of superlattice.

  2. b.

    0.2 μm of Ohmic contact (99% Ag/1% Sb for n-type).

  3. c.

    Two layers of 0.7 μm aluminium; one deposited on the legs (i.e. both p- and n-type), the other deposited on the connector.

  4. d.

    Two layers of 2 μm indium; one deposited on the legs, the other deposited on the connector.

  5. e.

    0.1 μm layer of insulating nitride (Si3N4) for preventing electrical leakages to the connector substrate.

  6. f.

    530 μm layer of Si substrate that is used in forming the connector.

Fig. 1
figure 1

a Geometrical design representing the Ge/SiGe TEG-module (b) Expanded view of the different layers and connections labelled a-f

Full size image

2.2 Thermoelectric material properties

The thermoelectric material properties required for the FEM are the thermal conductivity, Seebeck coefficients and electrical conductivity (refer to Table 1). A low thermal conductivity is desirable in order to minimize the conduction of thermal energy from the hot region to the cold region. This will aid the generation of a high Seebeck voltage. The Seebeck coefficient,α refers to the induced voltage per temperature difference across the material while the electrical conductivity, σ is a measure of the ease of flow of the valence electrons in the material.

Table 1 Estimated Material properties used in the FEM simulations
Full size table

It is important to note that the thermal conductivities for the p-type and n-type materials are within the region 4–6 W/mK. However, the value of 26.5 W/mK presented in Table 1 is the value obtained after the connection of the p- and n- leg to form the TEG module. This anomalous high value is as a result of the effect of thermal contact resistance in the circuit. Similarly, The alpha, α and sigma, σ values prior to connection are 112 µV/K and 4099 S/m for the p-type and 269 µV/K and 9400 S/m for the n-type. However, due to electrical contact resistance present in the connection of the p- and n- legs, the values become much lower as presented in Table 1.

Again, it is important to note that the SiGe Buffer layers and Si substrate are intrinsic and thus, are not expected to conduct. Hence \(x\) values between 0 and 1 can be assigned to its electrical conductivity, σ and seebeck coefficient, α as indicated in Table 1. These small values do not affect the performance of the circuit.

2.2.1 Boundary conditions

Boundary conditions are mathematical expressions of the thermal (and/or electrical) conditions at the boundaries or surfaces of the problem domain [10]. In the present FEM, Dirichlet boundary conditions are applied at the following boundaries: the voltage at the bottom of the p-leg is set to ground (i.e. V0 = 0), while the temperatures at the top and bottom surface of the TEG module are set to the measured temperatures, Tc and Th respectively (see Fig. 2).

Fig. 2
figure 2

Set boundary conditions for FE simulation of the TEG module

Full size image

2.3 Development of the governing equations

The governing equations used to model the TEG module are based on the heat flow equation given by:

$$\rho C\frac{\partial T}{\partial t}.u+\nabla .\mathrm{q}=\mathrm{Q}$$
(1)

and the continuity of electric charge equation given by:

$$\nabla .\left(\mathrm{J}+\frac{\partial \mathrm{D}}{\partial \mathrm{t}}\right)=0$$
(2)

which are coupled by the set of thermoelectric equations (Eqs. 3 and 4)

$$J=\sigma (E-\alpha .\nabla \mathrm{T})$$
(3)
$$q=\pi J-\kappa \nabla T$$
(4)

where \(\rho , C, u, \mathrm{q},\mathrm{ Q},\mathrm{ J},\mathrm{ D}, \sigma , \mathrm{E}, \alpha , \pi , \kappa\) are: resistivity, Heat capacity, mobility, generated or absorbed heat, overall generated or absorbed heat, current density, electric displacement, electrical conductivity, Electric field intensity, Seebeck coefficient, Peltier coefficient and thermal conductivity respectively.

2.4 Meshing of the TEG module

The final stage in developing the FEM is the meshing or discretization of the TEG module. Both tetrahedral and swept meshes are used to discretize the TEG module. The choice of these meshes was basically to help reduce the number of mesh elements and consequently, decreases the processing time, without affecting the accuracy of the results.

A total of 15,972 tetrahedral elements were used to discretize the TEG module (see Fig. 3(a) and (b)). Also the mesh sizes were varied between coarse and fine meshing and the results remained relatively the same with an insignificance deviation of < 0.6%.

Fig. 3
figure 3

a Meshed diagram for FEM of Ge/SiGe-based TEG (b) Expanded view of a single element with its coordinate vertices

Full size image

The FE software (COMSOL Multiphysics®) has an inbuilt function that formulates the equilibrium equations for the individual elements shown in Fig. 3(a). A system of equations based on the nodal coordinates of each element is generated and solved. Hence, an approximate solution of the governing equations (described in Sect. 2.3) is obtained.

3 Finite element simulations of the Ge/SiGe TEG

The FEM is used to generate temperature profiles and voltages in open circuit. It can also be used to generate results for close circuit voltages, load current, heat transfer and output power of the TEG device, from which the efficiency and power density can be derived. The temperature profile between the top and bottom surfaces is presented in Fig. 4(a) and the corresponding open circuit voltage is presented in Fig. 4(b).

Fig. 4
figure 4

a Temperature distribution for ΔΤ = 5.3 K; H represents superlattice height of 3.4 μm, (b) Corresponding voltage distribution (in open circuit)

Full size image

4 Discussion of result

The developed FEM can now be used to analyse the Ge/SiGe TEG module for improved performances. Firstly, it is used to show the effect of contact resistances (i.e. thermal and electrical resistance) on the device performance. Thereafter, it is used to optimize the Ge/SiGe TEG module for improved performances.

4.1 Demonstrating the effect of contact resistance.

Let M1 refer to the building of a TEG module that is void of thermal and electrical contact resistance; while M1 + contact refers to the building of the TEG module that is affected by contact resistance. Table 2 is used to show the material properties obtained for M1 and M1 + contact and the plots are presented in Figs. 5(a) and (b).

Table 2 Properties of M1 and M1 + contact
Full size table
Fig. 5
figure 5

Comparison of M 1 and M 1 + contact for (a) load voltage and (b) output power

Full size image

The plots in Fig. 5(a), suggest that the load voltage of the TEG module was by less than half, due to the presence of contact resistances in the device. The consequence of the contact resistance is also seen in the output power of Figs. 5(b).

The FEM study by Ebling et al. [11] also shows a similar trend. In their work [11], FEM simulations and experiment investigations were used to show that the geometrical design of the legs, the electrical contacts and soldering process affected the load voltage and output power of the TEG. The modules were made using Bismuth Telluride material. A decrease in ZT by a factor of about 4 was observed for the module arrangement when compared to the ZT of the individual materials. This decrease was attributed to the high contact resistances.

Hence the significance of the FEM in the present study is that it is able to show by how much the contact resistance can affect the output performance of the device

4.2 Geometrical optimization

The optimization of the geometry of the Ge/SiGe-based TEG module can be achieved by (a) the variation of the top and bottom substrate and (b) variation of the superlattice height. From the coupled set of thermoelectric equations given in Eqs. (3) and (4), it can be seen that the output performance of the TEG is dependent on both the material properties and the dimensions of the TEG as indicated in Table 1 above. Hence the variation of the dimensions of the TEG is expected to affect the output performance of the TEG.

Therefore, the significance of the FEM is that it is able to show the optimal dimension of the TEG that will yield maximum performance

4.2.1 Variation of the top and bottom substrate

These substrates have an original thickness of 530 μm. Three (3) different designs are considered; (a) the reduction of only the top substrate; (b) reduction of only the bottom substrate and (c) reduction of both top and bottom substrates. All three designs are then compared with the original design to determine which design produces a better performance. Figure 6(b, c and d) show the three designs in comparison to the original design in Fig. 6(a).

Fig. 6
figure 6

a Original design; variation of (b) bottom substrate (c) top substrate (d) top and bottom substrate;substrate thickness is reduced to 100 μm in all three cases

Full size image

The thickness of the top and bottom substrate is reduced from 530 μm to a minimum of 100 μm. Reduction of the substrate thickness of the Ge/SiGe material beyond 100 μm is possible but not practically reasonable because the sample will become too fragile for handling and is very susceptible to damage during the course of fabrication. The critical parameters that determine the performance of the TEG module, i.e. temperature difference across the superlattice – ΔTsuperlattice, open-circuit voltage – Voc, efficiency and generated output power, are compared for the four case studies.

Figure 7(1, 2, 3 and 4) presents the results obtained for the various geometrical configurations described in Fig. 6. The temperature difference across the superlattice, ΔTsuperlattice for the different configuration is estimated as shown in Fig. 7(1).

Fig. 7
figure 7

(1) Temperature difference across superlattice (2) corresponding open circuit voltage (3) efficiency and (4) output power generated for the geometrical configurations in Fig. 7

Full size image

It is observed that the thermal losses decrease with reduction in the substrate thickness; the largest ΔTsuperlattice is obtained for configuration (d). A similar trend has also been observed in the literature [12] whereby as the thickness of the substrate increases, the thermal loss in the substrate becomes larger than that in the thermoelements. Configurations (b) and (c) appear to have very close temperature differences. This implies that the thermal contributions from the bottom substrate are nearly the same as that of the top substrate. This is expected because both top and bottom substrates have the same surface to volume ratio for the p-leg and n-leg and both are made of the same material. Hence, with both substrates reduced as shown in configuration (d), twice the increase in ΔTsuperlattice can be observed. The corresponding open circuit voltage, Voc, for the four configurations is shown in Fig. 7(2). These voltages are dependent on ΔTsuperlattice based on the Seebeck effect principle. Therefore, the largest output voltage is also observed for configuration (d). Consequently, there is improvement in the effective efficiency and output power for configuration (d) as shown in Fig. 7(3) and (4).

4.2.2 Variation of the leg height of the superlattice

It has been shown in the Sect. 4.2a that configuration (d) produces the best performance considering thickness variations of the top and bottom substrates. Hence, this configuration is investigated further by considering variations in the superlattice height for the p- and n- leg. In this case, it is assumed that the p- and n- leg are of the same height. The leg heights are therefore varied between 1–4 μm. The respective plots for the various heights are presented in Fig. 8(a, b, c and d) for the temperature difference, open circuit voltage, output power and efficiency.

Fig. 8
figure 8

Effect of Leg height on the (a) Temperature difference across superlattice (b) corresponding open circuit voltage (c) Efficiency and (d) power output generated

Full size image

From Fig. 8(a), it can be seen that the temperature difference across the superlattice increases with increase in the leg height (or superlattice thickness) for the same heat input. This results to a corresponding increase in the open circuit Seebeck voltage, as shown in (b) and improved performances in the output power and efficiency, as shown in (c) and (d) respectively. From the results obtained, it can be deduced that the magnitude of the Seebeck voltage produced is dependent on the thickness of the superlattice layer.

Based on the results obtained in Fig. 8 and given the anisotropic nature of the superlattice structure, it can be inferred that the optimal way to take voltage measurement readings should be at the surface of the superlattice where its height is maximum. The cross-plane properties of the Ge/SiGe superlattices have been shown to yield better performances than the in-plane properties. Hence there has been ongoing research to engineer the cross plane properties to yield improved performances [13].

5 Conclusion

In this study, a computer tool (FEM) was developed to simulate the thermal and electrical dynamics of a real Ge/SiGe thermoelectric generator (TEG). The relevance of the developed FEM is that it produces significant insight about the TEG that may be difficult and time consuming to obtain experimentally. For example, it is able to show the effect of contact resistance on the performance of the TEG. the α and σ-values of the unicoupled TEG as compared to the individual p- and n- Ge/SiGe materials, was quite low due to the effect of electrical contact resistance and the κ - property was quite high due to the effect of thermal contact resistance and this resulted to the low voltage and output power that was generated by the TEG module. Hence future work can focus on modelling optimal designs that will help reduce the contact resistance to its barest minimum.

Furthermore, this study suggests an optimal way for taking voltage measurement, which is at the surface of the Ge/SiGe superlattice. The basis for this hypothesis is that the simulated voltage was found to increases with increase in superlattice height and the Ge/SiGe superlattice is anisotropic. Thus future work can focus on increasing the number of thermoelectric p- and n-legs and the joining of the legs should be targeted at the surface of the Ge/SiGe superlattice.