1 Introduction

Health monitoring of the structures is the necessity of time due to an increased risk. Elements made up of piezoelectric material gained wide scope as smart material following the increased demand for safety and stability of elements used in engineering structures. The converse application of the piezoelectric effect which is known as actuation can help to control deflection at critical points in the structure. Mechanical strain-induced related to applied electric charge is seen in selected ceramics present naturally which inspired the development of artificial ones like Lead Zirconate Titanate (PZT) to be used as smart material to control the deformation. Mechanical and electrical coupling detailed in terms of the constitutive formulation bringing the stress, strain, material property, electric charge is given in the study [50]. The astonishing work [13] on shape, active control of FGM plate through piezoelectric material layers with numerical modeling become the benchmark for further studies and application. In this study, the closed-loop system working with displacement feedback is used. Shape control for laminated composite beams and plates coupled with piezoelectric layers is conducted with element-free Galerkin’s method using first order shear deformation theory (FSDT), further from the finding of the study [22] it is suggested to locate actuator patches at high strain region for effective shape control. In the study [23] used a numerical solution with a radial basis function to perform static analysis and vibration control for a laminated composite plate using piezoelectric as a smart material. The numerical model developed in the study posses a better convergence rate than finite element method (FEM) based solution. Fiber-reinforced composites with piezo-layers are considered for static bending along with its control for FGM plate with a nonlinear variation of strains in study [32]. Simply supported at its edges two FGM layers are modeled with a homogeneous layer of a piezoelectric material sandwiched in between them to examine bending and free vibration analysis using state-space formulation in research conducted [7]. A Layer-wise approach in the finite element model for FGM plate coupled with piezoelectric layer is considered for static bending and dynamic analysis subjected to impulse loading, also the electric potential distribution is assumed layer-wise giving sufficiently accurate results [42]. FGM plate resting on elastic foundation [2] is analyzed for a three-dimensional exact solution with simply supported boundary condition which is integrated with piezoelectric layers using the Fourier series and state-space method. In the research effects of elastic foundation along with gradient index for electrical and mechanical loads is varied to study its effects. Geometric nonlinearity is taken into account while developing a mathematical model [3] for FGM with a numerical solution to get results for static bending under mechanical and electric loading. B-Spline finite strip method is used for static, vibration analysis of FGM plate coupled with skins of piezoelectric material in the study [25] demonstrating the advantage of B-Spline discretization over traditional FEM as it requires less electro-mechanical degrees of freedom. Reduction in stress concentration can be achieved through the smart application of piezoelectric material for host plate with a change in stiffness and thickness ratio is observed in the work done [11]. In the study [4] for composite beam coupled with piezoelectric patches genetic algorithm is used for optimizing shape control model based on Timoshenko’s beam theory and numerical solution through FEM. To study the free vibration analysis of FGM plate with piezoelectric layers in terms of combination for a power law, aspect ratio [36] used four variable plate theory employing an analytical approach with Navier’s solution for the simply supported case. Using FSDT based plate model [30] and cell-based smoothed discrete shear gap method while performing static shape and vibration control with closed-loop feedback algorithm based on displacement and velocity, further plate subjected to step, triangular, sinusoidal and explosive blast load is analyzed in the study. To handle complex boundary conditions for the Levy type plate model in case of smart FGM plate [1] used spectral method while performing free vibration analysis. Taking forward the smart application of piezoelectric material [40] studied impact analysis on carbon nano-tubes (CNT) reinforced composite plate using Reddy’s higher-order shear deformation theory [33], such that displacement is calculated with average acceleration Newmark’s time integration method. Cracked FGM plate is studied for the uni and bi-directional critical buckling loads using the discrete shear gap method in context of numerical solution for the extended finite element analysis. It is observed in the study [24] that crack geometry can be independent of mesh grid, mesh distortion can be controlled, triangular elements can be easily generated even for complex geometry. Internal defects of FGM plate are mapped [57] through isogeometric analysis using FSDT for study of thermal buckling in the plate. To perform dynamic analysis with piezoelectric layers as fiber-reinforced composites coupled to cross-ply laminated composite [37] followed the analytical solution scheme with Navier’s solution for the simply supported case of boundary conditions. In an interesting literature [49] study on the composite laminate microplate under the thermal environment is performed. The small scale effect is mapped properly through a combination of isogeometric analysis and modified couple stress theory under the bending and buckling effect. Reducing the stress concentrations, weight and/or improving the stiffness capacity is demonstrated through structural shape optimization using combination of extended isogeometric analysis and chaotic particle swarm optimization algorithm in the study [53] of structures with cutouts.

Plate theories following the equivalent single layer approach are well established in all domains of analysis like bending, buckling and vibration respectively. Classical work [18] was first to put forth a single layer model known as classical plate theory (CPT) gives accurate results only in the case of thin plates as the theory lacks incorporation of shear deformation effect. Later, second remarkable development [26] presented FSDT with the constant variation of shear strains through the thickness of plate which requires shear correction factor to get accurate results while performing complete analysis of thick plates. Higher order simple plate theory [33] considering the separated form of bending and shear deformation functions in the model is developed which is widely used. Results obtained from this theory were in good agreement with other higher order and three-dimensional plate theories as discussed in the study. The plate analysis model [33] was transformed into simple plate theory by splitting the transverse displacement into bending and shear with two separate functions for bending, shear each respectively minimizing the total number of governing variables to four was pioneering work [41]. Many researchers applied the basic logic of changing the shear deformation function by considering various mathematical forms satisfying the zero transverse shear stress condition, same models are listed and discussed in depth in this studies [29, 38]. Polynomial based function was proposed with a cubic variation of shear deformation function along the thickness direction as seen [15, 31, 35]. Another polynomial based function was proposed [43] which gives good results to incorporate shear deformation effect in thick plates using four variable theory. Applying the capability of trigonometric sine function [20, 45, 51] considered the shear deformation effect while developing the plate theory. Following the basic Taylor’s series expansion based on plate displacement field’s third term is assumed as hyperbolic shear deformation function was developed [44]. To map properly shear deformation, work done on plate analysis [16] proposed the use of an exponential function. All these models essentially follow the same logic of transverse shear stress to be zero at the top and bottom surface of the plate. Simple plate theory coupled with numerical method of isogeometric analysis through B-spline basis function such that \(C^{1}\) continuity is satisfied [55]. Complex problem of laminated plate with cutout is handled in effective and simpler manner in the study [58] using simple FSDT along with numerical solution. New refined simple plate theory based on the kinematics of plate deformation through theory of elasticity is proposed for analysis of FGM plate for bending, buckling and vibration analysis in the study [52]. The new five variable shear deformation theory is developed in study [39] for sandwich beams and plates while examining various shape functions related to shear deformations. In this study flexural analysis is studied for simply supported FGM plate using closed-form Navier’s solution. The small scale effect is mapped by proposing a new theory with three material scale parameters in the research [48]. In this study on the mechanical behavior of laminated composite plate is performed with free vibration analysis using Reddy’s plate theory [33].

The solution of a partial differential system developed with the interaction of two directional variables (u, v along x, y axes respectively) is complex especially when an analytical approach is used. The coupling of piezo layers to the core plate further elevates the complexity because of increased variables. To convert the partial differential system into ordinary applying the Fourier’s series [28] obtained the solution for the plate with all four edges to be simply supported. To consider the more complex case of two opposite edges simply supported while remaining two to be in a combination of simple, fixed, or free support [21] devised the solution. [56] provided tables that consisted of beam functions along with roots of characteristic equations such that the solution for clamped, free and simply supported boundary conditions for uniform beams is obtained. In this study [17] an extended kantrovich method is used for simplifying the partial differential equation of the plate problem to be converted into an ordinary one. The iterative solution procedure ensures the convergence of the results and is independent of the starting solution. [12] proposed a superposition method to deal with all types of boundary conditions such that the obtained result proves the applicability of the proposed method. [6] solved the problem on natural frequencies of a rectangular plate using Rayleigh–Ritz developed an approximate analytical method with orthogonal polynomial for solving the problem under study. Hierarchical trigonometric [5] set of functions is developed considering the bending and rotation modes at both ends of beams. Using trigonometric functions as a solution to beam bending for complex boundary conditions terms considered in solution going as higher as up to 2048 was not affected due to computer round-off error while with the same problem solved by polynomial based functions failed at an order of 47.

In the present study simple analytical bending mathematical model is developed based on four variable polynomial based shear deformation plate theory for FGM plate coupled with piezoelectric layers followed by closed form solution obtained with the use of beam functions [8, 46, 56]. The second part of the study consists of the smart application of piezoelectric material to achieve the shape control of the FGM plate through a closed-loop system based on the displacement feedback algorithm [30]. Simple polynomial to be used as shear deformation function [19, 27, 33, 41] which is further compared with other mathematical models to prove its robustness, improves the approach towards simplicity of the current model. Shear deformation functions based models with mathematical form oriented from Polynomial, Trigonometric, Hyperbolic, and Exponential are presented here. The governing system is obtained with the aid of the Principle of virtual work for basic mechanical variables while Maxwell’s condition is used to incorporate the part of the electrical variable. Flexural analysis of the FGM plate is presented as part of validation for the proposed model such that change in aspect ratio, material property, and boundary conditions are included. Smart application of piezoelectric material to control the static deflection of the FGM plate following the analytical approach in the form of a closed-loop system is developed with a demonstration in the form of numerical and graphical form. The novelty of the study is highlighted from the fact that in the field of plate analysis with a vast amount of literature available though every work appears similar, still the work presented here is unique in terms of the analytical approach to tackle the problem while most similar studies conducted it with a numerical approach.

Fig. 1
figure 1

Piezoelectric coupled FGM plate model

Full size image

2 Governing formulation

2.1 The displacement field

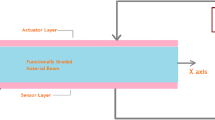
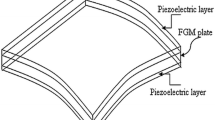
Articulating displacement field [41] such that transverse displacement is assumed to be separated in two components as bending and shear each respectively. Though four variable are present in the displacement field, present theory effectively maps the shear deformation effect in case of increase in thickness of plate when compared with CPT [18], FSDT [26]. Figure 1 shows piezoelectric coupled FGM plate with coordinate axes assumed while going through derivation of mathematical model. Core FGM layer is of thickness h, while piezo-layers are made of thickness \(h_{p}\). Size of plate is considered as \(a*b\) along x and y axes respectively.

$$\begin{aligned}&u=u-z\dfrac{\partial w_{b}}{\partial x}-(Fz)\dfrac{\partial w_{s}}{\partial x}\nonumber \\&v=v-z\dfrac{\partial w_{b}}{\partial y}-(Fz)\dfrac{\partial w_{s}}{\partial y} \nonumber \\&w=w_{b} + w_{s} \end{aligned}$$
(1)

Plate theories have evolved based on the role of shear deformation function [29, 38] in case of increase in the plate thickness. Starting from simple polynomial going upto complex combination of polynomial, trigonometric, hyperbolic and exponential functions the plate theories are now matured in all sense. Six plate theories considered in the this study are as given in Table 1 for studying performance of each mathematical form in terms of shear deformation function, leading to approval of simple plate theory based on the sixth polynomial (PolyF3) function to be used shape control study of FGM plate. To satisfy the condition of transverse shear stress to be zero at top and bottom surface of plate, \(Gz=1-\dfrac{\partial Fz}{\partial z}\) needs to be assumed.

Table 1 Plate theories based on shear deformation function in various mathematical forms
Full size table

2.2 Linear strains

Strains are given in Eq. (2) considering linear relation between strain–displacements for study of static bending and shape control of FGM plate through smart application of piezoelectric material.

$$\begin{aligned}&\mathcal E_{x}=\dfrac{\partial u}{\partial x}-z\dfrac{\partial ^{2} w_{b}}{\partial x^{2}}-(Fz)\dfrac{\partial ^{2} w_{s}}{\partial x^{2}}\nonumber \\&\mathcal E_{y}=\dfrac{\partial v}{\partial y}-z\dfrac{\partial ^{2} w_{b}}{\partial y^{2}}-(Fz)\dfrac{\partial ^{2} w_{s}}{\partial y^{2}} \nonumber \\&\gamma _{xz}= (G_{z}) \dfrac{\partial w_{s}}{\partial x} \nonumber \\&\gamma _{yz}= (G_{z}) \dfrac{\partial w_{s}}{\partial y} \nonumber \\&\gamma _{xy}=\dfrac{\partial u}{\partial y}+\dfrac{\partial v}{\partial x}-2z\dfrac{\partial ^{2} w_{b}}{\partial x \partial y} -2z\dfrac{\partial ^{2} w_{s}}{\partial x \partial y} \end{aligned}$$
(2)

2.3 Complementary stresses

The complementary stress–strain relations [50] for piezoelectric layers coupled to FGM plate are as given in Eq. (3).

$$\begin{aligned}&\sigma _{x}=\bar{Q}_{11} \mathcal E_{x}+\bar{Q}_{12} \mathcal E_{y}-e_{31} E_{z} \nonumber \\&\sigma _{y}=\bar{Q}_{21} \mathcal E_{x}+\bar{Q}_{22} \mathcal E_{y}-e_{32} E_{z} \nonumber \\&\sigma _{xz}=\bar{Q}_{44} \gamma _{xz}-e_{15} E_{x} \nonumber \\&\sigma _{yz}=\bar{Q}_{55} \gamma _{yz}-e_{24} E_{y} \nonumber \\&\sigma _{xy}=\bar{Q}_{66} \gamma _{xy} \end{aligned}$$
(3)

In above relations, \(\bar{Q}=Q\) is the constant assumed for FGM core plate while \(\bar{Q}=C\) for material of piezoelectric layers. The material property variation is mapped by power law [14, 34] through the thickness direction of the FGM plate. \(e_{15}, e_{24}, e_{31}, e_{32}\), \(e_{33}\) are piezoelectric constants and electric field intensity is given by \(E_{x}, E_{y}\) and \(E_{z}\) respectively. The material property elastic constants are given below along with the power law for through thickness material variation of FGM plate, assuming behavior of an isotropic material.

$$\begin{aligned}&\bar{Q}_{11}=\bar{Q}_{22}=\dfrac{E(z)}{(1-\mu _{z}^{2})},\\&\bar{Q}_{12}=\bar{Q}_{21}=\dfrac{\mu _{z}\,E(z)}{(1-\mu _{z}^{2})},\\&\bar{Q}_{44}=\bar{Q}_{55}=\bar{Q}_{66}=\dfrac{E(z)}{2\,[1+\mu _{z}]} \\&E(z)=E(m)+\Big [E(c)-E(m)\Big ]\Bigg (\dfrac{1}{2}+\dfrac{z}{h}\Bigg )^N\\ \end{aligned}$$

2.4 Principle of virtual work

To obtain the governing equations for piezoelectric coupled FGM plate principle of virtual work is used. Work done by transverse load q distributed over the surface of plate results in change of stress-strain over the volume domain of plate is considered [Eq. (4)].

$$\begin{aligned}&\int _{V} [\sigma _{x} \delta \mathcal E_{x} + \sigma _{y} \delta \mathcal E_{y} + \sigma _{xy} \delta \gamma _{xy}+ \sigma _{xz} \delta \gamma _{xz}+ \sigma _{yz} \delta \gamma _{yz} ]dV \nonumber \\&\qquad -\int _{0}^{a}\int _{o}^{b}q\,\delta (w_{b}+w_{s})dA=0 \end{aligned}$$
(4)

Simplifying Eq. (4) by taking out the thickness integrals of stress resultants given in Eq. (6) each with \(h_{T}=(h/2)+h_{p}\) and \(h_{B}=-(h/2)-h_{p}\) taken as the limits.

$$\begin{aligned}&\int _{0}^{a} \int _{0}^{b} \Bigg \lbrace N_{x} \dfrac{\partial \delta u}{\partial x}+N_{y} \dfrac{\partial \delta v}{\partial y} +N_{xy} \Bigg [\dfrac{\partial \delta u}{\partial y} + \dfrac{\partial \delta v}{\partial x} \Bigg ]\nonumber \\&\qquad - M^{b}_{x} \dfrac{\partial ^{2} \delta w_{b}}{\partial x^{2}} - M^{b}_{y} \dfrac{\partial ^{2} \delta w_{b}}{\partial y^{2}}- 2 M^{b}_{xy} \dfrac{\partial ^{2} \delta w_{b}}{\partial x \partial y} \nonumber \\&\qquad - M^{s}_{x} \dfrac{\partial ^{2} \delta w_{s}}{\partial x^{2}} - M^{s}_{y} \dfrac{\partial ^{2} \delta w_{s}}{\partial y^{2}}- 2 M^{s}_{xy} \dfrac{\partial ^{2} \delta w_{s}}{\partial x \partial y} \nonumber \\&\qquad + Q_{xz} \dfrac{\partial \delta w_{s}}{\partial x} + Q_{yz} \dfrac{\partial \delta w_{s}}{\partial y} \Bigg \rbrace dx dy \nonumber \\&\qquad -\int _{0}^{a}\int _{0}^{b}q\, \delta (w_{b}+w_{s})\,dx\,dy=0 \end{aligned}$$
(5)
$$\begin{aligned}&(N_{x}, N_{y}, N_{xy})=\int _{h_{B}}^{h_{T}} (\sigma _{x}, \sigma _{y}, \sigma _{xy})dz \nonumber \\&(M^{b}_{x}, M^{b}_{y}, M^{b}_{xy})=\int _{h_{B}}^{h_{T}} (\sigma _{x},\sigma _{y},\sigma _{xy})z dz \nonumber \\&(M^{s}_{x}, M^{s}_{y}, M^{s}_{xy})=\int _{h_{B}}^{h_{T}} (\sigma _{x},\sigma _{y},\sigma _{xy})(Fz)dz \nonumber \\&(Q_{xz}, Q_{yz})=\int _{h_{B}}^{h_{T}}(\sigma _{xz}, \sigma _{yz})(Gz)dz \end{aligned}$$
(6)

3 Governing equations

Collecting the coefficients of four virtual displacements (\(\delta u, \delta v, \delta w_{b}\) and \(\delta w_{s}\)) together as demonstrated in Eq. (7), is obtained by performing integration by parts for Eq. (5). The associated boundary conditions are presented in Table 2 valid along the plate edges coming out along with the governing equation.

$$\begin{aligned} \delta u \,:\,&\dfrac{\partial N_{x}}{\partial x}+ \dfrac{\partial N_{xy}}{\partial y} =0 \nonumber \\ \delta v \,:\,&\dfrac{\partial N_{y}}{\partial y}+ \dfrac{\partial N_{xy}}{\partial x} =0 \nonumber \\ \delta w_{b} \,:\,&\dfrac{\partial ^{2} M^{b}_{x}}{\partial x^{2}}+2\dfrac{\partial ^{2} M^{b}_{xy}}{\partial x\partial y}+\dfrac{\partial ^{2} M^{b}_{y}}{\partial y^{2}}+q_{w} =0 \nonumber \\ \delta w_{s} \,:\,&\dfrac{\partial ^{2} M^{s}_{x}}{\partial x^{2}}+2\dfrac{\partial ^{2} M^{s}_{xy}}{\partial x\partial y}+\dfrac{\partial ^{2} M^{s}_{y}}{\partial y^{2}} \nonumber \\&+\dfrac{\partial Q_{xz}}{\partial x}+\dfrac{\partial Q_{yz}}{\partial y}+q_{w} =0 \end{aligned}$$
(7)

In above equation term \(q_{w}\) is the simplified form of work done by transverse loading q, \(\bigg ( -\int _{0}^{a}\int _{o}^{b}q\,( \delta w_{b}+ \delta w_{s}) dx dy\bigg )\)

Table 2 Associated boundary conditions
Full size table

Final form of governing Eq. (8) is obtained by substituting for stresses in terms of strains in Eq. (6) for stress resultants. Later these expanded stress resultants are substituted in Eq. (7).

$$\begin{aligned}&A_{11} \dfrac{\partial ^{2} u}{\partial x^{2}}+A_{66} \dfrac{\partial ^{2} u}{\partial y^{2}}+(A_{12}+A_{66})\dfrac{\partial ^{2} v}{\partial x \partial y}-B_{11} \dfrac{\partial ^{3} w_{b}}{\partial x^{3}} \nonumber \\&\quad -(B_{12}+2B_{66})\dfrac{\partial ^{3} w_{b}}{\partial x \partial y^{2}}-B^{s}_{11} \dfrac{\partial ^{3} w_{s}}{\partial x^{3}}-(B^{s}_{12}+2B^{s}_{66}) \nonumber \\&\dfrac{\partial ^{3} w_{s}}{\partial x \partial y^{2}}+\mu _{1} \dfrac{\partial \varPi _{T}}{\partial x}+\mu _{2} \dfrac{\partial \varPi _{B}}{\partial x}=0 \end{aligned}$$
(8a)
$$\begin{aligned}&(A_{12}+A_{66})\dfrac{\partial ^{2} u}{\partial x \partial y}+A_{66} \dfrac{\partial ^{2} v}{\partial x^{2}}+A_{22} \dfrac{\partial ^{2} v}{\partial y^{2}}-(B_{12}+2B_{66})\nonumber \\&\dfrac{\partial ^{3} w_{b}}{\partial x^{2} \partial y}-B_{22} \dfrac{\partial ^{3} w_{b}}{\partial y^{3}}-(B^{s}_{12}+2B^{s}_{66})\dfrac{\partial ^{3} w_{s}}{\partial x^{2} \partial y}-B^{s}_{22} \dfrac{\partial ^{3} w_{s}}{\partial y^{3}}\nonumber \\&\quad +\mu _{3} \dfrac{\partial \varPi _{T}}{\partial y}+\mu _{4} \dfrac{\partial \varPi _{B}}{\partial y}=0\end{aligned}$$
(8b)
$$\begin{aligned}&B_{11} \dfrac{\partial ^{3} u}{\partial x^{3}}+(B_{12}+2B_{66})\dfrac{\partial ^{3} u}{\partial x \partial y^{2}}+(B_{12}+2B_{66})\dfrac{\partial ^{3} v}{\partial x^{2} \partial y}\nonumber \\&\quad +B_{22} \dfrac{\partial ^{3} v}{\partial y^{3}}-D_{11} \dfrac{\partial ^{4} w_{b}}{\partial x^{4}} -2(D_{12}+2D_{66}) \dfrac{\partial ^{4} w_{b}}{\partial x^{2} \partial y^{2}}\nonumber \\&\quad -D_{22}\dfrac{\partial ^{4} w_{b}}{\partial y^{4}}-D^{s}_{11} \dfrac{\partial ^{4} w_{s}}{\partial x^{4}}-2(D^{s}_{12}+2D^{s}_{66}) \dfrac{\partial ^{4} w_{s}}{\partial x^{2} \partial y^{2}} \nonumber \\&\quad -D^{s}_{22}\dfrac{\partial ^{4} w_{s}}{\partial y^{4}}+\mu _{5} \dfrac{\partial ^{2} \varPi _{T}}{\partial x^{2}}+\mu _{7} \dfrac{\partial ^{2} \varPi _{T}}{\partial y^{2}}+\mu _{6} \dfrac{\partial ^{2} \varPi _{B}}{\partial x^{2}}\nonumber \\&\quad +\mu _{8} \dfrac{\partial ^{2} \varPi _{B}}{\partial y^{2}}+q_{w}=0\end{aligned}$$
(8c)
$$\begin{aligned}&B^{s}_{11} \dfrac{\partial ^{3} u}{\partial x^{3}}+(B^{s}_{12}+2B^{s}_{66})\dfrac{\partial ^{3} u}{\partial x \partial y^{2}}+(B^{s}_{12}+2B^{s}_{66})\dfrac{\partial ^{3} v}{\partial x^{2} \partial y}\nonumber \\&\quad +B^{s}_{22} \dfrac{\partial ^{3} v}{\partial y^{3}} -D^{s}_{11} \dfrac{\partial ^{4} w_{b}}{\partial x^{4}}-2(D^{s}_{12}+2D^{s}_{66}) \dfrac{\partial ^{4} w_{b}}{\partial x^{2} \partial y^{2}}\nonumber \\&\quad -D^{s}_{22}\dfrac{\partial ^{4} w_{b}}{\partial y^{4}}-H^{s}_{11} \dfrac{\partial ^{4} w_{s}}{\partial x^{4}}-2(H^{s}_{12}+2H^{s}_{66}) \dfrac{\partial ^{4} w_{s}}{\partial x^{2} \partial y^{2}}\nonumber \\&\quad -H^{s}_{22}\dfrac{\partial ^{4} w_{s}}{\partial y^{4}}+A_{44}\dfrac{\partial ^{2} w_{s}}{\partial x^{2}}+A_{55}\dfrac{\partial ^{2} w_{s}}{\partial y^{2}}\end{aligned}$$
(8d)
$$\begin{aligned}&\quad +(\mu _{9}+\mu _{15}) \dfrac{\partial ^{2} \varPi _{T}}{\partial x^{2}}+(\mu _{11}+\mu _{17}) \dfrac{\partial ^{2} \varPi _{T}}{\partial y^{2}}\nonumber \\&\quad +(\mu _{10}+\mu _{16}) \dfrac{\partial ^{2} \varPi _{B}}{\partial x^{2}}+(\mu _{12}+\mu _{18}) \dfrac{\partial ^{2} \varPi _{B}}{\partial y^{2}}+q_{w}=0 \end{aligned}$$
(8e)

Elastic material property in the form of thickness integral are taken as;

$$\begin{aligned} (A_{11},&A_{12},A_{22},A_{66}) \nonumber \\&=\int _{-h/2}^{h/2} (Q_{11},Q_{12},Q_{22},Q_{66})dz\nonumber \\&\quad +2\int _{h/2}^{h_{T}} (C_{11},C_{12},C_{22},C_{66})dz \nonumber \\[3pt] (B_{11},&B_{12},B_{22},B_{66})\nonumber \\&=\int _{-h/2}^{h/2} (Q_{11},Q_{12},Q_{22},Q_{66} )\,z\,dz \nonumber \\&\quad +2\int _{h/2}^{h_{T}} (C_{11},C_{12},C_{22},C_{66})\,z \,dz \nonumber \\[3pt] (B^{s}_{11},&B^{s}_{12},B^{s}_{22},B^{s}_{66})\nonumber \\&=\int _{-h/2}^{h/2} (Q_{11},Q_{12},Q_{22},Q_{66} )\,(Fz)\,dz \nonumber \\&\quad +2\int _{h/2}^{h_{T}} (C_{11},C_{12},C_{22},C_{66})\,(Fz)\,dz \nonumber \\[3pt] (D_{11},&D_{12},D_{22},D_{66})\nonumber \\&=\int _{-h/2}^{h/2} (Q_{11},Q_{12},Q_{22},Q_{66})\,z^{2} \,dz \nonumber \\&\quad +2\int _{h/2}^{h_{T}} (C_{11},C_{12},C_{22},C_{66})\,z^{2}\,dz \nonumber \\[3pt] (D^{s}_{11},&D^{s}_{12},D^{s}_{22},D^{s}_{66})\nonumber \\&=\int _{-h/2}^{h/2} (Q_{11},Q_{12},Q_{22},Q_{66})\,z\, (Fz)\,dz \nonumber \\&\quad +2\int _{h/2}^{h_{T}} (C_{11},C_{12},C_{22},C_{66})\,z\,(Fz) dz \nonumber \\[3pt] (H^{s}_{11},&H^{s}_{12},H^{s}_{22},H^{s}_{66})\nonumber \\&=\int _{-h/2}^{h/2} (Q_{11},Q_{12},Q_{22},Q_{66})\, (Fz)^{2}\,dz\nonumber \\&\quad +2\int _{h/2}^{h_{T}} (C_{11},C_{12},C_{22},C_{66})\,(Fz)^{2}\,dz \nonumber \\[3pt] (A_{44}, A_{55})&=\int _{-h/2}^{h/2} (Q_{44},Q_{55})(Gz)^{2} dz\nonumber \\&\quad +2\int _{h/2}^{h_{T}} (C_{44},C_{55})(Gz)^{2} dz \end{aligned}$$
(9)

Electric properties along the thickness direction taken out as integrals to simply the formulation are given as below;

$$\begin{aligned} (\mu _{1},\mu _{3})&=\int _{h/2}^{h_{T}}(e_{31}, e_{32})\, \dfrac{\partial \varPhi _{T}}{\partial z} \,dz,\nonumber \\ (\mu _{2},\mu _{4})&=\int _{h_{B}}^{-h/2}(e_{31}, e_{32})\, \dfrac{\partial \varPhi _{B}}{\partial z} \,dz \nonumber \\ (\mu _{5},\mu _{7})&=\int _{h/2}^{h_{T}}(e_{31}, e_{32}) \,\dfrac{\partial \varPhi _{T}}{\partial z}z \,dz,\nonumber \\ (\mu _{6},\mu _{8})&=\int _{h_{B}}^{-h/2}(e_{31}, e_{32})\, \dfrac{\partial \varPhi _{B}}{\partial z}\,z\, dz \nonumber \\ (\mu _{9},\mu _{11})&=\int _{h/2}^{h_{T}}(e_{31}, e_{32}) \,\dfrac{\partial \varPhi _{T}}{\partial z}\,(Fz) \,dz, \nonumber \\ (\mu _{10},\mu _{12})&=\int _{h_{B}}^{-h/2}(e_{31}, e_{32})\, \dfrac{\partial \varPhi _{B}}{\partial z}\,(Fz) \,dz \nonumber \\ (\mu _{15},\mu _{17})&=\int _{h/2}^{h_{T}}(e_{15}, e_{24}) \,(Gz) \,\varPhi _{T} \,dz, \nonumber \\ (\mu _{16},\mu _{18})&=\int _{h_{B}}^{-h/2}(e_{15}, e_{24})\, (Gz)\,\varPhi _{B}\, dz \end{aligned}$$
(10)

4 Piezoelectric coupling

4.1 Electric potential function

Electrical potential function varying along the thickness of piezoelectric layers is second order polynomial verified in the study [54] with finite element which is used in present study. Same function was also used for free vibration analysis by [10] with FSDT and [36] with four variable refined plate theory to study free vibration analysis for FGM plate.

$$\begin{aligned} \varPhi _{T}= \varPi _{T} \Bigg [1-&\Bigg (\dfrac{z-h-h_{p}/2}{h_{p}/2}\Bigg )^{2} \Bigg ]\nonumber \\&\bigg \langle h/2 \le z \le (h/2)+h_{p} \bigg \rangle \end{aligned}$$
(11)
$$\begin{aligned} \varPhi _{B}= \varPi _{B} \Bigg [1-&\Bigg (\dfrac{-z-h-h_{p}/2}{h_{p}/2}\Bigg )^{2} \Bigg ]\nonumber \\&\bigg \langle -(h/2)-h_{p} \le z \le -h/2\bigg \rangle \end{aligned}$$
(12)

4.2 Electric displacement

Mechanical equilibrium is satisfied as per the detailed formulation given in section (3) with the four governing equations [Eq. (7)], similarly Maxwell’s electrical condition needs to be satisfied given in Eq. (14). The electric displacement is as detailed in Eq. (13) in terms of strain and electric field intensities.

$$\begin{aligned}&D_{x}=e_{15} \gamma _{xz}+\varOmega _{11} E_{x} \nonumber \\&D_{y}=e_{24} \gamma _{yz}+\varOmega _{22} E_{y} \nonumber \\&D_{z}=e_{31} \mathcal E_{x}+e_{32} \mathcal E_{y}+\varOmega _{33} E_{z} \end{aligned}$$
(13)

4.3 Fifth governing equation

Piezoelectric coupling increases number of variables to five hence additional equation is obtained by satisfying Maxwell’s electrical condition. Simplified form of this equation is given in Eq. (15), after substituting for electric displacement in Eq. (14).

$$\begin{aligned}&\int _{h/2}^{h_{T}} \Bigg (\dfrac{\partial D_{x}}{\partial x}+\dfrac{\partial D_{y}}{\partial y}+\dfrac{\partial D_{z}}{\partial z} \Bigg )dz \nonumber \\&\qquad + \int _{h_{B}}^{-h/2} \Bigg (\dfrac{\partial D_{x}}{\partial x}+\dfrac{\partial D_{y}}{\partial y}+\dfrac{\partial D_{z}}{\partial z} \Bigg )dz=0 \end{aligned}$$
(14)
$$\begin{aligned}&\qquad -\lambda _{5} \dfrac{\partial ^{2} w_{b}}{\partial x^{2}} -\lambda _{6} \dfrac{\partial ^{2} w_{b}}{\partial y^{2}}+\lambda _{1} \dfrac{\partial ^{2} w_{s}}{\partial x^{2}} +\lambda _{2} \dfrac{\partial ^{2} w_{s}}{\partial y^{2}}-\lambda _{7} \dfrac{\partial ^{2} \varPi _{T}}{\partial x^{2}}\nonumber \\&\qquad -\lambda _{9} \dfrac{\partial ^{2} \varPi _{T}}{\partial y^{2}}-\lambda _{8} \dfrac{\partial ^{2} \varPi _{B}}{\partial x^{2}} -\lambda _{10} \dfrac{\partial ^{2} \varPi _{B}}{\partial y^{2}}\nonumber \\&\qquad -\lambda _{12}\varPi _{T}-\lambda _{13}\varPi _{B}=0 \end{aligned}$$
(15)

The constants for thickness integrals based on the properties of piezoelectric layers are given below;

$$\begin{aligned} \lambda _{1}&=\int _{h/2}^{h_{T}}\Bigg (e_{15}(Gz)-e_{31}\dfrac{\partial Fz}{\partial z}\Bigg )\,dz\nonumber \\&\quad +\int _{h_{B}}^{-h/2}\Bigg (e_{15}(Gz)-e_{31}\dfrac{\partial Fz}{\partial z}\Bigg )\,dz\nonumber \\ \lambda _{2}&=\int _{h/2}^{h_{T}}\Bigg (e_{24}(Gz)-e_{32}\dfrac{\partial Fz}{\partial z}\Bigg )\,dz\nonumber \\&\quad +\int _{h_{B}}^{-h/2}\Bigg (e_{24}(Gz)-e_{32}\dfrac{\partial Fz}{\partial z}\Bigg )\,dz\nonumber \\ \lambda _{5}&=\int _{h/2}^{h_{T}}\,e_{31}\,dz+\int _{h_{B}}^{-h/2}\,e_{31}\,dz\nonumber \\ \lambda _{6}&=\int _{h/2}^{h_{T}}e_{32}\,dz+\int _{h_{B}}^{-h/2}e_{32}\,dz\nonumber \\ \lambda _{7}&=\int _{h/2}^{h_{T}}(\varOmega _{11}\varPhi _{T})\,dz,\lambda _{8}=\int _{h_{B}}^{-h/2}(\varOmega _{11}\varPhi _{B})\,dz\nonumber \\ \lambda _{9}&=\int _{h/2}^{h_{T}}(\varOmega _{22}\varPhi _{T})\,dz,\lambda _{10}=\int _{h_{B}}^{-h/2}(\varOmega _{22}\varPhi _{B})dz\nonumber \\ \lambda _{12}&=\int _{h/2}^{h_{T}} \varOmega _{33} \dfrac{\partial ^{2} \varPhi _{T}}{\partial z^{2}}\,dz\nonumber \\ \lambda _{13}&=\int _{h_{B}}^{-h/2} \varOmega _{33} \dfrac{\partial ^{2} \varPhi _{B}}{\partial z^{2}}\,dz \end{aligned}$$
(16)

4.4 Active feedback system

The constant displacement feedback control algorithm [30] is used for shape control of FGM plate assuming bottom piezoelectric layer acting as sensor while top acting as actuator given as \(\varPi _{T}= G_{d}*\varPi _{B}\). To convert the system in single input single output, the electric variable in bottom layer is assumed as \(\varPi _{B}=\varPi\).

5 Analytical solution

Five coupled equation forms complex system for bending analysis of FGM plate due to piezoelectric layers. Solution to be assumed for this highly coupled partial differential governing system is obtained for five basic variables based on the beam functions [8, 46, 56] considering the combination of simply supported and clamped boundary conditions. The expansion for variables is given in Eq. (17) based on satisfaction of geometric boundary conditions.

$$\begin{aligned}&u=\sum _{m=1}^{\infty } \sum _{n=1}^{\infty } U_{mn} \dfrac{\partial X_{m}}{\partial x} Y_{n}, \nonumber \\&v=\sum _{m=1}^{\infty } \sum _{n=1}^{\infty } V_{mn} X_{m} \dfrac{\partial Y_{n}}{\partial y}, \nonumber \\&w_{b}=\sum _{m=1}^{\infty } \sum _{n=1}^{\infty } W^{b}_{mn} X_{m} Y_{n}, \nonumber \\&w_{s}=\sum _{m=1}^{\infty } \sum _{n=1}^{\infty } W^{s}_{mn} X_{m} Y_{n}, \nonumber \\&\varPi =\sum _{m=1}^{\infty } \sum _{n=1}^{\infty } \varPi _{mn} X_{m} Y_{n} \end{aligned}$$
(17)

Simply-supported (SS):

$$\begin{aligned} \begin{aligned}&v=w_{b}=w_{s}=N_{x}=M^{b}_{x}=M^{s}_{x}=0\,at\,x=0, a\\[3pt]&u=w_{b}=w_{s}=N_{y}=M^{b}_{y}=M^{s}_{y}=0\,at\,y=0, b\\ \end{aligned} \end{aligned}$$

Clamped (CC):

$$\begin{aligned} \begin{aligned} u=v=w_{b}=\dfrac{\partial w_{b}}{\partial x}=\dfrac{\partial w_{b}}{\partial y}=w_{s}=\dfrac{\partial w_{s}}{\partial x}=\dfrac{\partial w_{s}}{\partial y}=0\\ at\,x=0,\,a \,and \,at\,y=0,\,b\\ \end{aligned} \end{aligned}$$

Table 3 consists beam shape functions which are obtained as a solution to frequency equation corresponding to beams with respective boundaries. The symbols used in Table 3 are interpreted as CC is clamped-clamped opposite edges, CS is clamped-simply supported while SS is for both opposite edges simply supported. To simplify the lengthy mathematical equations following coding is used such that \(\lambda _{m},\, \lambda _{n}\) are the roots of frequency equation.

$$\begin{aligned}&H\Big (\dfrac{\lambda _{m} x}{a}\Big )=sinh\Big (\dfrac{\lambda _{m} x}{a}\Big )-sin\Big (\dfrac{\lambda _{m} x}{a}\Big ), \\&H\Big (\dfrac{\lambda _{n} y}{b}\Big )=sinh\Big (\dfrac{\lambda _{n} y}{b}\Big )-sin\Big (\dfrac{\lambda _{n} y}{b}\Big ), \\&J\Big (\dfrac{\lambda _{m} x}{a}\Big )=cosh\Big (\dfrac{\lambda _{m} x}{a}\Big )-cos\Big (\dfrac{\lambda _{m} x}{a}\Big ), \\&J\Big (\dfrac{\lambda _{n} y}{b}\Big )=cosh\Big (\dfrac{\lambda _{n} y}{b}\Big )-cos\Big (\dfrac{\lambda _{n} y}{b}\Big ) \end{aligned}$$

The computer code adoptable stiffness matrix terms which can be used in any suitable programming tool obtained from the \(5*5\) order piezoelectric coupled FGM plate governing system when solution from Eq. (17) is substituted in Eqs. (8 and 15).

$$\begin{aligned} K_{11}&=A_{11}\,\varUpsilon _{12}+A_{66}\,\varUpsilon _{8},\\ K_{12}&=(A_{12}+A_{66})\,\varUpsilon _{8},\\ K_{13}&=-B_{11}\,\varUpsilon _{12}-(B_{12}+2\,B_{66})\,\varUpsilon _{8}, \\ K_{14}&=-B^{s}_{11}\,\varUpsilon _{12}-(B^{s}_{12}+2\,B^{s}_{66})\,\varUpsilon _{8},\\ K_{15}&=(\mu _{1}+\mu _{2})\,\varUpsilon _{6};\\[6pt] K_{21}&=(A_{12}+A_{66})\,\varUpsilon _{10}, \\ K_{22}&=A_{22}\,\varUpsilon _{4}+A_{66}\,\varUpsilon _{10},\\ K_{23}&=-B_{22}\,\varUpsilon _{4}-(B_{12}+2\,B_{66})\,\varUpsilon _{10},\\ K_{24}&=-B^{s}_{22}\,\varUpsilon _{4}-(B^{s}_{12}+2\,B^{s}_{66})\,\varUpsilon _{10},\\ K_{25}&=(\mu _{3}+\mu _{4})\,\varUpsilon _{2};\\[6pt] K_{31}&=B_{11}\,\varUpsilon _{13}+(B_{12}+2\,B_{66})\,\varUpsilon _{11}, \\ K_{32}&=(B_{12}+2\,B_{66})\,\varUpsilon _{11}+B_{22}\,\varUpsilon _{5},\\ K_{33}&=-D_{11}\,\varUpsilon _{13}-2\,(D_{12}+2\,D_{66})\,\varUpsilon _{11}\\&\quad -D_{22}\,\varUpsilon _{5},\\ K_{34}&=-D^{s}_{11}\,\varUpsilon _{13}-2\,(D^{s}_{12}+2\,D^{s}_{66})\,\varUpsilon _{11}\\&\quad -D^{s}_{22}\,\varUpsilon _{5},\\ K_{35}&=(\mu _{5}+\mu _{6})\,\varUpsilon _{9}+(\mu _{7}+\mu _{8})\,\varUpsilon _{3};\\[6pt] K_{41}&=B^{s}_{11}\,\varUpsilon _{13}+(B^{s}_{12}+2\,B^{s}_{66})\,\varUpsilon _{11}, \\ K_{42}&=(B^{s}_{12}+2\,B^{s}_{66})\,\varUpsilon _{11}+B^{s}_{22}\,\varUpsilon _{5},\\ K_{43}&=-D^{s}_{11}\,\varUpsilon _{13}-2\,(D^{s}_{12}+2\,D^{s}_{66})\,\varUpsilon _{11}\\&\quad -D^{s}_{22}\,\varUpsilon _{5},\\ K_{44}&=-H^{s}_{11}\,\varUpsilon _{13}-2\,(H^{s}_{12}+2\,H^{s}_{66})\,\varUpsilon _{11}\\&\quad -H^{s}_{22}\,\varUpsilon _{5}-A^{s}_{44}\,\varUpsilon _{9}-A^{s}_{55}\,\varUpsilon _{3},\\ K_{45}&=(\mu _{9}+\mu _{15}+\mu _{10}+\mu _{16})\,\varUpsilon _{9}\\&\quad +(\mu _{11}+\mu _{17}+\mu _{12}+\mu _{18})\,\varUpsilon _{3};\\[6pt] K_{51}&=0,\\ K_{52}&=0,\\ K_{53}&=-\lambda _{5}\,\varUpsilon _{9}-\lambda _{6}\,\varUpsilon _{3},\\ K_{54}&=\lambda _{1}\,\varUpsilon _{9}+\lambda _{2}\,\varUpsilon _{3},\\ K_{55}&=-((\lambda _{7}+\lambda _{8})\,\varUpsilon _{9}+(\lambda _{9}+\lambda _{10})\,\varUpsilon _{3}\\&\quad +(\lambda _{12}+\lambda _{13})\,\varUpsilon _{1}) \end{aligned}$$

Further simplified form of integrals used in stiffness terms valid over the area domain of plate are considered separately as given below to make formulation simple;

$$\begin{aligned} (\varUpsilon _{6},\,\varUpsilon _{8},\,\varUpsilon _{12})&=\int _{0}^{a}\int _{0}^{b}\Big (X^{'}_{m}\,Y_{n},\,X^{'}_{m}\,Y^{''}_{n},\\&\quad X^{'''}_{m}\,Y_{n}\Big )\,X^{'}_{m}\,Y_{n}\,dx\,dy,\\ (\varUpsilon _{2},\,\varUpsilon _{4},\,\varUpsilon _{10})&=\int _{0}^{a}\int _{0}^{b}\Big (X_{m}\,Y^{'}_{n},\,X_{m}\,Y^{'''}_{n},\\&\quad X^{''}_{m}\,Y^{'}_{n}\Big )\,X_{m}\,Y^{'}_{n}\,dx\,dy,\\ (\varUpsilon _{1},\,\varUpsilon _{3},\,\varUpsilon _{5})&=\int _{0}^{a}\int _{0}^{b}\Big (X_{m}\,Y_{n},\,X_{m}\,Y^{''}_{n},\\&\quad X_{m}\,Y^{''''}_{n}\Big )\,X_{m}\,Y_{n}\,dx\,dy,\\ (\varUpsilon _{7},\,\varUpsilon _{9},\,\varUpsilon _{11},\,\varUpsilon _{13})&=\int _{0}^{a}\int _{0}^{b}\Big (X^{'}_{m}\,Y^{'}_{n},\,X^{''}_{m}\,Y_{n},\\&\quad X^{''}_{m}\,Y^{''}_{n},\,X^{''''}_{m}\,Y_{n}\Big )\,X_{m}\,Y_{n}\,dx\,dy \end{aligned}$$

6 Numerical Validation

6.1 Comparative study

Numerical study begins with the validation and appreciation of simple polynomial based plate theory (PolyF3) through flexural analysis along with other plate theories listed in Table 1. The second part of the study showcases smart application of piezoelectric material for shape control of FGM plate in which the simple polynomial \(\Bigg (Fz=\dfrac{4 Z^{3}}{3 h_{t}^{2}}\Bigg )\) based plate theory (PolyF3) is used.

Table 3 Beam shape functions.
Full size table

In first part an FGM plate without considering piezoelectric layers made of metal (\(E_{m}=70\) GPa) on one side and ceramic (\(E_{c}=380\) GPa) on other side is examined. The value of Poisson’s ratio is considered to be constant \(\mu _{z}=0.3\). The load applied is sinusoidal with maximum ordinate \(q_{o}\) at the center. The values of non-dimensional [59] transverse deflection, stresses used are as given in Table 4. Table 5 gives the results for transverse deflection of simply supported plate for change in power law and length to thickness aspect ratio. In second example complete stress profile for FGM plate simply supported on all edges with \(a/h=10\) and variation in power law is analyzed whose results are given in Table 6. The combination of simply supported and clamped edges through analytical solution based on beam functions is validated in third example for FGM plate with change in power law as well as thickness ratio as given in Tables 7, 8 and 9, also the results are compared with numerical FEM solution based on four variable shear deformation theory.

Table 4 Non-dimensional deflection and stresses used in the study.
Full size table
Table 5 Non-dimensional deflection \(\bar{w}\) of SSSS plate under sinusoidal loading.
Full size table
Table 6 Dimensionless stress and deflections with change in power law \(\dfrac{a}{h}=10\)
Full size table
Table 7 Non-dimensional value of deflection \(\bar{w}\) for \(\dfrac{a}{h}=5\)
Full size table
Table 8 Non-dimensional value of deflection \(\bar{w}\) for \(\dfrac{a}{h}=10\)
Full size table
Table 9 Non-dimensional value of deflection \(\bar{w}\) for \(\dfrac{a}{h}=100\)
Full size table

6.2 Shape control

The main part of the study is to demonstrate smart application of piezoelectric material members for shape control of FGM plate. Consider the square FGM plate coupled with piezoelectric layers of sides 200 mm with core of thickness 5 mm while piezoelectric layers of 0.1 mm. The plate is subjected to uniform load of 100 \(N/m^{2}\). The FGM core is made of Ti–6Al–4V (Titanium-alloy) and Aluminum oxide with piezoelectric layers of PZT-G1195N. The material properties for same can be found in [30]. The parametric study for variation in constant displacement gain feedback \(G_{d}\) along with change in power law is performed whose results are given in Tables 10, 11, 12 and 13. Figures 2, 3, 4 and 5 shows the smart application of piezoelectric material for shape control through closed loop feedback control law based on displacement along with possible combination of boundary conditions. All the results in this part are obtained with simple plate theory (PolyF3).

Table 10 Deflection (m) of square SSSS FGM plate
Full size table
Table 11 Deflection (m) of square CCCC FGM plate.
Full size table
Table 12 Deflection (m) of square SCSC FGM plate.
Full size table
Table 13 Deflection (m) of square SSSC FGM plate.
Full size table
Fig. 2
figure 2

Shape control of square SSSS FGM plate

Full size image
Fig. 3
figure 3

Shape control of square CCCC FGM plate

Full size image
Fig. 4
figure 4

Shape control of square SCSC FGM plate

Full size image
Fig. 5
figure 5

shape control of square SSSC FGM plate

Full size image

7 Conclusion

The principle objective of developing a simple mathematical model for bending (flexural) analysis and shape control of the FGM plate is revealed through the detailed procedure along with numerical study presented here. The simple plate model helps in the analysis of plate structures encompassing deflection checks, shape control as an application towards the structural health monitoring. The simple polynomial based plate theory (PolyF3) greatly breaks it down in terms of computation process and time required for analysis of the plate with ensured accuracy. Complete flexural analysis effectively maps the robustness and applicability of presented mathematical model. To handle the complex boundary conditions with a view to extend the approach current model, beam function comes to great aid as part of approximate solution. After performing the in depth analysis and achieving shape control of FGM plate with help of piezoelectric material following inferences are drawn working on the path of objectives initially defined;

  • A mathematical model is presented with detailed formulation starting from the displacement field going up to governing equations with approximate analytical solution using beam functions satisfying the objective of study to develop simple mathematical model.

  • Polynomial based shear deformation function (PolyF3) gives accurate results when compared with trigonometric, hyperbolic, exponential functions as demonstrated in Tables 5, 6, 7, 8 and 9. Bending study along with complete flexural analysis of FGM plate using simple mathematical model performed in first part of study explores its capability.

  • The second important objective devised initially is to perform shape control of the FGM plate through smart application of piezoelectric material. In a closed loop system it is seen that increase in constant displacement feedback gain \(G_{d}\) in case of Ti–6Al–4V and Al\(_{2}\)O\(_{3}\) FGM plate decreases the transverse displacement as shown in Figs. 2, 3, 4 and 5 for a combination of clamped and simply supported boundary conditions.

  • Tabulated numerical results for control of deflection with change in \(G_{d}\), boundary conditions and power law are given in Tables 10, 11, 12 and 13 for the Ti–6Al–4V and Al\(_{2}\)O\(_{3}\) FGM plate, with a view to reinforce the strength of plate model in case of variation in input properties.

  • The present model successfully demonstrates its robustness in bending analysis along with the smart application of piezoelectric material to achieve shape control of FGM plate following a simple analytical approach compared to a complex numerical solution.

  • Though the current model is complete in all aspects of mathematical terms still the practical application of such concept is under progress. The cost of material especially piezoelectric is big lacking point for large scale application of practical study or actual physical use.

  • Another limitation of present study is the approximate analysis approach instead of complete three dimensional elastic solution. The beam function provides the approximate analytical solution based on satisfaction of geometric boundary condition.

  • Scope exists for the application of the presented governing system to perform vibration, buckling analysis along with active control and stability study on FGM plate with piezoelectric material.

  • The present model can extend its reach to partial three dimensional elastic analysis of plates by incorporating the thickness stretching effect such that strain in transverse (z-axis) is not equal to zero.