Error analysis of dual-hop DF relayed underlay cognitive networks over EGK fading channels

Abstract

In the presented work, we analyze an underlay cognitive relay network, with a decode and forward relay, for its error performance. The channel is modelled on extended generalized-K fading statistics. Interference temperature here is taken as a constraint which puts a limit on the secondary network transmit powers at the source and the relay. This is to ensure that the interference with the primary communication is kept to a minimum which is a mandatory condition for an underlay system. For the system under consideration, the computation of signal-to-noise ratio, respectively at the secondary relay and the destination, is the first step in our analysis. This is followed by the computation of the equivalent cumulative distribution functions. These quantities are then used for the calculation of the analytic expression for the probability of error of the dual-hop underlay system. Our results demonstrate how the error performance depends on different system parameters when working under the mentioned system constraints. Various numerical examples in the end illustrate how these parameters affect the system error performance of the relayed dual-hop underlay cognitive radio network.

1 Introduction

Over the years cognitive radio networks have evolved as a means to mitigate the spectrum scarcity problems by giving access of the licensed spectrum to unlicensed (secondary) user, either when the spectrum is free (overlay system) or simultaneously using it with the licensed (primary) user (underlay system). Some spectrum awareness methods, are employed by the secondary user to explore and then opportunistically utilize the spectrum holes (unused spectrum), in the interweave systems. This calls for collaborative spectrum sensing of the spectrum for its maximum utilization. At times a direct link between the source and the destination may not be feasible. This may be due to a long distance between these nodes or due to severe fading and shadowing in the communication channel. Introduction of relays in these networks improves the overall performance of these systems. In [1], decode-and-forward (DF) relays have been used for full duplex operation over a Nakagami-m channel, using power and location optimization. Network problems like imperfect channel state information [2, 3], and hardware impairments [4], can also be remedied significantly, by the implementation of relays in such networks. A DF relayed configuration is explored in [5] on a system using Nakagami-m characteristics, where the effect of interference temperature on the channel is also considered. Rayleigh distribution is used to estimate the performance of a DF relayed cognitive relay network (CRN) in [6], while in [7], Weibull fading channel is used to study the performance of a similar network. In [8], outage probability is analyzed for dual-hop DF relayed CRN over an EGK fading channel. Multi-hop networks using DF relays in Rayleigh fading channels with additive white Gaussian noise, are studied in [9] for the system working with interference temperature as a constraint. Final expressions for bit error rates for various modulation techniques are evaluated in the paper. Error performance of a DF relayed mixed RF-FSO channel is analyzed in [10], along with outage probability and channel capacity. RF channel in the work is taken to be having a generalized K fading distribution.

The work in this paper uses extended generalized-K (EGK) fading distribution as the channel model. This distribution, an extension of the generalized-K distribution, is a more suitable model for wireless channels, as it can approximate many types of fading and shadowing conditions encountered in radio environment. Also, it being a generalized distribution, most of the other channel distributions can be accurately approximated from it, either as special or limiting cases [11]. The authors in [12] prove this by determining the average probability of detection for various detection schemes, over various mentioned fading/shadowing channels as special cases of the EGK distribution. Error rate performance of M-PAM and M-QAM schemes in an EGK fading channel, in presence of generalized Gaussian noise is analyzed in [13]. The expression for average symbol error probability is derived in the paper, while average bit error probability of an AF relayed system over generalized fading channel is determined in [14]. Performance analysis of DF relayed underlay cognitive relay networks, over EGK fading channels, is conducted in [15], where outage probability and system ergodic capacity are explored for the considered CRN.

The presented work evaluates the error performance of a DF relayed CRN, operating with interference temperature I as the system constraint. Since the system considered here is an underlay systems, the primary and the secondary transmissions take place simultaneously, due to which the transmit power of the secondary user needs to be limited to ensure minimum interference to the primary communication. We choose the EGK fading distribution for this work, due to its already mentioned advantages. We begin the analysis with the determination of the signal-to-noise-ratio (SNR) of the secondary network, respectively at the relay and the destination nodes, with the help of its probability density function (PDF). Next we proceed to find the respective cumulative distribution functions (CDFs), which is followed by the determination of the analytic expression for the probability of error of the considered underlay CRN with a DF relay and a dual-hop configuration, over a channel with EGK fading characteristics.

Organization of the rest of the paper is as follows: Sect. 2 defines the system model and evaluates the equivalent CDF of the network. In Sect. 3, the expression for the probability of error, of the considered CRN, is derived. Simulation results are discussed in Sect. 4 and finally the conclusion of the paper is expressed in Sect. 5.

2 System model

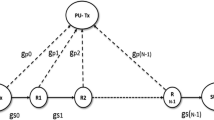
For the analysis, let us consider the underlay CRN shown in Fig. 1. It comprises a primary and a secondary network coexisting in the system, with each network having its source and destination. Additionally, the secondary network will use a DF relay. Due to severe shadowing and/or strong propagation attenuation in the secondary network, it is assumed that the direct connection between the source $S_s$ and the destination $D_s$ is not feasible. Hence it is only through the secondary relay $R_s$ that the end-to-end communication between $S_s$ and $D_s$ is possible. Assuming the primary source $P_s$ to be stationed at a considerable distance from the $R_s$ and the $D_s$ to interfere significantly with the secondary transmission [16], primary user network will be depicted only by the primary destination $D_p$, represented throughout in this work, by PU. This being an underlay system, the primary and secondary transmissions will take place simultaneously, which requires maintaining a strict control on the powers transmitted by $S_s$ and $R_s$. Terms $h_{sp}, h_{rp}, h_{sr}$ and $h_{rd}$ respectively, modeled on EGK fading characteristics due the advantages mentioned earlier, represent the channel coefficients for the links, $S_s-PU$, $R_s-PU$, $S_s-R_s$ and $R_s-D_s$. Due to the transmit power constraints at the secondary source and the relay [5], the powers that $S_s$ and $R_s$ can transmit, can not exceed the maximum transmit power P, available at these nodes. Since we have assumed no direct link between $S_s$ and $D_s$ and that these nodes can be connected only through $R_s$, it is clear that the data in the secondary network is communicated in two phases: the broadcasting phase, in which $S_s$ transmits to $R_s$ with the power $P_s$ and the forwarding phase, in which transmission takes place from $R_s$ to $D_s$ with the transmit power $P_r$. Let the SNRs of the signals at $R_s$ and $D_s$, for the links $S_s-R_s$ and $R_s-D_s$, under the interference constraint I, be denoted by $Z_1$ and $Z_2$ respectively. Under the assumption that P is greater than either $I/|h_{sp}|^2$ or $I/|h_{rp}|^2$, [5], $Z_1$ and $Z_2$ can be expressed as

$$\begin{aligned} Z_{1}= \frac{I}{|h_{sp}|^2}\frac{|h_{sr}|^2}{N_0} , Z_{2}= \frac{I}{|h_{rp}|^2}\frac{|h_{rd}|^2}{N_0} \end{aligned}$$

(1)

where $N_0$ denotes the variance of the additive white Gaussian noise.

Fig. 1

System model depicting a dual-hop DF relayed cognitive underlay network

The CDF of $Z_1$, $F_{Z_1}(\gamma )$, from [15], which uses the same system model, can be written as

$$\begin{aligned} F_{Z_1}(\gamma )&= {} \left( \frac{1}{\varGamma {\left( m_{sr}\right) }\varGamma {\left( m_{s_{sr}}\right) } \varGamma {\left( m_{sp}\right) }\varGamma {\left( m_{s_{sp}}\right) }}\right) \\&\quad\times H_{3,3}^{2,3}\left( \frac{\frac{\beta _{sr}\beta _{s_{sr}}}{{{\bar{\gamma }}}_{sr}}}{\frac{\beta _{sp}\beta _{s_{sp}}}{{{\bar{\gamma }}}_{sp}}}\frac{\gamma N_0}{I} \left| \begin{array}{c} (1,1), \left( 1-m_{sp},\frac{1}{\zeta _{sp}}\right) , \left( 1-m_{s_{sp}},\frac{1}{\zeta {s_{sp}}}\right) \\ \left( m_{sr},\frac{1}{\zeta _{sr}}\right) , \left( m_{s_{sr}},\frac{1}{\zeta {s_{sr}}}\right) ,\left( 0,1\right) \end{array}\right. \right) \end{aligned}$$

(2)

where the terms $m_{sp}$ and $m_{sr}$ define the severity of fading while $\zeta _{sp}$ and $\zeta _{sr}$ define the shaping factors of fading for the respective links. On the other hand, $m_{s_{sp}}$ and $m_{s_{sr}}$ and $\zeta _{s_{sp}}$ and $\zeta _{s_{sr}}$, represent the corresponding parameters for shadowing in the channel. Smaller values of these terms indicate more intense fading and shadowing. The term $\varGamma {(.)}=\int _{0}^{\infty }{t^{(z-1)}}exp(-t)dt, R(z)>0$ denotes the Gamma function [17] while $H_{p,q}^{m,n}[.]$ represents the Fox H-Function [20]. The average received SNR for each link is represented by ${\bar{\gamma }}_{sp}$, ${\bar{\gamma }}{sr}$, ${\bar{\gamma }}_{rp}$ and ${\bar{\gamma }}_{rd}$ and from [12] we get the values of $\beta$, for different links, to be $\beta _{sp}=\frac{\varGamma (m_{sp}+\frac{1}{\zeta _{sp}})}{\varGamma (m_{sp})}$, $\beta _{s_{sp}}=\frac{\varGamma (m_{s_{sp}}+\frac{1}{\zeta _{s_{sp}}})}{\varGamma (m_{s_{sp}})}$, $\beta _{sr}=\frac{\varGamma (m_{sr}+\frac{1}{\zeta _{sr}})}{\varGamma (m_{sr})}$ and $\beta _{s_{sr}}=\frac{\varGamma (m_{s_{sr}}+\frac{1}{\zeta _{s_{sr}}})}{\varGamma (m_{s_{sr}})}.$

Rewriting (2), we get

$$\begin{aligned} F_{Z_1}(\gamma )= A_1 H_{3,3}^{2,3}\left( \frac{C_{sr}}{C_{sp}}\frac{\gamma N_0}{I} \ \left| \begin{array}{c} (1,1),\left( \phi _1\right) \\ \left( \phi 2\right) ,\left( 0,1\right) \end{array}\right. \right) \end{aligned}$$

(3)

where $A_1=\frac{1}{\varGamma {\left( m_{sr}\right) }\varGamma {\left( m_{s_{sr}}\right) }\varGamma {\left( m_{sp}\right) }\varGamma {\left( m_{s_{sp}}\right) }}$, $\phi _1= \left[ \left( 1-m_{sp},\frac{1}{\zeta _{sp}}\right) ,\left( 1-m_{s_{sp}},\frac{1}{\zeta {s_{sp}}}\right) \right]$, $\phi _2 = \left[ \left( m_{sr},\frac{1}{\zeta _{sr}}\right) ,\left( m_{s_{sr}},\frac{1}{\zeta {s_{sr}}}\right) \right]$, $C_{sp} = \frac{\beta _{sp}\beta _{s_{sp}}}{{\bar{\gamma }}_{sp}}$ and $C_{sr} = \frac{\beta _{sr}\beta _{s_{sr}}}{{\bar{\gamma }}_{sr}}.$

Similarly

$$\begin{aligned} F_{Z_2}(\gamma )= A_2 H_{3,3}^{2,3}\left( \frac{C_{rd}}{C_{rp}}\frac{\gamma N_0}{I} \ \left| \begin{array}{c} (1,1),\left( \phi _3\right) \\ \left( \phi _4\right) ,\left( 0,1\right) \end{array}\right. \right) \end{aligned}$$

(4)

where $A_2=\frac{1}{\varGamma {\left( m_{rd}\right) }\varGamma {\left( m_{s_{rd}}\right) }\varGamma {\left( m_{rp}\right) }\varGamma {\left( m_{s_{rp}}\right) }}$, $\phi _3=\left[ \left( 1-m_{rp},\frac{1}{\zeta _{rp}}\right) ,\left( 1-m_{s_{rp}},\frac{1}{\zeta {s_{rp}}}\right) \right]$, $\phi _4 = \left[ \left( m_{rd},\frac{1}{\zeta _{rd}}\right) ,\left( m_{s_{rd}},\frac{1}{\zeta {s_{rd}}}\right) \right]$, $C_{rp} = \frac{\beta _{rp}\beta _{s_{rp}}}{{\bar{\gamma }}_{rp}}$ and $C_{rd} = \frac{\beta _{rd}\beta _{s_{rd}}}{{\bar{\gamma }}_{rd}}.$

The equivalent CDF of the system employing DF relays, from [15], can be written as

$$\begin{aligned} F_{eq}(\gamma )=F_{Z_1}(\gamma )+F_{Z_2}(\gamma )-F_{Z_1}(\gamma )F_{Z_2}(\gamma ) \end{aligned}$$

(5)

3 Probability of error

From [7], the probability of error is given by

$$\begin{aligned} P_e = \frac{a \sqrt{b}}{2 \sqrt{\pi }}{\int _{0}^{\infty }\frac{e^{-b\gamma }}{\sqrt{\gamma }}}F_{eq}(\gamma )d\gamma \end{aligned}$$

(6)

Substituting for $F_{eq}(\gamma )$ from (5), we can rewrite (6) as

$$\begin{aligned} P_e=\frac{a \sqrt{b}}{2 \sqrt{\pi }}\left( \underbrace{\int _{0}^{\infty }\frac{e^{-b\gamma }}{\sqrt{\gamma }}F_{Z_1}(\gamma )d\gamma }_{I_1} + \underbrace{\int _{0}^{\infty }\frac{e^{-b\gamma }}{\sqrt{\gamma }}F_{Z_2}(\gamma )d\gamma }_{I_2} - \underbrace{\int _{0}^{\infty }\frac{e^{-b\gamma }}{\sqrt{\gamma }}F_{Z_1}(\gamma )F_{Z_2}(\gamma )d\gamma }_{I_3}\right) \end{aligned}$$

(7)

To evaluate $P_e$, we need to evaluate $I_1, I_2$ and $I_3$ separately. From (7), we know that the integral $I_1$ is given by $I_1={\int _{0}^{\infty }\frac{e^{-b\gamma }}{\sqrt{\gamma }}F_{Z_1}(\gamma )d\gamma }$. Substituting for $F_{Z_1}(\gamma )$ from (3), we obtain $I_1$ as

$$\begin{aligned} I_1=A_1\int _{0}^{\infty }{e^{-b\gamma }{\gamma ^\frac{-1}{2}}} H_{3,3}^{2,3}\left( X_1\gamma \left| \begin{array}{c} (1,1),\left( \phi _1\right) \\ \left( \phi _2\right) ,\left( 0,1\right) \end{array}\right. \right) d\gamma \end{aligned}$$

(8)

where $X_1=\frac{C_{sr}N_0}{C_{sp}I}$. Using [18, Eq.(2.25.2.3)], we get the final expression for $I_1$ as

$$\begin{aligned} I_1=A_1 b^{\frac{-1}{2}}H_{4,3}^{2,4}\left( \frac{X_1}{b} \ \left| \begin{array}{c} \left( \frac{1}{2},1\right) ,(1,1), (\phi _1)\\ (\phi _2), (0,1) \end{array}\right. \right) \end{aligned}$$

(9)

Similarly, we get $I_2$ as

$$\begin{aligned} I_2=A_2 b^{\frac{-1}{2}}H_{4,3}^{2,4}\left( \frac{X_2}{b} \ \left| \begin{array}{c} \left( \frac{1}{2},1\right) ,(1,1),\left( \phi _3\right) \\ \left( \phi _4\right) ,\left( 0,1\right) \end{array}\right. \right) \end{aligned}$$

(10)

where $X_2=\frac{C_{rd}N_0}{C_{rp}I}$.

From (7), the integral $I_3$ is given as $I_3={\int _{0}^{\infty }\frac{e^{-b\gamma }}{\sqrt{\gamma }}F_{Z_1}(\gamma )F_{Z_2}(\gamma )d\gamma }$. Substituting for $F_{Z_1}(\gamma )$ and $F_{Z_2}(\gamma )$ from (3) and (4), we obtain $I_3$ as

$$\begin{aligned} I_3&= {} \int _{0}^{\infty }{e^{-b\gamma }{\gamma ^\frac{-1}{2}}} A_1 H_{3,3}^{2,3}\left( X_1\gamma \ \left| \begin{array}{c} (1,1),\left( \phi _1\right) \\ \left( \phi _2\right) ,\left( 0,1\right) \end{array}\right. \right) \\&\quad\times A_2 H_{3,3}^{2,3}\left( X_2\gamma \ \left| \begin{array}{c} (1,1),\left( \phi _3\right) \\ \left( \phi _4\right) ,\left( 0,1\right) \end{array}\right. \right) d\gamma \\ \end{aligned}$$

(11)

Substituting $e^{-b\gamma }=H_{0,1}^{1,0}\left( b\gamma \ \left| \begin{array}{c} -\\ (0,1) \end{array}\right. \right)$ from [18, Eq.(8.4.3.1)] in (11) and converting H-Functions into gamma functions using [19, Eq.(1.3, 1.3a)], we get

$$\begin{aligned} I_3&= {} \frac{A_1A_2}{{(2\varPi i)^{2}} }\int _{L_1}\int _{L_2}\frac{\varGamma \left( m_{rd}+\frac{s_1}{\zeta _{rd}}\right) {\varGamma \left( m_{s_{rd}}+\frac{s_1}{\zeta _{s_{rd}}} \right) }{\varGamma (-s_1)}{\varGamma \left( m_{sp}-\frac{s_1}{\zeta _{sp}}\right) }{\varGamma \left( m_{s_{sp}}-\frac{s_1}{\zeta _{s_{sp}}}\right) }}{\varGamma (1-s_1)} \\&\quad\times \frac{{\varGamma \left( m_{sr}+\frac{s_2}{\zeta _{sr}}\right) {\varGamma \left( m_{s_{sr}}+\frac{s_2}{\zeta _{s_{sr}}}\right) } {\varGamma (-s_2)}{\varGamma \left( m_{rp}-\frac{s_2}{\zeta _{rp}}\right) }{\varGamma \left( m_{s_{rp}}-\frac{s_2}{\zeta _{s_{rp}}}\right) }}}{\varGamma (1-s_2)} \\&\quad\times \left( \int _{0}^{\infty }H_{0,1}^{1,0}\left( b\gamma \ \left| \begin{array}{c} -\\ (0,1) \end{array}\right. \right) \gamma ^{\left( \frac{-1}{2}-s_1-s_2\right) }d\gamma \right) X_1^{-s_1}X_2^{-s_2} ds_1ds_2 \end{aligned}$$

(12)

Solving the inner integral in (12) using the identity [18, Eq.(2.25.2.1)], we get

$$\begin{aligned}&\int _{0}^{\infty }H_{0,1}^{1,0}\left( b\gamma \ \left| \begin{array}{c} -\\ (0,1) \end{array}\right. \right) \gamma ^{\left( \frac{-1}{2}-s_1-s_2\right) }d\gamma \\&\quad =b^{-(s_1+s_2+\frac{1}{2})}\varGamma {\left( s_1+s_2+\frac{1}{2}\right) } \end{aligned}$$

(13)

Substituting (13) in (12), and after manipulating the resultant equation, we get the closed form expression for $I_3$ as

$$\begin{aligned} I_3={A_1 A_2\sqrt{b}}H_{1,0\,:\,3,3\,:\,3,3}^{0,1\,:\,2,3\,:\,2,3}\left( \begin{array}{c} {\frac{X_1}{b}}\\ {\frac{X_2}{b}} \end{array} \ \left| \begin{array}{c} \left( {\frac{1}{2}},1\right) ;(1,1),(\phi _1);(1,1),(\phi _3) \\ -;(\phi _2),(0,1);(\phi _4),(0,1) \end{array}\right. \right) \end{aligned}$$

(14)

where $H_{p_1, q_1\,:\,p_2, q_2\,:\,p_3, q_3}^{m_1,n_1\,:\,m_2,n_2\,:\,m_3,n_3}(.)$ represents the extended generalized bivariate Fox H-Function (EGBFHF) [20, Eq.(2.57)]. This function is easily realizable with the help of MATLAB or MATHEMATICA, [21].

Substituting for $I_1, I_2$ and $I_3$ from (9), (10) and (14) in (7), we get the final expression for $P_e$ as

$$\begin{aligned} P_e&= {} \frac{a \sqrt{b}}{2 \sqrt{\pi }}\left[ {\frac{A_1}{\sqrt{b}}}H_{4,3}^{2,4}\left( \frac{X_1}{b} \ \left| \begin{array}{c} (\frac{1}{2},1),(1,1), (\phi _1)\\ (\phi _2), (0,1) \end{array}\right. \right) \right. \\&\quad +{\frac{A_2}{\sqrt{b}}}H_{4,3}^{2,4}\left( \frac{X_2}{b} \ \left| \begin{array}{c} \left( \frac{1}{2},1\right) ,(1,1),(\phi _3)\\ (\phi _4), (0,1) \end{array}\right. \right) \\&\quad - \left. {A_1 A_2\sqrt{b}} H_{1,0\,:\,3,3\,:\,3,3}^{0,1\,:\,2,3\,:\,2,3} \left( \begin{array}{c} {\frac{X_1}{b}}\\ {\frac{X_2}{b}} \end{array}\ \left| \begin{array}{c} \left( {\frac{1}{2}},1\right) ;(1,1),(\phi _1);(1,1),(\phi _3) \\ -;(\phi _2),(0,1);(\phi _4),(0,1) \end{array}\right. \right) \right] \end{aligned}$$

(15)

Using [22], for the values of a and b, $P_e$ for different modulation schemes can be evaluated.

4 Numerical results

We conduct the error performance analysis of a dual-hop, underlay CRN, using a DF relay over a channel having EGK fading statistics, in this work. The analysis is performed under interference temperature constraint, I, due to the proximity of primary user PU to the secondary system. Let us assume that (0, 0), (0, 1) and (0.5, 0) respectively are the initial coordinates of the source $S_s$, the destination $D_s$ and the relay $R_s$ in the secondary network. The initial position of primary is taken to be (0.5, 0.5). The link distances are assumed to be normalized. For the sake of generality, the propagation constant, $\alpha$, is taken as 4 for all the plots, assuming the area of operation to be urban. The shaping factors of fading and shadowing for the different links, $\zeta _{sp}, \zeta _{sr}, \zeta _{rp}, \zeta _{rd}, \zeta _{s_{sp}}, \zeta _{s_{sr}}$ and $\zeta _{s_{rp}}$ are all taken to be equal and denoted by $\zeta _k$. On the other hand, we study the effects of severity of fading and shadowing on the error probability of the system by denoting the severity factors, $m_{sp}, m_{sr}, m_{rp}, m_{rd}, m_{s_{sp}}, m_{s_{sr}}, m_{s_{rp}}$ and $m_{s_{rd}}$ by a single quantity $m_k$, which demonstrates its effect on the error probability of the system by taking different values in different plots. The error performance has been evaluated for four modulation schemes, BPSK, BFSK, QPSK and 8-PSK.

Fig. 2

Error probability vs $I/N_0$ for different values of PU position, keeping relay fixed at (0.5, 0) for $m_k=2$, $\zeta _k=1$. Modulation schemes used are BPSK, BFSK, QPSK and 8-PSK

Fig. 3

Variation in probability of error with $I/N_0$ for different values of $\gamma _{th}$ and for BPSK, BFSK, QPSK and 8-PSK. $m_k$ and $\zeta _k$ are kept constant at the values of 2 and 1 respectively while keeping relay position fixed at (0.5, 0) and PU at (0.5, 0.5).

Fig. 4

Change in error probability against $I/N_0$. $m_k$ is considered at the values of 1 and 4 respectively for BPSK, BFSK, QPSK and 8-PSK modulation schemes. $\zeta _k$ is assigned a value of 1 while keeping relay position fixed of (0.5, 0), PU at (0.5, 0.5) and $\gamma _{th}$ constant at 5 (dB)

Fig. 5

Variation of error probability against $I/N_0$ for different values of relay position for BPSK, BFSK, QPSK and 8-PSK modulation schemes. Severity $m_k$ is considered at the value of 2 while $\zeta _k$ is assigned a value of 1 while keeping PU at (0.5, 0.5) and $\gamma _{th}$ constant at 5 (dB)

In Fig. 2, we plot of the probability of error, $P_e$ against $I/N_0$, for different PU positions w.r.t its initial coordinates, (0.5, 0.5). The threshold SNR, $\gamma _{th}$ is kept constant at 5 dB as is the relay position at (0.5, 0). Throughout this plot, we keep severity and shaping factor of fading and shadowing, $m_k=2$ and $\zeta _k=1$, respectively. The general observation here is that the probability of error decreases with $I/N_0$, for both the PU positions and all the modulation schemes considered here. We further observe that the error probability against $I/N_0$, for all the modulation schemes, is more when PU is less distant from the secondary source and the relay. In the current case, it means that $P_e$ is higher when PU is at (0.44, 0.44), than when it is at (0.66, 0.66). Thus we can say in general that $P_e$ decreases with the increase of PU distance from the secondary network, when the relay position and $\gamma _{th}$ are held constant at the initial values. Also, from the plots it can be clearly observed that BPSK shows better error performance when compared with BFSK, QPSK and 8-PSK for both the PU positions. It simply implies that BPSK consistently has a lower probability of error irrespective of whether the primary is far from the secondary network or close to it while 8-PSK gives the worst error performance. This behaviour can be predicted from analytic results as well because the Euclidean distances between the signal points decreases with the increase in the value of M in M-ary modulation schemes, thereby increasing the error probability while decreasing the bandwidth.

Figure 3, illustrates the effect of threshold SNR $\gamma _{th}$, on the plot of the $P_e$ versus $I/N_0$. The relay and the primary continue to be at their starting positions of (0.5, 0) and (0.5, 0.5) respectively. Severity parameter $m_k$, is assigned the value 2 while $\zeta _k$ is kept constant at 1 in this observation. The plot clearly depicts that the error probability reduces as $I/N_0$ increases, for all the the values of $\gamma _{th}$ in all the modulation schemes, i.e., BPSK, BFSK, QPSK and 8-PSK. $P_e$, however, is observed to be smaller for lower values of $\gamma {th}$, like 0 dB, as compared to higher values like 15 dB. Also BPSK seems to have better error performance, followed by BFSK, for both the the values of $\gamma _{th}$, while 8-PSK seems to perform the worst. This conclusion can be reached analytically also because, higher values of $M$ in M-ary modulation schemes result in an increase in the probability of error and a decrease in the bandwidth of the signal, thereby improving its spectral performance.

Figure 4 demonstrates how $P_e$ changes with $I/N_0$, when we vary $m_k$, while $\zeta _k$ is kept constant at 1. Threshold SNR $\gamma _{th}$ is held constant at 5 dB and the PU and the relay are respectively fixed at (0.5, 0.5) and (0.5, 0). Clearly it can be observed from the graph that the drop in error probability with increasing $I/N_0$, is considerably more when the value of $m_k$ is higher (4 in this case), i.e. when fading is less severe as compared to lower values of $m_k$ (e.g $m_k=1$), which implies more severe fading. This is obvious from analytic results as well. This observation has been made for the considered modulation schemes, BPSK, BFSK, QPSK and 8-PSK. BPSK seems to have better error performance compared to QPSK and BFSK while 8-PSK performs the worst as far as severity of fading is concerned. For still higher values of M, like 16-PSK, 32-PSK, the probability of error increases further and approaches 1. This is along the expected lines only as higher values of M in M-ary modulation schemes are employed to decrease the bandwidth, which comes at the cost of increased error probability due to reduced Euclidean distances between the signal points. Thus we can safely conclude that the probability of error will be less pronounced when severity of fading is less, like in this case, when $m_k =4$, for all the considered modulations schemes.

Figure 5 depicts the plot of probability of error against the interference to noise power density ratio, $I/N_0$, for different relay positions keeping PU at its initial position of (0.5, 0.5). While $m_k$ and $\zeta _k$ are assigned the values of 2 and 1 respectively, $\gamma _{th}$ is held constant at 5 dB. From the plot it is evident that, for all the considered modulation schemes like BPSK, BFSK, QPSK and 8-PSK, the error probability shows a drop with increasing $I/N_0$. It can also be observed that when $R_s$ is further removed from the central point [(0.9, 0) in this case], $P_e$ is higher than when it is closer [(0.4, 0) in this case]. Hence it can be concluded that that the optimal position for the relay in this system model is closer to the middle of the link between $S_s$ and $D_s$. Also it can be observed that $P_e$ is more for 8-PSK than any other modulation scheme while it is lowest for BPSK in general. This again follows the general rule that $P_e$ is higher for higher values of M in M-ary modulation schemes while bandwidth used is lower. This is true for analytical results as well.

5 Conclusion

In the presented work, error analysis of a DF relayed underlay CRN is carried out. The channel used for the analysis has an EGK fading distribution. The analysis is performed with the interference temperature taken as the constraint. This constraint in turn imposes an upper limit on the powers transmitted by the secondary source and the relay nodes. The error analysis of the combination of EGK fading channel in cognitive radio scenario, under the constraint of interference temperature, with dual-hop DF relaying, for the mentioned modulation schemes, has been has not been attempted before, to the best of my knowledge. Several steps constitute the analysis, which starts with the determination of SNRs, PDFs and CDFs of the signals at various nodes in the network, and then the derivation of the equivalent CDF of the system from those terms. The analysis concludes with the determination the analytic expression for the probability of error of the underlay cognitive radio system. Various simulation results are included to exhibit the effect of different system parameters like the severity of fading and shadowing, the link distance between the primary and the secondary networks, the numerical values of $I/N_0$ and $\gamma _{th}$ etc., on the error probability for different modulation schemes in the system. The overall observation is that the PU distance from the secondary network and the severity of fading and shadowing, have a higher impact on the error performance of the system under consideration as compared to other factors. The error performance of the system has been evaluated for various modulation schemes like BPSK, BFSK, QPSK and 8-PSK and it is concluded that BPSK give the best error performance and 8-PSK the worst. This is in agreement with established facts and theory that higher the value of M, the lower the system error performance and that the increased bandwidth efficiency is acquired with the increase in M in M-ary modulation schemes, at the cost of system error performance.