Introduction

The investigation of nonlinear oscillations in constructions was crucial for comprehending the dynamics of diverse engineering systems, including bridges, buildings, and aerospace structures. Nonlinear dynamics are essential in determining how suspension bridges respond to wind and seismic forces [1]. Nonlinear electrical circuits were commonly encountered in electronic devices and systems. Understanding and analyzing their behavior is crucial for designing reliable and efficient electronic systems. For example, nonlinear oscillations in electronic oscillators and chaotic behavior in nonlinear circuits have applications in communication systems and signal processing [2]. Nonlinear dynamics were crucial for representing a range of biological systems, such as brain networks, heart rhythms, and biochemical activities. Comprehending these interactions was crucial for identifying illnesses and creating effective treatments. Nonlinear oscillations in cardiac cells played a vital role in comprehending arrhythmia and cardiac synchronization [3]. Nonlinear dynamics were commonly observed in chemical reaction systems, particularly in intricate reaction networks and catalytic reactions. Comprehending and managing these dynamics were crucial for maximizing chemical processes and creating effective reactors. One instance of oscillatory behavior, such as the Belousov-Zhabotinsky reaction, displayed complex nonlinear dynamics that have the possibility of is used in biochemical oscillators and the creation of patterns [4]. Nonlinear control mechanisms were present in a range of applications, such as robotics, automobile control, and systems for aerospace. To develop efficient control approaches for complex systems, a comprehensive comprehension of their nonlinear dynamics was essential. Nonlinear control techniques, such as sliding mode management and adaptable control, are employed to stabilize and regulate intricate nonlinear systems [5]. Nonlinear vibrations are present in a range of mechanical systems, such as spinning machinery, engines, and gearboxes. Comprehending and examining nonlinear vibrations were essential for identifying problems, forecasting component malfunctions, and enhancing machine dependability. These references provided further insights into the applications of nonlinear dynamics in different engineering and scientific fields. Oscillatory networks were widely present in both natural and engineering domains, appearing in many phenomena such as the rhythmic pulsation of a heart and the vibrations of a bridge. Although linear oscillations may be described relatively simply, real-world systems often display nonlinear behavior that defies basic study. Nonlinear oscillations, which were influenced by their amplitude and can exhibit complicated and unpredictable behavior, were a subject of fascination and difficulty for scientists and engineers [6]. In physics and engineering, dynamic regulations are often represented as a nonlinear differential equation that lacks a precise solution. Traditional approaches such as perturbation methods or numerical techniques are employed to establish the correct relationship between frequency and amplitude and forecast their dynamic responses. This enabled a thorough comprehension of the quantitative as well as qualitative characteristics [7].

The HFF, which was created by Ji-Huan He, was a fundamental component of the homotopy perturbation method (HPM). This formula employs a blend of the HPM and an averaging technique to approximate the frequency of nonlinear oscillators [8]. HFF was renowned for its simplicity and efficiency, making it highly effective in dealing with weakly nonlinear oscillators without the need for significant processing resources. The analytical expression establishes a correlation between the frequency of oscillation and the amplitude, which is particularly beneficial in systems with moderate nonlinearity. The HFF derived by He was extensively utilized in engineering and physics, particularly in mechanical systems such as beam oscillations and electrical circuits. It has proven to be highly useful in addressing a wide range of issues in these domains [9]. Significantly, it has proven to be highly beneficial in acquiring closed-form analytical solutions for oscillators, notably those of the Duffing variety [10]. The Duffing frequency, proposed by He, has become a valuable mathematical tool for studying the periodic solutions that exist in nonlinear oscillators. The frequency formula developed by He has gained significant attention due to its clear, simple, and effective nature, ever since it was introduced in a ground-breaking review study [11]. The technical community rapidly became interested in it due to its clarity and empirical verification [12]. Further study has focused on improving and increasing the accuracy of HFF [13, 14]. Furthermore, its usability has been expanded to include a wide range of oscillator types, such as fractal oscillators and damping oscillators, highlighting its flexibility and significance in the field of nonlinear dynamics exploration [15, 16].

The NPA provided a novel viewpoint, circumventing the repetitive improvement of perturbation methods. Instead than depending on minor deviations from a known solution, the NPA aimed to directly reflect the intrinsic complexities of the nonlinear system. This methodology, unconstrained by the limitations of minor perturbations, offers insights into a wider spectrum of system behaviour, particularly those that may be disregarded or unattainable using conventional perturbation approaches. El-Dib [17] specifically examined the presence of strong nonlinearities, including quadratic nonlinearity, in oscillatory systems. The formulae were specifically developed to address systems with pronounced or unique nonlinearities, providing a hardy solution in cases where conventional methods may be ineffective. This formula was renowned for its capacity to handle complex nonlinearities, offering precise frequency estimations in systems where the nonlinearity has a substantial impact on the system’s behavior. The damping coefficient of the nonlinear oscillator can be determined using El-Dib’s formulae [17]. Moreover, these formulae have the capability to incorporate nonlinear quadratic forces into the frequency equation of the oscillating system. It frequently entails more intricate mathematical operations in comparison to HFF. The efficacy of El-Dib’s technique was demonstrated in complicated systems, including high-energy physics, sophisticated engineering applications, and systems where the assumptions of weak nonlinearity are not applicable [17]. The NPA was widely employed in the study of dynamical systems and the stability of Electrohydrodynamics. The NPA was utilized to analyse the temporal delay of the Van der Pol oscillator [18]. The NPA was used to examine the effectiveness of the time-delayed controller in controlling nonlinear oscillations [19]. The NPA was used to analyse other highly nonlinear oscillators [20]. The study investigated various controllers to dampen the oscillations of a hybrid oscillator using the NPA method [21]. Regarding the field of hydrodynamic stability, an analysis was conducted on diverse problems involving several classes of non-Newtonian fluids, in different geometries and under various external stresses [22,23,24,25].

In relation to the utilization of the NPA and its remarkable results, the results that followed are to be centred:

  1. 1.

    The nonlinear ODE was identical to the alternate comparable linear ODE that was generated by the NPA.

  2. 2.

    These two equations are perfectly congruent when employing this approach.

  3. 3.

    All conventional methods employ Taylor expansion to mitigate the complexity of the given problem in the presence of restoring forces.

  4. 4.

    This current plan has eradicated this susceptibility.

  5. 5.

    The NPA facilitated the investigation of the problem’s stability analysis, in contrast to other conventional methodologies.

  6. 6.

    The unique method seems to be a user-friendly, pragmatic, and captivating tool. It can be utilized to study many forms of nonlinear oscillators.

According to an approach that minimizes the average difference between the two systems, a non-linear second order dynamical system may be transformed into a system with a linear structure [26]. It was demonstrated that the substitution was distinct and simple to implement as long as the averaging operator possessed particular characteristics. The averages of the functions of the linearized solution were used to represent the parameters of the alternative linear scheme. A study of certain methods that could be used with both highly and weakly nonlinear problems was given [9]. The resulting approximations of analytical solutions were also true across the whole solution domain. The drawbacks of conventional perturbation techniques were demonstrated. Estimating the periodic behaviour of a nonlinear oscillator is of utmost importance in engineering. Several approaches, including HFF, max–min approach, and HPM have been extensively studied as the simplest techniques for analyzing nonlinear oscillators [27]. To enhance the accuracy of predicting the frequency, a mathematical explanation of HFF was presented, incorporating a weighted average. Additionally, alternative techniques were proposed for strongly nonlinear oscillators, which are both straightforward and justified [28]. The results revealed that the method yielded an approximately precise response. A highly effective method for quickly determining the amplitude-frequency connection of a nonlinear oscillator was also made available by the study. The connection between a nonlinear vibration system’s frequency and amplitude was crucial for the design of packaging systems and micro electromechanical system [29]. The study presented a straightforward method to predict frequencies of nonlinear oscillators with varying initial conditions. Upon comparing the results with those obtained through the HPM, a significant level of concurrence was observed. In order to include the damping nonlinear oscillator, a developed HFF was derived. After converting the nonlinear oscillator to a linear damping model that was based on the conservative restoring force, the frequency resulting from the odd nonlinear damping force’s presence was determined. A numerical solution that demonstrated the great accuracy of the estimated frequency was scrutinised with the analytical solution.

In light of the aforementioned aspects, the current problem aims to adopt the NPA with their advantage to analyze some highly nonlinear ODEs. To crystalize the presentation of the problem, the rest of the paper is divided into five Sections to help in the presentation clearer. We briefly review and demonstrate the NPA’s explanation in Sect. "A Brief Explanation of NPA". Three nonlinear differential equations from the real world are examined using the NPA in Sect. "Application". In Sect. "Conclusions", a summary of the examinations in the current investigation is given. 

A Brief Explanation of NPA

Consider a highly nonlinear ODE of the form:

$$\eta^{\prime \prime} + F(\eta ,\,\eta^{\prime},\,\eta^{\prime \prime}) + G(\eta ,\,\eta^{\prime},\,\eta^{\prime \prime}) = H(\eta ,\,\eta^{\prime},\,\eta^{\prime \prime}),$$
(1)

where \(F(\eta ,\,\eta^{\prime},\,\eta^{\prime \prime})\) as well as \(G(\eta ,\,\eta^{\prime},\,\eta^{\prime \prime})\) are third-order secular functions. Simultaneously, \(H(\eta ,\,\eta^{\prime},\,\eta^{\prime \prime})\) is a quadratic function. These functions may be represented as:

$$\begin{aligned}&{F(\eta ,\,\eta^{\prime},\,\eta^{{\prime} {{\prime}}}) = \alpha_1 \eta^{\prime} + \beta_1 \eta^2 \eta^{\prime}+\gamma_1 \eta^{{\prime}{3}}+ \delta_1 \eta^{{\prime} {\prime}}\eta^{{\prime}{2}} ,} \\ &{G(\eta ,\,\eta^{\prime},\,\eta^{{\prime} {{\prime}}}) = \omega^2 \eta + \gamma_2 \eta \eta^{{\prime} {2}} + \delta_2 \eta^3 + \tau_2 \eta^{{\prime \prime}}\eta^2 ,}\\ &{H(\eta ,\,\eta^{\prime},\,\eta^{{\prime} {{\prime}}})= \alpha_3 \eta \eta^{\prime} + \beta_3 \eta^{{\prime} {2}} + \gamma_3 \eta^2 + \delta_3 \eta^{\prime}\eta^{{\prime} {\prime}} + \tau_3 \eta \eta^{{\prime} {\prime}}}, \end{aligned}$$
(2)

where \(\omega\) denotes the natural frequency and \(\alpha_k ,\,\beta_k ,\,\gamma_k ,\,\delta_k ,\,\tau_k \,\,(k = 1,\,2,\,3)\) are physical constants.

As previously shown throughout the classical perturbation methodologies [1], the first two-functions produce secular terms, whereas the third one does not create any secular terms.

Now, the NPA aims mainly to obtain an alternative linear ODE. For this purpose, three constants will be determined to construct the required linear ODE. To accomplish this, an initial solution of the given linear OLE can be represented as previously shown [17].

Based on the HFF, the NPA looks for a linear ODE that is similar to the original nonlinear ODE. In certainty, the simple harmonic motion and the ideal linear ODE behave similarly. Consequently, the guessing answer function may be thought of as a cosine wave with a final frequency that will be chosen at the end of the methodology process. Therefore, to reformulate the nonlinear system using the NPA, one needs to provide a new solution that fulfils the initial conditions (ICs). This is the recommended course of action:

Therefore, a guessing solution of the Eq. (1) is supposed in the form:

$$\eta = A\cos \Omega t,$$
(3)

Herein the ICs are given as:\(\eta (0) = A\), and \(\eta^{\prime}(0) = 0\).

The parameter \(\Omega\) represents the total frequency, which will be determined later.

The intended linear ODE can be articulated as:

$$\eta^{\prime \prime} + \sigma \eta^{\prime} + \varpi^2 \eta = \Lambda$$
(4)

As previously shown El-Dib [17] and Moatimid et al. [18,19,20,21,22,23,24,25], the above three parameters may be evaluated as:

$$\sigma = \int_0^{2\pi /\Omega } {\eta \, F(\eta ,\eta ,\eta^{\prime \prime})} \,dt/\int_0^{2\pi /\Omega } {\eta^2 } dt$$
(5)

Consider an equivalent frequency \(\varpi\), such that it can be obtained in terms of a function of the equivalent frequency as follows:

$$\varpi^2 = \int_0^{2\pi /\Omega } {\eta \,G(\eta ,\eta^{\prime},\eta^{\prime \prime})} dt/\int_0^{2\pi /\Omega } {\eta^2 } dt = \varpi^2 (\Omega ).$$
(6)

Therefore, the calculation of the non-uniformity part \(\Lambda\) shall be carried out by substituting:\(\eta \to \frac{A}{2},\,\eta^{\prime} \to \frac{A\Omega }{2},\) and \(\,\eta^{\prime \prime} \to \frac{A\Omega^2 }{2}\). It is worth mentioning that El-Dib [17] and Moatimid et al. [18,19,20,21,22,23,24,25] holds true only until the quadratic power. For more convenience, Eq. (4) may be written in a suitable normal form by using the substitution:

$$\eta (t) = f(t)Exp( - \sigma t/2).$$
(7)

Inserting Eq. (7) into Eq. (4), one gets

$$f^{\prime \prime} + \left( {\varpi^2 - \frac{\sigma^2 }{4}} \right)f = \Lambda \,Exp(\sigma t/2).$$
(8)

Finally, the total frequency is given by \(\Omega^2 = \varpi^2 - \frac{\sigma^2 }{4}\).

Application

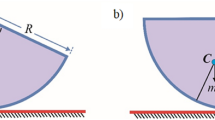
Let us consider a mechanical structure of a uniform conservative beam, with invariable length \(l\), see (Fig. 1). It is hinged at the base to a rotational spring with stiffness \(K_r\) and carries a lumped mass \(M\) at an arbitrary intermediate point \(s = d\) along the beam span. The beam’s thickness is restricted to be small according to its length, allowing the influence of shearing deformation and rotary inertia to be ignored. Such oscillating systems are referred to as autonomous conservative oscillators, and their operation is controlled by the following severely nonlinear ODE with fifth-order nonlinearity [30,31,32] is given as:

Fig. 1
figure 1

Describes the structure of a uniform conservative beam

Full size image

The governing equation of motion is given as:

$$\ddot{x}(1 + b_1 x^2 + b_2 x^4 ) + \Gamma x + a_1 x\dot{x}^2 + a_2 x^3 \dot{x}^2 + a_3 x^3 + a_5 x^5 = 0.$$
(9)

where \(\Gamma ,a_1 ,a_2 ,a_3 ,a_5 ,b_1 ,\) and \(b_2\) are arbitrary physical parameters that depend on the parameters \(l,d,K_{r}\), and \(M\) given in the Fig. 1.

The initial solution is given by Eq. (3) with their ICs.

Following the parallel process as given in the previous section, it follows the equivalent linear ODE is given by

$$\ddot{u} + \Omega^2 u = 0,$$
(10)

where

$$\Omega = \sqrt {{\frac{8\Gamma + 6a_3 A^2 + 5a_5 A^4 }{{8 + [6b_1 - 2a_1 - (a_2 - 5b_2 )A^2 ]A^2 }}}} .$$
(11)

It should be noted that Eq. (1) is the same as previously shown [31].

For more convenience, the original nonlinear ODE as given in Eq. (9) can have a solution that is the same as those used by the final linear ODE as given in Eq. (10), acknowledging the NPA. It is also helpful to link the NPA of the equivalent linear ODE as given in (10), which is created by the MS, with the NS of the original Eq. (9).

$$A = 0.5,\,\,\Gamma = 0.5,\,\,a_1 = 0.1,\,\,a_2 = 0.2,\,\,\,a_3 = 0.3,\,\,a_5 = - 1.2,\,b_1 = 1,\,\,b_2 = 0.2.$$

In Fig. 2, the NS and NPA are displayed and matched. Great dependability about them is seen to demonstrate the great accuracy of the used NPA, in which the outcomes are quite trustworthy concerning one another. According to MS, the absolute inaccuracy is 0.0141729.

Fig. 2
figure 2

Shows the comparison between the NS and NPA

Full size image

The analytic non-perturbative solution is explored in portions (a) and (b) of Fig. 3 at \(\Gamma ( = 1,2,3)\) when \(t \in [0,10]\,s\) and \(t \in [0,100]\,s[0,100]\)\(\,s\), respectively. The inspection of the drawn waves shows that they have periodic behaviour with the same amplitude and the oscillations’ number increases with the increase of \(\Gamma\) value. The phase plane diagrams corresponding to the illustrated curves in Fig. 3b are presented in Fig. 4 to assert that these waves have stationary manner during the investigated interval of time.

Fig. 3
figure 3

Shows the time-dependent solution when \(\Gamma ( = 1,2,3)\)

Full size image
Fig. 4
figure 4

Shows the diagram of the phase plane when \(\Gamma ( = 1,2,3)\)

Full size image

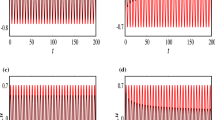
The inspection in the drawn curves in Figs. 5a, 6a, 7a, 8a, 9a, 10a shows the variation of the NPA with time in which they are plotted when \(\Gamma ( = 1,2,3),\)\(a_1 ( = 0.1,0.4,0.9),\)\(a_2 ( = 0.2,0.4,0.8),\) \(a_3 ( = 0.3,0.6,0.9),\) \(a_5 ( = 1.2,0.5,1.5),\) \(b_1 ( = 1,1.5,2),\) and \(b_2 ( = 0.2,0.5,0.8)\), respectively. It is important to mention that all other parameters were considered constant for each figure, except for analysing the variation in the specific parameter at the top of each diagram. With a careful look at these shapes, it can be said that we are dealing with periodic waves that represent the NPA during the studied time interval. Moreover, it is found that the number of oscillations increases, as in Figs. 5a, 7a, 8a, 9a, while remaining unchanged, as in Figs. 6a and 10a. On the other side, the amplitude of these waves doesn’t change. Therefore, these parameters significantly impact the behaviour of the solution. The corresponding figures to the temporal behavior of the NPA at the same values of the parameters are drawn in the diagrams (5b), (6b), (7b), (8b), (9b), and (10b). Based on these graphs, whether of temporal behaviour or phase plane, it can be said that these solutions are stable and free of chaotic phenomena.

Fig. 5
figure 5

Explores the time-dependent solution at \(a_1 ( = 0.1,0.4,0.9)\) and the corresponding phase plane diagram

Full size image
Fig. 6
figure 6

Presents \(u(t)\) at \(a_2 ( = 0.2,0.4,0.8)\) and the curves in \(u\dot{u}\) plane

Full size image
Fig. 7
figure 7

Reveals \(u(t)\) at \(a_3 ( = 0.3,0.6,0.9)\) and the curves in \(u\dot{u}\) plane

Full size image
Fig. 8
figure 8

Shows \(u(t)\) at \(a_5 ( = 1.2,0.5,1.5)\) and the curves in \(u\dot{u}\) plane

Full size image
Fig. 9
figure 9

Shows \(u(t)\) at \(b_1 ( = 1,1.5,2)\) and the curves in \(u\dot{u}\) plane

Full size image
Fig. 10
figure 10

Describes \(u(t)\) at \(b_2 ( = 0.2,0.5,0.8)\) and the curves in \(u\dot{u}\) plane

Full size image

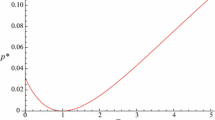
To express the stability and instability zones of the obtained solutions, Eq. (11) has been graphed in view of the aforementioned parameters. These areas are calculated as indicated in the Figs. 11, 12, 13, 14 when \(\Gamma ,a_1 ,a_2 ,a_3 ,a_5 ,b_1 ,\) and \(b_2\). It is shown that the stability areas increase as the values of these parameters decrease. It is observed that these areas vary with changes in each parameter. One can say that drawing stability and instability zones may provide insights on:

  • a. Clear demarcation of zones helps in identifying the parameters’ ranges where the system remains stable.

  • b. Highlighting instability zones allows for a better understanding of the conditions under which the system may fail or behave unpredictably.

  • c. Observing how stability and instability zones change with variations in parameters provides insights into which parameters are most critical for maintaining stability.

  • d. Engineers and designers can use these zones to optimize the design by adjusting parameters to expand the stability regions, thus enhancing the system’s robustness and performance.

  • e. Identifying the precise boundaries and behavior within these zones can direct future research efforts to better understand underlying phenomena and improve theoretical models.

Fig. 11
figure 11

Presents the stability zones in the plane \(A\,\Omega^2\) at: (a) \(\Gamma ( = 1,2,3)\), (b) \(a_1 ( = 0.1,0.4,0.9)\)

Full size image
Fig. 12
figure 12

Presents the stability zones in the plane \(A\,\Omega^2\) at: (a) \(a_2 ( = 0.2,0.4,0.8)\), (b) \(a_3 ( = 0.3,0.6,0.9)\)

Full size image
Fig. 13
figure 13

Presents the stability zones in the plane \(A\,\Omega^2\) at: (a)\(a_5 ( = 1.2,0.5,1.5)\), (b)\(b_1 ( = 1,1.5,2)\)

Full size image
Fig. 14
figure 14

Presents the stability zones in the plane \(A\,\Omega^2\) at: \(b_2 ( = 0.2,0.5,0.8)\)

Full size image

Special case (1)

Let’s examine the given equation of motion that describes the movement of a particle sliding down a parabola while the parabola \(z = \mu x^2\) itself is rotating around its axis with angular velocity \(\gamma\) [33], see Fig. 15.

Fig. 15
figure 15

Depicts the motion of a sliding particle on a parabola

Full size image

The equation that governs the motion of the first special case can be expressed as follows:

$$\ddot{x}(1 + 4q^2 x^2 ) + \lambda^2 x + 4q^2 x\dot{x}^2 = 0,$$
(12)

where \(q\) and \(\lambda\) are two arbitrary physical parameters that depend on the parameters \(m,\gamma\), and \(\mu\) given in the Fig. 15.

It should be mentioned that the previous problem was analyzed using the modified HPM together with the Laplace transforms [34]. The multiple time scales method was also adopted to inspect the stability profile.

The initial solution is given by: \(v = B\cos \Theta t\), with the ICs \(v(0) = B\) and \(\dot{v}(0) = 0\).

The equivalent equation is given by

$$\ddot{v} + \Theta^2 v = 0.$$
(13)

As previously shown in the general case, one finds the equivalent frequency as

$$\Theta^2 = \frac{\lambda^2 }{{1 + 2B^2 q^2 }}.$$
(14)

Equation (14) is identical to what was previously demonstrated [31], and it should be highlighted. The formula (14) reads that the system is always stable.

The NS and NPA are depicted in Fig. 16 and correspond to a sample chosen as \(\lambda = 0.3,\,q = 0.2,\) and \(B = 0.5.\) Additionally, it proves advantageous to establish a comparison between the NS of the Eq. (12) and the NPA, which is associated with the linear ODE as displayed in Eq. (13), by using the MS, see Fig. 16. The absolute error between them is 0.00215.

Fig. 16
figure 16

Displays the evaluation concerning the NS and NPA for case (1)

Full size image

The curves in Fig. 17 are determined based on different parameter values \(q( = 0.2,0.6,0.8)\) and \(\lambda ( = 0.3,0.5,0.8)\) at \(B = 0.5\). Parts (17a) and (17b) are drawn when \(\lambda = 0.3\), while portions (18a) and (18b) are drawn when \(q = 0.2\). Based on the NPA of the ODE (12), one can predict that the waves for the solution of this equation will be periodic. This prediction has been verified through the graphical representation of this equation, as seen in Figs. 17a, 18a. It is noted that the oscillation’s number rises in proportion to the increase in \(q\) and \(\lambda\) values, i.e., the wavelengths of these waves increase. According to the periodicity of the plotted waves, one can conclude that their behaviour is stable, which is verified by the graphed closed curves in the plane \(v\dot{v}\), as explored in Figs. 17b, 18b.

Fig. 17
figure 17

Illustrates the solution \(v(t)\) and their phase plane diagram at: (a, b) \(q( = 0.2,0.6,0.8)\)

Full size image
Fig. 18
figure 18

Illustrates the solutions \(v(t)\) and their corresponding phase plane diagrams at: (c, d) \(\lambda ( = 0.3,0.5,0.8)\)

Full size image

Case 2: Tapered beam

Because they uniquely combine efficiency, economy, and aesthetics, the three pillars of structural art, tapered elements are being employed more frequently in the building sector. For engineering constructions with varying stiffness throughout their length, such as tree branches, turbine blades, bridges, etc., a tapered beam is a useful model. The following nonlinear differential equation [36,37,38] can be used to represent a tapered beam’s fundamental vibration mode:

The governing equation of motion for the present case, can be obtained From Eq. (9) at \(a_1 = b_1 = \varepsilon ,a_2 = b_2 = a_5 = 0,\Gamma = 1,\) and \(a_2 = \beta\) in the form:

$$\ddot{x}(1 + \varepsilon x^2 ) + x + \varepsilon x\dot{x}^2 + \beta x^3 = 0.$$
(15)

The initial solution is given by \(y = C\cos \Psi t\), with the ICs \(y(0) = C\) and \(\dot{y}(0) = 0\).

The equivalent equation is given by

$$\ddot{y} + \Psi^2 y = 0,$$
(16)

where

$$\Psi^2 = \frac{4 + 3\beta C^2 }{{4 + 2C^2 \varepsilon }}.$$
(17)

It ought to be noted that Eq. (17) is the same as what was previously shown [33]. The formula (16) reads that the system is always stable.

The NS and NPA are shown in Fig. 19 and counterpart for a sample chosen as \(\beta = 0.3,\,\varepsilon = 0.2,\) and \(C = 0.5\).

Fig. 19
figure 19

Shows the assessment regarding the NS and NPA for case 2

Full size image

The high accuracy of the NPA is found, where the outcomes are consistent with the NS of Eq. (15), as explored in Fig. 19. It is observed that there is high consistency between the graphed solutions of NPA and the NS. The absolute error, according to MS, is 0.0020.

The temporal variations of the NPA of the linear ODE (16) at different values of the parameters \(\varepsilon ( = 0.2,0.5,0.9)\) and \(\lambda ( = 0.3,0.6,0.8)\) when \(C = 0.5\) have been drawn in Figs. 20a, 21a, respectively. A large number of periodic oscillations have been observed in these figures according to the considered parameters, which are calculated in view of Eq. (16). This number decreases to some extent with the increase of \(\varepsilon\) and \(\lambda\). Based on this periodicity, closed curves in the plane \(y\dot{y}\) are graphed, which assert that the amplitude of any wave will be stationary through the investigated time interval; see Figs 20b, 21b.

Fig. 20
figure 20

Describes the solutions \(y(t)\) and their phase plane diagrams at: (a, b) \(\varepsilon ( = 0.2,0.5,0.9)\)

Full size image
Fig. 21
figure 21

Describes the solutions \(y(t)\) and their phase plane diagrams at: (a, b) \(\beta ( = 0.3,0.6,0.8)\)

Full size image

Case 3: Mathews and Lakshmanan Oscillator

Mathews and Lakshmanan [39] demonstrated a non-linear nature, adhering to a motion equation such as:

$$(1 + kx^2 )\,\ddot{x} + \alpha x - kx\dot{x}^2 = 0.$$
(18)

The initial solution is given by \(z = R\cos \Delta t\), with the ICs: \(z(0) = R\) and \(\dot{z}(0) = 0\).

The equivalent equation is given by

$$\ddot{z} + \Delta^2 z = 0,$$
(19)

where

$$\Delta^2 = \frac{\alpha }{1 + kR^2 }.$$
(20)

It ought to be noted that Eq. (20) is the same as what has been shown before [31].

The consistency between the NS of Eq. (18) and the NPA of Eq. (19) at \(k = 2,A = 0.5,\) and \(\alpha = 1\) is shown in Fig. 22. It is noted that the drawn waves have periodic behaviour with the same amplitude. Therefore, these solutions are free of chaos.

Fig. 22
figure 22

Presents the great consistency between the NS and NPA for case 3

Full size image

Curves in Figs. 23, 24 show the variation in the values of the parameters \(\alpha ( = 1,2,3)\) and \(k( = 1,2,3)\) on the behavior of the NPA. Figure 23a, 23b are diagrammed when \(A = 0.5,\) and \(k = 2\), while Fig. 24a, 24b are plotted at \(A = 0.5,\) and \(\alpha = 1\). Periodic waves are noticed in these parts. The wavelengths of the presented waves decrease and increase with the increase of \(\alpha\) and \(k\) values, respectively, as seen in Fig. 23a, b. The plots of the phase plane for the presented solutions in Fig. 24a, b are graphed in closed symmetric curves, as seen in Figs. 23b, 24b to provide an explanation of the consistent pattern of the acquired NPA.

Fig. 23
figure 23

Explores the solutions \(z(t)\) and their phase plane diagram at: (a, b) \(\alpha ( = 1,2,3)\)

Full size image
Fig. (24
figure 24

Explores the solutions \(z(t)\) and their phase plane diagram at: (a, b) \(k( = 1,2,3)\)

Full size image

Conclusions

A generalized equation is developed for an assemblage of traditional oscillators exhibiting substantial nonlinearity that is not quite solvable. Due to the growing interest in the topic of nonlinear oscillators, the main objective of the current inquiry is to use the generalized HFF to analyze the analytical interpretations for particular types of extremely nonlinear oscillators. A general example is provided, drawing on several technical and scientific disciplines as well as three specific instances. The novel approach is noticeably straightforward and demands less computational effort and time compared to previous perturbation procedures employed in this particular domain. The NPA, or inventive method, is the name given to this ground-breaking strategy, which essentially turns the nonlinear ODE into a linear one. The process results in a new frequency that is similar to linear ODE, much like in a straightforward harmonic situation. The results from this uncomplicated methodology not only show great agreement with the numerical findings but also show to be more accurate than the results from other well-known approximate methodologies when analyzed for physiologically significant specialized examples. A simplified description of the NPA is provided for the readers’ advantage. A numerical evaluation using MS is used to verify the theoretical conclusions. The NS and theoretical replies both displayed excellent consistency. It is common knowledge that all traditional perturbation methods use the Taylor expansion to increase the restoring forces when they are present, which lowers the difficulty of the current problem. The susceptibility is eradicated when the NPA is present. Additionally, the use of NPA allows for a more comprehensive examination of the stability analysis of the matter, which was previously unattainable through conventional methods. Consequently, when evaluating the NS approximation for highly nonlinear oscillators, the NPA is a more reliable source. Although it may be readily modified to solve different nonlinear issues, the NPA serves as a valuable tool across the domains of mechanical engineering and applied sciences.

As a progress work, the NPA can be extended to include a system of coupled equations. This direction very important in the area of the dynamical system as well as in the hydrodynamics stability to involve the problem of coupled interfaces.