A Two-Temperature Nonlocal Poro-Thermoelastic Solid Via Higher-Order Time-Derivatives Model with Phase Lag

Abstract

Purpose

The present study has depicted the effect of gravitational on a two-temperature nonlocal poro-thermoelastic solid.

Methods

The multi-phase-lag model and fractional derivatives are used to tackle the issue. Through normal mode analysis, analytical formulas for the variable fields are derived. Using appropriate boundary conditions, the physical fields are calculated and the numerical computations have been carried out with the help of MATLAB programming.

Results

Through a careful comparison of the numerical data, the impacts of gravity, fractional derivative order, and locatiy on the behavior of physical fields are described.

Conclusion

Physical variables are affected by nonlocal thermoelasticity, fractional derivative order as well as the gravity field.

Introduction

To explore an integral equation that exists in the tautochrone problem’s description, Abel et al. [1] used fractional calculus. The relationship between non-integer order derivatives (FD) and the linear theory of viscoelasticity was introduced by Caputo and Mainardi [2, 3]. The concepts of FD and integral to a fractional order were introduced by Miller and Ross [4] and Podlubny [5] to a variety of methodologies and alternate definitions of fractional derivatives. Povstenko solved the non-integer order heat conduction equation and the associated thermal stress problem [6]. Youssef [7] used a one-dimensional problem that he solved to discuss how the FD affected all physical areas. The thermoelastic materials with voids and heat equation with FD were studied by Bachher et al. [8], and Hobiny et al. [9].

Due to many applications in the fields of geophysics, plasma physics, and related topics, increasing attention is being devoted to the interaction between fluids such as water and thermo elastic solids, which is the domain of the theory of poro-thermoelasticity. The field of poro-thermoelasticity has a wide range of applications, especially in studying the effect of using waste materials on the disintegration of asphalt concrete mixture (ACM). Nunziato and Cowin [10] introduced a concept for porous materials in which the skeleton or matrix components are elastic and the interstices are empty of substance. Cowin and Puri [11] were the first to present the conventional pressure vessel difficulties for linear elastic materials with vacancies. Marin [12] investigated the thermoelasticity of substances having voids within their effect zone. Numerous investigations on porous thermoelastic materials can be found in the references [13,14,15,16,17] in the literature.

The classical theory of elastic deformation often ignores the gravity effect. The first person to look into how the gravitational field affects wave propagation in solids was Bromwich [18]. Vinh and Seriani [19] investigated Rayleigh waves in an orthotropic elastic medium under the gravitational field. Abd-Alla et al. [20] depicted how rotation, initial stress, and gravity field affected Rayleigh wave propagation in a homogeneous orthotropic material. The issue of a thermoelastic medium with temperature-dependent properties for three models under the influence of gravity was formulated by Othman et al. [21]. Plane waves of a two-temperature fiber-reinforced thermoelastic material were discussed by Said and Othman [22]. In Refs. [23,24,25,26,27,28,29,30,31,32,33,34], you can find more significant papers on the subject.

An innovative multi-phase-lag model for a nonlocal porous thermoelastic medium with two temperatures is described in the current study using an FD-based model. To solve the resulting non-dimensional equations, normal mode analysis is needed to convert the non-dimensional partial differential equations into eighth-ordinary differential equations. The variables in question are contrasted both with and without a gravitational field and a nonlocal parameter. A comparison of the variables under investigation with and without FD is also conducted.

The Description of the Problem and the Fundamental Relations

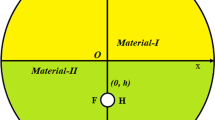
A two-temperature nonlocal poro-thermoelastic medium that is gravitationally influenced and occupies the half-space $(x \ge 0)\,.$ Thus displacement vector is $\vec{u} = (u,0,w),\,\,\,v = 0.$ The surface of a half-space is subjected to a thermal shock which is a function of z and t. Thus, all quantities considered will be functions of the time variable t and the coordinates x and z $\left( {\frac{\partial }{\partial y} = 0} \right)$ (Fig. 1).

Fig. 1

Nonlocal poro-thermoelastic medium under the effect of gravity

The stress–strain relationship, according to Hetnarski and Eslami [35] and Eringen [36], is as follows:

$$\left( {1 - \varepsilon^{2} \,\nabla^{2} } \right)\,\,\,\sigma_{ij} = \lambda \,e_{kk} \delta_{ij} + 2 \mu \,e_{ij} - \gamma \,\theta \,\delta_{ij\,} + b\psi \,\delta_{ij\,} ,$$

(1)

The equations of motion as Othman et al. [21].

$$\rho \,\ddot{u}_{i} = \sigma_{ji,\,j} + F_{i} ,$$

(2)

where $F_{1} = \rho \,g\,\frac{\partial \,w}{{\partial \,x}},\,\,\,\,\,\,F_{2} = 0,\,\,\,\,\,F_{3} = - \rho \,g\,\frac{\partial \,u}{{\partial \,x}}\,.$

$$\beta \,\psi_{,\;ii} - be - \alpha_{1} \,\psi - \alpha_{2} \,\psi_{,\;t} + \alpha_{3\,} \theta = \rho \alpha_{4\,} (1 - \varepsilon^{2} \nabla^{2} )\psi_{,\;tt} ,$$

(3)

The heat conduction equation as Zenkour [37]

$$I^{s - 1} K\left( {1 + \sum\limits_{r = 1}^{N} {\frac{{\tau_{\theta }^{r} }}{r!}} \frac{{\partial^{r} }}{{\partial t^{r} }}} \right)\nabla^{2} \Phi = \left( {\delta + \tau_{0} \frac{\partial }{\partial t} + \sum\limits_{r = 1}^{N} {\frac{{\tau_{q}^{r + 1} }}{(r + 1)!}} \frac{{\partial^{r + 1} }}{{\partial t^{r + 1} }}} \right)\left( {\rho C_{E} \theta_{,t} + \gamma T_{0} e_{,t} + \alpha_{3} T_{0} \psi_{,t} } \right),$$

(4)

$$\Phi - \theta = n\Phi_{,ii} ,\quad \Phi_{,ii} = \nabla^{2} \Phi .$$

(5)

According to Miller and Ross [4] and Podlubny [5]:

$$I^{s} f(t) = \frac{1}{\Gamma (s)}\int\limits_{0}^{t} {\frac{1}{{(t - \tau )^{1 - s} }}f(\tau )d} \tau ,\quad 0 < s < 1$$

(6)

where $\Gamma (s)$ is the Gamma function and $f(t)$ is a Lebesgue integrable continuous function.

Introducing Eqs. (1) in Eqs. (2), we get

$$\rho \left( {1 - \varepsilon^{2} \nabla^{2} } \right)\frac{{\partial^{2} u}}{{\partial t^{2} }} = (\lambda + 2\mu )\frac{{\partial^{2} u\,}}{{\partial x^{2} }} + (\lambda + \mu )\frac{{\partial^{2} w}}{\partial x\partial z} + \mu \frac{{\partial^{2} u}}{{\partial z^{2} }} - \gamma \frac{\partial \theta }{{\partial x}} + b\frac{\partial \psi }{{\partial x}} + \rho g\left( {1 - \varepsilon^{2} \nabla^{2} } \right)\frac{\partial w}{{\partial x}},$$

(7)

$$\rho \left( {1 - \varepsilon^{2} \nabla^{2} } \right)\frac{{\partial^{2} w}}{{\partial t^{2} }} = (\lambda + 2\mu )\frac{{\partial^{2} w}}{{\partial z^{2} }} + (\lambda + \mu )\frac{{\partial^{2} u}}{\partial x\partial z} + \mu \frac{{\partial^{2} w}}{{\partial x^{2} }} - \gamma \frac{\partial \theta }{{\partial z}} + b\frac{\partial \psi }{{\partial z}} - \rho g\left( {1 - \varepsilon^{2} \nabla^{2} } \right)\frac{\partial u}{{\partial x}},$$

(8)

The following non-dimensional variables are considered:

$$\begin{gathered} (x^{\prime},z^{\prime},\varepsilon^{\prime},u^{\prime},w^{\prime}) = \frac{1}{{l_{0} }}(x,z,\varepsilon ,u,w),\quad \left( {t^{\prime},\tau_{q}^{\prime } ,\tau_{0}^{\prime } ,\tau_{\theta }^{\prime } } \right) = \frac{{c_{0} }}{{l_{0} }}(t,\tau_{q} ,\tau_{0} ,\tau_{\theta } ),\quad \theta^{\prime} = \frac{\gamma \theta }{{\lambda + 2\mu }},\quad \Phi^{\prime } = \frac{\gamma \Phi }{{\lambda + 2\mu }}, \hfill \\ \sigma^{\prime}_{ij} = \frac{{\sigma_{ij} }}{\mu },\quad g^{\prime} = \frac{{l_{0} }}{{c_{0}^{2} }}g,\quad \psi^{\prime} = \psi ,\quad l_{0} = \sqrt {\frac{{K^{*} }}{{\rho C_{E} T_{0} }}} ,\quad c_{0} = \sqrt {\frac{\lambda + 2\mu }{\rho }} \hfill \\ \end{gathered}$$

(9)

Using Eqs. (9) in Eqs. (3–5) and (7), (8), we get

$$\,\,(1 - \varepsilon^{2} \nabla^{2} )\,\,\frac{{\partial^{{2}} u\,}}{{\partial \,t^{{2}} }} = \,\,\frac{{\partial^{{2}} u\,}}{{\partial \,x^{{2}} }} + A_{1} \frac{{\partial^{{2}} w\,}}{\partial \,x\,\,\partial \,z\,} + A_{2} \frac{{\partial^{{2}} u\,}}{{\partial \,z^{{2}} }} - \frac{\partial \,\theta \,}{{\partial \,x}} + A_{3} \frac{\partial \,\psi \,}{{\partial \,x}} + g\,\,(1 - \varepsilon^{2} \nabla^{2} )\,\,\frac{\partial \,w\,}{{\partial \,x}},$$

(10)

$$(1 - \varepsilon^{2} \nabla^{2} )\,\frac{{\partial^{{2}} w\,}}{{\partial \,t^{{2}} }} = \,\,\frac{{\partial^{{2}} w\,}}{{\partial \,z^{{2}} }} + A_{1} \frac{{\partial^{{2}} u\,}}{\partial \,x\,\,\partial \,z\,} + A_{2} \frac{{\partial^{{2}} w\,}}{{\partial \,x^{{2}} }} - \frac{\partial \,\theta \,}{{\partial \,z}} + A_{3} \frac{\partial \,\psi \,}{{\partial \,z}} - g\,\,(1 - \varepsilon^{2} \nabla^{2} )\,\,\frac{\partial \,u\,}{{\partial \,x}},$$

(11)

$$I^{s - 1} \left( {1 + \sum\limits_{r = 1}^{N} {\frac{{\tau_{\theta }^{r} }}{r!}} \frac{{\partial^{r} }}{{\partial t^{r} }}} \right)\nabla^{2} \Phi = \left( {\delta + \tau_{0} \frac{\partial }{\partial t} + \sum\limits_{r = 1}^{N} {\frac{{\tau_{q}^{r + 1} }}{(r + 1)!}} \frac{{\partial^{r + 1} }}{{\partial t^{r + 1} }}} \right)(A_{4} \theta_{,t} + A_{5} e_{,t} + A_{6} \psi_{,t} ),$$

(12)

$$\psi_{,ii} - A_{7} \,e - \,A_{8} \,\psi - A_{9} \,\psi_{,t} + A_{10} \,\theta = A_{11} \,(1 - \varepsilon^{2} \nabla^{2} )\psi_{,tt} ,$$

(13)

$$\Phi - \theta = A_{12} \,\Phi_{,ii} ,$$

(14)

where $e = \,\frac{\partial \,u}{{\partial \,x}} + \,\frac{\partial \,w}{{\partial \,z}},$ $A_{i}$ are given in the appendix.

The Solution of the Problem

The following form is how we define the normal mode analysis for the physical variable as Said et al. [38]:

$$[\,u,\,w,\,\theta ,\Phi , \psi ,\,\,\sigma_{ij} \,](x,\,z,\,t) = [ u^{*} ,w^{*} ,\,\theta^{*} , \Phi^{*} ,\,\,\psi^{*} ,\,\sigma_{ij}^{*} ](z)\,\exp (m\,t + {\text{i}}\,ax),$$

(15)

where $m$ is a complex constant, ${\text{i}} = \sqrt { - 1} ,$$a$ is the wave number in the $x -$ direction, and $u^{*} (z),w^{*} (z),\,\theta^{*} (z),$ $\Phi^{*} (z),\psi^{*} (z),\,\,\,\sigma_{ij}^{*} (z)$ are the amplitudes of the field quantities.

Adding Eq. (15) to Eqs. (10–14), we obtain

$$[N_{1} {\text{D}}^{2} - N_{2} ]\,u^{*} - \,[N_{3} \,{\text{D}}^{2} - N_{4} {\text{D}} + N_{5} ]\,w^{*} - {\text{i}}a\,[N_{8} - A_{12} {\text{D}}^{2} ]\,\Phi^{*} + {\text{i}}aA_{3} \psi^{*} = \,0,$$

(16)

$$\,[N_{3} \,{\text{D}}^{2} + N_{4} {\text{D}} + N_{5} ]\,u^{*} + [N_{6} {\text{D}}^{2} - N_{7} ]w^{*} - {\text{D}}\,[N_{8} - A_{12} {\text{D}}^{2} ]\,\Phi^{*} + A_{3} {\text{D}}\,\psi^{*} = \,0,$$

(17)

$$\,{\text{i}}a\;N_{11} \;u^{*} + \,\,N_{11} \,{\text{D}}\;\,w^{*} + ( - N_{14} {\text{D}}^{2} + N_{15} \,{)}\Phi^{*} { + }N_{16} \,\psi^{*} = 0,$$

(18)

$$iaA_{7} u^{*} + A_{7} Dw^{*} - A_{10} (N_{8} - A_{12} D^{2} )\Phi^{*} - \left( {N_{12} D^{2} - N_{13} } \right)\psi^{*} = 0.$$

(19)

where $N_{i}$ are given in the appendix and $D = \frac{d}{dz}.$

Solving Eqs. (16–19), we get:

$$\left( {D^{8} - B\;D^{6} + C\;D^{4} - ED^{2} + F} \right)\{ \,u^{*} (z),\;w^{*} (z),\;\Phi^{*} (z),\;\,\psi^{*} (z)\,\} = 0,$$

(20)

where $B,C,E,F$ are given in the appendix.

Equation (20) can be expressed as

$$\left( {D^{2} - k_{1}^{2} } \right)\left( {D^{2} - k_{2}^{2} } \right)\left( {D^{2} - k_{3}^{2} } \right)\left( {D^{2} - k_{4}^{2} } \right)u^{*} (z) = 0,$$

(21)

where $k_{j}^{2} \,(\,j = 1,\,2,\,3,\,4\,)$ are the roots of the following equation: $k^{{8}} - B\,k^{{6}} + C\,k\,^{{4}} - E\,k^{{2}} + F = {0}$.

The bounded solution of Eq. (21), can be written as:

$$u^{*} (z) = \sum\limits_{j = 1}^{4} {G_{j} } \,\exp ( - k_{j} z),$$

(22)

$$w^{*} (z) = \sum\limits_{j = 1}^{4} {R_{1j} \,G_{j} } \,\exp ( - k_{j} z),$$

(23)

$$\Phi^{*} (z) = \sum\limits_{j = 1}^{4} {R_{2j} \,G_{j} } \,\exp ( - k_{j} z),$$

(24)

$$\theta^{*} (z) = \sum\limits_{j = 1}^{4} {R_{3j} \,G_{j} } \,\exp ( - k_{j} z),$$

(25)

$$\psi^{*} (z) = \sum\limits_{j = 1}^{4} {R_{4j} \,G_{j} } \,\exp ( - k_{j} z),$$

(26)

Using the above equations, we get

$$\sigma_{zz}^{*} (z) = \sum\limits_{j = 1}^{4} {R_{5j} \,G_{j} } \,\exp ( - k_{j} z),$$

(27)

$$\sigma_{xz}^{*} (z) = \sum\limits_{j = 1}^{4} {R_{6j} G_{j} } \,\exp ( - k_{j} z),$$

(28)

where $k_{j} \,(\,j = 1,\,2,\,3,\,4\,)$ is positive, $R_{ij}$ are given in the appendix.

Boundary Conditions

In the physical problem, we should suppress the positive exponentials that are unbounded at infinity. To get the constants $G_{j} ,(j = 1,2,3,4).$ we take the following boundary conditions:

(a) The mechanical boundary condition that traction is free

$$\sigma_{xz} = 0.$$

(29)

(b) The mechanical boundary condition that the surface of the half-space is subjected to mechanical force.

$$\sigma_{zz} = - f\,{(}x{,}t{)} = - f_{0} \,e^{{m\,t + {\text{i}}\,a\,x}}$$

(30)

(c) The thermal boundary condition on the surface of the half-space is

$$\theta = 0.$$

(31)

(d) At the free surface, we can take the change in the volume fraction field of voids as

$$\frac{\partial \psi }{{\partial z}} = 0\,.$$

(32)

where $f_{0}$ is a constant and $f\,{(}x{,}t{)}$ is an arbitrary function.

From Eqs. (25–28) in Eqs. (29–32), we can obtain

$$\sum\limits_{j = 1}^{4} {R_{3j} G_{j} = 0} ,\quad \sum\limits_{j = 1}^{4} {R_{5j} G_{j} = - f_{0} } ,\quad \sum\limits_{j = 1}^{4} {R_{\;6j} G_{j} = 0} \,,\quad \sum\limits_{j = 1}^{4} {k_{j} R_{\;4j} G_{j} = 0} \,,$$

(33)

We get at a system of four equations after solving the previous system of Eqs. (30). We can get the following results by using the inverse matrix method:

$$\left( {\begin{array}{*{20}c} {G_{1} } \\ {G_{2} } \\ {G_{3} } \\ {G_{4} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {k_{1} R_{41} } & {k_{2} R_{42} } & {k_{3} R_{43} } & {k_{4} R_{44} } \\ {R_{31} } & {R_{32} } & {R_{33} } & {R_{34} } \\ {R_{51} } & {R_{52} } & {R_{53} } & {R_{54} } \\ {R_{61} } & {R_{62} } & {R_{63} } & {R_{64} } \\ \end{array} } \right)^{ - 1} \left( {\begin{array}{*{20}c} 0 \\ 0 \\ { - f_{0} } \\ 0 \\ \end{array} } \right).$$

(34)

Numerical Results

To investigate the influence of gravity, nonlocal parameter, and fractional derivatives order (FDO) on a porous thermoelastic media, as well as to clarify theoretical results and contrast them with the refined-phase-lag (RPL), dual-phase-lag (DPL), and Lord–Shulman (L–S) theory: We offer some numerical results for the following physical constants in this section as Said et al. [38]:

$$\lambda = 7.78\, \times 10^{9} \,{\text{N}}\,{.}\,{\text{m}}^{{ - {2}}} ,\,\,\mu = 3.78\, \times 10^{10} \,{\text{N}}\,{.}\,{\text{m}}^{{ - {2}}} ,\,\,\,\rho = 8954\,\,{\text{kg}}\,{.}\,{\text{m}}^{{ - {3}}} ,\,\,\,C_{E} = 383\,\,{\text{J}}\,{\text{.kg}}^{{ - {1}}} {.}\,{\text{K}}^{{ - {1}}} \,,\,\,\,\,\alpha_{t} = 1.78\,\, \times \,10^{ - 3} \,{\text{K}}^{{ - {1}}} {,}\,\,f_{0} = 7 \times 10^{ - 4} ,\,\tau_{q} = 9\, \times 10^{ - 2} \,{\text{s}},$$

$$\tau_{0} = 9\, \times 10^{ - 2} \,{\text{s}},\,\quad \tau_{\theta } = 7\, \times 10^{ - 2} \,{\text{s}},\,\,\,\,\,\,\,K^{*} = 386\,{\text{w}}\,{.}\,{\text{m}}^{{ - {1}}} {.}\,{\text{K}}^{{ - {1}}} {\text{.s}}^{{ - {1}}} {,}\,\,\,\,\,\,\,\,b = 1.6 \times 10^{7} \,{\text{N}}\,{.}\,{\text{m}}^{{ - {2}}} ,\,\,\,\,\,\,\alpha_{1} = 1.47\, \times 10^{10} {\text{N}}\,{.}\,{\text{m}}^{{ - {2}}} ,\,\alpha_{2} = 1.78\, \times 10^{ - 12} {\text{N}}\,{.}\,{\text{m}}^{{ - {2}}} ,\,\,\,\,m = m_{0} + i\xi ,$$

$$m_{0} = 2.0,\,\,\,\,\xi = 0.0,\,\,K = 700\,{\text{w}}\,{.}\,{\text{m}}^{{ - {1}}} {.}\,{\text{K}}^{{ - {1}}} ,\,\,a = 0.35,\;\delta = 1,\;s = 0.5,\;n = 0.9,\;\;\;T_{0} = 293\,{\text{K}},\,\,\,\,\,\alpha_{3} = 2\, \times 10^{5} {\text{N}}\,{.}\,{\text{m}}^{{ - {2}}} ,\,\,\,\,\,\,\alpha_{4} = 1.753\, \times 10^{ - 15} {\text{N}}\,{.}\,{\text{m}}^{{ - {2}}} ,$$

$\beta = 2 \times 10^{11} N.m^{ - 2} ,\quad x = 1.5$.

Figures 2, 3, 4, 5, 6 show comparisons between the displacement component $w,$ the thermodynamic temperature $\theta ,$ the conductive temperature $\Phi ,$ the change in the volume fraction field $\psi ,$ and the stress component $\sigma_{zz}$ in the absence ($\varepsilon = 0$) and presence ($\varepsilon = 0.9$) of nonlocal parameter. Figure 2 represents that the variation of vertical displacement $w$ starts from positive values. Values of $w$ decrease in the range $0 \le z \le 18$ for $\varepsilon = 0,0.9.$ The local parameter decreases values of $w.$ Figure 3 demonstrates that the distribution of the thermodynamic temperature $\theta$ start with a zero value and obeys the boundary condition at $z = 0$. In the context of the three theories, $\theta$ begins with decreasing to a minimum value and then increases for local and nonlocal theories. The nonlocal parameter increases the magnitude of $\theta$. Figure 4 shows the variations of the conductive temperature $\Phi$ and depicts that it begins from positive values except in the (RPL) and (L-S) theories for $\varepsilon = 0.9,$ its begin from a negative values. In the context of three theories without locality, $\Phi$ begins with decreasing in the range $0 \le z \le 13.5,$ and then becomes nearly constant. In the context of the (RPL) and (L-S) theories with locality, $\Phi$ begins with increasing in the range $0 \le z \le 13.5,$ and then becomes nearly constant. Figure 5 exhibits that the distribution of the volume fraction field $\psi$ begins from positive values in the context of the three theories. $\psi$ decreases in the range $0 \le z \le 18$ for $\varepsilon = 0,0.9.$ Figure 6 depicts that variations of the stress component $\sigma_{zz}$ begin with a negative value and satisfy the boundary conditions. The values of the stress component $\sigma_{zz}$ increase in the range $0 \le z \le 4,$ but decrease in the range $4 \le z \le 18,$ for $\varepsilon = 0,0.9.$ While the values of $\sigma_{zz}$ converge to zero with increasing distance $z$ at $z \ge 18,$ for $\varepsilon = 0,0.9.$

Fig. 2

Vertical displacement distribution $w$ for local and nonlocal theories

Fig. 3

Thermal temperature distribution $\theta$ for local and nonlocal theories

Fig. 4

Distribution of the conductive temperature $\Phi$ for local and nonlocal theories

Fig. 5

Volume fraction field distribution $\psi$ for local and nonlocal theories

Fig. 6

Distribution of stress component $\sigma_{zz}$ for local and nonlocal theories

Figures 7, 8, 9, 10 show the comparison between the displacement component $w,$ the thermodynamic temperature $\theta ,$ the change in the volume fraction field $\psi ,$ and the stress component $\sigma_{xz}$ in the absence ($g = 0$) and the presence ($g = 9.8$) of the gravity field. Figure 7 displays that the variations of vertical displacement $w$ begin from positive values. The values of $w$ decrease in the range $0 \le z \le 18$. Figure 8 shows that the variation of the thermodynamic temperature $\theta$ starts from a positive value and obeys boundary condition. In the context of the three theories and in the absence of the gravity field, $\theta$ begins with decreasing reach a minimum value in the range $0 \le z \le 2.7$, then increases in the range $2.7 \le z \le 18$. In the context of the three theories and in the presence of gravity, the values of $\theta$ begin with decreasing reach a minimum in the range $0 \le z \le 3.5,$ then increase in the range $3.5 \le z \le 18$. Figure 9 exhibits that the distribution of the volume fraction field $\psi$ begins from positive values. In the absence and presence of the gravity field, values of $\psi$ decrease reach a minimum value in the range $0 \le z \le 18$. Figure 10 depicts that the distribution of the stress component $\sigma_{xz}$ begins with a zero value and satisfies the boundary conditions. In the absence of the gravity field, values $\sigma_{xz}$ decrease in the range $0 \le z \le 1,$ but increase in the range $1 \le z \le 6.5\,.$ In the presence of the gravity field, values $\sigma_{xz} ,$ decrease in the range $0 \le z \le 1.2,$ but increase in the range $1.2 \le z \le 9\,.$

Fig. 7

Vertical displacement distribution $w$ in the absence and presence of the gravity

Fig. 8

Thermal temperature distribution $\theta$ in the absence and presence of the gravity

Fig. 9

The change in volume fraction field $\psi$ in the absence and presence of the gravity

Fig. 10

Distribution of stress component $\sigma_{xz}$ in the absence and presence of the gravity

Figures 11, 12, 13 show the comparison between the displacement component $u,$ the thermodynamic temperature $\theta ,$ and the stress component $\sigma_{zz}$ based on the (RPL) model and the (DPL) model in the absence ($s = 0$) and presence ($s = 0.9$) of the fractional derivative order. Figure 11 shows the variations of the displacement component $u,$ and depict that it begins from negative values. $u$ begins with increasing in the range $0 \le z \le 18,$ while the values of $u$ converge to zero with increasing distance $z$ at $z \ge 18,$ for $s = 0,0.9.$ Figure 12 shows that the distribution of the thermodynamic temperature $\theta ,$ obeys the boundary condition at $z = 0$. In the context of the two theories, $\theta$ begins with decreasing reach its a minimum value in the range $0 \le z \le 4$ for $s = 0,0.9.$ Values of $\theta$ increase in the range $4 \le z \le 18$ for $s = 0,0.9.$ Figure 13 shows that the distribution of the stress component $\sigma_{zz}$ begins with an increasing in the range $0 \le z \le 4,$ but a decreasing in the range $4 \le z \le 18$ for $s = 0,0.9.$ While the values of $\sigma_{zz}$ converge to zero with increasing distance $z$ at $18 \le z$ for $s = 0,0.9.$

Fig. 11

Distribution of displacement $u$ in the absence and presence of fractional derivative order

Fig. 12

Thermal temperature distribution $\theta$ in the absence and presence of fractional derivative order

Fig. 13

Distribution of stress component $\sigma_{zz}$ in the absence and presence of fractional derivative order

In the context of the RPL model, Figs. 14 and 15 provide 3D surface curves for the displacement component $w$ and the change in the volume fraction field $\psi$. These curves are used to examine the nonlocal poro-thermoelastic solid under the influence of the gravity field. These numbers are crucial for understanding how these physical values relate to the vertical component of distance.

Fig.14

Vertical displacement distribution $w$ in the context of the refined phase-lag model

Fig. 15

The change in volume fraction field $\psi$ in the context of the refined phase-lag (RPL) model

Conclusion

We demonstrated the impact of the gravity field and the FDO in a nonlocal poro-thermoelastic solid in the current problem using the (RPL) model, the (DPL) model, and the (L–S) theory. We can infer the following conclusions from the discussion above:

• (a) The locality has had a significant impact on the physical fields, which is evident from Figs. 2, 3, 4, 5, 6.

• (b) Gravity has had a significant impact on the physical fields, as illustrated in Figs. 7, 8, 9, 10.

• (c) The FDO has had a considerable impact on the physical fields, as indicated by Figs. 11, 12, 13.

• (d) All functions are continuous, and all physical value distributions have moved closer and closer to zero.

• (e) The issue has been mathematically resolved using normal mode analysis. That is applicable to a wide range of problems in hydrodynamics.

• (f) The result motivates us to investigate poro-thermoelastic materials as a new class of applicable materials.

Appendix

$A_{1} = \frac{\lambda + \mu }{{\rho \,c_{0}^{2} }},$ $A_{2} = \frac{\mu }{{\rho \,c_{0}^{2} }},$ $A_{3} = \frac{b}{{\rho \,c_{0}^{2} }},$ $A_{4} = \frac{{\rho \,c_{E} \,c_{0} \,l_{0} }}{k},$ $A_{5} = \frac{{\gamma^{2} \,T_{0} \,c_{0} \,l_{0} }}{(\lambda + 2\mu )k},$ $A_{6} = \frac{{\alpha_{3} \,A_{5} }}{\gamma },$ $A_{7} = \frac{{b\,l_{0}^{2} \,}}{\beta },$ $A_{8} = \frac{{\alpha_{1} \,l_{0}^{2} \,}}{\beta },$ $A_{9} = \frac{{\alpha_{2} \,c_{0} \,l_{0}^{2} \,}}{\beta },$ $A_{10} = \frac{{\alpha_{3} \,l_{0}^{2} \,}}{\beta }\,(\frac{\lambda + 2\mu }{\gamma }),$ $A_{11} = \frac{{\rho \,\alpha_{4} \,c_{0}^{2} \,}}{\beta },$ $A_{12} = \frac{n\,}{{l_{0}^{2} }},$ $N_{1} = A_{2} + \varepsilon^{2} m^{2} ,$ $N_{2} = m^{2} + a^{2} + \varepsilon^{2} m^{2} a^{2} ,$ $N_{3} = {\text{i}}\,a\,g\,\varepsilon^{2} ,$ $N_{4} = {\text{i}}\,a\,A_{1} ,$

$N_{5} = - {\text{i}}\,a\,g{(1 + }\varepsilon^{2} \,a^{2} \,{)},$ $N_{6} = 1 + m^{2} \,\varepsilon^{2} ,$ $N_{7} = m^{2} + a^{2} \,\varepsilon^{2} \,m^{2} + a^{2} \,A_{2} ,$ $N_{8} = (1 + A_{12} \,a^{2} ),$ $N_{9} = 1 + m^{*} \sum\limits_{r = 1}^{N} {\,\frac{{\tau_{\theta }^{r} }}{r!}\,\,m^{r} } ,$ $\,m^{*} = e^{ - mt} \,t^{ - s} \,\sum\limits_{j = 1}^{\infty } {\,\,\frac{{(mt)^{\,j} }}{\Gamma (j + 1 - s)}} \,,$ $N_{10} = \delta + \tau_{\theta } m + \sum\limits_{r = 1}^{N} {\,\frac{{\tau_{q}^{r + 1} }}{(r + 1)!}\,\,m^{r + 1} } ,$ $N_{11} = mA_{5} N_{10} ,$ $N_{12} = 1 + m^{2} A_{11} \varepsilon^{2} ,$ $N_{13} = a^{2} + mA_{9} + A_{8} + m^{2} A_{11} + m^{2} A_{11} \varepsilon^{2} a^{2} ,$ $N_{14} = mA_{4} A_{12} N_{10} + N_{9} ,$ $N_{15} = mA_{4} N_{8} N_{10} + N_{9} a^{2} ,$ $N_{16} = mA_{6} N_{10} ,$ $h_{1} = - N_{1} ,$ $h_{2} = {\text{i}}aN_{3} ,$ $h_{3} = N_{2} {\text{ + i}}aN_{4} ,$ $h_{4} = {\text{i}}aN_{5} ,$ $h_{5} = N_{3} ,$ $h_{6} = {\text{i}}aN_{6} - N_{4} ,$ $h_{7} = N_{5} ,$ $h_{8} = {\text{i}}aN_{7} ,$ $h_{9} = N_{1} N_{16} ,$ $h_{10} = N_{2} N_{16} - a^{2} A_{3} N_{11} ,$ $h_{11} = N_{3} N_{16} ,$ $h_{12} = {\text{i}}aA_{3} N_{11} - N_{4} N_{16} ,$ $h_{13} = N_{5} N_{16} ,$ $h_{14} = {\text{i}}a(A_{12} N_{16} + A_{3} N_{14} ),$ $h_{15} = {\text{i}}a(N_{8} N_{16} + A_{3} N_{15} ),$ $h_{16} = N_{3}^{2} N_{12} N_{15} + N_{3}^{2} N_{13} N_{14} + N_{4}^{2} N_{12} N_{14} - A_{3} A_{7} N_{1} N_{14} - A_{7} A_{12} N_{1} N_{16} ,$$h_{17} = A_{12} N_{1} N_{11} N_{13} + A_{12} N_{2} N_{11} N_{12} + N_{1} N_{8} N_{11} N_{12} + N_{1} N_{6} N_{12} N_{15} + N_{1} N_{6} N_{13} N_{14} ,$$h_{18} = N_{1} N_{7} N_{12} N_{14} + N_{2} N_{6} N_{12} N_{14} - 2N_{3} N_{5} N_{12} N_{14} + A_{10} A_{12} N_{3}^{2} N_{16} - A_{3} A_{10} A_{12} N_{1} N_{11} ,$$h_{19} = A_{10} A_{12} N_{1} N_{6} N_{16} + 2{\text{i}}aA_{12} N_{4} N_{11} N_{12} + a^{2} A_{12} N_{6} N_{11} N_{12} ,$$h_{20} = N_{3}^{2} N_{13} N_{15} + N_{4}^{2} N_{12} N_{15} + N_{4}^{2} N_{13} N_{14} + N_{5}^{2} N_{12} N_{14} - A_{3} A_{7} N_{1} N_{15} - A_{3} A_{7} N_{2} N_{14} ,$$h_{21} = N_{2} N_{8} N_{11} N_{12} - A_{7} A_{12} N_{2} N_{16} - A_{7} N_{1} N_{8} N_{16} + A_{12} N_{2} N_{11} N_{13} + N_{1} N_{8} N_{11} N_{13} ,$$h_{22} = N_{1} N_{6} N_{13} N_{15} + N_{1} N_{7} N_{12} N_{15} + N_{1} N_{7} N_{13} N_{14} + N_{2} N_{6} N_{12} N_{15} + N_{2} N_{6} N_{13} N_{14} ,$$h_{23} = N_{2} N_{7} N_{12} N_{14} - 2N_{3} N_{5} N_{12} N_{15} - 2N_{3} N_{5} N_{13} N_{14} + A_{10} A_{12} N_{4}^{2} N_{16} \, + A_{10} N_{3}^{2} N_{8} N_{16} ,$$h_{24} = A_{10} A_{12} N_{1} N_{7} N_{16} - A_{3} A_{10} N_{1} N_{8} N_{11} + A_{10} A_{12} N_{2} N_{6} N_{16} - 2A_{10} A_{12} N_{3} N_{5} N_{16} + A_{10} N_{1} N_{6} N_{8} N_{16} ,$$h_{25} = 2{\text{i}}aA_{12} N_{4} N_{11} N_{13} - 2{\text{i}}aA_{3} A_{7} N_{4} N_{14} - 2{\text{i}}aA_{7} A_{12} N_{4} N_{16} + 2{\text{i}}aN_{4} N_{8} N_{11} N_{12} - a^{2} A_{3} A_{7} N_{6} N_{14} ,$$h_{26} = a^{2} A_{12} N_{6} N_{11} N_{13} - a^{2} A_{7} A_{12} N_{6} N_{16} + a^{2} A_{12} N_{7} N_{11} N_{12} + a^{2} N_{6} N_{8} N_{11} N_{12} - a^{2} A_{3} A_{10} A_{12} N_{6} N_{11} ,$$h_{27} = - 2{\text{i}}aA_{3} A_{10} A_{12} N_{4} N_{11} - A_{3} A_{10} A_{12} N_{2} N_{11} ,$$h_{28} = N_{4}^{2} N_{13} N_{15} + N_{5}^{2} N_{12} N_{15} + N_{5}^{2} N_{13} N_{14} - A_{3} A_{7} N_{2} N_{15} - A_{7} N_{2} N_{8} N_{16} + N_{2} N_{8} N_{11} N_{13} ,$$h_{29} = N_{2} N_{6} N_{13} N_{15} + N_{2} N_{7} N_{12} N_{15} + N_{2} N_{7} N_{13} N_{14} - 2N_{3} N_{5} N_{13} N_{15} + A_{10} A_{12} N_{5}^{2} N_{16} ,$$h_{30} = A_{10} A_{12} N_{2} N_{7} N_{16} - A_{3} A_{10} N_{2} N_{8} N_{11} + A_{10} N_{1} N_{7} N_{8} N_{16} + A_{10} N_{2} N_{6} N_{8} N_{16} - 2A_{10} N_{3} N_{5} N_{8} N_{16} ,$$h_{31} = 2{\text{i}}aN_{4} N_{8} N_{11} N_{13} - 2{\text{i}}aA_{7} N_{4} N_{8} N_{16} - a^{2} A_{3} A_{7} N_{6} N_{15} - a^{2} A_{3} A_{7} N_{7} N_{14} - a^{2} A_{7} A_{12} N_{7} N_{16} ,$$h_{32} = a^{2} A_{12} N_{7} N_{11} N_{13} - a^{2} A_{7} N_{6} N_{8} N_{16} + a^{2} N_{6} N_{8} N_{11} N_{13} + a^{2} N_{7} N_{8} N_{11} N_{12} - a^{2} A_{3} A_{10} A_{12} N_{7} N_{11} ,$$h_{33} = - a^{2} A_{3} A_{10} N_{6} N_{8} N_{11} - 2iaA_{3} A_{10} N_{4} N_{8} N_{11} - 2{\text{i}}aA_{3} A_{7} N_{4} N_{15} + A_{10} N_{4}^{2} N_{8} N_{16} + N_{1} N_{7} N_{13} N_{15} ,$$h_{34} = N_{5}^{2} N_{13} N_{15} + N_{2} N_{7} N_{13} N_{15} + A_{10} N_{5}^{2} N_{8} N_{16} - a^{2} A_{3} A_{7} N_{7} N_{15} - a^{2} A_{7} N_{7} N_{8} N_{16} ,$$h_{35} = a^{2} N_{7} N_{8} N_{11} N_{13} + A_{10} N_{2} N_{7} N_{8} N_{16} - a^{2} A_{3} A_{10} N_{7} N_{8} N_{11} ,$ $B = \frac{{L_{1} }}{L},$ $C = \frac{{L_{2} }}{L},$ $E = \frac{{L_{3} }}{L},$ $F = \frac{{L_{4} }}{L},$

$L_{1} = h_{16} + h_{17} + h_{18} + h_{19} ,$ $L_{2} = h_{20} + h_{21} + h_{22} + h_{23} + h_{24} + h_{25} + h_{26} + h_{27} ,$ $L_{3} = h_{28} + h_{29} + h_{30} + h_{31} + h_{32} + h_{33} ,$ $L_{4} = h_{34} + h_{35} ,$ $L = N_{3}^{2} N_{12} N_{14} + A_{12} N_{1} N_{11} N_{12} + N_{1} N_{6} N_{12} N_{14} ,$

$R_{1j} = \frac{{h_{1} k_{j}^{3} - h_{2} k_{j}^{2} + h_{3} k_{j} - h_{4} }}{{\,h_{6} k_{j}^{2} - h_{5} k_{j}^{3} - h_{7} k_{j} - h_{8} }},$ $R_{2j} = \frac{{(h_{9} k_{j}^{2} \, - h_{10} ) + (h_{12} k_{j} - h_{11} k_{j}^{2} - h_{13} )R_{1j} \,}}{{h_{15} \, - h_{14} k_{j}^{2} }},$ $R_{3j} = (N_{8} - A_{12} k_{j}^{2} )R_{2j} ,$ $R_{4j} = \frac{{(N_{14} k_{j}^{2} - N_{15} )R_{2j} + N_{11} k_{j} R_{1j} \, - {\text{i}}aN_{11} }}{{N_{16} }},$ $R_{5j} = \frac{{{\text{i}}a\lambda - (\lambda + 2\mu )k_{j} R_{1j} - (\lambda + 2\mu )R_{3j} + bR_{4j} }}{{\mu (1 - \varepsilon^{2} k_{j}^{2} + \varepsilon^{2} a^{2} )}},$ $R_{6j} = \frac{{ - k_{j} + {\text{i}}aR_{1j} }}{{1 - \varepsilon^{2} k_{j}^{2} + \varepsilon^{2} a^{2} }}$.