Skip to main content
SpringerLink
Log in

Nonlinear Forced Vibration of a Concentrated Mass Loaded Axially Moving Plate Considering the Gravity Effect

  • Original Paper
  • Published:
Journal of Vibration Engineering & Technologies Aims and scope Submit manuscript

Abstract

Purpose

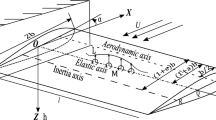
Considering the transportation structure in the factory is responsible for transporting materials, thus when analysing the axially moving characteristics of the conveyor belt in operation, the effect of the load must be considered.

Methods

Based on Von Karman’s nonlinear plate theory, the motion equations of the system are established using the assumed mode method and Hamilton’s principle. The effects of the concentrated mass positions on the dynamic characteristics of the system are analyzed. The stability properties of the system are analyzed by solving the generalized eigenvalue problem. The amplitude–frequency response curves of the transverse generalized displacements of the system are drawn and analyzed by numerical calculation.

Results

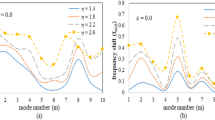
The effects of the concentrated mass position, the axially moving velocity, and the external excitation amplitude on the nonlinear amplitude–frequency responses of the system are studied. The results show that the concentrated mass position has significant effects on the natural frequency of the system. All the amplitude–frequency response curves of the system under the harmonic excitation show the hardening type nonlinearity. The concentrated mass and the axially moving velocity have a great influence on the first- and second-order resonances of the system. With the excitation amplitude, axially moving velocity, and concentrated mass changing, the system appears complex nonlinear response phenomena.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig.1
Fig.2
Fig.3
Fig. 4
Fig. 5
Fig.6
Fig.7
Fig. 8
Fig.9
Fig.10
Fig.11
Fig.12
Fig.13
Fig.14
Fig.15
Fig.16
Fig.17
Fig.18
Fig.19

Similar content being viewed by others

Data Availability

The data that support the findings of this study are available from the corresponding author on reasonable request.

References

  1. Ghayesh MH, Amabili M, Païdoussis MP (2012) Nonlinear vibrations and stability of an axially moving beam with an intermediate spring support: two-dimensional analysis. Nonlinear Dyn 70:335–354

    Article  MathSciNet  Google Scholar 

  2. Zhang YW, Yuan B, Fang B, Chen LQ (2017) Reducing thermal shock-induced vibration of an axially moving beam via a nonlinear energy sink. Nonlinear Dyn 87:1159–1167

    Article  Google Scholar 

  3. Yang TZ, Fang B (2012) Stability in parametric resonance of an axially moving beam constituted by fractional order material. Arch Appl Mech 82:1763–1770

    Article  Google Scholar 

  4. Wang YQ, Liang L, Guo XH (2013) Internal resonance of axially moving laminated circular cylindrical shells. J Sound Vib 332(24):6434–6450

    Article  ADS  Google Scholar 

  5. Wu Z, Zhang Y, Yao G (2023) Natural frequency and stability analysis of axially moving functionally graded carbon nanotube-reinforced composite thin plates. Acta Mech 234:1009–1031

    Article  MathSciNet  Google Scholar 

  6. Ding H, Chen LQ (2010) Galerkin methods for natural frequencies of high-speed axially moving beams. J Sound Vib 329(17):3484–3494

    Article  ADS  Google Scholar 

  7. Chu C, Al-Furjan MSH, Kolahchi R, Farrokhian A (2023) A nonlinear Chebyshev-based collocation technique to frequency analysis of thermally pre/post-buckled third-order circular sandwich plates. Commun Nonlinear Sci Numer Simul 118:107056

    Article  MathSciNet  Google Scholar 

  8. Wan PH, Al-Furjan MSH, Kolahchi R, Shan L (2023) Application of DQHFEM for free and forced vibration, energy absorption, and post-buckling analysis of a hybrid nanocomposite viscoelastic rhombic plate assuming CNTs’ waviness and agglomeration. Mech Syst Signal Process 189:110064

    Article  Google Scholar 

  9. Al-Furjan MSH, Shan L, Shen X, Kolahchi R, Rajak DK (2022) Combination of FEM-DQM for nonlinear mechanics of porous GPL-reinforced sandwich nanoplates based on various theories. Thin Wall Struct 178:109495

    Article  Google Scholar 

  10. Kolahchi R, Kolahdouzan F (2021) A numerical method for magneto-hygro-thermal dynamic stability analysis of defective quadrilateral graphene sheets using higher order nonlocal strain gradient theory with different movable boundary conditions. Appl Math Model 91:458–475

    Article  MathSciNet  Google Scholar 

  11. Kolahchi R, Safari M, Esmailpour M (2016) Dynamic stability analysis of temperature-dependent functionally graded CNT-reinforced visco-plates resting on orthotropic elastomeric medium. Compos Struct 150:255–265

    Article  Google Scholar 

  12. Hajmohammad MH, Nouri AH, Zarei MS, Kolahchi R (2019) A new numerical approach and visco-refined zigzag theory for blast analysis of auxetic honeycomb plates integrated by multiphase nanocomposite facesheets in hygrothermal environment. Engineering with Computers 35(4):1141–1157

    Article  Google Scholar 

  13. Wang YB, Fang XR, Ding H, Chen LQ (2023) Quasi-periodic vibration of an axially moving beam under conveying harmonic varying mass. Appl Math Model 123:644–658

    Article  MathSciNet  Google Scholar 

  14. Zhou YF, Wang ZM (2019) Dynamic instability of axially moving viscoelastic plate. Eur J Mech A Solids 73:1–10

    Article  MathSciNet  Google Scholar 

  15. Qiao Y, Yao G (2022) Stability and nonlinear vibration of an axially moving plate interacting with magnetic field and subsonic airflow in a narrow gap. Nonlinear Dyn 110:3187–3208

    Article  Google Scholar 

  16. Lu SF, Xue N, Zhang W, Song XJ, Ma WS (2021) Dynamic stability of axially moving graphene reinforced laminated composite plate under constant and varied velocities. Thin Walled Struct 167:108176

    Article  Google Scholar 

  17. Mao XY, Ding H, Chen LQ (2019) Internal resonance of a supercritically axially moving beam subjected to the pulsating speed. Nonlinear Dyn 95:631–651

    Article  Google Scholar 

  18. An C, Su J (2014) Dynamic analysis of axially moving orthotropic plates: Integral transform solution. Appl Math Comput 228:489–507

    MathSciNet  Google Scholar 

  19. Lin CC (1997) Stability and vibration characteristics of axially moving plates. Int J Solids Struct 34(24):3179–3190

    Article  Google Scholar 

  20. Zhang YW, She GL, Ding HX (2023) Nonlinear resonance of graphene platelets reinforced metal foams plates under axial motion with geometric imperfections. Eur J Mech A Solids 98:104887

    Article  MathSciNet  Google Scholar 

  21. Cao T, Hu YD (2023) Magnetoelastic primary resonance and bifurcation of an axially moving ferromagnetic plate under harmonic magnetic force. Commun Nonlinear Sci Numer Simul 117:106974

    Article  MathSciNet  Google Scholar 

  22. Yao G, Xie Z, Zhu L, Zhang Y (2021) Nonlinear vibrations of an axially moving plate in aero-thermal environment. Nonlinear Dyn 105:2921–2933

    Article  Google Scholar 

  23. Ding H, Lim CW, Chen LQ (2018) Nonlinear vibration of a traveling belt with non-homogeneous boundaries. J Sound Vib 424:78–93

    Article  ADS  Google Scholar 

  24. Zhang YW, She GL (2023) Nonlinear low-velocity impact response of graphene platelet-reinforced metal foam cylindrical shells under axial motion with geometrical imperfection. Nonlinear Dyn 111:6317–6334

    Article  Google Scholar 

  25. Ding HX, She GL (2023) Nonlinear resonance of axially moving graphene platelet-reinforced metal foam cylindrical shells with geometric imperfection. Archiv Civ Mech Eng 23:97

    Article  Google Scholar 

  26. Ding HX, She GL (2023) Nonlinear primary resonance behavior of graphene platelet-reinforced metal foams conical shells under axial motion. Nonlinear Dyn 111:13723–13752

    Article  Google Scholar 

  27. Amabili M, Carra S (2012) Experiments and simulations for large-amplitude vibrations of rectangular plates carrying concentrated masses. J Sound Vib 331(1):155–166

    Article  ADS  Google Scholar 

  28. Amabili M (2010) Geometrically nonlinear vibrations of rectangular plates carrying a concentrated mass. J Sound Vib 329(21):4501–4514

    Article  ADS  Google Scholar 

  29. Amabili M, Pellegrini M, Righi F, Vinci F (2006) Effect of concentrated masses with rotary inertia on vibrations of rectangular plates. J Sound Vib 295(1–2):1–12

    Article  ADS  Google Scholar 

  30. Zhong Z, Liu A, Pi YL, Deng J, Lu H, Li S (2019) Analytical and experimental studies on dynamic instability of simply supported rectangular plates with arbitrary concentrated masses. Eng Struct 196:109288

    Article  Google Scholar 

  31. Sebastian U, Łukasz K, Michał O (2021) The non-linear vibrations of simply supported column loaded by the mass element. Appl Math Model 89(Part 1): 700–709

  32. Eftekhari SA (2015) A note on mathematical treatment of the Dirac-delta function in the differential quadrature bending and forced vibration analysis of beams and rectangular plates subjected to concentrated loads. Appl Math Model 39(20):6223–6242

    Article  MathSciNet  Google Scholar 

  33. Pirmoradian M, Torkan E, Karimpour H (2018) Parametric resonance analysis of rectangular plates subjected to moving inertial loads via IHB method. Int J Mech Sci 142–143:191–215

    Article  Google Scholar 

  34. Du SJ, Xu A, Li FM, Hosseini SM (2022) Vibration characteristics of irregular plates with a lumped mass: Theory and experiment. Thin Walled Struct 179:109588

    Article  Google Scholar 

  35. Wang GX, Ding H, Chen LQ (2020) Dynamic effect of internal resonance caused by gravity on the nonlinear vibration of vertical cantilever beams. J Sound Vib 474:115265

    Article  Google Scholar 

  36. Culver D, Dowell E (2016) High frequency analysis of a plate carrying a concentrated nonlinear spring-mass system. J Sound Vib 379:84–105

    Article  ADS  Google Scholar 

  37. Amabili M (2008) Nonlinear vibrations and stability of shells and plates. Cambridge University Press, New York

    Book  Google Scholar 

  38. Nematollahi MS, Mohammadi H (2019) Geometrically nonlinear vibration analysis of sandwich nanoplates based on higher-order nonlocal strain gradient theory. Int J Mech Sci 156:31–45

    Article  Google Scholar 

  39. Reddy JN (1984) Energy principles and variational methods in applied mechanics, Wiley

  40. Hatami S, Ronagh HR, Azhari M (2008) Exact free vibration analysis of axially moving viscoelastic plates. Comput Struct 86(17–18):1738–1746

    Article  Google Scholar 

  41. Doedel EJ, Fairgrieve TF, Sandstede B, Champneys AR, Kuznetsov YA, Wang X (2024) AUTO-07P: continuation and bifurcation software for ordinary differential equations

  42. Ermentrout B (2019) The software for the numerical simulation and bifurcation analysis of dynamical systems. Spartan user interface XPP/XPPAUT homepage

  43. Dhooge A, Govaerts W, Kuznetsov YA, Meijer HGE, Sautois B (2008) New features of the software MatCont for bifurcation analysis of dynamical systems. Math Comput Model Dyn Syst 14(2):147–175

    Article  MathSciNet  Google Scholar 

  44. Yao G, Zhang YM (2016) Dynamics and stability of an axially moving plate interacting with surrounding airflow. Meccanica 51:2111–2119

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

This research is supported by the Natural Science Foundation of Liaoning (2020-MS-092).

Funding

The funding has been received from Natural Science Foundation of Liaoning Province with Grant no. 2020-MS-092.

Author information

Authors and Affiliations

  1. School of Mechanical Engineering and Automation, Northeastern University, Shenyang, 110819, China

    Mingjun Song & Guo Yao

Authors
  1. Mingjun Song
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Guo Yao
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Guo Yao.

Ethics declarations

Conflict of Interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Song, M., Yao, G. Nonlinear Forced Vibration of a Concentrated Mass Loaded Axially Moving Plate Considering the Gravity Effect. J. Vib. Eng. Technol. (2024). https://doi.org/10.1007/s42417-024-01299-y

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s42417-024-01299-y

Keywords

Search

Navigation