Skip to main content
SpringerLink
Log in

Vibroacoustic Analysis in the Thermal Environment of PCLD Sandwich Beams with Frequency and Temperature Dependent Viscoelastic Cores

  • Original Paper
  • Published:
Journal of Vibration Engineering & Technologies Aims and scope Submit manuscript

Abstract

Introduction

The impact of vibrations excited by incident sound fields has become a major concern today, due to its influence on the performance of systems and installations. Vibrations have the potential to cause considerable dynamic disturbances and instabilities, which can lead to significant structural and functional damage. Consequently, it is crucial to control vibration phenomena right from the system design phase. To solve the problem of vibration, it is sometimes possible to increase the damping level of the structure by incorporating a damping treatment.

Objective

The aim of this paper is to present a simplified numerical approach to study the vibro-acoustic responses of structures with PCLD “Passive Constrained Layer Damping” treatment in the thermal environment, taking into account the frequency and temperature dependence of the different viscoelastic behavior laws.

Material and Methods

The modal stability procedure MSP is based on the finite element method in order to discretize and formulate the equation of motion. The asymptotic numerical method “ANM” is applied to approximate the solution of complex eigenvalue problems and construct the modal basis. The variability of the frequency responses is evaluated by a Monte Carlo simulation (MCS) combined with MSP and ANM to evaluate the stochastic behavior of a sandwich beam with random properties.

Results

The comparison with the direct frequency responses (DFR) demonstrates that the results are highly satisfactory in terms of the validity of the present MSP approach. A comparative study of viscoelastic behavior models was carried out to evaluate their damping properties provided to the structure. The viscoelastic materials provide significant damping particularly for amplitudes corresponding to the high frequencies. This is in contrast to the responses obtained without the viscoelastic layer.

Conclusion

The obtained results show the importance of viscoelastic damping, which has a significant effect on the vibro-acoustic behavior, implying the improvement of the damping of the structure, especially for large frequencies and high temperatures.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20

Similar content being viewed by others

References

  1. Kerwin EM (1959) Damping of flexural waves by a constrained viscoelastic layer. J Acoust Soc Am 31:952–962

    Article  Google Scholar 

  2. Ross D, Ungar EE, Kerwin EM (1959) Flexural vibrations by means of viscoelastic laminate. In: ASME structure damping, pp 48–87.

  3. Ungar EE, Ross D, Kerwin EM (1959) Damping of flexural vibration by alternate viscoelastic and elastic layers. ASME, Cambridge, MA

    Google Scholar 

  4. Yi-Yuan Y (1962) Damping of flexural vibrations of sandwich plates. J Aerosp Sci 29:790–803

    Article  Google Scholar 

  5. Mead DJ, Markus S (1969) The forced vibration of a three-layer, damped sandwich beam with arbitrary boundary conditions. J Sound Vibr 10:163–175

    Article  Google Scholar 

  6. Pan HH (1969) Axisymmetrical vibrations of a circular sandwich shell with a viscoelastic core layer. J Sound Vib 9:338–348

    Article  Google Scholar 

  7. Markus S (1976) Damping properties of layered cylindrical shells, vibrating in axially symmetric modes. J Sound Vib 48:511–524

    Article  Google Scholar 

  8. DiTaranto RA (1965) Theory of vibratory vending for elastic and viscoelastic layered finite-length beams. J Appl Mech 32:881. https://doi.org/10.1115/1.3627330

    Article  Google Scholar 

  9. Rao DK (1978) Frequency and loss factors of sandwich beams under various boundary conditions. J Mech Eng Sci 20:271–282

    Article  Google Scholar 

  10. Cai C, Zheng H, Liu GR (2004) Vibration analysis of a beam with PCLD Patch. Appl Acoust 65:1057–1076

    Article  Google Scholar 

  11. Cai C, Zheng H, Chung HJ, Zhang ZJ (2006) Vibration analysis of a beam with an active constraining layer damping patch. Smart Mater Struct 15:147–156

    Article  Google Scholar 

  12. Irazu L, Elejabarrieta MJ (2017) The effect of the viscoelastic film and metallic skin on the dynamic properties of thin sandwich structures. Compos Struct 176:407–419. https://doi.org/10.1016/j.compstruct.2017.05.038

    Article  Google Scholar 

  13. Daya EM, Potier-Ferry M (2001) A numerical method for nonlinear eigenvalue problems application to vibrations of viscoelastic structures. J Comput Struct 79:533–541

    Article  MathSciNet  Google Scholar 

  14. Daya EM, Azrar L, Potier-Ferry M (2004) An amplitude equation for the non-linear vibration of viscoelastically damped sandwich beams. J Sound Vib 271:789–813

    Article  Google Scholar 

  15. Bilasse M, Daya M, Azrar L (2010) Linear and nonlinear vibrations analysis of viscoelastic sandwich beams. J Sound Vib 329(2010):4950–4969. https://doi.org/10.1016/j.jsv.2010.06.012

    Article  Google Scholar 

  16. Arvin H, Sadighi M, Ohadi AR (2010) A numerical study of free and forced vibration of composite sandwich beam with viscoelastic core. Compos Struct 92:996–1008. https://doi.org/10.1016/j.compstruct.2009.09.047

    Article  Google Scholar 

  17. Moita JS, Araújo AL, Martins P, Mota Soares CM, Mota Soares CA (2011) A finite element model for the analysis of viscoelastic sandwich structures. Comput Struct 89(2011):1874–1881. https://doi.org/10.1016/j.compstruc.2011.05.008

    Article  Google Scholar 

  18. Rezvani SS, Kiasat MS (2018) Analytical and experimental investigation on the free vibration of a floating composite sandwich plate having viscoelastic core. Arch Civil Mech Eng 18:1241–1258

    Article  Google Scholar 

  19. Landier J (1993) Modélisation et étude expérimentale des propriétés amortissantes des tôles sandwich. PhD thesis, Université de Metz

  20. Kiasat MS, Zhang G, Ernst L, Wisse G (2001) Creep behavior of a molding compound and its effect on packaging process stresses. In: Electronic components and technology conference, pp 931–938

  21. Li X, Kaiping Yu (2015) Vibration and acoustic responses of composite and sandwich panels under thermal environment. J Comput Struct 131:1040–1049

    Article  Google Scholar 

  22. Jeyaraj P, Padmanabhan C, Ganesan N (2008) Vibration and acoustic response of an isotropic plate in a thermal environment. J Vib Acoust. https://doi.org/10.1115/1.2948387

    Article  Google Scholar 

  23. Zhao X, Geng Q, Li Y (2013) Vibration and acoustic response of an orthotropic composite laminated plate in a hygroscopic environment. J Acoust Soc Am 133:1433–1442

    Article  Google Scholar 

  24. Geng Q, Li Y (2012) Analysis of dynamic and acoustic radiation characters for a flat plate under thermal environments. Int J Appl Mech 4:1250028

    Article  Google Scholar 

  25. Liu D, Li X (1996) An overall view of laminate theories based on displacement hypothesis. J Compos Mater 30:1539–1561

    Article  Google Scholar 

  26. Jeyaraj P, Ganesan N, Padmanabhan C (2009) Vibration and acoustic response of a composite plate with inherent material damping in a thermal environment. J Sound Vib 320:322–338

    Article  Google Scholar 

  27. Geng Q, Li Y (2014) Solutions of dynamic and acoustic responses of a clamped rectangular plate in thermal environments. J Vib Control 22:1593–1603

    Article  MathSciNet  Google Scholar 

  28. Hamdaoui M, Druesne F, Daya EM (2015) Variability analysis of frequency dependent visco-elastic three-layered beams. J Comput Struct 131:238–247

    Article  Google Scholar 

  29. Haberman M (2007) Design of high loss viscoelastic composites through micromechanical modeling and decision based material by design. PhD thesis Woodruff School of Mechanical Engineering, Georgia

  30. Junger MC, Feit D (1993) Sound structures and their interaction, 2nd edn. The Acoustical Society of America, USA

    Google Scholar 

  31. Ruzzene M (2004) Vibration and sound radiation of sandwich beams with honeycomb truss core. J Sound Vib 277:741–763

    Article  Google Scholar 

  32. Druesne F, Hamdaoui M, Lardeur P, Daya EM (2016) Variability of dynamic responses of frequency dependent visco-elastic sandwich beams with material and physical properties modeled by spatial random fields. J Comput Struct 152:316–323

    Article  Google Scholar 

  33. Cochelin B, Damil N, Potier-Ferry M (2007) Méthode Asymptotique Numérique. Hermès Science Publications, New Castle

    Google Scholar 

  34. Damil N (1999) An iterative method based upon Padé approximants. Commun Numer Methods Eng 15:701–708

    Article  MathSciNet  Google Scholar 

  35. Tekili S, Khadri Y, Karmi Y (2020) Dynamic analysis of sandwich beam with viscoelastic core under moving loads. Mechanik 26:325–330

    Article  Google Scholar 

  36. Trindade M, Benjeddou A, Ohayon R (2000) Modeling of frequency dependent viscoelastic materials for active–passive vibration damping. J Vib Acoust 122:169–174

    Article  Google Scholar 

Download references

Funding

This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.

Author information

Authors and Affiliations

  1. Laboratoire LRTAPM, Université Badji-Mokhtar Annaba, BP 12, 23000, Annaba, Algeria

    Yacine Karmi, Sabiha Tekili, Youcef Khadri & Haithem Boumediri

Authors
  1. Yacine Karmi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Sabiha Tekili
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Youcef Khadri
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Haithem Boumediri
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yacine Karmi.

Ethics declarations

Conflict of Interest

The authors declare no conflict of interest in preparing this article.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendices

Appendix A. Element Matrices

$$ \begin{gathered} \left[ M \right]^{e} = \hfill \\ \left( {\rho_{1} S_{1} + \rho_{3} S_{3} } \right)\int \limits_{0}^{{L^{e} }} \left( {\left[ {N_{u} } \right]^{T} \left[ {N_{u} } \right] + \frac{{h_{2}^{2} }}{4}\left[ {N_{\beta } } \right]^{T} \left[ {N_{\beta } } \right]} \right){\text{d}}x + h_{2} \left( {\rho_{1} S_{1} - \rho_{3} S_{3} } \right)\int \limits_{0}^{{L^{e} }} \left( {\left[ {N_{\beta } } \right]^{T} \left[ {N_{u} } \right]} \right){\text{d}}x \hfill \\ + \left( {\rho_{3} S_{3} h_{3} - \rho_{1} S_{1} h_{1} } \right) \int \limits_{0}^{{L^{e} }} \left( {\left[ {N_{w,x} } \right]^{T} \left[ {N_{u} } \right]} \right){\text{d}}x - \frac{{h_{2} }}{2}\left( {\rho_{1} S_{1} h_{1} + \rho_{2} S_{2} h_{2} } \right)\int \limits_{0}^{{L^{e} }} \left( {\left[ {N_{w,x} } \right]^{T} \left[ {N_{\beta } } \right]} \right){\text{d}}x \hfill \\ + \frac{1}{4}\left( {\rho_{1} S_{1} h_{1}^{2} + \rho_{3} S_{3} h_{3}^{2} } \right) \int \limits_{0}^{{L^{e} }} \left( {\left[ {N_{w,x} } \right]^{T} \left[ {N_{w,x} } \right]} \right){\text{d}}x + \left( {\rho_{2} S_{2} } \right) \int \limits_{0}^{{L^{e} }} \left( {\left[ {N_{u} } \right]^{T} \left[ {N_{u} } \right]} \right){\text{d}}x \hfill \\ + \left( {E_{1} S_{1} + E_{3} S_{3} + E_{2} S_{2} } \right)\int \limits_{0}^{{L^{e} }} \left( {\left[ {N_{w,xx} } \right]^{T} \left[ {N_{w,xx} } \right]} \right){\text{d}}x \, \hfill \\ \end{gathered} $$
(42)
$$ \begin{gathered} \left[ {K\left( \omega \right)} \right]^{e} = \hfill \\ \left( {E_{1} S_{1} + E_{3} S_{3} } \right)\int \limits_{0}^{{L^{e} }} \left( {\left[ {N_{u,x} } \right]^{T} \left[ {N_{u,x} } \right] + \frac{{h_{2}^{2} }}{4}\left[ {N_{\beta ,x} } \right]^{T} \left[ {N_{\beta ,x} } \right]} \right){\text{d}}x + h_{2} \left( {E_{1} S_{1} - E_{3} S_{3} } \right)\int \limits_{0}^{{L^{e} }} \left( {\left[ {N_{\beta ,x} } \right]^{T} \left[ {N_{u,x} } \right]} \right){\text{d}}x \hfill \\ + \left( {E_{3} S_{3} h_{3} - E_{1} S_{1} h_{1} } \right) \int \limits_{0}^{{L^{e} }} \left( {\left[ {N_{w,xx} } \right]^{T} \left[ {N_{u,x} } \right]} \right){\text{d}}x + \left( {E_{2} S_{2} } \right) \int \limits_{0}^{{L^{e} }} \left( {\left[ {N_{u,x} } \right]^{T} \left[ {N_{u,x} } \right]} \right){\text{d}}x \hfill \\ - \frac{{h_{2} }}{2}\left( {E_{1} S_{1} h_{1} + E_{3} S_{3} h_{3} } \right) \int \limits_{0}^{{L^{e} }} \left( {\left[ {N_{w,xx} } \right]^{T} \left[ {N_{\beta ,x} } \right]} \right){\text{d}}x + \left( {E_{1} I_{1} + E_{3} I_{3} } \right) \int \limits_{0}^{{L^{e} }} \left( {\left[ {N_{w,xx} } \right]^{T} \left[ {N_{w,xx} } \right]} \right){\text{d}}x \hfill \\ + \frac{1}{4}\left( {E_{1} S_{1} h_{1}^{2} + E_{3} S_{3} h_{3}^{2} } \right) \int \limits_{0}^{{L^{e} }} \left( {\left[ {N_{w,xx} } \right]^{T} \left[ {N_{w,xx} } \right]} \right){\text{d}}x + \left( {E_{2} I_{2} } \right)\int \limits_{0}^{{L^{e} }} \left( {\left[ {N_{\beta ,x} } \right]^{T} \left[ {N_{\beta ,x} } \right]} \right){\text{d}}x \hfill \\ + \left( {\frac{{E_{2} S_{2} }}{{2\left( {1 + \upsilon_{c} } \right)}}} \right) \int \limits_{0}^{{L^{e} }} \left( {\left[ {N_{\beta } } \right]^{T} \left[ {N_{\beta } } \right] + 2\left[ {N_{\beta } } \right]^{T} \left[ {N_{w,x} } \right] + \left[ {N_{w,x} } \right]^{T} \left[ {N_{w,x} } \right]} \right){\text{d}}x \, \hfill \\ \end{gathered} $$
(43)
$$ \left\{ F \right\}^{e} = \int \limits_{0}^{{L^{e} }} P\left( {x,t} \right)\left[ {N_{w} \left( x \right)} \right]^{T} $$
(44)

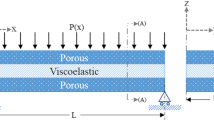
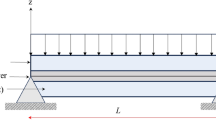
The simply supported sandwich beam is subjected to a moving load with a constant speed as shown in Fig. 1, the dynamic force is defined by:

$$ P\left( {x,t} \right) = P_{0} \delta \left( {x,vt} \right){ } $$
(45)

Replacing Eq. (45) in Eq. (46), the nodal force vector becomes:

$$ \left\{ F \right\}^{e} = P_{0} \left[ {N_{w} \left( {vt} \right)} \right]^{T} $$
(46)

Appendix B. Stiffness Matrix Decomposition

$$ \begin{gathered} \left[ {K_{0} } \right]^{e} = \left( {E_{1} S_{1} + E_{3} S_{3} } \right) \int \limits_{0}^{{L^{e} }} \left( {\left[ {N_{u,x} } \right]^{T} \left[ {N_{u,x} } \right] + \frac{{h_{2}^{2} }}{4}\left[ {N_{\beta ,x} } \right]^{T} \left[ {N_{\beta ,x} } \right]} \right){\text{d}}x + h_{2} \left( {E_{1} S_{1} - E_{3} S_{3} } \right) \int \limits_{0}^{{L^{e} }} \left( {\left[ {N_{\beta ,x} } \right]^{T} \left[ {N_{u,x} } \right]} \right){\text{d}}x \hfill \\ + \left( {E_{3} S_{3} h_{3} - E_{1} S_{1} h_{1} } \right) \int \limits_{0}^{{L^{e} }} \left( {\left[ {N_{w,xx} } \right]^{T} \left[ {N_{u,x} } \right]} \right){\text{d}}x + \left( {E_{0} S_{2} } \right)\int \limits_{0}^{{L^{e} }} \left( {\left[ {N_{u,x} } \right]^{T} \left[ {N_{u,x} } \right]} \right){\text{d}}x \hfill \\ - \frac{{h_{2} }}{2}\left( {E_{1} S_{1} h_{1} + E_{3} S_{3} h_{3} } \right) \int \limits_{0}^{{L^{e} }} \left( {\left[ {N_{w,xx} } \right]^{T} \left[ {N_{\beta ,x} } \right]} \right){\text{d}}x + \left( {E_{1} I_{1} + E_{3} I_{3} } \right)\int \limits_{0}^{{L^{e} }} \left( {\left[ {N_{w,xx} } \right]^{T} \left[ {N_{w,xx} } \right]} \right){\text{d}}x \hfill \\ + \frac{1}{4}\left( {E_{1} S_{1} h_{1}^{2} + E_{3} S_{3} h_{3}^{2} } \right) \int \limits_{0}^{{L^{e} }} \left( {\left[ {N_{w,xx} } \right]^{T} \left[ {N_{w,xx} } \right]} \right){\text{d}}x + \left( {E_{0} I_{2} } \right) \int \limits_{0}^{{L^{e} }} \left( {\left[ {N_{\beta ,x} } \right]^{T} \left[ {N_{\beta ,x} } \right]} \right){\text{d}}x \hfill \\ + \left( {\frac{{E_{0} S_{2} }}{{2\left( {1 + \upsilon_{2} } \right)}}} \right) \int \limits_{0}^{{L^{e} }} \left( {\left[ {N_{\beta } } \right]^{T} \left[ {N_{\beta } } \right] + 2\left[ {N_{\beta } } \right]^{T} \left[ {N_{w,x} } \right] + \left[ {N_{w,x} } \right]^{T} \left[ {N_{w,x} } \right]} \right){\text{d}}x \, \hfill \\ \end{gathered} $$
(47)
$$ \begin{gathered} \left[ {K_{c} } \right]^{e} = S_{2} \int \limits_{0}^{{L^{e} }} \left( {\left[ {N_{u,x} } \right]^{T} \left[ {N_{u,x} } \right]} \right){\text{d}}x + I_{2} \int \limits_{0}^{{L^{e} }} \left[ {N_{\beta ,x} } \right]^{T} \left[ {N_{\beta ,x} } \right]{\text{d}}x \hfill \\ + \frac{{S_{2} }}{{2\left( {1 + \upsilon_{2} } \right)}} \int \limits_{0}^{{L^{e} }} \left( {\left[ {N_{w,x} } \right]^{T} \left[ {N_{w,x} } \right] + \left[ {N_{\beta } } \right]^{T} \left[ {N_{w,x} } \right] + \left[ {N_{w,x} } \right]^{T} \left[ {N_{\beta } } \right] + \left[ {N_{\beta } } \right]^{T} \left[ {N_{\beta } } \right]} \right){\text{d}}x \, \hfill \\ \end{gathered} $$
(48)

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Karmi, Y., Tekili, S., Khadri, Y. et al. Vibroacoustic Analysis in the Thermal Environment of PCLD Sandwich Beams with Frequency and Temperature Dependent Viscoelastic Cores. J. Vib. Eng. Technol. 12, 3575–3594 (2024). https://doi.org/10.1007/s42417-023-01065-6

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s42417-023-01065-6

Keywords

Search

Navigation