Skip to main content
SpringerLink
Log in

Dynamic Stress Response Analysis of Circular Inclusions in Inhomogeneous Media With Trigonometric Variations in Modulus and Density Under Shear Horizontal Waves

  • Original Paper
  • Published:
Journal of Vibration Engineering & Technologies Aims and scope Submit manuscript

Abstract

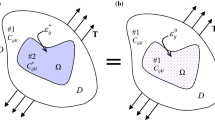
Functionally gradient materials (FGMs) are widely used in nuclear, military, automotive, and aerospace fields due to the excellent properties. The mechanical properties and stability analysis of functionally graded structures are particularly significant; this study closely links the design theory and research on the physical mechanism of FGMs by proposing an analytical method for the investigation of the propagation of elastic waves in inhomogeneous media with modulus and density variations (including composite media with homogeneous inclusions); this method uses the design theory for special functional materials based on the theory and method for modeling elastic wave propagation in homogeneous media. As an example, the dynamic stress response caused by homogeneous circular inclusions contained in an inhomogeneous medium with trigonometric variation in the modulus and density is analyzed under shear horizontal waves. The effects of the inhomogeneity parameters, reference wavenumber of the substrate, and properties of the circular inclusion relative to those of the substrate on the dynamic stress concentration factor (DSCF) around the circular inclusion are investigated; the results show that the inhomogeneity of the substrate is the primary factor affecting the degree of dynamic stress concentration at the boundary of the inclusion and may lead to a DSCF value of up to several hundred; this work not only helps to advance the fundamental understanding of the structure–response relationships of FGMs, but also provides theoretical reference for the structure design.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Gibson RF (2010) A review of recent research on mechanics of multifunctional composite materials and structures - Sciencedirect. Compos Struct 92(12):2793–2810

    Article  Google Scholar 

  2. Chigrin DN, Lavrinenko AV, Yarotsky DA et al (2018) All-dielectric one-dimensional periodic structures for total omnidirectional reflection and partial spontaneous emis-sion control. J Light Technol 17:2018–2024

    Article  Google Scholar 

  3. Mcgrath DT, Pyati VP (2016) Periodic structure analysis using a hybrid finite element method. Radio Sci 31:1173–1179

    Article  ADS  Google Scholar 

  4. Lin CY, Huang YH, Chen WT (2018) Multimodal suppres-sion of vibration in smart flexible beam using piezoelec-tric electrode-based switching control. Mechatronics 53:152–167

    Article  Google Scholar 

  5. Shen HJ, Wen JH, Yu DL et al (2014) Stability of fluid-conveying periodic shells on an elastic foundation with external loads. J Fluids Struct 46:134–148

    Article  ADS  Google Scholar 

  6. Xia Z, Mao K, Wei S et al (2017) Application of genetic algorithm-support vector regression model to predict damping of cantilever beam with particle damper. J Low Freq Noise V A 36:138–147

    Article  Google Scholar 

  7. Wu C, Liu XX, Lian DY et al (2010) Preparation of metal Cu film and the research of the infrared emissivity properties. Surface Technol 39(2):34–37

    CAS  Google Scholar 

  8. Sheng X, Zhao CY, Yi Q et al (2018) Engineered metabarrier as shield from longitudinal waves: band gap properties and optimization mechanisms. J Zhejiang Univ-Sci A Appl Phys Eng 19(9):663–675

    Article  Google Scholar 

  9. Zhang JL, Yao H, Du J et al (2016) Low-frequency sound insulation characteristics in the cabin based on local resonance type phononic crystal. J Silic 44(10):1440–1445 ((in Chinese with English abstract))

    CAS  Google Scholar 

  10. Huang J, Shi Z (2015) Vibration reduction of plane waves us-ing periodic in-filled pile barriers. J Geotech Geoenviron Eng 141(6):04015018

    Article  Google Scholar 

  11. Wang QC, Wang JC, Zhao DP et al (2016) Investigation of terahertz waves propagating through far infrared/CO2 laser stealth-compatible coating based on one-dimensional photonic crystal. Infrared Phys Technol 79:144–150

    Article  CAS  ADS  Google Scholar 

  12. Miao L, Shi JM et al (2016) Heterogeneous doped one-dimensional photonic crystal with low emissivity in infrared atmospheric window. Opt Eng 55(5):057101

    Article  ADS  Google Scholar 

  13. Arpin KA, Losego MD et al (2013) Three-dimensional self-assembled photonic crystals with high temperature stability for thermal emission modification. Nat Commun 4:2630

    Article  PubMed  ADS  Google Scholar 

  14. Kawasaki A, Watanabe R (1997) Concept and P/M fabrication of functionally gradient materials. Ceram Int 23(1):73–83

    Article  CAS  Google Scholar 

  15. Sun JI, Zhou ZG, Wang B (2005) A permeable crack in functionally graded piezoelectric /piezomagnetic materials. Acta Mech Sin 37(1):9–14

    Google Scholar 

  16. Petrov VM, Srinivasan G (2008) Enhancement of magnetoelectric coupling in functionally graded ferroelectric and ferromagnetic bilayers. Phys Rev B 78(18):2599–2604

    Article  Google Scholar 

  17. Kong Y, Liu J, Nie G (2016) Propagation characteristics of SH waves in a functionally graded piezomagnetic layer on PMN-0.29PT single crystal substrate. Mech Res Commun 73:107–112

    Article  Google Scholar 

  18. Du J, Xian K, Yong YK et al (2010) SH-SAW propagation in layered functionally graded piezoelectric material structures loaded with viscous liquid. Acta Mech 212(3–4):271–281

    Article  Google Scholar 

  19. Cao X, Shi J, Jin F (2012) Lamb wave propagation in the functionally graded piezoelectric–piezomagnetic material plate. Acta Mech 223(5):1081–1091

    Article  MathSciNet  Google Scholar 

  20. Singh BM, Rokne J (2013) Propagation of SH waves in layered functionally gradient piezoelectric–piezomagnetic structures. Philos Mag 93(14):1690–1700

    Article  CAS  ADS  Google Scholar 

  21. Martin PA (2009) Scattering by a cavity in an exponentially graded half-space. J Appl Mech 76(3):031009

    Article  Google Scholar 

  22. Hei BP, Yang ZL, Wang Y, Liu DK (2014) Dynamic analysis of elastic waves by an arbitrary cavity in an inhomogeneous medium with density variation. Math Mech Solids 21(8):931–940

    Article  MathSciNet  Google Scholar 

  23. Hei BP, Yang ZL, Sun BT, Wang Y (2015) Modelling and analysis of the dynamic behavior of inhomogeneous continuum containing a circular inclusion. Appl Math Model 39(23–24):7364–7374

    Article  MathSciNet  Google Scholar 

  24. Zhang XM, Qi H, Sun XL (2017) Scattering of SH-wave by a circular cavity in radial inhomogeneous piezoelectric medium. Explos Shock Waves 37(03):464–470 ((in Chinese with English abstract))

    Google Scholar 

  25. Liu DK, Gai BZ, Tao GY (1982) Applications of the method of complex functions to dynamic stress concentrations. Wave Mot 4:293–304

    Article  MathSciNet  ADS  Google Scholar 

  26. Li ZL, Liu DK (1995) Wave in solid. Science Press, Beijing

    Google Scholar 

Download references

Funding

Scientific Research Fund of Institute of Engineering Mechanics, China Earthquake Administration (Grant No.2021EEEVL0201) and National Natural Science Foundation of China (U2239252) and the program for Innovative Research Team in China Earthquake Administration.

Author information

Authors and Affiliations

  1. Key Laboratory of Earthquake Engineering and Engineering Vibration, Institute of Engineering Mechanics, China Earthquake Administration, Harbin, China

    Gui-xin Zhang & Zai-lin Yang

  2. Key Laboratory of Earthquake Disaster Mitigation, Ministry of Emergency Management, Harbin, China

    Gui-xin Zhang

  3. College of Aerospace and Civil Engineering, Harbin Engineering University, Harbin, 150001, China

    Yun Zhu & Zai-lin Yang

  4. Institute of Defense Engineering, AMS, PLA, Beijing, 100850, China

    Yun Zhu, Jian Zhao & Yi-cun Chen

Authors
  1. Gui-xin Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yun Zhu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Zai-lin Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Jian Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Yi-cun Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Zai-lin Yang.

Ethics declarations

Conflict of Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, Gx., Zhu, Y., Yang, Zl. et al. Dynamic Stress Response Analysis of Circular Inclusions in Inhomogeneous Media With Trigonometric Variations in Modulus and Density Under Shear Horizontal Waves. J. Vib. Eng. Technol. 12, 2393–2408 (2024). https://doi.org/10.1007/s42417-023-00986-6

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s42417-023-00986-6

Keywords

Search

Navigation