Skip to main content
SpringerLink
Log in

Nonlinear Vibration Analysis of Fractional Viscoelastic Nanobeam

  • Original Paper
  • Published:
Journal of Vibration Engineering & Technologies Aims and scope Submit manuscript

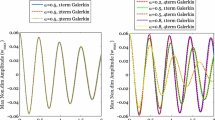
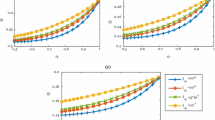
Abstract

Purpose

Considering the size-dependent influence ignored by classical continuum mechanics, a new non-classical Euler–Bernoulli beam model is proposed in this paper. The new fractional viscoelastic nanobeam model is set up using the fractional Kelvin–Voigt viscoelastic model and Hamilton’s principle. And the new model studies the total effects of nonlocal elasticity, modified couple stress, and surface energy.

Methods

The model represented the fractional integral-partial differential governing equation is solved by Galerkin’s and predictor–corrector methods. First, the effects of nonlocal elasticity, modified couple stress, surface energy, and their coupling impact on the nonlinear time response of free vibration of fractional viscoelastic nanobeam are analyzed. Then, in the frame of nonlocal couple-stress elasticity and surface energy theory, the effects of different parameters on the nonlinear time responses of free and forced vibration of fractional viscoelastic nanobeam are discussed.

Results and Conclusion

The numerical results show that the fractional order must be considered in the modeling of viscoelastic nanobeam, and the system’s damping enhances by the increase of fractional order. Moreover, owing to the correlation between fractional order and excitation frequency, the nonlinear time responses of fractional order to free and forced vibration are different.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21

Similar content being viewed by others

Data Availability

The data for the results of this study are available from the corresponding author.

References

  1. Wang B, Dündar MA, Nötzel R, Karouta F, He S, van der Heijden RW (2010) Photonic crystal slot nanobeam slow light waveguides for refractive index sensing. Appl Phys Lett 97(15):151105

    Google Scholar 

  2. On BB, Altus E (2010) Stochastic surface effects in nanobeam sensors. Probabilist Eng Mech 25(2):228–234

    Google Scholar 

  3. Duan JS, Rach R, Wazwaz AM (2013) Solution of the model of beam-type micro-and nano-scale electrostatic actuators by a new modified Adomian decomposition method for nonlinear boundary value problems. Int J NonLin Mech 49:159–169

    Google Scholar 

  4. Deotare PB, Kogos LC, Bulu I, Lončar M (2013) Photonic crystal nanobeam cavities for tunable filter and router applications. IEEE J Sel Top Quant 19(2):3600210

    Google Scholar 

  5. Fegadolli WS, Pavarelli N, O’Brien P, Njoroge S, Almeida VR, Scherer A (2015) Thermally controllable silicon photonic crystal nanobeam cavity without surface cladding for sensing applications. ACS Photonics 2(4):470–474

    Google Scholar 

  6. Bauer S, Pittrof A, Tsuchiya H, Schmuki P (2011) Size-effects in TiO2 nanotubes: diameter dependent anatase/rutile stabilization. Electrochem Commun 13(6):538–541

    Google Scholar 

  7. Xiao S, Hou W (2006) Studies of size effects on carbon nanotubes’ mechanical properties by using different potential functions. Fuller Nanotub Car N 14(1):9–16

    MathSciNet  Google Scholar 

  8. Chowdhury R, Adhikari S, Wang C, Scarpa F (2010) A molecular mechanics approach for the vibration of single-walled carbon nanotubes. Comp Mater Sci 48(4):730–735

    Google Scholar 

  9. Sun CT, Zhang H (2003) Size-dependent elastic moduli of platelike nanomaterials. J Appl Phys 93(2):1212–1218

    Google Scholar 

  10. Zhang H, Sun CT (2004) Nanoplate model for platelike nanomaterials. AIAA J 42(10):2002–2009

    Google Scholar 

  11. Kröner E (1967) Elasticity theory of materials with long range cohesive forces. Int J Solids Struct 3(5):731–742

    MATH  Google Scholar 

  12. Eringen AC (1972) Nonlocal polar elastic continua. Int J Eng Sci 10(1):1–16

    MathSciNet  MATH  Google Scholar 

  13. Eringen AC (1983) On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J Appl Phys 54(9):4703–4710

    Google Scholar 

  14. Eringen AC (2002) Nonlocal continuum field theories. Springer Science & Business Media, Berlin

    MATH  Google Scholar 

  15. Baǧdatli SM (2015) Non-linear vibration of nanobeams with various boundary condition based on nonlocal elasticity theory. Compos Part B-Eng 80:43–52. https://doi.org/10.1016/j.compositesb.2015.05.030

    Article  Google Scholar 

  16. Yapanmis BE, Togun N, Baǧdatli SM, Akkoca S (2021) Magnetic field effect on nonlinear vibration of nonlocal nanobeam embedded in nonlinear elastic foundation. Struct Eng Mech 79(6):723–735. https://doi.org/10.12989/sem.2021.79.6.723

    Article  Google Scholar 

  17. Yapanmis BE (2022) Nonlinear vibration and internal resonance analysis of microbeam with mass using the modified coupled stress theory. J Vib Eng Technol. https://doi.org/10.1007/s42417-022-00694-7

    Article  Google Scholar 

  18. Yapanmis BE, Baǧdatli SM (2022) Investigation of the non-linear vibration behaviour and 3:1 internal resonance of the multi supported nanobeam. Z Naturforsch A 77(4):305–321. https://doi.org/10.1515/zna-2021-0300

    Article  Google Scholar 

  19. Dell’Isola F, Andreaus U, Placidi L (2015) At the origins and in the vanguard of peridynamics, non-local and higher-gradient continuum mechanics: an underestimated and still topical contribution of Gabrio Piola. Math Mech Solids 20(8):887–928

    MathSciNet  MATH  Google Scholar 

  20. Dell’Isola F, Della Corte A, Esposito R, Russo L (2016) Some cases of unrecognized transmission of scientific knowledge: from antiquity to Gabrio Piola’s peridynamics and generalized continuum theories. Gen Continua Models Class Adv Mater 42:77–128. https://doi.org/10.1007/978-3-319-31721-2_5

    Article  MathSciNet  Google Scholar 

  21. Mindlin RD (1964) Micro-structure in linear elasticity. Arch Ration Mech An 16(1):28–34

    MathSciNet  MATH  Google Scholar 

  22. Mindlin RD (1965) Second gradient of strain and surface-tension in linear elasticity. Int J Solids Struct 14(1):22–25

    Google Scholar 

  23. Toupin R (1962) Elastic materials with couple-stresses. Arch Ration Mech An 11(1):385–414

    MathSciNet  MATH  Google Scholar 

  24. Mindlin RD, Tiersten HF (1962) Effects of couple-stresses in linear elasticity. Arch Ration Mech An 11:34–37

    MathSciNet  Google Scholar 

  25. Eringen AC (1972) Linear theory of nonlocal elasticity and dispersion of plane waves. Int J Eng Sci 10(5):425–450

    MATH  Google Scholar 

  26. Gurtin ME, Murdoch AI (1975) A continuum theory of elastic material surfaces. Arch Ration Mech An 57(4):291–323

    MathSciNet  MATH  Google Scholar 

  27. Gurtin ME, Murdoch AI (1978) Surface stress in solids. Int J Solids Struct 14(2):431–440

    MATH  Google Scholar 

  28. Wang LY, Han HJ (2021) Vibration and buckling analysis of piezoelectric nanowires based on surface energy density. Acta Mech Solida Sin 34:425–436. https://doi.org/10.1007/s10338-020-00210-y

    Article  Google Scholar 

  29. Wang LY, Ou ZY (2022) Modeling and analysis of the static bending of piezoelectric nanowires with the consideration of surface effects. J Braz Soc Mech Sci 44:329

    Google Scholar 

  30. Mandelbrot BB (1983) The fractal geometry of nature. Macmillan, London

    Google Scholar 

  31. Klimek M (2001) Fractional sequential mechanics-models with symmetric fractional derivative. Czech J Phys 51(12):1348–1354

    MathSciNet  MATH  Google Scholar 

  32. Riewe F (1997) Mechanics with fractional derivatives. Phys Rev E 55(3):3581

    MathSciNet  Google Scholar 

  33. Podlubny I (1999) Fractional differential equations. Academic Press, San Diego

    MATH  Google Scholar 

  34. Rossikhin YA, Shitikova MV (1997) Applications of fractional calculus to dynamic problems of linear and nonlinear hereditary mechanics of solids. Appl Mech Rev 50(3):15–67

    Google Scholar 

  35. Magin RL, Ovadia M (2008) Modeling the cardiac tissue electrode interface using fractional calculus. J Vib Control 14(9–10):1431–1442

    MATH  Google Scholar 

  36. Machado JT, Costa AC, Quelhas MD (2011) Fractional dynamics in DNA. Commun Nonlinear Sci 16(8):2963–2969

    MATH  Google Scholar 

  37. Heymans N (2008) Dynamic measurements in long-memory materials: fractional calculus evaluation of approach to steady state. J Vib Control 14(9–10):1587–1596

    MATH  Google Scholar 

  38. De Espíndola JJ, Bavastri CA, Lopes EMDO (2008) Design of optimum systems of viscoelastic vibration absorbers for a given material based on the fractional calculus model. J Vib Control 14(9–10):1607–1630

    MathSciNet  MATH  Google Scholar 

  39. Lazarević MP (2006) Finite time stability analysis of PD \(\alpha\) fractional control of robotic time-delay systems. Mech Res Commun 33(2):269–279

    MathSciNet  MATH  Google Scholar 

  40. Cervera J, Baños A (2008) Automatic loop shaping in QFT using CRONE structures. J Vib Control 14(9–10):1513–1529

    MathSciNet  MATH  Google Scholar 

  41. Vinagre BM, Podlubny I, Hernandez A, Feliu V (2000) Some approximations of fractional order operators used in control theory and applications. Fract Calc Appl Anal 3(3):231–248

    MathSciNet  MATH  Google Scholar 

  42. Frederico GS, Torres DF (2008) Fractional conservation laws in optimal control theory. Nonlinear Dyn 53(3):215–222

    MathSciNet  MATH  Google Scholar 

  43. Calderón AJ, Vinagre BM, Feliu V (2006) Fractional order control strategies for power electronic buck converters. Signal Process 86(10):2803–2819

    MATH  Google Scholar 

  44. Panda R, Dash M (2006) Fractional generalized splines and signal processing. Signal Process 86(9):2340–2350

    MATH  Google Scholar 

  45. Vinagre BM, Feliu V (2002) Modeling and control of dynamic system using fractional calculus: application to electrochemical processes and flexible structures. In: Proceedings of the Forty-first IEEE Conference on Decision and Control. University of Castilla-La Mancha, Castilla-La Mancha, pp 214–239

  46. Xu J, Chen Y, Tai Y, Xu X, Shi G, Chen N (2020) Vibration analysis of complex fractional viscoelastic beam structures by the wave method. Int J Mech Sci 167:105204. https://doi.org/10.1016/j.ijmecsci.2019.105204

    Article  Google Scholar 

  47. Di Paola M, Heuer R, Pirrotta A (2013) Fractional visco-elastic Euler-Bernoulli beam. Int J Solids Struct 50(22–23):3505–3510. https://doi.org/10.1016/j.ijmecsci.2013.02.007

    Article  Google Scholar 

  48. Barretta R, Marotti de Sciarra F, Pinnola FP, Vaccaro MS (2022) On the nonlocal bending problem with fractional hereditariness. Meccanica 57(4):807–820. https://doi.org/10.1007/s11012-021-01366-8

    Article  MathSciNet  MATH  Google Scholar 

  49. Pinnola FP, Barretta R, Marotti de Sciarra F, Pirrotta A (2022) Analytical solutions of viscoelastic nonlocal timoshenko beams. Mathematics 10(3):477. https://doi.org/10.3390/math10030477

    Article  Google Scholar 

  50. Alotta G, Di Paola M, Failla G, Pinnola FP (2018) On the dynamics of non-local fractional viscoelastic beams under stochastic agencies. Compos Part B-Eng 137:102–110. https://doi.org/10.1016/j.compositesb.2017.10.014

    Article  Google Scholar 

  51. Devillanova G, Marano GC (2016) A free fractional viscous oscillator as a forced standard damped vibration. Fract Calc Appl Anal 19(2):319–356. https://doi.org/10.1515/fca-2016-0018

    Article  MathSciNet  MATH  Google Scholar 

  52. Oskouie MF, Ansari R, Sadeghi F (2017) Nonlinear vibration analysis of fractional viscoelastic Euler-Bernoulli nanobeams based on the surface stress theory. Acta Mech Solida Sin 30(4):416–424. https://doi.org/10.1016/j.camss.2017.07.003

    Article  Google Scholar 

  53. Oskouie MF, Ansari R (2017) Linear and nonlinear vibrations of fractional viscoelastic Timoshenko nanobeams considering surface energy effects. Appl Math Model 43:337–350. https://doi.org/10.1016/j.apm.2016.11.036

    Article  MathSciNet  MATH  Google Scholar 

  54. Ansari R, Oskouie MF, Gholami R (2016) Size-dependent geometrically nonlinear free vibration analysis of fractional viscoelastic nanobeams based on the nonlocal elasticity theory. Physica E 75:266–271. https://doi.org/10.1016/j.physe.2015.09.022

    Article  Google Scholar 

  55. Ansari R, Oskouie MF, Sadeghi F, Bazdid-Vahdati M (2015) Free vibration of fractional viscoelastic Timoshenko nanobeams using the nonlocal elasticity theory. Physica E 74:318–327. https://doi.org/10.1016/j.physe.2015.07.013

    Article  Google Scholar 

  56. Ansari R, Oskouie MF, Rouhi H (2017) Studying linear and nonlinear vibrations of fractional viscoelastic Timoshenko micro-/nano-beams using the strain gradient theory. Nonlinear Dyn 87(1):695–711. https://doi.org/10.1007/s11071-016-3069-6

    Article  MATH  Google Scholar 

  57. Hosseini-Hashemi S, Behdad S, Fakher M (2020) Vibration analysis of two-phase local/nonlocal viscoelastic nanobeams with surface effects. Eur Phys J Plus 135(2):1–18. https://doi.org/10.1140/epjp/s13360-020-00148-7

    Article  Google Scholar 

  58. Loghman E, Kamali A, Bakhtiari-Nejad F, Abbaszadeh M (2021) Nonlinear free and forced vibrations of fractional modeled viscoelastic FGM micro-beam. Appl Math Model 92:297–314. https://doi.org/10.1016/j.apm.2020.11.011

    Article  MathSciNet  MATH  Google Scholar 

  59. Loghman E, Bakhtiari-Nejad F, Kamali A, Abbaszadeh M, Amabili M (2021) Nonlinear vibration of fractional viscoelastic micro-beams. Int J Nonlin Mech 137:103811. https://doi.org/10.1016/j.ijnonlinmec.2021.103811

    Article  MATH  Google Scholar 

  60. Nešić N, Cajić M, Karličić D, Obradović A, Simonović J (2022) Nonlinear vibration of a nonlocal functionally graded beam on fractional visco-Pasternak foundation. Nonlinear Dyn 107(3):2003–2026

    Google Scholar 

  61. Farokhi H, Ghayesh MH, Amabili M (2013) Nonlinear dynamics of a geometrically imperfect microbeam based on the modified couple stress theory. Int J Eng Sci 68:11–23. https://doi.org/10.1016/j.ijengsci.2013.03.001

    Article  MathSciNet  MATH  Google Scholar 

  62. Eldred LB, Baker WP, Palazotto AN (1995) Kelvin-Voigt versus fractional derivative model as constitutive relations for viscoelastic materials. AIAA J 33(3):547–550

    MATH  Google Scholar 

  63. Grzesikiewicz W, Wakulicz A, Zbiciak A (2013) Non-linear problems of fractional calculus in modeling of mechanical systems. Int J Mech Sci 70:90–98. https://doi.org/10.1016/j.ijmecsci.2013.02.007

    Article  Google Scholar 

  64. Lu P, He LH, Lee HP, Lu C (2006) Thin plate theory including surface effects. Int J Solids Struct 43(16):4631–4647. https://doi.org/10.1016/j.ijsolstr.2005.07.036

    Article  MATH  Google Scholar 

  65. Lü CF, Lim CW, Chen WQ (2009) Size-dependent elastic behavior of FGM ultra-thin films based on generalized refined theory. Int J Solids Struct 46(5):1176–1185

    MATH  Google Scholar 

  66. Sun K, Wang X, Sprott JC (2010) Bifurcations and chaos in fractional-order simplified Lorenz system. Int J Bifurcat Chaos 20(4):1209–1219. https://doi.org/10.1142/S0218127410026411

    Article  MathSciNet  MATH  Google Scholar 

  67. Diethelm K (1997) An algorithm for the numerical solution of differential equations of fractional order. Electron Trans Numer Anal 5(1):1–6

    MathSciNet  MATH  Google Scholar 

  68. Diethelm K, Ford NJ (2002) Analysis of fractional differential equations. J Math Anal Appl 265(2):229–248

    MathSciNet  MATH  Google Scholar 

  69. Diethelm K, Ford NJ, Freed AD (2002) A predictor-corrector approach for the numerical solution of fractional differential equations. Nonlinear Dyn 29(1):3–22

    MathSciNet  MATH  Google Scholar 

Download references

Funding

This work is supported by the National Natural Science Foundation of China (11862014).

Author information

Authors and Affiliations

  1. School of Science, Lanzhou University of Technology, Lanzhou, Gansu, People’s Republic of China

    Meifeng Qiu, Dongxia Lei & Zhiying Ou

Authors
  1. Meifeng Qiu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Dongxia Lei
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Zhiying Ou
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

All the authors contributed to the study.

Corresponding author

Correspondence to Zhiying Ou.

Ethics declarations

Conflict of Interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Qiu, M., Lei, D. & Ou, Z. Nonlinear Vibration Analysis of Fractional Viscoelastic Nanobeam. J. Vib. Eng. Technol. 11, 4015–4038 (2023). https://doi.org/10.1007/s42417-022-00799-z

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s42417-022-00799-z

Keywords

Search

Navigation