Skip to main content
SpringerLink
Log in

Free Vibration Analysis of AFGPM Non-uniform Beam: A Mathematical Modeling

  • Original Paper
  • Published:
Journal of Vibration Engineering & Technologies Aims and scope Submit manuscript

Abstract

Purpose

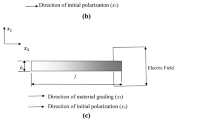
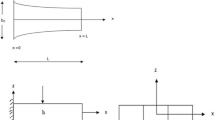
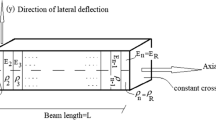
This work is an extension of the previously published work. In this study vibration behavior of an axially functionally graded piezoelectric material (AFGPM) non-uniform beam is investigated. The material properties are assumed to vary continuously along the length according to a power law. The polynomial function is used to define the width of the beam at the specific cross section. Two types of boundary conditions are taken into consideration, i.e. clamped-clamped (C-C) and clamped-free (C-F).

Methods

Hamilton's theory is adopted to model the equations of motion. The results are obtained using the generalized differential quadrature (GDQ) method.

Results

The effects of the degree of a polynomial function, boundary conditions, taper ratio, geometric parameter and volume fraction index on natural frequencies are reported.

Conclusions

The natural frequency increases with the increase in the degree of polynomial under the C-C boundary condition. However, the rate of increment is somewhat slow with the increment of the divergence of the beam. It may be revealed that the natural frequency decreases with the increase in degree of polynomial. Moreover, the decrement rate is faster with the increment of the convergence of the beam. The same variation is observed for higher values n. The natural frequency decreases with the increase in the degree of polynomial under the C-F boundary condition. However, the decrement rate is promptly with the increment of the divergence of the beam. It may be revealed that the natural frequency increases with the increase in the degree of polynomial. Although, the rate of decrement is somewhat prompt with the increment of the convergence of the beam. The same variation is observed for higher values of n. It can be seen that with the increase in slenderness ratio, the natural frequency decreases under both types of boundary conditions. It can be revealed that the natural frequency becomes almost same after 35 (l/h > 35) for all degrees of polynomial. It is found that with the increase in the volume fraction index, natural frequency decrease for both the convergent and divergent beams.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. Gupta B, Sharma P, Rathore SK (2022) A new numerical modeling of an axially functionally graded piezoelectric beam. J Vib Eng Technol 13:1–6

    Google Scholar 

  2. Liu B, Chen H, Cao W (2019) A novel method for tailoring elasticity distributions of functionally graded porous materials. Int J Mech Sci 1(157):457–470

    Google Scholar 

  3. Hajheidari P, Stiharu I, Bhat R (2020) Performance of non-uniform functionally graded piezoelectric energy harvester beams. J Intell Mater Syst Struct 31(13):1604–1616

    Google Scholar 

  4. Wu CC, Kahn M, Moy W (1996) Piezoelectric ceramics with functional gradients: a new application in material design. J Am Ceram Soc 79(3):809–812

    Google Scholar 

  5. Almajid A, Taya M, Takagi K, Li JF, Watanabe R. (2002) Fabrication and modeling of porous FGM piezoelectric actuators. In: Smart Structures and Materials 2002: Smart Structures and Integrated Systems 2002 Jul 15 (Vol. 4701, pp. 467–476). International Society for Optics and Photonics.

  6. Rubio WM, Vatanabe SL, Paulino GH, Silva EC. Functionally graded piezoelectric material systems–a multiphysics perspective. Computational Chemistry of Solid State Materials. 2011.

  7. Sharma P (2021) Vibration analysis of FGPM beam: a review. Mater Today Proc 1(44):1384–1390

    MathSciNet  Google Scholar 

  8. Komijani M, Reddy JN, Ferreira AJ (2014) Nonlinear stability and vibration of pre/post-buckled microstructure-dependent FGPM actuators. Meccanica 49(11):2729–2745

    MathSciNet  MATH  Google Scholar 

  9. Li YS, Feng WJ, Cai ZY (2014) Bending and free vibration of functionally graded piezoelectric beam based on modified strain gradient theory. Compos Struct 1(115):41–50

    Google Scholar 

  10. Ebrahimi F, Salari E (2016) Analytical modeling of dynamic behavior of piezo-thermo-electrically affected sigmoid and power-law graded nanoscale beams. Appl Phys A 122(9):1–24

    Google Scholar 

  11. Sharma P (2019) Vibration analysis of functionally graded piezoelectric actuators. Springer, New York, NY

    Google Scholar 

  12. Sharma P, Parashar SK (2016) Free vibration analysis of shear-induced flexural vibration of FGPM annular plate using generalized differential quadrature method. Compos Struct 1(155):213–222

    Google Scholar 

  13. Sharma P (2018) Efficacy of harmonic differential quadrature method to vibration analysis of FGPM beam. Compos Struct 1(189):107–116

    Google Scholar 

  14. Parashar SK, Sharma P (2016) Modal analysis of shear-induced flexural vibration of FGPM beam using generalized differential quadrature method. Compos Struct 1(139):222–232

    Google Scholar 

  15. Komijani M, Gracie R (2016) Nonlinear thermo-electro-mechanical dynamic behavior of FGPM beams. Compos Struct 15(150):208–218

    Google Scholar 

  16. Ebrahimi F, Daman M (2017) Nonlocal thermo-electromechanical vibration analysis of smart curved FG piezoelectric Timoshenko nanobeam. Smart Struct Syst 20(3):351–368

    Google Scholar 

  17. Ebrahimi F, Fardshad RE (2018) Modeling the size effect on vibration characteristics of functionally graded piezoelectric nanobeams based on Reddy’s shear deformation beam theory. Adv Nano Res 6(2):113

    Google Scholar 

  18. Maruani J, Bruant I, Pablo F, Gallimard L (2017) A numerical efficiency study on the active vibration control for a FGPM beam. Compos Struct 15(182):478–486

    Google Scholar 

  19. Derayatifar M, Tahani M, Moeenfard H (2017) Nonlinear analysis of functionally graded piezoelectric energy harvesters. Compos Struct 15(182):199–208

    Google Scholar 

  20. Chen M, Chen H, Ma X, Jin G, Ye T, Zhang Y, Liu Z (2018) The isogeometric free vibration and transient response of functionally graded piezoelectric curved beam with elastic restraints. Results Phys 1(11):712–725

    Google Scholar 

  21. Heshmati M, Amini YJ (2019) A comprehensive study on the functionally graded piezoelectric energy harvesting from vibrations of a graded beam under travelling multi-oscillators. Appl Math Model 1(66):344–361

    MathSciNet  MATH  Google Scholar 

  22. Cai B, Zhou L (2019) A coupling electromechanical inhomogeneous cell-based smoothed finite element method for dynamic analysis of functionally graded piezoelectric beams. Adv Mater Sci Eng 6:2019

    Google Scholar 

  23. Fatehi P, Mahzoon M, Farid M (2021) Piezoelectric energy harvesting from nonlinear dynamics of functionally graded plate under multi-moving loads and masses. Mech Based Des Struct Mach 27:1–20

    Google Scholar 

  24. Jing HX, He XT, Du DW, Peng DD, Sun JY (2020) Vibration analysis of piezoelectric cantilever beams with bimodular functionally-graded properties. Appl Sci 10(16):5557

    Google Scholar 

  25. Wang YQ (2018) Electro-mechanical vibration analysis of functionally graded piezoelectric porous plates in the translation state. Acta Astronaut 1(143):263–271

    Google Scholar 

  26. Wang YQ, Zu JW (2018) Speed-dependent nonlinear broadband vibrations of smart functionally graded piezoelectric material plates. J Intell Mater Syst Struct 29(8):1764–1776

    Google Scholar 

  27. Sharma A (2022) Effect of porosity on active vibration control of smart structure using porous functionally graded piezoelectric material. Compos Struct 15(280):114815

    Google Scholar 

  28. Wang YQ, Liu YF, Zu JW (2019) Analytical treatment of nonlocal vibration of multilayer functionally graded piezoelectric nanoscale shells incorporating thermal and electrical effect. Eur Phys J Plus 134(2):1–5

    Google Scholar 

  29. Fang X, Hu Y, Zhu C, An S, Chen L (2022) Size-dependent vibration of laminated functionally graded curved beams covered with piezoelectric layers. Mech Adv Mater Struct 4:1

    Google Scholar 

  30. Sh EL, Kattimani S, Vinyas M (2022) Nonlinear free vibration and transient responses of porous functionally graded magneto-electro-elastic plates. Arch Civil Mech Eng 22(1):1–26

    Google Scholar 

  31. Wang YQ, Liu YF, Yang TH (2019) Nonlinear thermo-electro-mechanical vibration of functionally graded piezoelectric nanoshells on Winkler-Pasternak foundations via nonlocal Donnell’s nonlinear shell theory. Int J Struct Stab Dyn 19(09):1950100

    MathSciNet  Google Scholar 

  32. Liu YF, Wang YQ (2019) Thermo-electro-mechanical vibrations of porous functionally graded piezoelectric nanoshells. Nanomaterials 9(2):301

    MathSciNet  Google Scholar 

  33. Chai Q, Wang YQ (2022) Traveling wave vibration of graphene platelet reinforced porous joined conical-cylindrical shells in a spinning motion. Eng Struct 1(252):113718

    Google Scholar 

  34. Ye C, Wang YQ (2021) Nonlinear forced vibration of functionally graded graphene platelet-reinforced metal foam cylindrical shells: internal resonances. Nonlinear Dyn 104(3):2051–2069

    Google Scholar 

  35. Teng MW, Wang YQ (2021) Nonlinear forced vibration of simply supported functionally graded porous nanocomposite thin plates reinforced with graphene platelets. Thin-Walled Struct 1(164):107799

    Google Scholar 

  36. Xu H, Wang YQ (2022) Differential transformation method for free vibration analysis of rotating Timoshenko beams with elastic boundary conditions. Int J Appl Mech. https://doi.org/10.1142/S1758825122500466

    Article  Google Scholar 

  37. Sharma P, Gupta B, Rathore SK, Khinchi A, Gautam M (2022) Computational characteristics of an exponentially functionally graded piezoelectric beam. Int J Int Design Manuf (IJIDeM) 31:1–7

    Google Scholar 

  38. Sharma P (2021) Numerical study of grid distribution effect on accuracy of GDQ method of FGPM actuator. Mater Today Proc 1(45):5706–5708

    MathSciNet  Google Scholar 

  39. Zhang SQ, Huang ZT, Zhao YF, Ying SS, Ma SY (2021) Static and dynamic analyses of FGPM cylindrical shells with quadratic thermal gradient distribution. Compos Struct 1(277):114658

    Google Scholar 

  40. Lyu Z, Liu W, Liu C, Zhang Y, Fang M (2021) Thermo-electro-mechanical vibration and buckling analysis of a functionally graded piezoelectric porous cylindrical microshell. J Mech Sci Technol 35(10):4655–4672

    Google Scholar 

  41. Yi H, Sahmani S, Safaei B (2020) On size-dependent large-amplitude free oscillations of FGPM nanoshells incorporating vibrational mode interactions. Arch Civil Mech Eng 20(2):1–23

    Google Scholar 

  42. Huang W, Tahouneh V (2021) Frequency study of porous FGPM beam on two-parameter elastic foundations via Timoshenko theory. Steel Compos Struct Int J 40(1):139–156

    Google Scholar 

  43. Zhou K, Hu Z, Hua H (2021) Investigation of the nonstationary stochastic response of functionally graded piezoelectric material plates with general boundary conditions. Appl Math Model 1(96):315–335

    MathSciNet  MATH  Google Scholar 

  44. Tian W, Zhao T, Yang Z (2021) Nonlinear electro-thermo-mechanical dynamic behaviors of a supersonic functionally graded piezoelectric plate with general boundary conditions. Compos Struct 1(261):113326

    Google Scholar 

  45. Susheel C (2021) Shape and vibration control of spherical shell using functionally graded piezoelectric materials. Advances in engineering design. Springer, Singapore, pp 61–73

    Google Scholar 

  46. Pradhan KK, Chakraverty S (2021) Vibration of functionally graded piezoelectric material beams. New paradigms in computational modeling and its applications. Elsevier, Amsterdam, pp 11–34

    Google Scholar 

  47. Shen Y, Zhang P, He W, Xu M, Duan Q (2021) Transverse vibration responses of the in-plane-wise functionally graded piezoelectric composite plates. Mech Adv Mater Struct 20:1–7

    Google Scholar 

  48. Singh R, Sharma P (2021) Vibration analysis of an axially functionally graded material non-prismatic beam under axial thermal variation in humid environment. J Vib Control 9:10775463211037150

    Google Scholar 

  49. Lezgy-Nazargah M, Vidal P, Polit O (2013) An efficient finite element model for static and dynamic analyses of functionally graded piezoelectric beams. Compos Struct 1(104):71–84

    Google Scholar 

  50. Bellman R, Kashef BG, Casti J (1972) Differential quadrature: a technique for the rapid solution of nonlinear partial differential equations. J Comput Phys 10(1):40–52

    MathSciNet  MATH  Google Scholar 

  51. Bert CW, Malik M (1996) Differential quadrature method in computational mechanics: a review. Appl Mech Rev 49(1):1–28

    Google Scholar 

  52. Shu C (2012) Differential quadrature and its application in engineering. Springer Science & Business Media

    Google Scholar 

  53. Parashar SK, Von Wagner U, Hagedorn P (2004) A modified Timoshenko beam theory for nonlinear shear-induced flexural vibrations of piezoceramic continua. Nonlinear Dyn 37(3):181–205

    MATH  Google Scholar 

Download references

Funding

This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Rajasthan Technical University, Kota, 324010, India

    Barkha Gupta, Pankaj Sharma & S. K. Rathore

Authors
  1. Barkha Gupta
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Pankaj Sharma
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. S. K. Rathore
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Barkha Gupta.

Ethics declarations

Conflict of interest

The authors declare no conflict of interest in preparing this article.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gupta, B., Sharma, P. & Rathore, S.K. Free Vibration Analysis of AFGPM Non-uniform Beam: A Mathematical Modeling. J. Vib. Eng. Technol. 11, 2945–2954 (2023). https://doi.org/10.1007/s42417-022-00722-6

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s42417-022-00722-6

Keywords

Search

Navigation