Skip to main content
SpringerLink
Log in

Dynamic Behaviors of Thermal–Electric Imperfect Functionally Graded Piezoelectric Sandwich Microplates Based on Modified Couple Stress Theory

  • Original Paper
  • Published:
Journal of Vibration Engineering & Technologies Aims and scope Submit manuscript

Abstract

Introduction

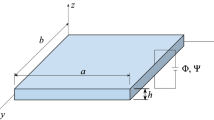
Based on the modified couple stress theory and the hyperbolic tangential mixed shear deformation theory, the free vibration and the transient responses of the functionally graded piezoelectric (FGP) sandwich microplates with considering the thermal–electric effects are investigated.

Methods

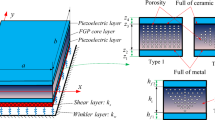
By introducing the porosity volume fraction, the perfect FGP sandwich mocroplate are destroyed and porous FGP sandwich plates are constructed. Electro-elastic material properties of porous FGP microplate vary across the thickness based on the modified power-law model. The governing equations derived from Hamilton's principle are solved analytically.

Results

By comparisons with the FEM simulation results and the previous results in the literature, the accuracy of the present established models is confirmed. Then the influences of thermal loadings, porosity volune fraction, material gradation, length scale to thickness ratios and facesheet thickness on the dynamic behaviors of FGP sandwich microplates are discussed.

Significance

These research can provide a theoretical basis for the accurate design of smart structures made of functionally graded piezoelectric materials.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  1. Rasool M, Kamran B (2021) Free vibration response of smart sandwich plates with porous CNT-reinforced and piezoelectric layers. Appl Mathl Model 96:66–79

    Article  MathSciNet  MATH  Google Scholar 

  2. Stassi S, Cauda V, Ottone C et al (2015) Flexible piezoelectric energy nanogenerator based on ZnO nanotubes hosted in a polycarbonate membrane. Nano Energy 13(36):474–481

    Article  Google Scholar 

  3. Mehrabi H, Hamedi M, Aminzahed I (2020) A novel design and fabrication of a micro-gripper for manipulation of micro-scale parts actuated by a bending piezoelectric. Microsys Technol 26(5):1563–1571

    Article  Google Scholar 

  4. Kumar S, Bhushan A (2022) Investigation of static and dynamic characteristics of an electrostatically actuated rectangular microplate with axial internal stress and transverse pressure. J Vib Eng Technol. https://doi.org/10.1007/s42417-022-00602-z

    Article  Google Scholar 

  5. Bakhsheshy A, Mahbadi H (2019) The effect of multidimensional temperature distribution on the vibrational characteristics of a size-dependent thick bi-directional functionally graded microplate. Noise Vib Worldw 50(9–11):267–290

    Article  Google Scholar 

  6. Chen Y, Zhang M, Su Y et al (2021) Coupling analysis of flexoelectric effect on functionally graded piezoelectric cantilever nanobeams. Micromachines 12(6):595

    Article  Google Scholar 

  7. Sator L, Sladek V, Sladek J (2020) Analysis of coupling effects in FGM piezoelectric plates by a meshless method. Compos Struct 244:112256

    Article  Google Scholar 

  8. Li C, Li S, Yao L et al (2015) Nonlocal theoretical approaches and atomistic simulations for longitudinal free vibration of nanorods/nanotubes and verification of different nonlocal models. Appl Math Model 39(15):4570–4585

    Article  MathSciNet  MATH  Google Scholar 

  9. Shen JP, Li C (2017) A semi-continuum-based bending analysis for extreme-thin micro/nano-beams and new proposal for nonlocal differential constitution. Compos Struct 172:210–220

    Article  Google Scholar 

  10. Rabczuk T, Ren H, Zhuang X (2019) A nonlocal operator method for partial differential equations with application to electromagnetic waveguide problem. Comput Mater Con 59(1):31–55

    Google Scholar 

  11. Ashoori MA, Mahmoodi MJ (2013) A micro-scale modeling of Kirchhoff plate based on modified strain-gradient elasticity theory. Eur J Mech A Solids 40:50–59

    Article  MathSciNet  MATH  Google Scholar 

  12. Gao XL, Huang JX, Reddy JN (2013) A non-classical third-order shear deformation plate model based on a modified couple stress theory. Acta Mech 224:2699–2718

    Article  MathSciNet  MATH  Google Scholar 

  13. Li YS, Pan E (2015) Static bending and free vibration of a functionally graded piezoelectric microplate based on the modified couple stress theory. Int J Eng Sci 97:40–59

    Article  MathSciNet  MATH  Google Scholar 

  14. Jankowski PJ, Żur KK, Kim J et al (2021) On the piezoelectric effect on stability of symmetric FGM porous nanobeams. Compos Struct 267:113880

    Article  Google Scholar 

  15. Liu C, Yu J, Zhang X et al (2020) Reflection behavior of elastic waves in the functionally graded piezoelectric microstructures. Eur J MechA-Solid 81:103955

    Article  MathSciNet  MATH  Google Scholar 

  16. Tham VV, Tran HQ, Tu TM (2021) Vibration characteristics of piezoelectric functionally graded carbon nanotube-reinforced composite doubly-curved shells. Appl Math Mech 42(6):819–840

    MathSciNet  MATH  Google Scholar 

  17. Sharifi Z, Khordad R, Gharaati A et al (2019) An analytical study of vibration in functionally graded piezoelectric nanoplates: nonlocal strain gradient theory. Appl Math Mech 40(12):1723–1740

    Article  MathSciNet  MATH  Google Scholar 

  18. Eftekhari SA, Hashemian M, Toghraie D (2020) Optimal vibration control of multi-layer micro-beams actuated by piezoelectric layer based on modified couple stress and surface stress elasticity theories. Physica A 546:123998

    Article  MathSciNet  MATH  Google Scholar 

  19. Yu P, Leng W, Peng L et al (2021) The bending and vibration responses of functionally graded piezoelectric nanobeams with dynamic flexoelectric effect. Results Phys 28:104624

    Article  Google Scholar 

  20. Wang A, Chen H, Zhang W (2019) Nonlinear transient response of doubly curved shallow shells reinforced with graphene nanoplatelets subjected to blast loads considering thermal effects. Compos Struct 225:111063

    Article  Google Scholar 

  21. Chen Z, Wang A, Qin B et al (2020) Investigation on free vibration and transient response of functionally graded graphene platelets reinforced cylindrical shell resting on elastic foundation. Eur Phys J Plus 135(7):582

    Article  Google Scholar 

  22. Salami SJ (2017) Low velocity impact response of sandwich beams with soft cores and carbon nanotube reinforced face sheets based on extended high order sandwich panel theory. Aerosp Sci Technol 66:165–176

    Article  Google Scholar 

  23. Wang Y, Zhou A, Fu T et al (2020) Transient response of a sandwich beam with functionally graded porous core traversed by a non-uniformly distributed moving mass. Int J Mech Des 16(3):519–540

    Google Scholar 

  24. Li ZN, Hao YX, Zhang W et al (2018) Nonlinear transient response of functionally graded material sandwich doubly curved shallow shell using new displacement field. Acta Mech Solida Sin 31(1):108–126

    Article  Google Scholar 

  25. Ren S, Meng G, Cheng F et al (2020) Transient responses of functionally graded magneto-electro-elastic structures with holes in thermal environment using stabilized node-based smoothed radial point interpolation method. Int J Mech Sci 185:105870

    Article  Google Scholar 

  26. Langdon GS, Gabriel S, von Klemperer CJ et al (2021) Transient response and failure of medium density fibreboard panels subjected to air-blast loading. Compos Struct 273:114253

    Article  Google Scholar 

  27. Chanda A, Sahoo R (2021) Trigonometric zigzag theory for free vibration and transient responses of cross-ply laminated composite plates. Mech Mater 155:103732

    Article  Google Scholar 

  28. Zhang J, Zhu X, Yang X et al (2019) Transient nonlinear responses of an auxetic honeycomb sandwich plate under impact loads. Int J Impact Eng 2019(134):103383

    Article  Google Scholar 

  29. Alibeigloo A (2021) Transient response analysis of sandwich cylindrical panel with FGM core subjected to thermal shock. Int J Mech Mater Des 17(3):707–719

    Article  Google Scholar 

  30. Sadiq SE, Jweeg MJ, Bakhy SH (2020). The effects of honeycomb parameters on transient response of an aircraft sandwich panel structure. IOP Conference Series: Materials Science and Engineering. IOP Publishing 928 (2): 022126.

  31. Saha P, Mandal KK (2021) Transient responses of laminated composite plates. Asian J Civil Eng 22(1):137–157

    Article  Google Scholar 

  32. Liu J, Hao C, Ye W et al (2021) Free vibration and transient dynamic response of functionally graded sandwich plates with power-law non-homogeneity by the scaled boundary finite element method. Comput Method Appl M 376:113665

    Article  MATH  Google Scholar 

  33. Zhou L, Tang J, Tian W et al (2021) A multi-physics coupling cell-based smoothed finite element micromechanical model for the transient response of magneto-electro-elastic structures with the asymptotic homogenization method. Thin Wall Struct 165:107991

    Article  Google Scholar 

  34. Wattanasakulpong N, Ungbhakorn V (2014) Linear and nonlinear vibration analysis of elastically restrained ends FGM beams with porosities. Aerosp Sci Technol 32(1):111–120

    Article  Google Scholar 

  35. Thai HT, Vo TP (2013) A size-dependent functionally graded sinusoidal plate model based on a modified couple stress theory. Compos Struct 96:376–383

    Article  Google Scholar 

  36. Mahi A, Bedia Ei AA, Tounsi A (2015) A new hyperbolic shear deformation theory for bending and free vibration analysis of isotropic functionally graded sandwich and laminated composite plates. Appl Mathl Model 39(9):2489–2508

    Article  MathSciNet  MATH  Google Scholar 

  37. Reddy JN (2004) Mechanics of laminated composite plates and shells, 2nd edn. CRC Press, New York

    MATH  Google Scholar 

  38. Ren H, Zhuang X, Rabczuk T (2020) A nonlocal operator method for solving partial differential equations. Comput Methods Appl Mech Eng 358:112621

    Article  MathSciNet  MATH  Google Scholar 

  39. Anitescu C, Atroshchenko E, Alajlan N et al (2019) Artificial neural network methods for the solution of second order boundary value problems. Comput Mater Con 59(1):345–359

    Google Scholar 

  40. Guo H, Rabczuk T, Zhuang X (2019) A deep collocation method for the bending analysis of Kirchhoff plate. Comput Mater Con 59(2):433–456

    Google Scholar 

  41. Zhuang X, Guo H, Alajlan N et al (2021) Deep autoencoder based energy method for the bending, vibration, and buckling analysis of Kirchhoff plates with transfer learning. Eur J Mech A -Solid 87:104225

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors gratefully acknowledge the support from the Beijing Natural Science Foundation (No.1222006) and the Natural Science Foundation of China (Grant Nos.11732005, 12172339).

Author information

Authors and Affiliations

  1. School of Mechanical and Electrical Engineering, Beijing Information Science and Technology University, Beijing, 100192, China

    Feng-Lian Li, Shi-Jie Fan, Yu-Xin Hao, Li Yang & Mei Lv

Authors
  1. Feng-Lian Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Shi-Jie Fan
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yu-Xin Hao
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Li Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Mei Lv
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Feng-Lian Li.

Ethics declarations

Conflicts of Interest

The authors declare that they have no competing interests and do not have any conflict of interests regarding the publication of this manuscript.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, FL., Fan, SJ., Hao, YX. et al. Dynamic Behaviors of Thermal–Electric Imperfect Functionally Graded Piezoelectric Sandwich Microplates Based on Modified Couple Stress Theory. J. Vib. Eng. Technol. 11, 2387–2401 (2023). https://doi.org/10.1007/s42417-022-00709-3

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s42417-022-00709-3

Keywords

Search

Navigation