Explicit Formulas for Optimal Parameters of Friction Dynamic Vibration Absorber Attached to a Damped System Under Various Excitations

Abstract

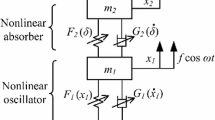
In this paper, a damped one degree-of-freedom system equipped with a friction dynamic vibration absorber is considered. The optimal parameters: tuning frequency ratio and friction slip load are derived for various excitations: harmonic force, random force, harmonic base acceleration, and random base acceleration. The random excitation is modeled as Gaussian white noise, with constant power spectral density. First, a linearization technique is used to solve the equations of motion. Then, the optimization is conducted analytically for the undamped system, it is based on viscous absorber parameters. Finally, explicit formulas for the damped system are determined using curve fitting methods. The present paper has the advantage of determining analytically the optimal parameters of the friction absorber. It is found that the proposed formulas lead to optimal response, rapidly and accurately.

Appendices

Appendix 1

For harmonic force, defining the dimensionless time as $\tau ={\omega }_{1}t$, and dividing Eqs. (5) by m₁ for the first, and by m₂ for the second, the equations of motion are expressed as follows:

$$\begin{array}{*{20}c} {\omega_{1}^{2} \ddot{x}_{1} + \frac{{c_{1} }}{{m_{1} }}\omega_{1} \dot{x}_{1} + \frac{{k_{1} }}{{m_{1} }}x_{1} + \frac{{k_{2} }}{{m_{1} }}\left( {x_{1} - x_{2} } \right) + \frac{\mu N}{{m_{1} }}{\text{sign}}\left( {\dot{x}_{1} - \dot{x}_{2} } \right) = \frac{{F_{0} }}{{m_{1} }}e^{i\omega \tau } ,} \\ {\omega_{1}^{2} \ddot{x}_{2} - \frac{{k_{2} }}{{m_{2} }}\left( {x_{1} - x_{2} } \right) - \frac{\mu N}{{m_{2} }}{\text{sign}}\left( {\dot{x}_{1} - \dot{x}_{2} } \right) = 0,} \\ \end{array}$$

(43)

where $\omega = \frac{\Omega }{{\omega_{1} }}$, $\omega_{1}^{2} \ddot{x}_{1} = \omega_{1}^{2} \frac{{{\text{d}}^{2} x_{1} \left( \tau \right)}}{{{\text{d}}\tau^{2} }} = \frac{{{\text{d}}^{2} x_{1} \left( t \right)}}{{{\text{d}}t^{2} }}$, $\omega_{1}^{2} \ddot{x}_{2} = \omega_{1}^{2} \frac{{{\text{d}}^{2} x_{2} \left( \tau \right)}}{{{\text{d}}\tau^{2} }} = \frac{{{\text{d}}^{2} x_{2} \left( t \right)}}{{{\text{d}}t^{2} }}$, $\omega_{1} \dot{x}_{1} = \omega_{1} \frac{{{\text{d}}x_{1} \left( \tau \right)}}{{{\text{d}}\tau }}$, $\omega_{1} \dot{x}_{2} = \omega_{1} \frac{{{\text{d}}x_{2} \left( t \right)}}{{{\text{d}}t}}$ Then, dividing Eqs. (43) by${\omega }_{1}^{2}$, the equations become:

$$\begin{array}{*{20}c} {\ddot{x}_{1} + 2\xi_{1} \dot{x}_{1} + x_{1} + r\omega_{{\text{a}}}^{2} \left( {x_{1} - x_{2} } \right) + \frac{\mu N}{{m_{1} \omega_{1}^{2} }}{\text{sign}}\left( {\dot{x}_{1} - \dot{x}_{2} } \right) = \frac{{F_{0} }}{{m_{1} \omega_{1}^{2} }}e^{i\omega \tau } ,} \\ {\ddot{x}_{2} - \omega_{{\text{a}}}^{2} \left( {x_{1} - x_{2} } \right) - \frac{\mu N}{{m_{2} \omega_{1}^{2} }}{\text{sign}}\left( {\dot{x}_{1} - \dot{x}_{2} } \right) = 0,} \\ \end{array}$$

(44)

where $r = \frac{{m_{2} }}{{m_{1} }},\;\omega_{{\text{a}}} = \frac{{\omega_{2} }}{{\omega_{1} }},\;\xi_{1} = \frac{{c_{1} }}{{2m_{1} \omega_{1} }},\;\omega_{1} = \sqrt {\frac{{k_{1} }}{{m_{1} }}} ,\;\omega_{2} = \sqrt {\frac{{k_{2} }}{{m_{2} }}} .$

The displacement x_s is introduced, it is defined as:

$$x_{s} = \frac{{F_{0} }}{{m_{1} \omega_{1}^{2} }}.$$

Now, dividing Eqs. (44) by x_s, the following equations are obtained:

$$\begin{array}{*{20}c} {\ddot{y}_{1} + 2\xi_{1} \dot{y}_{1} + y_{1} + r\omega_{{\text{a}}}^{2} \left( {y_{1} - y_{2} } \right) + \delta {\text{sign}}\left( {\dot{y}_{1} - \dot{y}_{2} } \right) = e^{i\omega \tau } ,} \\ {\ddot{y}_{2} - \omega_{{\text{a}}}^{2} \left( {y_{1} - y_{2} } \right) - \frac{\delta }{r}{\text{sign}}\left( {\dot{y}_{1} - \dot{y}_{2} } \right) = 0,} \\ \end{array}$$

(45)

where $y_{1} = \frac{{x_{1} }}{{x_{s} }},y_{2} = \frac{{x_{2} }}{{x_{s} }},\delta = \frac{\mu N}{{F_{0} }}.$

Appendix 2

For harmonic acceleration, using the dimensionless time $\tau ={\omega }_{1}t$, and dividing Eqs. (8) by m₁ for the first, and by m₂ for the second, the equations of motion are expressed as follows

$$\begin{array}{*{20}c} {\omega_{1}^{2} \ddot{x}_{1} + \frac{{c_{1} }}{{m_{1} }}\omega_{1} \dot{x}_{1} + \frac{{k_{1} }}{{m_{1} }}x_{1} + \frac{{k_{2} }}{{m_{1} }}\left( {x_{1} - x_{2} } \right) + \frac{\mu N}{{m_{1} }}{\text{sign}}\left( {\dot{x}_{1} - \dot{x}_{2} } \right) = - G_{0} e^{i\omega \tau } ,} \\ {\omega_{1}^{2} \ddot{x}_{2} - \frac{{k_{2} }}{{m_{2} }}\left( {x_{1} - x_{2} } \right) - \frac{\mu N}{{m_{2} }}{\text{sign}}\left( {\dot{x}_{1} - \dot{x}_{2} } \right) = - G_{0} e^{i\omega \tau } .} \\ \end{array}$$

(46)

Then, dividing Eqs. (46) by ${\omega }_{1}^{2}$, the equations become:

$$\begin{array}{*{20}c} {\ddot{x}_{1} + 2\xi_{1} \dot{x}_{1} + x_{1} + r\omega_{a}^{2} \left( {x_{1} - x_{2} } \right) + \frac{\mu N}{{m_{1} \omega_{1}^{2} }}{\text{sign}}\left( {\dot{x}_{1} - \dot{x}_{2} } \right) = - \frac{{G_{0} }}{{\omega_{1}^{2} }}e^{i\omega \tau } ,} \\ {\ddot{x}_{2} - \omega_{a}^{2} \left( {x_{1} - x_{2} } \right) - \frac{\mu N}{{m_{2} \omega_{1}^{2} }}{\text{sign}}\left( {\dot{x}_{1} - \dot{x}_{2} } \right) = - \frac{{G_{0} }}{{\omega_{1}^{2} }}e^{i\omega \tau } .} \\ \end{array}$$

(47)

The displacement x_s is introduced, it is defined as:

$$x_{s} = \frac{{G_{0} }}{{\omega_{1}^{2} }}.$$

Now, dividing Eqs. (47) by x_s, the following equations are obtained:

$$\begin{array}{*{20}c} {\ddot{y}_{1} + 2\xi_{1} \dot{y}_{1} + y_{1} + r\omega_{{\text{a}}}^{2} \left( {y_{1} - y_{2} } \right) + \delta {\text{sign}}\left( {\dot{y}_{1} - \dot{y}_{2} } \right) = - e^{i\omega \tau } ,} \\ {\ddot{y}_{2} - \omega_{{\text{a}}}^{2} \left( {y_{1} - y_{2} } \right) - \frac{\delta }{r}{\text{sign}}\left( {\dot{y}_{1} - \dot{y}_{2} } \right) = - e^{i\omega \tau } .} \\ \end{array}$$

(48)

Appendix 3

For random force, dividing Eqs. (21) by m₁ for the first, and by m₂ for the second, the equations of motion are expressed as follows:

$$\begin{array}{*{20}c} {\omega_{1}^{2} \ddot{x}_{1} + \frac{{c_{1} }}{{m_{1} }}\omega_{1} \dot{x}_{1} + \frac{{k_{1} }}{{m_{1} }}x_{1} + \frac{{k_{2} }}{{m_{1} }}\left( {x_{1} - x_{2} } \right) + \frac{\mu N}{{m_{1} }}{\text{sign}}\left( {\dot{x}_{1} - \dot{x}_{2} } \right) = \frac{F}{{m_{1} }},} \\ {\omega_{1}^{2} \ddot{x}_{2} - \frac{{k_{2} }}{{m_{2} }}\left( {x_{1} - x_{2} } \right) - \frac{\mu N}{{m_{2} }}{\text{sign}}\left( {\dot{x}_{1} - \dot{x}_{2} } \right) = 0.} \\ \end{array}$$

(49)

Then, dividing Eqs. (49) by ${\omega }_{1}^{2}$, the equations become:

$$\begin{array}{*{20}c} {\ddot{x}_{1} + 2\xi_{1} \dot{x}_{1} + x_{1} + r\omega_{a}^{2} \left( {x_{1} - x_{2} } \right) + \frac{\mu N}{{m_{1} \omega_{1}^{2} }}{\text{sign}}\left( {\dot{x}_{1} - \dot{x}_{2} } \right) = \frac{F}{{m_{1} \omega_{1}^{2} }},} \\ {\ddot{x}_{2} - \omega_{{\text{a}}}^{2} \left( {x_{1} - x_{2} } \right) - \frac{\mu N}{{m_{2} \omega_{1}^{2} }}{\text{sign}}\left( {\dot{x}_{1} - \dot{x}_{2} } \right) = 0.} \\ \end{array}$$

(50)

The displacement x_s is introduced, it is defined as:

$$x_{s} = \sqrt {\frac{{2\pi S_{0} \omega_{1} }}{{k_{1}^{2} }}} .$$

Dividing Eqs. (50) by x_s, the following equations are obtained:

$$\begin{array}{*{20}c} {\ddot{y}_{1} + 2\xi_{1} \dot{y}_{1} + y_{1} + r\omega_{{\text{a}}}^{2} \left( {y_{1} - y_{2} } \right) + \delta {\text{sign}}\left( {\dot{y}_{1} - \dot{y}_{2} } \right) = f,} \\ {\ddot{y}_{2} - \omega_{{\text{a}}}^{2} \left( {y_{1} - y_{2} } \right) - \frac{\delta }{r}{\text{sign}}\left( {\dot{y}_{1} - \dot{y}_{2} } \right) = 0.} \\ \end{array}$$

(51)

Appendix 4

For random acceleration, dividing Eqs. (32) by m₁ for the first, and by m₂ for the second, the equations of motion are expressed as follows:

$$\begin{array}{*{20}c} {\omega_{1}^{2} \ddot{x}_{1} + \frac{{c_{1} }}{{m_{1} }}\omega_{1} \dot{x}_{1} + \frac{{k_{1} }}{{m_{1} }}x_{1} + \frac{{k_{2} }}{{m_{1} }}\left( {x_{1} - x_{2} } \right) + \frac{\mu N}{{m_{1} }}{\text{sign}}\left( {\dot{x}_{1} - \dot{x}_{2} } \right) = - G,} \\ {\omega_{1}^{2} \ddot{x}_{2} - \frac{{k_{2} }}{{m_{2} }}\left( {x_{1} - x_{2} } \right) - \frac{\mu N}{{m_{2} }}{\text{sign}}\left( {\dot{x}_{1} - \dot{x}_{2} } \right) = - G.} \\ \end{array}$$

(52)

Then, dividing Eqs. (52) by ${\omega }_{1}^{2}$, the equations become:

$$\begin{array}{*{20}c} {\ddot{x}_{1} + 2\xi_{1} \dot{x}_{1} + x_{1} + r\omega_{{\text{a}}}^{2} \left( {x_{1} - x_{2} } \right) + \frac{\mu N}{{m_{1} \omega_{1}^{2} }}{\text{sign}}\left( {\dot{x}_{1} - \dot{x}_{2} } \right) = - \frac{G}{{\omega_{1}^{2} }},} \\ {\ddot{x}_{2} - \omega_{{\text{a}}}^{2} \left( {x_{1} - x_{2} } \right) - \frac{\mu N}{{m_{2} \omega_{1}^{2} }}{\text{sign}}\left( {\dot{x}_{1} - \dot{x}_{2} } \right) = - \frac{G}{{\omega_{1}^{2} }}.} \\ \end{array}$$

(53)

The displacement x_s is introduced, it is defined as:

$$x_{s} = \sqrt {\frac{{2\pi S_{0} }}{{\omega_{1}^{3} }}} .$$

Now, dividing Eqs. (53) by x_s, the following equations are obtained:

$$\begin{array}{*{20}c} {\ddot{y}_{1} + 2\xi_{1} \dot{y}_{1} + y_{1} + r\omega_{a}^{2} \left( {y_{1} - y_{2} } \right) + \delta {\text{sign}}\left( {\dot{y}_{1} - \dot{y}_{2} } \right) = - g,} \\ {\ddot{y}_{2} - \omega_{a}^{2} \left( {y_{1} - y_{2} } \right) - \frac{\delta }{r}{\text{sign}}\left( {\dot{y}_{1} - \dot{y}_{2} } \right) = - g.} \\ \end{array}$$

(54)

Appendix 5

The fminimax optimization as defined in the MATLAB User’s Guide and Optimization Toolbox:

$$x \, = \, f\min i\max ({\kern 1pt} Y_{1} ,x_{0} ,A,b,A_{{{\text{eq}}}} ,b_{{{\text{eq}}}} ,l_{{\text{b}}} ,u_{{\text{b}}} ).$$

All the parameters of the optimization procedure are listed in Table

Table 5 Parameters of the optimization procedure

5. There are no equality or inequality constraints in this problem.