Stability and Synchronous Characteristics of Dual-Rotors Vibrating System Considering the Material Effects

Abstract

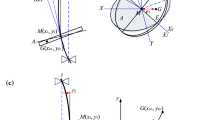
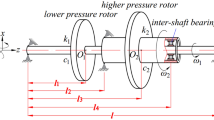
The stability and synchronization characteristics of vibrating system cannot be ignored to get a better form of motion. In the present work the stability and synchronous characteristics of dual-rotors vibrating system considering the material effects are studied. Firstly, the equations of motion about the vibrating system are solved using Lagrange theory, Newton’s laws of motion and momentum theorem. Then the stability of the system is discussed based on the theory of nonlinear dynamics and Poincare theory using numerical simulation. Further the effect rules of material with different mass on phase difference of dual-rotors are revealed. Finally, the reliability and correctness of theoretical analysis and numerical simulation are verified approximately based on a prototype experiment in which the amplitude errors of vertical displacement about test point P1 and P2 are within the allowable limits of experimental error. It can be concluded that the stability of the system and the synchronous characteristics of dual-rotors decline with the mass ratio of material to vibrating body increasing.

Appendix

$m_{0}$ :

Mass of vibrating body

$m_{i}$ :

Mass of eccentric rotor $i{\kern 1pt} {\kern 1pt} {\kern 1pt} (i = 1,2)$

$m$ :

Mass of material

$M$ :

The total Mass of the vibrating system $M = m_{0} + m_{1} + m_{2}$

$g$ :

Acceleration of gravity

$k_{j}$ :

Stiffness coefficient of springs in $j$-direction $j{\kern 1pt} {\kern 1pt} {\kern 1pt} (j = x,y,\psi )$

$f_{j}$ :

Damping coefficient of damper in $j$-direction $j{\kern 1pt} {\kern 1pt} {\kern 1pt} (j = x,y,\psi )$

$f_{1} ,f_{2}$ :

Damping coefficients of the exciter shaft of dual-rotors

$r_{i}$ :

Rotation radius of eccentric rotor $i{\kern 1pt} {\kern 1pt}$($i =$ 1, 2)

$r$ :

Rotation radius of dual-rotors

$l_{i}$ :

Distance between o and o₁/ o₂ $i{\kern 1pt} {\kern 1pt}$($i =$ 1, 2)

$J_{m}$ :

Rotational inertia of vibrating body

$\omega_{m}$ :

Average speed of the eccentric rotor in a cycle

$n$ :

Number of periods of the force

$x_{0} ,y_{0}$ :

Initial value of displacement in $j$-direction $j{\kern 1pt} {\kern 1pt} {\kern 1pt} (j = x,y)$

$\psi_{0} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \dot{\psi }_{0}$ :

Initial value of displacement and velocity in $\psi$-direction

$R$ :

Recovery coefficient

$\beta$ :

The angle between $\overline{oo} {}_{2}$ and $x$-direction

$\varphi_{i}$ :

Angular displacement of eccentric rotor $i{\kern 1pt} {\kern 1pt}$($i =$ 1, 2)

$\varphi$ :

The average phase angle

$\alpha$ :

Phase difference of dual-rotors $\alpha = \varphi_{1} - \varphi_{2}$

$\rho_{i} {\kern 1pt} {\kern 1pt}$ :

Magnification factor of amplitude $(i = x,y,\psi )$

${\kern 1pt} \rho_{j}^{\prime } {\kern 1pt} {\kern 1pt} {\kern 1pt}$ :

Magnification factor of amplitude $(j = x,y)$

$\gamma_{i}$ :

Lagging angle of phase $(i = x,y,\psi )$

$\gamma_{j}^{\prime }$ :

Lagging angle of phase $(j = x,y)$

$T$ :

Kinetic energy of the system

$V$ :

Potential energy of the system

$F_{f}$ :

Friction force

$F_{N}$ :

Supporting force

$F_{mx} ,F_{my}$ :

Nonlinear forces of vibrating body exerted by the material

$T_{R1} ,T_{R2}$ :

Electromagnetic torques of dual-rotors

$\Delta \ddot{x},\Delta \ddot{y},\Delta \ddot{x}_{ - } ,\Delta \ddot{x}_{ + }$ :

Relative accelerations

$t_{a}$ :

Starting time of forward sliding motion

${\kern 1pt} \varphi_{a}$ :

Starting angle of forward sliding motion

$t_{c}$ :

Starting time of backward sliding motion

$\varphi_{c}$ :

Starting angle of backward sliding motion

$t_{b}$ :

Ending time of forward sliding motion

$t_{d}$ :

Ending time of backward sliding motion

$\varphi_{b}$ :

Ending angle of forward sliding motion

$\varphi_{d}$ :

Ending angle of backward sliding motion

$t_{e}$ :

Starting time of hop motion

$\varphi_{e}$ :

Starting angle of hop motion

$t_{f}$ :

Ending time of hop motion

$\varphi_{f}$ :

Ending angle of hop motion

$a_{{{\text{I}}x}} ,a_{{{\text{I}}y}}$ :

Equivalent accelerations

$\Delta t$ :

Impact time

$t_{g}$ :

Starting time of relative rest phase

$\varphi_{g}$ :

Starting angle of relative rest phase

$t_{h}$ :

Ending time of relative rest phase

$\varphi_{h}$ :

Ending angle of relative rest phase