Simultaneous Optimization of Launch Vehicle Stage and Trajectory Considering Flight-Requirement Constraints

Abstract

A conceptual design of a launch vehicle encompasses various disciplines, such as structural design, aerodynamics, propulsion systems, flight control, and stage sizing. This paper focuses on optimizing trajectory and stage size. Traditional approaches used for the conceptual design of a launch vehicle conduct the stage and trajectory designs sequentially, often leading to high computational complexity and suboptimal results. This paper presents an optimization framework that addresses both trajectory optimization and staging in an integrated way. The proposed framework aims to minimize the lift-off mass while satisfying the constraints on flight requirements (e.g., maximum dynamic pressure and the impact points of separated parts). A case study demonstrates the advantage of the proposed framework compared to the traditional sequential optimization approach.

1 Introduction

The performance of launch vehicles plays a critical role in space exploration. Optimization of launch vehicle performance considers multiple disciplines such as structural design, aerodynamics, propulsion, flight control, and stage sizing. During the conceptual design phase, crucial decisions regarding various factors are made, significantly influencing the final design of the launch vehicle. Stage sizing and trajectory design are two interconnected key elements in the conceptual design process of a launch vehicle.

The optimal staging process minimizes the lift-off mass by efficiently allocating each stage’s structural and propellant masses while generating a sufficient velocity increment to carry the payload into the target orbit. The trajectory optimization procedure determines the optimal ascent trajectory of a launch vehicle to maximize the payload mass delivered to the target orbit. The trajectory optimization involves flight simulations and evaluating velocity losses during flight. As velocity losses influence the need for more velocity increments, optimal staging and trajectory optimization are interrelated.

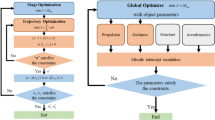
Traditional approaches adopt a sequential staging and trajectory optimization procedure, followed by iterations for convergence [1, 2]. The designer first allocates the stage masses based on the target orbit, engine characteristics, and structural mass ratio based on the assumption of velocity loss terms. Then, trajectory optimization using the stage information is conducted, considering flight-requirement constraints and yielding the computed velocity loss terms. This procedure continues until the assumed and computed velocity loss terms converge. Past studies demonstrated the effectiveness of the approach above utilizing sequential design and iterations. However, this approach often fails to capture the inter dependencies between each element, leading to a suboptimal design. Moreover, the computational complexity of these tasks makes the conceptual design procedure challenging.

This study combines optimal stage sizing and trajectory optimization in the conceptual design phase. The proposed optimization framework enables obtaining an optimal design by simultaneously considering constraints based on flight requirements, which often lead to suboptimal designs in the traditional sequential method. The other advantageous property is its reduced computational complexity. Unlike the iterative approach, the proposed optimization framework requires solving the integrated optimization problem only once, streamlining the process and reducing the risk of algorithm divergence.

The remainder of this paper is organized as follows. Section 2 provides a brief overview of previous studies. Section 3 introduces the integrated framework for optimizing the stage size and launch trajectory. Section 4 presents several case studies to validate and compare the developed framework to traditional approaches. Lastly, Sect. 5 concludes the paper and discusses potential future research directions.

2 Preliminaries

2.1 Optimal Staging of a Launch Vehicle

The optimal stage sizing (P_S) of a launch vehicle determines the mass distributions (propellant and stage masses) for each vehicle stage to put the payload into the target orbit. The propulsion system capability (specific impulse or equivalently effective exhaust velocity) and the structural characteristics (mass fraction) are external parameters for the optimal sizing problem. Malina first proposed an efficient optimal sizing approach for multi-stage rockets [3], and many studies utilized the approach for the optimal staging of launch vehicles [4,5,6,7,8,9]. This section provides a concise overview of previous studies on the optimal staging problem.

We assume the exhaust velocity of the propulsion system and the structural mass fraction for each stage are given parameters used in the optimal staging problem. Note that the structural mass fraction for stage k (ε_k) is the ratio of the structural mass (m_s,k) to the sum of the structural and propellant (m_p,k) masses defined as follows:

$$ \varepsilon_{k} \equiv \frac{{m_{s,k} }}{{m_{s,k} + m_{p,k} }}. $$

(1)

In addition, we define m_pl,k as the mass considered as the payload of the k^th stage, equivalent to the sum of the masses of the upper stages and payload. Note that the value corresponds to the initial mass of the (k + 1)^th stage of the launch vehicle (m_i,k+1), which is the mass immediately after separating the k^th stage (see Fig. 1)

$$ m_{pl,k} = m_{\text{PL}} + \sum\limits_{j = k + 1}^{n} (m_{s,j} + m_{p,j} ) = \left\{ {\begin{array}{*{20}c} {m_{i,k + 1} \;\;\;(k < n)} \\ {m_{\text{PL}} \;\;\;\;\;\;(k = n)} \\ \end{array} } \right. .$$

(2)

Fig. 1

Mass components of a multi-stage launch vehicle

The mass ratio of each stage (µ_k) is the ratio between the initial mass (m_i,k) and the final mass (m_f,k) after consuming the whole propellant of the stage

$$ \mu_{k} \equiv \frac{{m_{i,k} }}{{m_{f,k} }} = \frac{{m_{i,k} }}{{m_{i,k} - m_{p,k} }} = \frac{{m_{s,k} + m_{p,k} + m_{pl,k} }}{{m_{s,k} + m_{pl,k} }}. $$

(3)

Based on the definitions above, the relationship between the initial and payload masses of the k^th stage can be derived as follows:

$$ \frac{{m_{i,k} }}{{m_{pl,k} }} = \frac{{m_{i,k} }}{{m_{i,k} - m_{p,k} - m_{s,k} }} = \frac{{\mu_{k} (1 - \varepsilon_{k} )}}{{1 - \mu_{k} \varepsilon_{k} }}. $$

(4)

Therefore, the ratio of the lift-off mass to the payload mass (m_Lift-off/m_PL) is expressed as follows:

$$\begin{aligned} \frac{{m_{{\text{Lift - off}}} }}{{m_{{{\text{PL}}}} }} &= \frac{{m_{i,1} }}{{m_{pl,1} }} \times \frac{{m_{pl,1} }}{{m_{pl,2} }} \times \cdots \times \frac{{m_{pl,n} }}{{m_{{{\text{PL}}}} }} \\ &= \frac{{m_{i,1} }}{{m_{pl,1} }} \times \frac{{m_{i,2} }}{{m_{pl,2} }} \times \cdots \times \frac{{m_{i,n} }}{{m_{pl,n} }}\\& = \prod\limits_{k = 1}^{n} {\frac{{\mu_{k} (1 - \varepsilon_{k} )}}{{1 - \mu_{k} \varepsilon_{k} }}}. \end{aligned}$$

(5)

The velocity increment generated by each stage can be calculated using Tsiolkovsky’s rocket equation. The total velocity increment of the launch vehicle is obtained by summing the velocity increments produced by all stages as follows:

$$ \sum\limits_{k = 1}^{n} \Delta v_{k} = \sum\limits_{k = 1}^{n} v_{ex,k} \ln \mu_{k}. $$

(6)

The velocity increment calculated by Eq. (6) should be greater than or equal to the required velocity increment (Δv_req) to put the payload into the target orbit. Hence, the optimal stage sizing problem can be formulated as follows:

[P_S: Optimization of the stage size].

For given values of v_ex,i, ε_k, and Δv_req

$$ \mathop {\min }\limits_{{\mu_{1} , \cdots ,\mu_{n} }} \prod\limits_{k = 1}^{n} \frac{{\mu_{k} (1 - \varepsilon_{k} )}}{{1 - \mu_{k} \varepsilon_{k} }}, $$

(7)

subject to

$$ \sum\limits_{k = 1}^{n} {v_{{ex,k}} \ln \mu _{k} - \Delta v_{{{\text{req}}}} } \ge 0. $$

(8)

One can solve the formulated optimization problem by introducing the Lagrange multiplier and applying a numerical root-finding procedure [10]. Based on the obtained optimal mass ratios (µ_k^*), the optimal mass and velocity increment of each stage (m_p,k^*, m_s,k^*, Δv_k^*) can be calculated.

2.2 Considering Velocity Losses

While various studies have addressed the optimal staging problem described in the previous section, early studies did not consider velocity losses. Instead, they determined the required velocity increment (Δv_req) using the target orbital velocity (v_f) and the initial velocity due to the Earth’s rotation (v_i). However, the actual flight of a rocket involves the velocity losses caused by various sources (e.g., gravity, steering, aerodynamic drag, and pressure difference at the engine exit).

Gravity loss is the speed reduction required to overcome the Earth’s gravity during a flight. Steering loss occurs when a vehicle’s thrust vector is not parallel to the velocity vector, resulting in the thrust not being fully used to increase the speed of the launch vehicle. Drag loss represents the deceleration caused by the aerodynamic force during the ascent of the launch vehicle. Pressure loss refers to the reduction in speed resulting from decreased thrust relative to vacuum thrust due to atmospheric pressure. The velocity loss, which is caused by the cumulative effect of these velocity loss components, significantly reduces the final speed of the launch vehicle. Consequently, the velocity loss necessitates a larger velocity increment provided by the rocket, and its consideration for optimal stage sizing is critical.

Some studies assessed the required velocity increment (Δv_req) with v_f, v_i, and Δv_Loss values (Δv_req = v_f – v_i + Δv_Loss) [10, 11], making compensation for velocity losses proportional to the velocity increment for each stage. However, the velocity loss for each stage does not necessarily scale proportionately to the velocity increment allocated to the stage, potentially leading to a suboptimal design [12]. Other recent studies adopted a different approach [14,15,16,17]. Instead of simply adding the loss terms to Δv_req, they obtained the ideal velocity increment for each stage under the loss-free condition. Then, they assigned the velocity loss from stage k (Δv_Loss,k) to Δv_k. Since Δv_Loss,k is directly linked to the flight trajectory, any modification to a stage size may lead to a change in velocity loss associated with the stage. Consequently, the methodology iteratively solves the trajectory optimization problem and the stage sizing problem, yielding an optimal launch vehicle size design. Although this methodology showed reasonable performance, the iterative process does not always obtain an optimal design due to the inter-dependencies among stage sizing, trajectory, and velocity losses. The trajectory under flight-requirement constraints may differ from the constraint-free condition, and the velocity losses also be affected and changed accordingly. In the iterative approach, the constraints on flight requirements can only be handled implicitly using the velocity losses during the optimal staging process. Particularly, one can observe that the process converges to a suboptimal design when imposing constraints related to the flight-requirement, such as maximum dynamic pressure and range-safety constraints.

Jamilnia [10] proposed simultaneous optimization of staging and trajectory, but the absence of a discussion on flight-requirement constraints limited capturing advantages in the simultaneous optimization process. Jo [13] employed simultaneous optimization while optimizing the size of the rocket family. However, this work did not deal with the range-safety constraints for flight (e.g., impact points of separated stages and fairing), which is a crucial flight-requirement.

Note that the new framework proposed in this paper can simultaneously consider various constraints on flight requirements and efficiently obtain the optimal solution. The case study section of this paper provides the discussions on implementation details and the advantages of the proposed framework.

2.3 Instantaneous Impact Point (IIP) for Launch Safety

An IIP is the touch-down point of a launch vehicle in case of the immediate termination of the propelled flight. Monitoring the IIP during launch operation is one of the most crucial tasks for ensuring the safety of space launch vehicles [18, 19]. A multi-stage expendable launch vehicle separates the lower stage(s), which drops to the Earth’s surface. The trajectory of a launch vehicle should be carefully designed so that the collision risk of the separated stage is minimized [20]. The position and velocity of a launch vehicle determine its impact point. Considering that the stage sizing determines the velocity increment, the integrated design of the vehicle stage and launch trajectory can effectively address the issue of range-safety constraint along with the launch capability (i.e., maximized payload-mass ratio) [17]. Figure 2 illustrates the concept of the IIP.

Fig. 2

Impact point of separated stage

Accuracy and speed are two critical features required for IIP prediction used in a range-safety system. Therefore, studies for IIP modeling and computation have focused on two primary objectives: enhancing the prediction accuracy and accelerating the computation. Montenbruck et al. [21, 22] calculated the IIP based on the assumption that the launch vehicle experiences a constant downward gravitational acceleration in the LVLH coordinate system. They compensated for the modeling errors (e.g., earth curvature, gravitational acceleration, and aerodynamic drag) by introducing the correction terms for the calculation. On the other hand, the Keplerian algorithm used Kepler’s two-body problem as the basis to predict the IIP. This methodology is considered more suitable for operating space launch vehicles than the past approach based on the constant-gravity assumption. The algorithm introduced in references [23] and [24] calculates the IIP while assuming that the vehicle’s motion without propulsion is subject to only Kepler’s central gravitational acceleration. These algorithms employed an iterative procedure to determine the IIP. Alternatively, Ahn and Roh [25] proposed a Keplerian algorithm without iterations, reducing the potential issues related to the computational burden caused by excessive iterations. Ahn and Seo [26] improved the algorithm to reflect the atmospheric drag and oblateness of the Earth based on the response-surface method. Their approach modeled the correction terms for the flight angles and time with the current position and vector as inputs and improved the prediction accuracy of the IIP significantly. Nam and Ahn [27] introduced the concept of the adjusted instantaneous impact point (AIIP) to improve the flight safety (termination) decision-making process based on the IIP. The AIIP considers the potential delay between the flight termination command generation and the actual engine cut-off by using the “Delta IIP.” They developed the analytical formula representing the time derivatives of IIP due to the external force (thrust) to compute the Delta IIP. They showed that AIIP-based decision-making could reduce the chances of undetected collision risk and unnecessary flight termination, improving flight-safety operations.

The next section presents a framework that can optimize the launch vehicle stages and flight trajectory integratively while considering the range-safety constraints on the IIP.

3 Simultaneous Optimization Framework

The optimization framework proposed in this study consists of three modules. The first module is a flight simulation module that simulates the motion of a launch vehicle. It uses the specification of the launch vehicle, flight sequence, and the histories of attitude angles as input parameters and generates the vehicle’s states (e.g., mass, position/velocity, and velocity loss terms) by integrating the dynamic equations. The second module takes the state variables (output of the first module) and computes output variables associated with flight-requirement constraints (e.g., flight environment, range-safety, orbital elements, and radar tracking). Various coordinate transformation and conversion formulae are used to calculate the output variables from the states. One of the important output variables associated with range-safety operations is the IIP, which is explained in detail in the previous section. The last module formulates the simultaneous stage/trajectory design as a nonlinear optimization problem and solves it using a gradient-based algorithm.

The proposed framework discretizes the entire flight time (from lift-off to orbit insertion) into multiple intervals referred to as Phases. For example, Phase p is the time interval starting/terminating at t_p–1 and t_p, respectively (= [t_p–1, t_p]). While trajectory optimization is an optimal control problem involving continuous states and input in nature, parameter discretization enables designers to handle the problem together with stage sizing in a single optimization framework. Note that the duration of a phase involving active thrust is subject to change depending on the propellant mass of each stage, while the duration of an unpropelled phase remains constant. Phases are designed in such a way that important flight events (e.g., stage/fairing separations, ignition/cut-off of an engine) occur at the end of each phase (t_p). Figure 3 illustrates the configuration of a phase using discretized time points.

Fig. 3

Example of phase configuration

The framework assumes the exhaust velocity (v_ex,k) and structural mass fraction (ε_k) as given constant parameters. The decision variables of the optimization problem are the angles representing the thrust directions at discretized time points (θ(t_p) and ψ(t_p)) and the structural masses of each stage (m_s,k), which constitute the input variables of the first module along with the propellant masses. Note that the structural masses determine the propellant masses of each stage (m_p,k) based on the constant structural mass fraction assumption. Its objective is to minimize the lift-off mass of the launch vehicle while satisfying the specified constraints on the target orbit insertion and flight requirements. The constraints of the optimal design problem are imposed on the output variables of the second module (e.g., altitude, inertial speed, flightpath angle, inclination angle, dynamic pressure and IIP) at discretized time points. Figure 4 shows the architecture of the simultaneous optimization framework proposed in this paper.

Fig. 4

Architecture of the proposed optimization framework

The following subsections explain the detailed implementation of three modules constituting the proposed framework.

3.1 Flight Simulation Module

The flight simulation module implements a 3-degree-of-freedom point mass model. This module computes the position (r), velocity (v), and velocity loss values (Δv_Loss) over simulation time by integrating the differential equations describing the vehicle dynamics. The dynamic equations describing the vehicle motion at each phase are as follows:

$$ \frac{{d{\varvec{r}}}}{dt} = {\varvec{v}}, $$

(9)

$$ \frac{{d{\varvec{v}}}}{dt} = \left( {{\varvec{f}}_{T} + {\varvec{f}}_{a} + {\varvec{f}}_{g} } \right)/m, $$

(10)

$$ \dot{m}_{p,j} = \frac{{T_{v,j} }}{{v_{ex,j} }}, $$

(11)

$$ \frac{{d\Delta v_{L,p} }}{dt}{ = }\frac{{p_{a} A_{e,j} }}{m}, $$

(12)

$$ \frac{{d\Delta v_{L,d} \, }}{dt} = \frac{{||{\varvec{f}}_{a} ||}}{m}, $$

(13)

$$ \frac{{d\Delta v_{L,g} }}{dt}{ = }\frac{{||{\varvec{f}}_{g} ||\sin \gamma }}{m}, $$

(14)

$$ \frac{{d\Delta v_{L,s} }}{dt}{ = }\frac{{||\varvec{f}_{\varvec{T}} ||(1 - \cos \delta )}}{m}. $$

(15)

Equations (9–11) represent the translational motion of the launch vehicle expressed in an Earth-Centered Inertial (ECI) coordinate frame. In these equations, m is the mass of the launch vehicle expressed as follows:

$$ m = m_{{{\text{PL}}}} + \sum\limits_{k = j}^{n} {(m_{{s,k}} + m_{{p,k}} ) + s \times m_{{{\text{fairing}}}} }. $$

(16)

In Eq. (16), j is the index representing the currently active stage, and s is a binary indicator variable whose value is one before fairing separation and zero afterward. Three force components (f_a, f_g, and f_T) are defined as follows:

$$ {\varvec{f}}_{T} = \left( {v_{ex,j} \dot{m}_{p,j} (t) - A_{e,j} p_{a} } \right){\varvec{e}}_{T}, $$

(17)

$$ {\varvec{f}}_{a} = - \frac{1}{2}\rho_{a} C_{D} S_{{{\text{ref}}}} ||{\varvec{v}}_{r} ||{\varvec{v}}_{r}, $$

(18)

$$ {\varvec{f}}_{g} = m({\varvec{g}}_{c} + {\varvec{g}}_{p} ) = m\left\{ { - \frac{\mu }{{||{\varvec{r}}||^{3} }}{\varvec{r}} + {\varvec{g}}_{p} } \right\}. $$

(19)

In these equations, e_T is a unit vector representing the thrust direction defined by the pitch and yaw angles (θ and ψ), and p_a / ρ_a are the atmospheric pressure/density from the 1976 U.S. standard atmosphere model [28]. C_D is an aerodynamic coefficient calculated through linear interpolation using external input values. Also, g_c and g_p are the central and perturbed (considering J₂ term) gravity acceleration vectors, respectively. Equations (12–15) are the differential equations for velocity loss components: pressure loss (Δv_L,p), drag loss (Δv_L,d), gravity loss (Δv_L,g), and steering loss (Δv_L,s), respectively.

The launch position and velocity determine the initial states of the first phase. Also, the final states of phase p determine the initial states of phase (p + 1). These relationships are expressed as follows:

$$ \left[ {\begin{array}{*{20}c} {{\varvec{r}}_{i}^{(p + 1)} } \\ {{\varvec{v}}_{i}^{(p + 1)} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{\varvec{r}}_{f}^{(p)} } \\ {{\varvec{v}}_{f}^{(p)} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{\varvec{r}}(t_{p} )} \\ {{\varvec{v}}(t_{p} )} \\ \end{array} } \right]. $$

(20)

3.2 Output Generation Module

The output generation module computes various output variables using the state variables (r, v, m_k), which are the outputs of the first module. The module first computes the position and velocity elements expressed in various coordinate frames using coordinate transformations. Utilizing the position and velocity vectors expressed in various coordinate systems, the flight status variables, such as dynamic pressure, flight path angle, and angle of attack, are calculated. The orbital elements needed for setting boundary conditions on orbit insertion in the optimization module are calculated by transforming the inertial position/velocity into six parameters [29]. The flight-safety related variables (e.g., IIP) are computed based on the procedures presented in reference [25, 30, 31]. Table 1 outlines the selected output variables (notations, descriptions, and units) computed in the second module.

Table 1 Selected output variables from the second module

3.3 Nonlinear Optimization Module

The nonlinear optimization module formulates and optimizes the problem of minimizing lift-off mass with constraints on the target orbit insertion and other flight requirements (e.g., range-safety). The problem is formulated as follows:

[P_I: Integrated optimization of stage and trajectory of a launch vehicle]

$$ \mathop {\min }\limits_{{\varvec{x}}} m_{{\text{Lift-off}}}, $$

(21)

$$ {\varvec{x}} = [m_{s,k} ,\theta_{f}^{p} ,\psi_{f}^{p} ]\;\;\;\;(1 \le k \le N,\;\;1 \le p \le P), $$

(22)

subject to

$$ \varepsilon_{k} = m_{s,k} /(m_{s,k} + m_{p,k} ). $$

(23)

Equations (9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20)

$$ \left[ {\begin{array}{*{20}c} {h_{f}^{P} } \\ {\gamma_{f}^{P} } \\ {(v_{I} )_{f}^{P} } \\ {i_{f}^{P} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {h_{req} } \\ {\gamma_{req} } \\ {(v_{I} )_{req} } \\ {i_{req} } \\ \end{array} } \right], $$

(24)

$$ \alpha^{p} = 0,\;\;(p \in \Pi_{G} ), $$

(25)

$$ q(t) \le q_{\max }, $$

(26)

$$ (\varphi_{I}^{k} )_{L} \le \varphi_{I}^{{S_{k} }} \le (\varphi_{I}^{k} )_{U} ,\;(\varphi_{I}^{F} )_{L} \le \varphi_{I}^{{S_{F} }} \le (\varphi_{I}^{F} )_{U}, $$

(27)

$$ (\lambda_{I}^{k} )_{L} \le \lambda_{I}^{{S_{k} }} \le (\lambda_{I}^{k} )_{U} ,\;(\lambda_{I}^{F} )_{L} \le \lambda_{I}^{{S_{F} }} \le (\lambda_{I}^{F} )_{U}. $$

(28)

Equation (21) is the objective function of the nonlinear optimization problem, which is the minimization of the lift-off mass of the vehicle for a given target mission and payload mass. Equation (22) defines the decision variables for the problem: structural mass of stages (m_s,k) and discretized angles defining thrust direction ($\theta_{f}^{p}$ and $\psi_{f}^{p}$). We select the final pitch and yaw angles at the end of each phase for design variables and use linear interpolation to determine the angles within the phase. Equation (23) represents a constraint on the structural mass fraction (ε_k), determining the propellant mass (m_p,k). Vehicle dynamics expressed as Eqs. (9)–(20) are imposed as constraints as well. As explained previously, the differential equations are integrated numerically and create the output variables representing the flight status, IIP and orbital elements, which are used to define constraints expressed in Eqs. (24)–(28). Equation (24) includes the constraints for target orbit insertion specifying the final altitude, flightpath angle, inertial velocity, and inclination angle. Equation (25) represents the constraint that the angle of attack should be zero during the gravity turn, where Π_G is the set of phases that belong to the gravity-turn period. Equation (26) describes the constraint on the dynamic pressure the vehicle experiences throughout the ascending flight. Equations (27)–(28) impose the range-safety constraints [20]. These constraints define allowable limits for the impact point of a separated part, constraining both the latitude and longitude values to fall within specified lower and upper bounds. The primary objective of these constraints is to ensure that the separated part follows a trajectory that leads to its impact within a predefined safe area. By setting boundaries on both latitude and longitude, the constraints effectively mitigate the potential risk associated with the separated components, enhancing launch safety. In these equations, superscript S_k and S_F represent the phases at which the k^th stage and payload fairing are separated, respectively.

Sometimes, the designer may impose additional constraints, such as the structural load (expressed by the product of the dynamics pressure and aerodynamic angle) and thermal heating. Equalities or inequalities (e.g., g(x) ≤ 0, h(x) = 0) can express these additional constraints.

4 Case Study

This section presents a case study demonstrating the effectiveness of the proposed framework to optimize the stage size and trajectory of a launch vehicle simultaneously. We set up the mission of delivering a 3000 kg payload to a circular target orbit (altitude: 300 km, inclination: 80 deg). The characteristics of the structural and propulsion systems for Korean Space Launch Vehicle II (KSLV-II, Nuri) are used for this case study (e.g., structural mass fraction, specific impulse, and thrust). Table 2 summarizes the specifications of the KSLV-II vehicle used for this case study [32]. Note that the nozzle exit area was estimated based on the expressed differences between the vacuum and sea level thrust of the engine, and the reference area was utilized by the reported diameter of KSLV-II [33]. The structural mass values presented in this table were used as the initial guess for the decision variables.

Table 2 Reference design for case study-specification of KSLV-II

We implemented the proposed simultaneous optimization framework and the method proposed by Koch [14] for comparison. Koch’s algorithm requires iterations between trajectory optimization and staging problems. The convergence criterion for Koch’s algorithm was selected as 0.1% error for the maximum payload obtained from the trajectory optimization. The case study uses MATLAB on a Windows 11 operating system with an Intel i5-13600 K processor and 64 GB of RAM. The sequential quadratic programming (SQP) provided by MATLAB Optimization Toolbox was used as the numerical optimization algorithm. We conducted three case studies on redesigning KSLV-II using the proposed framework. During the case study, essential flight requirements were considered (e.g., maintaining zero angle of attack during the gravity turn, limiting maximum dynamic pressure, and range-safety constraint). Each case introduces additional constraints to the optimization problem, allowing us to conduct a step-by-step analysis of the influence constraining the flight trajectory.

Case I considers the gravity-turn condition for the flight-requirement constraint (Eq. 25), Case II additionally considers the dynamic pressure constraint (Eqs. 25, 26), and Case III considers the gravity turn and the IIP-range constraints (Eqs. 25, 27, and 28) for the optimization.

Table 3 exhibits the optimization results for Case I obtained using the traditional staging-trajectory iteration and the simultaneous optimization. The simultaneous optimization method presented in this paper showed a distinct advantage by treating both the stage mass and attitude as a design variable within a single nonlinear optimization problem. This approach leads to improved solutions with a lighter objective function compared to a traditional approach that handles staging and trajectory optimization separately. The simultaneous optimization method resulted in a lower Δv_Loss and a 7.2% reduction in the lift-off mass than the traditional algorithm, supporting the advantage of the proposed framework.

Table 3 Case I (Constraint on gravity turn) results

Table 4 presents the results for Case II. The maximum dynamic pressure value used for the constraint (q_max) is 40 kPa. One can observe that the proposed framework yields the objective function (lift-off mass) 6.8% smaller than the traditional approach involving the iteration between the trajectory design and staging. In addition, the computation time spent on the proposed framework (28 s) was significantly shorter than that of the traditional approach (4766 s), which is caused by the large number of iterations (405). Figure 5 shows the optimal trajectories obtained by both methodologies. The launch vehicle design obtained through the simultaneous optimization framework moves slightly more vertically.

Table 4 Case II (Constraints on gravity turn and dynamic pressure) results

Fig. 5

Optimized trajectories obtained by the two methods

In the conventional iterative-approach, the value of velocity losses can vary significantly as the stage size of the launch vehicle changes during iteration. Reduction in the lift-off mass results in significant acceleration during the early phases after launch, leading to a relatively higher speed at the same altitude and an increase in the dynamic pressure. To satisfy the dynamic pressure constraint, the flight trajectory needs to be adjusted, varying the velocity loss terms. Thus, the flight requirements serve as incentives for changes at each stage mass during the design-iteration process. The magnitude of these changes can significantly impact the convergence time of the traditional approach or even fail to converge in the worst-case scenario. In contrast, the proposed framework solves the nonlinear-optimization problem by simultaneously considering the trajectory and staging. Therefore, the framework can successfully reflect flight-requirement constraints in staging decisions, yielding the solution more efficiently.

Table 5 presents the results for Case III, which constrains the IIP of the separated first stage. This constraint ensures that the separated parts falls within the safe area and does not pose risks to human populations or cross borders. The upper limit of the IIP longitude is set as 128.3°E, and the zero angle of attack constraint during the gravity-turn period is imposed as well.

Table 5 Case III (Constraints on gravity turn and IIP of Stage 1) results

Figure 6 visualizes the trajectory of the current position and IIP of the vehicle on the map. Since the target orbit is prograde, the launch vehicle flies eastward. Therefore, as the first stage size increases, the separated first stage’s impact point shifts eastward. Hence, when there is a constraint on the maximum allowable longitude of the first stage impact point, it is necessary to design the first stage smaller so that the velocity increment allocated to the first stage decreases. The velocity increment values achieved by the first stage are 3296 m/s (Case I) and 3076 m/s (Case III), respectively, showing this tendency. Note that the traditional optimization approach failed to obtain the solution for Case III (procedure diverged after iteration 6), showing its vulnerability to design problems involving complex constraints.

Fig. 6

Trajectories (position and IIP) and range-safety constraint shown on the map

5 Conclusions

This study has introduced a new framework to optimize a launch vehicle’s trajectory and stage size simultaneously. The proposed simultaneous optimization framework obtains an efficient stage size design while effectively handling the constraints caused by flight requirements. By appropriately discretizing the variables in the optimal control problem of the launch vehicle’s ascending flight and integrating them with the optimal staging problem, the framework transforms the iterative multidisciplinary design optimization process into a single nonlinear-optimization problem.

Unlike the iterative methods utilized in previous studies, the proposed framework demonstrates improved quality of solution, convergence characteristics, and computational efficiency. The framework not only simplifies the design optimization process but also contributes to a reduction in computational time. Validation of the proposed framework through three case studies highlights the effectiveness of the simultaneous-optimization approach with faster computation speed and lighter lift-off mass on the obtained design.

A potential direction for future research is to extend the framework to address design issues specific to reusable launch vehicles. In addition, integrating the optimization framework with other design disciplines in the launch vehicle’s conceptual design phase is a potential avenue. For example, linking the structural mass fraction, which is a fixed value in the proposed framework, to other design variables could facilitate an iterative-design process for the structural mass fraction during the initial design stage of the launch vehicle.