Dynamic output feedback control strategy for a satellite orbital model within negative-imaginary systems theory framework

Abstract

This article presents the synthesis of a dynamic output feedback controller for a satellite orbital system confronted with uncertainties. The investigated method transforms the closed-loop system, synthesized by the controller, into an $\alpha$-strictly negative-imaginary system. It utilizes the DC-loop gain condition associated with negative-imaginary systems theory to demonstrate robust stability of the satellite orbital system in the presence of uncertainties. Furthermore, the synthesized negative-imaginary closed-loop system exhibits notable time-domain performance. The numerical simulation outcomes presented in this article validate the investigated synthesis method.

1 Introduction

This article explores the orbit control of a benchmark satellite dynamic model in a geostationary orbit (refer to Fig. 1). The orbit control problem generally refers to the challenge of precisely controlling the trajectory and orientation of spacecraft or satellites in orbit around a celestial body. This problem is crucial for maintaining stable and efficient operations of space missions, including satellite positioning, attitude control, and orbital maneuvers. Satellites, as free-floating bodies in space, experience diverse forces of varying intensities throughout their orbital motion, originating from a range of sources. These forces frequently disrupt the satellite’s intended orbit, causing deviations from the desired trajectory. Therefore, difficulties in orbit control related to positioning satellites within a specified orbit are quite common.

The Negative Imaginary (NI) systems theory has gained considerable interest in recent years, mainly owing to its straightforward internal stability condition for interconnected systems, which is solely dependent on the DC loop gain [1]. This theory has demonstrated broad applicability in addressing various real-world engineering challenges. The concept of negative-imaginary systems was initially proposed by Lanzon and Petersen in [1] to address robust control challenges in flexible structure dynamic models. Since then, numerous articles exist in the literature, concentrating on robustness analysis and controller synthesis frameworks for a range of dynamical systems (refer to [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19], etc.). The negative-imaginary (NI) characteristic of a system G(s) is determined by analyzing the properties of the imaginary part of its frequency response $G(j\omega )$. This attribute can be expressed equivalently as $j\left( G(j\omega )-G(j\omega )^{*}\right) \ge 0, \ \forall \omega \in \left( 0, \ \infty \right)$. For NI systems, the phase lag falls within the range of 0 to $-\pi$, resulting in Nyquist diagrams lying completely below the real axis for all positive frequencies. There is a close relationship between negative-Imaginary systems theory and positive real (PR) systems theory, particularly for linear time-invariant (LTI) systems, however, the applicability of PR systems theory is limited to systems with relative degrees of zero or one. In contrast, negative-imaginary systems theory expands this range of applicability to include systems with relative degrees between zero and two.

Classical feedback control techniques and some advanced control algorithms are generally used to calculate and execute precise orbit maneuvers in order to achieve the desired trajectory of a satellite. The literature extensively discusses the orbit control problem, and those interested can refer [20,21,22,23,24,25] for a comprehensive survey of results. In [25], an $H_{\infty }$ static state feedback controller is designed for satellite under the assumption that real-time state signals can be precisely transmitted. This assumption allows for the employment of a full state feedback controller when all the states are available for measurement. Since a satellite system consists of six degrees of freedom (DOF): three translational and three rotational. Consequently, it could encompass a maximum of twelve distinct states. These states include linear position, linear velocity, angular position, and angular velocity. Acquiring measurements for all these states may require the purchase of very expensive sensors, potentially making the implementation of a state feedback controller cost-ineffective. This article addresses the aforementioned facts by employing a dynamic output feedback control scheme for geostationary satellite orbital system. Moreover, the PR systems theory framework operates with rates, such as force to velocity or torque to angular velocity, requiring a rate sensor, which is impractical. In contrast, NI systems theory relies on a position sensor, which is practical. Since a satellite orbital system also involves force (torque) inputs and position (attitude) measurements, the motivation for selecting the NI systems theory-based control approach for the orbital system is firmly rooted in its practical realities.

Fig. 1

Geostationary orbit satellite

Several research efforts are devoted to addressing the challenge of synthesizing controllers that result in a negative-imaginary (NI) closed-loop system. As an illustration, the article [19, 26] investigates the synthesis of a state feedback controller using an LMI-based approach, with a focus on imposing the negative-imaginary (NI) property in the closed-loop system. The state feedback controller is synthesized in [10] to achieve a negative imaginary (NI)/strictly negative imaginary (SNI) closed-loop system based on an algebraic Riccati equation (ARE). In the context of negative-imaginary (NI) synthesis, aimed at enhancing time-domain transient performance, the paper [27] develops a state-feedback NI controller by incorporating the principles of $\alpha$- and D- pole placement to enforce the NI property within the closed-loop system. In [12], the authors presented methods for synthesizing static state feedback and dynamic output feedback controllers while ensuring the closed-loop NI property. However, the synthesis techniques presented in [12] are complex and fail to tackle the problem of output performance. The research described in [17, 28, 29] focused on solving the NI synthesis problem while ensuring $H_{\infty }$ closed-loop performance. The method in [17] included the initial design of an NI controller, followed by the minimization of its deviation from another synthesized $H_{\infty }$ controller. However, it’s important to note that minimizing the distance between the two controllers does not ensure the preservation of any specific property of the $H_{\infty }$ controller by the NI controller. The literature in [28, 29] centers around the development of a dynamic output feedback controller aimed at achieving an SNI closed-loop system. This controller is designed to be robust against uncertainties within the NI class while satisfying specific DC gain criteria. Furthermore, the resulting closed-loop system exhibits notable time-domain performance. This article further extends the dynamic output feedback control scheme based on NI systems theory, as outlined in [28, 29], and applies this approach to a satellite orbital system. It is also worth noting that the output-feedback control method holds greater importance in real-world applications. The major contribution of this article is the successful implementation of an NI systems theory-based dynamic output feedback control scheme for a benchmark satellite orbital model.

The structure of the rest of the paper is as follows: Sect. 2 introduces fundamental concepts related to basic negative-imaginary (NI) systems theory to augment the reader’s comprehension of the paper. In Sect. 3, a generalized state-space model of satellite orbital dynamics is formulated. Section 4 elaborates on the dynamic output feedback control scheme for a satellite orbital system based on NI system theory. The analysis of results and numerical simulations is presented in Sect. 5. Finally, Sect. 6 offers a concise conclusion to the paper.

2 Preliminaries

This section presents the formal definitions and fundamental key concepts of negative imaginary systems, which are essential for the scope of this article.

Definition 1

[2, 3, 26, 30,31,32] A transfer-function matrix $G(s)\in {\mathbb {R}}^{n\times n}$ is called a negative-imaginary (NI) system if it fulfills the following criteria:

• 1. G(s) has no poles in the region $\left\{ s\in {\mathbb {C}}: {\mathfrak {Re}}\left\{ s\right\} >0\right\} ;$

• 2. For all $\omega \in \left( 0,\infty \right)$ such that $j\omega$ is not a pole of G(s), the inequality $j\left[ G(j\omega )-G(j\omega )^{*}\right] \ge 0$ holds.

• 3. For any $\omega \in \left( 0, \infty \right)$, if $s=j\omega _{0}$ is a pole of G(s), then it is a simple pole. Additionally, the corresponding residue matrix $R_{0}$, defined as $R_{0}\triangleq \lim \limits _{s\rightarrow j\omega _{0}}\left( s-j\omega _{0}\right) jG(s)\ge 0$

• 4. If $s=0$ is the pole of G(s), then $\displaystyle \lim _{s\rightarrow 0}s^{p}G(s)=0$ for each integer $p\ge 3$, and $\displaystyle \lim _{s\rightarrow 0}s^{2}G(s)\ge 0$

• 5. If $s=j\infty$ is a pole of G(s), then $\displaystyle \lim _{\omega \rightarrow \infty }\frac{G(j\omega )}{\left( j\omega \right) ^2}\le 0$ and $\displaystyle \lim _{\omega \rightarrow \infty }\frac{G(j\omega )}{\left( j\omega \right) ^p}=0$ for all integer $p\ge 3$

Definition 2

[2, 3, 26, 30, 31] A transfer-function matrix $G(s) \in {\mathbb {R}}^{n\times n}$ is said to be a strictly negative-imaginary (SNI) system if it meets the following conditions:

• 1. All poles of G(s) must reside in the region $\left\{ s\in {\mathbb {C}}: {\mathfrak {Re}}\left\{ s\right\} <0\right\} ;$

• 2. The inequality $j\left[ G(j\omega )-G(j\omega )^{*}\right] >0$ must hold for all $\omega \in \left( 0. \infty \right)$.

Definition 3

[33] Let $\left( A, B, C, D \right)$ be a minimal state-space realization of a square real-rational proper transfer function matrix $G(s)\in {\mathcal {R}}^{m\times m}$, where $A\in {\mathbb {R}}^{n\times n}, B\in {\mathbb {R}}^{n\times m}, C\in {\mathbb {R}}^{m\times n}, D\in {\mathbb {R}}^{m\times m}$, and $m\le n$. Then, G(s) is called lossless negative-imaginary system if and only if $D=D^{T}$, and there exists a real matrix $Q=Q^T\ge 0, Q\in {\mathbb {R}}^{n\times n}$, such that

$$\begin{aligned} \begin{bmatrix} QA+A^{T}Q &{} QB-A^{T}C^{T}\\ B^{T}Q-CA &{} CB+(CB)^{T} \end{bmatrix}&=0 \end{aligned}$$

(1)

Definition 4

[19] For a given non-negative real constant $\alpha$, an LTI system with a real-rational proper transfer function G(s) is called asymptotically $\alpha$-stable if the real part of every pole $\lambda _i$ of G(s) is less than $-\alpha$, i.e., ${\mathfrak {Re}}\left[ \lambda _i \right] <-\alpha$.

Definition 5

[18] For a given real constant $\alpha >0$, a transfer-function matrix $G(s)\in {\mathcal {R}}^{m\times m}$ with state-space realization $\left[ \begin{array}{c|c} A &{} B\\ \hline C &{} D \end{array}\right]$ and $D=D^T$ is said to be $\alpha$-strictly negative imaginary ($\alpha$-SNI) if there exists a real matrix $P=P^{T}>0$ such that

$$\begin{aligned} \begin{aligned} AP+PA^T+2\alpha P&\le 0 \\ B+APC^T&= 0 \end{aligned} \end{aligned}$$

(2)

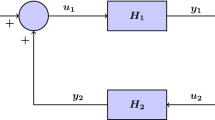
The criterion for internal stability within the positive feedback interconnection of NI (Negative Imaginary) and SNI (Strictly Negative Imaginary) systems is stated in following theorem.

Theorem 1

[1, 30] If $G_{1}(s)$ is considered a stable NI system and $G_{2}(s)$ is identified as an SNI system, the positive feedback interconnection of $G_{1}(s)$ and $G_{2}(s)$, illustrated in Fig. 2, ensures internal stability if and only if $\lambda _{max}\left[ G_{2}(0)G_{1}(0)\right] <1$. Additionally, for this internal stability to hold, it is necessary that either $G_{1}(\infty )=0$ or $G_{1}(\infty )G_{2}(\infty )=0$, and $G_{2}(\infty )\ge 0$.

Fig. 2

Positive-feedback interconnection of negative-imaginary (NI) systems

3 Dynamic model of a satellite orbital system

The geostationary orbit comprises two primary phases associated with the satellite’s orbit control. The initial phase involves the transition from the geostationary-transfer orbit (GTO) to the ultimate geostationary orbit (GEO). The subsequent phase, also denoted as the mission stage, is typically anticipated to extend beyond 10 years. Our emphasis in this research is on the mission stage, where the satellite resides in geostationary orbit, specifically for control system design.

The non-linear dynamics of satellite orbital system is described by the following second-order differential equations [34]

(3a)

(3b)

where r denotes the distance between the Earth’s center and the satellite’s center, R is the radius of earth, $m_s$ is the mass of the satellite under operational geostationary conditions and $\theta$ is angular position of satellite. Additionally, the thrust forces $F_1$ and $F_2$ act on the satellite in the radial and tangential directions, respectively. To facilitate a better understanding of the problems, we carry out the normalization of time, distance, and force variables into dimensionless quantities by utilizing the following relationship

$$\begin{aligned} \tau&=\frac{t}{\sqrt{\frac{r}{g}}}; \ \rho =\frac{r}{R}; \\ u_{1}&=\frac{F_{1}}{m_{s}g}; \ u_{2}=\frac{F_{2}}{m_{s}g} \end{aligned}$$

Hence, the expressions governing the orbital motion of the satellite (3) can be formulated as

(4a)

(4b)

Remark 1

In the context of geostationary conditions, the choice for the periodic reference orbit necessitates it to be circular, maintaining a constant angular velocity. Specifically, setting .

If we define the state vectors as are the state vectors, the state-space representation of a non-linear model for a satellite orbital system can be described as follows:

(5)

The satellite model undergoes linearization based on the specified nominal orbit parameters $x_0$ and $u_{0}$, where

It is important to highlight that, in this context, the nominal orbit parameters do not represent an equilibrium point but rather the periodic solutions of the state equations (5).

Remark 2

In the context of satellite motion, a periodic solution would describe an orbit in which the satellite returns to the same position after a certain fixed period of time. Periodic orbits can be stable, meaning that small perturbations won’t cause the satellite to deviate significantly from its desired path. Periodic solutions can help with station-keeping maneuvers, which involve making periodic adjustments to the satellite’s orbit to counteract the effects of perturbations.

By employing the periodic nominal orbit parameters and using the dot symbol $\left( \cdot \right)$ for , the following linearized satellite orbital system in state-space form is derived.

$$\begin{aligned} \begin{aligned} {\dot{x}}&=Ax+Bu,\\ y&=Cx \end{aligned} \end{aligned}$$

(6)

with

The system defined by (6) is vulnerable to external disturbances in a practical working environment, and the impact of the disturbance signal could negatively influence the anticipated normal system outputs $\rho$ and $\theta$. Therefore, we have considered the disturbance signal $\Omega$ in the system (6) with disturbance input matrix $B_{\omega }=\left[ 1\ 0\ 1\ 0\right] ^{T}$. Hence state-space model along with controlled output Z and measured output $Y=\left[ y_1\ y_2\right] ^{T}$ can be expressed as

$$\begin{aligned} \begin{aligned} {\dot{X}}&=A X+B_{\omega } \Omega +B U\\ Z&=C_{z}X\\ Y&=CX, \end{aligned} \end{aligned}$$

(7)

where $C_{z}=\left[ 0\ 0\ 1\ 0 \right] .$ To fulfill the demands of real-world scenarios, it is crucial to simultaneously consider the following key aspects:

• 1. Parametric uncertainty: Because of detection inaccuracies or complex forces among objects in space, the online determination of the satellite’s angular velocity $\omega$ faces challenges. This situation is typically described as

  $$\begin{aligned} \omega =\omega _{0}\left( 1+\delta \right) \end{aligned}$$

  (8)

  where $\omega _0$ represents the theoretical angular velocity, and $\delta$ indicates the extent of uncertainty.

• 2. Input constraint: The consideration of control input constraints becomes crucial in any space mission, where limitations on thrust equipment and the restricted quantity of fuel impose constraints on the force applied for orbit control. Therefore, it is essential to confine the actual control input force within a specific range, expressed as

  

  (9)

  where $U_{max}$ represents the maximum control input force.

Hence, the state-space model with parametric uncertainty can be written as

$$\begin{aligned} \begin{aligned} {\dot{X}}&={\tilde{A}} X+B_{\omega } \Omega +B U\\ Z&=C_{z}X\\ Y&=CX, \end{aligned} \end{aligned}$$

(10)

where ${\tilde{A}}=A+\Delta$.

Fig. 3

a LFT diagram for dynamic output-feedback controller synthesis; b positive-feedback interconnection of Negative-Imaginary systems

For the uncertain matrix $\Delta$ in (10), we consider a norm-bounded condition , where $\beta$ is a positive value determined by $\delta$. If DC gain of any uncertain system $\Delta (s)$ is less than or equal to infinity norm of uncertain matrix $\Delta$ i.e. , then the uncertainty of the system (10) can be realized by the following DC gain condition:

$$\begin{aligned} \Delta (0)\le \frac{1}{\beta }\ \ \text {for any}\ \ \beta >0 \end{aligned}$$

(11)

4 Dynamic output feedback control method

This section offers a concise overview of the synthesis method used for a dynamic-output feedback controller in a satellite orbital system, leading to the $\alpha$-SNI closed-loop system. The variable $\alpha$ determines the decay rate of the NI feedback system and serves as an indicator of the system’s performance. In this methodology, it is not necessary for the satellite orbital system model G(s) and its controller K(s) to be an NI system. However, it is essential for the resulting closed-loop system and the associated uncertainty $\Delta (s)$ to exhibit the NI property.

4.1 Formulation of control problem

Consider the generalized state-space model of the orbital system (10), which is characterized by the subsequent set of state-equations:

$$\begin{aligned} G: {\left\{ \begin{array}{ll} {\dot{X}}=A X+B_{\omega } \Omega +B U\\ Z=C_{z}X+D_{z\omega }\Omega +D_{z}U\\ Y=CX+D_{\omega }\Omega , \end{array}\right. } \end{aligned}$$

(12)

where $X\in {\mathbb {R}}^n, U\in {\mathbb {R}}^{n_u}, Y\in {\mathbb {R}}^{n_y}, \Omega \in {\mathbb {R}}^{m}, Z\in {\mathbb {R}}^{m}, A\in {\mathbb {R}}^{n\times n}, B_{\omega }\in {\mathbb {R}}^{n\times m}, B\in {\mathbb {R}}^{n\times n_{u}}, C_{z}\in {\mathbb {R}}^{m\times n}$, and $C\in {\mathbb {R}}^{n_{y}\times n}$ with $n=4,n_{u}=2,n_{y}=2,m=1$ are given in Eqs. (6) and (7). The matrices $D_{z\omega }=0, D_{z}=0_{1\times 2}$ and $D_{\omega }=0_{2\times 1}$ are known.

Consider the block diagram shown in Fig. 3. The primary goal is to design a dynamic output-feedback controller K(s)

$$\begin{aligned} K(s): {\left\{ \begin{array}{ll} {\dot{X}}_{k}=A_{k}X_{k}+B_{k}Y\\ U=C_{k}X_{k}+D_{k}Y \end{array}\right. } \end{aligned}$$

(13)

for the satellite orbital system (12). This controller aims to guarantee that the nominal closed-loop system $T_{z\omega }(s)$, formed through the lower-linear fractional transformation (LFT) between the generalized system model G(s) and the controller K(s), conforms to an $\alpha$-strictly negative-imaginary ($\alpha$-SNI) system. Additionally, the system is required to demonstrate robust stability against all stable, strictly-proper negative-imaginary (NI) uncertainties $\Delta (s)$ that satisfy the condition (11). Note that the state-space realization of the closed-loop system $T_{z\omega }(s)$ from $\Omega$ to Z is obtained as

$$\begin{aligned} T_{z\omega }(s)&= \left[ \begin{array}{c|c} A_{cl} &{} B_{cl}\\ \hline C_{cl} &{} D_{cl} \end{array}\right] = \left[ \begin{array}{c|c} \begin{matrix} A+BD_{k}C &{} BC_{k}\\ B_{k}C &{} A_{k} \end{matrix}&{} \begin{matrix} B_{\omega }+BD_{k}D_{\omega }\\ B_{k}D_\omega \end{matrix}\\ \hline \begin{matrix} C_{z} &{} &{} &{} &{} 0 \end{matrix}&D_{z\omega } \end{array}\right] \end{aligned}$$

(14)

4.2 Controller synthesis method

The subsequent theorem outlines the necessary conditions for determining the dynamic-output feedback controller K(s) which transform closed-loop system (14) into an $\alpha$-SNI system with a user-specified value of $\alpha >0$. This controller ensures stability in the feedback loop, even in the presence of any stable, strictly-proper negative-imaginary uncertainty $\Delta (s)$ that satisfies DC-gain condition (11).

Theorem 2

[28, 29] Consider the generalized system model G is given by (12) with $m\le 2n$, $D_{z\omega }=D_{z\omega }^{T},\ D_{z}=0$, $\left( A, B\right)$ controllable and $\left( A, C\right)$ observable. If, for given $\beta >0$ and $\alpha >0$, there exist matrices ${\tilde{A}}\in {\mathbb {R}}^{n\times n}, {\tilde{B}}\in {\mathbb {R}}^{n\times n_{y}}, {\tilde{C}}\in {\mathbb {R}}^{n_{u}\times n}$ and ${\tilde{D}}\in {\mathbb {R}}^{n_{u}\times n_{y}}$ and symmetric matrices $P\in {\mathbb {R}}^{n\times n}$ and $S\in {\mathbb {R}}^{n\times n}$ such that the following set of conditions

$$\begin{aligned}&\left[ \begin{array}{c|c} \begin{matrix} \Phi _{11}+2\alpha P &{} \Phi _{12}+2\alpha I\\ \star &{} \Phi _{22}+2\alpha S \end{matrix}&{} \begin{matrix} PB_{\omega }+{\tilde{B}}D_{\omega }+{\tilde{A}}C_{z}^{T}\\ \Phi _{23} \end{matrix}\\ \hline \begin{matrix} \star &{} &{} &{} &{} &{} \star \end{matrix}&0 \end{array}\right] \le 0, \end{aligned}$$

(15)

$$\begin{aligned}&\begin{bmatrix} P &{} I\\ I &{} S \end{bmatrix}>0, \end{aligned}$$

(16)

$$\begin{aligned}&C_{z}SC_{z}^{T}+D_{z\omega }<\beta I, \end{aligned}$$

(17)

holds with the following shorthand

$$\begin{aligned} \Phi _{11}&:=PA+A^{T}P+{\tilde{B}}C+C^{T}{\tilde{B}}^{T} \end{aligned}$$

(18a)

$$\begin{aligned} \Phi _{12}&:={\tilde{A}}+\left( A+B{\tilde{D}}C\right) ^{T} \end{aligned}$$

(18b)

$$\begin{aligned} \Phi _{22}&:=AS+SA^{T}+B{\tilde{C}}+{\tilde{C}}^{T}B^T \end{aligned}$$

(18c)

$$\begin{aligned} \Phi _{23}&:=B_{\omega }+B{\tilde{D}}D_{\omega }+ASC_{z}^{T}+B{\tilde{C}}C_{z}^{T} \end{aligned}$$

(18d)

and the symbol $\star$ denotes the symmetric entries within the LMIs, then an internally stabilizing dynamic output-feedback controller K(s), as described in (13), is obtained by using the following matrices

$$\begin{aligned} D_{k}&={\tilde{D}}, \end{aligned}$$

(19a)

$$\begin{aligned} C_{k}&=\left( {\tilde{C}}-D_{k}CS \right) M^{-T}, \end{aligned}$$

(19b)

$$\begin{aligned} B_{k}&=N^{-1}\left( {\tilde{B}}-PBD_{k} \right) , \end{aligned}$$

(19c)

$$\begin{aligned} A_{k}&=N^{-1}\left( {\tilde{A}}\right. \nonumber \\&\quad \left. -PAS-NB_{k}CS-PBC_{k}M^{T}-PBD_{k}CS \right) M^{-T}, \end{aligned}$$

(19d)

where M and N represent square, non-singular solutions to the algebraic equation $MN^{T}=1-SP$. Moreover, controller K(s) transforms the closed-loop system $T_{z\omega }(s)$ as described in (14) into an $\alpha$-SNI system and ensures robust stability of the generalized system model G in closed-loop against all stable strictly proper NI uncertainties $\Delta (s)$ satisfying $\lambda _{max}\left( \Delta (0) \right) \le \frac{1}{\beta }$.

Proof of this theorem can be found in [28, 29].

Remark 3

The selection of $\alpha > 0$ is arbitrary; however, selecting a large value for $\alpha$ may result in high control effort, potentially causing actuator saturation. Therefore, considering the limited power of the actuator, we must choose $\alpha$ in a way that ensures the control input force satisfies the condition (9). Additionally, an excessively high value of $\alpha$ will result in a reduced range of uncertainties for which the closed-loop system maintains robust stability. Moreover, the increased performance requirements for the closed-loop system tend to diminish its robustness. Therefore, a natural requirement arises for balancing the robustness and performance of the closed-loop system.

Remark 4

The application of Theorem 2 indicates that the closed-loop system will remain robustly stable against the class of NI uncertainties $\Delta (s)$, provided that the DC gain of $\Delta (s)$ remains less than or equal to $\frac{1}{\beta }$. This implies that in the scenario of a flexible system with collocated force input and position output, if we use a truncated model of the system as our generalized plant G(s) for controller synthesis and consider the remaining modes as unmodeled dynamics $\Delta (s)$, then the outcome of Theorem 2 will ensure robust stability against these unmodeled dynamics $\Delta (s)$ as long as the DC gain of the unmodeled dynamics is less than or equal to $\frac{1}{\beta }$. This assurance arises from the conditions (15) and (17) in Theorem 2, ensuring that the closed-loop system is $\alpha$-SNI and has a DC-gain less than $\frac{1}{\beta }$, respectively.

5 Simulations and results analysis

In this section, we discuss the numerical simulation outcomes for the output-feedback control of the satellite orbital system (12).

The following parameters for a geostationary satellite are employed in this study: The universal gravitational constant, denoted as G, is $6.673 \times 10^{-11}\ \text {m}^{3}\ \text {kg}^{-1}\ \text {s}^{-2}$; the mass of the Earth, denoted as $M_E$, is $5.974 \times 10^{24}$ kg; the radius of the Earth, denoted as R, is $6.367 \times 10^{6}$ m; the mass of the satellite under operational geostationary conditions, represented as $m_s$, is 300 kg and the acceleration due to gravity, denoted as g, is $9.81\ \text {m}\ \text {s}^{-2}$. With the utilization of these determined values, the calculation of parameters for the satellite orbital system (12) can be straightforwardly performed. The turn rate of the satellite orbit, denoted as $\omega$, is determined as $2\pi /\text {day}=7.29\times 10^{-5}$ rad/s. The normalized nominal orbit turn rate, represented as $\omega _{0}$, is then calculated as $\omega \times \sqrt{\frac{R}{g}}= 0.0587$. The geostationary nominal orbit radius, denoted as $r_{0}$, is evaluated using the formula $\left( \frac{GM_E}{\omega ^2}\right) ^{1/3}=4.22\times 10^{7}$ m. Additionally, the normalized geostationary nominal orbit radius, denoted as $\rho _{0}$, is determined as $\frac{r_0}{R}= 6.6279$

Remark 5

The ratio $\rho _0$ of the orbital radius of a GEO satellite $(r_0)$ to Earth’s radius R should be equal to approximately 6.6279 to maintain a stable geostationary orbit. This value is derived from the requirements of a geostationary orbit, where the orbital period of the satellite aligns with the Earth’s rotational period. This constraint ensures that the satellite orbits at the right altitude to complete one orbit around the Earth in the same amount of time it takes the Earth to complete one rotation. As a result, the satellite appears stationary relative to the Earth’s surface, which is a key characteristic of GEO orbits. Satellite operators use this ratio to manage and control GEO satellites’ orbits. If the ratio exceeds the specified value, adjustments may be required to lower the satellite’s altitude and bring it back into a stable geostationary orbit. Conversely, if the ratio is below the specified value, altitude adjustments may be needed to raise the satellite to the correct geostationary altitude.

On substituting $\omega _{0}$ and $\rho _{0}$ in the satellite orbital model (6), the following state-space matrices for generalized system model (12) is obtained

The poles of the dynamic model for satellite orbital motion are given by $p_{1,2,3,4}=0,0,\pm j0.059$. It is evident that two poles are located at the origin, and the other two lie on the imaginary axis, indicating system instability. Additionally, the presence of poles on the imaginary axis, specifically the eigenvalue pair $\pm j0.059$, suggests the inclusion of oscillatory modes within the system. Furthermore, it can be verified that the controllability of $\left( A, B\right)$ and observability of $\left( A, C\right)$ hold true. Also, note that the satellite orbital model (12) is a lossless negative-imaginary system. This can be verified using Definition 3. Since $D = D^{T}$ and upon solving (1), we find a positive-definite symmetric matrix i.e., $Q=Q^{T}>0$, where

Consider $\Delta (s)$ is an NI uncertainty with $\Delta (\infty )=0$ and $\Delta (0)\le 1$ i.e. $\beta =1$. By selecting $\alpha =0.9$, LMIs (15), (16), and (17) are solved using the CVX toolbox [35] with SEDUMI solver, and the following feasible solutions are obtained.

By fixing the value of $M=I_{4\times 4}$, we can get $N=I_{4\times 4}-PS$. The following controller matrices $A_{k}, B_{k}, C_{k}$ and $D_{k}$ of (13) are then uniquely computed for this M and N by utilizing the relationships specified in (19)

(20)

The transfer function describing the closed-loop system (14) between disturbance input $\Omega$ and controlled output Z is derived as

$$\begin{aligned} T_{z\omega }(s)=\frac{\left( s+1.4709\right) \left( s^2 + 13.4 s + 125.7 \right) \left( s^2 + 4.504 s + 8.253\right) \left( s^2 + 2.995 s + 5.492\right) }{\left( s+1.2061\right) \left( s+5.0743\right) \left( s^2 + 10.06s + 96.54 \right) \left( s^2 + 2.794 s + 5.61 \right) \left( s^2 + 3.238 s + 5.114 \right) } \end{aligned}$$

The poles $\lambda _{i}$ of the closed-loop system $T_{z\omega }(s)$ can be obtained by computing the eigenvalues of the matrix $A_{cl}$ using (14) and it is given by

$$\begin{aligned} \lambda _{i}\left( A_{cl} \right) ={\left\{ \begin{array}{ll}-1.2061,\ -1.397 \pm j1.9128,\\ -1.619 \pm j1.5788,\\ \ -5.0743,\ -5.0304 \pm j8.4401,\end{array}\right. } \end{aligned}$$

(21)

Fig. 4

a Nyquist plot of $T_{z\omega }(s),\ \omega \in \left( 0\ \infty \right)$; b anti-hermitian plot of $T_{z\omega }(s)$

The Nyquist plot for $T_{z\omega }(s)$ with $\omega$ ranging from 0 to $\infty$, along with the plot of ${\underline{\lambda }}\left( j\left[ T_{z\omega }(j\omega )-T_{z\omega }(j\omega )^{*}\right] \right)$, is illustrated in Fig. 4. It can be confirmed from (21) and Fig. 4 that $T_{z\omega }(s)$ is an $\alpha$-SNI system with ${\mathfrak {R}}\left[ \lambda _{i}\left( A_{cl} \right) \right] <-0.9$ for all i. As $T_{z\omega }(0)=0.87684$, it follows that $\lambda _{\text {max}}\left( T_{z\omega }(0)\Delta (0) \right) <1$, ensuring robust stability in the closed-loop system against any NI uncertainty $\Delta (s)$ having $\Delta (0)\le 1$ via Theorem 1.

To demonstrate the practicality of the synthesis approach, we investigate the issue of disturbance attenuation in two cases (a) when pulse disturbance having amplitude 0.1 with Ton = 1s acting to satellite, and (b) when white noise disturbance with an intensity=1 is affecting the satellite, both in presence of two arbitrarily selected strictly proper NI uncertainties $\Delta _{1}(s)=\frac{1}{s+20}$ and $\Delta _{2}(s)=\frac{1}{s+5}$, under zero initial condition.

Remark 6

Pulse disturbances, characterized by sudden and short-duration forces, might be suitable for simulating specific events or impacts on the satellite, whereas white noise disturbances can represent random and uncorrelated disturbances, making them suitable for simulating the cumulative effects of various random factors over time. This could include micro-meteoroid impacts, sensor noise or other sources of uncertainty.

Fig. 5

a Controlled-output response Z with pulse disturbance input; b controlled-output response Z with white noise disturbance input

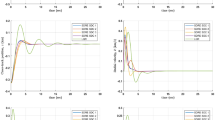
The controlled output response Z of closed-loop system $T_{z\omega }(s)$ in nominal and perturbed conditions for both disturbance cases (a) and (b) are shown in Fig. 5. Figure 5 shows that the designed controller K(s) is effectively eliminating the effects of the disturbance signals on the system and it also shows that the deviation of the output response from nominal to perturbed conditions is very small. The states response of closed-loop system $T_{z\omega }(s)$ for case (a) and case (b) are shown in Figs. 6 and 7 respectively. The findings in Figs. 6 and 7 demonstrate that the percentage deviation of responses for all states from the nominal to perturbed conditions are consistently remains within $10\%$. Moreover, Fig. 6 reveals that the transient phase of every state decays only for the first 2 seconds, after which it reaches zero states or target position.

Fig. 6

The states response of closed-loop system $T_{z\omega }(s)$ under both nominal and perturbed conditions, subject to a pulse disturbance under the zero initial conditions; a $x_{1}$; b $x_{2}$; c $x_{3}$; d $x_{4}$

Fig. 7

The states response of closed-loop system $T_{z\omega }(s)$ under both nominal and perturbed conditions, subject to white noise disturbance under the zero initial conditions; a $x_{1}$; b $x_{2}$; c $x_{3}$; d $x_{4}$

Finally, consider the closed-loop system between reference inputs and measured outputs and it is given by

$$\begin{aligned} T_{yu}(s)&= \left[ \begin{array}{c|c} A_{cl} &{} B_{cl}\\ \hline C_{cl} &{} D_{cl} \end{array}\right] \nonumber \\&= \left[ \begin{array}{c|c} \begin{matrix} A+BD_{k}C &{} BC_{k}\\ B_{k}C &{} A_{k} \end{matrix}&{} \begin{matrix} B+BD_{k}D_{\omega }\left( I_{1\times 3}\right) \\ B_{k}D_{\omega }\left( I_{1\times 3}\right) \end{matrix}\\ \hline \begin{matrix} C+\left( I_{1\times 3}\right) D_{z}D_{k}C &{} \left( I_{3\times 1}\right) D_{z}C_{k} \end{matrix}&D_{z\omega } \end{array}\right] \end{aligned}$$

(22)

where I denotes the identity matrix. Assume that initial position of satellite is $x_{0}=\left[ \rho _0,\ 0,\ \omega _{0}\tau ,\ \omega _{0}\right] =\left[ 6.6279,\ 0,\ 6.266,\ 0.0595\right]$ at time $t=0$. In addition, we simplify our analysis by considering that the initial state $x(0)=\left[ 6.6279,\ 0,\ 6.266,\ 0.0595,\ 0,\ 0,\ 0,\ 0\right]$. This assumption implies that the satellite remains stationary prior to time $t = 0.$ The output response Y of the closed-loop system (22) to initial conditions is illustrated in Fig. 8. Figure 8 shows that the transient phase of outputs $\rho$ and $\theta$ decays only for the first 3 seconds, after which it reaches zero or target position. The states response of the feedback system (22) is shown in Fig. 9. Figure 9 illustrates that the controller effectively guides the system from its initial states to zero states. To check the robust stability of the closed-loop system $T_{yu}(s)$, we again apply Theorem 1. Since we obtained , it follows that $\lambda _{\text {max}}\left( T_{yu}(0)\Delta (0)\right) < 1$, ensuring robust stability in the closed-loop system against any uncertainty $\Delta (s)$, provided that $\Delta (0) \le 1$. Moreover, it is essential to investigate the limitation imposed by the maximum control input i.e. units. Figure 10 provides a visual representation of how control inputs varies along radial and tangential direction. As depicted in the graph, the most substantial variation occurs in the control input along tangential direction. It is worth noting that the highest control input well below the prescribed maximum limit of 1000 units. This finding confirms that the controller’s design effectively maintains adherence to the input constraints. To demonstrate the robustness in the output response of the closed-loop system $T_{yu}(s)$ to initial conditions, we consider an uncertainty of $\Delta (0) = 0.8$ with percentage deviations of $20\%$ from the nominal value. The output response of the closed-loop system $T_{yu}(s)$ in presence of uncertainty is shown in Fig. 11.

Fig. 8

The output response Y(t) of the closed-loop system $T_{yu}(s)$ to initial conditions

Fig. 9

The states response of the closed-loop system $T_{yu}$ between reference inputs and measured outputs

Fig. 10

Control inputs for satellite orbital system

Figure 12 illustrates a geostationary orbit undergoing a 10% deviation from the required ratio of $\rho _{0} = 6.6279$. The diagram demonstrates that the disturbed orbit re-stabilized to its nominal state within just 4 h, thereby maintaining a stable geostationary position. Finally, the trajectory of the geostationary satellite orbit, governed by the nonlinear differential equations (3), with force inputs $F_{1}=u_{1}m_{s}g$ and $F_{2}=u_{2}m_{s}g$, where $u_1$ and $u_2$ represent control inputs in the radial and tangential directions, is also depicted in Fig. 13.

Fig. 11

Output response Y of the closed-loop system $T_{yu}(s)$ to initial conditions in presence of uncertainty

Fig. 12

Radial error or drift vs time

Fig. 13

Trajectory of geostationary satellite orbit with control inputs

6 Conclusion

In this study, we explore dynamic output feedback control strategies for a satellite orbit dynamic model using NI theory. The primary objective is to achieve a specified level of stability within the feedback system. The article begins by presenting the dynamic equations governing the satellite orbital system and its generalized state-space model. We employ an NI synthesis approach for the satellite orbital system, utilizing the $\alpha$-Strictly Negative Imaginary (SNI) framework to ensure a minimum prescribed decay-rate for the synthesized feedback system. Moreover, the article incorporates a robustness analysis of stability for positive-feedback control within the satellite orbital system, taking into account uncertain conditions. The resulting NI closed-loop system demonstrates notable time-domain performance. The numerical simulation results provided in this study offer support for the effectiveness of the proposed synthesis method.