Introduction

Research literature has firmly established that there are individual differences in how children’s mathematical knowledge and skills develop (e.g. Dowker, 2015; MacKay & De Smedt, 2019). This domain of study is important since children’s varied approaches to strategy use offer insights into their underlying understandings and conceptualizations (Lester, 2007). For the domain of fractions, research has focused on varying aspects of elementary school children’s development of fraction procedures and concepts such as the development of the measure fraction sub-construct (e.g. Norton & Wilkins, 2010), reasoning with multiplicative relationships (e.g. Boyce & Norton, 2016; Hackenberg, 2010), and children’s conceptual and procedural knowledge when learning fractions (e.g. Lenz et al., 2019). While the focus on the development of fraction concepts and skills has contributed immensely to the literature on individual differences, much more remains to be explored, such as the link between the different fraction sub-constructs (Middleton et al., 2015).

The fraction construct can have five different meanings depending on the context (Kieren, 1980). These include the measure, part-whole, quotient, operator and ratio sub-constructs. In exploring children’s understanding of the partitive quotient sub-construct, several studies (e.g. Empson et al., 2006; Lamon, 2012; Streefland, 1991) have used fair sharing tasks such as ‘how much does each person receive when four pizzas are shared fairly among five friends?’ The children in the present study also explored similar tasks. Behr and Post (1993) describe the partitive quotient sub-construct in procedural terms as follows: (a) starting with two quantities; (b) treating one of them as a divisor and the other as the dividend; and (c) obtaining a single quantity result by the process of partitive division. In other words, in a fair sharing situation where \(x\div y=\frac xy\), the numerator maps to the dividend and the denominator to the divisor (Charles & Nason, 2000; Empson et al., 2006).

Existing literature suggests that children will only have a deep and complete understanding of the fraction construct when their classroom instruction addresses all the different sub-constructs (Boyce & Norton, 2016; Kieren, 1993; Middleton et al., 2015; Steffe & Olive, 2010). There is therefore a need for research that focuses on children’s knowledge development from one fraction sub-construct to another.

Internationally, children’s fraction instruction in school typically begins with the part-whole sub-construct (Čadež & Kolar, 2018; Torbeyns et al., 2015) and “many students have yet to construct fraction understandings beyond part-whole comparisons by the time they reach middle school” (age 11) (Boyce & Norton, 2016, p. 10). According to English and Halford (1995), a part-whole conceptualization involves (1) recognizing that the parts in the whole are equal, (2) identifying the total number of equal parts (e.g. eight), (3) identifying the number of shaded equal parts (e.g. three) and (4) coordinating the number of shaded parts and the total number of parts to obtain the fraction, \(\frac{3}{8}\). While much attention has been given in the academic literature to the part-whole sub-construct, this has not been extended to the partitive quotient meaning of fractions (Hackenberg, 2010).

To date, a limited number of studies (e.g. Charalambous & Pitta-Pantazi, 2007; Charles & Nason, 2000; Nunes, 2008) has explicitly focused on how another fraction sub-construct knowing emerges from existing part-whole knowledge. Furthermore, the few studies that have investigated the impact of the part-whole meaning of fractions on the development of the partitive quotient sub-construct have provided mixed findings. On the one hand, researchers have found that previous part-whole learning inhibits children’s knowledge attainment of other fraction sub-constructs, including the partitive quotient sub-construct (e.g. Charles & Nason, 2000; Kerslake, 1986). On the other hand, other findings have suggested that the part-whole and partitive quotient understandings can emerge relatively seamlessly alongside each other with appropriate support from instruction (e.g. Naik & Subramaniam, 2008; Nunes, 2008).

Considering that the part-whole meaning of fractions is still, most often, the first fraction sub-construct that children learn in the classroom, it is notable that research on how other meanings of fractions develop from initial part-whole knowledge is still sparse (Amato, 2005), although “there is a research base on how children’s thinking about fractions could progress” (Empson, 2011). The present research, which draws from a larger study (see George, 2017), aims to address this research gap by examining 9-year old children’s engagement with partitive quotient tasks after having been only taught the part-whole sub-construct of fractions in school. This paper does not aim to evaluate whether one way of engagement is more optimal than another. Instead, it aims at examining the potential influence of the part-whole sub-construct through an analysis of within and cross-individual variation in children’s emerging approaches to partitive quotient tasks with the view of contributing to the advancement of existing evidence and understanding of the nature of this influence.

The current research differs from existing, cross-sectional research work (e.g. Charles & Nason, 2000; Empson et al., 2006) in that it aimed to explore children’s engagement with partitive quotient problems in more than one problem solving session that took place close in time, as part of a microgenetic research design. It also deviates from existing studies that have examined children’s engagement with the partitive quotient sub-construct over time in the context of teaching situations (e.g. Empson & Levi, 2011; Streefland, 1991), in that it sought to investigate children’s exploration of the partitive quotient sub-construct before they had been exposed to related explicit instruction at school.

Exploring differences and changes in strategy use when children engage with novel partitive quotient tasks is significant for informing teaching that aims to support children making meaningful connections between existing and new knowledge in their development of fraction knowledge. This research has sought answers for the following research questions:

  • 1. What strategies do 9-year-old children who have only been taught the part-whole fraction sub-construct use to find the fraction associated with solving partitive quotient problems in a sequence of problem-solving sessions?

  • 2. How does children’s strategy use change when they engage with multiple partitive quotient problems in a sequence of problem-solving sessions?

Strategies for Finding the Fraction in Partitive Quotient Tasks: Previous Research

Previous empirical literature on children’s solving of partitive quotient problems reveals that children use several correct and incorrect approaches. In this section, we provide exemplars from the research base to show the diversity in children’s engagement. Streefland’s (1991) study, which was conducted in the Netherlands, involved children whose first encounter with fractions was with the partitive quotient sub-construct, but who had previously engaged extensively with whole numbers. He found that when faced with a problem in which the number of items was less than the number of sharers, such as share six pancakes among eight people, children used several correct repeated addition strategies. These included: 1/8 + 1/8 + 1/8 + 1/8 + 1/8 + 1/8 and 1/8 + 1/8 = 2/8; 2/8 + 1/8 = 3/8 etc. Empson and Levi (2011) described the repeated addition approach where one item is shared at a time as additive coordination.

In Streefland’s (1991) study, when the number of items was greater than the number of individuals in the sharing situation, such as, share five eggs among four people, children used several strategies, such as:

  • 1 + ¼ = 1 ¼ where each person got a whole and then ¼ from the last egg (Correct)

  • 1 + ¼ = 2/4 since 1 + 1 = 2 and 4 remains as is (Incorrect).

For the incorrect solution ‘1 + ¼ = 2/4’, some of the children made the error of operating with the fraction symbols in the same way as with whole numbers and performed the operation of addition on the numerators and denominators individually. Streefland (1991) reports that most of the children in his sample operated in this way at several points during their engagement with the partitive quotient problems and that this phenomenon was particularly stubborn, even when the teacher/researcher made specific efforts to counteract it.

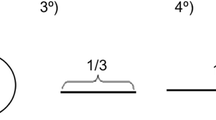
Charles and Nason (2000) conducted research in Australia with twelve year 3 (aged 7.9–8.3) children. They only used tasks where the number of items was less than the number of sharers. Similar to Streefland (1991), Charles and Nason’s (2000) research participants used repeated addition, but further to this, some children did not only partition each item into the same number of pieces, but partitioned the items being shared in two or more ways. For example, for the problem of ‘share three pizzas among four people’, two children partitioned two items into two pieces each and the third into four pieces. The children then found the fraction that each person received by adding two fractions, ½ + ¼, to obtain an answer of ¾ (Fig. 1). Another way in which some children in Charles and Nason’s (2000) study quantified each person’s share was by an immediate verbalization of the answer as \(\frac{\mathrm{number of items}}{\mathrm{number of people}}\) “without partitioning and sharing of the objects” (p. 200). The two aforementioned approaches have been also reported in a study conducted by Empson et al. (2006) with a sample of 112 children in varied grades in the USA.

Fig. 1
figure 1

Authors’ representation for illustrating the partitioning for sharing three items among four people in Charles and Nason’s (2000) work

Full size image

A novel approach reported for some of the children in Charles and Nason’s (2000) research was a strategy that involved finding the denominator of the fraction by adding the total number of pieces from partitioning the items and determining the numerator by adding the number of pieces that children distributed to each of the sharers. For example, in sharing two items among four people, after partitioning each of the two items into half and distributing the pieces, the child quantified each person’s share as “one part out of four equal parts” (Charles & Nason, 2000, pp. 204-205). This way of working is in contrast to strategies reported in Streefland (1991) whose sample appeared to act exclusively on the fraction symbols, adding the numerators and denominators separately.

Empson and Levi (2011) described the additive coordination strategy that involved children sharing groups of items. For example, for the problem ‘share six cakes among eight children’, children who employed this strategy noticed that two cakes can be shared among eight people by sharing each cake into fourths. Each person then received one-fourth from each pair of cakes. In total, each person received three-fourths cake.

The final approach presented in this section relates to the research conducted by Charles and Nason (2000) and involves a child sharing one pizza between two people. After sharing the pizza into eight, the child “incorrectly quantified each person’s share as ¼ instead of 4/8” (p. 204). In so doing, the child appeared to treat each person’s share as a unit fraction in which the denominator represented the number of pieces each person received. Charles and Nason (2000) stated that the child appeared “to confuse the number of pieces in each person’s share (4) with the number of pieces in the whole (8) when he was generating the fraction denominator” (p. 204).

Theoretical Underpinning

In this study, we view the process by which learners engage with a novel task as being underpinned by cognitive constructivist ideas of development, whereby individuals, starting from existing knowledge and competencies, construct knowledge and make sense of new experiences (Boaler, 2015; Martin & Towers, 2016; Steffe & Olive, 2010). On this basis, the theoretical idea of ‘met-befores’ put forward by McGowen and Tall (2010) has informed this research. McGowen and Tall (2010) define the notion of ‘met-befores’ as “a mental structure that we have now as a result of experiences we have met-before” (p. 171). They point out that where the acquisition of new knowledge is concerned, ‘met-befores’ function in supportive and/or preventative roles, depending on the varying contexts. In other words, ‘met-befores’ can either promote or impede present and/or future knowledge construction.

The notion that previous knowings and experiences or ‘met-befores’ influence the development of new knowledge is well established in the domain of fractions (Charles & Nason, 2000; Steffe & Olive, 2010; Tzur & Simon, 2004). Previous research suggests that two ‘met-befores’—whole numbers and the part-whole sub-construct—appear to interfere with children’s knowledge construction related to the partitive quotient sub-construct (e.g. Charalambous & Pitta-Pantazi, 2007; Ni & Zhou, 2005; Norton & Wilkins, 2010; Streefland, 1991).

Knowledge of whole numbers has been found to influence children’s solving of partitive quotient problems such as ‘share three continuous items among four people’ (e.g. Streefland, 1991). After partitioning the three items into four, which represents the number of people sharing, the child finds the fraction amount by adding all the numerators and denominators of the fraction symbols separately, as follows: \(\frac{1}{4}\) + \(\frac{1}{4}\) + \(\frac{1}{4}\) = \(\frac{1 + 1 + 1}{4 + 4 + 4}\) to get an answer of \(\frac{3}{12}.\)

Another ‘met-before’ that appears to interfere with a child’s knowledge construction of the partitive quotient is the part-whole relationship (e.g. Charles & Nason, 2000; Mack, 1990). Charles and Nason (2000) report that some of the children in their study found that the fraction for quantifying each person’s share in a partitive quotient situation corresponded to: Total number of pieces given to each person/Total number of pieces in all the items. This is because some of the children appeared to conceptualize the task using the part-whole sub-construct by forming one unit from the various numbers of continuous items. They denoted the number of pieces in all the items as the denominator of their fraction and the total number of pieces each person received in all the items as the numerator. Charalambous and Pitta-Pantazi (2007) also support Charles and Nason’s (2000) finding. Citing results from their data analysis based on a sample of 646 fifth and sixth graders in Cyprus, they report that the partitive quotient task of: ‘Three pizzas are evenly divided among four children. How much pizza will each child get?’ was associated directly with the part-whole fraction sub-construct. They considered this reasonable, because, “due to the numbers used in the problem, students could also use a part-whole representation to solve this problem” (p. 307).

Moving from whole numbers to the part-whole meaning of fractions and then to the partitive quotient sub-construct is cognitively demanding for children because of the associated changes in the nature of the unit or the whole (Lamon, 2012; Siegler et al., 2013). In Charles and Nason (2000, p. 214) when solving partitive quotient problems, children who quantified a person’s share using the part-whole notion “regularly suffered ‘loss of whole’”. The researchers explained that when children attempted to find each person’s share, they did not think of the number of pieces in each one whole unit. Instead, they considered the number of pieces in all the units. In line with Mack’s (1990) study, the children in Charles and Nason’s (2000) research appeared to attempt to form the single whole or unit that they were accustomed to during their previous experiences with fractions as part-whole.

The study reported in this paper focused on exploring and examining inter- and intra-individual variations in strategy use by children who were engaging with the novel partitive quotient fraction sub-construct, following previous formal knowledge of the part-whole fraction sub-construct and whole numbers, as developed through explicit instruction at school. Therefore, the notion of ‘met-befores’ provides a relevant and useful theoretical basis for viewing and interpreting children’s ways of working.

Methods

Research Design

The research applied a qualitative, microgenetic design (Voutsina et al., 2019; Siegler, 1995). Microgenetic research involves intensive observation of learners’ problem solving behaviour, including verbalizations and/or actions, as they engage in similar types of tasks, over short periods of time, when their knowledge of a concept or use of particular problem solving strategies is developing (Chinn, 2006; Siegler, 2006). This provides an avenue for collecting the type of fine-grained information that is necessary for understanding change processes in learning (Luwel et al., 2008) and the development of knowledge.

Microgenetic research designs produce very rich data; however, both the data collection and analysis processes are particularly effort- and time-consuming. Consequently, microgenetic studies typically involve either a small sample or a small number of sessions or both, to allow fine-grained analysis of data stemming from more than one trial with the same type of task over more than one session. This is essential for examining transition phases in learners’ behaviour (Flynn et al., 2006). One limitation related to the microgenetic research design is related to the need for multiple sessions. For children, this may lead to boredom and/or frustration. The number of tasks or sessions must therefore be carefully chosen so that a balance between collecting the data needed and managing concerns related to participant tiredness is achieved. For the current research, before the main data collection, we conducted a pilot study with a different group of children of the same age. This pilot study indicated that eight sessions were sufficient to collect data on potential changes in children’s strategy use within a short, specific time frame of sessions whilst maintaining children’s interest in the task.

Within the field of mathematics education, the microgenetic approach has been applied to explore areas such as children’s strategy discovery and use in single-digit addition and additive problem solving (e.g. Siegler & Crowley, 1991), strategy use in multiple-step tasks (e.g. Voutsina, 2012), strategy choices in algebraic problem solving (e.g. Nussbaumer et al., 2014), single-digit multiplication strategies (e.g. Van der Ven et al., 2012) and strategies employed by college students for fraction magnitude comparison (e.g. Fazio et al., 2016).

Microgenetic methods are “designed specifically to address questions” such as “how do various components of students’ prior knowledge interact with new information to produce change… do learners build on prior knowledge… or do they partly sidestep old knowledge and try to set it aside as they construct new understandings” (Chinn, 2006, p. 441). Further to this, this design “is well suited to capture the dynamic of competition among strategies” (Kuhn, 1995, p. 134). For this reason, a microgenetic approach was deemed to be appropriate to use for the current study which aims at examining the kind of strategies that children use, when they engage with novel, for them, partitive quotient tasks.

Research Participants

Nine year 5 children (three girls and six boys), aged 9–10 years participated in the study. A non-probability sampling technique was employed. Children were chosen from two schools, purposively, on the basis of whether they were likely to verbalize their thoughts as they worked on problems; whether they wanted to participate and had a regular attendance record. Since the aim of the study was to conduct dense observations and intensively analyze the data as each child engaged with the eight tasks across more than one session, there was a small number of research participants (Kuhn, 1995). The aim was to gain in-depth insights into the potential qualitative variation of strategy use and changes from close, detailed qualitative analysis of data from more than one problem solving session rather than from a single point in time from a larger sample. The objective of the analysis was to make inferences that can contribute to theoretical reasoning (Bryman, 2016) about children’s emergent partitive quotient approaches. Review of the elementary school mathematics curriculum (ages 5–11), textbooks used by the two schools and a discussion with the children’s teachers confirmed that the children had been taught the part-whole meaning of fractions at school and the partitive quotient problems were novel for them.

This research forms part of doctoral work undertaken in the UK. Consequently, the British Education Research Association (BERA, 2018) ethical guidelines in relation to parental consent and children’s assent for participation were followed (British Educational Research Association, 2018). Further to this, ethical approval was sought and obtained from the researchers’ academic institution.

Data Collection

Video-recorded, one-to-one task-based interviews (Maher & Sigley, 2014) were used as the data collection tool. The data were collected by the first author over a 6-week period in the first term of the academic year and consisted of the verbalizations and written work of the research participants as they engaged in solving eight partitive quotient problems. Children solved problems associated with sharing a number of continuous items among b people, such as share three cakes among four people. The tasks that were used had been adapted from previous empirical research (Charles & Nason, 2000; Lamon, 2012; Streefland, 1991). The main change related to the contexts of problem situations within which the tasks were embedded. In particular, the following two contexts were used to introduce tasks that involved situations of sharing cake and pizza, respectively:

  • a. Grade 5 decided to have a bring-and-share picnic day. Everyone decided that rectangular cakes would be brought and shared among the class. Over the next few days, we are going to share different numbers of cakes among different numbers of children so that each person in a group gets the same amount of cake and no cake is left over.

  • b. Harry’s mum makes rectangular pizzas to share with family and friends. Over the next few days, we are going to share different numbers of pizzas among different numbers of people so that each person gets the same amount of pizza and no pizza is left over.

Table 1 shows two task examples, one from each context, and the number of items and people in each of the eight tasks (T01–T08).

Table 1 Task details
Full size table

A combination of even and odd numbers was used. The smallest number of items that was included was two, since for one item, the number of ways of solving the problem is limited. For tasks T04 and T06, the number of items and people involved in the fair-sharing task had a common factor, which could potentially elicit a wide variety of ways of engaging with the tasks. The sharing situation in one task, T02, involved a number of items that was more than the number of people. This task was to elicit the generation of improper fractions or mixed numbers. The tasks were ordered so that the first and last task involved the smallest and largest number of people sharing, respectively. The order of the other tasks was randomly assigned.

The participants, generally, engaged with two tasks on a weekly basis. Interviews were at most 30 min long. In the fair sharing tasks, cakes and pizzas were represented using rectangular region models as relevant to each task, printed on A4 paper. We chose to use rectangular, bar models because previous research has shown that it is easier for children to work with the bar model, as compared to the circular model (e.g. Keijzer & Terwel, 2001). Additionally, in doing so, we followed previous empirical research conducted within the framework of constructivist ideas and approaches in which children used representational diagrams such as bar models as they engaged with different fraction problems (Ball, 1993; Hunt & Tzur, 2017; Norton & D'Ambrosio, 2008; Simon, 2019). In making this choice, Ball (1993) informs that:

Fruitful representational contexts are framed clearly enough to facilitate the development of sound mathematical understandings and skill in students. Fraction bars, pie diagrams, number lines—all these can help to focus learners on certain key features of fractions, such as the meanings of fractional terms. At the same time, the context is sufficiently open to afford students opportunities to explore—to make conjectures and follow important mathematical tangents. (p. 6)

Therefore, students’ use of representational diagrams, such as bar models, is considered as a critical component of individual’s knowledge construction.

The interviewer (first author of the paper) prompted the children to describe and explain their strategies by asking questions such as: “How did you figure that out?”, “How do you know?” After a first solution to the problem had been given, the interviewer prompted children to think of other ways for sharing the items by asking the question: “How else can you share [number of items] among [number of people]?”

Data Analysis

As a starting point, the categorization of strategies was based on the set of possible strategies for finding the fraction that have been identified in previous literature presented earlier in the paper. In instances where the strategy used by a research participant did not match any of the strategies reported in existing empirical research, a new short description and an associated code were created. Table 2 presents the description of each strategy identified, one example of data from the present research that illustrates each strategy (pseudonyms have been used) and references to previous research that has also identified a particular strategy.

Table 2 Description and exemplars of strategies used
Full size table

One of the strategies shown in Table 2 resulted in a correct fraction to the partitive quotient problem (strategy B: number of pieces per person/number of pieces in one item) and three were incorrect (strategies A: number of pieces per person/number of pieces in all items, C: number of pieces per person/number of items, and D: 1/number of pieces per person from the items). Three of these strategies have been reported in previous empirical literature (strategies A, B, D) and one (strategy C) has not been reported before, as far as the authors are aware. Following from this, the analysis closely examined individual strategy use across the eight tasks with a focus on inter-individual differences and intra-individual changes of strategy use. Findings from this line of analysis are presented in the following section.

Strategy Use Across the Eight Task-Based Interviews

Figure 2 shows the distribution of the four strategies for finding the fraction across research participants and tasks. The inter- and intra-individual variation of engagement with the tasks is also presented. Each colour represents a different strategy. Cells of different colours within one task-based interview (e.g. T02 for Samuel), show that the child has used more than one strategy to quantify each person’s share within the same task. Beyond the first solution, children generally provided alternative solutions for each task when the question ‘How else can you share the same number of items among the same number of people?’ was asked. The most common way of operating, however, was for the children to use a single strategy type for a given task. This is depicted by the single colour in a given cell for most of the tasks. The colours depict the strategies that the children used across all the different solutions that they provided across the tasks.

Fig. 2
figure 2

Distribution of strategies across children and tasks

Full size image

Strategy A (number of pieces per person/number of pieces in all items) was used most often, followed by strategy B (number of pieces per person/number of pieces in one item). Specifically, seven of the research participants (David, Kenny, Karen, Mary, Gabriel, Samuel, Harry) used strategy A on at least one occasion over the eight task-based interviews, whereas six children used strategy B. While both strategies A and B were most often utilised, five children used strategy A predominantly (for at least five of the eight tasks), while one child (Harry) used strategy B. In addition, three out of the five children (Karen, Mary, Gabriel) who applied strategy A as their main strategy, also used strategy B. Six children used strategy B at some point of their engagement with the eight tasks but only two of the children in this study applied this as their strategy of choice across all tasks.

It is important to note that the individual strategies that the children used have been presented in this section to provide the basis for exploring intra- and inter-individual strategy use across eight partitive quotient tasks. This individual strategy use that aligned largely with previous research is not the primary focus of this paper. The key findings relate to children’s strategy shifts and variation of strategy use within and between individuals across the multiple tasks as shown in Fig. 2.

Shifts in Strategy Use Across Eight Partitive Quotient Tasks

Across the eight tasks, three children (David, Kenny, Rebecca) used a single strategy and six of the nine children used more than one strategy for quantifying each person’s share (Fig. 2). In this section, we present indicative examples of children who used more than one strategy across the tasks. Of the six children who used two strategies, three children (Mary, Samuel, Harry) used these within a given task-based interview. Tables 3 and 4 provide indicative examples of shifts observed between strategies A (number of pieces per person/number of pieces in all items) and B (number of pieces per person/number of pieces in one item) in Harry’s and Samuel’s reports, respectively, in response to the researcher’s (R) questions, illustrating different variations of strategy use across more than one task.

Table 3 Harry’s strategy use across the tasks
Full size table
Table 4 Samuel’s strategy use across the tasks
Full size table

Harry’s engagement with tasks T02, T04, T05, T06 and T08 are presented. In T02, the number of items was greater than the number of people sharing. T04 and T06 present tasks preceding and subsequent to the notable shift between strategies A (number of pieces per person/number of pieces in all items) and B (number of pieces per person/number of pieces in one item) occurring in T05. T08 presents Harry’s solving approach at the end of the task-based interviews. In the case of Samuel, tasks were chosen from the start, middle and end of the sequence of task-based interviews. Harry used strategy B until T05. In T05, for one solution within a given task he appeared to utilize strategy A instead. Subsequently, he reverted to strategy B and did not use strategy A again. In obtaining the fractions 2/16 and 2/14, Harry, for the first time, combined the individual cakes to form two wholes, each with a number of equal parts; 14 and 16. He then appeared to apply part-whole knowings in finding the fractions with the denominator equal to the total number of pieces in the newly formed ‘single cake’ and the numerator of each fraction equal to the number of pieces each sharer received. It is unclear what prompted this way of working; perhaps the specific way of partitioning the two diagrams, which did not appear for other tasks. In T04, Harry distributed four pieces of cake to the sharers, one from each diagram, but did not appear to apply a part-whole conceptualization of forming a new single item strategy before finding the fraction.

Samuel used both strategies A (number of pieces per person/number of pieces in all items) and B (number of pieces per person/number of pieces in one item) for seven out of the eight tasks (Table 4). For strategy B, Samuel, like Harry, appeared to use a part-whole conceptualization where the unit is one whole. To obtain this whole he added the pieces from the different items which became the denominator of the fraction and then totalled the number of pieces that each person received from all the items and denoted this as the numerator. Samuel’s use of strategy A may also have incorporated the use of a part-whole lens. The unit or whole for this solution consisted of each equally partitioned individual cake. Samuel appeared to equate the sum of each fraction obtained from the individual items to the fraction obtained when individual items were combined to form one item. Throughout the tasks, Samuel shifted consistently from using strategy B, which resulted to a correct solution, to strategy A, which resulted to an erroneous solution. We do not have concrete evidence for what might have underlaid this shift. However, the prompt “How else can you share [number of items] among [number of people]?” that was part of the tasks, might be linked with this observation. It might be that the need to respond to this question, and think of another way of sharing the items, resulted to an unsuccessful attempt for an alternative solution. Samuel’s return to the application of the correct strategy B for his first attempt in every subsequent task provides a basis for this speculation. Furthermore, his correct initial attempt for every task indicates his capability to apply an appropriate approach to partitive quotient tasks even though his subsequent shift to an erroneous approach suggests some limitations in his grasp of the partitive quotient sub-construct.

The other three children (Karen, Gabriel and Jack) who used two strategies across the tasks used a single strategy for multiple solutions to one given task, then switched to another, different strategy for a subsequent task (See Tables 5 and 6). This differentiates these children’s way of working from Mary, Samuel and Harry who used two different strategies within a given task-based interview. Karen (Table 5) used strategy A (number of pieces per person/number of pieces in all items) for T01, where the number of items was less than the number of people sharing. In T02, she used strategy B (number of pieces per person/number of pieces in one item) when the number of items was more than the number of people sharing. For T03, which was similar to T01 in that the number of items was less than the number of people sharing, she reverted to strategy A and continued to do so until T08. Therefore, in using strategy A, similar to Samuel, Karen appeared to combine the individual items being shared to get a ‘new’, single whole consisting of the total number of individual pieces. This is a key error that children who used strategy A made. To find the numerator, Karen identified the number of pieces each person would receive. She then verbalized that this number is ‘out of’ the denominator or total number of pieces comprising the new unit. The act of joining the individual items to form a new whole and the phrase ‘out of’ suggest that it is plausible that a part-whole lens was applied to the task.

Table 5 Karen’s strategy use across the tasks
Full size table
Table 6 Jack’s strategy use across the tasks
Full size table

Jack’s strategy use across the eight tasks (Table 6) was unique in that he was the only child who employed strategy C (number of pieces per person/number of items). After using strategy B (number of pieces per person/number of pieces in one item) for the first three tasks, he switched to using the strategy C, for T04 and for the remainder of the tasks. Empson (2011) captures our conclusion in relation to strategy C when she notes that in solving partitive quotient problems, individuals often used strategies that were seemingly inconsistent with their previous ways of working.

Discussion

The data stemming from more than one problem-solving session with each child show seven different variations of problem-solving strategy use over the eight partitive quotient tasks. The strategy use presented here does not constitute a typical picture of how children who have primarily been exposed to the part-whole fraction sub-construct engage with the partitive quotient meaning of fractions, in general. For a different sample of children, other variations could emerge. The findings are noteworthy since this study reveals differences in strategy use and changes across and within individual children who have only been previously exposed to the part-whole sub-construct as part of explicit instruction at school. The study also reveals several instances of when (see Fig. 2) and how the part-whole fraction sub-construct interfered with children’s engagement with the partitive quotient problems across the eight sessions. This has not been reported in previous cross-sectional research or in studies where teaching was involved (e.g. Empson & Levi, 2011). In this regard, the findings from this study add to the mixed findings related to the impact of the part-whole meaning of fractions on the development of the partitive quotient sub-construct. The present findings also provide new evidence for intra- and inter-individual variation in strategy use and strategy selection in tasks related to the partitive-quotient meaning of fractions which is consistent with fraction magnitude comparison research (Siegler et al., 2013).

Most children in this study (five out of nine), who had only been taught the part-whole meaning of fractions, applied strategy A (number of pieces per person/number of pieces in all items) as their strategy of choice for quantifying each person’s share in the problem contexts. Three out of the five children who applied strategy A as their strategy of choice, at some point in engaging with the tasks, used strategy B (number of pieces per person/number of pieces in one item), but abandoned its use entirely, later on in their engagement with the problems.

The choice of strategy A (number of pieces per person/number of pieces in all items) is noteworthy because it suggests that the children used a part-whole lens in finding the fraction to the partitive quotient problems. The children who used strategy A appeared to be using the steps put forward by English and Halford (1995), presented earlier in the paper, but instead of denoting the numerator as the number of the shaded parts, the children denoted the numerator as the number of pieces each person received. The children in this study found the denominator by determining the total number of parts in all the items shared. This contrasts with Streefland (1991) whose research participants appeared to be influenced by the whole number ‘met-before’ as they acted exclusively on the fraction symbols by adding all the numerators and denominators separately to obtain the fraction each sharer received. The children in the current study acted on and used the drawings that they had created to derive their fraction to quantify each person’s share as ‘Total number of pieces given to each person/Total number of pieces in all the items’. Therefore, we do not consider the whole number ‘met-before’ to be applicable here. Instead, it appears that similar to some of the children in Charles and Nason’s (2000) study, some of the children in this study interpreted the task through a part-whole lens and therefore used a part-whole approach (strategy A) for finding the fraction.

Consistent with Kieren (1993) and R. Tzur (personal communication, August 12, 2019), we connect this observation with the children’s long-standing exposure to the part-whole fraction sub-construct as part of their elementary school mathematics experience. Tzur and Simon (2004) concur with this reasoning and posit that it is a predictable outcome that children’s established conceptions of mathematical topics “interfere with their learning of new conceptions” (p. 300). They add that when learners initially engage with a new concept or construct, they may utilize existing knowledge incorrectly resulting in incorrect answers as was observed for most of the children in this study. Further to this, the part-whole interference exhibited by the children appears to be grounded in their partial understanding of what constitutes the whole or unit within the context of the part-whole sub-construct. Behr and Post (1992) state that the concept of the whole underpins the varied fraction sub-constructs, but that the conventional part-whole situation that children encounter in elementary school is that of a single continuous item partitioned into a number of equal parts, which represents one whole or unit. Rarely, if ever, do children encounter part-whole situations where the unit consists of multiple units (Hackenberg et al., 2016; Kieren, 1993). Children’s limited conceptualization of the part-whole and use of strategy A (number of pieces per person/number of pieces in all items) could therefore be linked to previous engagement with the part-whole which involves single and not multiple units (Behr & Post, 1992; Kieren, 1993).

The part-whole fraction sub-construct in the current research assumed the role of a preventative ‘met-before’ (Tall, 2013). This notion is well-established in mathematics education but has been given a variety of labels such as epistemological obstacle (Sierpinska, 1990) or conceptual obstacle which is an “obstacle that has a cognitive nature that can be explained in terms of mathematical structures and concepts that underlie students’ earlier learning experiences” (Zaslavsky, 1997, p. 20). Some researchers suggest that the interference of ‘met-befores’ is an inevitable and useful part of children’s knowledge construction (Steffe & Olive, 2010; Tzur & Simon, 2004). Although some ‘met-befores’ such as whole numbers or the part-whole present a hurdle to the acquisition of new knowledge, ultimately they serve a constructive role as individuals reorganize existing knowledge to accommodate new knowledge (Empson, 2011). This perceived ‘obstacle’ is an opportunity for individuals to refine and extend their mathematical knowledge.

While we conclude that a part-whole lens appeared to interfere with most of the children’s engagement with partitive quotient tasks, the findings show differences and interesting variations in how the part-whole sub-construct interfered and at which points of children’s repeated engagements with the tasks. On the one hand, David and Kenny did not deviate from the use of strategy A (number of pieces per person/number of pieces in all items) regardless of whether the number of items being shared was greater than or less than the number of sharers. On the other hand, this task characteristic may have had an impact on Karen and Mary who only used strategy A when the number of items was less than the number of sharers. Empson (2011) asserts that children’s strategies in solving partitive quotient problems do not always align to expected responses but are “a function of specific quantities in the problem” as well as the previous knowledge of children (p. 581). Samuel used strategies A (number of pieces per person/number of pieces in all items) and B (number of pieces per person/number of pieces in one item) alongside each other. Streefland (1991) categorized this way of working as having an absence of cognitive conflict in situations where different results are obtained to the same problem. A child accepts both answers as correct because different methods are involved. However, Streefland’s (1991) research found that the natural number interfered with children’s learning of the partitive quotient meaning of fractions. In this research, this cognitive conflict is aligned to the part-whole sub-construct and not natural numbers.

While the main ‘met-befores’ that are related to the partitive quotient sub-construct include whole numbers and the part-whole sub-construct, this research suggests that other ‘met-befores’ may also apply. For Rebecca, who quantified each person’s share as ‘1/number of pieces per person from the items’ (see Table 2), neither whole numbers nor the part-whole sub-construct ‘met-befores’ apply. This way of working suggests that Rebecca may think that all fractions are unit fractions with a numerator of one and that it is the denominator that denotes ‘number of parts shaded or number of parts each person receives’. In this case, the unit fraction would be considered to function as a ‘met-before’ that impeded finding the correct fraction for the partitive quotient task. For Jack, it is difficult to discern which, if any, ‘met-before’ is applicable to his fraction solution. In solving partitive quotient problems, children will invariably encounter conflicts and take detours that divert, prolong, or even stall their progress towards a mature understanding of the sub-construct (Middleton et al., 2015; Streefland, 1991).

The findings reported here are based on data collected during individual, task-based interviews. In interpreting the findings, the particular context of data collection and situation-specific nature of the data need to be considered. While we consider that the analysis of data based on more than one session with the same type of problem provided a strong basis for the description and examination of problem solving behaviour, children’s behaviour was in response to the particular situation and the researcher’s questions within a specific number of sessions. The study does not capture how the reported variations in each of the children’s emergent approaches further develop as children advance their understanding and conceptualization of the partitive quotient sub-construct. Also, the research does not capture how the observed variations hold or change within other contexts, such as classroom-based activities and tasks, or everyday contexts, as this was beyond the scope of this study.

The focus of the current research on investigating entities that require fine-grained analysis over multiple sessions, as per the microgenetic design, necessitated a small number of participants. Future research could further explore the arguments put forward and aforementioned explanations of children’s strategy use in larger scale studies, longitudinally and within different contexts. Further research on the factors that may affect and trigger shifts in children’s strategy use within the same task and across similar tasks will also be useful. This could contribute to researchers’ and educators’ understanding of children’s trajectories of learning of the partitive quotient sub-construct in a holistic way.

In capturing and comparing multiple snapshots of individual children’s engagement with novel for them partitive quotient tasks, the current study reveals some of the detours and decisions that children take regarding their ways of solving these problems, which may not always be accurate. This can inform theoretical reasoning in relation to how the part-whole sub-construct and the concept of a unit interfere, as met-befores, in children’s engagement with partitive quotient problems.

Conclusion

In this study, we found that 9–10-year-old children displayed different variations of strategy use when solving novel, partitive quotient problems. While the part-whole sub-construct appeared to interfere with most of the children’s engagement with partitive quotient tasks, our findings show inter- and intra-individual variations in this interference and different points of interference in individual children’s engagement with the tasks, across more than one session. In addition, the present research suggests that it is plausible that children’s use of a part-whole conceptualization in engaging with the partitive quotient fraction sub-construct is linked to their potentially limited understanding of the concept of a unit or whole. Therefore, teaching and curriculum design that emphasises the concept of a unit in the different fraction sub-construct contexts could potentially facilitate and support the transition from one fraction sub-construct to another in the context of elementary school mathematics.

The findings highlight the need for teaching that introduces different fraction sub-constructs to learners early in their schooling so that one meaning of fractions does not become representative of all fraction knowledge. Stemming from this is a consideration of the order in which fraction sub-constructs are taught. We do not consider that categorically stating which fraction sub-construct is most appropriate to teach first or next is of central importance. Rather, the present study highlights the importance of informing varied decisions as to the order in which to teach the fraction sub-constructs by knowledge of the different understandings and conceptualizations that students bring with them in their engagement with novel fraction sub-constructs. We concur with Prediger’s (2008, p. 15) point that ‘obstacles’ in children’s developing fraction conceptions should be viewed as opportunities and that developing our understanding of the nature of different kinds of obstacles, such as the ‘met-befores’ reported here, is significant. This is because this knowledge can inform instructional approaches that aim to support children’s integration and reorganization, where necessary, of prior and new knowledge. Internationally, the part-whole meaning of fractions is still, predominantly, the first fraction sub-construct that children encounter and engage with over a substantial period of time in school, across different countries and educational contexts. Therefore, the findings of this study and aforementioned educational considerations are relevant and significant for the teaching and learning of fractions in education contexts internationally.