Skip to main content
SpringerLink
Log in

Non-linear finite element formulations of reinforced concrete haunched beam (RCHB)

  • Original Paper
  • Published:
Asian Journal of Civil Engineering Aims and scope Submit manuscript

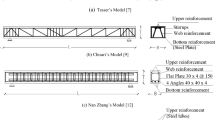
Abstract

Generally, a reinforced concrete haunched beam (RCHB) is used in the structure for increasing shear capacity at support and reduce self-weight of the structure to minimize cost. Large depth at support expresses stronger characteristics of beam. Therefore, classical strong column and weak beam theory may have violated which shows harmful effect of structure during lateral loading. However, in the present study, linear and non-linear formulae are developed for the 5-noded line elements of RCHB and parametric studies are performed under gravity loading. In parametric studies, the depth of the beam is reduced for the formation of haunch with the variations of haunch angles and lengths. Newly developed non-linear formulations are compared with the ETABS (18.1.1) which represents a good-fit of results up to a haunch angle of 7° and results vary after crossing this angle because of some consideration of present formulations responsible for these variations. Also, these formulations are compared with the Godínez-Domínguez et al. (Eng Struct 105: 99–122, 2015) experimental and numerical results which show similar variations of results like ETABS because of the same reason involved herewith. Most of the cases, forces, and displacements of RCHB are deviated from the haunch angle of 3° based on parametric studies. In addition, acceptance criteria meet when displacements of life safety and collapse preventions are 1.6 and 2.3 times of code prescribed maximum allowable displacement. The non-linear model and solution technique of present research can exhibit acceptance level of RCHB because of residual stress generation of the iterative process although results vary from ETABS and previous studies which indicates that further scope will have for the enhancement of present formulations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19

Similar content being viewed by others

Abbreviations

L :

Length of haunch beam

h y :

Depth of haunch

L i :

Length of haunch

N j :

Nodes

e#i :

Elements

K ei :

Elements stiffness matrixes

I i :

Moment of inertia of elements

E :

Elastic modulus of haunch beam

b :

Width of haunch beam

K G :

Global stiffness matrix in global coordinate

i :

Number of elements (1, 2, 3 and 4)

j :

Number of nodes (1, 2, 3, 4 and 5)

M ij :

Fixed end moments

F ij :

Fixed end forces

δ j :

Vertical translational nodal displacements

θ j :

Rotational nodal displacements

\(F_{ij}^{N}\) :

Nodal forces

\(M_{ij}^{N}\) :

Nodal moments

\(H_{i1}^{N}\) :

Hardening parameter of first stage of iteration

\({\text{d}}M_{i1}^{N}\) :

Change of moment

\({\text{d}}\varepsilon_{pi1}^{N}\) :

Change of plastic curvature

\(M_{pi1}^{N}\) :

Maximum plastic moment

\(M_{ei}\) :

Maximum elastic moment

\({\text{d}}\varepsilon_{i1}^{N}\) :

Change of total curvature

\({\text{d}}\varepsilon_{ei}\) :

Change of elastic curvature

\(M_{0}\) :

Maximum moment at yield of confinement (steel and concrete)

\(EI_{ik}^{N}\).:

Flexural rigidity at kth stage

\(H_{ik}^{N}\) :

Hardening parameter

\(K_{eik}^{N}\) :

Element stiffness matrix

\(K_{Gk}^{N}\) :

Global stiffness matrix

\(\psi_{{\left( {ij} \right)k}}^{N}\) :

Residual forces

\(\varphi_{jk}^{N}\) :

Nodal displacements

\(f_{{\left( {ij} \right)k}}^{N}\) :

Elements fixed end moment and forces

\(\Delta \varphi_{jk}^{N}\) :

Incremental nodal displacements

\(\varphi_{{j\left( {k + 1} \right)}}^{N}\) :

Nodal displacements at (k + 1)th stage

\(\theta_{{j\left( {k + 1} \right)}}^{N}\) :

Nodal rotational displacements

\({\text{d}}M_{ik}^{N}\) :

Changes of moments at (k + 1)th stage

\(\left( {EI} \right)_{{T\left( {ik} \right)}}^{N}\) :

Tangential flexural rigidity

\(H_{{i\left( {k + 1} \right)}}^{N}\) :

Hardening parameter at (k + 1)th stage

\(f_{{\left( {ij} \right)k}}^{NN}\) :

Nodal forces

\(f_{{\left( {ij} \right)k}}^{NF}\) :

Fixed end moments and forces at individual nodes

k :

Successive number loading stage

r :

Maximum number loading stage

\(w_{{\text{c}}}\) :

Unit weight of concrete

\(f_{c}^{^{\prime}}\) :

Cylindrical strength of concrete

N :

Notation of non-linearity

References

  • ACI. (2014). Building code requirements for structural concrete. American Concrete Institute.

    Google Scholar 

  • Ahmed, A.E.-R.M. (1982). Repeated loading effect on the behaviour of haunched R.C. beams. Assiut University.

    Google Scholar 

  • Ahmed, A.E.-R.M., Farghal, O. A., Sayed, A. M., & Yassen, O. A. (2018). Numerical analysis of statical shear behaviour of reinforced concrete haunched beams strengthened by using externally bounded steel plates by ANSYS program. Journal of Scientific and Engineering Research, 5(2), 210–223.

    Google Scholar 

  • Albegmprli, H. M., Abdulkadir, Ç., Gulsan, M. E., & Kurtoglu, A. E. (2015). Reliability analysis of reinforced concrete haunched beams shear capacity based on stochastic nonlinear FE analysis. Computers and Concrete, 15, 259–277.

    Article  Google Scholar 

  • Albegmprli, H. M., Gülşan, M. E., & Cevik, A. (2019). Comprehensive experimental investigation on mechanical behavior for types of reinforced concrete haunched beam. Advances in Concrete Construction, 7(1), 39–50.

    Google Scholar 

  • Allawi, A. A.-M., 2007. Stiffness matrix for haunched members with including effect of transverse shear deformations. Springer Eng. & Technology, 25, 1226–1236.

    Google Scholar 

  • Arzani, H., Kaveh, A., & Kamalinejad, M. (2019). Optimal design of pitched roof rigid frames with non-prismatic members using quantum evolutionary algorithm. Periodica Polytechnica Civil Engineering, 63(2), 593–607.

    Google Scholar 

  • ASCE, SEI. (2014). Seismic evaluation and retrofit of existing buildings (41st–13th ed.). American Society of Civil Engineers.

    Book  Google Scholar 

  • BNBC. (2021). Bangladesh national building code. Ministry of Housing and Public Works.

    Google Scholar 

  • Chenwei, H., & Matsumoto, K. (2015). Shear failure mechanism of reinforced concrete haunched beams. Journal of JSCE, 3, 230–245.

    Article  Google Scholar 

  • Godínez-Domínguez, E. A., Tena-Colunga, A., & Juárez-Luna, G. (2015). Nonlinear finite element modeling of reinforced concrete haunched beams designed to develop a shear failure. Engineering Structures, 105, 99–122.

    Article  Google Scholar 

  • Gulsan, M. E., Albegmprli, H. M., & Cevik, A. (2018). Finite element and design code assessment of reinforced concrete haunched beams. Structural Engineering and Mechanics, 66, 423–438.

    Google Scholar 

  • IBC. (2012). International building code. International Code Council.

    Google Scholar 

  • Jaafer, A. A., & Abdulghani, A. W. (2018). Nonlinear finite element analysis for reinforced concrete haunched beams with opening. Materials Science and Engineering, 454, 121.

    Google Scholar 

  • Kaveh, A., Izadifard, R., & Mottaghi, L. (2019a). Optimal design of planar RC frames considering CO2 emissions using ECBO, EVPS and PSO metaheuristic algorithms. Journal of Building Engineering, 28, 1–11.

    Google Scholar 

  • Kaveh, A., Kabir, M. Z., & Bohlool, M. (2019b). Optimum design of three-dimensional steel frames with prismatic and non-prismatic elements. Engineering with Computers, 36, 1011–1027.

    Article  Google Scholar 

  • Kaveh, A., Mottaghi, L., & Izadifard, R. (2021). An integrated method for sustainable performance-based optimal seismic design of RC frames with non-prismatic beams. Scientia Iranica A, 28(5), 2596–2612.

    Google Scholar 

  • Mottaghi, L., Izadifard, R. A., & Kaveh, A. (2021). Factors in the relationship between optimal CO2 emission and optimal cost of the RC frames. Periodica Polytechnica Civil Engineering, 65(1), 1–14.

    Google Scholar 

  • Sadavare, J. V., & Tande, S. N. (2021). Study of haunched beam frame subjected to various load conditions. International Research Journal of Engineering and Technology (IRJET), 08(05), 1334–1342.

    Google Scholar 

  • Sangave, P. & Nampalli, P. (2015). Linear And Non-Linear Analysis of Reinforced Concrete Frames With Members of Varying Inertia. IOSR Journal of Mechanical and Civil Engineering, 12, 50–59.

    Google Scholar 

  • Tena-Colunga, A., Hans, I. A., & Oscar, M. G. (2008). Behavior of reinforced concrete haunched beams subjected to static shear loading. Engineering Structures, 30, 478–492.

    Article  Google Scholar 

  • Vijayan, V., & Jolly, A. (2016). Structural behaviour of reinforced concrete haunched beam. International Journal of Scientific & Engineering Research, 7(10), 93–97.

    Google Scholar 

Download references

Funding

No external funding was used.

Author information

Authors and Affiliations

  1. Department of Civil Engineering, Bangladesh University of Engineering and Technology, BNUS Research Room, Dhaka, 1000, Bangladesh

    Md. Foisal Haque

Authors
  1. Md. Foisal Haque
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Md. Foisal Haque.

Ethics declarations

Conflict of interest

The author declares that he has no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Haque, M.F. Non-linear finite element formulations of reinforced concrete haunched beam (RCHB). Asian J Civ Eng 23, 1029–1064 (2022). https://doi.org/10.1007/s42107-022-00462-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s42107-022-00462-8

Keywords

Search

Navigation