PDMATLAB2D: A Peridynamics MATLAB Two-dimensional Code

Abstract

PDMATLAB2D is a meshfree peridynamics implementation in MATLAB suitable for simulation of two-dimensional fracture problems. The purpose of this code is twofold. First, it provides an entry-level peridynamics computational tool for educational and training purposes. Second, it serves as an accessible and easily modifiable computational tool for peridynamics researchers who would like to adapt the code for a multitude of peridynamics simulation scenarios. The current version of the code implements a bond-based brittle elastic peridynamic model and a critical stretch criterion for bond breaking. However, the code is designed to be extendable for other peridynamic models and computational features. In this paper, we provide an overview of the code structure and functions with illustrative examples. Due to the integrated computation and postprocessing MATLAB capabilities, PDMATLAB2D can serve as an effective testbed for testing new constitutive models and advanced numerical features for peridynamics computations.

Appendices

Appendix A. Derivation of a Microelastic Bond-Based PD Model

In this appendix, we derive the functional form of a microelastic bond-based PD model, following [1].

Let a bond-based PD pairwise force function be $\textbf{f}(\varvec{\eta },\textbf{x}^\prime , \textbf{x},t)$ with $\varvec{\eta }, \textbf{x}^\prime , \textbf{x}\in \mathbb {R}^3$ and $t\geqslant 0$, where $\varvec{\eta }: = \textbf{u}(\textbf{x}^\prime ,t) - \textbf{u}(\textbf{x},t)$. Then, by the linear admissibility condition:

$$\begin{aligned} \textbf{f}(-\varvec{\eta },\textbf{x}, \textbf{x}^\prime ,t) = -\textbf{f}(\varvec{\eta },\textbf{x}^\prime , \textbf{x},t), \qquad \forall \varvec{\eta },\textbf{x}^\prime , \textbf{x} \in \mathbb {R}^3, \quad t \geqslant 0, \end{aligned}$$

(A1)

and by the angular admissibility condition:

$$\begin{aligned} (\varvec{\xi } + \varvec{\eta }) \times \textbf{f}(\varvec{\eta },\textbf{x}^\prime , \textbf{x},t) = \textbf{0}, \qquad \forall \varvec{\eta },\textbf{x}^\prime , \textbf{x} \in \mathbb {R}^3, \quad t \geqslant 0, \end{aligned}$$

(A2)

where $\varvec{\xi }: = \textbf{x}^\prime - \textbf{x}$. By (A1) and (A2), we can express the pairwise force function as follows:

$$\begin{aligned} \textbf{f}(\varvec{\eta },\textbf{x}^\prime , \textbf{x},t) = F(\varvec{\eta },\textbf{x}^\prime , \textbf{x},t)(\varvec{\xi } + \varvec{\eta }), \end{aligned}$$

(A3)

where F is a symmetric scalar-valued function:

$$\begin{aligned} F(-\varvec{\eta },\textbf{x}, \textbf{x}^\prime ,t) = F(\varvec{\eta },\textbf{x}^\prime , \textbf{x},t), \qquad \forall \varvec{\eta },\textbf{x}^\prime , \textbf{x} \in \mathbb {R}^3, \quad t \geqslant 0. \end{aligned}$$

(A4)

For a microelastic material, the following condition holds:

$$\begin{aligned} \nabla _{\varvec{\eta }}\times \textbf{f}(\varvec{\eta },\textbf{x}^\prime , \textbf{x},t) = \textbf{0},\qquad \forall \varvec{\eta },\textbf{x}^\prime , \textbf{x} \in \mathbb {R}^3, \quad t \geqslant 0. \end{aligned}$$

(A5)

Assuming F is continuously differentiable on $\varvec{\eta }$, we have:

$$\begin{aligned} \nabla _{\varvec{\eta }}\times \textbf{f}(\varvec{\eta },\textbf{x}^\prime , \textbf{x},t)&= \varepsilon _{ijk}\frac{\partial }{\partial \eta _i}\left( f_j(\varvec{\eta },\textbf{x}^\prime , \textbf{x},t) \right) \textbf{e}_k\\&= \varepsilon _{ijk}\frac{\partial }{\partial \eta _i}\left( F(\varvec{\eta },\textbf{x}^\prime , \textbf{x},t)(\xi _j + \eta _j) \right) \textbf{e}_k\\&= \varepsilon _{ijk}\frac{\partial F}{\partial \eta _i}(\varvec{\eta },\textbf{x}^\prime , \textbf{x},t)(\xi _j + \eta _j)\textbf{e}_k\\&= \frac{\partial F}{\partial \varvec{\eta }}(\varvec{\eta },\textbf{x}^\prime , \textbf{x},t)\times (\varvec{\xi } + \varvec{\eta }), \end{aligned}$$

where $\varepsilon _{ijk}$ is the Levi-Civita symbol, $\{\textbf{e}_k\}_{k=1,2,3}$ is the set of standard Cartesian unit vectors, and we used Einstein summation convention for repeated indices. Then, by (A5), we have

$$\begin{aligned} \frac{\partial F}{\partial \varvec{\eta }}(\varvec{\eta },\textbf{x}^\prime , \textbf{x},t) = A(\varvec{\eta },\textbf{x}^\prime , \textbf{x},t)(\varvec{\xi } + \varvec{\eta }), \end{aligned}$$

where A is a scalar-valued function. Note that

$$\begin{aligned} \frac{\partial }{\partial \eta _i} (\Vert \varvec{\xi } + \varvec{\eta }\Vert ) = \frac{{\xi }_i + {\eta }_i}{\Vert \varvec{\xi } + \varvec{\eta }\Vert }, i=1,2,3. \end{aligned}$$

Consequently, we can express F as follows:

$$\begin{aligned} F (\varvec{\eta },\textbf{x}^\prime , \textbf{x},t) = H(\Vert \varvec{\xi } + \varvec{\eta }\Vert ,\textbf{x}^\prime , \textbf{x},t), \end{aligned}$$

(A6)

where $H(p,\textbf{x}^\prime , \textbf{x},t)$ with $p=\Vert \varvec{\xi } + \varvec{\eta }\Vert$ is a scalar-valued function continuously differentiable on p.

Combining (A6) and (A3), we can express the microelastic bond-based PD pairwise force function as follows:

$$\begin{aligned} \textbf{f}(\varvec{\eta },\textbf{x}^\prime , \textbf{x},t) = f(\Vert \varvec{\xi } + \varvec{\eta }\Vert ,\textbf{x}^\prime , \textbf{x},t)\frac{\varvec{\xi } + \varvec{\eta }}{\Vert \varvec{\xi } + \varvec{\eta }\Vert }, \end{aligned}$$

(A7)

where f is a scalar-valued function given by

$$\begin{aligned} f(\Vert \varvec{\xi } + \varvec{\eta }\Vert ,\textbf{x}^\prime , \textbf{x},t) = \Vert \varvec{\xi } + \varvec{\eta }\Vert H(\Vert \varvec{\xi } + \varvec{\eta }\Vert ,\textbf{x}^\prime , \textbf{x},t). \end{aligned}$$

Appendix B. Derivation of the Maximum Grid Perturbation in GridGenerator

Consider a rectangular cell centered at node i with coordinates $(x_i,y_i)$ with edge lengths $\Delta x$ and $\Delta y$ in the x- and y-directions, respectively, and assume a perturbation of the cell vertices. For simplicity, in the derivations below, we assume only three of the four vertices are perturbed, and we denote these by A, B, and C, as illustrated in Fig. 13. The perturbed vertices are denoted by $A^\prime$, $B^\prime$, and $C^\prime$, respectively (see Fig. 13), and the region of admissible new positions for a given vertex after perturbation is given by a rectangular region of size $2\alpha \Delta x \times 2\alpha \Delta y$ centered at the vertex (see Fig. 13), where $\alpha$ is a given parameter. We seek the value of the parameter $\alpha$ for which $C^\prime$ falls on the line connecting $A^\prime$ and $B^\prime$ (see Fig. 13), which represents the limiting value for which the shape of the deformed cell remains convex.

Fig. 13

Representation of perturbation of the vertices of a cell centered at node i with coordinates $(x_i,y_i)$. The cell dimensions are $\Delta x$ and $\Delta y$ in the x- and y-directions, respectively. The unperturbed cell vertices are represented by blue circles, whereas the perturbed cell vertices are represented by orange circles. Only the vertices A, B, and C are perturbed, and their corresponding vertices after perturbation are $A^\prime$, $B^\prime$, and $C^\prime$, respectively. The region of perturbation for each of these vertices is represented by an empty rectangle with green dashed border line. The size of the rectangle is defined as a fraction of the original cell via a parameter $\alpha$

Consider the following three vertices:

$$\begin{aligned} A&:= (x_i - \tfrac{\Delta x}{2}, y_i - \tfrac{\Delta y}{2}),\\ B&:= (x_i + \tfrac{\Delta x}{2}, y_i + \tfrac{\Delta y}{2}),\\ C&:= (x_i + \tfrac{\Delta x}{2}, y_i - \tfrac{\Delta y}{2}). \end{aligned}$$

To consider the worst case scenario, we assume the following perturbed vertices (see Fig. 13):

$$\begin{aligned} A^\prime&:= (x_i - \tfrac{\Delta x}{2} + \alpha \Delta x, y_i - \tfrac{\Delta y}{2} - \alpha \Delta y),\\ B^\prime&:= (x_i + \tfrac{\Delta x}{2}+ \alpha \Delta x, y_i + \tfrac{\Delta y}{2}- \alpha \Delta y),\\ C^\prime&:= (x_i + \tfrac{\Delta x}{2}- \alpha \Delta x, y_i - \tfrac{\Delta y}{2}+ \alpha \Delta y). \end{aligned}$$

Let the line connecting the nodes $A^\prime$ and $B^\prime$ be

$$\begin{aligned} y(x) = a_1 x + a_0, \end{aligned}$$

(B8)

where $a_1$ and $a_0$ are parameters. The slope of the line $a_1$ is given by

$$\begin{aligned} a_1 = \frac{\Delta y}{\Delta x}. \end{aligned}$$

(B9)

Substituting $a_1$ in (B8) and evaluating the line at the vertex $A^\prime$, we have

$$\begin{aligned} y_i - \tfrac{\Delta y}{2} - \alpha \Delta y = \frac{\Delta y}{\Delta x} (x_i - \tfrac{\Delta x}{2} + \alpha \Delta x) + a_0, \end{aligned}$$

from which $a_0$ can be obtained:

$$\begin{aligned} a_0 = y_i - \frac{\Delta y}{\Delta x}x_i - 2\alpha \Delta y. \end{aligned}$$

(B10)

We now substitute the coordinates of $C^\prime$ in the line given by (B8) with coefficients given by (B9) and (B10):

$$\begin{aligned} y_i - \tfrac{\Delta y}{2}+ \alpha \Delta y&= a_1 (x_i + \tfrac{\Delta x}{2}- \alpha \Delta x) + a_0 \\&= \frac{\Delta y}{\Delta x} (x_i + \tfrac{\Delta x}{2}- \alpha \Delta x) + y_i - \frac{\Delta y}{\Delta x}x_i - 2\alpha \Delta y, \end{aligned}$$

from which we obtain, after some algebraic manipulations,

$$\begin{aligned} \alpha = \frac{1}{4}. \end{aligned}$$

Appendix C. Derivation of c and $s_0$

This appendix presents derivations of the expressions of the micromodulus constant c and critical stretch $s_0$ for the GPMB model (see Sect. 2.1) in two-dimensional plane elasticity, following analogous derivations for the PMB model in three dimensions [26].

1.1 C.1 Micromodulus Constant

The micromodulus constant c can be obtained by equating the PD macroelastic energy density and the strain energy density from the classical theory of elasticity, under a suitable deformation.

Consider a static isotropic extension given by $\textbf{u}(\textbf{x}) = \bar{s} \textbf{x}$ with $\bar{s}$ constant. In this case, $\varvec{\eta } = \bar{s} \varvec{\xi }$, which results in a constant stretch: $s(\Vert \varvec{\xi } + \varvec{\eta }\Vert ,\Vert \varvec{\xi }\Vert ) = \bar{s}$ for all $\varvec{\eta },\varvec{\xi } \in \mathbb {R}^2$. Then, we can express the macroelastic energy density of the GPMB model for a point $\textbf{x}$ in the bulk of a body (assuming $\mu \equiv 1$) as follows (see (7) and (10)):

$$\begin{aligned} W&= \frac{1}{4} h \int _{\mathcal {H}}c\, \omega (\Vert \varvec{\xi }\Vert ) \, \bar{s}^2 \Vert \varvec{\xi }\Vert d{\varvec{\xi }}, \end{aligned}$$

where we used the change of variable $\textbf{x}^\prime = \textbf{x}+\varvec{\xi }$ and

$$\begin{aligned} \mathcal {H} := \{ \varvec{\xi } \in \mathbb {R}^2: \Vert \varvec{\xi }\Vert \leqslant \delta \} \end{aligned}$$

is the neighborhood around the origin (cf. (2)). Using polar coordinates,

$$\begin{aligned} W = \frac{1}{4} c h \bar{s}^2 \int _{0}^{2\pi } \int _0^\delta \, \omega (r) r \, r dr d\theta = c \frac{\pi }{2} h \left( \int _0^\delta \, \omega (r) r^2 dr \right) \bar{s}^2. \end{aligned}$$

(C11)

Note that the arguments of W have been omitted. The time dependence has been omitted because the imposed deformation is static; the spatial dependence, on the other hand, has been omitted because the macroelastic energy density is spatially independent in the bulk of a body for an isotropic extension. Below, we similarly omit these arguments for clarity.

The integral in (C11) can be computed by direct computation for the influence functions presented in Sect. 2.1.1, resulting in the following expressions:

$$\begin{aligned} \begin{aligned} \int _0^\delta \, \omega _0(r) r^2 dr = \frac{\delta ^3}{3}, \quad \int _0^\delta \, \omega _1(r) r^2 dr = \frac{\delta ^3}{12}, \quad \int _0^\delta \, \omega _3(r) r^2 dr = \frac{\delta ^3}{15}, \\ \int _0^\delta \, \omega _5(r) r^2 dr = \frac{5\delta^3}{84}, \quad \int _0^\delta \, \omega _7(r) r^2 dr = \frac{\delta^3}{18}. \end{aligned} \end{aligned}$$

(C12)

Plane strain: In classical linear elasticity, the strain energy density for an isotropic material in a state of plane strain is given by (see, e.g., [53]):

$$\begin{aligned} W^{C\varepsilon } = \frac{E}{2(1+\nu )(1-2\nu )} \left[ (1-\nu ) (\varepsilon _{11}^2 + \varepsilon _{22}^2) + 2 \nu \varepsilon _{11} \varepsilon _{22} + 2(1 - 2\nu ) \varepsilon _{12} \right] , \end{aligned}$$

(C13)

where E is the Young’s modulus, $\nu$ is the Poisson’s ratio, and $\varepsilon _{ij}$ with $i,j = 1,2$ are the components of the infinitesimal strain tensor:

$$\begin{aligned} \varepsilon _{ij} := \frac{1}{2}\left( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i} \right) , \quad i, j = 1,2. \end{aligned}$$

For the isotropic extension given by $\textbf{u}(\textbf{x}) = \bar{s} \textbf{x}$, we have $\varepsilon _{11} = \varepsilon _{22} = \bar{s}$ and $\varepsilon _{12} = 0$. Then,

$$\begin{aligned} W^{C\varepsilon } = \frac{E}{2(1+\nu )(1-2\nu )} \left[ (1-\nu ) (\bar{s}^2 +\bar{s}^2) + 2 \nu \bar{s}^2 \right] = \frac{E \bar{s}^2}{(1+\nu )(1-2\nu )}. \end{aligned}$$

In the case of plane strain, two-dimensional isotropic bond-based PD models are restricted to a Poisson’s ratio of $\nu = 1/4$ [38, 53]. In this case,

$$\begin{aligned} W^{C\varepsilon } = \frac{8}{5}E \bar{s}^2. \end{aligned}$$

(C14)

Assuming $W = W^{C\varepsilon }$, we thus obtain from (C11) and (C14):

$$\begin{aligned} c = \frac{16}{5\pi }\frac{E}{ \displaystyle h \int _0^\delta \, \omega (r) r^2 dr}, \end{aligned}$$

(C15)

where the result depends on the choice of influence function. Using (C12), the resulting expressions corresponding to the different influence functions are summarized in Sect. 3.4 (see Table 2 (top row)).

Plane stress: In classical linear elasticity, the strain energy density for an isotropic material in a state of plane stress is given by (see, e.g., [53]):

$$\begin{aligned} W^{C\sigma } = \frac{E}{2(1-\nu ^2)} \left[ \varepsilon _{11}^2 + \varepsilon _{22}^2 + 2 \nu \varepsilon _{11} \varepsilon _{22} + 2(1 - \nu ) \varepsilon _{12} \right] . \end{aligned}$$

(C16)

For the isotropic extension given by $\textbf{u}(\textbf{x}) = \bar{s} \textbf{x}$, we have (recall $\varepsilon _{11} = \varepsilon _{22} = \bar{s}$ and $\varepsilon _{12} = 0$)

$$\begin{aligned} W^{C\sigma } = \frac{E}{2(1-\nu ^2)} \left[ \bar{s}^2 + \bar{s}^2 + 2 \nu \bar{s}^2 \right] = \frac{E \bar{s}^2}{(1-\nu )} . \end{aligned}$$

In the case of plane stress, two-dimensional isotropic bond-based PD models are restricted to a Poisson’s ratio of $\nu = 1/3$ [38, 53]. In this case,

$$\begin{aligned} W^{C\sigma } = \frac{3}{2} E \bar{s}^2. \end{aligned}$$

(C17)

Assuming $W = W^{C\sigma }$, we thus obtain from (C11) and (C17):

$$\begin{aligned} c = \frac{3}{\pi } \frac{E}{\displaystyle h \int _0^\delta \, \omega (r) r^2 dr}, \end{aligned}$$

(C18)

where the result again depends on the choice of influence function. Using (C12), the resulting expressions corresponding to the different influence functions are summarized in Sect. 3.4 (see Table 2 (bottom row)).

Remark 10

We observe that, while the expressions for the micromodulus constant c in (C15) and (C18) depend on h, in practice, h cancels out when c is substituted in expressions for the computation of PD quantities (see, e.g., (1)).

1.2 C.2 Critical Stretch

Fig. 14

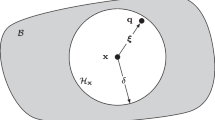
Illustration of the integration for the computation of the fracture energy $G_0$ in (C19) in two dimensions, analogously to [26]. Given a fracture surface, we compute the energy per unit area collectively provided by the pairwise potentials of all the bonds connecting any point on the left side of the fracture surface along a line perpendicular to the surface with distance $0 < x \leqslant \delta$ to points within their neighborhood on the right side of the fracture surface

To compute the critical stretch $s_0$, we assume any bond breaks irreversibly when it reaches the critical stretch. Then, we consider a fracture surface (see illustration in Fig. 14), compute the total energy per unit area released by breaking all the bonds crossing that surface, and compare the result to the fracture energy $G_0$.

Mimicking the calculations in [26], adapted to a two-dimensional case (see Fig. 14), we have (cf. (10))

$$\begin{aligned} G_0 = h \int _{0}^\delta \int _{x}^\delta \int _{-\cos ^{-1}(x/r)}^{\cos ^{-1}(x/r)} \left( \frac{1}{2} c \, \omega (r) s_0^2 r \right) r d \theta d r dx. \end{aligned}$$

(C19)

We now have

$$\begin{aligned} G_0 = \frac{1}{2} c h s_0^2 \int _{0}^\delta \int _{x}^\delta \omega (r) r^2 2\cos ^{-1}(x/r) d r dx. \end{aligned}$$

Changing the order of integration, we obtain

$$\begin{aligned} G_0 = c h s_0^2 \int _{0}^\delta \int _{0}^r \omega (r) r^2 \cos ^{-1}(x/r) dxd r. \end{aligned}$$

Using the change of variable $a = x/r$, we have

$$\begin{aligned} G_0&= ch s_0^2 \int _{0}^\delta \int _{0}^1 \omega (r) r^2 \cos ^{-1}(a) r da d r = c hs_0^2 \int _{0}^\delta \omega (r) {r^3} \left[ \int _{0}^1 \cos ^{-1}(a) da \right] d r\\&= c hs_0^2 \int _{0}^\delta \omega (r) r^3 d r, \end{aligned}$$

where

$$\begin{aligned} \int _{0}^1 \cos ^{-1}(a) da = 1. \end{aligned}$$

The critical stretch $s_0$ can then be expressed as follows:

$$\begin{aligned} s_0 = \sqrt{\frac{G_0}{c h \displaystyle \int _{0}^\delta \omega (r) r^3 dr}}. \end{aligned}$$

(C20)

The integral in (C20) can be computed by direct computation for the influence functions presented in Sect. 2.1.1, resulting in the following expressions:

$$\begin{aligned} \begin{aligned} \int _0^\delta \, \omega _0(r) r^3 dr = \frac{\delta ^4}{4}, \quad \int _0^\delta \, \omega _1(r) r^3 dr = \frac{\delta ^4}{20}, \quad \int _0^\delta \, \omega _3(r) r^3 dr = \frac{\delta ^4}{28}, \\ \int _0^\delta \, \omega _5(r) r^3 dr = \frac{5\delta^4}{168}, \quad \int _0^\delta \, \omega _7(r) r^3 dr = \frac{7\delta^4}{264}. \end{aligned} \end{aligned}$$

(C21)

Using these expressions as well as the expressions for the micromodulus constant c from Sect. 3.4 (see Table 2) in (C20), the resulting expressions for the critical stretch corresponding to the different influence functions are summarized in Sect. 3.4 (see Table 3) for both plane strain (top row) and plane stress (bottom row).

Appendix D. Quadratic Deformation Test for the ForceEnergyDensity Function

Consider a quadratic static deformation given by a displacement field $\textbf{u}(x,y) =(v(x,y),w(x,y))$ of the following form:

$$\begin{aligned} v(x,y)&= V_{11}x^2 , \end{aligned}$$

(D22a)

$$\begin{aligned} w(x,y)&= 0, \end{aligned}$$

(D22b)

where $V_{11}$ is a constant. We would like to evaluate the internal force density and macroelastic energy density at a point $\textbf{x}$ in the bulk of a body for the GPMB model. For this purpose, we approximate these quantities by resorting to their linearization under the assumption that $\Vert \varvec{\eta }\Vert \ll \delta$. In this case, the stretch in (9) can be approximated via a Taylor expansion, as follows:

$$\begin{aligned} s(\Vert \varvec{\xi } + \varvec{\eta }\Vert ,\Vert \varvec{\xi }\Vert ) = s(\Vert \varvec{\xi }\Vert ,\Vert \varvec{\xi }\Vert ) + \frac{\partial s(\Vert \varvec{\xi } + \varvec{\eta }\Vert ,\Vert \varvec{\xi }\Vert )}{\partial \eta _i} \Big |_{\varvec{\eta } = \textbf{0}} \eta _i + \mathcal {O}(\Vert \varvec{\eta }\Vert ^2), \end{aligned}$$

(D23)

where we used Einstein summation convention for repeated indices, and we note that $s(\Vert \varvec{\xi }\Vert ,\Vert \varvec{\xi }\Vert ) = 0$ for all $\varvec{\xi }\in \mathbb {R}^2$ (see (9)). Expressing the stretch as follows:

$$\begin{aligned} s(\Vert \varvec{\xi } + \varvec{\eta }\Vert ,\Vert \varvec{\xi }\Vert ) = \frac{1}{\Vert \varvec{\xi }\Vert }\sqrt{(\xi _1 + \eta _1)^2 + (\xi _2 + \eta _2)^2} - 1, \end{aligned}$$

where $\varvec{\xi } = (\xi _1,\xi _2)$ and $\varvec{\eta } = (\eta _1,\eta _2)$, we can easily compute

$$\begin{aligned} {\frac{\partial s(\Vert \varvec{\xi } + \varvec{\eta }\Vert ,\Vert \varvec{\xi }\Vert )}{\partial \eta _i} }= \frac{1}{\Vert \varvec{\xi }\Vert }\frac{(\xi _i + \eta _i)}{\Vert \varvec{\xi } + \varvec{\eta }\Vert }, \quad i = 1,2, \end{aligned}$$

which results in (see (D23))

$$\begin{aligned} s(\Vert \varvec{\xi } + \varvec{\eta }\Vert ,\Vert \varvec{\xi }\Vert ) \approx \frac{\varvec{\xi }\cdot \varvec{\eta } }{\Vert \varvec{\xi }\Vert ^2}, \end{aligned}$$

where we omitted terms of order $\mathcal {O}(\Vert \varvec{\eta }\Vert ^2)$. The GPMB pairwise force function (6) with (8) and pairwise potential function (cf. (10)) can then be approximated (assuming $\mu \equiv 1$ and omitting the time dependence) as follows:

$$\begin{aligned} \textbf{f}(\varvec{\eta },\textbf{x}^\prime ,\textbf{x})&\approx c\,\omega (\Vert \varvec{\xi }\Vert ) \, \frac{1}{\Vert \varvec{\xi }\Vert ^3}(\varvec{\xi }\cdot \varvec{\eta })\varvec{\xi } ,\end{aligned}$$

(D24)

$$\begin{aligned} w(\varvec{\eta },\textbf{x}^\prime ,\textbf{x})&\approx \frac{1}{2} c\,\omega (\Vert \varvec{\xi }\Vert ) \, \frac{1}{\Vert \varvec{\xi }\Vert ^3}(\varvec{\xi }\cdot \varvec{\eta })^2 . \end{aligned}$$

(D25)

Using the linearized expression for the pairwise force function and pairwise potential function given in (D24) and (D25), respectively, we compute the internal force density and macroelastic energy density for a point $\textbf{x}$ in the bulk of a body under the quadratic deformation given in (D22a) and (D22b). To this end, we first note that, in this case, the relative displacement is given by

$$\begin{aligned} \varvec{\eta }&= ( V_{11}(x^\prime )^2 - V_{11} x^2,0) = ( V_{11}(x + \xi _1)^2 - V_{11} x^2,0) \\&= ( V_{11}(x^2 + 2x \xi _1 + \xi _1^2) - {V_{11}} x^2,0) = ( V_{11}(2x \xi _1 + \xi _1^2) ,0). \end{aligned}$$

We then obtain,

$$\begin{aligned} \varvec{\xi }\cdot \varvec{\eta }&= (\xi _1,\xi _2) \cdot ( V_{11}(2x \xi _1 + \xi _1^2) ,0) = V_{11}(2x \xi _1^2 + \xi _1^3). \end{aligned}$$

Then,

$$\begin{aligned} f_1(\varvec{\eta },\textbf{x}^\prime ,\textbf{x})&\approx c\, \omega (\Vert \varvec{\xi }\Vert ) \, \frac{1}{\Vert \varvec{\xi }\Vert ^3}V_{11}(2x \xi _1^3 + \xi _1^4) ,\\ f_2(\varvec{\eta },\textbf{x}^\prime ,\textbf{x})&\approx c\, \omega (\Vert \varvec{\xi }\Vert ) \, \frac{1}{\Vert \varvec{\xi }\Vert ^3}V_{11}(2x \xi _1^2 + \xi _1^3)\xi _2 ,\\ w(\varvec{\eta },\textbf{x}^\prime ,\textbf{x})&\approx \frac{1}{2} c\, \omega (\Vert \varvec{\xi }\Vert ) \, \frac{1}{\Vert \varvec{\xi }\Vert ^3} V_{11}^2 (4x^2 \xi _1^4 + 4x \xi _1^5 + \xi _1^6). \end{aligned}$$

The components of the internal force density at $\textbf{x}$ are given by:

$$\begin{aligned} F_1(\textbf{x})& = h \int _{\mathcal {H}_\textbf{x}} f_1(\varvec{\eta },\textbf{x}^\prime ,\textbf{x}) d{\textbf{x}^\prime } \approx h \int _{\mathcal {H}_\textbf{x}} c\,\omega (\Vert \varvec{\xi }\Vert ) \, \frac{1}{\Vert \varvec{\xi }\Vert ^3}V_{11}(2x \xi _1^3 + \xi _1^4) d{\textbf{x}^\prime }\\&= h \int _{\mathcal {H}_\textbf{x}} c\,\omega (\Vert \varvec{\xi }\Vert ) \, \frac{1}{\Vert \varvec{\xi }\Vert ^3}V_{11} \xi _1^4 d{\textbf{x}^\prime } =h \int _{0}^{2\pi } \int _0^{\delta } c \, \omega (r) \, \frac{1}{r^3} V_{11}(r\cos (\theta ))^4 r dr d\theta \\&= \frac{3\pi }{4} ch V_{11} \int _0^{\delta } \, \omega (r) r^2 dr,\\ F_2 (\textbf{x})& = h\int _{\mathcal {H}_\textbf{x}} f_2(\varvec{\eta },\textbf{x}^\prime ,\textbf{x}) d{\textbf{x}^\prime } \approx 0, \end{aligned}$$

where we used antisymmetry to eliminate the term with $\xi _1^3$ in the expression for $F_1(\textbf{x})$ and to conclude that $F_2 (\textbf{x}) \approx 0$. Using the expressions for c for plane strain (C15) and plane stress (C18), we obtain

$$\begin{aligned} F_1(\textbf{x})&\approx \left\{ \begin{array}{cc} \frac{12}{5} V_{11} E, &{} \text{ Plane } \text{ strain}, \\ \frac{9}{4} V_{11} E, &{} \text{ Plane } \text{ stress}, \\ \end{array} \right. \end{aligned}$$

(D26a)

$$\begin{aligned} F_2 (\textbf{x})&\approx 0. \end{aligned}$$

(D26b)

We now compute the macroelastic energy density at $\textbf{x}$:

$$\begin{aligned} W(\textbf{x})& = \frac{1}{2}h\int _{\mathcal {H}_\textbf{x}} w(\varvec{\eta },\textbf{x}^\prime ,\textbf{x}) d{\textbf{x}^\prime } \approx \frac{1}{4} h\int _{\mathcal {H}_\textbf{x}} c\,\omega (\Vert \varvec{\xi }\Vert ) \, \frac{1}{\Vert \varvec{\xi }\Vert ^3} V_{11}^2 (4x^2 \xi _1^4 + 4x \xi _1^5 + \xi _1^6) d{\textbf{x}^\prime }\\&= \frac{1}{4}h \int _{\mathcal {H}_\textbf{x}} c\, \omega (\Vert \varvec{\xi }\Vert ) \, \frac{1}{\Vert \varvec{\xi }\Vert ^3} V_{11}^2 (4x^2 \xi _1^4 + \xi _1^6) d{\textbf{x}^\prime }\\&=\frac{1}{4}h \int _{0}^{2\pi } \int _0^{\delta }c \, \omega (r) \, \frac{1}{r^3} V_{11}^2 (4x^2 (r\cos (\theta ))^4 + (r\cos (\theta ))^6) r dr d\theta \\&=\frac{1}{4} c hV_{11}^2 \int _0^{\delta } \, \omega (r) \, \frac{1}{r^3} \left( 4x^2 \frac{3\pi }{4} r^4 + \frac{5\pi }{8} r^6\right) r dr \\&=\frac{\pi }{32} c hV_{11}^2 \int _0^{\delta } \, \omega (r) \, \left( 24x^2 r^2 + 5 r^4\right) dr. \end{aligned}$$

Using the expressions for c for plane strain (C15) and plane stress (C18), we can express the macroelastic energy density, as follows:

• Plane strain

  $$\begin{aligned} \begin{aligned} W(\textbf{x})&\approx \frac{\pi }{32} \frac{16}{5\pi } \frac{E}{\displaystyle h \int _0^{\delta } \omega (r) r^2 dr} h V_{11}^2 \int _0^{\delta } \, \omega (r) \, \left( 24x^2 r^2 + 5 r^4\right) dr\\&= \frac{E V_{11}^2}{10} \left[ 24x^2 + 5\, \frac{\displaystyle \int _0^{\delta } \, \omega (r) r^4 dr}{\displaystyle \int _0^{\delta }\, \omega (r) r^2 dr} \right] . \end{aligned} \end{aligned}$$

  (D27)

• Plane stress

  $$\begin{aligned} \begin{aligned} W(\textbf{x})&\approx \frac{\pi }{32} \frac{3}{\pi } \frac{E}{\displaystyle h\int _0^{\delta } \omega (r) r^2 dr} h V_{11}^2 \int _0^{\delta } \, \omega (r) \, \left( 24x^2 r^2 + 5 r^4\right) dr \\&= \frac{3EV_{11}^2 }{32} \left[ 24x^2 + 5 \, \frac{\displaystyle \int _0^{\delta } \, \omega (r) \, r^4 dr }{\displaystyle \int _0^{\delta }\, \omega (r) r^2 dr} \right] . \end{aligned} \end{aligned}$$

  (D28)

We now have

$$\begin{aligned} \begin{aligned} \int _0^\delta \, \omega _0(r) r^4 dr = \frac{\delta ^5}{5}, \quad \int _0^\delta \, \omega _1(r) r^4 dr = \frac{\delta ^5}{30}, \quad \int _0^\delta \, \omega _3(r) r^4 dr = \frac{3\delta ^5}{140},\\ \int _0^\delta \, \omega _5(r) r^4 dr = \frac{\delta ^5}{60}, \quad \int _0^\delta \, \omega _7(r) r^4 dr = \frac{7\delta ^5}{495}. \end{aligned} \end{aligned}$$

(D29)

Using the expressions given in (C12) and (D29) in (D27) and (D28), we obtain the results reported in Table D1.

Table D1 Macroelastic energy density for a point $\textbf{x} = (x,y)$ in the bulk of a body under the quadratic deformation given in (D22a) and (D22b)

Remark 11

Given the quadratic deformation in (D22a) and (D22b), the strain components are: $\varepsilon _{11} = 2V_{11}x$, $\varepsilon _{12} = 0$, and $\varepsilon _{22} = 0$. Consequently, the corresponding strain energy density in classical linear elasticity, for the case of plane strain (for $\nu = 1/4$), is (see (C13))

$$\begin{aligned} W^{C\varepsilon } = \frac{E (1-\nu )}{2(1+\nu )(1-2\nu )} (2V_{11}x)^2 = \frac{12}{5}E V_{11}x^2 \end{aligned}$$

and, for the case of plane stress (for $\nu = 1/3$), is (see (C16))

$$\begin{aligned} W^{C\sigma } = \frac{E}{2(1-\nu ^2)} (2V_{11}x)^2 = \frac{9}{4}E V_{11}x^2, \end{aligned}$$

which correspond to the expressions reported in Table D1, in the limit as $\delta \rightarrow 0$.

Remark 12

The stress–strain relation in plane-strain classical linear elasticity is given by:

$$\begin{aligned} \left[ \begin{array}{c} \sigma _{11}\\ \sigma _{22}\\ \sigma _{12} \\ \end{array} \right] = \frac{E}{(1+\nu )(1-2\nu )} \left[ \begin{array}{ccc} 1-\nu &{} \nu &{} 0\\ \nu &{} 1-\nu &{} 0 \\ 0 &{} 0 &{} \tfrac{1}{2}(1-2\nu ) \end{array} \right] \left[ \begin{array}{c} \varepsilon _{11}\\ \varepsilon _{22}\\ 2\varepsilon _{12} \\ \end{array} \right] , \end{aligned}$$

(D30)

where $\sigma _{ij}$, $i,j=1,2$, are the components of the stress tensor and $\varepsilon _{ij}$, $i,j=1,2$, are the components of the strain tensor, and where E is the Young’s modulus and $\nu$ is the Poisson’s ratio. Under the quadratic deformation given in (D22a) and (D22b), $\varepsilon _{11} = 2V_{11}x$, $\varepsilon _{12} = 0$, and $\varepsilon _{22} = 0$, and we get (for $\nu = 1/4$):

$$\begin{aligned} \sigma _{11}&= \frac{12}{5}E V_{11}x,\\ \sigma _{22}&= \frac{4}{5}E V_{11}x,\\ \sigma _{12}&= 0. \end{aligned}$$

The internal force density is given by $\textbf{F}^{\text{CE}}: = \nabla \cdot \varvec{\sigma }$, which, in component form in this case, is:

$$\begin{aligned} F_1^{\text{CE}}&= \frac{\partial \sigma _{11}}{\partial x} + \frac{\partial \sigma _{12}}{\partial y} = \frac{12}{5}V_{11}E ,\\ F_2^{\text{CE}}&= \frac{\partial \sigma _{12}}{\partial x} + \frac{\partial \sigma _{22}}{\partial y} = 0. \end{aligned}$$

Similarly, the stress–strain relation in plane-stress classical linear elasticity is given by:

$$\begin{aligned} \left[ \begin{array}{c} \sigma _{11}\\ \sigma _{22}\\ \sigma _{12} \\ \end{array} \right] = \frac{E}{(1-\nu ^2)} \left[ \begin{array}{ccc} 1 &{} \nu &{} 0\\ \nu &{} 1 &{} 0 \\ 0 &{} 0 &{} \tfrac{1}{2}(1-\nu ) \end{array} \right] \left[ \begin{array}{c} \varepsilon _{11}\\ \varepsilon _{22}\\ 2\varepsilon _{12} \\ \end{array} \right] . \end{aligned}$$

(D31)

Under the quadratic deformation given in (D22a) and (D22b), $\varepsilon _{11} = 2V_{11}x$, $\varepsilon _{12} = 0$, and $\varepsilon _{22} = 0$, and we get (for $\nu = 1/3$):

$$\begin{aligned} \sigma _{11}&= \frac{9}{4} E V_{11} x,\\ \sigma _{22}&= \frac{3}{4} E V_{11}x,\\ \sigma _{12}&= 0. \end{aligned}$$

The internal force density, in component form in this case, is:

$$\begin{aligned} F_1^{\text{CE}}&= \frac{9}{4}V_{11}E ,\\ F_2^{\text{CE}}&= 0. \end{aligned}$$

The results for both plane strain and plane stress coincide with the ones in (D26a) and (D26b); i.e., for the given quadratic deformation, the linearized GPMB model possesses the same internal force density (for points in the bulk of a body) as in classical linear elasticity.

Appendix E. Intersection of Two Line Segments

This section describes a method for determining if two line segments in a plane intersect. It is a planar treatment of the line segment intersection algorithm found in [54].

Consider two line segments in the xy-plane. Without loss of generality, one may select points $\textbf{p}$ and $\textbf{q}$ and directions $\textbf{r}$ and $\textbf{s}$ so that the line segments are defined parametrically as:

$$\begin{aligned} \textbf{L}_\textbf{p}(t) := \textbf{p} + t \textbf{r}, \quad t \in [0,1] \end{aligned}$$

(E32)

and

$$\begin{aligned} \textbf{L}_\textbf{q}(u) := \textbf{q} + u \textbf{s}, \quad u \in [0,1]. \end{aligned}$$

(E33)

An illustration is shown in Fig. 15.

Fig. 15

Illustration of line segments $\textbf{L}_{\textbf{p}}(t)$ with endpoints $\textbf{p}$ and $\mathbf {p+r}$ and $\textbf{L}_{\textbf{q}}(u)$ with endpoints $\textbf{q}$ and $\mathbf {q+s}$

We start by determining if the two line segments are parallel, which is easily determined by calculating the cross product $\textbf{r} \times \textbf{s}$. Specifically, $\textbf{r} \times \textbf{s} = \textbf{0}$ implies that the line segments are parallel and $\textbf{r} \times \textbf{s} \ne \textbf{0}$ implies that the line segments are not parallel. The two cases are treated separately, starting with parallel line segments.

Line Segments are Parallel ($\textbf{r} \times \textbf{s} = \textbf{0}$)

The next step is to determine if the line segments are collinear, which is true if and only if $\textbf{q}-\textbf{p}$ is parallel to $\textbf{r}$, i.e., $(\textbf{p}-\textbf{q}) \times \textbf{r} = \textbf{0}$. If the line segments are not collinear, they clearly do not intersect. On the other hand, if the line segments are collinear, one must check whether they overlap. This is accomplished by writing the endpoints $\textbf{p}$ and $\mathbf {p+r}$ of the line segment $\textbf{L}_{\textbf{p}}$ in terms of the line segment $\textbf{L}_{\textbf{q}}$:

$$\begin{aligned} \textbf{p} = \textbf{q} + u_0 \textbf{s} \quad \text {and} \quad \textbf{p} + \textbf{r} = \textbf{q} + u_1 \textbf{s}. \end{aligned}$$

(E34)

Solving for $u_0$ and $u_1$ in (E34) yields

$$\begin{aligned} u_0 = \frac{(\textbf{p}-\textbf{q})\cdot \textbf{s}}{ \textbf{s} \cdot \textbf{s}} \quad \text {and} \quad u_1 = \frac{(\textbf{p}+\textbf{r}-\textbf{q})\cdot \textbf{s}}{ \textbf{s} \cdot \textbf{s}} = u_0 + \frac{\textbf{r}\cdot \textbf{s}}{ \textbf{s} \cdot \textbf{s}}. \end{aligned}$$

(E35)

There is no overlap if and only if $\max \left\{ u_0, u_1 \right\} < 0$ or $\min \left\{ u_0, u_1\right\} > 1$. Geometrically, these two conditions imply that along the line containing the two line segments, $\textbf{L}_{\textbf{p}}$ is entirely to the left of $\textbf{L}_{\textbf{q}}$ or $\textbf{L}_{\textbf{p}}$ is entirely to the right of $\textbf{L}_{\textbf{q}}$. Next, line segments which are not parallel are considered.

Line Segments are not Parallel ($\textbf{r} \times \textbf{s} \neq \textbf{0}$)

The line segments intersect if there exist $u_0$ and $t_0$ in the interval [0, 1] such that

$$\begin{aligned} \textbf{L}_\textbf{p}(t_0) = \textbf{L}_\textbf{q}(u_0) \Rightarrow \textbf{p} + t_0 \textbf{r} = \textbf{q} + u_0 \textbf{s}. \end{aligned}$$

(E36)

This may be determined by solving for $t_0$ and $u_0$. In (E36), subtracting $\textbf{p}$ and then taking the cross product with respect to $\textbf{s}$ results in (note that $\textbf{s} \times \textbf{s} = \textbf{0}$)

$$\begin{aligned} t_0 (\textbf{r} \times \textbf{s}) = (\textbf{q}-\textbf{p}) \times \textbf{s}. \end{aligned}$$

(E37)

Since $\textbf{r},\textbf{s},$ and $\textbf{q}-\textbf{p}$ are in the xy-plane, the first two components of the cross products in (E37) are zero. We conclude

$$\begin{aligned} t_0 = \frac{\left( (\textbf{q}-\textbf{p}) \times \textbf{s} \right) _z}{ \left( \textbf{r} \times \textbf{s} \right) _z}, \end{aligned}$$

(E38)

where the subscript z signifies the third component of the vector. Similarly, in (E36), subtracting $\textbf{q}$ and then taking the cross product with respect to $\textbf{r}$ results in (note that $\textbf{r} \times \textbf{r} = \textbf{0}$)

$$\begin{aligned} u_0 (\textbf{s} \times \textbf{r}) = (\textbf{p} - \textbf{q}) \times \textbf{r} \Rightarrow u_0 = \frac{ \left( (\textbf{p} - \textbf{q}) \times \textbf{r} \right) _z}{ \left( \textbf{s} \times \textbf{r} \right) _z} = \frac{ \left( (\textbf{q} - \textbf{p}) \times \textbf{r} \right) _z}{ \left( \textbf{r} \times \textbf{s} \right) _z}. \end{aligned}$$

(E39)

If $u_0,t_0 \in [0,1]$, one may conclude that the line segments intersect. Otherwise, they do not.

Appendix F. Numerical Computation of the Internal Force Density and Macroelastic Energy Density

We present numerical computations of the internal force density $\textbf{F}$ and macroelastic energy density W to check the correctness of their computation by the ForceEnergyDensity function (see Sect. 3.5). For this purpose, we consider a domain $\Omega = (0,1)\times (0,1)$ and we impose a deformation on all the nodes in the domain. We choose a PD horizon $\delta = 0.2$ and a Young’s modulus $E = 1$ in consistent units. To check the computation of W, we consider an isotropic extension with constant stretch $\bar{s} = 0.1$ for which $W = 8E\bar{s}^2/5$ for plane strain (see (C14)) and $W = 3E\bar{s}^2/2$ for plane stress (see (C17)). To check the computation of $\textbf{F}$, we consider a quadratic deformation given by $\textbf{u}({x,y}) = (V_{11}x^2,0)$ with $V_{11} = 0.01$ for which $\textbf{F} \approx (12 V_{11}E/5,0)$ for plane strain and $\textbf{F} \approx (9 V_{11}E/4,0)$ for plane stress (see (D26a) and (D26b)).⁶ Table F2 reports the corresponding results for a point in the bulk of the body, for a discretization given by a uniform grid of grid spacing $\Delta x = \Delta y = \delta /6$, using the function TestForceEnergyDensity based on the computations for uniform grids over rectangular domains (see Sect. 3.5); the same results are obtained based on the computations for general grids.

Table F2 Computation of the macroelastic energy density W and the x-component of the internal force density ($F_1$), at a node in the bulk of a body, for the case of an isotropic extension with constant stretch $\bar{s} = 0.1$ and a quadratic deformation given by $\textbf{u}({x,y} ) = (V_{11}x^2,0)$ with $V_{11} = 0.01$, respectively. The computation employs $\delta = 0.2$ and a uniform grid of grid spacing $\Delta x = \Delta y = \delta /6$. The rightmost column provides reference values computed with the analytical expressions of the corresponding quantities for the continuum case. We report results for both plane strain and plane stress assumptions for the different influence functions. The values reported are computed with the TestForceEnergyDensity function

Remark 13

The results reported in Table F2 depend on the particular discretization chosen. A comparative study between the different partial-area algorithms is presented in [42]. Note that for the case of $\omega _{0.5}$, the accuracy of the PA-AC algorithm is reduced compared to the case where ω₀ is used; this is expected since evaluating ω_0.5 at quadrature points outside the neighborhood returns a zero value, as opposed to $\omega _0$.

Remark 14

The selection of problems and quantities reported in Table F2 was based on having quantities that neither vanish nor change for the different influence functions, for brevity. For the isotropic extension case, the internal force density $\textbf{F}$ vanishes for points in the bulk of a body, so we only report the macroelastic energy density W. For the quadratic deformation case, the y-component of the internal force density ($F_2$) vanishes (see (D26b)), while the macroelastic energy density W varies for different influence functions (see Table D1), so we only report the x-component of the internal force density ($F_1$).

Appendix G. Numerical Computation of the Fracture Energy

We present a numerical computation of the fracture energy to confirm the expressions of the critical stretch reported in Sect. 3.4 (see Table 3) by computing a numerical analogue of (C19), as described below.

Let us consider a vertical line representing a surface at $x=0$. We numerically approximate the energy per unit area resulting from all the interactions between points along a horizontal line to the left of the vertical line and their neighboring points on the right side of the vertical line, under the assumption that all the corresponding bonds are critically stretched. For this purpose, we discretize the horizontal line with a set of line segments of length $\Delta x$, and we discretize the space on the right side of the vertical line with a uniform grid of cells of area $\Delta x \Delta y$. We then sum all the pairwise potentials of the bonds connecting the nodes centered at the line segments to their neighboring cells while weighting each pairwise potential by the product of the line segment length and the neighboring area. An illustration of the system is presented in Fig. 16. This calculation is inspired by the numerical computations of nonlocal tractions presented in [55].

Choose a horizon $\delta = 1$ and a grid spacing $\Delta x = \Delta y= \delta /6$, and let a domain be $\Omega = (-1,1)\times (-1-\tfrac{\Delta y}{2},1+\tfrac{\Delta y}{2})$, which is uniformly discretized based on the grid spacing. Let the point intersecting the horizontal and vertical lines be $\textbf{x}_0 = (x_0,y_0)$. Define the set $\mathcal {S}^{\text{L}}$ of nodes on the horizontal line on the left side of the vertical line within $\Omega$ (see green nodes in Fig. 16):

$$\begin{aligned} \mathcal {S}^{\text{L}} :=\{ (x_0 - \tfrac{\Delta x}{2}, y_0), \ldots , (x_0 - \delta + \tfrac{\Delta x}{2}, y_0) \} \end{aligned}$$

and the set $\mathcal {S}^{\text{R}}$ of nodes on the right side of the vertical line within $\Omega$ (see black nodes in Fig. 16) as:

$$\begin{aligned} \mathcal {S}^{\text{R}} :=\{ x_0 + \tfrac{\Delta x}{2}, \ldots , x_0 + \delta - \tfrac{\Delta x}{2} \} \times \{ y_0 - \delta ,\ldots ,y_0 + \delta \}, \end{aligned}$$

which is built as a Cartesian product. Let $\textbf{x}_i^{\text{L}} \in \mathcal {S}^{\text{L}}, {i = }1, \ldots , N^{\text{L}},$ and $\textbf{x}_{{{j}}}^{\text{R}} \in \mathcal {S}^{\text{R}}, {j=}1, \ldots , N^{\text{R}},$ be the reference positions of the nodes within each set. A numerical analogue of (C19), $G^h_0$, can be expressed as follows:

$$\begin{aligned} G^h_0:= h\sum _{i = 1}^{N^{\text{L}}} {\sum _{j\in \hat{\mathcal{F}}^{\text{R}}_i}} \frac{1}{2} c\, \omega (\Vert {\hat{\textbf{x}}^{\text{R}}_{j(i)}} - \textbf{x}^{\text{L}}_i \Vert) s_0^2 \Vert {\hat{\textbf{x}}^{\text{R}}_{j(i)}} - \textbf{x}^{\text{L}}_i\Vert \Delta x {\hat{A}^{\text{R}}_{j(i)}}, \end{aligned}$$

(G40)

where $\hat{\mathcal{F}}^{\text{R}}_i$ is a set of indices corresponding to the quadrature points for the two inner integrals in (C19), $\hat{\textbf{x}}^{\text{R}}_{j(i)}$ is the jth quadrature point, and $\hat{A}^{\text{R}}_{j(i)}$ is the corresponding jth quadrature weight associated with node i located at $\textbf{x}_i^{\text{L}}$ (cf. (14)).

Let the Young’s modulus be $E = 1$ and the fracture energy be $G_0 = 1$ in consistent units. We compute $G^h_0$ for both plane strain and plane stress assumptions for the different influence functions, and we compare the results with $G_0$. These results are reported in Table G3. Note that the value of $c h s_0^2$ is the same for both plane strain and plane stress (cf. (C20)), for each influence function, so we report both results together.

Fig. 16

Illustration of a domain discretization for the numerical computation of the fracture energy in (G40). We consider a vertical line representing a surface (thick magenta line) at $x=0$. The computation considers all the bonds connecting nodes on a horizontal line to the left of the vertical line (green nodes) and their neighbor cells on the right side of the vertical line. The intersecting point between the horizontal and vertical lines is $(x_0,y_0) = (0,0)$. For clarity, the intersection between the boundary of the neighborhood of the rightmost node on the horizontal line and the cells to the right side of the vertical line is plotted in blue. The figure is produced with the PlotNumericalFractureEnergy function. Figure adapted from [55]

Table G3 Computation of the fracture energy using (G40) for the system illustrated in Fig. 16. The computation employs a horizon $\delta = 1$ and a uniform grid of grid spacing $\Delta x = \Delta y = \delta /6$. The Young’s modulus is taken as $E=1$ and the fracture energy is also taken as $G_0= 1$ in consistent units. The micromodulus constant c and the critical stretch $s_0$ are computed with the PDBondConstants function using the expressions in Sect. 3.4 (see Tables 2 and 3, respectively). The computations reported in the table are computed with the TestCriticalStretch function

Appendix H. Input Decks for Numerical Examples

1.1 H.1 WavePropagation Input Deck

1.2 H.2 CrackBranching Input Deck