Peridynamic Formulation for Higher-Order Plate Theory

Abstract

In this study, a new peridynamic model is presented for higher-order plate theory. The formulation is derived by using Euler-Lagrange equation and Taylor’s expansion. The formulation is verified by considering two benchmark problems including simply supported and clamped plates subjected to transverse loading. Moreover, mixed (simply supported-clamped) boundary conditions are also considered to investigate the capability of the current formulation for mixed boundary conditions. Peridynamic results are compared with finite element analysis results and a very good agreement was obtained between the two approaches.

1 Introduction

Classical continuum mechanics (CCM) developed by Cauchy has been widely used for the analysis of deformation behaviour of materials and structures. Although CCM has been very successful in dealing with numerous complex problems of engineering, it encounters difficulties if the displacement field is discontinuous. This situation mainly arises when cracks occur inside the solution domain. In this case, the partial derivatives in the governing equations of CCM become invalid along the crack surfaces. Moreover, as the technology advances and nanoscale structures become a significant interest, accurate material characteristic at such a small scale cannot always be captured by CCM since CCM does not have a length scale parameter.

To overcome the aforementioned issues related with CCM, a new continuum mechanics formulation, peridynamics, was proposed by Silling [1]. The governing equations of peridynamics (PD) are in the form of integro-differential equations and do not contain any spatial derivatives. Therefore, they are always valid even if the displacement field is discontinuous. Moreover, it has a length scale parameter, horizon, which can be utilized to model structures at nanoscale. According to dell’Isola et al. [2], the origins of peridynamics go back to Piola. Since its introduction, there has been rapid development in peridynamics research especially during the last years. PD has been applied to analyze different material systems including metals [3], composites [4, 5], concrete [6] and graphene [7]. Moreover, it is not limited to elasticity behaviour and PD-based plasticity [8], viscoelasticity [9] and viscoplasticity [10] formulations are available. In addition, PD equations have been extended to other fields to perform heat transfer [11], diffusion [12], porous flow [13] and fluid flow [14] analyses. An extensive review on peridynamics is given in Javili et al. [15].

Simplied structures including beams, plates and shells can also be represented in PD framework. Taylor and Steigmann [16] introduced a two-dimensional model for thin plates. Diyaroglu et al. [17] developed a PD Euler-beam formulation which was further extended to Kirchhoff plates by Yang et al. [18]. The effect of transverse shear deformation in thick plates was taken into account by Diyaroglu et al. [19] by developing PD Timoshenko beam and Mindlin plate formulations. O’Grady and Foster [20, 21] proposed Euler beam and Kirchhoff plate formulations by utilizing non-ordinary state-based peridynamics. Chowdhury et al. [22] developed a state-based PD formulation suitable for linear elastic shells.

In this study, a new PD formulation is presented for higher-order plate theory suitable for analysis of thick plates. The formulation is developed by using Euler-Lagrange equations and Taylor’s expansion. The formulation does not have any limitation on material constants as in bond-based peridynamics. The developed formulation is validated by considering two benchmark problems and peridynamic results are compared against finite element analysis results.

2 Higher-Order Plate Formulation

The displacement field of any material point, u(x, y, z, t),v(x, y, z, t) and w(x, y, z, t), can be represented in terms of the displacement field of a material point on the mid-plane, u(x, y, 0, t), v(x, y, 0, t) and w(x, y, 0, t), by using Taylor’s expansion as

$$ u\left(x,y,z,t\right)={\left.u\right|}_{z=0}+{\left.\frac{\partial u}{\partial z}\right|}_{z=0}\mathrm{z}+\frac{1}{2}{\left.\frac{\partial^2u}{\partial {z}^2}\right|}_{z=0}{z}^2+\frac{1}{3!}{\left.\frac{\partial^3u}{\partial {z}^3}\right|}_{z=0}{z}^3+\cdots $$

(1a)

$$ v\left(x,y,z,t\right)={\left.v\right|}_{z=0}+{\left.\frac{\partial v}{\partial z}\right|}_{z=0}\mathrm{z}+\frac{1}{2}{\left.\frac{\partial^2v}{\partial {z}^2}\right|}_{z=0}{z}^2+\frac{1}{3!}{\left.\frac{\partial^3v}{\partial {z}^3}\right|}_{z=0}{z}^3+\cdots $$

(1b)

$$ w\left(x,y,z,t\right)={\left.w\right|}_{z=0}+{\left.\frac{\partial w}{\partial z}\right|}_{z=0}\mathrm{z}+\frac{1}{2}{\left.\frac{\partial^2w}{\partial {z}^2}\right|}_{z=0}{z}^2+\frac{1}{3!}{\left.\frac{\partial^3w}{\partial {z}^3}\right|}_{z=0}{z}^3+\cdots $$

(1c)

In this study, only flexural deformations are taken into consideration. Thus, eliminating axial deformation effects and higher-order terms in Eqs. (1), the components of the displacement field can be expressed as

$$ u\left(x,y,z,t\right)=\mathrm{z}{\theta}_x\left(x,y,t\right)+{z}^3{\theta}_x^{\ast}\left(x,y,t\right) $$

(2a)

$$ v\left(x,y,z,t\right)=z{\theta}_y\left(x,y,t\right)+{z}^3{\theta}_y^{\ast}\left(x,y,t\right) $$

(2b)

$$ w\left(x,y,z,t\right)=\mathrm{w}\left(\mathrm{x},\mathrm{y},\mathrm{t}\right)+{z}^2{w}^{\ast}\left(x,y,t\right) $$

(2c)

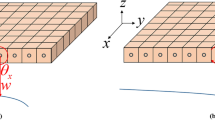
where θ_x, θ_y, ${\theta}_x^{\ast }$, ${\theta}_y^{\ast }$ and w^∗ are introduced as five new independent variables, respectively, which are defined as (see Fig. 1)

$$ {\theta}_x\left(x,y,t\right)={\left.\frac{\partial u}{\partial z}\right|}_{z=0} $$

(3a)

$$ {\theta}_y\left(x,y,t\right)={\left.\frac{\partial v}{\partial z}\right|}_{z=0} $$

(3b)

$$ {\uptheta}_x^{\ast}\left(x,y,t\right)=\frac{1}{3!}{\left.\frac{\partial^3u}{\partial {z}^3}\right|}_{z=0} $$

(3c)

$$ {\uptheta}_y^{\ast}\left(x,y,t\right)=\frac{1}{3!}{\left.\frac{\partial^3v}{\partial {z}^3}\right|}_{z=0} $$

(3d)

$$ {w}^{\ast}\left(x,y,t\right)=\frac{1}{2}{\left.\frac{\partial^2w}{\partial {z}^2}\right|}_{z=0} $$

(3e)

Fig. 1

Independent variables for each material point in higher-order plate theory

In order to simplify the expressions, hereafter, w(x, y, t), θ(x, y, t), w^∗(x, y, t) and θ^∗(x, y, t) will be written simply as w, θ, w^∗ and θ^∗, respectively.

After utilizing the displacement relationships given in Eqs. (2), strain-displacement relationships of 3-dimensional elasticity can be expressed as

$$ {\varepsilon}_{11}=z\frac{\partial {\theta}_1}{\partial {x}_1}+{z}^3\frac{\partial {\theta}_1^{\ast }}{\partial {x}_1} $$

(4a)

$$ {\varepsilon}_{22}=z\frac{\partial {\theta}_2}{\partial {x}_2}+{z}^3\frac{\partial {\theta}_2^{\ast }}{\partial {x}_2} $$

(4b)

$$ {\varepsilon}_{33}=2z{w}^{\ast } $$

(4c)

$$ {\varepsilon}_{12}={\varepsilon}_{21}=\frac{1}{2}\left[z\left(\frac{\partial {\theta}_1}{\partial {x}_2}+\frac{\partial {\theta}_2}{\partial {x}_1}\right)+{z}^3\left(\frac{\partial {\theta}_1^{\ast }}{\partial {x}_2}+\frac{\partial {\theta}_2^{\ast }}{\partial {x}_1}\right)\right] $$

(4d)

$$ {\varepsilon}_{13}={\varepsilon}_{31}=\frac{1}{2}\left[\left({\theta}_1+\frac{\partial w}{\partial {x}_1}\right)+{z}^2\left(3{\theta}_1^{\ast }+\frac{\partial {w}^{\ast }}{\partial {x}_1}\right)\right] $$

(4e)

$$ {\varepsilon}_{23}={\varepsilon}_{32}=\frac{1}{2}\left[\left({\theta}_2+\frac{\partial w}{\partial {x}_2}\right)+{z}^2\left(3{\theta}_2^{\ast }+\frac{\partial {w}^{\ast }}{\partial {x}_2}\right)\right] $$

(4f)

with x₁ = x, x₂ = y.

These strain-displacement relationships can be also expressed in following form by using indicial notation:

$$ {\varepsilon}_{ij}=\frac{1}{2}\left[z\left(\frac{\partial {\theta}_I}{\partial {x}_J}+\frac{\partial {\theta}_J}{\partial {x}_I}\right)+{z}^3\left(\frac{\partial {\theta}_I^{\ast }}{\partial {x}_J}+\frac{\partial {\theta}_J^{\ast }}{\partial {x}_I}\right)\right]{\delta}_{Ii}{\delta}_{Jj}+\frac{1}{2}\left[\left({\theta}_I+\frac{\partial w}{\partial {x}_I}\right)+{z}^2\left(3{\theta}_I^{\ast }+\frac{\partial {w}^{\ast }}{\partial {x}_I}\right)\right]\left({\delta}_{Ii}{\delta}_{3j}+{\delta}_{3i}{\delta}_{Ij}\right)+2z{w}^{\ast }{\delta}_{3i}{\delta}_{3j} $$

(5)

where i, j = 1, 2, 3 and I, J = 1, 2. Note that this convention where capital letter indices, e.g., I, J, K, … vary from 1 and 2, and lowercase letter indices, e.g., i, j, k, … vary from 1, 2 and 3, will be applied throughout this study.

Assuming the material is isotropic and obeys 3-dimensional constitutive relationship, the stress components can be expressed as

$$ {\sigma}_{ij}={C}_{ij kl}{\varepsilon}_{kl} $$

(6)

where C_ijkl is the elastic modulus tensor which is defined as

$$ {C}_{ij kl}=\frac{E}{2\left(1+\nu \right)}\left({\delta}_{il}{\delta}_{jk}+{\delta}_{ik}{\delta}_{jl}\right)+\frac{E\nu}{\left(1+\nu \right)\left(1-2\nu \right)}{\delta}_{ij}{\delta}_{kl} $$

(7)

with E and ν being elastic (Young’s) modulus and Poisson’s ratio, respectively. Substituting Eq. (7) into (6) yields:

$$ {\sigma}_{ij}=\frac{E}{\left(1+\nu \right)}{\varepsilon}_{ij}+\frac{E\nu}{\left(1+\nu \right)\left(1-2\nu \right)}{\varepsilon}_{ll}{\delta}_{ij} $$

(8)

The strain energy density is defined as:

$$ \mathrm{W}=\frac{1}{2}{\sigma}_{ij}{\varepsilon}_{ij} $$

(9)

Inserting Eqs. (8) and (5) into Eq. (9) and rearranging the indices gives the expression of strain energy density as

$$ W=\frac{G}{2}\left[{z}^2\left(\frac{\partial {\theta}_I}{\partial {x}_J}\frac{\partial {\theta}_I}{\partial {x}_J}+\frac{\partial {\theta}_I}{\partial {x}_J}\frac{\partial {\theta}_J}{\partial {x}_I}+\frac{\partial {\theta}_I}{\partial {x}_I}\frac{\partial {\theta}_J}{\partial {x}_J}\right)+{z}^6\left(\frac{\partial {\theta}_I^{\ast }}{\partial {x}_J}\frac{\partial {\theta}_I^{\ast }}{\partial {x}_J}+\frac{\partial {\theta}_I^{\ast }}{\partial {x}_J}\frac{\partial {\theta}_J^{\ast }}{\partial {x}_I}+\frac{\partial {\theta}_I^{\ast }}{\partial {x}_I}\frac{\partial {\theta}_J^{\ast }}{\partial {x}_J}\right)+2{z}^4\left(\frac{\partial {\theta}_{\mathrm{I}}}{\partial {x}_J}\frac{\partial {\theta}_I^{\ast }}{\partial {x}_J}+\frac{\partial {\theta}_I}{\partial {x}_J}\frac{\partial {\theta}_J^{\ast }}{\partial {x}_I}+\frac{\partial {\theta}_I^{\ast }}{\partial {x}_I}\frac{\partial {\theta}_J}{\partial {x}_J}\right)\right]+\frac{G\left(4\nu -1\right)}{2\left(1-2\nu \right)}\left({z}^2\frac{\partial {\theta}_I}{\partial {x}_I}\frac{\partial {\theta}_J}{\partial {x}_J}+2{z}^4\frac{\partial {\theta}_I^{\ast }}{\partial {x}_I}\frac{\partial {\theta}_J}{\partial {x}_J}+{z}^6\frac{\partial {\theta}_I^{\ast }}{\partial {x}_I}\frac{\partial {\theta}_J^{\ast }}{\partial {x}_J}\right)+\frac{G}{2}\left[{\left({\theta}_I+\frac{\partial w}{\partial {x}_I}\right)}^2+{z}^4{\left(3{\theta}_I^{\ast }+\frac{\partial {w}^{\ast }}{\partial {x}_I}\right)}^2+2{z}^2\left({\theta}_I+\frac{\partial w}{\partial {x}_I}\right)\left(3{\theta}_I^{\ast }+\frac{\partial {w}^{\ast }}{\partial {x}_I}\right)\right]+\frac{4G}{1-2\nu}\left({z}^2{w}^{\ast}\left[\left(1-\nu \right){w}^{\ast }+\nu \frac{\partial {\theta}_I}{\partial {x}_I}\right]+{z}^4\nu {w}^{\ast}\frac{\partial {\theta}_I^{\ast }}{\partial {x}_I}\right) $$

(10)

The average strain energy density for a particular material point on the mid-plane can be obtained by integrating the strain energy density function, Eq. (10), through the transverse direction and divided by the thickness as

$$ W=\frac{1}{h}{\int}_{-h/2}^{h/2} Wdz=\frac{G}{2}\left[\frac{h^2}{12}\left(\frac{\partial {\theta}_I}{\partial {x}_J}\frac{\partial {\theta}_I}{\partial {x}_J}+\frac{\partial {\theta}_I}{\partial {x}_J}\frac{\partial {\theta}_J}{\partial {x}_I}+\frac{\partial {\theta}_I}{\partial {x}_I}\frac{\partial {\theta}_J}{\partial {x}_J}\right)+\frac{h^6}{448}\left(\frac{\partial {\theta}_I^{\ast }}{\partial {x}_J}\frac{\partial {\theta}_I^{\ast }}{\partial {x}_J}+\frac{\partial {\theta}_I^{\ast }}{\partial {x}_J}\frac{\partial {\theta}_J^{\ast }}{\partial {x}_I}+\frac{\partial {\theta}_I^{\ast }}{\partial {x}_I}\frac{\partial {\theta}_J^{\ast }}{\partial {x}_J}\right)+2\frac{h^4}{80}\left(\frac{\partial {\theta}_I}{\partial {x}_J}\frac{\partial {\theta}_I^{\ast }}{\partial {x}_J}+\frac{\partial {\theta}_I}{\partial {x}_J}\frac{\partial {\theta}_J^{\ast }}{\partial {x}_I}+\frac{\partial {\theta}_I^{\ast }}{\partial {x}_I}\frac{\partial {\theta}_J}{\partial {x}_J}\right)\right]+\frac{G\left(4\nu -1\right)}{2\left(1-2\nu \right)}\left(\frac{h^2}{12}\frac{\partial {\theta}_I}{\partial {x}_I}\frac{\partial {\theta}_J}{\partial {x}_J}+2\frac{h^4}{80}\frac{\partial {\theta}_I^{\ast }}{\partial {x}_I}\frac{\partial {\theta}_J}{\partial {x}_J}+\frac{h^6}{448}\frac{\partial {\theta}_I^{\ast }}{\partial {x}_I}\frac{\partial {\theta}_J^{\ast }}{\partial {x}_J}\right)+\frac{G}{2}\left[{\left({\theta}_I+\frac{\partial w}{\partial {x}_I}\right)}^2+\frac{h^4}{80}{\left(3{\theta}_I^{\ast }+\frac{\partial {w}^{\ast }}{\partial {x}_I}\right)}^2+2\frac{h^2}{12}\left({\theta}_I+\frac{\partial w}{\partial {x}_I}\right)\left(3{\theta}_I^{\ast }+\frac{\partial {w}^{\ast }}{\partial {x}_I}\right)\right]+\frac{4G}{1-2\nu}\left(\frac{h^2}{12}{w}^{\ast}\left[\left(1-\upnu \right){w}^{\ast }+\nu \frac{\partial {\theta}_I}{\partial {x}_I}\right]+\frac{h^4}{80}\nu {w}^{\ast}\frac{\partial {\theta}_I^{\ast }}{\partial {x}_I}\right) $$

(11)

3 Peridynamic Higher-Order Plate Formulation

PD is a new continuum mechanics formulation. It is within the class of non-local continuum mechanics where material points that are within an influence domain, horizon, H, can interact with each other. The governing equations of peridynamics are in integro-differential equation form and can be written as

$$ \rho \left(\boldsymbol{x}\right)\ddot{\boldsymbol{u}}\left(\boldsymbol{x},t\right)={\int}_H\mathbf{f}\left({\boldsymbol{u}}^{\prime },\boldsymbol{u},{\boldsymbol{x}}^{\prime },\boldsymbol{x}\right) dV^{\prime }+\boldsymbol{b}\left(\boldsymbol{x},t\right) $$

(12)

where ρ is the density, $\ddot{\boldsymbol{u}}$ and u represent acceleration and displacement and t denotes time. b(x, t) corresponds to body load vector and is utilized to apply external load. As shown in Fig. 2, f(u^′ , u, x^′ , x) represents the peridynamic interaction (bond) force between two interacting material points located at x and x^′.

Fig. 2

Peridynamic interaction force between two material points [23]

Obtaining analytical solution for Eq. (12) is usually not possible. Instead, numerical techniques such as meshless approach are widely utilized. Therefore, the PD equations of motion for a material point k can be expressed in discrete form as

$$ {\rho}_{(k)}{\ddot{\boldsymbol{u}}}_{(k)}={\sum}_{j=1}^N{\mathbf{f}}_{(k)(j)}{V}_{(j)}+{\boldsymbol{b}}_{(k)} $$

(13)

where N indicates the total number of family members inside the horizon of material point k and V represents the material point volume.

The PD equations of motion can be derived by utilizing Euler-Lagrange equation as

$$ \frac{d}{dt}\frac{\partial L}{\partial {\dot{\boldsymbol{u}}}_{(k)}}-\frac{\partial L}{\partial {\boldsymbol{u}}_{(k)}}=0 $$

(14)

where L = T − U is the Lagrangian. The system’s kinetic energy, T, and potential energy, U, can be expressed as

$$ T=\frac{1}{2}{\sum}_k\rho {\dot{\boldsymbol{u}}}_{(k)}\cdotp {\dot{\boldsymbol{u}}}_{(k)}{V}_{(k)} $$

(15a)

and

$$ U={\sum}_k{W}_{(k)}{V}_{(k)}-{\sum}_k{\boldsymbol{b}}_{(k)}\cdotp {\boldsymbol{u}}_{(k)}{V}_{(k)} $$

(15b)

where u_(k) and b_(k) are the generalized displacement vector and generalized body force density vector, respectively, which in this study can be defined as

$$ {\boldsymbol{u}}_{(k)}={\left(\ {\theta}_x^{(k)}\kern0.5em {\theta}_y^{(k)}\kern0.5em \begin{array}{cc}{\theta}_x^{\ast (k)}& \begin{array}{cc}{\theta}_y^{\ast (k)}& \begin{array}{cc}{w}_{(k)}& {w}_{(k)}^{\ast}\end{array}\end{array}\end{array}\right)}^T $$

(16a)

and

$$ {\mathbf{b}}_{(k)}={\left({b}_{mx}^{(k)}\kern0.5em \begin{array}{cc}{b}_{my}^{(k)}& \begin{array}{cc}0& \begin{array}{cc}0& \begin{array}{cc}{b}_z^{(k)}& 0\end{array}\end{array}\end{array}\end{array}\right)}^T $$

(16b)

Here, the entries of the body force density vector, b_m and b_z, correspond to moment and transverse force, respectively. The generalized velocity vector, $\dot{\boldsymbol{u}}\left(x,y,z,t\right)$, can be obtained by taking derivative with respect to time from Eq.(2) as:

$$ \dot{\boldsymbol{u}}\left(x,y,z,t\right)=\left\{\begin{array}{c}\mathrm{z}{\dot{\theta}}_x+{z}^3{\dot{\theta}}_x^{\ast}\\ {}z{\dot{\theta}}_y+{z}^3{\dot{\theta}}_y^{\ast}\\ {}\dot{\mathrm{w}}+{z}^2{\dot{w}}^{\ast}\end{array}\right\} $$

(17)

Thus, inserting Eq. (17) into (15a), integrating throughout the thickness and dividing by the thickness gives the (average) kinetic energy of the system as

$$ T=\frac{1}{2h}\sum \limits_k{\rho}_{(k)}\left[\frac{h^3}{12}\left({\dot{\theta}}_I^{(k)}{\dot{\theta}}_I^{(k)}\right)+\frac{h^7}{448}\left({\dot{\theta}}_I^{\ast (k)}{\dot{\theta}}_I^{\ast (k)}\right)+2\frac{h^5}{80}\left({\dot{\theta}}_I^{(k)}{\dot{\theta}}_I^{\ast (k)}\right)+h{\dot{w}}_{(k)}^2+\frac{h^5}{80}{\left({\dot{w}}_{(k)}^{\ast}\right)}^2+2\frac{h^3}{12}{\dot{w}}_{(k)}{\dot{w}}_{(k)}^{\ast}\right]{V}_{(k)} $$

(18)

with h being the thickness of the plate. The first term of Euler-Lagrange equation can be obtained by substituting Eq. (18) into Eq. (14) as

$$ \frac{d}{dt}\frac{\partial L}{\partial {\dot{\boldsymbol{u}}}_{(k)}}={\rho}_{(k)}\left\{\begin{array}{c}\begin{array}{c}\frac{h^2}{12}{\ddot{\theta}}_{\mathrm{I}}^{(k)}+\frac{h^4}{80}{\ddot{\theta}}_I^{\ast (k)}\\ {}\frac{h^6}{448}{\ddot{\theta}}_I^{\ast (k)}+\frac{h^4}{80}{\ddot{\theta}}_I^{(k)}\\ {}{\ddot{w}}_{(k)}+\frac{h^2}{12}{\ddot{w}}_{(k)}^{\ast}\end{array}\\ {}\frac{h^4}{80}{\ddot{w}}_{(k)}^{\ast }+\frac{h^2}{12}{\ddot{w}}_{(k)}\end{array}\right\}{V}_{(k)} $$

(19)

Unlike the classical elasticity theory, according to PD theory, the strain energy density function has a non-local characteristic such that the strain energy of a particular material point k depends on both its displacement and all other material points in its family and can be expressed as

$$ {W}_{(k)}={W}_{(k)}\left({\boldsymbol{u}}_{(k)},{\boldsymbol{u}}_{\left({1}^k\right)},{\boldsymbol{u}}_{\left({2}^k\right)},{\boldsymbol{u}}_{\left({3}^k\right)},\cdots \right) $$

(20)

where u_(k) is the displacement vector of material point k and ${\boldsymbol{u}}_{\left({i}^k\right)}$ (i = 1, 2, 3, ⋯) is the displacement vector of the ith material point inside the horizon of the material point k.

The total potential energy stored in the body can be obtained by summing potential energies of all material points including strain energy and energy due to external loads as

$$ U={\sum}_k{W}_{(k)}\left({\boldsymbol{u}}_{(k)},{\boldsymbol{u}}_{\left({1}^k\right)},{\boldsymbol{u}}_{\left({2}^k\right)},{\boldsymbol{u}}_{\left({3}^k\right)},\cdots \right){V}_{(k)}-{\sum}_k{\boldsymbol{b}}_{(k)}{\boldsymbol{u}}_{(k)}{V}_{(k)} $$

(21)

Thus, the second term of the Euler-Lagrange equation can be written as

$$ -\frac{\partial L}{\partial {\boldsymbol{u}}_{(k)}}=\frac{\partial }{\partial {\boldsymbol{u}}_{(k)}}{\sum}_n{W}_{(n)}\left({\boldsymbol{u}}_{(n)},{\boldsymbol{u}}_{\left({1}^n\right)},{\boldsymbol{u}}_{\left({2}^n\right)},{\boldsymbol{u}}_{\left({3}^n\right)},\cdots \right){V}_{(n)}-\frac{\partial }{\partial {\boldsymbol{u}}_{(k)}}{\sum}_n{\boldsymbol{b}}_{(n)}{\boldsymbol{u}}_{(n)}{V}_{(n)}={\sum}_n\frac{\partial {W}_{(n)}}{\partial {\boldsymbol{u}}_{(k)}}\left({\delta}_{nk}+{\delta}_{n{i}^k}\right){V}_{(n)}-{\sum}_n{\boldsymbol{b}}_{(n)}{\delta}_{nk}{V}_{(n)}=\left(\frac{\partial {W}_{(k)}}{\partial {\boldsymbol{u}}_{(k)}}{V}_{(k)}+{\sum}_j\frac{\partial {W}_{(j)}}{\partial {\boldsymbol{u}}_{(k)}}{V}_{(j)}\right)-{\boldsymbol{b}}_{(k)}{V}_{(k)} $$

(22)

Inserting Eqs. (22) and (19) into the Euler-Lagrange equation yields

$$ {\rho}_{(k)}\left\{\begin{array}{c}\begin{array}{c}\frac{h^2}{12}{\ddot{\theta}}_I^{(k)}+\frac{h^4}{80}{\ddot{\theta}}_I^{\ast (k)}\\ {}\frac{h^6}{448}{\ddot{\theta}}_I^{\ast (k)}+\frac{h^4}{80}{\ddot{\theta}}_I^{(k)}\\ {}{\ddot{w}}_{(k)}+\frac{h^2}{12}{\ddot{w}}_{(k)}^{\ast}\end{array}\\ {}\frac{h^4}{80}{\ddot{w}}_{(k)}^{\ast }+\frac{h^2}{12}{\ddot{w}}_{(k)}\end{array}\right\}{V}_{(k)}=-\left\{\begin{array}{c}\begin{array}{c}\frac{\partial {W}_{(k)}}{\partial {\theta}_I^{(k)}}{V}_{(k)}+{\sum}_j\frac{\partial {W}_{(j)}}{\partial {\theta}_I^{(k)}}{V}_{(j)}\\ {}\frac{\partial {W}_{(k)}}{\partial {\theta}_I^{\ast (k)}}{V}_{(k)}+{\sum}_j\frac{\partial {W}_{(j)}}{\partial {\theta}_I^{\ast (k)}}{V}_{(j)}\\ {}\frac{\partial {W}_{(k)}}{\partial {w}_{(k)}}{V}_{(k)}+{\sum}_j\frac{\partial {W}_{(j)}}{\partial {w}_{(k)}}{V}_{(j)}\end{array}\\ {}\frac{\partial {W}_{(k)}}{\partial {w}_{(k)}^{\ast }}{V}_{(k)}+{\sum}_j\frac{\partial {W}_{(j)}}{\partial {w}_{(k)}^{\ast }}{V}_{(j)}\end{array}\right\}+\left\{\begin{array}{c}\begin{array}{c}{b}_{mI}^{(k)}\\ {}0\\ {}{b}_z^{(k)}\end{array}\\ {}0\end{array}\right\}{V}_{(k)} $$

(23)

In order to express the strain energy density function given in Eq. (9) in PD form for a particular material point k, it is necessary to transform all the differential terms into an equivalent form of integration and the nonlocalized strain energy density function should be in accordance with the form given in Eq.(20). As derived in the Appendix, the strain energy density function for the material point k and its family member j can be expressed as

$$ {W}_{(k)}=\frac{G}{2}\frac{12}{\pi {\delta}^3{h}^2}\left[\frac{h^3}{12}{\sum}_i\frac{{\left[\left({\theta}_I^{\left({i}^k\right)}-{\theta}_I^{(k)}\right){n}_I^{\left({i}^k\right)(k)}\right]}^2}{\xi_{\left({i}^k\right)(k)}}{V}_{\left({i}^k\right)}+\frac{h^7}{448}{\sum}_i\frac{{\left[\left({\theta}_I^{\ast \left({i}^k\right)}-{\theta}_I^{\ast (k)}\right){n}_I^{\left({i}^k\right)(k)}\right]}^2}{\xi_{\left({i}^k\right)(k)}}{V}_{\left({i}^k\right)}+2\frac{h^5}{80}{\sum}_i\frac{\left({\theta}_I^{\left({i}^k\right)}-{\theta}_I^{(k)}\right)\left({\theta}_J^{\ast \left({i}^k\right)}-{\theta}_J^{\ast (k)}\right)}{\xi_{\left({i}^k\right)(k)}}{n}_I^{\left({i}^k\right)(k)}{n}_J^{\left({i}^k\right)(k)}{V}_{\left({i}^k\right)}\right]+\frac{G\left(4\nu -1\right)}{2\left(1-2\nu \right)}\frac{1}{h}{\left(\frac{2}{\pi {\delta}^2h}\right)}^2\left(\begin{array}{c}\frac{h^3}{12}{\left(\sum \limits_i\frac{\theta_I^{\left({i}^k\right)}-{\theta}_I^{(k)}}{\xi_{\left({i}^k\right)(k)}}{n}_I^{\left({i}^k\right)(k)}{V}_{\left({i}^k\right)}\right)}^2\\ {}+2\frac{h^5}{80}{\sum}_i\frac{\theta_I^{\ast \left({i}^k\right)}-{\theta}_I^{\ast (k)}}{\xi_{\left({i}^k\right)(k)}}{n}_I^{\left({i}^k\right)(k)}{V}_{\left({i}^k\right)}{\sum}_i\frac{\theta_J^{\left({i}^k\right)}-{\theta}_J^{(k)}}{\xi_{\left({i}^k\right)(k)}}{n}_J^{\left({i}^k\right)(k)}{V}_{\left({i}^k\right)}\\ {}+\frac{h^7}{448}{\left({\sum}_i\frac{\theta_I^{\ast \left({i}^k\right)}-{\theta}_I^{\ast (k)}}{\xi_{\left({i}^k\right)(k)}}{n}_I^{\left({i}^k\right)(k)}{V}_{\left({i}^k\right)}\right)}^2\end{array}\right)+\frac{G}{2}\frac{3}{\pi {\delta}^3{h}^2}\left[h{\sum}_i\frac{{\left({w}_{\left({i}^k\right)}-{w}_{(k)}+\frac{\theta_I^{(k)}+{\theta}_I^{\left({i}^k\right)}}{2}{\xi}_{\left({i}^k\right)(k)}{n}_I^{\left({i}^k\right)(k)}\right)}^2}{\xi_{\left({i}^k\right)(k)}}{V}_{\left({i}^k\right)}+\frac{h^5}{80}{\sum}_{i^k}\frac{{\left({w}_{\left({i}^k\right)}^{\ast }-{w}_{(k)}^{\ast }+3\frac{\theta_I^{\ast (k)}+{\theta}_I^{\ast \left({i}^k\right)}}{2}{\xi}_{\left({i}^k\right)(k)}{n}_I^{\left({i}^k\right)(k)}\right)}^2}{\xi_{\left({i}^k\right)(k)}}{V}_{\left({i}^k\right)}+2\frac{h^3}{12}{\sum}_{i^k}\frac{\left({w}_{\left({i}^k\right)}-{w}_{(k)}+\frac{\theta_I^{(k)}+{\theta}_I^{\left({i}^k\right)}}{2}{\xi}_{\left({i}^k\right)(k)}{n}_I^{\left({i}^k\right)(k)}\right)\left({w}_{\left({i}^k\right)}^{\ast }-{w}_{(k)}^{\ast }+3\frac{\theta_J^{\ast (k)}+{\theta}_J^{\ast \left({i}^k\right)}}{2}{\xi}_{\left({i}^k\right)(k)}{n}_J^{\left({i}^k\right)(k)}\right)}{\xi_{\left({i}^k\right)(k)}}{V}_{\left({i}^k\right)}\right]+\frac{4G}{1-2\nu}\frac{3}{\pi {\delta}^3{h}^2}\left(\frac{h^3}{12}{\sum}_{i^k}\frac{w_{(k)}^{\ast }+{w}_{\left({i}^k\right)}^{\ast }}{2}\left[\nu \left({\uptheta}_I^{\left({i}^k\right)}-{\uptheta}_I^{(k)}\right){n}_I^{\left({i}^k\right)(k)}+\frac{1-\nu }{2}\frac{w_{(k)}^{\ast }+{w}_{\left({i}^k\right)}^{\ast }}{2}{\xi}_{\left({i}^k\right)(k)}\right]{V}_{\left({i}^k\right)}+\frac{h^5}{80}\nu {\sum}_{i^k}\frac{w_{(k)}^{\ast }+{w}_{\left({i}^k\right)}^{\ast }}{2}\left({\uptheta}_I^{\ast \left({i}^k\right)}-{\uptheta}_I^{\ast (k)}\right){n}_I^{\left({i}^k\right)(k)}{V}_{\left({i}^k\right)}\right) $$

(24a)

$$ {W}_{(j)}=\frac{G}{2}\frac{12}{\pi {\delta}^3{h}^2}\left[\frac{h^3}{12}{\sum}_i\frac{{\left[\left({\theta}_I^{\left({i}^j\right)}-{\theta}_I^{(j)}\right){n}_I^{\left({i}^j\right)(j)}\right]}^2}{\xi_{\left({i}^j\right)(j)}}{V}_{\left({i}^j\right)}+\frac{h^7}{448}{\sum}_i\frac{{\left[\left({\theta}_I^{\ast \left({i}^j\right)}-{\theta}_I^{\ast (j)}\right){n}_I^{\left({i}^j\right)(j)}\right]}^2}{\xi_{\left({i}^j\right)(j)}}{V}_{\left({i}^j\right)}+2\frac{h^5}{80}{\sum}_i\frac{\left({\theta}_I^{\left({i}^j\right)}-{\theta}_I^{(j)}\right)\left({\theta}_J^{\ast \left({i}^j\right)}-{\theta}_J^{\ast (j)}\right)}{\xi_{\left({i}^j\right)(j)}}{n}_I^{\left({i}^j\right)(j)}{n}_J^{\left({i}^j\right)(j)}{V}_{\left({i}^j\right)}\right]+\frac{G\left(4\nu -1\right)}{2\left(1-2\nu \right)}\frac{1}{h}{\left(\frac{2}{\pi {\delta}^2h}\right)}^2\left(\frac{h^3}{12}{\left({\sum}_i\frac{\uptheta_I^{\left({i}^j\right)}-{\uptheta}_I^{(j)}}{\xi_{\left({i}^j\right)(j)}}{n}_I^{\left({i}^j\right)(j)}{V}_{\left({i}^j\right)}\right)}^2+2\frac{h^5}{80}{\sum}_i\frac{\uptheta_I^{\ast \left({i}^j\right)}-{\uptheta}_I^{\ast (j)}}{\xi_{\left({i}^j\right)(j)}}{n}_I^{\left({i}^j\right)(j)}{V}_{\left({i}^j\right)}{\sum}_i\frac{\uptheta_J^{\left({i}^j\right)}-{\uptheta}_J^{(j)}}{\xi_{\left({i}^j\right)(j)}}{n}_J^{\left({i}^j\right)(j)}{V}_{\left({i}^j\right)}+\frac{h^7}{448}{\left({\sum}_i\frac{\uptheta_I^{\ast \left({i}^j\right)}-{\uptheta}_I^{\ast (j)}}{\xi_{\left({i}^j\right)(j)}}{n}_I^{\left({i}^j\right)(j)}{V}_{\left({i}^j\right)}\right)}^2\right)+\frac{G}{2}\frac{3}{\pi {\delta}^3{h}^2}\left[h{\sum}_i\frac{{\left({w}_{\left({i}^j\right)}-{w}_{(j)}+\frac{\theta_I^{(j)}+{\theta}_I^{\left({i}^j\right)}}{2}{\xi}_{\left({i}^j\right)(j)}{n}_I^{\left({i}^j\right)(j)}\right)}^2}{\xi_{\left({i}^j\right)(j)}}{V}_{\left({i}^j\right)}+\frac{h^5}{80}{\sum}_i\frac{{\left({w}_{\left({i}^j\right)}^{\ast }-{w}_{(j)}^{\ast }+3\frac{\theta_I^{\ast (j)}+{\theta}_I^{\ast \left({i}^j\right)}}{2}{\xi}_{\left({i}^j\right)(j)}{n}_I^{\left({i}^j\right)(j)}\right)}^2}{\xi_{\left({i}^j\right)(j)}}{V}_{\left({i}^j\right)}+2\frac{h^3}{12}{\sum}_i\frac{\left({w}_{\left({i}^j\right)}-{w}_{(j)}+{\theta}_I^{(j)}{\xi}_{\left({i}^j\right)(j)}{n}_I^{\left({i}^j\right)(j)}\right)\left({w}_{\left({i}^j\right)}^{\ast }-{w}_{(j)}^{\ast }+3{\theta}_J^{\ast (j)}{\xi}_{\left({i}^j\right)(j)}{n}_J^{\left({i}^j\right)(j)}\right)}{\xi_{\left({i}^j\right)(j)}}{V}_{\left({i}^j\right)}\right]+\frac{4G}{1-2\nu}\frac{3}{\pi {\delta}^3{h}^2}\left\{\frac{h^3}{12}{\sum}_i\frac{w_{(j)}^{\ast }+{w}_{\left({i}^j\right)}^{\ast }}{2}\left[\nu \left({\uptheta}_I^{\left({i}^j\right)}-{\uptheta}_I^{(j)}\right){n}_I^{\left({i}^j\right)(j)}+\frac{1-\nu }{2}\frac{w_{(j)}^{\ast }+{w}_{\left({i}^j\right)}^{\ast }}{2}{\xi}_{\left({i}^j\right)(j)}\right]{V}_{\left({i}^j\right)}+\frac{h^5}{80}\nu {\sum}_i\frac{w_{(j)}^{\ast }+{w}_{\left({i}^j\right)}^{\ast }}{2}\left({\uptheta}_I^{\ast \left({i}^j\right)}-{\uptheta}_I^{\ast (j)}\right){n}_I^{\left({i}^j\right)(j)}{V}_{\left({i}^j\right)}\right\} $$

(24b)

where n₁ = cos φ, n₂ = sin φ with φ being the bond angle with respect to x-axis.

Substituting these PD strain energy expressions into Eq. (23) yields the final PD equations of motion for higher-order plate theory as:

$$ {\rho}_{(k)}\left(\frac{h^2}{12}{\ddot{\theta}}_L^{(k)}+\frac{h^4}{80}{\ddot{\theta}}_L^{\ast (k)}\right)=\frac{24G}{\pi {\delta}^3{h}^2}\left[\frac{h^3}{12}{\sum}_j\frac{\theta_I^{(j)}-{\theta}_I^{(k)}}{\xi_{(j)(k)}}{n}_I^{(j)(k)}{n}_L^{(j)(k)}{V}_{(j)}+\frac{h^5}{80}{\sum}_j\frac{\theta_I^{\ast (j)}-{\theta}_I^{\ast (k)}}{\xi_{(j)(k)}}{n}_I^{(j)(k)}{n}_L^{(j)(k)}{V}_{(j)}\right]+\frac{G\left(4\nu -1\right)}{1-2\nu }{\left(\frac{2}{\pi {\delta}^2h}\right)}^2\frac{1}{h}\left[\frac{h^3}{12}{\sum}_j\frac{n_L^{(j)(k)}}{\xi_{(j)(k)}}\left({\sum}_i\frac{\theta_I^{\left({i}^k\right)}-{\theta}_I^{(k)}}{\xi_{\left({i}^k\right)(k)}}{n}_I^{\left({i}^k\right)(k)}{V}_{\left({i}^k\right)}+{\sum}_i\frac{\theta_I^{\left({i}^j\right)}-{\theta}_I^{(j)}}{\xi_{\left({i}^j\right)(j)}}{n}_I^{\left({i}^j\right)(j)}{V}_{\left({i}^j\right)}\right){V}_{(j)}+\frac{h^5}{80}{\sum}_j\frac{n_L^{(j)(k)}}{\xi_{(j)(k)}}\left({\sum}_i\frac{\theta_I^{\ast \left({i}^k\right)}-{\theta}_I^{\ast (k)}}{\xi_{\left({i}^k\right)(k)}}{n}_I^{\left({i}^k\right)(k)}{V}_{\left({i}^k\right)}+{\sum}_i\frac{\theta_I^{\ast \left({i}^j\right)}-{\theta}_I^{\ast (j)}}{\xi_{\left({i}^j\right)(j)}}{n}_I^{\left({i}^j\right)(j)}{V}_{\left({i}^j\right)}\right){V}_{(j)}\right]-\frac{3G}{\pi {\delta}^3{h}^2}\left[h{\sum}_j{n}_L^{(j)(k)}\left({w}_{(j)}-{w}_{(k)}+\frac{\theta_I^{(j)}+{\theta}_I^{(k)}}{2}{\xi}_{(j)(k)}{n}_I^{(j)(k)}\right){V}_{(j)}+\frac{h^3}{12}{\sum}_j{n}_L^{(j)(k)}\left({w}_{(j)}^{\ast }-{w}_{(k)}^{\ast }+3\frac{\theta_I^{\ast (k)}+{\theta}_I^{\ast (j)}}{2}{\xi}_{(j)(k)}{n}_I^{(j)(k)}\right){V}_{(j)}\right]+\frac{\mathrm{G}}{1-2\nu}\frac{12}{\pi {\delta}^3h}\frac{1}{h}\left(\frac{h^3}{12}{\sum}_j\nu \left({w}_{(k)}^{\ast }+{w}_{(j)}^{\ast}\right){n}_L^{(j)(k)}{V}_{(j)}\right)+{b}_{mL}^{(k)} $$

(25a)

$$ {\rho}_{(k)}\left(\frac{h^6}{448}{\ddot{\theta}}_I^{\ast (k)}+\frac{h^4}{80}{\ddot{\theta}}_I^{(k)}\right)=\frac{24G}{\pi {\delta}^3{h}^2}\left[\frac{h^7}{448}\left({\sum}_j\frac{\theta_I^{\ast (j)}-{\theta}_I^{\ast (k)}}{\xi_{(j)(k)}}{n}_I^{(j)(k)}{n}_L^{(j)(k)}{V}_{(j)}\right)+\frac{h^5}{80}\left({\sum}_j\frac{\theta_I^{(j)}-{\theta}_I^{(k)}}{\xi_{(j)(k)}}{n}_I^{(j)(k)}{n}_L^{(j)(k)}{V}_{(j)}\right)\right]+\frac{G\left(4\nu -1\right)}{1-2\nu }{\left(\frac{2}{\pi {\delta}^2h}\right)}^2\frac{1}{h}\left[\frac{h^5}{80}{\sum}_j\frac{n_L^{(j)(k)}}{\xi_{(j)(k)}}\left({\sum}_i\frac{\uptheta_I^{\left({i}^k\right)}-{\theta}_I^{(k)}}{\xi_{\left({i}^k\right)(k)}}{n}_I^{\left({i}^k\right)(k)}{V}_{\left({i}^k\right)}+{\sum}_i\frac{\theta_I^{\left({i}^j\right)}-{\theta}_I^{(j)}}{\xi_{\left({i}^j\right)(j)}}{n}_I^{\left({i}^j\right)(j)}{V}_{\left({i}^j\right)}\right){V}_{(j)}+\frac{h^7}{448}{\sum}_j\frac{n_L^{(j)(k)}}{\xi_{(j)(k)}}\left({\sum}_i\frac{\theta_I^{\ast \left({i}^k\right)}-{\theta}_I^{\ast (k)}}{\xi_{\left({i}^k\right)(k)}}{n}_I^{\left({i}^k\right)(k)}{V}_{\left({i}^k\right)}+{\sum}_i\frac{\theta_I^{\ast \left({i}^j\right)}-{\theta}_I^{\ast (j)}}{\xi_{\left({i}^j\right)(j)}}{n}_I^{\left({i}^j\right)(j)}{V}_{\left({i}^j\right)}\right){V}_{(j)}\right]-\frac{9G}{\pi {\delta}^3{h}^2}\left[\frac{h^5}{80}{\sum}_j\left({w}_{(j)}^{\ast }-{w}_{(k)}^{\ast }+3\frac{\uptheta_I^{\ast (k)}+{\theta}_I^{\ast (j)}}{2}{\xi}_{(j)(k)}{n}_I^{(j)(k)}\right){n}_L^{(j)(k)}{V}_{(j)}+\frac{h^3}{12}{\sum}_j\left({w}_{(j)}-{w}_{(k)}+\frac{\theta_I^{(j)}+{\theta}_I^{(k)}}{2}{\xi}_{(j)(k)}{n}_I^{(j)(k)}\right){n}_L^{(j)(k)}{V}_{(j)}\right]+\frac{G}{1-2\nu}\frac{12}{\pi {\delta}^3{h}^2}\left(\frac{h^5}{80}{\sum}_j\nu \left({w}_{(k)}^{\ast }+{w}_{(j)}^{\ast}\right){n}_L^{(j)(k)}{V}_{(j)}\right) $$

(25b)

$$ {\rho}_{(k)}\left({\ddot{w}}_{(k)}+\frac{h^2}{12}{\ddot{w}}_{(k)}^{\ast}\right)=\frac{6G}{\pi {\delta}^3{h}^2}\left[h{\sum}_j\left(\frac{w_{(j)}-{w}_{(k)}}{\xi_{(j)(k)}}+\frac{\theta_I^{(k)}+{\theta}_I^{(j)}}{2}{n}_I^{(j)(k)}\right){V}_{(j)}+\frac{h^3}{12}{\sum}_j\left(\frac{w_{(j)}^{\ast }-{w}_{(k)}^{\ast }}{\xi_{\left(\mathrm{j}\right)(k)}}+\frac{3}{2}\left({\theta}_I^{\ast (k)}+{\theta}_I^{\ast (j)}\right){n}_I^{(j)(k)}\right){V}_{(j)}\right]+{b}_z^{(k)} $$

(25c)

$$ {\rho}_{(k)}\left(\frac{h^4}{80}{\ddot{w}}_{(k)}^{\ast }+\frac{h^2}{12}{\ddot{w}}_{(k)}\right)=\frac{6G}{\pi {\delta}^3{h}^2}\left[\frac{h^5}{80}{\sum}_j\left(\frac{w_{(j)}^{\ast }-{w}_{(k)}^{\ast }}{\xi_{(j)(k)}}+\frac{3}{2}\left({\theta}_I^{\ast (k)}+{\theta}_I^{\ast (j)}\right){n}_I^{(j)(k)}\right){V}_{(j)}+\frac{h^3}{12}{\sum}_j\frac{w_{(j)}-{w}_{(k)}}{\xi_{(j)(k)}}+\frac{\theta_I^{(k)}+{\theta}_I^{(j)}}{2}{n}_I^{(j)(k)}{V}_{(j)}\right]-\frac{E}{\left(1+\nu \right)\left(1-2\nu \right)}\frac{6}{\pi {\delta}^3h}\frac{1}{h}\left\{\frac{h^3}{12}{\sum}_j\left[\nu \left({\uptheta}_I^{(j)}-{\uptheta}_I^{(k)}\right){n}_I^{(j)(k)}+\left(1-\nu \right)\frac{w_{(k)}^{\ast }+{w}_{(j)}^{\ast }}{2}{\xi}_{(j)(k)}\right]{V}_{(j)}+\frac{h^5}{80}{\sum}_j\nu \left({\uptheta}_I^{\ast (j)}-{\uptheta}_I^{\ast (k)}\right){n}_I^{(j)(k)}{V}_{(j)}\right\} $$

(25d)

Note that when the Poisson’s ratio is ν = 0.25, PD equations of motion will have simpler forms:

$$ {\rho}_{(k)}\left(\frac{h^2}{12}{\ddot{\theta}}_L^{(k)}+\frac{h^4}{80}{\ddot{\theta}}_L^{\ast (k)}\right)=\frac{48}{5}\frac{E}{\pi {\delta}^3h}\frac{1}{h}\left[\frac{h^3}{12}{\sum}_j\frac{\theta_I^{(j)}-{\theta}_I^{(k)}}{\xi_{(j)(k)}}{n}_I^{(j)(k)}{n}_L^{(j)(k)}{V}_{(j)}+\frac{h^5}{80}{\sum}_j\frac{\theta_I^{\ast (j)}-{\theta}_I^{\ast (k)}}{\xi_{(j)(k)}}{n}_I^{(j)(k)}{n}_L^{(j)(k)}{V}_{(j)}\right]-\frac{6}{5}\frac{E}{\pi {\delta}^3h}\frac{1}{h}\left[h{\sum}_j{n}_L^{(j)(k)}\left({w}_{(j)}-{w}_{(k)}+\frac{\theta_I^{(k)}+{\theta}_I^{(j)}}{2}{\xi}_{(j)(k)}{n}_I^{(j)(k)}\right){V}_{(j)}+\frac{h^3}{12}{\sum}_j{n}_L^{(j)(k)}\left({w}_{(j)}^{\ast }-{w}_{(k)}^{\ast }+3\frac{\theta_I^{\ast (k)}+{\theta}_I^{\ast (j)}}{2}{\xi}_{(j)(k)}{n}_I^{(j)(k)}\right){V}_{(j)}\right]+\frac{12}{5}\frac{E}{\pi {\delta}^3h}\frac{1}{h}\left(\frac{h^3}{12}{\sum}_j\left({w}_{(k)}^{\ast }+{w}_{(j)}^{\ast}\right){n}_L^{(j)(k)}{V}_{(j)}\right)+{b}_{mL}^{(k)} $$

(26a)

$$ {\rho}_{(k)}\left(\frac{h^6}{448}{\ddot{\theta}}_I^{\ast (k)}+\frac{h^4}{80}{\ddot{\theta}}_I^{(k)}\right)=\frac{48}{5}\frac{E}{\uppi {\delta}^3h}\frac{1}{h}\left[\frac{h^7}{448}\left({\sum}_j\frac{\theta_I^{\ast (j)}-{\theta}_I^{\ast (k)}}{\xi_{(j)(k)}}{n}_I^{(j)(k)}{n}_L^{(j)(k)}{V}_{(j)}\right)+\frac{h^5}{80}\left({\sum}_j\frac{\theta_I^{(j)}-{\theta}_I^{(k)}}{\xi_{(j)(k)}}{n}_I^{(j)(k)}{n}_L^{(j)(k)}{V}_{(j)}\right)\right]-\frac{18}{5}\frac{E}{\pi {\delta}^3h}\frac{1}{h}\left[\frac{h^5}{80}{\sum}_j\left({w}_{(j)}^{\ast }-{w}_{(k)}^{\ast }+3\frac{\theta_I^{\ast (k)}+{\theta}_I^{\ast (j)}}{2}{\xi}_{(j)(k)}{n}_I^{(j)(k)}\right){n}_L^{(j)(k)}{V}_{(j)}+\frac{h^3}{12}{\sum}_j\left({w}_{(j)}-{w}_{(k)}+\frac{\theta_I^{(k)}+{\theta}_I^{(j)}}{2}{\xi}_{(j)(k)}{n}_I^{(j)(k)}\right){n}_L^{(j)(k)}{V}_{(j)}\right]+\frac{12}{5}\frac{E}{\pi {\delta}^3h}\frac{1}{h}\left(\frac{h^5}{80}{\sum}_j\left({w}_{\left(\mathrm{k}\right)}^{\ast }+{w}_{(j)}^{\ast}\right){n}_L^{(j)(k)}{V}_{(j)}\right) $$

(26b)

$$ {\rho}_{(k)}\left({\ddot{w}}_{(k)}+\frac{h^2}{12}{\ddot{w}}_{(k)}^{\ast}\right)=\frac{12}{5}\frac{E}{\pi {\delta}^3h}\frac{1}{h}\left[h{\sum}_j\left(\frac{w_{(j)}-{w}_{(k)}}{\xi_{(j)(k)}}+\frac{\theta_I^{(k)}+{\theta}_I^{(j)}}{2}{n}_I^{(j)(k)}\right){V}_{(j)}+\frac{h^3}{12}{\sum}_j\left(\frac{w_{(j)}^{\ast }-{w}_{(k)}^{\ast }}{\xi_{(j)(k)}}+\frac{3}{2}\left({\theta}_I^{\ast (k)}+{\theta}_I^{\ast (j)}\right){n}_I^{(j)(k)}\right){V}_{(j)}\right]+{b}_z^{(k)} $$

(26c)

$$ {\rho}_{(k)}\left(\frac{h^4}{80}{\ddot{w}}_{(k)}^{\ast }+\frac{h^2}{12}{\ddot{w}}_{(k)}\right)=\frac{12}{5}\frac{E}{\pi {\delta}^3h}\frac{1}{h}\left[\frac{h^5}{80}{\sum}_j\left(\frac{w_{(j)}^{\ast }-{w}_{(k)}^{\ast }}{\xi_{(j)(k)}}+\frac{3}{2}\left({\theta}_I^{\ast (k)}+{\theta}_I^{\ast (j)}\right){n}_I^{(j)(k)}\right){V}_{(j)}+\frac{h^3}{12}{\sum}_j\frac{w_{(j)}-{w}_{(k)}}{\xi_{(j)(k)}}+\frac{\theta_I^{(k)}+{\theta}_I^{(j)}}{2}{n}_I^{(j)(k)}{V}_{(j)}\right]-\frac{12}{5}\frac{E}{\pi {\delta}^3h}\frac{1}{h}\left\{\frac{h^3}{12}{\sum}_j\left[\left({\uptheta}_I^{(j)}-{\uptheta}_I^{(k)}\right){n}_I^{(j)(k)}+3\frac{w_{(k)}^{\ast }+{w}_{(j)}^{\ast }}{2}{\xi}_{(j)(k)}\right]{V}_{(j)}+\frac{h^5}{80}{\sum}_j\left({\uptheta}_I^{\ast (j)}-{\uptheta}_I^{\ast (k)}\right){n}_I^{(j)(k)}{V}_{(j)}\right\} $$

(26d)

4 Boundary Conditions

In this study, the displacement boundary conditions are applied by introducing a fictitious boundary layer, R_c, outside the boundary of the actual material domain as shown in Fig. 3. The width of this layer can be chosen as the size of the horizon for the Poisson’s ratio value of ν = 1/4 or double size of the horizon for the Poisson’s ration of ν ≠ 1/4. This is mainly because the size of the influence domain is equal to double size of the horizon for ν ≠ 1/4. Two common types of boundary conditions, i.e. clamped and simply supported, are explained below for PD higher-order plate formulation.

Fig. 3

Actual, R and fictitious, R_c solution domains

4.1 Clamped Condition

To implement the clamped boundary condition, a fictitious boundary layer is created outside the actual material domain. If the horizon size is chosen as δ = 3∆x, the size of the fictitious domain can be specified as 3∆x for ν = 1/4 or 6∆x for ν ≠ 1/4 in which the discretization size is ∆x. The clamped boundary condition constrains zero transverse displacement and zero rotation for the material points adjacent to the clamped end. In this study, this can be achieved by enforcing symmetrical displacement fields for w and w^∗ and anti-symmetrical displacement fields for θ_I and ${\theta}_I^{\ast }$ (I = 1, 2), respectively, to the material points in the fictitious region with respect to the actual displacement field as (see Fig. 4)

Fig. 4

Application of clamped boundary condition

$$ {w}_{(k)(i)}={w}_{(k)\left(-i\right)},\kern0.5em {w}_{(k)(i)}^{\ast }={w}_{(k)\left(-i\right)}^{\ast } $$

(27a)

$$ {\theta}_I^{(k)(i)}=-{\theta}_I^{(k)\left(-i\right)},\kern0.5em {\theta}_I^{\ast (k)(i)}=-{\theta}_I^{\ast (k)\left(-i\right)} $$

(27b)

$$ {w}_{(k)(1)}={w}_{(k)\left(-1\right)}=\kern0.5em {w}_{(k)(1)}^{\ast }={w}_{(k)\left(-1\right)}^{\ast }=0 $$

(27c)

(i = 1,2,…,6 for ν ≠ 1/4, i = 1,2,3 for ν = 1/4)

4.2 Simply Supported Condition

To implement the simply supported boundary condition, a fictitious boundary layer is created outside the actual material domain as in the clamped boundary condition. If the horizon size is chosen as δ = 3∆x, the size of the fictitious domain can be specified as 3∆x for ν = 1/4 or 6∆x for ν ≠ 1/4. The simply supported boundary condition constrains zero transverse displacement for the material points adjacent to the constrained boundary. In this study, this can be achieved by enforcing anti-symmetrical displacement fields for w and w^∗ and symmetrical displacement fields for θ_I and ${\theta}_{\mathrm{I}}^{\ast }$ (I = 1, 2), respectively, to the material points in the fictitious region with respect to the actual displacement field as (see Fig. 5)

$$ {w}_{(k)(i)}=-{w}_{(k)\left(-i\right)},\kern0.5em {w}_{(k)(i)}^{\ast }=-{w}_{(k)\left(-i\right)}^{\ast } $$

(28a)

$$ {\theta}_I^{(k)(i)}={\theta}_I^{(k)\left(-i\right)},\kern0.5em {\theta}_I^{\ast (k)(i)}={\theta}_I^{\ast (k)\left(-i\right)} $$

(28b)

Fig. 5

Application of simply supported boundary condition

(for i = 1,2,…,6 if ν ≠ 1/4, for i = 1,2,3 if ν = 1/4)

5 Numerical Results

In order to verify the PD formulation for a higher-order plate theory, two numerical examples are considered for simply supported and clamped boundary conditions. The PD solutions are compared with the corresponding finite element (FE) analysis results.

5.1 Simply Supported Plate Subjected to Transverse Loading

A simply supported plate with a length and width of L = W = 1m and a thickness of h = 0.2m is considered as shown in Fig. 6. The Young’s modulus and Poisson’s ratio of the plate are E = 200GPa and ν = 1/4, respectively. The model is discretized into one single row of material points along with the thickness direction and the distance between material points is ∆x = 1/70 m. The horizon size is chosen as δ = 3.015∆x. A fictitious region is introduced outside the edges as the external boundaries with a width of δ. The plate is subjected to a distributed transverse load of p = 100N/m through the y-centre line. The line load is converted to a body load of $b=\frac{pW}{2\left(\frac{w}{\Delta x}\right)\Delta V}=1.25\times {10}^4N/{m}^3$ and it is distributed to two columns of material points through the centre line as shown in Fig. 7.

Fig. 6

Simply supported plate subjected to transverse loading

Fig. 7

Application of transverse loading in PD model and fictitious region

The FE model of the plate is created by using SOLID185 element in ANSYS with 50 elements along the length and width, and 8 elements along the thickness. Boundary conditions below were applied in ANSYS as:

$$ {\displaystyle \begin{array}{c}u\left(0,y,0\right)=u\left(L,y,0\right)=u\left(x,0,0\right)=u\left(x,W,0\right)=0\\ {}v\left(0,y,0\right)=v\left(L,y,0\right)=v\left(x,0,0\right)=v\left(x,W,0\right)=0\\ {}w\left(0,y,0\right)=w\left(L,y,0\right)=w\left(x,0,0\right)=w\left(x,W,0\right)=0\end{array}} $$

As depicted in Fig. 8, the transverse displacement variation results along the central x-axis and y-axis obtained from PD and FE analyses are compared with each other and a very good agreement is obtained between the two approaches.

Fig. 8

Variation of transverse displacements along a central x-axis and b central y-axis

5.2 Clamped Plate Subjected to Transverse Loading

A clamped plate with a length and width of L = W = 1m and a thickness of h = 0.15m is considered as shown in Fig. 9. Young’s modulus and Poisson’s ratio of the plate are E = 200GPa and ν = 0.3, respectively. The model is discretized into one single row of material points along with the thickness and the distance between material points is ∆x = 1/70 m. The horizon size is chosen as δ = 3.015∆x. A fictitious region is introduced outside the edges as the external boundaries with a width of 2δ. The plate is subjected to a distributed transverse load of p = 100N/m through the y-centre line. The line load is converted to a body load of $\mathrm{b}=\frac{pW}{2\left(\frac{w}{\Delta x}-2\right)\Delta V}=1.3021\times {10}^4N/{m}^3$ and it is distributed to two columns of material points through the centre line as shown in Fig. 10.

Fig. 9

Clamped plated subjected to transverse loading

Fig. 10

Application of transverse loading in PD model and fictitious region

The FE model of the plate is created by using the SOLID185 element in ANSYS with 50 elements along the length and width, and 8 elements along the thickness. Boundary conditions below were applied in ANSYS as:

$$ {\displaystyle \begin{array}{c}u\left(0,y,z\right)=u\left(L,y,z\right)=u\left(x,0,z\right)=u\left(x,W,z\right)=0\\ {}v\left(0,y,z\right)=v\left(L,y,z\right)=v\left(x,0,z\right)=v\left(x,W,z\right)=0\\ {}w\left(0,y,0\right)=w\left(L,y,0\right)=w\left(x,0,0\right)=w\left(x,W,0\right)=0\end{array}} $$

PD results for transverse deflection obtained along the central x-axis and y-axis are compared against FE results as shown in Fig. 11. PD results agree very well with FE results.

Fig. 11

Variation of transverse displacements along a central x-axis and b central y-axis

5.3 Plate Subjected to Transverse Loading and Mixed (Simply Supported-Clamped) Boundary Conditions

In the final numerical case, a mixed (simply supported-clamped) boundary condition is considered, as shown in Fig. 12. The plate has a length and width of L = W = 1m and a thickness of h = 0.2m. The material properties are same as in the previous case. The plate is subjected to a distributed transverse load of p = 100N/m through the y-centre line. The line load is converted to a body load of $b=\frac{pW}{2\left(\frac{w}{\Delta x}\right)\Delta V}=1.25\times {10}^4N/{m}^3$ and it is distributed to two columns of material points through the centre line. The top and bottom edges of the plate are subjected to clamped boundary condition, whereas the left and right edges of the plate are subjected to simply supported boundary condition.

Fig. 12

Simply supported-clamped plated subjected to transverse loading

The FE model of the plate is created by using the SOLID185 element in ANSYS with 50 elements along the length and width, and 8 elements along the thickness. Boundary conditions below were applied in ANSYS as:

$$ {\displaystyle \begin{array}{c}u\left(0,y,0\right)=u\left(L,y,0\right)=u\left(x,0,z\right)=u\left(x,W,z\right)=0\\ {}v\left(0,y,0\right)=v\left(L,y,0\right)=v\left(x,0,z\right)=v\left(x,W,z\right)=0\\ {}w\left(0,y,0\right)=w\left(L,y,0\right)=w\left(x,0,0\right)=w\left(x,W,0\right)=0\end{array}} $$

Transverse deflection results obtained along the central x-axis and y-axis are shown in Fig. 13 and PD and FE results agree very well with each other demonstrating that the current formulation is capable of considering mixed boundary conditions.

Fig. 13

Variation of transverse displacements along a central x-axis and b central y-axis

6 Conclusions

In this study, a new peridynamic model was presented for higher-order plate theory. The formulation was derived by using Euler-Lagrange equation and Taylor’s expansion. The formulation was verified by considering two benchmark problems including simply supported and clamped plates subjected to transverse loading. Moreover, mixed (simply supported-clamped) boundary conditions are also considered to investigate the capability of the current formulation for mixed boundary conditions. Peridynamic results were compared with finite element analysis results and a very good agreement was obtained between the two approaches. Therefore, it can be concluded that the developed approach can be used as an alternative approach for problems in which higher-order plate theory is applicable.

Appendix

In this section, the derivation of the PD form of strain energy density function given in Eq. (11) is presented. To clarify the derivation, strain energy density expression is separated into four parts:

$$ W={W}_1+{W}_2+{W}_3+{W}_4 $$

(29)

where

$$ {W}_1=\frac{E}{4\left(1+\nu \right)}\frac{1}{h}\left[\frac{h^3}{12}\left(\frac{\partial {\theta}_I}{\partial {x}_J}\frac{\partial {\theta}_I}{\partial {x}_J}+\frac{\partial {\theta}_I}{\partial {x}_J}\frac{\partial {\theta}_J}{\partial {x}_I}+\frac{\partial {\theta}_I}{\partial {x}_I}\frac{\partial {\theta}_J}{\partial {x}_J}\right)+\frac{h^7}{448}\left(\frac{\partial {\theta}_I^{\ast }}{\partial {x}_J}\frac{\partial {\theta}_I^{\ast }}{\partial {x}_J}+\frac{\partial {\theta}_I^{\ast }}{\partial {x}_J}\frac{\partial {\theta}_J^{\ast }}{\partial {x}_I}+\frac{\partial {\theta}_I^{\ast }}{\partial {x}_I}\frac{\partial {\theta}_J^{\ast }}{\partial {x}_J}\right)+2\frac{h^5}{80}\left(\frac{\partial {\theta}_I}{\partial {x}_J}\frac{\partial {\theta}_I^{\ast }}{\partial {x}_J}+\frac{\partial {\theta}_I}{\partial {x}_J}\frac{\partial {\theta}_J^{\ast }}{\partial {x}_I}+\frac{\partial {\theta}_I^{\ast }}{\partial {x}_I}\frac{\partial {\theta}_J}{\partial {x}_J}\right)\right] $$

(30a)

$$ {W}_2=\frac{E\left(4\nu -1\right)}{4\left(1+\nu \right)\left(1-2\nu \right)}\frac{1}{h}\left(\frac{h^3}{12}\frac{\partial {\theta}_I}{\partial {x}_I}\frac{\partial {\theta}_J}{\partial {x}_J}+2\frac{h^5}{80}\frac{\partial {\theta}_I^{\ast }}{\partial {x}_I}\frac{\partial {\theta}_J}{\partial {x}_J}+\frac{h^7}{448}\frac{\partial {\theta}_I^{\ast }}{\partial {x}_I}\frac{\partial {\theta}_J^{\ast }}{\partial {x}_J}\right) $$

(30b)

$$ {W}_3=\frac{E}{4\left(1+\nu \right)}\frac{1}{h}\left[h{\left({\theta}_I+\frac{\partial w}{\partial {x}_I}\right)}^2+\frac{h^5}{80}{\left(3{\theta}_I^{\ast }+\frac{\partial {w}^{\ast }}{\partial {x}_I}\right)}^2+2\frac{h^3}{12}\left({\theta}_I+\frac{\partial w}{\partial {x}_I}\right)\left(3{\theta}_I^{\ast }+\frac{\partial {w}^{\ast }}{\partial {x}_I}\right)\right] $$

(30c)

$$ {W}_4=\frac{2E}{\left(1+\nu \right)\left(1-2\nu \right)}\frac{1}{h}\left(\frac{h^3}{12}{w}^{\ast}\left[\left(1-\nu \right){w}^{\ast }+\nu \frac{\partial {\theta}_I}{\partial {x}_I}\right]+\frac{h^5}{80}\nu {w}^{\ast}\frac{\partial {\theta}_I^{\ast }}{\partial {x}_I}\right) $$

(30d)

Transforming W₁ into PD form

As shown in Fig. 14 in the Appendix, the function θ can be expressed by using Taylor’s expansion up to 1st-order terms about point x as

$$ {\theta}_I\left(\boldsymbol{x}+\boldsymbol{\xi} \right)-{\theta}_I\left(\boldsymbol{x}\right)=\frac{\partial {\theta}_I\left(\boldsymbol{x}\right)}{\partial {x}_J}\xi {n}_J $$

(31a)

$$ {\theta}_K\left(\boldsymbol{x}+\boldsymbol{\xi} \right)-{\theta}_K\left(\boldsymbol{x}\right)=\frac{\partial {\theta}_K\left(\boldsymbol{x}\right)}{\partial {x}_L}\xi {n}_L $$

(31b)

where ξ = |ξ| and unit direction vector n is defined as

$$ \mathbf{n}=\left\{\begin{array}{c}{n}_1\\ {}{n}_2\end{array}\right\}=\left\{\begin{array}{c}\cos \varphi \\ {}\sin \varphi \end{array}\right\} $$

(32)

Fig. 14

Peridynamic interaction between two material points

Multiplying Eq. (A31a) by (A31b) gives

$$ \frac{\left[{\theta}_I\left(\boldsymbol{x}+\boldsymbol{\xi} \right)-{\theta}_I\left(\boldsymbol{x}\right)\right]\left[{\theta}_K\left(\boldsymbol{x}+\boldsymbol{\xi} \right)-{\theta}_K\left(\boldsymbol{x}\right)\right]}{\xi }=\frac{\partial {\theta}_I\left(\boldsymbol{x}\right)}{\partial {x}_J}\frac{\partial {\theta}_K\left(\boldsymbol{x}\right)}{\partial {x}_L}\xi {n}_J{n}_L $$

(33)

Multiplying both sides of Eq. (A33) yields

$$ \frac{\left[{\theta}_I\left(\boldsymbol{x}+\boldsymbol{\xi} \right)-{\theta}_I\left(\boldsymbol{x}\right)\right]\left[{\theta}_K\left(\boldsymbol{x}+\boldsymbol{\xi} \right)-{\theta}_K\left(\boldsymbol{x}\right)\right]}{\xi }{n}_R{n}_S=\frac{\partial {\theta}_I\left(\boldsymbol{x}\right)}{\partial {x}_J}\frac{\partial {\theta}_K\left(\boldsymbol{x}\right)}{\partial {x}_L}\xi {n}_J{n}_L{n}_R{n}_S $$

(34)

Considering x as a fixed point, integrating both sides of Eq. (A34) over a circular domain with centre of x and radius of δ result in:

$$ {\int}_0^{2\pi }{\int}_0^{\delta}\frac{\left[{\theta}_I\left(\boldsymbol{x}+\boldsymbol{\xi} \right)-{\theta}_I\left(\boldsymbol{x}\right)\right]\left[{\theta}_K\left(\boldsymbol{x}+\boldsymbol{\xi} \right)-{\theta}_K\left(\boldsymbol{x}\right)\right]}{\xi }{n}_R{n}_S\xi d\xi d\varphi =\frac{\partial {\theta}_I\left(\boldsymbol{x}\right)}{\partial {x}_J}\frac{\partial {\theta}_K\left(\boldsymbol{x}\right)}{\partial {x}_L}{\int}_0^{2\pi }{\int}_0^{\delta}\xi {n}_J{n}_L{n}_R{n}_S\xi d\xi d\varphi =\frac{\partial {\theta}_I\left(\boldsymbol{x}\right)}{\partial {x}_J}\frac{\partial {\theta}_K\left(\boldsymbol{x}\right)}{\partial {x}_L}\left({\delta}_{JL}{\delta}_{RS}+{\delta}_{JR}{\delta}_{LS}+{\delta}_{JS}{\delta}_{LR}\right)\frac{\pi {\delta}^3}{12}=\frac{\pi {\delta}^3}{12}\left(\frac{\partial {\theta}_I\left(\boldsymbol{x}\right)}{\partial {x}_J}\frac{\partial {\theta}_K\left(\boldsymbol{x}\right)}{\partial {x}_J}{\delta}_{RS}+\frac{\partial {\theta}_I\left(\boldsymbol{x}\right)}{\partial {x}_R}\frac{\partial {\theta}_K\left(\boldsymbol{x}\right)}{\partial {x}_S}+\frac{\partial {\theta}_I\left(\boldsymbol{x}\right)}{\partial {x}_S}\frac{\partial {\theta}_K\left(\boldsymbol{x}\right)}{\partial {x}_R}\right) $$

(35)

Multiply both sides of Eq. (A35) by δ_RIδ_SK yields:

$$ {\int}_0^{2\pi }{\int}_0^{\delta}\frac{\left[{\theta}_I\left(\boldsymbol{x}+\boldsymbol{\xi} \right)-{\theta}_I\left(\boldsymbol{x}\right)\right]\left[{\theta}_K\left(\boldsymbol{x}+\boldsymbol{\xi} \right)-{\theta}_K\left(\boldsymbol{x}\right)\right]}{\xi }{n}_R{n}_S{\delta}_{RI}{\delta}_{SK}\xi d\xi d\varphi =\frac{\pi {\delta}^3}{12}\left(\frac{\partial {\theta}_I\left(\boldsymbol{x}\right)}{\partial {x}_J}\frac{\partial {\theta}_K\left(\boldsymbol{x}\right)}{\partial {x}_J}{\delta}_{RS}+\frac{\partial {\theta}_I\left(\boldsymbol{x}\right)}{\partial {x}_R}\frac{\partial {\theta}_K\left(\boldsymbol{x}\right)}{\partial {x}_S}+\frac{\partial {\theta}_I\left(\boldsymbol{x}\right)}{\partial {x}_S}\frac{\partial {\theta}_K\left(\boldsymbol{x}\right)}{\partial {x}_R}\right){\delta}_{RI}{\delta}_{SK} $$

(36)

Rearranging the indices gives:

$$ \frac{\partial {\theta}_I\left(\boldsymbol{x}\right)}{\partial {x}_J}\frac{\partial {\theta}_I\left(\boldsymbol{x}\right)}{\partial {x}_J}+\frac{\partial {\theta}_I\left(\boldsymbol{x}\right)}{\partial {x}_I}\frac{\partial {\theta}_J\left(\boldsymbol{x}\right)}{\partial {x}_J}+\frac{\partial {\theta}_I\left(\boldsymbol{x}\right)}{\partial {x}_J}\frac{\partial {\theta}_J\left(\boldsymbol{x}\right)}{\partial {x}_I}=\frac{12}{\pi {\delta}^3}{\int}_0^{2\pi }{\int}_0^{\delta}\frac{\left[{\theta}_I\left(\boldsymbol{x}+\boldsymbol{\xi} \right)-{\theta}_I\left(\boldsymbol{x}\right)\right]\left[{\theta}_K\left(\boldsymbol{x}+\boldsymbol{\xi} \right)-{\theta}_K\left(\boldsymbol{x}\right)\right]}{\xi }{n}_I{n}_K\xi d\xi d\varphi $$

(37)

which can be written in discretized form as:

$$ \frac{\partial {\theta}_I^{(k)}}{\partial {x}_J}\frac{\partial {\theta}_I^{(k)}}{\partial {x}_J}+\frac{\partial {\theta}_I^{(k)}}{\partial {x}_I}\frac{\partial {\theta}_I^{(k)}}{\partial {x}_J}+\frac{\partial {\theta}_I^{(k)}}{\partial {x}_J}\frac{\partial {\theta}_I^{(k)}}{\partial {x}_I}=\frac{12}{\pi {\delta}^3h}{\sum}_i\frac{\left({\theta}_I^{\left({i}^k\right)}-{\theta}_I^{(k)}\right)\left({\theta}_J^{\left({i}^k\right)}-{\theta}_J^{(k)}\right)}{\xi_{\left({i}^k\right)(k)}}{n}_I^{\left({i}^k\right)(k)}{n}_J^{\left({i}^k\right)(k)}{V}_{\left({i}^k\right)} $$

(38a)

Following a similar approach, the following expressions can also be obtained:

$$ \frac{\partial {\theta}_I^{\ast (k)}}{\partial {x}_J}\frac{\partial {\theta}_I^{\ast (k)}}{\partial {x}_J}+\frac{\partial {\theta}_I^{\ast (k)}}{\partial {x}_I}\frac{\partial {\theta}_I^{\ast (k)}}{\partial {x}_J}+\frac{\partial {\theta}_I^{\ast (k)}}{\partial {x}_J}\frac{\partial {\theta}_I^{\ast (k)}}{\partial {x}_I}=\frac{12}{\pi {\delta}^3h}{\sum}_i\frac{\left({\theta}_I^{\ast \left({i}^k\right)}-{\theta}_I^{\ast (k)}\right)\left({\theta}_J^{\ast \left({i}^k\right)}-{\theta}_J^{\ast (k)}\right)}{\xi_{\left({i}^k\right)(k)}}{n}_I^{\left({i}^k\right)(k)}{n}_J^{\left({i}^k\right)(k)}{V}_{\left({i}^k\right)} $$

(38b)

$$ \frac{\partial {\theta}_I^{(k)}}{\partial {x}_J}\frac{\partial {\theta}_I^{\ast (k)}}{\partial {x}_J}+\frac{\partial {\theta}_I^{(k)}}{\partial {x}_I}\frac{\partial {\theta}_I^{\ast (k)}}{\partial {x}_J}+\frac{\partial {\theta}_I^{(k)}}{\partial {x}_J}\frac{\partial {\theta}_I^{\ast (k)}}{\partial {x}_I}=\frac{12}{\pi {\delta}^3h}{\sum}_i\frac{\left({\theta}_I^{\left({i}^k\right)}-{\theta}_I^{(k)}\right)\left({\theta}_J^{\ast \left({i}^k\right)}-{\theta}_J^{\ast (k)}\right)}{\xi_{\left({i}^k\right)(k)}}{n}_I^{\left({i}^k\right)(k)}{n}_J^{\left({i}^k\right)(k)}{V}_{\left({i}^k\right)} $$

(38c)

Substituting Eqs. (38) into (A30a) results in

$$ {W}_1^{(k)}=\frac{E}{4\left(1+\nu \right)}\frac{1}{h}\frac{12}{\pi {\delta}^3h}\left[\frac{h^3}{12}\left({\sum}_i\frac{\left({\theta}_I^{\left({i}^k\right)}-{\theta}_I^{(k)}\right)\left({\theta}_J^{\left({i}^k\right)}-{\theta}_J^{(k)}\right)}{\xi_{\left({i}^k\right)(k)}}{n}_I^{\left({i}^k\right)(k)}{n}_J^{\left({i}^k\right)(k)}{V}_{\left({i}^k\right)}\right)+\frac{h^7}{448}\left({\sum}_i\frac{\left({\theta}_I^{\ast \left({i}^k\right)}-{\theta}_I^{\ast (k)}\right)\left({\theta}_J^{\ast \left({i}^k\right)}-{\theta}_J^{\ast (k)}\right)}{\xi_{\left({i}^k\right)(k)}}{n}_I^{\left({i}^k\right)(k)}{n}_J^{\left({i}^k\right)(k)}{V}_{\left({i}^k\right)}\right)+2\frac{h^5}{80}\left({\sum}_i\frac{\left({\theta}_I^{\left({i}^k\right)}-{\theta}_I^{(k)}\right)\left({\theta}_J^{\ast \left({i}^k\right)}-{\theta}_J^{\ast (k)}\right)}{\xi_{\left({i}^k\right)(k)}}{n}_I^{\left({i}^k\right)(k)}{n}_J^{\left({i}^k\right)(k)}{V}_{\left({i}^k\right)}\right)\right] $$

(39)

Transform W₂ into PD form:

If we recall the expression given in Eq. (31a)

$$ {\theta}_I\left(\boldsymbol{x}+\boldsymbol{\xi} \right)-{\theta}_I\left(\boldsymbol{x}\right)=\frac{\partial {\theta}_I\left(\boldsymbol{x}\right)}{\partial {x}_J}\xi {n}_J. $$

(40)

and multiply Eq. (A40) by the direction vector n_K yields:

$$ \frac{\theta_I\left(\boldsymbol{x}+\boldsymbol{\xi} \right)-{\theta}_I\left(\boldsymbol{x}\right)}{\xi }{n}_K=\frac{\partial {\theta}_I\left(\boldsymbol{x}\right)}{\partial {x}_J}{n}_J{n}_K $$

(41)

Considering x as a fixed point, integrating both sides of Eq. (A41) over a circular domain with centre of x and radius of δ result in:

$$ {\int}_0^{2\pi }{\int}_0^{\delta}\frac{\theta_I\left(\boldsymbol{x}+\boldsymbol{\xi} \right)-{\theta}_I\left(\boldsymbol{x}\right)}{\xi }{n}_K\xi d\xi d\varphi =\frac{\partial {\theta}_I\left(\boldsymbol{x}\right)}{\partial {x}_J}{\int}_0^{2\pi }{\int}_0^{\delta }{n}_J{n}_K\xi d\xi d\varphi =\frac{\partial {\theta}_I\left(\boldsymbol{x}\right)}{\partial {x}_J}\frac{\pi {\delta}^2}{2}{\delta}_{JK}=\frac{\partial {\theta}_I\left(\boldsymbol{x}\right)}{\partial {x}_K}\frac{\pi {\delta}^2}{2} $$

(42)

Multiplying both sides of Eq. (A42) with δ_IK gives

$$ \frac{\partial {\theta}_I\left(\boldsymbol{x}\right)}{\partial {x}_I}=\frac{2}{\pi {\delta}^2}{\int}_0^{2\pi }{\int}_0^{\delta}\frac{\theta_I\left(\boldsymbol{x}+\boldsymbol{\xi} \right)-{\theta}_I\left(\boldsymbol{x}\right)}{\xi }{n}_I\xi d\xi d\varphi $$

(43a)

Rewriting Eq. (A43a) with another index, J gives:

$$ \frac{\partial {\theta}_J\left(\boldsymbol{x}\right)}{\partial {x}_J}=\frac{2}{\pi {\delta}^2}{\int}_0^{2\pi }{\int}_0^{\delta}\frac{\theta_J\left(\boldsymbol{x}+\boldsymbol{\xi} \right)-{\theta}_J\left(\boldsymbol{x}\right)}{\xi }{n}_J\xi d\xi d\varphi $$

(43b)

Multiplying Eq. (A43a) with (A43b) yields:

$$ \frac{\partial {\theta}_I\left(\boldsymbol{x}\right)}{\partial {x}_I}\frac{\partial {\theta}_J\left(\boldsymbol{x}\right)}{\partial {x}_J}={\left(\frac{2}{\pi {\delta}^2}\right)}^2{\int}_0^{2\pi }{\int}_0^{\delta}\frac{\theta_I\left(\boldsymbol{x}+\boldsymbol{\xi} \right)-{\theta}_I\left(\boldsymbol{x}\right)}{\xi }{n}_I\xi d\xi d\varphi {\int}_0^{2\pi }{\int}_0^{\delta}\frac{\theta_J\left(\boldsymbol{x}+\boldsymbol{\xi} \right)-{\theta}_J\left(\boldsymbol{x}\right)}{\xi }{n}_J\xi d\xi d\varphi $$

(44)

which can be written in discretized form as

$$ \frac{\partial {\theta}_I^{(k)}}{\partial {x}_I}\frac{\partial {\theta}_J^{(k)}}{\partial {x}_J}={\left(\frac{2}{\pi {\delta}^2}\right)}^2{\sum}_i\frac{\theta_I^{\left({i}^k\right)}-{\theta}_I^{(k)}}{\xi_{\left({i}^k\right)(k)}}{n}_I^{\left({i}^k\right)(k)}{V}_{\left({i}^k\right)}{\sum}_i\frac{\theta_J^{\left({i}^k\right)}-{\theta}_J^{(k)}}{\xi_{\left({i}^k\right)(k)}}{n}_J^{\left({i}^k\right)(k)}{V}_{\left({i}^k\right)} $$

(45a)

Following a similar approach, the following expressions can also be obtained:

$$ \frac{\partial {\theta}_I^{\ast (k)}}{\partial {x}_I}\frac{\partial {\theta}_J^{(k)}}{\partial {x}_J}={\left(\frac{2}{\pi {\delta}^2}\right)}^2{\sum}_i\frac{\theta_I^{\ast \left({i}^k\right)}-{\theta}_I^{\ast (k)}}{\xi_{\left({i}^k\right)(k)}}{n}_I^{\left({i}^k\right)(k)}{V}_{\left({i}^k\right)}{\sum}_i\frac{\theta_J^{\left({i}^k\right)}-{\theta}_J^{(k)}}{\xi_{\left({i}^k\right)(k)}}{n}_J^{\left({i}^k\right)(k)}{V}_{\left({i}^k\right)} $$

(45b)

$$ \frac{\partial {\theta}_I^{\ast (k)}}{\partial {x}_I}\frac{\partial {\theta}_J^{\ast (k)}}{\partial {x}_J}={\left(\frac{2}{\pi {\delta}^2}\right)}^2{\sum}_i\frac{\theta_I^{\ast \left({i}^k\right)}-{\theta}_I^{\ast (k)}}{\xi_{\left({i}^k\right)(k)}}{n}_I^{\left({i}^k\right)(k)}{V}_{\left({i}^k\right)}{\sum}_i\frac{\theta_J^{\ast \left({i}^k\right)}-{\theta}_J^{\ast (k)}}{\xi_{\left({i}^k\right)(k)}}{n}_J^{\left({i}^k\right)(k)}{V}_{\left({i}^k\right)} $$

(45c)

Substituting Eqs. (A44) into (A30b) results in

$$ {W}_2^{(k)}=\frac{E\left(4\nu -1\right)}{4\left(1+\nu \right)\left(1-2\nu \right)}\frac{1}{h}{\left(\frac{2}{\pi {\delta}^2}\right)}^2\left(\frac{h^3}{12}{\sum}_i\frac{\theta_I^{\left({i}^k\right)}-{\theta}_I^{(k)}}{\xi_{\left({i}^k\right)(k)}}{n}_I^{\left({i}^k\right)(k)}{V}_{\left({i}^k\right)}{\sum}_i\frac{\theta_J^{\left({i}^k\right)}-{\theta}_J^{(k)}}{\xi_{\left({i}^k\right)(k)}}{n}_J^{\left({i}^k\right)(k)}{V}_{\left({i}^k\right)}+2\frac{h^5}{80}{\sum}_i\frac{\theta_I^{\ast \left({i}^k\right)}-{\theta}_I^{\ast (k)}}{\xi_{\left({i}^k\right)(k)}}{n}_I^{\left({i}^k\right)(k)}{V}_{\left({i}^k\right)}{\sum}_i\frac{\theta_J^{\left({i}^k\right)}-{\theta}_J^{(k)}}{\xi_{\left({i}^k\right)(k)}}{n}_J^{\left({i}^k\right)(k)}{V}_{\left({i}^k\right)}+\frac{h^7}{448}{\sum}_i\frac{\theta_I^{\ast \left({i}^k\right)}-{\theta}_I^{\ast (k)}}{\xi_{\left({i}^k\right)(k)}}{n}_I^{\left({i}^k\right)(k)}{V}_{\left({i}^k\right)}{\sum}_i\frac{\theta_J^{\ast \left({i}^k\right)}-{\theta}_J^{\ast (k)}}{\xi_{\left({i}^k\right)(k)}}{n}_J^{\left({i}^k\right)(k)}{V}_{\left({i}^k\right)}\right) $$

(46)

Transform W₃ into PD form:

Similar to Eq. (A31a), the following relationship can be written as:

$$ \mathrm{w}\left(\boldsymbol{x}+\boldsymbol{\xi} \right)-\mathrm{w}\left(\boldsymbol{x}\right)=\frac{\mathrm{\partial w}\left(\boldsymbol{x}\right)}{\partial {x}_I}\xi {n}_I $$

(47a)

$$ \frac{\theta_I\left(\boldsymbol{x}+\boldsymbol{\xi} \right)+{\theta}_I\left(\boldsymbol{x}\right)}{2}\xi {n}_I={\theta}_I\left(\boldsymbol{x}\right)\xi {n}_I $$

(47b)

Combining Eq. (A47a) with (A47b) yields:

$$ \frac{\theta_I\left(\boldsymbol{x}+\boldsymbol{\xi} \right)+{\theta}_I\left(\boldsymbol{x}\right)}{2}\upxi {n}_I+\mathrm{w}\left(\boldsymbol{x}+\boldsymbol{\xi} \right)-\mathrm{w}\left(\boldsymbol{x}\right)=\frac{\mathrm{\partial w}\left(\boldsymbol{x}\right)}{\partial {x}_I}\xi {n}_I+{\theta}_I\left(\mathbf{x}\right)\upxi {n}_I $$

(48a)

Rewriting Eq. (A48a) with another index, J gives:

$$ \frac{\theta_J\left(\boldsymbol{x}+\boldsymbol{\xi} \right)+{\theta}_J\left(\boldsymbol{x}\right)}{2}\upxi {n}_J+\mathrm{w}\left(\boldsymbol{x}+\boldsymbol{\xi} \right)-\mathrm{w}\left(\boldsymbol{x}\right)=\frac{\mathrm{\partial w}\left(\boldsymbol{x}\right)}{\partial {x}_J}\xi {n}_J+{\theta}_J\left(\mathbf{x}\right)\upxi {n}_J $$

(48b)

Multiplying Eq. (A48a) with (A48b) and then dividing each term by ξ results in:

$$ \frac{\left[\frac{\theta_I\left(\boldsymbol{x}+\boldsymbol{\xi} \right)+{\theta}_I\left(\boldsymbol{x}\right)}{2}\upxi {n}_I+\mathrm{w}\left(\boldsymbol{x}+\boldsymbol{\xi} \right)-\mathrm{w}\left(\boldsymbol{x}\right)\right]\left[\frac{\theta_J\left(\boldsymbol{x}+\boldsymbol{\xi} \right)+{\theta}_J\left(\boldsymbol{x}\right)}{2}\upxi {n}_J+\mathrm{w}\left(\boldsymbol{x}+\boldsymbol{\xi} \right)-\mathrm{w}\left(\boldsymbol{x}\right)\right]}{\xi }=\left(\frac{\mathrm{\partial w}\left(\boldsymbol{x}\right)}{\partial {x}_I}+{\theta}_I\left(\mathbf{x}\right)\right)\left(\frac{\mathrm{\partial w}\left(\boldsymbol{x}\right)}{\partial {x}_J}+{\theta}_J\left(\mathbf{x}\right)\right)\xi {n}_I{n}_J $$

(49)

Considering x as a fixed point, integrating both sides of Eq. (A49) over a circular domain with centre of x and radius of δ yield:

$$ {\int}_0^{2\pi }{\int}_0^{\delta}\frac{\left[\frac{\theta_I\left(\boldsymbol{x}+\boldsymbol{\xi} \right)+{\theta}_I\left(\boldsymbol{x}\right)}{2}\upxi {n}_I+\mathrm{w}\left(\boldsymbol{x}+\boldsymbol{\xi} \right)-\mathrm{w}\left(\boldsymbol{x}\right)\right]\left[\frac{\theta_J\left(\boldsymbol{x}+\boldsymbol{\xi} \right)+{\theta}_J\left(\boldsymbol{x}\right)}{2}\upxi {n}_J+\mathrm{w}\left(\boldsymbol{x}+\boldsymbol{\xi} \right)-\mathrm{w}\left(\boldsymbol{x}\right)\right]}{\xi}\xi d\xi d\varphi =\left(\frac{\mathrm{\partial w}\left(\boldsymbol{x}\right)}{\partial {x}_I}+{\theta}_I\left(\mathbf{x}\right)\right)\left(\frac{\mathrm{\partial w}\left(\boldsymbol{x}\right)}{\partial {x}_J}+{\theta}_J\left(\mathbf{x}\right)\right){\int}_0^{2\pi }{\int}_0^{\delta}\xi {n}_I{n}_J d\xi d\varphi =\left(\frac{\mathrm{\partial w}\left(\boldsymbol{x}\right)}{\partial {x}_I}+{\theta}_I\left(\mathbf{x}\right)\right)\left(\frac{\mathrm{\partial w}\left(\boldsymbol{x}\right)}{\partial {x}_J}+{\theta}_J\left(\mathbf{x}\right)\right)\frac{\pi {\delta}^3}{3}{\delta}_{IJ}=\frac{\pi {\delta}^2}{3}\left(\frac{\mathrm{\partial w}\left(\boldsymbol{x}\right)}{\partial {x}_I}+{\theta}_I\left(\boldsymbol{x}\right)\right)\left(\frac{\mathrm{\partial w}\left(\boldsymbol{x}\right)}{\partial {x}_I}+{\theta}_I\left(\boldsymbol{x}\right)\right) $$

(50)

which gives:

$$ \left(\frac{\mathrm{\partial w}\left(\boldsymbol{x}\right)}{\partial {x}_I}+{\theta}_I\left(\boldsymbol{x}\right)\right)\left(\frac{\mathrm{\partial w}\left(\boldsymbol{x}\right)}{\partial {x}_I}+{\theta}_I\left(\boldsymbol{x}\right)\right)=\frac{3}{\pi {\delta}^2}{\int}_0^{2\pi }{\int}_0^{\delta}\frac{{\left[\frac{\theta_I\left(\boldsymbol{x}+\boldsymbol{\xi} \right)+{\theta}_I\left(\boldsymbol{x}\right)}{2}\xi {n}_I+w\left(\boldsymbol{x}+\boldsymbol{\xi} \right)-w\left(\boldsymbol{x}\right)\right]}^{\mathbf{2}}}{\xi}\xi d\xi d\varphi $$

(A51)

Eq. (A51) can be written in a discretized form as

$$ \left(\frac{\partial {\mathrm{w}}_{(k)}}{\partial {x}_I}+{\theta}_I^{(k)}\right)\left(\frac{\partial {\mathrm{w}}_{(k)}}{\partial {x}_I}+{\theta}_I^{(k)}\right)=\frac{3}{\pi {\delta}^3h}{\sum}_i\frac{{\left({w}_{\left({i}^k\right)}-{w}_{(k)}+\frac{\theta_I^{(k)}+{\theta}_I^{(j)}}{2}{\xi}_{\left({i}^k\right)(k)}{n}_I^{\left({i}^k\right)(k)}\right)}^2}{\xi_{\left({i}^k\right)(k)}}{V}_{\left({i}^k\right)} $$

(52a)

Following a similar approach, the following expressions can also be obtained

$$ \left(3{\theta}_I^{\ast (k)}+\frac{\partial {w}_{(k)}^{\ast }}{\partial {x}_I}\right)\left(3{\theta}_I^{\ast (k)}+\frac{\partial {w}_{(k)}^{\ast }}{\partial {x}_I}\right)=\frac{3}{\pi {\delta}^3h}{\sum}_{i^k}\frac{{\left({w}_{\left({i}^k\right)}^{\ast }-{w}_{(k)}^{\ast }+3\frac{\theta_I^{\ast (k)}+{\theta}_I^{\ast (j)}}{2}{\xi}_{\left({i}^k\right)(k)}{n}_I^{\left({i}^k\right)(k)}\right)}^2}{\xi_{\left({i}^k\right)(k)}}{V}_{\left({i}^k\right)} $$

(52b)

and

$$ \left(\frac{\partial {\mathrm{w}}_{(k)}}{\partial {x}_I}+{\theta}_I^{(k)}\right)\left(3{\theta}_I^{\ast (k)}+\frac{\partial {w}_{(k)}^{\ast }}{\partial {x}_I}\right)=\frac{3}{\pi {\delta}^3h}{\sum}_{i^k}\frac{\left({w}_{\left({i}^k\right)}-{w}_{(k)}+\frac{\theta_I^{(k)}+{\theta}_I^{(j)}}{2}{\xi}_{\left({i}^k\right)(k)}{n}_I^{\left({i}^k\right)(k)}\right)\left({w}_{\left({i}^k\right)}^{\ast }-{w}_{(k)}^{\ast }+3\frac{\theta_J^{\ast (k)}+{\theta}_J^{\ast (j)}}{2}{\xi}_{\left({i}^k\right)(k)}{n}_J^{\left({i}^k\right)(k)}\right)}{\xi_{\left({i}^k\right)(k)}}{V}_{\left({i}^k\right)} $$

(52c)

Substituting Eqs. (24) into (30c) results in:

$$ {W}_3^{(k)}=\frac{G}{2}\frac{3}{\pi {\delta}^3{h}^2}\left[h{\sum}_i\frac{{\left({w}_{\left({i}^k\right)}-{w}_{(k)}+\frac{\theta_I^{(k)}+{\theta}_I^{(j)}}{2}{\xi}_{\left({i}^k\right)(k)}{n}_I^{\left({i}^k\right)(k)}\right)}^2}{\xi_{\left({i}^k\right)(k)}}{V}_{\left({i}^k\right)}+\frac{h^5}{80}{\sum}_{i^k}\frac{{\left({w}_{\left({i}^k\right)}^{\ast }-{w}_{(k)}^{\ast }+3\frac{\theta_J^{\ast (k)}+{\theta}_J^{\ast (j)}}{2}{\xi}_{\left({i}^k\right)(k)}{n}_J^{\left({i}^k\right)(k)}\right)}^2}{\xi_{\left({i}^k\right)(k)}}{V}_{\left({i}^k\right)}+2\frac{h^3}{12}{\sum}_{i^k}\frac{\left({w}_{\left({i}^k\right)}-{w}_{(k)}+\frac{\theta_I^{(k)}+{\theta}_I^{(j)}}{2}{\xi}_{\left({i}^k\right)(k)}{n}_I^{\left({i}^k\right)(k)}\right)\left({w}_{\left({i}^k\right)}^{\ast }-{w}_{(k)}^{\ast }+3\frac{\theta_J^{\ast (k)}+{\theta}_J^{\ast (j)}}{2}{\xi}_{\left({i}^k\right)(k)}{n}_J^{\left({i}^k\right)(k)}\right)}{\xi_{\left({i}^k\right)(k)}}{V}_{\left({i}^k\right)}\right] $$

(53)

Transform W ₄ into PD form:

Multiplying both sides of Eq. (3a) by ν yields:

$$ \nu \left[{\theta}_I\left(\boldsymbol{x}+\boldsymbol{\xi} \right)-{\theta}_I\left(\boldsymbol{x}\right)\right]=\nu \frac{\partial {\theta}_I\left(\boldsymbol{x}\right)}{\partial {x}_J}\xi {n}_J $$

(54a)

w^∗(x) can be Taylor expanded as

$$ \frac{w^{\ast}\left(\boldsymbol{x}+\boldsymbol{\xi} \right)+{w}^{\ast}\left(\boldsymbol{x}\right)}{2}{n}_K={w}^{\ast}\left(\boldsymbol{x}\right){n}_K $$

(54b)

Multiplying Eq. (A54a) by Eq. (A54b) gives

$$ \nu \frac{w^{\ast}\left(\boldsymbol{x}+\boldsymbol{\xi} \right)+{w}^{\ast}\left(\boldsymbol{x}\right)}{2}\left[{\theta}_I\left(\boldsymbol{x}+\boldsymbol{\xi} \right)-{\theta}_I\left(\boldsymbol{x}\right)\right]{n}_K=\nu {w}^{\ast}\left(\boldsymbol{x}\right)\frac{\partial {\theta}_I\left(\boldsymbol{x}\right)}{\partial {x}_J}\xi {n}_J{n}_K $$

(55)

Considering x as a fixed point, integrating both sides of Eq. (A55) over a circular domain with centre of x and radius of δ result in:

$$ {\int}_0^{2\pi }{\int}_0^{\delta}\nu \frac{w^{\ast}\left(\boldsymbol{x}+\boldsymbol{\xi} \right)+{w}^{\ast}\left(\boldsymbol{x}\right)}{2}\left[{\theta}_I\left(\boldsymbol{x}+\boldsymbol{\xi} \right)-{\theta}_I\left(\boldsymbol{x}\right)\right]{n}_K\xi d\xi d\varphi =\nu {w}^{\ast}\left(\boldsymbol{x}\right)\frac{\partial {\theta}_I\left(\boldsymbol{x}\right)}{\partial {x}_J}{\int}_0^{2\pi }{\int}_0^{\delta}\xi {n}_J{n}_K\xi d\xi d\varphi =\nu {w}^{\ast}\left(\boldsymbol{x}\right)\frac{\partial {\theta}_I\left(\boldsymbol{x}\right)}{\partial {x}_J}\frac{\pi {\delta}^3}{3}{\delta}_{JK}=\nu {w}^{\ast}\left(\boldsymbol{x}\right)\frac{\partial {\theta}_I\left(\boldsymbol{x}\right)}{\partial {x}_K}\frac{\pi {\delta}^3}{3} $$

(56)

Multiplying both sides of Eq. (A56) by δ_IK yield:

$$ \nu {w}^{\ast}\left(\boldsymbol{x}\right)\frac{\partial {\theta}_I\left(\boldsymbol{x}\right)}{\partial {x}_I}=\frac{3}{\pi {\delta}^3}{\int}_0^{2\pi }{\int}_0^{\delta}\nu \frac{w^{\ast}\left(\boldsymbol{x}+\boldsymbol{\xi} \right)+{w}^{\ast}\left(\boldsymbol{x}\right)}{2}\left[{\theta}_I\left(\boldsymbol{x}+\boldsymbol{\xi} \right)-{\theta}_I\left(\boldsymbol{x}\right)\right]{n}_I\xi d\xi d\varphi $$

(57)

Adding both sides of Eq. (A57) with (1 − ν)(w^∗(x))² and performing some algebraic manipulation gives:

$$ {w}^{\ast}\left(\boldsymbol{x}\right)\left(\left(1-\nu \right){w}^{\ast}\left(\boldsymbol{x}\right)+\nu \frac{\partial {\theta}_I\left(\boldsymbol{x}\right)}{\partial {x}_I}\right)=\frac{3}{\pi {\delta}^3}{\int}_0^{2\pi }{\int}_0^{\delta}\nu \frac{w^{\ast}\left(\boldsymbol{x}+\boldsymbol{\xi} \right)+{w}^{\ast}\left(\boldsymbol{x}\right)}{2}\left[{\theta}_I\left(\boldsymbol{x}+\boldsymbol{\xi} \right)-{\theta}_I\left(\boldsymbol{x}\right)\right]{n}_I\xi d\xi d\varphi +\left(1-\nu \right){\left(\frac{w^{\ast}\left(\boldsymbol{x}+\boldsymbol{\xi} \right)+{w}^{\ast}\left(\boldsymbol{x}\right)}{2}\right)}^2=\frac{3}{\pi {\delta}^3}{\int}_0^{2\pi }{\int}_0^{\delta}\nu \frac{w^{\ast}\left(\boldsymbol{x}+\boldsymbol{\xi} \right)+{w}^{\ast}\left(\boldsymbol{x}\right)}{2}\left[{\theta}_I\left(\boldsymbol{x}+\boldsymbol{\xi} \right)-{\theta}_I\left(\boldsymbol{x}\right)\right]{n}_I\xi d\xi d\varphi +\left(1-\nu \right){\left(\frac{w^{\ast}\left(\boldsymbol{x}+\boldsymbol{\xi} \right)+{w}^{\ast}\left(\boldsymbol{x}\right)}{2}\right)}^2\frac{\int_0^{2\pi }{\int}_0^{\delta}\frac{\xi }{2}\xi d\xi d\varphi}{\int_0^{2\pi }{\int}_0^{\delta}\frac{\xi }{2}\xi d\xi d\varphi}=\frac{3}{\pi {\delta}^3}{\int}_0^{2\pi }{\int}_0^{\delta}\nu \frac{w^{\ast}\left(\boldsymbol{x}+\boldsymbol{\xi} \right)+{w}^{\ast}\left(\boldsymbol{x}\right)}{2}\left[{\theta}_I\left(\boldsymbol{x}+\boldsymbol{\xi} \right)-{\theta}_I\left(\boldsymbol{x}\right)\right]{n}_I\xi d\xi d\varphi +\frac{3}{\pi {\delta}^3}{\int}_0^{2\pi }{\int}_0^{\delta}\frac{1-\nu }{2}{\left[\frac{w^{\ast}\left(\boldsymbol{x}+\boldsymbol{\xi} \right)+{w}^{\ast}\left(\boldsymbol{x}\right)}{2}\right]}^2\xi \xi d\xi d\varphi =\frac{3}{\pi {\delta}^3}{\int}_0^{2\pi }{\int}_0^{\delta }{w}^{\ast}\left(\boldsymbol{x}\right)\left(\nu \left[{\theta}_I\left(\boldsymbol{x}+\boldsymbol{\xi} \right)-{\theta}_I\left(\boldsymbol{x}\right)\right]{n}_I+\frac{1-\nu }{2}\frac{w^{\ast}\left(\boldsymbol{x}+\boldsymbol{\xi} \right)+{w}^{\ast}\left(\boldsymbol{x}\right)}{2}\xi \right)\xi d\xi d\varphi $$

(58)

Eq. (A58) can be written in discretized form as

$$ {w}_{(k)}^{\ast}\left(\left(1-\nu \right){w}_{(k)}^{\ast }+\nu \frac{\partial {\uptheta}_I^{(k)}}{\partial {x}_I}\right)=\frac{3}{\pi {\delta}^3h}{\sum}_{i^k}\frac{w_{(k)}^{\ast }+{w}_{\left({i}^k\right)}^{\ast }}{2}\left[\nu \left({\uptheta}_I^{\left({i}^k\right)}-{\uptheta}_I^{(k)}\right){n}_I^{\left({i}^k\right)(k)}+\frac{1-\nu }{2}\frac{w_{(k)}^{\ast }+{w}_{\left({i}^k\right)}^{\ast }}{2}{\xi}_{\left({i}^k\right)(k)}\right]{V}_{\left({i}^k\right)} $$

(59a)

Following a similar approach, the following expression can also be obtained:

$$ {w}_{(k)}^{\ast}\frac{\partial {\theta}_I^{\ast (k)}}{\partial {x}_I}=\frac{3}{\pi {\delta}^3h}{\sum}_{i^k}\frac{w_{(k)}^{\ast }+{w}_{\left({i}^k\right)}^{\ast }}{2}\left({\uptheta}_I^{\ast \left({i}^k\right)}-{\uptheta}_I^{\ast (k)}\right){n}_I^{\left({i}^k\right)(k)}{V}_{\left({i}^k\right)} $$

(59b)

Inserting Eqs. (A59) and into (A30d) yields:

$$ {W}_4^{(k)}=\frac{2E}{\left(1+\nu \right)\left(1-2\nu \right)}\frac{3}{\pi {\delta}^3h}\frac{1}{h}\left(\frac{h^3}{12}{\sum}_{i^k}\frac{w_{(k)}^{\ast }+{w}_{\left({i}^k\right)}^{\ast }}{2}\left[\nu \left({\uptheta}_I^{\left({i}^k\right)}-{\uptheta}_I^{(k)}\right){n}_I^{\left({i}^k\right)(k)}+\frac{1-\nu }{2}\frac{w_{(k)}^{\ast }+{w}_{\left({i}^k\right)}^{\ast }}{2}{\xi}_{\left({i}^k\right)(k)}\right]{V}_{\left({i}^k\right)}+\frac{h^5}{80}\nu {\sum}_{i^k}\frac{w_{(k)}^{\ast }+{w}_{\left({i}^k\right)}^{\ast }}{2}\left({\uptheta}_I^{\ast \left({i}^k\right)}-{\uptheta}_I^{\ast (k)}\right){n}_I^{\left({i}^k\right)(k)}{V}_{\left({i}^k\right)}\right) $$

(60)

Finally, combining Eqs. (A39), (A46), (A53) and (A60) gives the strain energy density of material point k in PD form as:

$$ {W}_{(k)}={W}_1^{(k)}+{W}_2^{(k)}+{W}_3^{(k)}+{W}_4^{(k)}=\frac{G}{2}\frac{12}{\pi {\delta}^3{h}^2}\left[\frac{h^3}{12}{\sum}_i\frac{{\left[\left({\theta}_I^{\left({i}^k\right)}-{\theta}_I^{(k)}\right){n}_I^{\left({i}^k\right)(k)}\right]}^2}{\xi_{\left({i}^k\right)(k)}}{V}_{\left({i}^k\right)}+\frac{h^7}{448}{\sum}_i\frac{{\left[\left({\theta}_I^{\ast \left({i}^k\right)}-{\theta}_I^{\ast (k)}\right){n}_I^{\left({i}^k\right)(k)}\right]}^2}{\xi_{\left({i}^k\right)(k)}}{V}_{\left({i}^k\right)}+2\frac{h^5}{80}{\sum}_i\frac{\left({\theta}_I^{\left({i}^k\right)}-{\theta}_I^{(k)}\right)\left({\theta}_J^{\ast \left({i}^k\right)}-{\theta}_J^{\ast (k)}\right)}{\xi_{\left({i}^k\right)(k)}}{n}_I^{\left({i}^k\right)(k)}{n}_J^{\left({i}^k\right)(k)}{V}_{\left({i}^k\right)}\right]+\frac{G\left(4\nu -1\right)}{2\left(1-2\nu \right)}\frac{1}{h}{\left(\frac{2}{\pi {\delta}^2h}\right)}^2\left(\begin{array}{c}\frac{h^3}{12}{\left({\sum}_i\frac{\theta_I^{\left({i}^k\right)}-{\theta}_I^{(k)}}{\xi_{\left({i}^k\right)(k)}}{n}_I^{\left({i}^k\right)(k)}{V}_{\left({i}^k\right)}\right)}^2\\ {}+2\frac{h^5}{80}{\sum}_i\frac{\theta_I^{\ast \left({i}^k\right)}-{\theta}_I^{\ast (k)}}{\xi_{\left({i}^k\right)(k)}}{n}_I^{\left({i}^k\right)(k)}{V}_{\left({i}^k\right)}{\sum}_i\frac{\theta_J^{\left({i}^k\right)}-{\theta}_J^{(k)}}{\xi_{\left({i}^k\right)(k)}}{n}_J^{\left({i}^k\right)(k)}{V}_{\left({i}^k\right)}\\ {}+\frac{h^7}{448}{\left({\sum}_i\frac{\theta_I^{\ast \left({i}^k\right)}-{\theta}_I^{\ast (k)}}{\xi_{\left({i}^k\right)(k)}}{n}_I^{\left({i}^k\right)(k)}{V}_{\left({i}^k\right)}\right)}^2\end{array}\right)+\frac{G}{2}\frac{3}{\pi {\delta}^3{h}^2}\left[h{\sum}_i\frac{{\left({w}_{\left({i}^k\right)}-{w}_{(k)}+\frac{\theta_I^{(k)}+{\theta}_I^{\left({i}^k\right)}}{2}{\xi}_{\left({i}^k\right)(k)}{n}_I^{\left({i}^k\right)(k)}\right)}^2}{\xi_{\left({i}^k\right)(k)}}{V}_{\left({i}^k\right)}+\frac{h^5}{80}{\sum}_{i^k}\frac{{\left({w}_{\left({i}^k\right)}^{\ast }-{w}_{(k)}^{\ast }+3\frac{\theta_I^{\ast (k)}+{\theta}_I^{\ast \left({i}^k\right)}}{2}{\xi}_{\left({i}^k\right)(k)}{n}_I^{\left({i}^k\right)(k)}\right)}^2}{\xi_{\left({i}^k\right)(k)}}{V}_{\left({i}^k\right)}+2\frac{h^3}{12}{\sum}_{i^k}\frac{\left({w}_{\left({i}^k\right)}-{w}_{(k)}+\frac{\theta_I^{(k)}+{\theta}_I^{\left({i}^k\right)}}{2}{\xi}_{\left({i}^k\right)(k)}{n}_I^{\left({i}^k\right)(k)}\right)\left({w}_{\left({i}^k\right)}^{\ast }-{w}_{(k)}^{\ast }+3\frac{\theta_J^{\ast (k)}+{\theta}_J^{\ast \left({i}^k\right)}}{2}{\xi}_{\left({i}^k\right)(k)}{n}_J^{\left({i}^k\right)(k)}\right)}{\xi_{\left({i}^k\right)(k)}}{V}_{\left({i}^k\right)}\right]+\frac{4G}{1-2\nu}\frac{3}{\pi {\delta}^3{h}^2}\left(\frac{h^3}{12}{\sum}_{i^k}\frac{w_{(k)}^{\ast }+{w}_{\left({i}^k\right)}^{\ast }}{2}\left[\nu \left({\uptheta}_I^{\left({i}^k\right)}-{\uptheta}_I^{(k)}\right){n}_I^{\left({i}^k\right)(k)}+\frac{1-\nu }{2}\frac{w_{(k)}^{\ast }+{w}_{\left({i}^k\right)}^{\ast }}{2}{\xi}_{\left({i}^k\right)(k)}\right]{V}_{\left({i}^k\right)}+\frac{h^5}{80}\nu {\sum}_{i^k}\frac{w_{(k)}^{\ast }+{w}_{\left({i}^k\right)}^{\ast }}{2}\left({\uptheta}_I^{\ast \left({i}^k\right)}-{\uptheta}_I^{\ast (k)}\right){n}_I^{\left({i}^k\right)(k)}{V}_{\left({i}^k\right)}\right) $$

(61)