Utility of classical insurance risk models for measuring the risks of cyber incidents

Abstract

We demonstrate that the classical insurance risk models yield significant advantages in the context of cyber risk analysis. This model exhibits commendable attributes in terms of both computational efficiency and predictive capabilities. Utilizing several compound point risk models, we derive the conditional Value-at-Risk and Tail Value-at-Risk predictions for the cumulative breach size within specified time intervals. To verify the reliability of our method, we conduct backtesting exercises, comparing our predictions with actual breach sizes.

1 Introduction

In recent decades, the escalation of cyber incidents has paralleled the rapid advancement of Information Technology. Consequently, certain non-life insurance companies have introduced cyber-risk insurance, underscoring the importance of accurately assessing the risks associated with cyber incidents. Cyber risk analysis is a globally prominent and dynamically evolving field, with numerous researchers contributing to its discourse.

Some recent and notable studies include the works of Farkas et al. (2021), Woods and Böhme (2021), Eling et al. (2022), Peters et al. (2023), and many more as referenced in these papers provide valuable insights and references for further exploration of the topic. Research focusing on the mathematical and technical aspects of cyber risk quantification and predictive distribution has been conducted relatively long. For example, Maillart and Sornette (2010) claim that the breach size distribution of cyber incidents seems heavy-tailed. Peng et al. (2016) discussed predicting cyber attack rates using marked point processes. Xu et al. (2018) employed ACD (Autoregressive Conditional Duration) and ARMA-GARCH models to characterize the frequency and magnitude of cyber incidents, respectively. Sun et al. (2021) categorized cyber incident data into business sectors and leveraged copulas to forecast cyber risks at the organizational level. These papers delve into complex modeling, statistical methods, and risk assessment techniques to better understand cyber risk. In recent years, increasing tools such as machine learning and AI has attracted further attention to computational demands. For example, Zhan et al. (2015) harnessed machine learning techniques for forecasting incident frequency, integrating extremal theory and time-series analysis to enhance predictive accuracy.

On the other hand, these approaches may incur substantial computational costs, and the opacity of these AI models can introduce challenges in their interpretability. One of these challenges is the “black box” nature of many machine learning algorithms, making it difficult to interpret and understand the inner workings of these models. Furthermore, in the field of cyber risk analysis, there is a growing interest in combining machine learning methods with statistical (theoretical) methods. These hybrid methods are often referred to as “gray methods.” The need to strike a balance between methods’ transparency and effectiveness is an ongoing concern in this area of research.

In this paper, we dare to shed light on the classical model again to recognize the usefulness of a simple model. The model we employed adheres to classical actuarial practices. It offers simplicity, ease of comprehension, and computational efficiency, which are advantageous in practical applications. It is also powerful enough to predict risk quantification in the future. We shall demonstrate the efficacy of classically employed risk models, particularly those involving composite point processes, in achieving substantial risk reduction without incurring substantial computational expenses. Even when Monte Carlo simulations are necessary, the model’s straightforward nature and explicitly computable structure make it a valuable tool for efficiently assessing and managing cyber risks. This aligns with the actuarial principle of using well-understood and computationally manageable risk analysis and management models.

In our cyber risk analysis, we will adopt a quite simple compound risk model, a classic paradigm in insurance risk assessment: Let N be a random variable representing the frequency of cyber incidents occurring within a defined period, and $U_{i}$ be the breach size of the ith incident involving information leakage, with the common distribution $F_{U}$. Then the total amount of breaches, say S, is given by

$$\begin{aligned} S=\sum _{i=1}^{N}U_{i};\qquad U_{i}\overset{i.i.d.}{\sim }F_{U}. \end{aligned}$$

(1.1)

While it may be considered a straightforward model, it boasts a reasonable degree of expressiveness and is supported by various distribution approximations, making it possible for easy statistical inference. As in Awiszus et al. (2023) and Dacorogna and Kratz (2023), the classification of cyber risks is complex, and such a classical frequency-severity approach may have limitations. However, we usually employ this model within a single period but adapt it to encompass multi-period risks, which is the novelty of our paper, and still propose statistical inference for point processes; see Sect. 3. We revisit this classic risk model, highlighting its potential and demonstrating that it can effectively predict cyber risks with ingenuity even within its classical framework.

Nonetheless, constructing a more detailed model needs an elaborate examination of actual data. Thus, before introducing a specific model, we shall look at the dataset employed in this paper. We use an open dataset given by Privacy Rights Clearinghouse (2023). It includes information about cyber incidents in the United States, with a public date, breach size, type of breach, and business field, among others. To get the model insight, let us review the data. Figure 1 presents a distribution of breach sizes for each incident recorded between 2005 and 2020, exhibiting a pronounced long (heavy) right tail. In this paper, as in Maillart and Sornette (2010), we assume that the tail function $\overline{F}_U(x):=1-F_U(x)$ conforms to the concept of being ‘regularly varying’ with the index $-\kappa$, where $\kappa \ge 0$ is a key parameter:

$$\begin{aligned} \lim _{x\rightarrow \infty }\dfrac{\overline{F}_U(tx)}{\overline{F}_U(x)}=t^{-\kappa }\quad \hbox { for all}\ t>0, \end{aligned}$$

which is denoted as

$$\begin{aligned} \overline{F}_U \in {\mathscr {R}}_{-\kappa }. \end{aligned}$$

Furthermore, we should note that this breach data encompasses numerous instances of zero values (i.e., 0-inflated), signifying the occurrence of cyberattacks without resulting in any information leakage. Since our primary interest lies in evaluating the actual damage risk stemming from cyberattacks, our focus is on assessing tail risk, involving the calculation of ’Value-at-Risk’ (VaR) and ’Tail Value-at-Risk’ (TVaR), both of which are commonly established tail risk metrics. Given that these metrics are reliant on the tail properties of the distribution, we employ the ’Peaks-Over-Threshold’ method from extreme value theory and model the tail distribution using the ’generalized Pareto distribution (GPD),’ as outlined in Theorem A.1. This approach serves as the standard procedure for dealing with data characterized by heavy tails; see, e.g., Embrechts et al. (2003) or Resnick (2008), among others.

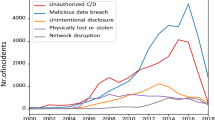
Figure 2 illustrates the time series of frequencies spanning the years 2005–2020, suggesting that the frequency of cyber incidents should be addressed through the modeling of a stochastic (point) process, as opposed to being represented by a single random variable N as previously discussed. We assert that modeling this dynamic time series of frequencies is pivotal to our analysis. In Sect. 3, we will introduce and elaborate upon several stochastic processes to address this modeling challenge.

Based on the observations presented in Fig. 3, it is evident that breach sizes have exhibited a significant increase since 2016. While the precise cause of this trend remains uncertain, it is likely influenced by a legislative amendment in 2015, which mandated the reporting of cyber attack data in the United States. Consequently, some of the leakage data recorded before 2016 may have been consolidated and reported in 2016, thus affecting the accuracy and continuity of the breach size time-series data. Furthermore, it’s important to note that the data available for 2005 and beyond 2019 is notably limited, as numerous breaches during these periods have yet to be formally recorded. As a result, we have chosen to focus our data analysis on the period from 2006 to 2018.

Considering these factors, we have divided the data into two distinct cases: Case 1, our primary dataset, excludes data recorded after 2016 due to the observed shift in frequency tendencies, as previously discussed. Case 2 encompasses all available data and serves as a reference, as summarized in Table 1.

Table 1 Usage of data

Considering this dataset’s distinctive attributes, we introduce specific models in the subsequent section. The outcomes of our data analysis employing these dedicated models are presented in Sect. 4, culminating with the paper’s conclusions in Sect. 5.

Fig. 1

Breach size of single incident

Fig. 2

Frequency (monthly)

Fig. 3

Breach size (monthly)

2 Multi-period compound risk models

As described in Sect. 1, we expand upon the single-period model (1.1) to formulate a multi-period framework. In this multi-period analysis, we partition the observation period into distinct segments, presupposing that the cumulative breach count within each period has a potentially different compound risk model. On the other hand, when examining the breach size distribution, as shown in Fig. 1, we presume a common heavy-tailed distribution spanning all the observation periods:

• Let $N_{k}$ be a random variable describing the frequency of breaches in kth period, satisfying that there exists some ${\epsilon }>0$ such that

  $$\begin{aligned} \sum _{r=0}^{\infty }(1+{\epsilon })^r {{\mathbb {P}}}(N_k=r)<\infty , \end{aligned}$$

  which corresponds to the condition (A.1) in Theorem A.4.

• Let $U^{(k)}:=\{U_{1}^{(k)}, U_{2}^{(k)},..., U_{N_{k}}^{(k)}\}$ be the sets of breach sizes of each incident occurring in kth period with $U_{i}^{(k)}\overset{i.i.d}{\sim }F_{U}$, and assume that there exists a constant $\kappa >1$ such that

  $$\begin{aligned} \overline{F}_U \in {\mathscr {R}}_{-\kappa }. \end{aligned}$$

  (2.1)

• For $t\in {\mathbb {N}}$, let ${\mathscr {F}}_{0}$ and ${\mathscr {F}}_{t}$ be a $\sigma$-field such that ${\mathscr {F}}_{0}:=\{\emptyset ,\Omega \}$ and, by induction,

  $$\begin{aligned} {\mathscr {F}}_{t}:={\mathscr {F}}_{t-1}\vee \sigma (N_{t};U^{(t)}),\quad t=1,2,\dots . \end{aligned}$$

Then, the total amount of breaches in the kth period is given by

$$\begin{aligned} S_k = \sum _{i=1}^{N_k} U_i^{(k)}, \quad k = 1,2,\dots , \end{aligned}$$

and we are interested in the following conditional (Tail-) Value-at-Risk:

$$\begin{aligned} {\left\{ \begin{array}{ll} & VaR_{\alpha }^{(t)}(S_{k}):=\inf \{x\ge 0\ |\ {{\mathbb {P}}}(S_{k}\le x|{\mathscr {F}}_{t})\ge \alpha \}\\ & TVaR_{\alpha }^{(t)}(S_{k}):=\dfrac{1}{1-\alpha }\displaystyle \int _{\alpha }^{1}VaR_{u}^{(t)}(S_{k})\,du \end{array}\right. },\quad k>t. \end{aligned}$$

(2.2)

To approximate these risk measures in heavy-tailed situations, the following result by, e.g., Biagini and Ulmer (2009), Theorem 2.5 is useful. More detailed asymptotic estimates are given in Theorem A.4 in Appendix. See also Böcker and Klüppelberg (2005), Peters et al. (2013) and references therein.

Theorem 2.1

(Biagini and Ulmer 2009) Suppose that the index in (2.1) satisfies $\kappa >1$. Then, as $\alpha \rightarrow 1$, it holds that

$$\begin{aligned} VaR^{(t)}_{\alpha }(S_k)&\sim VaR_{\beta ^{(t)}_k}(U); \\ TVaR^{(t)}_{\alpha }(S_k)&\sim \frac{\kappa }{\kappa -1}VaR_{\beta ^{(t)}_k}(U) \end{aligned}$$

where

$$\begin{aligned} \beta ^{(t)}_k:=1-\frac{(1-\alpha )}{{\mathbb {E}}[N_k|{\mathscr {F}}_t]}. \end{aligned}$$

(2.3)

Let us explore an further approximation for $VaR_{\beta ^{(t)}_k}(U)$, which facilitates the explicit computation of $VaR^{(t)}_{\alpha }(S_k)$ and $TVaR^{(t)}_{\alpha }(S_k)$. Given that $\beta ^{(t)}_k \rightarrow 1\ a.s.$ as $\alpha \rightarrow 1$ for any values of k and t, we can approximate$VaR_{\beta ^{(t)}_k}(U)$ as $\beta ^{(t)}_k\rightarrow 1$ through the conventional arguments inherent to extreme value theory, as outlined below: it follows for any $u\in {\mathbb {R}}$ that

$$\begin{aligned} F_{U}(x)&= \overline{F}_{U}(u)F_{U}(x-u|u)+F_{U}(u), \end{aligned}$$

where $F_{U}(x-u|u):= [F_{U}(x)-F_{U}(u)]/\overline{F}_{U}(u)$. When $x = VaR_{\beta _k^{(t)}}(U)$ and $u>0$ is “large enough”, Theorem A.1 gives the following approximation of $VaR_{\beta _k^{(t)}}(U)$ by replacing $F_{U}(x-u|u)$ with a generalized Pareto distribution (GPD) $G_{\xi ,\sigma }(x-u)$:

$$\begin{aligned} VaR_{\beta _k^{(t)}}(U)&= F_U^{-1}(\beta ^{(t)}_k) \nonumber \\&\sim u+G_{\xi ,\sigma }^{-1}\left(1-\frac{1-\beta _k^{(t)}}{\overline{F}_{U}(u)}\right) =u+\frac{\sigma }{\xi }\left\{ \left( \frac{\overline{F}_{U}(u)}{1-\beta _k^{(t)}}\right) ^{\xi }-1\right\} . \end{aligned}$$

(2.4)

See Theorem A.4 for details of the validation of this formula. The value for u is determined using the Peaks-Over-Threshold method, a standard approach within this context. The estimation of the parameters $\xi$ and $\sigma$ from the data is elaborated upon in Sect. 4.

Remark 2.2

Thus, the fact that the conditional (Tail) VaR can be written explicitly is a major advantage in numerical calculations. Since the risk measures we need to compute are ${\mathscr {F}}_t$-conditional random quantities, their prediction requires Monte Carlo calculations based on their distribution. With complex models, even a single computation of a risk measure requires a Monte Carlo calculation, which must be repeated many times to examine its distribution. Our method eliminates the initial Monte Carlo calculation; see also Remark 3.1.

3 Specific models for frequencies

3.1 Negative binomial model

We assume that the distribution of $N_k\ (k=1,2,\dots )$ will change according to the period. However, assuming a single distribution for each time period typically provides only a limited amount of data for estimating that distribution. To address this limitation, we further divide each period into several sub-periods, such that for a given integer $m\in {\mathbb {N}}$, we express the frequency $N_k$ as a sum of individual sub-period frequencies:

$$\begin{aligned} N_k := N_{k,1} + N_{k,2} + \dots + N_{k,m}, \end{aligned}$$

(3.1)

where m is the number of the sub-period and $N_{k,j}\ (j=1,\dots ,m)$ is the number of breaches in the sub-period $k_j$. We make the following assumptions to guide our analysis:

• [NB1] $N_{k,j}(j=1,...,m)$ are i.i.d. random variables, each of which follows a geometric distribution $N_{k,j}\overset{i.i.d}{\sim }Ge(p_k)$, where the parameter $p_k$ is constant during the kth period: for $p_k\in (0,1)$,

  $$\begin{aligned} {{\mathbb {P}}}(N_{k,j} = r) = (1-p_k)p_k^r,\quad r=1,2,.... \end{aligned}$$

Then the distribution of $N_k$, which is the i.i.d. sum of geometric variables becomes the negative binomial distribution $N_{k}\sim NBin(m, p_k)$:

$$\begin{aligned} {{\mathbb {P}}}(N_k = r) = {m + r - 1 \atopwithdelims ()r}(1 - p_k)^m p_k^r,\quad r=1,2,\dots . \end{aligned}$$

Note that

$$\begin{aligned} {\mathbb {E}}[N_k] = \frac{mp_k}{1-p_k}. \end{aligned}$$

(3.2)

Moreover, under this assumption, the condition (A.1) in Theorem A.4 is obvious since $p_k<1$.

We further assume a time series model for $\{p_k\}_{k=1,2,\dots }$:

• [NB2] The value of the parameter $p_{k}$ changes stochastically according to k, and the logit transformation of $p_{k}$, say $\text{ logit }p_k:=\log p_k/(1-p_k)$ follows an ARIMA(p, d, q) process:

  $$\begin{aligned} \text{ logit }\,p_{k}-\text{ logit }\,p_{k-d}=c+{\epsilon }_{k}+\sum _{i=1}^{p}\,\phi _{i}\text{ logit }\,p_{k-i}+\sum _{i=1}^{q}\theta _{i}{\epsilon }_{k-i}, \end{aligned}$$

  where ${\epsilon }_{k}\overset{i.i.d}{\sim }{\mathscr {N}}(0,\sigma ^{2})$, $c\in {\mathbb {R}}$, and $\sigma >0$. $\theta _{i}$ and $\phi _{i}$ are the regression coefficients.

To compute the approximated (T)VaR, we require the prediction of the conditional expectation

$$\begin{aligned} {\mathbb {E}}[N_k|{\mathscr {F}}_t],\quad k > t \end{aligned}$$

based on observations $(N_{k,1},N_{k,2},\dots , N_{k,m})_{k=1,2,\dots ,t}$. Given that m observations $N_{k,j}\,(j=1,\dots ,m)$ are independently and identically distributed samples from a geometric distribution with parameter $p_k$, the log-likelihood is expressed as

$$\begin{aligned} L_n(p_k):= \sum _{j=1}^m \log (1-p_k)p_k^{N_{k,j}}, \end{aligned}$$

and the MLE of $p_k$ up to time t is computed as

$$\begin{aligned} \widehat{p}_k:= 1 - \frac{1}{1 + N_k/m},\quad k=1,\dots ,t. \end{aligned}$$

If $\widehat{p}_k\,(k=1,\dots t)$ provides a reliable estimate of $p_k$, we can assume that these estimated values approximately satisfy the ARIMA process described in [NB2]. Consequently, we can proceed to estimate the parameters $(p,d,q; c,\phi _i,\vartheta _i,\sigma )$ based on the sequence $\{\widehat{p}_k\}{k=1,\dots t}$, resulting in $(\widehat{p},\widehat{d},\widehat{q}; \widehat{c},\widehat{\phi }_i,\widehat{\vartheta }_i,\widehat{\sigma })$.

Subsequently, the logit of $p_k^{(t)}:=p_k|_{{\mathscr {F}}_t}$, representing the ’future’ parameter conditional on ${\mathscr {F}}_t$, can be predicted through the estimated ARIMA$(\widehat{p},\widehat{d},\widehat{q})$ model, as follows:

$$\begin{aligned} \text{ logit }\,p_k^{(t)}= \widehat{c} + \text{ logit }\,p^{(t)}_{k-\widehat{d}} + {\epsilon }_{k}+\sum _{i=1}^{\widehat{p}}\widehat{\phi }_{i}\text{ logit }\,p_{k-i}^{(t)}+\sum _{i=1}^{\widehat{q}}\widehat{\theta }_{i}{\epsilon }_{k-i},\quad {\epsilon }_k \sim {\mathscr {N}}(0,\widehat{\sigma }^{2}). \end{aligned}$$

Generating a sample of $p^{(t)}_k$ as well as the expression (3.2), we have the predictor

$$\begin{aligned} {\mathbb {E}}[N_k|{\mathscr {F}}_t]\approx \frac{m p^{(t)}_k}{1-p^{(t)}_k},\quad k>t, \end{aligned}$$

and the predictor of $\beta ^{(t)}_k$ in (2.3) is given by

$$\begin{aligned} \widehat{\beta }^{(t)}_k:=1-\frac{(1-\alpha )(1-p^{(t)}_k)}{mp_k^{(t)}}. \end{aligned}$$

Remark 3.1

Since $VaR_{\widehat{\beta }^{(t)}_k }(U)$ is a random variable via $p_k^{(t)}$ that follows ARIMA model, we must estimate its distribution to predict $VaR_{\widehat{\beta }^{(t)}_k }(U)$. This involves generating random samples of $VaR_{\widehat{\beta }^{(t)}_k }(U)$. By repeating the aforementioned procedure, for example, B times, and obtaining predictor values $\widehat{\beta }^{(t)}_{k,1},\widehat{\beta }^{(t)}_{k,2}, \dots ,\widehat{\beta }^{(t)}_{k,B}$, we accumulate a set of B samples of $VaR_\beta (U)$:

$$\begin{aligned} \widehat{{\varvec{V}}}:=\left\rbrace VaR_{\widehat{\beta }^{(t)}_{k,1} }(U), VaR_{\widehat{\beta }^{(t)}_{k,2} }(U), \dots , VaR_{\widehat{\beta }^{(t)}_{k,B} }(U) \right\lbrace . \end{aligned}$$

Consequently, a predictor for $VaR_{\widehat{\beta }^{(t)}_k }(U)$ can be approximated as

$$\begin{aligned} VaR_{\widehat{\beta }^{(t)}_k }(U) \approx \textrm{mean}(\widehat{{\varvec{V}}}) = \frac{1}{B}\sum _{j=1}^B VaR_{\widehat{\beta }^{(t)}_{k,j}}(U), \end{aligned}$$

and each $VaR_{\widehat{\beta }^{(t)}_{k,j}}(U)$ is calculated according to the formula in (2.4); see Sect. 4 for the practical procedure. Moreover, the $\alpha$-confidence interval is given by

$$\begin{aligned} [\widehat{{\mathbb {V}}}_{(1-\alpha )/2}, \widehat{{\mathbb {V}}}^{(1-\alpha )/2}],\quad \alpha \in (0,1), \end{aligned}$$

where ${\mathbb {V}}_{(1-\alpha )/2}$ and ${\mathbb {V}}^{(1-\alpha )/2}$ are the lower and upper $(1-\alpha )/2$-empirical quantile for $\widehat{{\varvec{V}}}$, respectively.

In this procedure, if $VaR_{\widehat{\beta }^{(t)}_{k,j}}(U)$ had to be calculated again by Monte Carlo, it would be a significant computational cost. However, in our simple model approach, this can be written in explicit form, which significantly reduces the amount of computation.

3.2 Compound Poisson model

The second candidate for N is the compound Poisson process with stochastic intensity. We maintain the structure of Eq. (3.1) for $N_k$ but alter the distribution of $N_{k,j}$ to follow the Poisson distribution. We make the following assumptions:

• [CP1] $N_{k,j} (j=1,...,m)$ are independent and identically distributed random variables, each of which conforms to a Poisson distribution, denoted as $N_{k,j}\overset{i.i.d}{\sim }Po(\Lambda _k/m)$. Here, the parameter $\Lambda _k$ remains constant throughout the $k^{th}$ period, with $\Lambda _k > 0$: for $\Lambda _k > 0$,

  $$\begin{aligned} {{\mathbb {P}}}(N_{k,j} = r) = e^{-\Lambda _k/m}\frac{(\Lambda _k/m)^\ell }{\ell !},\quad \ell =0,1,2,\dots . \end{aligned}$$

• [CP2] The value of the parameter $\Lambda _{k}$ changes depending on k. In particular, log transfomation of $\Lambda _{k}(:=\displaystyle \log \Lambda _{k})$ follows ARIMA(p, d, q) process, i.e.

  $$\begin{aligned} \log \Lambda _{k}-\log \Lambda _{k-d}=c+{\epsilon }_{k}+\sum _{i=1}^{p}\phi _{i}\log \Lambda _{k-i}+\sum _{i=1}^{q}\theta _{i}{\epsilon }_{k-i}, \end{aligned}$$

  where ${\epsilon }_{k}\overset{i.i.d}{\sim }{\mathscr {N}}(0,\sigma ^{2})$.

Under the condition [CP1], it is evident that the condition in Eq. (A.2) from Theorem A.4 holds, given that $N_k\sim Po(\Lambda _k)$.

We follow the same procedure as the previous section to predict ${\mathbb {E}}[N_k|{\mathscr {F}}_t]\ (k>t)$. To commence, we estimate each $\Lambda _k/m\ (k=1,2,\dots ,t)$ based on observations $(N_{k,1},N_{k,2},\dots , N_{k,m})_{k=1,2,\dots ,t}$ through the MLE:

$$\begin{aligned} \frac{\widehat{\Lambda }_k}{m} = \frac{N_{k,1} + \dots + N_{k,m}}{m} = \frac{N_k}{m}\quad \Leftrightarrow \quad \widehat{\Lambda }_k = N_k. \end{aligned}$$

Next, if the $\widehat{\Lambda }_k$ estimates the true $\Lambda _k$ well, then we can regards that $\{\log \widehat{\Lambda }_k\}_{k\in {\mathbb {N}}}$ follows the ARIMA(p, d, q), and that $\Lambda _k^{(t)} = \Lambda _k|_{{\mathscr {F}}_t}$ is predicted by

$$\begin{aligned} \log \Lambda _{k}^{(t)}-\log \Lambda _{k-\widehat{d}}^{(t)} =\widehat{c}+{\epsilon }_{k}+\sum _{i=1}^{\widehat{p}}\widehat{\phi }_{i}\log \Lambda _{k-i}^{(t)}+\sum _{i=1}^{\widehat{q}}\widehat{\theta }_{i}{\epsilon }_{k-i},\quad {\epsilon }_k\sim {\sim }{\mathscr {N}}(0,\widehat{\sigma }^{2}), \end{aligned}$$

where all the unknown parameters are estimated from $\{\log \widehat{\Lambda }_k\}_{k=1,2,\dots t}$.

Since ${\mathbb {E}}[N_k]=\Lambda _k$, we approximate ${\mathbb {E}}[N_k|{\mathscr {F}}_t]$ as follows:

$$\begin{aligned} {\mathbb {E}}[N_k|{\mathscr {F}}_t] \approx \Lambda _k^{(t)},\quad k>t, \end{aligned}$$

and the predictor of $\beta _k^{(t)}$ is given by

$$\begin{aligned} \widehat{\beta }_k^{(t)} = 1 - \frac{1-\alpha }{\Lambda _k^{(t)}}. \end{aligned}$$

Then the $VaR_{\widehat{\beta }_k^{(t)}}$ is predicted by the same procedure as in Remark 3.1.

3.3 Hawkes processes

The third candidate for N is represented by a Hawkes process $\widetilde{N}=(\widetilde{N}t){t\ge 0}$, which is a point process characterized by stochastic intensity: for given ${\mathscr {F}}_t$,

$$\begin{aligned} \lambda _t=\mu +\sum _{t_{i}<t}g(t-t_{i}), \end{aligned}$$

(3.3)

where $\mu \ge 0$, g is a kernel function, and $t_{i}$ is the $i_{th}$ incident time.

We suppose that $\widetilde{N}_k$ is the number of incidents up to time k. Then our $N_k$, which is the number of incident in the $k^{th}$ period, is given by

$$\begin{aligned} N_k = \widetilde{N}_{k} - \widetilde{N}_{k-1}. \end{aligned}$$

Given that obtaining the expectation ${\mathbb {E}}[\widetilde{N}_k]$ is typically challenging, we make an additional assumption concerning the kernel function g, which assumes the form

$$\begin{aligned} g_\vartheta (x)=\alpha \beta \exp (-\beta x),\quad x\in {\mathbb {R}}, \end{aligned}$$

(3.4)

with a parameter $\vartheta =(\alpha ,\beta ) \in {\mathbb {R}}_{+}^2$. Importantly, we assume that the parameter $\vartheta$ remains constant across periods (k), whereas in Sects. 3.1 and 3.2, we had assumed period-dependent $\vartheta$ values.

According to Lesage et al. (2020), the expectation of the Hawkes process with the kernel (3.4) is written as

$$\begin{aligned} {\mathbb {E}}[\widetilde{N}_{t}]=\frac{\mu }{1-\alpha }t-\frac{\mu \alpha }{\beta (1-\alpha )^{2}}\left[1-\exp \{-(1-\alpha )\beta t\}\right], \end{aligned}$$

(3.5)

although it is generally hard to find the explicit expression of the expectation of a Hawkes process.

Next, we check the condition (A.2) in Theorem A.4. According to Daley and Vere-Jones (2003),

$$\begin{aligned} {{\mathbb {P}}}(\widetilde{N}_k - \widetilde{N}_{k-1}=r)={\mathbb {E}}\Biggl [\exp \left( -\int _{k-1}^{k}\lambda _{s}\,ds\right) \frac{(\int _{k-1}^{k}\lambda _{s}\,ds)^{r}}{r!}\Biggr ]. \end{aligned}$$

Hence it follows for any ${\epsilon }>0$ that

$$\begin{aligned} \sum _{r=0}^\infty (1+{\epsilon })^r {{\mathbb {P}}}(N_k=r)&= \sum _{r=0}^\infty (1+{\epsilon })^r {{\mathbb {P}}}(\widetilde{N}_k - \widetilde{N}_{k-1}=r)\\&= \sum _{r=0}^{\infty }(1+{\epsilon })^{r}\cdot {\mathbb {E}}\Biggl [\exp \left( -\int _{k-1}^{k}\lambda _{s}ds\right) \dfrac{(\int _{k-1}^{k}\lambda _{s}ds)^{r}}{r!}\Biggr ]\\&= {\mathbb {E}}\Biggl [\sum _{r=0}^{\infty }\exp \left( -\int _{k-1}^k \lambda _{s}ds\right) \dfrac{\{(1+{\epsilon })\int _{k-1}^{k}\lambda _{s}ds\}^{r}}{r!}\Biggr ]\\&= {\mathbb {E}}\Biggl [\exp \left( {\epsilon }\int _{k-1}^{t}\lambda _{s}ds\right) \sum _{r=0}^{\infty }\exp \left\{ -(1+{\epsilon })\int _{k-1}^{k}\lambda _{s}ds\right\} \\&\quad \times \dfrac{\{(1+{\epsilon })\int _{k-1}^{k}\lambda _{s}ds\}^{r}}{r!}\Biggr ]\\&= {\mathbb {E}}\Biggl [\exp \left( {\epsilon }\int _{k-1}^{k}\lambda _{s}ds\right) \Biggr ] < \infty . \end{aligned}$$

To estimate the parameters $\vartheta = (\mu ,\alpha ,\beta )$, we require knowledge of the incident times $t_i$, which are not available in the PRC dataset [18]. Only the date of each incident is provided. Consequently, we resort to a hypothetical stochastic generation of incident times and substitute these with random numbers to construct an estimator for the parameters. This process is iterated multiple times, and the estimated values of $\widehat{\vartheta }$ are computed by averaging these estimators.

Given that numerous incident times occur within a single day, an approximation in which the times are assumed to be uniformly distributed throughout a day is generally acceptable. The averaging process will help mitigate any errors. In practical terms, we follow these steps:

• 1. Generate the quasi-occurrence times $t_i < t$ uniformly within a daily scale, denoted as $\tau _1,\dots , \tau _{N_k}$.

• 2. Estimate the $\vartheta =(\mu ,\alpha ,\beta )$ by the maximum likelihood method, where the likelihood function is given by

  $$\begin{aligned} L(\mu ,\alpha ,\beta ):= \sum _{j=1}^{N_k} \log \lambda _{\tau _j} - \int _0^t \lambda _s\,ds \end{aligned}$$

• 3. Iterate this procedure B times, and compute the MLE $\widehat{\vartheta }^{t,j} = (\widehat{\mu }^{(t,j)}, \widehat{\alpha }^{(t,j)}, \widehat{\beta }^{(t,j)})$ in the $j^{th}$ step $(j=1,2,\dots ,B)$. Then, aggregate these individual estimates as follows:

  $$\begin{aligned} \widehat{\vartheta }^{(t)} = \frac{1}{B}\sum _{j=1}^B \widehat{\vartheta }^{(t,j)}. \end{aligned}$$

  This approach allows us to estimate the parameters $\vartheta$ with repeated sampling and averaging for enhanced accuracy.

From the expression (3.5), we have the approximation

$$\begin{aligned} {\mathbb {E}}[\widetilde{N}_k|{\mathscr {F}}_t] \approx \frac{\widehat{\mu }^{(t)}}{1-\widehat{\alpha }^{(t)}}k-\frac{\widehat{\mu }^{(t)}\widehat{\alpha }^{(t)}}{\widehat{\beta }^{(t)}(1-\widehat{\alpha }^{(t)})^{2}}\left\rbrace 1-\exp \left[-(1-\widehat{\alpha }^{(t)})\widehat{\beta }^{(t)}k\right]\right\lbrace =: \Pi _k^{(t)},\quad k>t. \end{aligned}$$

Since $N_k = \widetilde{N}_k - \widetilde{N}_{k-1}$, the predictor of $\beta _k^{(t)}$ is given by

$$\begin{aligned} \widehat{\beta }_k^{(t)} = 1 - \frac{1-\alpha }{\Pi _k^{(t)} - \Pi _{k-1}^{(t)}}. \end{aligned}$$

Remark 3.2

It’s important to note that in this particular model, the predictor for $\widehat{\beta }_k^{(t)}$ in the future is not subject to randomness. This is because the model assumes that the parameter values remain constant. As a result, there is no need to follow the procedure outlined in Remark 3.1. The value of $VaR_{\widehat{\beta }_k^{(t)}}$ is solely determined by the estimated value of $\widehat{\beta }_k^{(t)}$.

3.4 Approximation and estimation of $F_U$

Across all the models described above, we maintain the assumption:

$$\begin{aligned} \overline{F}_U \in {\mathscr {R}}_{-\kappa },\quad \kappa >1. \end{aligned}$$

which enables us to apply Theorem A.1, and for ‘large $u>0$’, we can approximate

$$\begin{aligned} F_U(x|u) \approx G_{\xi ,\sigma }(x), \end{aligned}$$

where $\xi \ge 0$ and $\sigma >0$ represent the parameters. Determining a ‘suitable’ value for $u>0$ is crucial. The Peaks-Over-Threshold (POD) method is a widely recognized approach for selecting a threshold $u>0$. We make this determination visually by utilizing the mean excess (ME)-plot. Further details can be found in Embrechts et al. (2003), Section 6.5.

As an example, Fig. 4 displays the ME-plot for Case 2 (2006–2016); refer to Table 1. We can opt for a threshold such as $u=6.6\times 10^6\ (\mathrm {6.6e+06})$. Subsequently, we estimate the parameters $\xi$ and $\sigma$ using data that exceeds this threshold u, employing the maximum likelihood method as outlined in Embrechts et al. (2003), Section 6.5.1. These estimated values are denoted as $\widehat{\xi }{u}^{(t)}$ and $\widehat{\sigma }{u}^{(t)}$. It’s important to note that $t=2013$ in Case 1 and $t=2016$ in Case 2. The estimated values are presented in Table 2.

Fig. 4

Mean excess plot (Case 2: 2006–2016)

Table 2 Estimated values of $\xi$ and $\sigma$ (MLE) with the threshold u

Furthermore, based on these estimated values, we conducted the Kolmogorov–Smirnov (KS) goodness-of-fit test for the estimated probability density function: $G_{\widehat{\xi }{u}^{(t)}, \widehat{\sigma }{u}^{(t)}}$. The KS test statistics are provided in Table 3, and we found that the hypothesis stating the distribution of $U_i>u$ follows a Generalized Pareto Distribution (GPD) was not rejected at the 5% significance level in both Cases 1 and 2. For your reference, these density functions are depicted in Fig. 5.

Table 3 KS-test

Fig. 5

Estimated density of GPD with data; Case 1 (left) and Case 2 (right)

4 Data analysis: prediction of tail risks

Utilizing each of the models previously outlined, namely NB (negative binomial), CP (compound Poisson), and HK (Hawkes process), we estimate the conditional (Tail) Value-at-Risk as described in Remark 3.1.

In the NB and CP models, we set $m=7$ to represent a week, where $N_{kj}$ signifies the number of incidents on the jth day of the kth week. Under each model, we generate 1000 samples of $VaR_{\beta _k^{(t)}}(U)$ and $TVaR_{\beta _k^{(t)}}(U)$, calculate the mean, and determine the 95% confidence interval. Subsequently, we compare these results with the test data in Cases 1 and 2, respectively.

4.1 Negative Binomial model

Table 4 provides the results of estimating the ARIMA process for $p_k$ as assumed in [NB2]. We select the values of (p, d, q) using Akaike’s Information Criteria (AIC) through maximum likelihood estimation (MLE).

We estimate the 99% and 99.9% (Tail) VaR and present the results in Figs. 6 and 7 alongside the testing data for backtesting.

Table 4 Estimation of ARIMA process for $p_k$ in [NB2]

Fig. 6

NB model, Case 1: 99% and 99.9% (T)VaR with breaches in 2014–2015

Fig. 7

NB model, Case 2: 99% and 99.9% (T)VaR with breaches in 2017–2018

4.2 Compound Poisson model

Table 5 is estimating the result of the ARIMA process for $\Lambda _k$ assumed in [CP2]. AIC also selects the parameter (p, d, q). We show 99% and 99.9% (Tail) VaR in Figs. 8 and 9.

Table 5 Estimation of ARIMA process for $\Lambda _k$ in [CP2]

Fig. 8

CP model, Case 1: 99% and 99.9% (T)VaR with breaches in 2014–2015

Fig. 9

CP model, Case 2: 99% and 99.9% (T)VaR with breaches in 2017–2018

4.3 Hawkes Process

We present the backtesting results for the HK models in Figs. 10 and 11. As mentioned at the end of Sect. 3.3, the values of $VaR_{\widehat{\beta }_k^{(t)}}(U)$ $(k=1,2,\dots )$ are computed deterministically based on the estimated values of $\widehat{\beta }_k^{(t)}$. Consequently, we cannot provide confidence intervals for the VaR as in the other models; see also Remark 3.2.

Fig. 10

HK model, Case 2: 99% and 99.9% (T)VaR with breaches in 2014–2015

Fig. 11

HK model, Case 2: 99% and 99.9% (T)VaR with breaches in 2017–2018

4.4 Back testing the models

We provide the backtesting results in Tables 6, 7, 8 and 9, where:

• ‘95%-lower’ represents the rate at which the actual breaches are less than the 95%-lower bound of the confidence interval.

• ‘95%-upper’ indicates the rate at which the actual breaches are less than the 95%-upper bound of the confidence interval.

• ‘Mean’ represents the rate at which the actual breaches are less than the mean of the Monte Carlo samples of (T)VaR. This can be considered as the risk reserve for the insurer of the cyber risks.

From a theoretical perspective, these rates (especially ‘Mean’) are expected to be close to 99% in VaR and even higher in TVaR because TVaR is a more conservative risk measure than VaR.

The results show that the 99%-VaR behaves as the theory suggests, and TVaR is more conservative, which appears to be sufficient for risk management. In Case 1, each rate is around 99% for VaR, while in Case 2, they are slightly underestimated but not far from 99%. This outcome is reasonable considering the trend changes since 2016, as discussed in the Introduction.

Figures 6, 7, 8, 9, 10 and 11 illustrate that the results with NB and CP are similar, making it challenging to determine which is superior. The HK model yields slightly inferior results compared to the other two, even though it is often used to analyze cyber risks. Hence, the NB and CP models are sufficiently suitable for practical risk management, and there may be no compelling reason to opt for the HK model, which involves more complex estimation and modeling processes.

Table 6 Empirical test for $VaR_{0.99}$

Table 7 Empirical test for $VaR_{0.999}$

Table 8 Empirical test for $TVaR_{0.99}$

Table 9 Empirical test for $TVaR_{0.999}$

Table 10 p-values for binomial backtesting of $VaR_{0.99}$. Bold letters are the results where $H_0$ is rejected at a significance level of 10%

Table 11 p-values for binomial backtesting of $VaR_{0.999}$. Bold letters are the results where $H_0$ is rejected at a significance level of 10%

The above empirical backtesting may need to be revised: backtesting of VaR and TVaR is described in detail in Bayer and Dimitriadis (2022) and Nolde and Ziegel (2017), and R packages are available. However, they did not work well on our dataset. The exact reasons are unclear, but in particular, during the computational process, irregular matrices appeared and the errors could not be removed until the end. This may be due to the peculiarities of our data. As mentioned in the Introduction, our data are not partly recorded as correct time stamps. This is a drawback of this open data, and hence, the distribution of the data is rather biased.

Therefore, as a standard backtest for VaR, we conducted a backtest using the binomial distribution mentioned in the Basel documents (Bank for International Settlements 2013) (Tables 10 and 11). This method serves our purpose here, as it is a method that can be described in the framework of the Nolde and Ziegel (2017) backtest and can be used without any distributional assumptions on the loss data (see Nolde and Ziegel 2017, Example 1). The null hypothesis in our test is the following:

$H_0$: The sequence of our predicted $\{VaR_{\alpha }^{(t)}\}_{t\in {\mathbb {N}}}$ is conditionally calibrated (certainly the value-at-risk with level $\alpha$).

Table 10 shows that the p-value for the HK model is relatively small, e.g., $H_0$ is rejected at a significance level of 5% for the HK-Mean, Case 2, but is at a level of stable acceptance for both NB and CP (in the Mean). Also, from Table 11, the performance of HK is somewhat inferior to the other two models, as is also the case at the 99.9% level. It is safe to say that very classical models such as NB and CP are also adequate in practical terms, at least in our dataset.

Remark 4.1

All existing methods for backtesting against TVaR rely on the distribution of the loss data and/or the asymptotic variance of the test statistic. In particular, it was difficult to find a suitable method for TVaR backtesting, as the loss data in this case was heavy-tailed, and even the existence of variance was doubtful. Due to those limitations, only the above-mentioned empirical results are identified here.

5 Conclusion and future works

We extend the classical (single-period) insurance risk model to a multi-period framework for more effective cyber risk assessment. By evaluating the performance of different models, including the negative binomial model, Poisson process, and Hawkes process, you provide valuable insights into their ability to predict VaR and TVaR in future periods.

Our data analysis revealed that both the negative binomial and Poisson models effectively predict VaR and TVaR for cyber risks. However, there was no significant difference in their performance, suggesting that either of these models can be used effectively for risk assessment. Surprisingly, the Hawkes model, which is commonly used for predicting cyber risks, did not exhibit superior performance in this specific dataset.

Our study demonstrates that a classical and simple model can effectively manage cyber risks. The explicit calculations and low computational costs make this approach practical and accessible. Moreover, the straightforward statistical procedures involved in this model make it a valuable tool for cyber risk assessment. This research emphasizes the importance of using models that are not only effective but also easy to implement in practice.

On the other hand, recent survey studies related to cyber risk and insurance, such as Awiszus et al. (2023) and Dacorogna and Kratz (2023), have pointed out that while emphasizing the importance and utility of the classical actuarial approach, it is difficult to address the complexity of cyber risk data using only the classical frequency-severity approach. This suggests that there is still room for development in the direct application of our classical model. However, it should not be forgotten that the explicit expressiveness of the simple classical model has computational advantages, which cannot be ignored in practice. Furthermore, in the above studies, the use of a single-period model is assumed for frequency modeling. Our novelty lies in extending this to a multi-period model and addressing its statistical inference. Awiszus et al. (2023) mention using a Cox process for frequency modeling, but this approach does not yield explicit expressions for VaR or TVaR. Our approach emphasizes explicitness. Making our multi-period model the standard benchmark model and incorporating the characteristics of cyber risk may serve as a trigger for more complex modeling.

Despite using the PRC data [18], the largest dataset available to our knowledge, several issues still need to be solved. First, many cyber incidents have likely yet to be disclosed. Open databases for cyber attacks may help address this. Secondly, inaccuracies in the incident dates are a concern. The reported dates in PRC are not necessarily when the breaches occurred but when they were made public. As a result, some incidents may be reported long after they occurred, akin to the Incurred But Not Reported (IBNR) concept in insurance. This issue needs further attention in future research.

While we used all data without categorization in our data analysis, the trends may differ depending on the type of breaches. For instance, some incidents, such as hacking or insider breaches, may be malicious, while others could result from negligence, like administrative errors. Additionally, the trends may vary based on business sectors such as companies, educational institutions, and medical facilities. Consequently, future analyses should ideally be based on more finely categorized and detailed data. Unfortunately, such data are not readily available as open-source, and developing a comprehensive database is still an ongoing challenge. The cyber risk analysis field would greatly benefit from establishing more extensive and categorized datasets for improved insights and risk management.

Appendix

Theorem A.1

Let F be a (proper) distribution function with $F(x) <1$ for any $x\in {\mathbb {R}}$. There exists $\kappa >0$ such that $\overline{F}\in {\mathscr {R}}_{-\kappa }$ if and only if there exists a positive function $b(u)\rightarrow \infty$ as $u\rightarrow \infty$ such that

$$\begin{aligned} \lim _{u\rightarrow \infty }\sup _{0<x<\infty }|F(x|u)-G_{\xi ,b(u)}(x)|=0, \end{aligned}$$

where $F(x|u):={{\mathbb {P}}}(X-u\le x|X>u)$ and $\xi =1/\kappa$, and $G_{\xi ,\sigma }$ is the generalized Pareto distribution (GPD) with the distribution function given by

$$\begin{aligned} G_{\xi ,\sigma }(x)= {\left\{ \begin{array}{ll} 1-\left( 1+\dfrac{\xi }{\sigma }x\right) ^{-1/\xi } & (\xi \ne 0)\\ 1-e^{-x/\sigma } & (\xi =0) \end{array}\right. }. \end{aligned}$$

Proof

See Embrechts et al. (2003), Theorem 3.4.13. $\square$

Lemma A.2

Let S is a compound risk model given in (1.1), and suppose that N satisfies

$$\begin{aligned} \sum _{r=0}^{\infty }(1+{\epsilon })^{r}\cdot {{\mathbb {P}}}(N=r)<\infty \end{aligned}$$

for some ${\epsilon }>0$. Then, it holds that

$$\begin{aligned} \overline{F}_{S}(x)\sim {\mathbb {E}}[N]\cdot \overline{F}_{U}(x),\quad x\rightarrow \infty . \end{aligned}$$

Proof

See Embrechts et al. (2003), Theorem 1.3.9. $\square$

Lemma A.3

For $\kappa >1$ and $\overline{F}_U \in {\mathscr {R}}_{-\kappa }$, there exists a function $L(x) \in {\mathscr {R}}_0$ such that

$$\begin{aligned} \int _x^\infty \overline{F}_U(y)\,dy \sim L(x) \frac{x^{1-\kappa }}{\kappa - 1},\quad x\rightarrow \infty . \end{aligned}$$

Proof

See Grandell (1997), p.181. $\square$

Theorem A.4

Let S is a compound risk model given in (1.1), and suppose that $F_U$ is a (proper) distribution function with $F_U(x) <1$ for any $x\in {\mathbb {R}}$, and that $\overline{F}_{U}\in {\mathscr {R}}_{-\kappa }$ where $\kappa >1$. Moreover, suppose that there exists some ${\epsilon }>0$ such that

$$\begin{aligned} \sum _{r=0}^{\infty }(1+{\epsilon })^{r}\cdot {{\mathbb {P}}}(N=r)<\infty . \end{aligned}$$

(A.1)

Then it follows for $\beta :=1-\dfrac{1-\alpha }{{\mathbb {E}}[N]}$ that

$$\begin{aligned} {\left\{ \begin{array}{ll} VaR_{\alpha }(S)\sim VaR_{\beta }(U)\\ TVaR_{\alpha }(S)\sim \dfrac{\kappa }{\kappa -1}VaR_{\beta }(U) \end{array}\right. },\ \alpha \rightarrow 1. \end{aligned}$$

(A.2)

Furthermore, taking a sequence $u=u(\alpha ) \uparrow \infty$ such that

$$\begin{aligned} \lim _{\alpha \uparrow 1}\frac{1-\alpha }{1-F_U(u(\alpha ))} \in (0,{\mathbb {E}}[N]), \end{aligned}$$

(A.3)

it holds that

$$\begin{aligned} VaR_{\beta }(U)\sim u(\alpha )+\dfrac{\sigma }{\xi }\left\{ \left( \dfrac{\overline{F}_{U}(u(\alpha ))}{1-\beta }\right) ^{\xi }-1\right\} , \quad \alpha \rightarrow 1, \end{aligned}$$

(A.4)

where $\xi = 1/\kappa$ and $\sigma$ is a function of $u=u(\alpha )$.

Remark A.5

As an example, taking $u=u(\alpha )$ such that, for a constant $\gamma \in (0,1)$,

$$\begin{aligned} u(\alpha ) = F_U^{-1}\left(1 - \gamma ^{-1}\frac{1 - \alpha }{{\mathbb {E}}[N]}\right), \end{aligned}$$

then we have $u(\alpha )\rightarrow \infty$ as $\alpha \uparrow 1$, and that

$$\begin{aligned} \lim _{\alpha \uparrow 1} \frac{1-\alpha }{1-F_U(u(\alpha ))} = \gamma {\mathbb {E}}[N] \in (0,{\mathbb {E}}[N]), \end{aligned}$$

which satisfies (A.3).

Proof

The asymptotic equivalency (A.2) is shown in Biagini and Ulmer (2009), Theorem 2.5, so we omit the details. See also Shimizu (2018).

As for the statement (A.4), we note the following decomposition of $F_U$: for any $u<x$,

$$\begin{aligned} F_U(x)&= \overline{F}_U(u) \frac{ \overline{F}_U(x) - \overline{F}_U(u) }{\overline{F}_U(u) } + F_U(u) \nonumber \\&= \overline{F}_U(u) \frac{{{\mathbb {P}}}(U\le x) - {{\mathbb {P}}}(U\le u)}{{{\mathbb {P}}}(U>u) } + F_U(u) \nonumber \\&= \overline{F}_U(u) F_U(x-u|u)+ F_U(u). \end{aligned}$$

(A.5)

We see from Theorem A.1 that there exists a function $\sigma =b(u)\uparrow \infty$ such that

$$\begin{aligned} r_u(x):= F_U(x-u|u) - G_{\xi ,\sigma }(x-u) \rightarrow 0,\quad u\rightarrow \infty \end{aligned}$$

uniformly in $x>u$ and that, for $x= VaR_\beta (U)$, we have

$$\begin{aligned} \frac{G_{\xi ,\sigma }(VaR_\beta (U)-u)}{F_U(VaR_\beta (U)-u|u)} = 1 - \frac{1 - F_U(u)}{\beta - F_U(u)} r_u(VaR_\beta (U)), \end{aligned}$$

and

$$\begin{aligned} r_u(VaR_\beta (U)) \rightarrow 0, \end{aligned}$$

as $u\rightarrow \infty$ and $\beta \rightarrow 1$. Here we note that, under (A.3) with $u=u(\alpha )$,

$$\begin{aligned} 0< \frac{1 - F_U(u)}{\beta - F_U(u)} =\frac{1}{ 1 - \frac{1-\alpha }{1 - F_U(u)}\frac{1}{{\mathbb {E}}[N]} } = O(1)\quad (\alpha \rightarrow 1), \end{aligned}$$

which implies that

$$\begin{aligned} \frac{G_{\xi ,\sigma }(VaR_\beta (U)-u)}{F_U(VaR_\beta (U)-u|u)} = 1 -O(1)\cdot r_u(VaR_\beta (U)) \rightarrow 1 \end{aligned}$$

as $u=u(\alpha )$ and $\alpha \rightarrow 1$. Therefore, we see that

$$\begin{aligned} F_U(VaR_\beta (U)-u|u) \sim G_{\xi ,\sigma }(VaR_\beta (U)-u) \end{aligned}$$

under (A.3). Substituting x with $VaR_\beta (U)$ in both sides of (A.5), we have that

$$\begin{aligned} \beta \sim \overline{F}_U(u) G_{\xi ,\sigma }\left(VaR_\beta (U) - u\right)+ F_U(u), \quad \alpha \rightarrow 1, \end{aligned}$$

which concludes that

$$\begin{aligned} VaR_\beta (U) \sim u(\alpha ) + G^{-1}_{\xi ,\sigma }\left(1 - \frac{1-\beta }{\overline{F}_U(u)}\right) \sim u + \frac{\sigma }{\xi } \left\{ \left( \frac{\overline{F}_U(u)}{1-\beta } \right) ^\xi - 1\right\} ,\quad \alpha \rightarrow 1, \end{aligned}$$

with $u= u(\alpha )$ in (A.3). $\square$