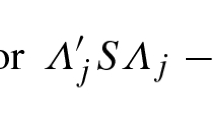Taylor’s power law and reduced-rank vector generalized linear models

Abstract

Taylor’s power law (TPL) from empirical ecological theory has had many explanations proposed for its widespread observation in data. We show that the class of reduced-rank vector generalized linear models (RR-VGLMs) for coupling two parameters from a statistical distribution linearly together creates hybrid models that satisfy TPL or very similar. These include the RR-negative binomial, RR-inverse Gaussian and RR-generalized Poisson distributions. Some advantages of RR-VGLMs include the handling of covariates and an implementation exists in the form of the VGAM R package. The software is demonstrated to show how these models may be fitted conveniently.

1 Introduction

In ecology, Taylor’s power law (TPL; (Taylor , 1961)) is a well-known empirical relationship between the mean and variance of population abundance. During the (over) half a century, since it was first proposed, it has captured the research attention of not only ecologists but mathematical statisticians, geneticists, epidemiologists and physicists attempting to explain it. There is now an almost voluminous literature on the subject; some recent work include Cohen and Huillet (2022) and De La Pena et al. (2022). Kendal (2004b) reviews Taylor’s power law and some of its possible causes.

In the context of living in an era where many modern statistical techniques exist and whose analyses may be performed with ease, the main purposes of this paper are:

• Give a short overview of Taylor’s power law (Sect. 3).

• Demonstrate how the VGAM R package and its statistical framework can fit regression models that accommodate, or bear strong similarities to, the mean-variance relationship of Taylor’s power law. In particular, the class of reduced-rank vector generalized linear models (RR-VGLMs) creates TPL-like models for continuous and discrete responses (Sect. 5). These hybrid models are either not well known or are novel. One advantage of the methodology is that it can adjust for covariates.

• Offer some interspersed musings about the above points to tie in connections between them.

The purposes are very modest and informally met. The overall conclusion is that Taylor’s power law currently remains at least partially inexplicable and there is still scope for considerable future work that could be directed into this area—ranging from almost totally empirical to purely theoretical research. Some parts of this article draws upon Jorgensen et al. (2011).

2 Data sets

This section describes the two data sets to be analyzed in Sect. 7. They are real and simulated data respectively. Some of the basics of VGLMs and RR-VGLMs described after this section are tied in with these data to help aid their explanation.

2.1 Pink Salmon data

The pinkbr data frame in ecofolio (Anderson et al. , 2019) is supplementary material to Krkosek et al. (2011) and used in Anderson et al. (2013). It concerns the abundance of pink salmon recruits for even years 1972–2008 in the Broughton Archipelago, BC, Canada. The data was downloaded from https://rdrr.io/github/seananderson/ecofolio. The following code sets things up for the RR-VGLM analysis of Sect. 7.1.

For convenience, we centered the covariate year. It is noted that each column, except for the first, represents the abundance of a different river in British Columbia, Canada, through time. For example, the Neekas River is located about 27 km from Klemtu, in Kitimat-Stikine Regional District. The data were collected by Fisheries and Oceans Canada.

Before performing the analysis, we first conduct the most naive analysis by fitting a LM to the sample log-variance versus log-means:

The basic plot is

The data does appear to be linear and the estimated slope is approximately 1.98.

2.2 Simulated data

The following code uses simulation to generate data and then the fits are compared to the true parameter estimates. The response is rounded to allow discrete distributions to be fitted, and the upward rounding is because 0 is not allowed for some continuous distributions—this may cause some slight bias.

Looking ahead to Sect. 7.2, the data satisfies (2) with

$$\begin{aligned} \alpha _2= 1 \end{aligned}$$

(1)

because, from (15), $a_{21} = 1$ and $\alpha _2= 2 - a_{21}$, based on rgamma(scale = scale, shape = shape) which has mean scale * shape. The estimates of $\alpha _1$ are obtained for both data sets in Sect. 7.

3 Some background

Taylor’s Power Law has been observed in many different species and ecosystems. Let $Y_{ij}$ denote the observed abundance, where $j=1,\ldots ,\mathcal{S}$ denote sites and $i=1,\ldots ,n_j$ denote replicates within a site. For example, the pink salmon data of Sect. 2.1 has $n_j=19$ and $\mathcal{S}=7$. TPL states that

$$\begin{aligned} \text{ Var }(Y_{ij}) ~=~ \alpha _1\, \mu _j^{\alpha _2}, ~~~ 0< \alpha _1, ~~ 0 < \alpha _2, \end{aligned}$$

(2)

for parameters $\alpha _1$ and $\alpha _2$. With data, the parameters may be estimated by regressing the log sample variance, $\log S_j^2$, on the log sample mean, $\log \overline{Y}_j$, assuming independence both between and within sites. With covariates one can rewrite (2) as

$$\begin{aligned} \text{ Var }(Y_{ij}|\varvec{x}_{ij}) ~=~ \alpha _1\left[ \mu _j(\varvec{x}_{ij}) \right] ^{\alpha _2}, ~~~ 0< \alpha _1, ~~ 0 < \alpha _2, \end{aligned}$$

(3)

to emphasize its dependency on $\varvec{x}_{ij}$. (However, see the comments regarding the $\varvec{x}_{i}$ notation in early part of Sect. 4.) Motivation for the need to handle covariates is given in Sect. 7. As an example, the pink salmon data has the sole covariate year.

Taylor (1961) described $\alpha _1$ as ‘a sampling or computing factor, depending upon the size of the sampling unit and on which estimate of variance is used’. This parameter may be estimated, e.g. Sect. 7 for both data sets. More importantly, he called $\alpha _2$ an ‘index of aggregation’ with $\alpha _2\rightarrow 0$ being ‘near-regular’, $\alpha _2= 1$ being ‘random’ and $\alpha _2\rightarrow \infty$ being ‘highly aggregated’. Illustrating (2) using 24 ecological data sets obtained from the literature, he obtained a sample mean and median $\widehat{\alpha }_2$ of 1.69 and 1.57 respectively, where estimates ranged from 0.7 to 3.08. In practice, $1< \widehat{\alpha }_2< 2$ is most commonly observed in data, and $\widehat{\alpha }_2< 1$ is uncommon because sites with high abundances tend to have higher variability.

TPL has been observed in many fields outside of ecology and consequently it has been called Taylor’s “universal” power law by some. Some examples include HIV-infected individuals (Anderson and May , 1988); physics (called fluctuation scaling, e.g. (Fronczak and Fronczak , 1990; De La Pena et al. , 2022)); genetics (e.g. (Kendal , 2004a)) and demography (e.g. (Bohk et al. , 2015)).

One problem with TPL is that the definition of aggregation is not universally agreed upon so that there are different measures of it (Routledge and Swartz , 1991; Pedigo and Buntin , 1994). In contrast to (2), Routledge and Swartz (1991) argue that

$$\begin{aligned} \text{ Var }(Y)= & {} A_1 \, \mu + A_2 \, \mu ^2, \end{aligned}$$

(4)

cf. the NEF-QVF models of Sect. 6.1. A good reference on indices of aggregation is Hurlbert (1990).

Several statistical distributions have been used to model aggregation and/or TPL. Some of the most popular of these include the negative binomial distribution (NBD; Sect. 5.4) and the log-series distribution. Magurran (2004) describes these as well as the lognormal distribution. Taylor et al. (1983) describe some shortcomings of the NBD for measuring aggregation and suggest using the log-variance log-mean relationship instead. A useful reference regarding diversity and species abundance is May (1975). Hill and Hamer (1998) describe problems distinguishing between the log-series and lognormal models.

A referee asked about the relation between TPL and allometry. The latter traditionally concerns the study of relationships of individual body size to shape, anatomy, physiology and behaviour. However, the past decade has seen a more macroscopic application of allometry, in particular, density-mass allometry (DMA) which asserts that the mean population density of a set of populations is a power-law function of the average body size of organisms. Combined TPL–DMA predicts that the variance of the population density is a power-law function of mean individual body mass, and the relationship is called “variance-mass allometry” (VMA). Empirical evidence for the TPL–DMA combination has been found in United States oak (Quercus spp.) (Cohen et al. , 2012) and New Zealand mountain beech (Fuscospora spp.) trees (Cohen et al. , 2016). In summary, the combination connects the variability of population density to the mean body mass of individuals.

4 The VGLM/RR-VGLM framework

Vector generalized linear models (VGLMs) are a class of models that can loosely thought of as multivariate GLMs applied to parameters $\theta _j$ (not necessarily a mean) to a model not necessarily from the exponential family. The data may be written $(\varvec{x}_i,\ \varvec{y}_i)$, $i=1,\ldots ,n$, assumed independently, with response $\varvec{y}_i$ and explanatory variables $\varvec{x}_i$ usually with an intercept $x_{i1}=1$. However, we are quite informal in writing $\varvec{x}$ in general, e.g.

• when the ith value of $\varvec{x}$ is not of interest, we can simply write $\varvec{x}$ as $(x_1,\ldots ,x_d)^T$, such as in (5), to reflect the variables only;

• In (7) for instance, we have $\eta _j$-specific covariates $x_{ikj}$ and we could write $\varvec{x}_{ij}= (x_{i1j},\ldots , x_{idj})^T$ so that $\varvec{x}_i$ contains all the $\varvec{x}_{ij}$. Thus, we use $\varvec{x}_i$ in general and we sometimes write it equivalently with $\varvec{x}_{ij}$ when concerning $\eta _j$. Thus, in (3), we could replace $\varvec{x}_{ij}$ by $\varvec{x}_{i}$ without contradiction.

These nuances in notation should hopefully not create confusion because its context is usually very clear.

The jth linear predictor is

$$\begin{aligned} g_j(\theta _j) ~=~ \eta _j ~=~ \varvec{\beta }_j^{T} \varvec{x}~=~ \sum _{k=1}^d \; \beta _{(j)k} \, x_{k}, ~~~ j=1, \ldots , M, \end{aligned}$$

(5)

for some parameter link function $g_j$ satisfying the usual properties. If $M>1$, then linear constraints between the regression coefficients are accommodated, as

$$\begin{aligned} \varvec{\eta }(\varvec{x}_i)= & {} \left( \begin{array}{c} \eta _1(\varvec{x}_i) \\ \vdots \\ \eta _M(\varvec{x}_i) \end{array} \right) ~=~ \sum _{k=1}^d \, \varvec{\beta }_{(k)} \, x_{ik} ~=~ \sum _{k=1}^d \, \textbf{H}_k \, \varvec{\beta }_{(k)}^{*} \, x_{ik}, \end{aligned}$$

(6)

for known user-specified constraint matrices $\textbf{H}_k$ of full column-rank (i.e. rank $\mathcal {R}_k=$ ncol($\textbf{H}_k$)), and $\varvec{\beta }_{(k)}^{*}$ is a possibly reduced set of regression coefficients to be estimated. Whilst trivial constraints are denoted by $\textbf{H}_k=\textbf{I}_M$, other common examples include parallelism ($\textbf{H}_k=\textbf{1}_M$, an $M\times 1$ matrix of ones), exchangeability, and intercept-only parameters $\eta _j=\beta _{(j)1}^*$.

The overall ‘large’ model matrix is written $\textbf{X}_{\textrm{VLM}}$, which equals $\textbf{X}_{\textrm{LM}} \otimes \textbf{I}_M$ with trivial constraints. For an $M=1$ model, $\textbf{X}_{\textrm{LM}}=[(x_{ik})]$ is the ‘smaller’ $n \times d$ model matrix. If a model has $\eta _j$-specific explanatory variables (e.g. a time-varying covariate) then (6) extends to

$$\begin{aligned} \varvec{\eta }_i&~=~&\varvec{o}_i + \sum _{k=1}^{d} \, \text{ Diag }(x_{ik1},\ldots ,x_{ikM}) \, \textbf{H}_k \, \varvec{\beta }_{(k)}^{*} \end{aligned}$$

(7)

with provision for offsets $\varvec{o}_i$. Equation (7) is the central formula for the xij feature or capability and is the most general for VGLMs.

Like ordinary GLMs (Nelder and Wedderburn , 1972; McCullagh and Nelder , 1989), maximum likelihood estimation for VGLMs is by the iteratively reweighted least squares (IRLS)/Fisher scoring algorithm. This requires the computation of the expected information matrices. For VGLMs, the log-likelihood is

$$\begin{aligned} \ell ~=~ \sum _{i=1}^n \; \log \, f(y_i; \varvec{\theta }) ~=~ \sum _{i=1}^n \, \ell _i \end{aligned}$$

where f is the probability density or mass function. The estimated variance-covariance matrix is

$$\begin{aligned} \widehat{\text{ Var }} \left( \widehat{\varvec{\beta }^{*}} \right)&~=~&\left( \textbf{X}_{\textrm{VLM}}^T \; \textbf{W}^{(a)} \; \textbf{X}_{\textrm{VLM}} \right) ^{-1}, \end{aligned}$$

(8)

evaluated at the final iteration a, where $\varvec{\beta }^{*}=(\varvec{\beta }_{(1)}^{*T},\ldots ,\varvec{\beta }_{(d)}^{*T})^T$ are all the regression coefficients to be estimated, and the maximum likelihood estimate is $\widehat{\varvec{\beta }^{*}}$. Here, suppressing a momentarily, $\textbf{W}=\text{ Diag }(\textbf{W}_1,\ldots ,\textbf{W}_m)$ is the block-diagonal working weights matrix with $\textbf{W}_i$ being $\text{ Var }(\partial \ell _i / \partial \varvec{\eta }_i)= E[ -\partial ^2 \ell _i / (\partial \varvec{\eta }_i \, \partial \varvec{\eta }_i^{\top })]$, giving rise to the Fisher scoring algorithm. That is, the expected information matrix for observation i are used. More information on the estimation of VGLMs can be found, e.g. in Yee (2008), Yee (2010) and Yee (2015, Ch.3).

As a topic, reduced-rank regression in statistics is a general technique for reducing the dimension or complexity of a regression model. It often results in lowering the number of regression coefficients estimated. Some references on the subject as a whole include Anderson (1951), Izenman (1975) who coined the phrase, Reinsel and Velu (1998), Izenman (2008, Ch.6), Bura et al. (2018), Forzani et al. (2019).

Reduced-rank VGLMs (RR-VGLMs; (Yee and Hastie , 2003; Yee , 2014)) are VGLMs where a subset of the $\textbf{H}_k$ are unknown and therefore estimated. RR-VGLMs stipulate that

$$\begin{aligned} \varvec{\eta }(\varvec{x})= & {} \textbf{B}_1^T \varvec{x}_{1} + \textbf{A}\, \varvec{\nu } \end{aligned}$$

(9)

where $\varvec{x}= (\varvec{x}_1^T, \varvec{x}_2^T)^T$, $\varvec{\nu }= \textbf{C}^T \varvec{x}_2=(\nu _1,\ldots ,\nu _R)^T$ is a vector of latent variables (linear combinations of the explanatory variables $\varvec{x}_2$ which may be considered explanatory variables in their own right), $\textbf{A}{}$ is $M \times R$ (with $\textbf{A}^T = (\textbf{I}_R \; \widetilde{\textbf{A}}^T)$ being convenient corner constraints used for identifiability—only the $(M-R)R$ elements of $\widetilde{\textbf{A}}$ are estimated) and $\textbf{C}{}$ is $p_2 \times R$. Here, $\dim (\varvec{x}) = d = p$ with $\dim (\varvec{x}_1) = p_1$, $\dim (\varvec{x}_2) = p_2$, and $p_1 + p_2 = d$. The $\textbf{A}{}$ and $\textbf{C}{}$ are estimated by an alternating algorithm, and $\textbf{B}= (\textbf{B}_1^T \; \textbf{B}_2^T)^T$ with $\textbf{B}_2 = \textbf{C}\, \textbf{A}^T$, a reduced-rank approximation of a subset of B. The submatrix $\textbf{B}_1$ is estimated too and normally this only contains the intercepts which the reduced-rank regression leaves unchanged. The rank R is ideally as low as possible in order to keep the model parsimonious (sometimes 1 or 2) and $\widehat{\textbf{B}}$ can be biplotted (Gabriel , 1971; Gower et al. , 2011) to show the relationship between the variables and linear predictors.

Important for this paper are statistical distributions with $M=2$ parameters that arise after reduced-rank regression is applied: with $R=1$ and $\textbf{A}= (1, a_{21})^T$, the corner constraint implies there is only one parameter to estimate. Then $g_1(\theta _1) = \eta _1$ and we couple the second parameter linearly to the first by

$$\begin{aligned} \eta _2= & {} t_1 + a_{21} \cdot \eta _1, \mathrm { say.} \end{aligned}$$

(10)

There are two variants where the second (Variant II) has $t_1 = 0$ and Variant I has $t_1 \ne 0$. Since $g_{j}$ is invertible then

$$\begin{aligned} \theta _2= & {} g_2^{-1} \left( t_1 + a_{21} \cdot g_1(\theta _1) \right) . \end{aligned}$$

(11)

This equation is central to this paper and Table 1 is a summary of some TPL-like models produced. The user can sometimes choose from a set of suitable link functions; therefore, there is a little flexibility in the class of models that can be possibly generated. In Sect. 5, we sketch a few details behind the table.

The VGAM R package (Yee , 2023) is an S4 (Chambers , 1998) implementation of the above. Although vglm() is probably the most widely used modelling function (which is superficially very similar to stats::glm()), we will mainly focus on rrvglm(). Over 100 distributions/models may be fitted and readers are directed to, e.g. Yee (2008), Yee (2015), Yee (2020) for information about its practical use. In this article, we show how VGAM can be used to fit certain models that are potentially useful for biodiversity analyses, as well as mentioning some of its advantages. In addition to many VGAM family functions for estimation, most are accompanied by dpqr-type functions e.g. genpoisson1() has rgenpois1() for generating random variates for the GP-1 distribution (Sect. 5.2). Regarding VGAM family functions, almost all have a zero argument which, when assigned NULL, forces no $\eta _j$ to be intercept-only, i.e. (5) holds for all $j=1,\ldots ,M$. (This detail is necessary for understanding the rightmost column of Table 1).

5 Reduced-rank models

In this section, the following result is used repeatedly. Suppose parameters $\theta _1$ and $\theta _2$ are both positive. For obvious reasons, in the VGLM/RR-VGLM framework, it is common to use the log-link as the default; then substituting $\eta _j = \log \theta _j$ into (10) yields

$$\begin{aligned} \theta _2= & {} K_1 \, \theta _1^{a_{21}} \end{aligned}$$

(12)

where $K_1 = e^{t_1}$ is a positive parameter to be estimated for Variant I and $K_1 = 1$ for Variant II. This derivation is continued in Sect. 5.5 where (12) is applied to the 2-parameter gamma distribution as a specific example.

5.1 The inverse Gaussian distribution

The canonical form of the inverse Gaussian distribution has density

$$\begin{aligned} f(y;\mu ,\lambda ) = \sqrt{\lambda /(2\pi y^3)} \; e^{ -\lambda (y-\mu )^2 / (2 y \mu ^2) }, ~~~~ y>0, ~~~~ \mu>0, ~~~~ \lambda >0 \end{aligned}$$

so that $E(Y)=\mu$ and $\text{ Var }(Y) = \mu ^3/\lambda$. The default for VGAM’s inv.gaussianff() is $\eta _1=\log \mu$ and $\eta _2=\log \lambda$. Applying (12) gives $\text{ Var }(Y) = {K_1^{-1}} \, \mu ^{3 - a_{21}}$, cf. (2).

5.2 The GP-1 distribution

Introduced by Consul and Jain (1973), the generalized Poisson distribution (GPD) handles overdispersion and therefore is a direct competitor of the NBD. Several variants have been proposed and the GP-1 (as named by Yang et al. (2009)) satisfies (2) when fitted as a RR-VGLM.

The GP-1 has probability mass function $\Pr (Y=y; \mu , \varphi ) =$

$$\begin{aligned} \displaystyle { \frac{\mu \left[ \, \mu + \left( \sqrt{\varphi }- 1\right) y \right] ^{y-1}}{ y! \; \varphi ^{y/2} \; \exp \left\{ \left[ \mu + \left( \sqrt{\varphi }- 1\right) y \right] / \sqrt{\varphi }\right\} }, } \quad y=0, 1, 2, \ldots , \infty , \quad 0 < \mu , \quad 1 \le \varphi . ~~~~ \end{aligned}$$

(13)

Then $E(Y)=\mu$ and $\text{ Var }(Y) = \mu \varphi$ where $\varphi$ is the dispersion index. Further information can be found in Consul (1989) and Consul and Famoye (1992).

The software default for genpoisson1() is $\eta _1 = \log \mu$ and $\eta _2 = \log \log \varphi$. However, by setting $\eta _2 = \log \varphi$, then (12) can be used to obtain $\text{ Var }(Y) = K_1 \cdot \mu ^{1+a_{21}}$, cf. (2).

Table 1 Summary of reduced-rank two-parameter families related to TPL. Parameters $\mu$, $t_1$, $a_{21}$ and $K_1$ are unknown and to be estimated. The final column is the family argument of the call rrvglm(y $\sim$ x2 + x3 + $\cdots$, family = $\ldots$) in VGAM. Variant I is used here throughout

5.3 The two-parameter gamma distribution

The 2-parameter gamma distribution has density function

$$\begin{aligned} f(y; \mu , \sigma ) ~=~ (\mu \, \Gamma (\sigma ))^{-1} \; e^{-\sigma y / \mu } \; (\sigma y / \mu )^{\sigma -1} \, \sigma \end{aligned}$$

(14)

for mean $\mu >0$, shape ${\sigma > 0}$, and ${y > 0}$. Then $\text{ Var }(Y) = \mu ^2 / \sigma$. By default, $\eta _1=\log \mu$ and $\eta _2=\log \sigma$, so the usual argument (12) yields

$$\begin{aligned} \text{ Var }(Y)= & {} {K_1^{-1}} \, \mu ^{2 - a_{21}}. \end{aligned}$$

(15)

5.4 The negative binomial distribution

Probably the most popular full-likelihood model for modelling overdispersion relative to the Poisson is the negative binomial distribution. For this, its genesis as a distribution arising from a gamma-distributed mean parameter of a Poisson is very well known. The NBD now has a large literature and Stoklosa et al. (2022) provides a recent and modern overview of the NBD within the context of ecological modelling.

It is noted that Stoklosa et al. (2022, Table 3) lists 17 R packages for performing NB regression. What advantage does VGAM have over other packages? One is that its statistical framework naturally allows a larger number of NB variants, e.g. NB-1, NB-2, NB-H, NB-P, NB-C, etc. using the nomenclature of Hilbe (2011). These simply emerge as special cases because of the ability to handle constraint matrices and apply reduced-rank regression. The $\varvec{x}_{ij}$ facility also allows $\eta _j$-specific covariates to be entered in—this is exploited in capture-recapture models based on the positive-Bernoulli distribution (see, e.g. (Yee et al. , 2015)). The NBD variants handled by VGAM are described in Yee (2015) and Yee (2020). Recently, Miranda-Soberanis and Yee (2023) solved the four-decades problem of estimating the NBD with its canonical link. One disadvantage of VGAM for NB regression is that Bayesian analyses are not supported.

For this paper, of special interest is the NB-P variant, also known as the reduced-rank NB ((Yee , 2014), RR-NB;). Following ?stats::NegBinomial, we use the NB probability mass function

$$\begin{aligned} \Pr (Y=y;\mu , k) ~=~ {y + k - 1 \atopwithdelims ()y} \, \left( \frac{\mu }{\mu +k} \right) ^y\, \left( \frac{k}{k+\mu } \right) ^k, ~~~ y=0,1,\ldots , \end{aligned}$$

(16)

having mean $\mu >0$ and index parameter $k>0$. Then $\text{ Var }(Y)=\mu +\mu ^2/k$ with Poisson limit $k \rightarrow \infty$.

Applying (12) to $\eta _1= \log \mu$ and $\eta _2= \log k$, then $\text{ Var }(Y)= \mu + {K_1^{-1}} \, \mu ^{2 - a_{21}}$ which is approximately (2) when $\mu$ is large. In terms of estimation, Greene (2008) and Winkelmann and Zimmermann (1995) develop one-off algorithms for fitting the RR-NB but these are unnecessarily complicated. In contrast, the alternating algorithm of Yee and Hastie (2003) operates for all RR-VGLMs and is much simpler.

5.5 RR-VGLM synthesis

Continuing on from (12), let’s use (14) to illustrate how RR-VGLMs can be fitted to estimate the two TPL parameters of (2). For this (2-parameter gamma) distribution we fit a RR-VGLM to all the data jointly by entering the site information as a factor. We convert the usual response data matrix into a long (or tall) vector to indicate the relative positions. As an example, the data set might be pinkbr in ecofolio (Sect. 2.1).

One complication of the following treatment is the necessity to convert a ‘short’ data set into a ‘long’ data set. For the models considered in this paper, the VGAM package treats each column of the response matrix as univariate response. Multiple responses are therefore permitted, e.g. rrvglm(cbind(y1, y2, y3) $\sim$ x2 + x3, ...), and this results in $\varvec{\eta }=(\varvec{\eta }_1^T,\varvec{\eta }_2^T,\ldots )^T$, i.e. separate linear predictors for each response which are concatenated into one large vector of linear predictors. In the following, index j corresponds to the columns of the response matrix.

The overall model is

$$\begin{aligned} \varvec{\eta }= & {} \left( \begin{array}{c} \eta _1 \\ \eta _2 \end{array} \right) ~=~ \left( \begin{array}{c} \log \, \mu _{ij} \\ \log \, \sigma _{ij} \end{array} \right) ~=~ \left( \begin{array}{c} \beta _{(1)1} \\ \beta _{(2)1} \end{array} \right) + \left( \begin{array}{c} 1 \\ a_{21} \end{array} \right) \nu _{ij} \end{aligned}$$

(17)

where $\nu _{i} = \nu _{ij} = \sum _{k=1}^S \, c_{2k} \, x_{2ik} + c_3\, x_{i3}$ is a latent variable and the summation is taken over all sites. Here, $x_{2ik}$ are dummy variables for the factor site effectively and $x_{i3}$ is a value of year. Also, $c_{2k}=0$ for the baseline level of a factor. Then

$$\begin{aligned} \mu _{ij}= & {} e^{\beta _{(1)1} + \nu _{ij}}, \\ \sigma _{ij}= & {} e^{\beta _{(2)1} + a_{21} [\beta _{(1)1} + \nu _{ij}] - a_{21} \beta _{(1)1} } ~=~ \mu _{ij} \cdot e^{\beta _{(2)1} - a_{21} \beta _{(1)1} }. \end{aligned}$$

Thus, $\text{ Var }(Y_{ij}) = \mu _{ij}^2 / \sigma _{ij} = \alpha _1\, \mu _{ij}^{\alpha _2}$ where

$$\begin{aligned} \alpha _2= & {} 2 - a_{21},\\ \alpha _1= & {} e^{a_{21} \beta _{(1)1} - \beta _{(2)1}}. \end{aligned}$$

The typical call has the form of

because the argument noRRR = $\sim$ 1 is the default (no reduced-rank regression is applied to the intercept, and the other terms in the formula are part of the latent variable). The estimate of $a_{21}$ may be obtained by Coef(fit)@A[2, 1].

The other distributions in this section follow a similar argument.

5.6 Estimation of the computing factor

With RR-VGLMs, the parameter $\alpha _1$ may sometimes be estimated. From Table 1, the inverse Gaussian and 2-parameter gamma have $\alpha _1=K_1^{-1}$ whereas the generalized Poisson has $\alpha _1=K_1$. The univariate normal has $\alpha _1=K_1^{2}$. The estimates for both data sets are given in Sect. 7.

6 Other models

6.1 NEF-QVF models

Jørgensen (1997) describes the class of dispersion models containing continuous and discrete distributions where the central notion is that the location and scale are generalized to position and dispersion. A special subclass of dispersion models is called natural exponential family (NEF) or exponential dispersion models. Morris (1982) showed that there are six exponential dispersion models which have a variance function that is a polynomial function of $\mu$ of degree 2 or less. These are called NEF-QVF (quadratic variance function), and in the notation of Morris and Lock (2009), QVFs satisfy

$$\begin{aligned} V(\mu )= & {} \upsilon _2 \, \mu ^2 + \upsilon _1 \, \mu + \upsilon _0, \end{aligned}$$

(18)

cf. (4). They are the binomial, Poisson, negative binomial, normal, gamma, and NEF-GHS (generalized hyperbolic secant distribution). The first three are discrete and the remainder are 2-parameter continuous distributions. The normal has constant variance function, the Poisson has a linear variance function, and the remaining four are quadratics in the mean. VGAM implements all except the NEF-GHS—they are binomialff(), poissonff(), negbinomial()/polyaR(), uninormal() and gamma2().

6.2 Tweedie models

For completeness, only we mention Tweedie exponential dispersion models (EDMs) which have been used for TPL analyses. The family has variance function $V(\mu ) = \mu ^{\xi }$ where $\xi \le 0$ or $\xi \ge 1$, and $\xi$ is called the Tweedie index parameter. The support when $1< \xi < 2$ is $[0, \infty )$ when $2 < \xi$ it is $(0, \infty )$, and when $\xi < 0$ it is $\mathbb {R}$. For more information, see e.g. Jørgensen (1987) and Dunn and Smyth (2018, ch.12).

Unfortunately, this family does not fit within the VGLM/VGAM framework, for several reasons: its probability function does not have a closed form, so the expected information cannot be computed, and ordinary maximum likelihood estimation for $\xi$ by Fisher scoring/IRLS is not possible.

7 Numerical examples

We now illustrate VGAM applied to both data sets described in Sect. 2. We first focus on estimating $\alpha _2$ and then on $\alpha _1$.

It is commented that the approach of covariate adjustment is imperative for any realistic data analysis. Without covariates (also called an intercept-only model by the author), (3) simplifies to (2). It is well known in regression analysis that an intercept-only (null) model is an extreme form and is often grossly inadequate in most applications. Carrying this over, we contend that one must also be able to handle covariates such as in (3), e.g. without such we could incur large biases and incorrect standard errors for $\alpha _2$ and $\alpha _1$. In the second example, year is a very important covariate which should not be omitted—for example, summary(iga.fit) indicates that year.long is very highly statistically significant by a Wald test (not shown below). In the first example, year is less important (e.g. summary(gp1.fit) yields a p-value of around 4%) and it is by luck that the naive $\widehat{\alpha }_2$ happens to be similar to the reduced-rank models.

7.1 Pink Salmon data

Continuing from Sect. 2.1, we set up some long vectors of the data first.

(Note that y.use.long has length 133 whereas y.long in Sect. 5.5 has length 19). Here are some RR-VGLMs fitted to the data.

The estimates are

The estimates are quite stable. Taking the sample mean, they suggest that $\alpha _2\approx 1.95$. This happens to be in agreement with the naive estimate of Sect. 2.1. Sometimes not all the standard errors for $a_{21}$ are available because the computation of the entire variance–covariance matrix of all the parameters is very difficult and finite-difference approximations can sometimes lead to the entire matrix not being positive-definite, however they are all available here:

Hence, an approximate 95% confidence interval for $\alpha _2$ based on the 2-parameter gamma is (1.94, 2.15), the GP-1 is (1.62, 2.13), the IG is (1.94, 2.15) and (1.94, 2.15) for the RR-NB.

Given several models and estimates, a natural question to ask is: which one is preferred? For this, we recommend using some standard goodness-of-fit measures, such as AIC and BIC. Applying the former to this data (BIC() gives the same ranking), we obtain the following.

It is seen that the RR-gamma and RR-GP1 are equally the best, followed by the NB-P by a whisker. The RR-inverse Gaussian model is markedly inferior. In this example, we only have a factor for site as an explanatory variable so there is a very limited range of models to choose from.

7.1.1 Estimation of the computing factor

Now for the estimation of $\alpha _1$, this can be obtained from the software as follows:

Although large, the values are reasonably concordant.

7.2 Simulated data

Continuing from Sect. 2.2, we repeat the estimation process for the simulated data.

The naive estimate is very poor since it overestimates grossly. This is because the ordinary sample means and variances do not adjust for the covariate year. In contrast,

The results are, cf. (1),

which show the estimated $\alpha _2$ is very near the truth for all distributions. Now for the confidence intervals for the $\alpha _2$:

Not all the confidence intervals cover unity and this might be because the $y_{ij}$ has been rounded upwards.

In terms of goodness-of-fit,

it is not surprising that the RR-gamma appears best, albeit, by a slim margin.

7.2.1 Estimation of the computing factor

Now to obtain $\widehat{\alpha }_1$,

These are all close to the true value $\alpha _1= 12$ assigned in Sect. 2.2.

8 Discussion

After more than six decades, Taylor’s power law remains as intriguing as when it was first proposed. Despite much effort directed towards it by cumulatively a disparate group of researchers, it remains at least partially inexplicable today. It is shown here that the VGLM/RR-VGLM framework potentially offers much for biodiversity analyses, especially in terms of regression with covariates. RR-VGLMs are a dimension reduction technique and even reducing a two-parameter problem to one dimension has been shown to be beneficial. The methodology presented here can be considered semiparametric because it is based on an assumed distribution that has been made more flexible. The data is used to ‘directly’ estimate the aggregation parameter in (2).

However, the statistical framework of Yee (2015) offers a lot more than just RR-VGLMs. Not mentioned here is spline smoothing for the vector generalized additive model (VGAM) class. This allows a data-driven type of analysis which is exploratory and it has become an exceedingly popular tool for the modern practitioner with data sets having continuous variables.

A reviewer asked whether it is possible to model a negative binomial point process by RR-VGLMs? (This question was motivated by the popular species distribution modelling (SDM) method MAXENT (Phillips et al. , 2006) being equivalent to Poisson point process, so it can be modelled by a GLM (Renner and Warton , 2013).) Our answer is negative: Diggle and Milne (1983) showed that a NB point process possessing three basic statistical properties expected in count data does not exist or would be difficult to construct. More recent work such as Ipsen and Maller (2017) relating to Gregoire (1984), whilst showing some promise for certain applications, is very complex and does not have the same simplicity of the Poisson point process described by Berman and Turner (1992) that is amenable to a GLM-like framework and used by Renner and Warton (2013).

The reviewer also asked whether it is possible to consider mixed effect models in VGLM? That is, could there be a class of vector generalized linear mixed models (VGLMMs)? The answer to this second good question is that adding random effects to the VGLM class would be a very useful feature to have so that VGLMMs are certainly possible. However, it would take much work to develop theoretically and then to implement it in R in such a way that it was upward compatible with existing VGAM functionality. Basically, it would involve applying an estimation technique, such as restricted maximum likelihood (REML), penalised quasi-likelihood (PQL), Markov Chain Monte Carlo (MCMC), or the Laplace approximation (adaptive Gaussian quadrature) to a log-likelihood belonging outside the exponential family. VGLMMs would extend the GLMM class greatly. A recent and nontechnical survey of GLMMs and R software for fitting such is Watson (2023).

In empirical research and observation, it seems that certain laws attract the attention of what becomes a devoted group of followers and researchers. In fact, simply stated empirical laws seem bound to attract the attention of the curious and often they seem to create cult followings. As another example, one could muse that Benford’s law ((Benford , 1938), also known as the law of first digits) shares at least four similarities to Taylor’s power law: it is empirical, is widely observed, is easily stated, and many have tried explaining it since being first put forth. Probably there are multiple reasons why such laws hold—not one ‘magic bullet’—but multiple reasons that coalesce to produce the observed outcome. Consequently, it takes a substantial amount of research time to establish all the pertinent reasons before exhausting the possibilities.