1 Introduction

It has been reported that chip flow can be controlled by coating or texturing tool surfaces [1], indicating that the condition of the tool–workpiece interface is important for cutting performance. The interface between the tool and workpiece during mechanical machining is subjected to extreme conditions, such as high temperature, high pressure, and high-speed sliding, as well as the constant generation of active new surfaces. Because of this complexity, many models have been proposed to describe the interfacial phenomena during processing [2]. For comprehension of the interfacial phenomena, various techniques have been attempted, such as lateral observation of the “secondary shear zone” reproduced by indentation [3] and visualization of the interface using a transparent sapphire tool [4].

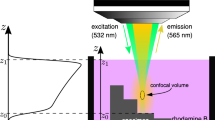
This study focused on the lubrication phenomenon at the tool–workpiece interface. As indicated by the difference in performance between wet and dry machining, the lubricant plays an important role at the tool–workpiece interface. However, the extent to which it penetrates and its role are not clear. The distribution of this lubricant is thought to affect machining performance. Indentation tests are effective for investigating machining phenomena. During indentation machining, various deformations occur depending on the angle of the tool tip [3]. Therefore, the establishment of an optical measurement method for monitoring interfacial liquid film distribution through a transparent indenter was set as the goal. However, the thickness of the lubricant film at this interface is extremely thin, approximately 1 μm thick [5]. In addition, the interface under indentation, where the lubricant film exists, is smooth and difficult to access vertically when the tip angle is sharp, even if the indenter is made of transparent materials such as glass and sapphire (Fig. 1). Therefore, this method must be able to measure liquid film thickness on steep and smooth surfaces. Nevertheless, many optical methods, such as spectroscopy, ellipsometry, and interferometry, have difficulty acquiring signals from these surfaces [6,7,8]. This study focuses on the principle of fluorescence, which makes it possible to acquire signals even from smooth and steep surfaces. Fluorescence is a phenomenon in which absorbed energy is subsequently emitted as light when fluorescent molecules return to their ground state after excitation, and it is characterized by a wide range of emissions [9]. The lubricant exhibits fluorescence when excited by ultraviolet light (UV); therefore, it is widely used in machining research, such as the evaluation of the profile of the cutting tool [10, 11]. When a lubricant is excited by UV light through a transparent indenter, fluorescence signals can be detected from the interfacial lubricant film, regardless of the surface properties of the workpiece (Fig. 2). The laser-induced fluorescence (LIF) method is used to calculate the liquid film thickness from the fluorescence intensity [12].

Fig. 1
figure 1

Accessibility of the lubricant film at the tool–workpiece interface. When the tip angle is sharp, it is difficult to observe it vertically

Full size image
Fig. 2
figure 2

Fluorescence signal detection from the steep interface

Full size image

When applying LIF to an indentation interface, it is necessary to evaluate the fluorescence signals. If the material property of the object is constant, it can be calibrated by measuring the film thickness [13]. However, in indentation tests for understanding the interfacial phenomena during machining, the material properties of the workpiece are expected to vary. In this situation, it is better to consider the amplification of the fluorescence signal owing to reflection at the workpiece surface to reduce the number of calibrations. The different reflectances of the workpiece surface and slope angle of the interface are expected to change the reflection and affect the signal intensity differently. Therefore, the purpose of this study was to develop a model of the fluorescence signal that considers the reflectance and angle of incidence for the measurement of interfacial liquid film thickness distribution, such as the lubricant in the indentation interface, and to verify the applicability of the proposed model to the calibration of absolute film thickness.

2 Proposed Principle of Interfacial Liquid Film Thickness Calibration

The basic model of the LIF method is shown in Fig. 3. When light of intensity I0 (mW/cm2) enters a liquid film of thickness L (µm), the intensity of the transmitted light Itrans (mW/cm2) can be expressed by Eq. (1) based on the Beer–Lambert law:

$$\begin{array}{*{20}c} {I_{\text{trans}} = I_{0} \exp \left( { - ACL} \right)} \\ \end{array}$$
(1)

where A (L/mol/µm) and C (mol/L) are the absorption coefficient and the solute concentration, respectively. The fluorescence intensity F (mW/mm2) is proportional to the absorbance Iabs (= I0 − Itrans) (mW/cm2) and quantum efficiency Q and is expressed as Eq. (2). If the film is sufficiently thin, it can be approximated using Eq. (3).

$$\begin{array}{*{20}c} {F = QI_{\text{abs}} = QI_{0} \left( {1 - \exp \left( { - ACL} \right)} \right)} \\ \end{array}$$
(2)
$$\begin{array}{*{20}c} {F \approx QI_{0} ACL} \\ \end{array}$$
(3)
Fig. 3
figure 3

Schematic of fluorescence excitation

Full size image

The range within which this approximation holds varies with the physical properties of each solute and must be investigated experimentally. If a liquid film is sandwiched between other materials, the incident light and emitted fluorescence cause multiple reflections at the interfaces, thereby amplifying the detected signal. This study aims to evaluate fluorescence signals by modeling multiple reflections. Figure 4 shows the vertical incidence of the excitation light on the fluorescent liquid film sandwiched between the cover glass and the workpiece. The amount of light absorbed by the liquid film during the first round trip of the incident excitation light between interfaces i1 (mW/cm2) is expressed as follows:

$$\begin{aligned} i_{1} = &\, t_{1} \left( \theta \right)I_{0} \left( {1 - \exp \left( { - ACL} \right)} \right) + R_{1} \left( {\theta_{\text{r}} } \right)t_{1} \left( \theta \right)I_{0} \exp \left( { - ACL} \right)\left( {1 - \exp \left( { - ACL} \right)} \right) \\ = &\, t_{1} \left( \theta \right)I_{0} \left( {1 - \exp \left( { - ACL} \right)} \right)\left( {1 + R_{1} \left( {\theta_{\text{r}} } \right)\exp \left( { - ACL} \right)} \right) \\ \end{aligned}$$
(4)

where t1(θ) and R1(θr) are the transmittance of the incident light at the upper interface and the reflectance of the incident light at the lower interface, respectively. Each parameter depends on the incidence angle θ (rad) and the reflection angle θr (rad). θr depends on θ and refractive indices of the materials involved (reflecting materials and liquid film). When the incidence is vertical, θ and θr are zero in Eq. (4). The absorbance at the kth round trip ik (mW/cm2) is expressed as follows:

$$\begin{array}{*{20}c} {i_{k} = \left( {R_{1} \left( {\theta_{\text{r}} } \right)r_{1} \left( {\theta_{\text{r}} } \right)\exp \left( { - 2ACL} \right)} \right)^{k - 1} i_{1} } \\ \end{array}$$
(5)

where r1(θr) is the reflectance of the incident light on the upper interface. In this situation, θr is zero. Therefore, the absorbance considering multiple reflections, Iabs (mW/cm2), can be expressed as follows:

$$\begin{aligned} I_{\text{abs}} = & \mathop \sum \limits_{k = 1}^{\infty } i_{k} \\ = & \frac{{t_{1} \left( 0 \right)I_{0} \left( {1 - {\text{exp}}\left( { - ACL} \right)} \right)\left( {1 + R_{1} \left( 0 \right){\text{exp}}\left( { - ACL} \right)} \right)}}{{1 - R_{1} \left( 0 \right)r_{1} \left( 0 \right){\text{exp}}\left( { - 2ACL} \right)}} \\ \end{aligned}$$
(6)
Fig. 4
figure 4

Multiple reflection model with vertical incidence

Full size image

If the film is sufficiently thin, the Maclaurin expansion approximates Eq. (6) to Eq. (7).

$$\begin{array}{*{20}c} {I_{\text{abs}} \approx \frac{{1 + R_{1} \left( 0 \right)}}{{1 - R_{1} \left( 0 \right)r_{1} \left( 0 \right)}}t_{1} \left( 0 \right)I_{0} ACL} \\ \end{array}$$
(7)

The fluorescence intensity F generated by multiplying the reflected excitation light is expressed as follows:

$$\begin{array}{*{20}c} {F = QI_{\text{abs}} } \\ \end{array}$$
(8)

Assuming that the wavelength ranges of absorbance and fluorescence are sufficiently far apart and that fluorescence self-absorption is negligible, the sum of the fluorescence on the optical path of the (k − 1)th and kth reflections between the interfaces fk (mW/cm2) can be expressed as follows:

$$\begin{array}{*{20}c} {f_{k} = \left( {R_{2} \left( {\theta_{\text{r}} } \right)r_{2} \left( {\theta_{\text{r}} } \right)} \right)^{k - 1} \left( {1 + R_{2} \left( {\theta_{\text{r}} } \right)} \right)t_{2} \left( {\theta_{\text{r}} } \right)F} \\ \end{array}$$
(9)

where R2(θr), r2(θr), and t2(θr) are the reflectance of the fluorescence on the lower interface, the reflectance of the fluorescence on the upper interface, and the transmittance of the fluorescence on the upper interface, respectively. In this situation, θr is zero. The sum of the detected fluorescence F0 (mW/cm2) is expressed as follows:

$$\begin{aligned} F_{0} = & \mathop \sum \limits_{k = 1}^{\infty } f_{k} \\ = & \frac{{1 + R_{1} \left( 0 \right)}}{{1 - R_{1} \left( 0 \right)r_{1} \left( 0 \right)}}\frac{{1 + R_{2} \left( 0 \right)}}{{1 - R_{2} \left( 0 \right)r_{2} \left( 0 \right)}}t_{1} \left( 0 \right)t_{2} \left( 0 \right)I_{0} QACL \\ \end{aligned}$$
(10)

A schematic of the liquid film inclined at θ (rad) is shown in Fig. 5. Considering that the excitation light intensity per unit area is cos θr times and the optical path length is 1/cos θr times due to the inclination of the wavefront to the cover glass, the absorbance is expressed like Eq. (7):

$$\begin{aligned} I_{\text{abs}} & \approx \frac{{1 + R_{1} \left( {\theta_{\text{r}} } \right)}}{{1 - R_{1} \left( {\theta_{\text{r}} } \right)r_{1} R_{1} \left( {\theta_{\text{r}} } \right)}}t_{1} \left( \theta \right)\left( {I_{0} {\text{cos}} \, \theta_{\text{r}} } \right)AC\left( {L/{\text{cos}}\, \theta_{\text{r}} } \right) \\ & = \frac{{1 + R_{1} \left( {\theta_{\text{r}} } \right)}}{{1 - R_{1} \left( {\theta_{\text{r}} } \right)r_{1} \left( {\theta_{\text{r}} } \right)}}t_{1} \left( \theta \right)I_{0} ACL \\ \end{aligned}$$
(11)

where as mentioned before, θr is the reflection angle depending on the incident angle θ and refractive indices of materials. The transmittance and reflectance depend on θ and θr, respectively. The sum of the fluorescence received at the objective lens parallel to the optical axis after multiple reflections Fθ (mW/cm2) is expressed as follows:

$$\begin{array}{*{20}c} {F_{\theta } = KI_{0} QACL} \\ \end{array}$$
(12)
$$\begin{array}{*{20}c} {K = \frac{{1 + R_{1} \left( {\theta_{\text{r}} } \right)}}{{1 - R_{1} \left( {\theta_{\text{r}} } \right)r_{1} \left( {\theta_{\text{r}} } \right)}}\frac{{1 + R_{2} \left( {\theta_{\text{r}} } \right)}}{{1 - R_{2} \left( {\theta_{\text{r}} } \right)r_{2} \left( {\theta_{\text{r}} } \right)}}t_{1} \left( \theta \right)t_{2} \left( {\theta_{\text{r}} } \right)} \\ \end{array}$$
(13)

where K is a coefficient characterized by reflectance. When θ is zero, Eq. (12) reverts to Eq. (10). Therefore, Eqs. (12) and (13) are defined as model equations. If the incident intensity and properties of the fluorescent material are accurately known, the thickness of the fluorescent film can be determined from the fluorescence intensity. However, it is difficult to accurately determine these parameters. Therefore, we calibrated these parameters. Once the known film thickness, L, was measured, the other coefficients were determined. However, measuring a known absolute film thickness remains challenging. Therefore, we aimed to evaluate the coefficients by making a step height in the cover glass on the fluorescent film and measuring the step in advance using a measuring instrument such as an atomic force microscope (AFM). This study proposes a simple and accurate fluorescence signal calibration method using the film thickness distribution derived from a cover glass with a step height (Fig. 6). The relative intensity ΔF corresponding to the cover glass step ΔL is expressed as follows:

$$\begin{array}{*{20}c} {\Delta F = KI_{0} QAC\Delta L} \\ \end{array}$$
(14)
Fig. 5
figure 5

Multiple reflection model with inclined incidence

Full size image
Fig. 6
figure 6

Concept of calibration using cover glass with step height

Full size image

Once the signal on the standard substrate is obtained, it can be corrected using Eq. (13), even when the workpiece material is changed. The absolute thickness was determined by measuring the surface profile of the cover glass. Herein, it is assumed that the change in incident intensity in the liquid film owing to the difference in reflectance between the substrate and the indenter is negligible. For a more accurate measurement, it can be compensated by an experimental approach using a calibration indenter with a step added to the surface or a virtual one by incorporating reflections at the substrate and indenter interface into the model.

3 Experimental Setup

3.1 Measurement System

The measurement system shown in Fig. 7 was constructed to verify the model and proposed method. The incident light is collimated by the collector lens and focused by the field lens to the rear focal point of the objective lens, where it enters the sample uniformly (Köhler illumination). The incident light is polarized in the x-direction using a polarized beam splitter (PBS). The fluorescence from the sample is assumed to be unpolarized and is captured by the objective lens (focal length f = 30 mm, working distance = 20.4 mm, numerical aperture (NA) = 0.30, estimated depth of focus =  ± 2.8 µm), separated from the incident light by PBS and long-pass filter and imaged on the cooled charge-coupled device. The field of view of the imaging system was 1.44 mm × 1.92 mm. A fluorescent dye solution (PMR-L10Y; Kokuyo Co., Ltd.) was used in this study. The absorption wavelength was approximately 390 nm, and the fluorescence emission peak was at 515 nm with a bandwidth (FWHM) of 80 nm (Fig. 8).

Fig. 7
figure 7

Measurement system. a Schematic and b photograph

Full size image
Fig. 8
figure 8

Fluorescence excitation (left peak) and emission (right peak) spectra of PMR-L10Y

Full size image

3.2 Sample Preparation

To evaluate the effect of reflectance experimentally, substrates with various reflectance values are required. There are several possible methods, such as preparing substrates of various materials or depositing metals on substrates under various conditions; we chose the latter because it is easier to maintain substrates with the same surface topography and control reflectance, a sample of which is shown in Fig. 9. The fluorescent liquid was sandwiched between a cover glass with a step height and gold-deposited substrate. A dove-shaped prism was used as the substrate to avoid backside reflections. Figure 10 shows the AFM height profile measurement and 500 nm step of the cover glass. In this experiment, the thickness was calibrated by obtaining the relative fluorescence intensity corresponding to this height.

Fig. 9
figure 9

Sample used to evaluate the effect of the substrate reflectance. The reflectance was controlled by deposited gold thickness. Light transmitted through the fluorescent liquid was reflected out of the sample by a dove prism

Full size image
Fig. 10
figure 10

Height profile of the cover glass and the step height measured with AFM

Full size image

Because it was difficult to measure the actual thickness of the deposited gold, measured reflectance values were used as parameters for the model. They were calculated using the following procedure: First, white light was incident on the substrate and reference mirror at two angles (0° and 45°), and the reflected light was detected using a spectrometer. The reflectance at each wavelength in air was calculated by multiplying the nominal reflectance of the mirror by the ratio of the reflected light intensity of the substrate to that of the mirror. The complex refractive indices of the substrates were determined from the calculated reflectance in air and converted into reflectance in liquid based on the Fresnel equation (Eq. (15)). The refractive index of the fluorescent liquid was assumed to be 1.33. In addition, the angle of refraction θr was calculated based on Snell’s law (Eq. (16)) when the excitation light was incident at 45° to the cover glass. The refractive index of the cover glass was set at 1.49.

$$\begin{array}{*{20}c} {R_{\text{s}} = \left| {\frac{{n_{1} {\text{cos}} \, \theta_{1} - n_{2} {\text{cos}} \, \theta_{2} }}{{n_{1} {\text{cos}} \, \theta_{1} + n_{2} {\text{cos}} \, \theta_{2} }}} \right|^{2} } \\ \end{array}$$
(15)
$$\begin{array}{*{20}c} {n_{1} {\text{sin}} \, \theta_{1} = n_{2} {\text{sin}} \, \theta_{2} } \\ \end{array}$$
(16)

where Rs is the S-polarized reflectance, n1 and n2 are the complex refractive indices, θ1 is the incidence angle, and θ2 is the refraction angle. Assuming an incident angle θ of 45° for the further experiment, the refraction angle θr was calculated as 32.1°. The reflectance values for each substrate are listed in Table 1. To verify the validity of this result, the reflectance of gold as bulk was calculated from the designed film thickness and Fresnel equation, in general agreement with the measured values: 0.27 (designed thickness 20 nm, λ = 390 nm), 0.25 (designed thickness 20 nm, λ = 515 nm), 0.38 (designed thickness 40 nm, λ= 390 nm), 0.49 (designed thickness 40 nm, λ = 515 nm), 0.38 (designed thickness 70 nm, λ = 390 nm), and 0.62 (designed thickness 70 nm, λ = 515 nm). The refractive indices of the respective materials were set as follows: fluorescent fluid was 1.33 (λ = 390 and 515 nm), both cover glass and dove prism were 1.47 (λ= 390 nm) and 1.46 (λ = 515 nm), and gold was 1.67 + 1.94i (λ = 390 nm) and 0.60 + 2.12i (λ = 515 nm). The transmittance of the cover glass was measured using a spectrometer. The transmittance t1 (λ = 390 nm) and t2 (λ = 515 nm) were 0.82 and 0.84, respectively.

Table 1 Measured reflectance at 45° incidence
Full size table

4 Experimental Confirmation of the Proposed Model

4.1 Linearity with Thickness

The proposed model assumes linearity between the liquid film thickness and the fluorescence intensity, as shown in Eq. (12). Before applying the model, the film thickness range over which this approximation is valid must be investigated. A linearly changed film thickness distribution was achieved by sandwiching the fluorescent fluid between tilted flat glasses for the fluorescence measurements (Fig. 11). In this configuration, the film thickness at each point can be estimated from the width of the liquid film D and thickness of the cover glass Lglass. In this experiment, D was 16.3 mm, and Lglass was 150 µm. Furthermore, this fluorescent liquid film was excited and measured every 150 µm in the x-direction. The intensity of the incident light I0 was 300 mW/cm2, and the exposure time was 1 s. The plane z = 0 was the focus. Thirty images were captured at the same location and the averaged image was used as the output. The pixel values of the same pixel in each image were extracted and are presented in Fig. 12a, with the value at x = 0 being zero. On the horizontal axis, the estimated film thickness at each point L(x) was plotted based on the equation L(x) = xLglass/D. This result suggests that the proposed model is valid for film thicknesses of 25 µm or less using the present measurement system. This study is particularly aimed at applications for thin film thicknesses below 1 µm, and linearity in this region needs to be confirmed. A graph plotting the pixel values per pixel for images containing x = 0 is shown in Fig. 12b. This suggests that the fluorescence intensity is linear, with a film thickness of approximately 1 µm.

Fig. 11
figure 11

Measurement of equidistant points on fluorescent liquid film with linear thickness distribution

Full size image
Fig. 12
figure 12

Measured fluorescence intensity with linear thickness distribution

Full size image

4.2 Linearity with Incident Light Intensity

In the proposed method, the fluorescence intensity was proportional to the incident light intensity. Once the linearity is confirmed, the proposed model can be used to compensate for the incident light intensity. To confirm this hypothesis, a fluorescent liquid film sandwiched between flat glasses was prepared. The film thickness was approximately 3 µm. The fluorescence from a constant point on the sample was acquired using a spectrometer by varying the incident light intensity, and the integral of the intensity was normalized and plotted, as shown in Fig. 13. The incident light intensity was varied from 0 to 560 mW/cm2. The exposure time was 100 ms. Thirty images were captured at the same location, and the averaged image was used as the output. The fluorescence intensity was plotted as the difference from that at zero incidence. This result confirms the linearity between the fluorescence intensity and incident light intensity in the present measurement system.

Fig. 13
figure 13

Fluorescence intensity with incident light intensity

Full size image

4.3 Effect of Substrate Reflectance

The contribution of substrate reflectance was experimentally evaluated to verify the proposed model. The fluorescent liquid sandwiched between a cover glass with a step height and substrates with various reflectances was imaged at 45° (Fig. 14). The intensity of the incident light I0 was 300 mW/cm2, and the exposure time was 1 s. Thirty images were captured at the same location, and the averaged image was used as the output. An example of the obtained image is shown in Fig. 15. The thickness profiles of the 1 mm in-focus line segment across the step are presented in Fig. 16. The figure shows the relative intensities as a function of position from x = 0 µm. Figure 17 shows the relationship between the difference in intensity ΔF at points x = 0 and 1000 µm (relative intensity) and the coefficient K characterized by reflectance, which was calculated from measured reflectance (Table 1) and measured transmittance based on Eq. (13). In Fig. 17, the points lie near the line approximated by the least-squares method, confirming the linearity of the relative intensity ΔF and the coefficient K, characterized by reflectance. This result indicated the validity of the proposed model, and the relationship between ΔF and K in this experiment was found to be ΔF = 1925.8 K. In this experiment, I0 was 300 mW/cm2, and ΔL was 0.5 µm. Based on the linearity confirmed thus far, the relationship between fluorescence intensity and each parameter in the present system was determined as follows:

$$\begin{array}{*{20}c} {\Delta F = 12.84KI_{0} \Delta L} \\ \end{array}$$
(17)
Fig. 14
figure 14

Setup of the measurement of effect of substrate reflectance. The incident light was S-polarized

Full size image
Fig. 15
figure 15

An example of obtained image. Contrast is adjusted

Full size image
Fig. 16
figure 16

Relative intensity at 45° slope angles corresponding to the step height. The legend indicates the designed thickness of the gold film deposited on the substrate

Full size image
Fig. 17
figure 17

Relationship between the relative intensity ΔF and the coefficient K characterized by reflectance. The legend indicates the designed thickness of the gold film deposited on the substrate

Full size image

5 Validation of Calibration of Interfacial Liquid Film Thickness in Indentation

Calibration using the proposed method was applied to an indentation interface and validated by comparing the measured thickness distribution, reflecting the surface topography of the workpiece, with the surface profile measured using a surface profiler. This comparison is difficult when the interface during indentation is observed because surface topography changes with machining. In this experiment, the thickness distribution of the liquid film between the preindented workpiece and the transparent indenter was measured instead of in-situ measurements. Although various angles could be assumed for the tip of the indenter, a surface with a 45° slope was prepared for the basic experiment in this study. A fluorescent liquid was applied to the preindented aluminum workpiece, and the fluorescence intensity at the interface was acquired when the transparent indenter was pressed against it. A right-angle prism was used as a transparent indenter. Its tip was chamfered, with a flat area approximately 500 µm wide. The interface was imaged by focusing on the plane of the dashed line in Fig. 18 using scratch markings on the surface of the workpiece. The intensity of the incident light I0 was 300 mW/cm2, and the exposure time was 1 s. Thirty images were captured at the same location and the averaged image was used as the output. The fluorescence intensity distribution was converted into thickness distribution based on Eq. (17). The results are shown as a color map in Fig. 18. Although the refractive index of the entire wavelength range should be considered in the calculation of K, the refractive index at the dominant wavelength was used for basic verification in this experiment. The refractive index of the workpiece was assumed to be that of aluminum (0.47 + 4.78i @390 nm, 0.82 + 6.28i @515 nm) [14]. The liquid film was assumed to exhibit a thickness distribution derived from the surface profile of the workpiece. The surface profiles of the three line segments, which were easy to identify based on the surface scratch markings, were measured using a surface profiler. The results are shown in Fig. 18. The same data processing as that for the surface profiler was applied to the thickness distribution measured using the proposed method, and the results are shown in Fig. 18 as thickness profiles. Based on Eq. (11), the fluorescence intensity emitted from the inclined liquid film in this model corresponds to the film thickness, which is defined as perpendicular to the slope. Thus, the results of the measurement using the proposed method of the inclined liquid film thickness at the indentation interface can be compared with the surface topography measured vertically by the surface profiler. The thickness and surface profiles agreed well for irregularities within the height of approximately 2–4 µm, thereby verifying the proposed calibration method.

Fig. 18
figure 18

Measurement of liquid film thickness distribution at the pseudo-indentation interface. The monochrome image shows fluorescence intensity distribution. Converted thickness distribution is shown in the color map. Thickness and surface profile on the three-line segments are shown in bottom. Both profiles are high-pass filtered

Full size image

6 Discussion

The model given in Eq. (12) does not consider scattering at the surface but only specular reflection. The actual sample in Fig. 18 had surface roughness; that is, the deviation of the model from the measurement results should be considered. Here, samples with various surface roughness values were measured, and the distribution of their fluorescence intensities was checked to confirm the feasibility of the proposed model. We sandwiched the fluorescent liquid between the standard sample with a roughness of Ra 0.4–3.2 µm and the cover glass with a step height and observed the signals for the step. The intensity of the incident light I0 was 300 mW/cm2, and the exposure time was 1 s. Figure 19 shows the fluorescence intensity distribution; the wavy profile reflects the shape of the sample. However, the signal for the step was almost constant, regardless of the surface roughness. This implies that the proposed model is valid, even for rough surfaces. Rough surfaces diffuse the incident light into their surroundings as scattered light. This scattered light also contributes to the excitation of fluorescent liquid (Fig. 20). Although the specular reflection component of a certain ray is attenuated owing to scattering, fluorescence by light scattered from the surrounding surfaces exists. Consequently, the fluorescence intensity remained nearly constant. In other words, because the light energy incident on the field remained the same regardless of the roughness of the measurement surface, the total amount of fluorescence energy was assumed to remain the same. However, notably, the lateral resolution is likely to deteriorate. Consequently, a reasonable film thickness distribution can be measured even for a rough workpiece, as shown in Fig. 18.

Fig. 19
figure 19

Signals for the step with various surface roughness

Full size image
Fig. 20
figure 20

Excitation by multiple reflections (left) and scattered light (right)

Full size image

7 Conclusion

The purpose of this study was to observe the tool–workpiece interface during mechanical machining through a transparent indenter using the LIF method. A measurement model was proposed to estimate the thickness of the fluorescent solution film from the fluorescence intensity when using fluorescent solutions to measure the surface topography. A calibration method for the parameters of the measurement model was proposed, and the results of the surface topography measurements under indentation were in good agreement with those measured using a surface profiler. These results confirm the validity of the proposed model. Simultaneously, we demonstrated the possibility of in-situ measurement of machining conditions under indentation using this method.