1 Introduction

Structural elements of integrated electronic circuits are often formed by grating-like structures with very small periods. These lamellar gratings are affected by line-edge roughness that has been identified as the ultimate limiting factor in the production of nanostructured surfaces in the semiconductor industry [1]. State-of-the-art integrated electronic circuits are produced in several steps and any misplacement of the edge position can lead to a complete failure of the features [2]. Therefore, at present, almost 50% of the processes in production consist of metrology [3]. An in-line nondestructive method with high throughput and sensitivity is sought.

Methods based on scatterometry are used as in-line metrology [3, 4]. Overlay metrology is used to characterize displacements between patterned layers with optical wavelengths. However, the accuracy is limited when asymmetry is present on the studied targets [2]. Grazing-incidence small-angle X-ray scattering (GISAXS) has been proposed as an alternative method for characterizing nanostructured surfaces. However, the elongated footprint leads to experimental [5] and data analysis challenges [6]. A recent comparison between EUV scatterometry and GISAXS has shown the potential of using softer X-rays to characterize nanostructured surfaces [7]. The characterization of nanostructures using X-ray (or EUV) scattering data relies on optimization methods based on a forward model. Forward models must be as faithful to the experimental conditions and as versatile as possible [8, 9] for a reliable reconstruction of the parameters and their uncertainties. Therefore, knowledge of the role of line-edge roughness in diffracted intensities is essential. A Debye–Waller factor (DWF) has been considered to account for the roughness in the scattered intensities [8, 10, 11–15]. Moreover, the applicability of the DWF in the reconstruction of binary gratings has been proposed [10, 16, 17]. Recently, the limits of application of the DWF for the characterization of three-dimensional nanostructures have been reported [9]. In the presence of roughness, the light gets scattered out of the diffraction orders producing a structured scattering pattern, where different phenomena have been identified [12, 13, 18]. However, the characterization and analysis of nanostructures based on the diffuse scattering pattern are rather complex [19].

Previous reports have indicated that the diffuse scattering signal from lamellar gratings can be decomposed in the analysis of the different frequencies [20,21,22]. This possibility would mean that in the absence of dynamical scattering, the diffuse scattering can be explained by the superposition of periodic binary samples. In this regard, the redistribution of the intensity for lamellar gratings with periodic roughness has been theoretically and experimentally investigated in the framework of critical-dimension small-angle X-ray scattering (CD-SAXS) [22,23,24] and EUV-scatterometry [20, 25]. Ultimately, the effect of the height of the structure, which is neglected in binary gratings, plays a crucial role in the distribution of the diffuse scattering [13]. In this manner, it was shown that the superposition of periodic binary gratings of different amplitudes could not explain the diffuse scattering pattern from stochastic samples [13, 26]. Additionally, the reported studies considered different types of line-edge roughness. According to the correlation between the edges of the lines, we can have line edge roughness (LER, correlated edges) or line width roughness (LWR, totally anti-correlated). The roughness types are distinguishable by the scattering out of the diffraction orders [13, 20] as predicted by Fourier optics using binary gratings [20].

In this work, we reviewed some of those concepts already reported for the characterization of line-edge roughness and the distinction between line-edge roughness and line-width roughness. We extend the previous reports with other types of roughness distributions. Chirped roughness and a combination of LER and LWR with different correlation lengths and amplitudes are also included in this sample set. We show that the chirped roughness can also be explained by the superposition of binary gratings with periodic roughness. However, for the explanation of the diffuse scattering from stochastic roughness, this demonstration is not applicable. The roughness along the lines as well as the correlation between the lines and the height of the structures must be considered.

2 Experimental Details

2.1 Sample Set

The set of samples was produced in the framework of the European Research Program Horizon 2020 to improve and benchmark the existing metrology methods in the semiconductor industry [27]. The investigated sample consists of 11 fields etched on silicon, as shown in Table 1. The reference grating is of 100-nm pitch and a nominal line width of 30 nm. The other fields are designed with a dedicated type of roughness: line edge roughness (LER), line width roughness (LWR), or a combination of both, and a dedicated roughness distribution (periodic, chirped, or random). A roughness-basis cell was designed depending on the type, distribution, amplitude (\(\delta \)), and correlation length (\(L_c\)) of the roughness (for the stochastic samples) or roughness pitch (\(p_r\)). This roughness-basis cell is repeated to cover the grating area, which is approximately 8 mm × 0.5 mm. The subset with periodic roughness has a sinusoidal profile with a roughness pitch \(p_r\) of 180 nm. The subset with chirped roughness has a roughness pitch \(p_r\) that continuously varies from \(p_{r_1} = \) 90 nm to \(p_{r_2} = \) 360 nm over the length of \(l = \) 3600 nm following

$$\begin{aligned} y(x) = \delta \sin { \left( \phi _0 +2 \uppi x \left( f_{p_{r_1}} + \frac{{\Delta} f_{p_r}}{2 l} x \right) \right) }, \end{aligned}$$
(1)

where \(f_{p_{r_1}} = \frac{1}{p_{r_1}}\) and \(\Delta {f_{p_r}} = \frac{1}{p_{r_1}}-\frac{1}{p_{r_2}}\). The initial phase is \(\phi _0\). Depending on LER and LWR, both edges of the lines would be in phase or out of phase, respectively. The roughness-basis cell of the chirped structure consists of the above signal and its mirrored profile. The x step size is given by the grid used in the manufacturing process and was 1 nm. For the stochastic roughness, different correlation lengths are considered, and for each the basis cell is 45 nm × 45 nm. Top-view SEM images from some of the samples are given in Fig. 1.

Fig. 1
figure 1

SEM top view images from the sample set. LER samples have a period of 75 nm; all other samples, 100 nm

Full size image
Table 1 List of structure patterns with the characteristics, where p is the pitch. The CD is the nominal line width of the structures, \(\delta \) is the maximum deviation of the line from a straight line, \(p_r\) is the roughness pitch and \(L_c\) the correlation length of the roughness
Full size table

2.2 Experimental Setup

The measurements were conducted at the SX700 beamline at PTB’s laboratory at the electron storage ring BESSY II. This beamline delivers a photon energy range from 50 to 1800 eV and it is under UHV [28]. For the measurements, the photon wavelength of the beam was selected as 13.5 nm. A monochromatic beam with wavevector \(\varvec {k}_i\) impinges on the sample at an incidence angle \(\alpha _i\) defined from the sample surface (Fig. 2). The elastically scattered beam with wavevector \(\varvec {k}_f\) propagates along an exit angle \(\alpha _f\) and an azimuth angle \(\theta _f\). The momentum transfer is given by \(\varvec {q}=\varvec {k}_f - \varvec {k}_i\),

$$\begin{aligned} \left( \begin{array}{c} q_x \\ q_y \\ q_z \end{array}\right) =k_0\left( \begin{array}{c} \cos (\theta _f)\cos (\alpha _f)-\cos (\alpha _i) \\ \sin (\theta _f)\cos (\alpha _f) \\ \sin (\alpha _f)+\sin (\alpha _i) \end{array} \right) , \end{aligned}$$
(2)

where \(k_0={2\uppi }/{\lambda }\). An EUV angle resolved scattering chamber [29] was used. This prototype does not allow the rotation of the incident angle but the sample can be azimuthally rotated. A back-illuminated CCD detector is placed at the end of the chamber, approximately \({15}\,{\hbox {mm}}\) from the sample and the incident angle is approximately \({31}\,{^{\circ }}\). The grating samples were mounted in conical geometry, i.e., with the grating lines parallel to the incoming beam. Because of the limitations of the setup, the angle of incidence and distance must be evaluated using the double periodicity of the samples with periodic roughness. The position of the diffraction orders is given by the intersection of the grating truncation rods and the Ewald sphere. If an additional periodicity exists along the line, satellite orders appear [8, 20, 25]. By azimuthally rotating the sample, the position of the orders of diffraction changes and the orders are no longer symmetrically distributed around the zeroth order.

Fig. 2
figure 2

Sketch of the experimental setup. The inset on the left shows the direct imaging of the grating fields by projection with a collimated beam. The black circle shows the beam footprint for the scatter measurements

Full size image

The positions of the diffraction orders are given by,

$$\begin{aligned} q_x & = {} n \frac{2\uppi }{p}\sin \varphi + m\frac{2\uppi }{p_r}\cos \varphi , \end{aligned}$$
(3)
$$\begin{aligned} q_y & = {} n\frac{2\uppi }{p}\cos \varphi + m\frac{2\uppi }{p_r}\sin \varphi , \end{aligned}$$
(4)

where n is the diffraction order given by the periodicity or pitch p and m is the satellite row given by the periodicity along the lines or pitch roughness, \(p_r\).

Using the above equations, the positions in \(q_z\) of the diffraction orders in reflecting condition, i.e., over the sample horizon, are

$$\begin{aligned} q_z&= k_0 \left[ \left( 1- \left( \frac{m\lambda }{p_r}\cos \varphi + \frac{n\lambda }{p}\sin \varphi + \cos \alpha _i \right) ^2 \right. \right. \nonumber \\&\qquad -\left. \left. \left( \frac{n\lambda }{p}\cos \varphi + \frac{m\lambda }{p_r} \sin \varphi \right) ^2 \right) ^{\!1/2} + \sin \alpha _i \right] . \end{aligned}$$
(5)

The illumination time is adapted to each target to allow high counting rates without overexposing the detector. For these measurements, a pinhole of \({320}\,{\hbox {mm}}\) was introduced in the beam path to reduce the footprint of the beam. Different samples scatter differently and the distribution of the intensity strongly depends on the period of the grating. Thus, the measurement time was estimated experimentally for each pitch size. The samples with a 75-nm pitch were measured for 10 s; the samples with a 100-nm pitch, for 20 s.

3 Results

All the samples were measured using EUV scatterometry with an incoming photon wavelength of 13.5 nm. Figure 3a shows the scattering pattern for the reference sample. Different distributions and amplitudes of the roughness lead to different scattering patterns (Figs. 3b and 4). Scattering patterns from samples with periodic or chirped roughness are dominated by the frequencies of the samples (Eqs. 3–5), as shown in Fig. 3b). The angular distribution of the scattering pattern from the samples with stochastic roughness (Fig. 4) is qualitatively different depending on the correlation length of the roughness. However, the intensity of the scattered light in (and out of) the diffraction orders highly depends on the amplitude of the roughness. The total intensity of the main diffraction orders (\(m=0\) in Eqs. 3–5) decreases with increasing roughness amplitudes. Small differences in the diffuse scattering are observed for different types or correlation lengths of the roughness (Fig. 5). The samples were separated according to the pitch because the intensity of the diffraction orders highly depends on the structure and form factors of the investigated sample. The roughness amplitudes considered for the plot correspond to the line-edge roughness analysis using SEM reported by Levi et al. [27]. For the reference grating, no roughness was considered in the design, but in previous studies it was reported to be approximately 1 nm [27].

Fig. 3
figure 3

a Scattering pattern of the reference sample (grating 1). b Scattering patterns for the samples with LER (top) and LWR (bottom). The scattering patterns from the samples with periodic roughness correspond to the nominal roughness \(\delta \) = 6 nm (on the left). The chirped roughness is on the right

Full size image
Fig. 4
figure 4

Scattering patterns for the samples with stochastic roughness. The correlation length is 50 nm on the left and 200 nm on the right

Full size image
Fig. 5
figure 5

Total intensity of the diffraction orders for the samples with a 75-nm pitch (samples with only LER) and b 100-nm pitch measured under the same conditions

Full size image

Figure 6 compares the trend of the ratio between the diffuse scattering and the diffracted light for EUV (at the incoming photon wavelength of 13.5 nm) and GISAXS. For GISAXS this ratio has been already studied for the applicability of the Debye–Waller factor for the characterization of three-dimensional nanostructures [9]. Despite the similar trend, there are differences on that ratio. GISAXS data correspond to the average of 21 different photon energies, while the EUV experiment corresponds to a single experimental setup using 13.5 nm as the incoming photon wavelength. The dark signal must be removed from the images obtained by the back-illuminated CCD detector, while in GISAXS the PILATUS detector allows single-photon counting. Additionally, inhomogeneities have also been observed in the CCD detector, and scattering events due to the defining-beam pinhole have been identified. These effects would contribute to the total intensity but not to the trend of the intensity within these measurements. To analyze the effect of different correlation lengths on the trend of the diffuse scattering, further studies are needed.

Fig. 6
figure 6

Ratio between the diffuse scattering and the diffracted intensities for the stochastic and reference samples using EUV scatterometry

Full size image

3.1 Differences Between LER and LWR

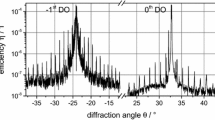
The recorded images for the different types of roughness (LER/LWR) show a distinct scattering pattern (Fig. 3b). The scattering patterns from samples with LER show no satellite order at the zeroth order of diffraction, see top image in Fig. 3b. In contrast, the samples with LWR have well-resolved satellite peaks at the zeroth order of diffraction. This difference has already been reported for samples with periodic roughness [13, 20] and can be qualitatively explained by using binary gratings in Fourier optics [20]. LER and LWR have different form factors that cause the satellite orders at the zeroth order to vanish or appear. Here, samples with chirped roughness are shown to also have this behavior. For the periodic and chirped roughness, the same phenomenon is observed. The scattering pattern is dominated by the periods on the sample, in the lateral direction, i.e., the pitch, and along the line. The angular distribution of the scattering out of the diffraction orders can be explained by the superposition of periodic binary gratings whose lines are fully correlated [20]. This assumption is also followed in the derivation of the Debye–Waller factor for lamellar gratings [10].

Fig. 7
figure 7

Scattering pattern of a sample with stochastic LER (top) and LWR (bottom) at 261 eV. This sample was reported elsewhere [13, 14]

Full size image

However, it has also been reported previously that stochastic LER or LWR has a distinct scattering pattern. Along the zeroth order of diffraction the same effect as the one observed for periodic roughness was reported [14, 25]. However, for the samples with LER, the maximum diffuse scattering signal is found between the orders and not along the orders. This is shown in Fig. 7, where the scattering patterns from another sample with dedicated roughness [14, 25] are shown. An analogous experimental setup was used. The sample detector distance from the center of the sample was 40 mm. The incoming photon energy of the beam was 261 eV, and the beam size was approximately 0.5 mm × 0.5 mm. The experimental realization and its preliminary results have already been reported elsewhere [14]. The behavior at the zeroth order of diffraction for samples with stochastic roughness might be explained following the superposition of periodic solutions without considering the correlation between the lines, as for the chirped roughness. The diffuse scattering observed between the orders cannot be explained by the simple superposition of the nanostructures without considering the correlation between the lines. The impact of the height on the diffuse scattering has been identified as a further parameter to be included in future theoretical models [25]. Additionally, the correlation between the lines affects the angular distribution of the scattering signal and may move scatter intensity to between the regular orders as shown in Fig. 8.

Fig. 8
figure 8

Fourier transform of a free-standing binary grating with chirped roughness and shifted-chirped roughness

Full size image

Figure 8 shows the Fourier transform of free-standing binary gratings with chirped roughness and one with shifted-chirped roughness. The first case is analogous to the ones reported here. In the latter case, the lines are shifted. The same frequencies of the roughness are chirped but have different starting frequencies, so that the lines are shifted to each other. For shifted roughness, a signal is also observed between the diffraction orders. Thus, the diffuse scattering must be explained including the height of the structures and considering the correlation between and along the lines [26]. This latter consideration is clearly explained here by considering a sample with chirped roughness and shifted-chirped roughness. The distribution of the diffuse scattering has also been shown to depend on the height of the structures [25]. Existing theories are based on the superposition of periodic rough gratings [10, 20, 21] where the effects of height and correlation of the lines are ignored.

3.2 Quantification of Periodic Roughness Amplitudes

The models that exist for the quantification and description of stochastic roughness using diffuse scattering are not sufficiently versatile. However, for the analysis of periodic-roughness-induced scattering, analytical methods exist [20, 22, 24]. Here, the applicability of two of these methods is discussed. The third one predicts the effect of LER using another form factor of the structure with little evidence [24].

For the analysis of the two-dimensional frequencies (pitch grating and pitch roughness) of the samples, the scattering patterns in Fig. 3 are converted into \(q_y\)-\(q_x\) coordinates, where \(q_x\) allows us to explore the pitch roughness-induced scattering.

Fig. 9
figure 9

Frequencies of the chirped and periodic structures for LER (a) and for LWR (b). The area along the first order and zeroth order of diffraction is shown for LER and LWR, respectively

Full size image

Figure 9 shows a cut at the first order of diffraction (\(q_y = \frac{2\uppi }{p}\)) and along \(q_x\) for LER and at the zeroth order of diffraction \(q_y=0\) for LWR. For LER, no modulation of the intensity is observed at the zeroth order of diffraction. For larger amplitudes of the roughness (see periodic cases), the intensity of the satellite orders increases as previous models predict [20, 22]. The two models used for comparison were developed in the framework of Fourier optics. The model of Kato et al. [20] is developed for EUV masks with sinusoidal profiles analyzed by EUV scatterometry. The model from Wang et al. [22] is developed for CD-SAXS, where the height of the structure is neglected and the roughness is considered in the form of boxes. The distribution of the intensity according to Kato’s model for LER is [20]

$$ {\text{model}}_{{{\text{LER}}}}^{\text K} = \frac{{I\left( {q_{y} ,m\frac{{2\uppi }}{{p_{r} }}} \right)}}{{I_{0} \left( {q_{y} ,0} \right)}} = J_{m}^{2} \left( {q_{y} \delta } \right), $$
(6)

where \(I_0(q_y,0)\) is the intensity of the diffraction orders of an undisturbed grating (an ideal reference grating). Considering that the roughness produces the dispersion of the scattering along \(q_x\), the addition of the kinematic scattering for each \(q_y\) coordinate would correspond to that of a non-rough grating. This assumption is used here to calculate the intensity of an undisturbed grating from the experimental data. The numerator \(I ( q_y, m \frac{2 \uppi }{p_{r}})\) corresponds to the intensity of the satellite orders (in this case the satellite row \(m = -1\)), and \(q_y\) corresponds to the position of the main diffraction order. The distribution of the intensity is given by a Bessel function of first kind of order m, \(J_m\). However, Wang’s model compares the diffracted intensity of the satellite orders with that of the main diffraction orders of the disturbed grating \(I(q_y,0)\). For the minus first satellite row, \(m=-1\), this is given by [22]

$$ {\text{model}}_{{{\text{LER}}}}^{W} = \frac{{I\left( {q_{y} ,m\frac{{2\uppi }}{{p_{r} }}} \right)}}{{I\left( {q_{y} ,0} \right)}} \approx \tan ^{2} \left( {q_{y} \delta } \right). $$
(7)
Fig. 10
figure 10

Comparison of the model of Wang (red) and Kato (black) for the redistribution of the scattered intensity for a lamellar grating with periodic LER (a) and for LWR (b). The measured data is represented by dots

Full size image

Figure 10a compares the measurement and the two models for the samples with LER. For the calculation of the models, the reported values for the roughness are used [27]. Both models predict that the satellite at the position of the zeroth order disappears.

For the case of LWR, the intensity of the orders on the satellite row (in this case \(m=-1\)) is compared to that of the diffraction orders. Using Kato’s model and derivation of the relative diffracted intensity [20, pp. 6460–6461] we have that,

$$ {\text{model}}_{{{\text{LWR}}}}^{{\text{K}}} {\text{ = }}\frac{{I \left( {{q}_{{y}} , - \frac{{{\text{2}}\uppi }}{{{p}_{r} }}} \right)}}{{{I}\left( {{{q}}_{{{y}}} ,{\text{0}}} \right)}}{\text{ = }}\cot ^{{\text{2}}} \left( {{{q}}_{{{y}}} \frac{{{{CD}}}}{{\text{2}}}} \right)\frac{{{{J}}_{{{1}}}^{{\text{2}}} \left( {{{q}}_{{{y}}} \delta } \right)}}{{{{J}}_{{\text{0}}}^{{\text{2}}} \left( {{{q}}_{{{y}}} \delta } \right)}} $$
(8)

for \(q_y \ne 0\). The case \(q_y=0\) is discussed separately [20, p. 6462] because of the divergence of the odd satellite rows [20]. The relation between the zeroth order of diffraction and the satellite at this position is [20]:

$$\begin{aligned} \frac{I \left( 0, - \frac{2 \uppi }{p_{r}}\right) }{I \left( 0,0\right) } = \left( \frac{\delta }{CD}\right) ^2. \end{aligned}$$
(9)

However, the theory of Wang et al. for the LWR does not analyze the behavior of the zeroth order’s satellite order as this is usually not measured in CD-SAXS [22]. Therefore, Wang’s method does not predict the main difference between LER and LWR. However, the model predicts the relative intensity of the diffraction and satellite orders for the other diffraction orders [22],

$$ {\text{model}}_{{{\text{LWR}}}}^{{\text{W}}} {\text{ = }}\frac{{{{I}}\left( {{{q}}_{{{y}}} , - \frac{{{\text{2}}\uppi }}{{{{p}}_{{{r}}} }}} \right)}}{{{{I}}\left( {{{q}}_{{{y}}} ,{\text{0}}} \right)}}{\text{ = }}\cot ^{{\text{2}}} \left( {{{q}}_{{{y}}} \frac{{{{CD}}}}{{\text{2}}}} \right)\tan ^{{\text{2}}} \left( {{{q}}_{{{y}}} \delta } \right) $$
(10)

Figure 10b compares the models for periodic LWR and the measurement data. The trend is predicted by both models, but Wang’s model fails to predict the intensity of the main distinguishing feature of LWR: the satellite order at the zeroth order of diffraction. For the extraction of the diffracted intensities, the patterns were corrected by the solid angle subtended by each pixel to that of the direct beam. The measured intensities (dots) partially follow the behavior of the models for LER and LWR. Previously, a similar analysis was conducted for samples with periodic roughness using the photon energy at 1 keV [13]. The models estimated poorly the amplitude of the roughness. Several reasons may be proposed for the different observed behavior. The photon energy and angle of incidence are different, as is the structure itself. Figures 7 and  4 show diffuse scattering patterns from different rough samples. The combination of the experimental conditions and the sample shape in Fig. 4 do not allow the observation of the modulation of the diffuse scattering by the height, while in Fig 7 it is clearly visible. Moreover, in previous analysis [13], the angle of incidence was rotated to measure the diffraction or the satellite orders. Each variation of the incident angle varies the \(q_z\) component. Thus, the resulting influence of the height on the scattering intensity is much larger.

The present study does not directly analyze the influence of the height distribution on the diffracted intensities. The angular distribution of the diffuse scattering intensity is an interplay between the form factor and structure factor of the grating, the amplitude and distribution of the roughness and the roughness type. It has been reported that different layouts of the roughness lead to different line shapes and thus, scatter differently [9]. However, these samples were produced in such a way that the influence of the line-edge roughness on the scattering pattern is rather large compared to other parameter variations on the sample. Within a sample structure, height might vary depending on the position of the line edge and thus redistribute the diffuse scattering.

4 Conclusions

A dedicated set of samples covering different types of roughness (LER or LWR) and different amplitudes, distributions (periodic, chirped, and stochastic) and correlation lengths was analyzed using EUV scatterometry. The already-reported behavior depending on the type of roughness has been verified. For the samples with LER, no satellite order is observed at the position of the zeroth order, while for LWR it is. Binary models, where the height of the structure is neglected, can explain the distribution of the scattered intensity between the diffraction and satellite orders in this specific case because the modulation caused by the height is not predominant.

The difference between the types of roughness is also shown for samples with chirped roughness. However, the superposition of different frequencies along a line does not explain the diffuse scattering. It is shown that the correlation of one edge to that of neighboring lines must be considered to better explain the distribution of the scattered intensities from stochastic samples. This consideration, together with models that also include the height of the structures, is essential for the further development of roughness analysis using EUV scattering.

It has also been shown that the intensity of the diffuse scattering depends on the amplitude of the roughness, however, further analysis is needed to conclude if the roughness correlation length is also playing a role.