1 Introduction

Cutting force modelling and analysis, as an important process indicator in micro-milling, can collectively reflect the various cutting process phenomena and dynamics such as size effect, chip formation, energy consumption and cutting heat partition, and the machining instability and chatter. It can also be correlated with the tool cutting performance particularly with the tool wear and tool life. Therefore, cutting force is seen as a key formulation to optimize the cutting process variables and tool geometries in micro-cutting processes. A number of cutting force models are proposed and studies for micro-cutting processes [1,2,3,4,5,6,7,8], which falls in four categories, i.e. analytical modelling [9,10,11,12], numerical modelling [7, 8, 13], empirical modelling [14,15,16,17] and hybrid modelling (combining the strengths of previous three modelling approaches). Davoudinejad et al. [18] proposed a 3D FEM for studying the cutting forces in full slot end milling process. The simulation and experimental results indicated that the effect of the run-out phenomenon was visible in the cutting force results and different cutting action could be significantly observed for the two teeth. He also investigated the influence of the worn tool affected by built-up edge (BUE) on micro-end milling process performance via FEM, which demonstrates that the predicted micro-milling cutting forces resulted affected by BUE with different teeth engagements [19]. Zhang et al. [20] proposed an analytical model by considering the minimum chip thickness effect, tool run-out (axial offset and tilt offset) and trochoidal trajectory to determine the cutting forces. These were seen as the most related influence factors in the force model and validated through experiments. Matsumura and Tamura [21] developed an analytical model to evaluate the effect of the cutter run-out on the cutting force in order to perform the milling operation properly. In addition, the experimental results from Kang et al. [22] presented that the effect of cutting edge radius on cutting forces was significant in the micro-scale milling. However, the modelling approaches and techniques developed so far are almost all focused on obtaining the absolute value of cutting forces. In ultraprecision and micro-cutting processes, the cutting forces are at the 0.1–1 N scale compared to that in conventional machining normally being at 100–1000 N scale. The accurate measurement and analysis of their absolute values are challenging and often not applicable particularly in-process and taking account of the cutting dynamics as normally required in industrial applications. In addition, the cutting process phenomenon above mentioned cannot be appropriately reflected as cutting force down to such a small scale. Moreover, most researches focus on the effects of cutting edge, tool run-out and dynamic modulation in cutting force models, while the effect of feed rate on the time delay and actual chip thickness is always ignored. As a result, micro-cutting force modelling by considering the instantaneous chip thickness and cutting dynamics comprehensively is still less understood. Therefore, dynamic cutting force modelling and understanding the dynamic aspects of the cutting force are becoming essentially important for micro-cutting particularly for developing the relevant in-process algorithms and analytics for smart micro-machining.

This paper presents an innovative dynamic cutting force model by considering instantaneous chip thickness in micro-milling and further investigates the scientific understanding of the relevant micro-cutting mechanics and the process dynamics. A comprehensive cutting force modelling, representing the micro-milling forces at the unit length, unit area and further at the unit volume, is proposed in order to establish scientific understanding of the underlying micro-cutting mechanics and physics in a multi-scale manner. This innovative modelling is expected to be industrial feasible and realistic compared to the existing models, and also to take account of the size effect, chip formation, tool wear mechanism and the cutting temperature partition, etc. in a quantitative analysis manner while with physical engineering meanings. The approach is evaluated and validated through well-designed experimental trials, which will likely help the micro-milling process optimization with the application to industrial micro-manufacturing.

2 Chip Thickness Modelling in Micro-milling

2.1 Analytical Chip Thickness

In conventional milling process, the chip thickness can be expressed by a sinusoidal function of feed per tooth approximately as below:

$$ h_{\text{c}} \left( \theta \right) = f_{\text{t}} \sin \theta $$
(1)

where hc(θ) represents the uncut chip thickness, ft is the feed per tooth and θ is the position angle of tool tip from the beginning position of cutting. This presents a good approximation of chip thickness in conventional milling process due to the feed rate is comparatively large.

However, in micro-milling with the scaled-down cutting variables, the function in Eq. (1) is not appropriate or accurate due to the real movement of the cutting tool centre is not taken into account. The tool diameter normally falls less than 1 mm even down to 100 μm, the feed rate usually ranges from 0.1 to 10 μm and the extremely small cutting edge radius cannot be ignored which means the chip thickness calculation in each revolution is even complex in micro-milling process. In addition, dynamic run-out of cutting tool normally ranges from 1 to 5 μm which is extremely tiny in conventional milling. However, the ratio of run-out to tool diameter becomes more significant in micro-milling. Thus, the run-out of tools needs to be considered in order to achieve a precise chip thickness prediction in each revolution. Bao and Tansel [9] proposed an analytical cutting force model which firstly considered the tool run-out effects. Zaman et al. [12] developed a model which determined the theoretical chip area at any specific angular position of the cutting tool tip. Li et al. [23] presented a new algorithm to calculate the actual chip thickness considering the trochoidal trajectory of tool tip with run-out and the minimum chip thickness (MCT) effects.

However, these methods and approaches mentioned above only considered the tool run-out in the machine coordinate system and overlooked the change of cutting tool geometry caused by the run-out of cutting tool. This study proposes a new algorithm to accurately calculate the chip thickness based on the real trajectory of tool tip in the workpiece coordinate system and the actual chip thickness is determined by comparing the nominal chip thickness with MCT at each calculation interval. As a result, this model simulates discontinuous chip formation at particular locations.

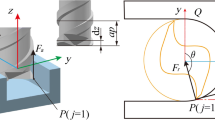
Figure 1 shows a micro-milling tool with a run-out of r at the angle α in workpiece coordinate system, in which the tool spins about the spindle centre O. Previous chip thickness models which include the tool run-out usually determine the tool rotates about the tool centre O′. The particular location of tool centre O′ can be expressed as

$$ \begin{aligned} x & = r\sin \left( {wt + \alpha } \right) + ft/60 \\ y & = r\cos \left( {wt + \alpha } \right) \\ \end{aligned} $$
(2)

where r is the run-out in µm, w is the angular velocity in rad/s, f is the feed rate in µm/min and α is the run-out location angle of actual tool centre in rad.

Fig. 1
figure 1

Tool run-out in micro-milling

Full size image

However, the tool actually rotates about spindle centre O and the rotational radius of each tool tip has changed that represented by red line in Fig. 1. Given the nominal radius of cutting tool, tool run-out and its location angle, the following expression of actual tool radius based on laws of cosines is obtained.

$$ R_{k} = \sqrt {R^{2} + r^{2} - 2Rr\cos \left( {2\pi /N*\left( {k - 1} \right) - \alpha } \right)} $$
(3)

where k is the tooth number, R is the nominal radius of cutting tool and N is the number of tool teeth. The actual velocity direction of tool tip is indicated by solid red arrow in comparison with the nominal direction indicated by dashed arrow shown in Fig. 1. The nominal rake angle of cutting tool is zero, whereas the actual rake angle becomes positive for tooth 1, while negative for tooth 2. The change of rake angle can be formulated by:

$$ \gamma_{\text{c}} = \left( { - 1} \right)^{k + 1} \cos^{ - 1} \left( {\frac{{R^{2} + R_{k}^{2} - r^{2} }}{{2RR_{k} }}} \right) $$
(4)

The change of rake angle can significantly affect the interaction between tool and workpiece. In addition, the change has further effects on the cutting process and tool performance. Thus, it is critical to take this into account when modelling the micro-milling process accurately. Knowing the actual radius of cutting tool and the actual rotation centre O moves along the x-axis at the speed of feed rate, the trajectory versus time of each tool tip can be expressed as:

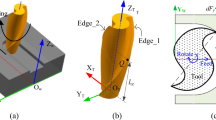
$$ \begin{aligned} x\left( {t,k} \right) & = \frac{ft}{60} + R_{k} \cos \left( {wt - \left( {k - 1} \right)\alpha } \right) \\ y\left( {t,k} \right) & = R_{k} \sin \left( {wt - \left( {k - 1} \right)\alpha } \right) \\ \end{aligned} $$
(5)

Figure 2 illustrates the real tool tip trajectory of a two-fluted mill in micro-milling process. It can be observed that the trajectory is more trochoidal rather than circular. The maximum chip thickness can be found that locates slightly behind 90° rotation angle as shown in this figure. Supposing the kth tool tip is located at point Pc (x, y) at rotation time t, the tool rotation centre is located at position Oc. Thus, the line PcOc has the following expression in the coordinate system:

$$ y = R_{k} \tan^{ - 1} \left( {wt - \left( {k - 1} \right)\alpha } \right)\left( {x - ft/60} \right) $$
(6)
Fig. 2
figure 2

Real tool tip trajectory in micro-milling

Full size image

PcOc represents the cutting edge at the kth tool path intersects with the trajectory of previous (k − 1)th cutting edge at point Pp (xp, yp), supposing the (k − 1)th tool tip reaches point Pp (xp, yp) at time tp and the tool rotation centre is point Op. Similarly, the line PpOp has the following expression:

$$ y_{\text{p}} = R_{k - 1} \tan^{ - 1} \left( {wt_{\text{p}} - \left( {k - 1 - 1} \right)\alpha } \right)\left( {x_{\text{p}} - ft_{\text{p}} /60} \right) $$
(7)

Since it can be observed that point Pp (xp, yp) is also on the line PcOc, by combining Eqs. (6) and (7), the coordinates of point Pp can be derived. Thus, the chip thickness can be seen as the distance between PcPp, which can be eventually expressed as:

$$ h\left( {t,k} \right) = R_{k} - P_{\text{p}} O_{\text{c}} = R_{k} - R_{k - 1} \cos \theta_{\text{p}} /\cos \theta $$
(8)

where θ is the position angle of kth tooth at time point t, and θp is the position angle of (k − 1)th tooth at time point tp. The Newton–Raphson iterative method is utilized to derive tp which satisfies Eq. (7) and the initial value is set to \( t_{\text{p}}^{0} = t - 2\pi /\left( {wN} \right) \).

Due to the uneven tool edge radius, another fact caused by the tool run-out is the change of entry and exit angles. Ideally, the tool entry and exit angles are 0° and 180°, respectively, in slot milling process, whereas the actual tool entry and exit angles of the kth tool tooth can be formulated as:

$$ \theta_{\text{en}}^{k} = \frac{3}{2}\pi + \frac{{\left( {f^{\prime } t_{1} } \right)^{2} + R_{k}^{2} - R_{k - 1}^{2} }}{{2f^{\prime } t_{1} R_{k} }} $$
(9)
$$ \theta_{\text{ex}}^{k} = \frac{3}{2}\pi - \frac{{\left( {f^{\prime } t_{2} } \right)^{2} + R_{k}^{2} - R_{k - 1}^{2} }}{{2f^{\prime } t_{2} R_{k} }} $$
(10)

where f′ is the feed rate per second, t1 and t2 are the time delay between two adjacent cutting tooth acting at the same position on the workpiece.

Figure 3 shows the evolution of the entry and exit angles for a two-flute milling tool along the change of run-out angle. The tool run-out value is fixed, and the actual radius of the 2nd tooth is larger than the 1st tooth at the run-out angle of 0°. The entry and exit angles are determined by the tool radius. The tooth with larger radius has larger entry and exit angle, which is determined by the fact that tool with larger radius starts to remove material prior to passing the vertical line and disengage with material beyond the vertical line shown in Fig. 2. Figure 4 shows the entry and exit angles of the two-flute milling tool at varied run-out while fixed angle. It indicates that the entry and exit angles for the 2nd tooth with larger tool radius hardly change; while for the 1st tooth, entry angle increases and exit angle decreases significantly, which means less engagement on the workpiece material in one revolution.

Fig. 3
figure 3

Entry and exit angles versus tool run-out angles (tool diameter = 1 mm, run-out = 1 µm)

Full size image
Fig. 4
figure 4

Entry angle and exit angles versus tool run-out magnitudes (tool diameter = 1 mm, run-out angle = 60°)

Full size image

2.2 Actual Chip Thickness

From previous research and experimental results, it has been discovered that for tungsten carbide tools, the MCT is around 15% of the tool cutting edge radius [24]. Due to the existence of MCT in micro-milling, cutting without chip formation occurs especially under the conditions of small feed rate or at the entering and exiting points during machining. If the actual chip thickness h(t, k) at time point t is less than the MCT, material deforms elastically or plastically instead of being removed. The residual material is added to uncut chip thickness in the next tooth revolution at the same position angle. This is repeatable until the accumulated chip thickness exceeds the MCT. As a result, chip formation will take place every two or more tooth passes depending on the uncut chip thickness and MCT. In this case, the actual chip thickness can be expressed as:

$$ h_{\text{a}} \left( {t + \Delta t,k + 1} \right) = h\left( {t,k} \right) + h\left( {t + \Delta t,k + 1} \right) $$
(11)

When the uncut chip thickness becomes larger than the MCT, the chips will be formed and removed at the calculated instantaneous chip thickness. The actual chip thickness is then equal to the calculated chip thickness at:

$$ h_{\text{a}} \left( {t,k} \right) = h\left( {t,k} \right) $$
(12)

Figure 5 shows the simulated chip thickness considering the MCT in the vicinity of entering point. The blue curve represents the trajectory of the tool tip, and the red line represents the actual profile after material being removed. It can be seen that due to the existence of cutting edge radius, chips can’t be formed at the beginning and material deforms plastically and recovers to certain level. Only on conditions that the uncut chip thickness exceeds the MCT, the machined profile overlaps with the tool tip trajectory.

Fig. 5
figure 5

Nominal and actual chip thicknesses and their resultant tool tip trajectory and actual machined profile

Full size image

3 Innovative Dynamic Cutting Force Modelling in Micro-milling

3.1 Orthogonal Cutting Force Modelling

Due to the cutting edge radius cannot be ignored, the cutting process in micro-milling is clearly divided into two distinct regimes. One is ploughing-dominant regime where material deforms plastically but no chips are formed; the other is shearing-dominant regime where material is removed with chips formation. The material splits and separates under the round cutting edge. As a result, the upper part forms the chip and the lower part flows beneath the tool and forms the machined surface.

When cutting takes place under MCT, the ploughing forces are assumed to be proportional to the volume of interface between workpiece and tool [6] computed by

$$ \begin{aligned} & {\text{d}}F_{\text{rp}} = (K_{\text{rp}} A_{\text{p}} + K_{\text{re}} ){\text{d}}z \\ & {\text{d}}F_{\text{tp}} = (K_{\text{tp}} A_{\text{p}} + K_{\text{te}} ){\text{d}}z \\ \end{aligned} $$
(13)

where Krp and Ktp are the radial and tangential ploughing coefficients, respectively; Ap is the ploughed area between the tool and workpiece [6]; Kre and Kte are the radial and tangential edge coefficients, respectively; dz is the axial height of each differential flute element;

When machining takes place at uncut chip thickness that larger than MCT, the tangential and radial cutting forces can be modelled as follows:

$$ \begin{aligned} & {\text{d}}F_{\text{rc}} = (K_{\text{rc}} h\left( {\theta_{i} \left( z \right)} \right) + K_{\text{re}} ){\text{d}}z \\ & {\text{d}}F_{\text{tc}} = (K_{\text{tc}} h\left( {\theta_{i} \left( z \right)} \right) + K_{\text{te}} ){\text{d}}z \\ \end{aligned} $$
(14)

where Kre and Kte are the radial and tangential cutting coefficients, respectively; h(θ i (z)) is the uncut chip thickness which is a function of tool position angle θ and axial height z.

The above cutting coefficients are related to the friction and pressure at the interface between tool and workpiece. These coefficients need to be calibrated against the model based on the experimental data. This can be achieved by curve fitting the cutting forces into the model and using least square methods to find the optimal coefficients.

By decomposing the radial and tangential cutting forces into the coordinate system and integration over the range of cutting depth, the forces can be expressed as:

$$ \begin{aligned} & F_{x} \left( {t,k} \right) = R\cot \beta \mathop \smallint \limits_{{\theta_{\text{en}} }}^{{\theta_{\text{ex}} }} \left( {K_{\text{rp}} A_{\text{p}} \sin \theta + K_{\text{re}} \sin \theta + K_{\text{tp}} A_{\text{p}} \cos \theta + K_{\text{te}} \cos \theta } \right){\text{d}}\theta \\ & F_{y} \left( {t,k} \right) = R\cot \beta \mathop \smallint \limits_{{\theta_{\text{en}} }}^{{\theta_{\text{ex}} }} \left( {K_{\text{rp}} A_{\text{p}} \cos \theta + K_{\text{re}} \cos \theta - K_{\text{tp}} A_{\text{p}} \sin \theta - K_{\text{te}} \sin \theta } \right){\text{d}}\theta \\ \end{aligned} $$
(15)

when h < hmin:

$$ \begin{aligned} & F_{x} \left( {t,k} \right) = R\cot \beta \mathop \smallint \limits_{{\theta_{\text{en}} }}^{{\theta_{\text{ex}} }} \left( {\begin{array}{*{20}c} {K_{\text{rc}} h\left( {\theta_{i} \left( z \right)} \right)\sin \theta + K_{\text{re}} \sin \theta + \cdots } \\ {K_{\text{tc}} h\left( {\theta_{i} \left( z \right)} \right)\cos \theta + K_{\text{te}} \cos \theta } \\ \end{array} } \right){\text{d}}\theta \\ & F_{y} \left( {t,k} \right) = R\cot \beta \mathop \smallint \limits_{{\theta_{\text{en}} }}^{{\theta_{\text{ex}} }} \left( {\begin{array}{*{20}c} {K_{\text{rc}} h\left( {\theta_{i} \left( z \right)} \right)\cos \theta + K_{\text{re}} \cos \theta - \cdots } \\ {K_{\text{tc}} h\left( {\theta_{i} \left( z \right)} \right)\sin \theta - K_{\text{te}} \sin \theta } \\ \end{array} } \right){\text{d}}\theta \\ \end{aligned} $$
(16)

when h ≥ hmin: where θen and θex are the entry angle and exit angle of cutting flute when it engages and disengages with material; β is the helix angle of the flute; dθ = dz/R * tanβ considering the influence of the helix angle.

It should be noted that as the chip thickness changes periodically, both ploughing-dominant cutting and shearing-dominant cutting will take place in each revolution. Thus, the cutting forces should be calculated using both Eqs. (15) and (16).

3.2 The Proposed Innovative Approach to Cutting Force Modelling

The afore-described modelling technique [6] can be used to predict the cutting forces. However, previous research and experiments show that cutting force in micro-machining is quite small down to the 0.1–1 N scale in magnitude. The direct usage of absolute cutting force imposes the technical challenge in accurate prediction of the micro-cutting forces particularly in the micro-cutting process. Furthermore, it is essential in developing the cutting force model for bridging the gaps between understanding the micro-cutting mechanics and the process optimization together with cutting performance enhancement. Therefore, an innovative cutting force modelling is proposed to provide quantitative analysis into micro-milling mechanics and the cutting process, which is further presented in detail below.

3.2.1 Cutting Force at Unit Length

The cutting force at the unit length can provide force distribution at the changing positions. Considering the existing helix angle, the total length of cutting flute engaged with material is expressed as follows:

$$ l = R\left( {\theta_{\text{ex}} - \theta_{\text{en}} } \right)/\sin \beta $$
(17)

Thus, the cutting force on unit length is represented as:

$$ F_{lx} \left( {t,k} \right) = \frac{{F_{x} \left( t \right)\cos \beta }}{{\left( {\theta_{\text{ex}} - \theta_{\text{en}} } \right)}};F_{ly} \left( {t,k} \right) = \frac{{F_{y} \left( t \right)\cos \beta }}{{\left( {\theta_{\text{ex}} - \theta_{\text{en}} } \right)}} $$
(18)

The cutting force at the unit length can be used to predict the burrs formation in micro-milling and likely render the foundation for the process optimization particularly in avoiding the burrs formation along the edges of micro-milled surface.

3.2.2 Cutting Force at Unit Area

The cross section of the chip generated in micro-milling is also a function of position angle that can be formulated as follows:

$$ s = \frac{R}{\sin \beta }\mathop \smallint \limits_{{\theta_{\text{en}} }}^{{\theta_{\text{ex}} }} h\left( {\theta_{i} \left( z \right)} \right){\text{d}}\theta $$
(19)

The cutting force on unit area is calculated as:

$$ F_{\text{sx}} \left( {t,k} \right) = \frac{{F_{x} \left( t \right)\sin \beta }}{{R\mathop \smallint \nolimits_{{\theta_{\text{en}} }}^{{\theta_{\text{ex}} }} h\left( {\theta_{i} \left( z \right)} \right){\text{d}}\theta }};\quad F_{\text{sy}} \left( {t,k} \right) = \frac{{F_{y} \left( t \right)\sin \beta }}{{R\mathop \smallint \nolimits_{{\theta_{\text{en}} }}^{{\theta_{\text{ex}} }} h\left( {\theta_{i} \left( z \right)} \right){\text{d}}\theta }} $$
(20)

The cutting force on unit area can be closely linked with the Young’s modulus of the workpiece material, which can provide insightful information on the chip formation and breakage, surface generation and even tool wears at both rake and flank surfaces of cutting tool [25].

3.2.3 Cutting Force at Unit Volume

The volume of material being removed in micro-milling can be expressed approximately as:

$$ {\text{d}}V = v{\text{d}}tR\cot \beta \mathop \smallint \limits_{{\theta_{\text{en}} }}^{{\theta_{\text{ex}} }} h\left( {\theta_{i} \left( z \right)} \right){\text{d}}\theta $$
(21)

The cutting force in the unit volume has the physical meaning, which can directly lead to the energy consumption in unit volume. The cutting energy consumption in a unit volume can be further represented in the following formulation:

$$ e = \frac{{Fv{\text{d}}t}}{{{\text{d}}V}} = \frac{F\tan \beta }{{R\mathop \smallint \nolimits_{{\theta_{\text{en}} }}^{{\theta_{\text{ex}} }} h\left( {\theta_{i} \left( z \right)} \right){\text{d}}\theta }} $$
(22)

The energy consumption on unit volume can be used to compute the cutting heat partition in the micro-milling tool, chips and workpiece. Scientific understanding and quantitative determination of the heat partition ratio in micro-milling are essentially important, as it can likely provide further quantitative analysis on the tool wear mechanism and cutting performance in the process.

4 Experimental Evaluation and Validation

4.1 Cutting Trials Design and Experimental Set-up

The experimental set-up is shown in Fig. 6. The workpiece is placed on top of a Kistler dynamometer 9256C2 via the bolted connection. Transfer function from the workpiece to the dynamometer is measured and compensated. Various milling tools are employed including the natural diamond and tungsten carbide single-fluted tools and also normal end mills with helix flutes. Experiments are conducted at varied feed rate and cutting speed to broadly study the machining process. The cutting parameters in the experiments are listed in Table 1.

Fig. 6
figure 6

Experiment set-up for evaluating and validating the cutting force modelling

Full size image
Table 1 Cutting process parameters used in micro-milling experiments
Full size table

4.2 Measurement of the Tool Run-out

The run-out of cutting tool and its position angle is measured at the tool tip. Various factors can contribute to the run-out magnitude such as manufacturing error, alignment error and tool dynamics. Previous research and experiments show that the most significant run-out error is introduced by the alignment error. This mainly consists of the parallel tool offset and tilt error. For most cases in the experiments, the tilt error has extremely small effect on the tool run-out as the small cutting depth adopted in cutting trials. Thus, the tool run-out error measurement is mainly focused on the tool parallel offset and its position angle.

The nominal diameter of cutting tool is firstly measured on the TESA-200 microscope. The rotational tool run-out is measured by using the capacitive sensor MicroSense 5810. To measure the location angle, two marks are attached to the tool in alignment with the opposite two tool tips, thus the increment angle is exactly 180°. The two marks are captured by the sensor, and the actual increment angle can be derived by calculating the angle between them. The position angle of the tool run-out can be determined by the difference. Tool run-out is measured at varied spindle speed adopted in the experiments. Figure 7 shows the tool run-out for 1-mm tungsten carbide tool. The magnitude is around 5–6 µm and the position angle is derived at 30° which is a constant for specified tool-holder pair.

Fig. 7
figure 7

Tool run-out magnitudes versus spindle speed

Full size image

4.3 Cutting Force Model Calibration and Validation

4.3.1 Parameters Calibration

Experiments are carried out at varied feed rate and spindle speed as shown in Table 1. The collected forces are used to compute the coefficients in the cutting force model. Due to the periodical change of chip thickness in each revolution, the machining process experiences both ploughing-dominant cutting and shearing-dominant cutting. The transition is determined by comparing the actual chip thickness with the MCT. The actual chip thickness is obtained based on the algorithm proposed. The MCT is around 15% of the cutting edge radius which is 1.4 μm [24]. The cutting forces are divided into two groups based on different cutting regimes. The ploughing and its edge coefficients are obtained by fitting forces into Eq. (13); the cutting and edge coefficients are obtained by fitting forces into Eq. (14). For this purpose, the least square method is adopted in which the coefficients are determined once the sum of squares of the error between predicted force and experimental results reaches the minimum:

$$ E = \mathop \sum \limits_{i = 1}^{n} \mathop \sum \limits_{j = 1}^{m} \left( {F_{\text{pre}} - F_{ \exp } } \right)^{2} $$
(23)

where n is the number of feed rates used in curve fitting, and m is the number of data points. Fpre is the predicted force by the model, and Fexp is the collected experimental force. In this study, five feed rates and 300 data points for each feed rate are used to calculate the coefficients. The obtained coefficients are shown in Table 2.

Table 2 Cutting force model coefficients for different cutting regimes
Full size table

4.3.2 Model Validation

Figure 8 plots the simulated and experimental cutting force by using the single-flute tool, which shows a good agreement. The peak difference between prediction and measurement results is less than 10%. The model can be used to predict the evolution and magnitude of the cutting force but fail to explain the fluctuation in real cutting forces due to the limitation of the modelling technique. These fluctuations, considering the machining process, are introduced by machine and tool vibrations. The single flute tungsten carbide tool is used, and only one chip is formed in each revolution. The predicted cutting forces are zero since the tool disengages material in the latter half revolution, while the measured forces show otherwise. The strong attachment of material attached to the tool which continues scratching the material and causes the fluctuation in the cutting force is the probable reason.

Fig. 8
figure 8

Comparison between the simulated and experimental cutting forces (slot-milling; single-flute tool; spindle rotational speed: 21,000 rpm; feed rate: 2 μm/tooth). a The simulated and experimental cutting forces in x-direction. b The simulated and experimental cutting forces in y-direction

Full size image

Figure 9 shows the predicted and measured cutting force using 1-mm two-flute milling tool by adopting the same modelling method. In this cutting trial, the measured run-out is 4.5 µm and its location angle is 79°, which results in the larger radius of 500.8 µm and the smaller one of 499.24 µm. The comparison shows a good agreement between the predicted and measured cutting forces. It also indicates that due to the existence of the tool run-out, cutting forces generated by one flute with larger radius is significantly larger than that generated by the flute with smaller radius.

Fig. 9
figure 9

Comparison between the simulated and experimental cutting forces (slot milling; two-flute tool; spindle speed: 18,000 rpm; feed rate: 3 μm/tooth). a The simulated and experimental cutting forces in x-direction. b The simulated and experimental cutting forces in y-direction

Full size image

The predicted cutting forces are also compared with the conventional cutting force model without considering the tool run-out and MCT effect. Figure 10 shows the comparison and it can be clearly observed that the conventional method can only predict periodical cutting force, which fluctuates with single amplitude and periodicity. It can also be seen that the amplitude of the periodical force is smaller than that generated with larger radius while larger than that generated with smaller radius in both predicted and measured forces, which results in smaller chip thickness.

Fig. 10
figure 10

Comparison between measured force in x-direction under proposed method and conventional method

Full size image

4.4 Model Interpretation of the Machining Process

The proposed model attempts to interpret the machining process at varied feed rates in three aspects, which are the resultant cutting force on unit length or area and the energy consumption in unit volume. For the single straight flute tools, the force on unit length is similar to the resultant force. Figure 11 shows the calculation results at different feed rates for both diamond and tungsten carbide tools.

Fig. 11
figure 11

Total cutting force at the unit length versus angular position (spindle rotational speed: 21,000 rpm). a tungsten carbide tool, b diamond tool

Full size image

It can be found that the magnitude of specific cutting force increases along with feed rate. The fluctuations are due to material impurity, tool vibration and different chip formation mechanism. It should be noted that the magnitude at proximity of 180° is higher than that at 0°, which is shown in both plots. This is probably due to the reason of intact chips being removed by the tool at 180°, while the tool just engages with material at 0° and doesn’t remove any material until chips are formed.

As for straight flute cutting tools, the cutting force on unit area and energy consumption on unit volume of material are the same from the point of mathematical computation. Figure 11 also indicates the stress exerted on the tool, at around 180°, the stress rises up dramatically from 50 to 500 GPa. Comparing with the major properties of tungsten carbide tool with shear modulus of 274 GPa, tensile strength of 344 MPa and compression strength of 2.7 GPa, it can be indicated that although the force magnitude is small, the stresses that the tool is exposed to are extremely large. This can be used to explain the tool wear in micro-milling process. The constituent elements of tool are gradually removed in every revolution.

Figures 12 and 14 plot the cutting energy consumption in the unit volume of materials being machined by using both tungsten carbide tools and diamond tools. It significantly shows that the energy consumption at the entry and exit proximity is much higher than that in the middle of revolution. In addition, at the exit proximity, the energy consumption rises up exponentially. From Fig. 12a, b, it can be observed that the order of magnitude can be 10 times higher for tungsten carbide tool, which is a strong indication of size effect due to the existence of relatively large cutting edge radius. However, the energy consumed in the middle of revolution does not change too much and mostly stays constant as can be seen in both plots. This indicates that when chips are formed, the energy consumption in unit volume of material does not change a lot along with the cutting depth. Comparing the energy consumed by using different tools, it can be found that more energy is depleted by using tungsten carbide tools, which is not only due to tool properties, but also the large cutting edge radius effects.

Fig. 12
figure 12

Energy consumption on unit volume at varied feed rates: a tungsten carbide tool, b diamond tool

Full size image

The proposed model is also applied to more general tools, i.e. tool with helix angle. For tungsten carbide tools with helix angle, the contact length at certain moment depends on the axial cutting depth and tool position angle. Since the tool is discretized in axial direction, the contact length can be approximated by considering the helix angle and axial depth of cut:

$$ L = \mathop \sum \limits_{1}^{n} d \times \tan^{ - 1} \beta $$
(24)

where d is the depth of incremental element, and β is the helix angle. The instantaneous volume of material can be approximated as follows:

$$ V = S \times v \times dt $$
(25)

where v is the cutting speed and dt is the data sampling interval, S is the contact area and it has following expression:

$$ S = \mathop \sum \limits_{1}^{n} \left( {h\left( {\theta ,k} \right) \times d \times \tan^{ - 1} \beta } \right) $$
(26)

Experiments are carried out at a wide range of feed rates from 1 to 14 μm/tooth. Figures 13 and 14 show that the force on unit cutting length has the similar form as the total resultant cutting force. This indicates that for such small depth of cut, the influence of the helix angle is not obvious. The energy consumption on unit volume of material shows that the size effect becomes less and less obvious with the feed rate increases. At lower feed rates, the chip thickness at the proximity of entry and exit points is close to the cutting edge radius. However, the chip thickness at the same position angle at larger feed rates is much higher than the cutting edge radius, thus, the chips are formed quickly and the cutting energy consumed on unit volume of material decreases quickly and drops by levels. It should be noted that as the feed rate becomes larger, the energy consumed on unit volume of material, on the contrary, becomes less as shown in Fig. 14. The zoom-in view shows that the difference among different feed rates also gets smaller. This result indicates that once chips are formed, the larger the cutting depth used, the less energy will be consumed on unit volume of material. The relation between them is not linear, which implies a sharper cutting edge will make material removal easier from another aspect. Based on these findings, we can also predict that the energy consumed on unit volume of material at same feed rate will increase due to more distinct size effect when tool wear occurs.

Fig. 13
figure 13

Total cutting forces on the unit cutting length at varied feed rates

Full size image
Fig. 14
figure 14

Cutting energy consumption on a unit volume of materials being machined at varied feed rates

Full size image

5 Conclusions

In this paper, an innovative investigation on the micro-milling mechanics is presented particularly focusing on the innovative dynamic cutting force modelling and its intrinsic relationships with micro-milling chip formation, minimum chip thickness (MCT), cutting temperature partition and surface generation, etc. further supported by experimental evaluation and validation. The main conclusions can be drawn as follows:

  1. 1.

    An innovative cutting force modelling approach is presented for computing the instantaneous chip thickness while taking account of the micro-milling tool run-out. It is found that the tool run-out has significant effects on the actual tool radius and cutting geometry in micro-milling. Furthermore, the MCT is also included in the associated new algorithm supported by computational procedures.

  2. 2.

    The cutting force model for the micro-milling process is developed in a multi-scale manner, including the cutting force at the unit length, specific cutting force at the unit area, and further cutting force or cutting energy consumption in the unit volume of materials being machined. This model is of significance in likely leading to better scientific understanding of micro-milling mechanics, which will help render the in-depth analysis of the sharp edge quality (burrs and voids) in micro-milling, chip formation, surface generation and micro-cutting heat and temperature partition.

  3. 3.

    Experimental cutting trials are conducted to validate the modelling approach and the cutting force model. The method to determine the tool run-out is introduced experimentally. For accurate measurement of cutting forces, a Kalman filter is developed and applied to compensate the distortion in cutting force signals due to the dynamic transmission characteristics of the tooling-workpiece system. Based on the compensated cutting forces, the cutting force model is calibrated and proved with the good agreement with experimental trials.

  4. 4.

    The cutting force modelling presented can be applied to scientifically interpret and better understand the underlying micro-cutting mechanics in the micro-milling process particularly linking to burrs-free machining, chip formation and surface generation, and the tool cutting performance and tool wear. Furthermore, the modelling and the associated analytics can likely be used to gauge the cutting process in real time and thus able to simulate the dynamic surface generation by combining a virtual micro-milling system and digital twin in the future.