Skip to main content
SpringerLink
Log in

Investigation of fuzzy semi-Markovian model for single unit systems with partial failure and Weibull distributed random laws

  • Original Research
  • Published:
International Journal of Information Technology Aims and scope Submit manuscript

Abstract

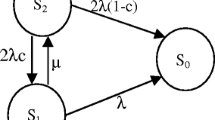
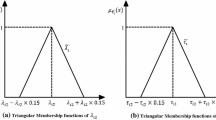
The prominent objective of present study is to investigate the fuzzy reliability measures of a semi-Markovian model under the concept of partial failure of the system, inspection, and abnormal environment. The stochastic model is developed using regenerative point technique. All the failure and repair rates followed Weibull distribution having fuzzy parameters defined using bell shaped membership function. All random variables are independent to each other, and repairs are perfect. The measures of system effectiveness are evaluated for various values of shape parameters with the help of the proposed algorithm. The numerical values of mean time to system failure and availability are evaluated based on the estimated values of the parameters.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

References

  1. Saini M, Dahiya O, Kumar A (2021) Modeling and availability analysis of data centre: a fuzzy approach. Int J Inf Technol 13(6):2453–2460

    Google Scholar 

  2. Saini M, Goyal D, Kumar A, Patil RB (2022) Availability optimization of biological and chemical processing unit using genetic algorithm and particle swarm optimization. Int J Qual Reliab Manag. https://doi.org/10.1108/IJQRM-08-2021-0283 (Vol. ahead-of-print No. ahead-of-print)

    Article  Google Scholar 

  3. Kumar A, Saini M, Gupta N, Sinwar D, Singh D, Kaur M, Lee HN (2022) Efficient stochastic model for operational availability optimization of cooling tower using metaheuristic algorithms. IEEE Access 10:24659–24677

    Article  Google Scholar 

  4. Kumar A, Goyal D, Sinwar D, Saini M (2022) Stochastic modeling and performance optimization of sludge digestion processing system using genetic algorithm. Int J Inform Technol 1–10

  5. Kumar A, Saini M (2018) Comparison of reliability characteristics of two semi-Markov repairable systems under degradation and abnormal environment. Life Cycle Reliab Saf Eng 7(4):257–268

    Article  Google Scholar 

  6. Kumar A, Pawar D, Malik SC (2019) Profit analysis of a warm standby non-identical unit system with single server performing in normal/abnormal environment. Life Cycle Reliab Saf Eng 8(3):219–226

    Article  Google Scholar 

  7. Aggarwal C, Malik SC (2020) A standby repairable system with rest of server between repairs. J Stat Manag Syst 23(8):1485–1496

    Google Scholar 

  8. Saini M, Gupta N, Kumar A (2021) Stochastic modeling and sensitivity analysis of condenser in steam turbine power plants. Glob Stoch Anal 8(2):101–119

    Google Scholar 

  9. Wang Z, Pan R (2021) Point and interval estimators of reliability indices for repairable systems using the Weibull generalized renewal process. IEEE Access 9:6981–6989

    Article  Google Scholar 

  10. Hussainy ST, Shabeer B (2021) A study on stochastic modelling of the repairable system. J Comput Math 5(2):76–82

    Google Scholar 

  11. Saini M, Devi K, Kumar A (2020) Stochastic modeling and profit evaluation of a redundant system with priority subject to Weibull densities for failure and repair. In: International Conference on Information and Communication Technology for Intelligent Systems. Springer, Singapore, pp 11–20

  12. Kishan R, Jain D (2014) Classical and Bayesian analysis of reliability characteristics of a two-unit parallel system with Weibull failure and repair laws. Int J Syst Assur Eng Manag 5(3):252–261

    Article  Google Scholar 

  13. Tyagi S, Kumar D, Kumar S (2019) Open source software: analysis of available reliability models keeping security in the forefront. Int J Inform Technol 1–10

  14. Das D, Tripathy CR, Tripathy PK, Kabat MR (2020) System reliability estimation of constrained multi-state computational grids. Int J Inf Technol 12(4):1419–1425

    Google Scholar 

  15. Kumar A, Saini M (2018) Stochastic modeling and cost-benefit analysis of computing device with fault detection subject to expert repair facility. Int J Inf Technol 10(3):391–401

    MathSciNet  Google Scholar 

  16. Zadeh LA (1965) Information and control. Fuzzy sets 8(3):338–353

    Google Scholar 

  17. Dutta P, Limboo B (2017) Bell-shaped fuzzy soft sets and their application in medical diagnosis. Fuzzy Inform Eng 9(1):67–91

    Article  Google Scholar 

  18. Temraz NSY (2021) Comparison of fuzzy semi-Markov models for one unit with mixed standby units with and without preventive maintenance using regenerative point method. Heliyon 7(8):e07717

    Article  Google Scholar 

  19. He Y, Chen Z, Zhao Y, Han X, Zhou D (2019) Mission reliability evaluation for fuzzy multistate manufacturing system based on an extended stochastic flow network. IEEE Trans Reliab 69(4):1239–1253

    Article  Google Scholar 

  20. Larsen EM, Ding Y, Li YF, Zio E (2020) Definitions of generalized multi-performance weighted multi-state K-out-of-n system and its reliability evaluations. Reliab Eng Syst Saf 199:105876

    Article  Google Scholar 

  21. Aghili SJ, Hajian-Hoseinabadi H (2017) Reliability evaluation of repairable systems using various fuzzy-based methods—a substation automation case study. Int J Electr Power Energy Syst 85:130–142

    Article  Google Scholar 

  22. Ding R, Liu Z, Xu J, Meng F, Sui Y, Men X (2021) A novel approach for reliability assessment of residual heat removal system for HPR1000 based on failure mode and effect analysis, fault tree analysis, and fuzzy Bayesian network methods. Reliab Eng Syst Saf 216:107911

    Article  Google Scholar 

  23. Kumar M (2020) A novel weakest t-norm based fuzzy fault tree analysis through qualitative data processing and its application in system reliability evaluation. J Intell Syst 29(1):977–993

    Article  Google Scholar 

  24. Pramanik R, Baidya DK, Dhang N (2021) Reliability assessment of three-dimensional bearing capacity of shallow foundation using fuzzy set theory. Front Struct Civ Eng 15(2):478–489

    Article  Google Scholar 

  25. Patrai K, Uprety I (2015) Reliability assessment of a degradable system with fuzzy lifetime distribution. In: International Conference on Computing, Communication & Automation. IEEE, pp 208–212

  26. Liu K, Dang W, Zou T, Lü C, Li P, Zhang H (2021) Reliability evaluation of two-phase degradation process with a fuzzy change-point. J Shanghai Jiaotong Univ (Sci) 1–6

  27. Kumar A, Saini M (2018) Mathematical modeling of sugar plant: a fuzzy approach. Life Cycle Reliab Saf Eng 7(1):11–22

    Article  MathSciNet  Google Scholar 

  28. Kumar A, Saini M (2018) Fuzzy availability analysis of a marine power plant. Mater Today: Proc 5(11):25195–25202

    Google Scholar 

  29. Dahiya OMBIR, Kumar ASHISH, Saini MONIKA (2019) An analysis of feeding system of sugar plant subject to coverage factor. Int J Mech Prod Eng Res Dev (IJMPERD) 9(1):495–508

    Google Scholar 

  30. Dahiya O, Kumar A, Saini M (2019) Mathematical modeling and performance evaluation of A-pan crystallization system in a sugar industry. SN Appl Sci 1(4):1–9

    Article  Google Scholar 

  31. Dahiya O, Kumar A, Saini M (2020) Modeling and analysis of concrete mixture plant subject to coverage factor and profust reliability approach. Life Cycle Reliab Saf Eng 9(3):273–281

    Article  Google Scholar 

  32. Khurshid S, Shrivastava AK, Iqbal J (2021) Effort based software reliability model with fault reduction factor, change point and imperfect debugging. Int J Inf Technol 13(1):331–340

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics and Statistics, Manipal University Jaipur, Jaipur, 303007, India

    Vijay Singh Maan, Monika Saini & Ashish Kumar

Authors
  1. Vijay Singh Maan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Monika Saini
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ashish Kumar
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ashish Kumar.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Maan, V.S., Saini, M. & Kumar, A. Investigation of fuzzy semi-Markovian model for single unit systems with partial failure and Weibull distributed random laws. Int. j. inf. tecnol. 14, 2971–2980 (2022). https://doi.org/10.1007/s41870-022-01070-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s41870-022-01070-0

Keywords

Search

Navigation