1 Introduction

The implementation of stricter pollution emission regulations by local governments and international organizations has resulted in a general decrease in pollutant concentrations worldwide (Baldasano et al. 2003). For example, recent global air quality studies conducted over the past decade reveal that noxious pollutants levels have been on the decline across most regions of the world (Venter et al. 2020). However, this decline does not hold true for all pollutants nor for all areas of the world (Lelieveld et al. 2015; Van Donkelaar et al. 2015). Concentrations of NO2 are routinely found to be at or near the safety threshold guidelines established by the World Health Organization (WHO) (WHO 2018). Particulate matter has also emerged as a critical environmental issue in Asia, with some areas experiencing concentrations in excess of 300 g/m3 (Gupta & Christopher 2009), far above the safety threshold. Furthermore, Ozone levels have consistently exceeded established guideline limits for many regions of the world, indicating that it remains a global problem of significant concern (EPA 2021; UNEP/WMO, 2011). Other studies have suggested that despite advancements in some regions (i.e. the Global North), developing nations and those with low average incomes (Global South) continue to experience comparatively high levels of air pollution (Brauer et al. 2016; Chowdhury et al. 2019; Shaddick et al. 2018). Moreover, as Global South countries continue to grow, there is a tendency for air pollution levels to increase further, thereby exacerbating the already dire situation (Baldasano et al. 2003; Mage et al. 1996). In fact, the Global South now accounts for roughly 80% of the world's population and has been marked by extensive urbanization, industrialization, and rampant deforestation (Bologna and Aquino 2020; Patinvoh and Taherzadeh 2019; United Nations 2019) which is associated with further degradation in air quality.

In addition to respiratory and other health related issues associated with a decline in air quality (Domingo and Rovira 2020), there are other important implications related to the ambient environment. Specifically, increases in air pollution are associated with an increase in LST (Cao et al. 2016). Research indicates that urban aerosols or haze is one of the leading factors for this increase because it can substantially exacerbate the Urban Heat Island (UHI) effect. Haze contributes to an increase in nighttime surface temperature UHI by approximately 0.7 ± 0.3˚C (mean ± 1 standard error). Notably, this effect varies spatially and tends to intensify with seasonal changes in humidity and the associated AOD (Cao et al. 2016). The utilization of remote sensing data is particularly advantageous when it comes to monitoring AOD. For instance, Biswas et al. (2017) utilized remote sensing to reveal that the highest AOD concentrations in India are observed during the pre-monsoon season (March–May) that gradually diminishes in the post-monsoon period (October–November). Others have used remote sensing to evaluate a more explicit connection between the AOD and LST (He 2022; Islam et al. 2022; Z. Liu et al. 2020; Perone 2022; Wu et al. 2022).

Increases in LST contribute to the UHI effect. The UHI effect is marked by elevated temperatures in metropolitan regions when contrasted with their rural counterparts. Given the relationship between air pollution and LST, the UHI effect can be partly attributed to the assimilation and preservation of heat by pollutants, including nitrogen oxides and particulate matter (Akbari et al. 2001; Kafy et al. 2022; Z. A. Rahaman et al. 2022a, b; Ruan et al. 2021), which work to alter the reflectance of the earth's surface and lead to changes in temperature (Bond et al. 2013). Moreover, studies have established that air pollution can exert a substantial influence on vegetation health which is an important urban heat regulator (Park et al. 2021). For example, Kumari et al. (2021) and others (Rahaman et al. 2023; Tian et al. 2020) have found that elevated levels of pollutants, such as ozone and sulfur dioxide, can harm vegetation and lead to fluctuations in surface temperatures.

The interplay between LST and air pollutants' concentration, pivotal for urban and environmental planning, can be discerned through the lens of remote sensing data and statistical analysis. Leveraging correlation and regression analyses, researchers have shed light on this intricate relationship, advocating for the integration of more nuanced methods like GWR and PCA to refine predictions' precision and locality. Henderson et al. (2007) demonstrated the application of Land Use Regression (LUR) in predicting nitrogen oxides and fine particulate matter concentrations, employing GIS-generated variables to construct models with enhanced spatial resolution (Henderson et al. 2007). This methodology echoes through the work of Hoek et al. (2008), who underscored LUR models' efficacy in modeling pollutants like NO2 and PM2.5 and called for models that incorporate additional predictors, such as wind direction, to increase applicability across various locales (Hoek et al. 2008). Further, Mo et al. (2021) reviewed LST reconstruction methods, categorizing them and emphasizing the importance of validating reconstructed LST datasets, a crucial step for the practical application of remote sensing in environmental studies (Mo et al. 2021). Voogt and Oke (2003) discussed the application of thermal remote sensing in urban areas, particularly in assessing urban heat islands, yet observed a lag in advancing beyond qualitative descriptions to quantitative analysis, suggesting a potential for incorporating PCA for deeper insights (Voogt and Oke 2003). Steinle et al. (2013) pointed towards a paradigm shift towards using sensor technology for detailed spatial and temporal monitoring of pollutant concentrations, which could significantly benefit from advanced statistical techniques including PCA (Steinle et al. 2013). While these studies collectively highlight advanced statistical methods' potential, such as GWR and PCA, in enhancing our understanding of pollution patterns, a direct examination of PCA in creating a pollutant index was not identified, indicating a possible research gap or an area ripe for further exploration.

The correlation between air pollution and LST, particularly in industrializing nations, is an area of growing global concern (Tan et al. 2010; Ahmed et al. 2023). Research has demonstrated a link between changes in land use, often due to industrialization, and intensification of UHI (L. Liu and Zhang 2011). The use of remote sensing data has also proven effective in assessing UHI, as exemplified by a study in Hong Kong (L. Liu and Zhang 2011). The potential exacerbation of worldwide global warming, due to the contribution of air pollutants to LST cannot be ignored, particularly given the prevalence of air pollution in many developing countries. To comprehensively evaluate the spatial–temporal connection of multiple air pollutants and LST, there is a pressing need for new spatial–temporal methods that leverage remote sensing data. Current research underscores the complex interplay between air pollutants, urban land use, and LST, but often falls short in capturing the nuanced dynamics over time and space due to limitations in traditional modeling approaches. For example, studies such as Weissert et al. (2019) and Zimmerman et al. (2020) have made significant strides in understanding pollution variability and the impact of local sources using low-cost sensors and land use regression models. However, these approaches may not fully exploit the potential of remote sensing data to capture the broader spatial extent and temporal variability of air quality and LST across diverse urban landscapes (Weissert et al. 2019; Zimmerman et al. 2020). The reliance on ground-level monitoring and local sensor networks, while invaluable for high-resolution local analysis, may not adequately represent the spatial heterogeneity and temporal patterns captured by satellite observations. This gap highlights the need to develop innovative methodologies that incorporate remote sensing data, enabling a more comprehensive understanding of how LST depends on air pollutants.

Bangladesh, particularly its capital city, Dhaka, has been identified as one of the most polluted urban areas worldwide in terms of air quality (IQAir 2020; Salam et al. 2021; Zaman et al. 2021). A report by the World Bank indicates that from 2018 to 2021, Bangladesh ranked second highest in air pollution levels due in part to rapid urbanization, uncontrolled vehicular regulations, and deforestation (Begum and Hopke 2019; THE WORLD BANK 2022) that are responsible for high levels of PM2.5 from the combustion of fossil fuels (gasoline, oil, and diesel), as well as PM10 from the burning of wood. The precipitous rise in air pollution has exacerbated the UHI phenomenon (Kafy et al. 2020, 2021; Naim and Kafy 2021). Although there is considerable research examining the connection between air pollutants and LST in various regions of Bangladesh, focusing on either single or multiple pollutants, the spatial–temporal relationship between multiple air pollutants and LST at a national scale remains unexplored. This study aims to elucidate the relationship between air pollutants and LST of Bangladesh by employing cloud-based spatial–temporal remote sensing data at the national level and develop a pollutant index, in order to identify the locations where air pollutants are increasing LST over time.

2 Methods

2.1 Study Area

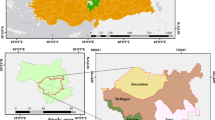
Situated in the southern region of Asia, Bangladesh is bordered by India to its west, north, and east, and Myanmar to its southeast. As of 2021, the country accommodates approximately 166.50 million people, which makes up 2.11% of the global population (Khatun et al. 2021). The south of the country opens onto the Bay of Bengal, offering a natural maritime outlet, with only sparse hills found in the northeastern and southeastern corners (Ali et al. 2023). The country's coordinates roughly fall between 20.34° and 26.39° North in latitude and 88.01° and 92.41° East in longitude.

Administratively, Bangladesh is divided into eight divisions, representing the second-tier administrative delineations. These divisions are Barisal, Chattagram (Chittagong), Dhaka, Khulna, Mymensingh, Rajshahi, Rangpur, and Sylhet. Each of these is further subdivided into districts, or 'Zilas', making up the third tier of the administrative structure. The country consists of 64 such districts. These districts are further divided into 'Upazilas' or sub-districts, forming the fourth administrative level. The smallest rural administrative units are the unions into which these Upazilas are divided. Conversely, urban areas in Bangladesh are systematically divided into administrative divisions known as wards and 'mahallas'. Bangladesh is composed of twelve distinct city corporation areas, as illustrated in Fig. 1. Dhaka, the nation's capital, is also its largest city. (Central Intelligence Agency 2022). Our study focuses predominantly on this fourth-tier administrative boundary for its analysis. Figure 1 illustrates a detailed map of the area under study.

Fig. 1
figure 1

Detailed map of the Study Area (Bangladesh) with its administrative boundaries

Full size image

2.2 Data

GEE was used to extract remote sensing data pertaining to air pollutants and LST. One of the significant advantages of utilizing GEE is its preprocessed data, which is readily available on a global scale through various remote sensing satellite sources (S. N. Rahaman et al. 2022a, b; S. N. Rahaman and Shermin 2022). The datasets utilized in this study cover November 2018 to June 2022 and includes LST, AOD, and measurements of NO2, CO, O3, SO2, and HCHO. All datasets, their source, and resolution are detailed in Table 1. The resolution of Sentinel-5p is slightly lower than MODIS, however, we did not resample as we are not directly analyzing the image but extracting the image data in feature (Angal et al. 2020). The project team created a custom processing algorithm using the GEE user interface to extract and process the data prior to use. The algorithm is detailed in Appendix I.

Table 1 List of remote sensing data
Full size table

Sentinel-5 Precursor (Sentinel-5P) is a cutting-edge satellite launched by the European Space Agency (ESA) that plays a vital role in monitoring Earth's atmosphere. Equipped with the TROPOMI (TROPOspheric Monitoring Instrument), Sentinel-5P provides high-resolution data on various air pollutants, including NO2, SO2, CO, HCHO, and O3. The satellite's ability to measure these pollutants daily on a global scale offers invaluable insights for understanding and addressing air quality issues, climate change, and public health impacts. Studies utilizing Sentinel-5P data have revealed significant variations in pollutant concentrations due to natural phenomena and human activities, such as the COVID-19 lockdowns, which led to observable decreases in NO2 and CO levels across many urban areas. Sentinel-5P's comprehensive and accurate atmospheric data support efforts to mitigate pollution and improve environmental policy making (Ayoobi et al. 2022; Goldberg et al. 2022; Levelt et al. 2022).

The MCD19A2.061 product represents a significant advancement in satellite-based monitoring of aerosols and air quality, utilizing the Multi-Angle Implementation of Atmospheric Correction (MAIAC) algorithm on both Terra and Aqua MODIS data to produce daily Land AOD at a 1 km spatial resolution (Lyapustin and Wang 2022). This high-resolution AOD data, including Optical_Depth_047, is critical for understanding atmospheric particles' effects on climate, weather, and human health. The MAIAC algorithm enhances AOD retrieval by dynamically isolating aerosol and land contributions, offering improved accuracy over traditional methods.

Several studies have validated and applied MCD19A2.061 data for air quality monitoring and research. For instance, Just et al. (2018) corrected measurement error in satellite AOD using machine learning, significantly improving air pollution modeling in the Northeastern USA (Just et al. 2018). Similarly, Just et al. (2020) utilized machine learning to enhance satellite-derived column water vapor measurements, demonstrating the potential to improve atmospheric correction and AOD retrieval accuracy (Just et al. 2020). Moreover, Li et al. (2019) developed a provisional surface reflectance product from Himawari-8 AHI using the MAIAC algorithm, highlighting the algorithm's versatility across different satellite platforms (Li et al. 2019). These studies underscore the value of high-resolution MAIAC AOD data for environmental monitoring and climate research, offering a deeper understanding of aerosol distribution and dynamics at local and regional scales.

The MOD11A2.061 product provides an 8-day composite of LST and emissivity at a 1 km spatial resolution, derived from the Terra platform's MODIS (Moderate Resolution Imaging Spectroradiometer) instrument (Giglio 2021). This dataset is crucial for a broad range of Earth science research, offering insights into the Earth's surface conditions, energy balance, and environmental changes.

Several studies have focused on evaluating and improving the accuracy and consistency of MODIS LST products. Wang et al. (2007) conducted a detailed evaluation of MODIS LST/emissivity products using ground-based measurements in a semi-desert site on the Tibetan Plateau, showing good agreement between satellite and ground observations, which underscores the reliability of MODIS data in capturing LST across diverse landscapes (K. Wang et al. 2007). Hulley and Hook (2011) aimed to generate consistent LST and emissivity products between ASTER and MODIS data, highlighting the importance of high-spatial-resolution emissivity products for various applications and the potential for improved utilization of MODIS data alongside higher resolution datasets like ASTER (Hulley and Hook 2011). Furthermore, Wang and Liang (2009) assessed ASTER and MODIS LST and emissivity products against long-term surface longwave radiation observations at SURFRAD sites, indicating that both datasets provide valuable temperature information but with noted differences due to their distinct spatial, spectral, and temporal resolutions (K. Wang and Liang 2009). Chen and Song (2011) integrated Terra/Aqua MODIS measurements for simultaneous retrieval of atmospheric temperature-humidity profiles and LST-emissivity, demonstrating a method to enhance retrieval accuracy by leveraging the complementary strengths of Terra and Aqua observations (Chen and Song 2011).

2.3 Spatial–Temporal Analysis

We utilized the Space Time Cube analysis in ArcGIS Pro 3.0.2 to examine LST and pollution over the study extent and time. The “Defined Locations” option was used to aggregate the spatial and temporal data for LST and air pollutants to discrete geographic locations to identify variations in spatial patterns over time. We use the fourth administrative boundary of Bangladesh as the defined locations and associated all the monthly LST and air pollutant data to each defined location (Fig. 1).

Each of the panels within the cube represents a bin with an independent time series temporal trend, which has been calculated utilizing the Mann–Kendall trend test. This test determines the rank correlation between the bin count or value and its respective time sequence. This approach enabled the examination of temporal trends for LST and air pollutant data, thus facilitating a more comprehensive understanding of the spatiotemporal patterns of these variables (ESRI 2021a; Kendall and Gibbons 1990; Mann 1945). The comparison between the bin values of each subsequent period involves adding one to the outcome if the first number (t) is less than the second (t + 1) and assigning a value of -1 if the opposite is true. In case of a tie, the resulting value is 0. The cumulative sum of each paired time period is then calculated. The absence of a discernible pattern over time will thus result in a value of zero. To ascertain the statistical significance of the difference between the observed total and the predicted sum, the variance of the values in the time series bin, the number of ties, and the number of periods are considered. A z-score and an associated p-value are used to track the trend for each binned time series. A low p-value indicates a high likelihood of a significant trend, while a positive/negative z-score implies an increasing/decreasing trend (ESRI 2021a). The test statistics S for the time series of air pollutants are calculated through Eq. (1),

$$S= \sum_{i=1}^{n-1}\sum_{j=i+1}^{n}{a}_{ij}$$
(1)

where,

$${a}_{ij}=sign\left({x}_{j}-{x}_{i}\right)=sign\left({R}_{j}-{R}_{i}\right)=\left\{\begin{array}{c}1\\ 0\\ -1\end{array} \begin{array}{c}{x}_{i}<{x}_{j}\\ {x}_{i}={x}_{j}\\ {x}_{i}>{x}_{j}\end{array}\right.$$
(2)

The ranks of xi and xj time series are defined as Ri and Rj, respectively. Assuming the data are independent and identically distributed, the mean and variance of S statistics are,

$$E\left(s\right)=0$$
(3)
$${V}_{o}\left(S\right)=\frac{n\left(n-1\right)\left(2n+5\right)}{18}$$
(4)

where n is the number of observations. This results in a reduction of the variance of S due to the existence of tied ranks (equal observations).

$${V}_{o}^{*}\left(S\right)=\frac{n\left(n-1\right)\left(2n+5\right)}{18}-\sum_{j=1}^{m}\frac{{t}_{j}\left({t}_{j}-1\right)\left(2{t}_{j}+5\right)}{18}$$
(5)

where m is the number of groups of tied ranks, each with tj tied observation. The methods iterate over the independent data and calculate the exact distribution of S. The method makes the S closer to a normal distribution with the observation increment, which means the more the study time, the more accurate the model.

2.4 Emerging Hotspot Analysis

We leveraged the Space Time Cube to identify temporal trends in pollution levels by identifying spatial hotspots that emerge or persist over time (Esri 2021a, b; Getis & Ord 1992; Ord and Getis 1995). This approach uses Getis-Ord local statistics on the reduction of variance value from Eq. (5) and uses Eq. (6) for calculating the z-score.

$${G}_{i}^{*}=\frac{\sum_{j=1}^{n}{w}_{i,j}{x}_{j}-\overline{X }\sum_{j=1}^{n}{w}_{i,j}}{S\sqrt{\frac{\left[n\sum_{j=1}^{n}{w}_{i,j}^{2}-{\left(\sum_{j=1}^{n}{w}_{i,j}\right)}^{2}\right]}{n-1}}}$$
(6)

where xj is the attribute value for feature j, wi,j is the spatial weight between feature i and j, and n is the total number of features. The calculation of \(\overline{X }\) and S is followed by Eqs. (7) and (8).

$$\overline{X }=\frac{\sum_{j=1}^{n}{x}_{j}}{n}$$
(7)
$$S=\sqrt{\frac{\sum_{j=1}^{n}{x}_{j}^{2}}{n}-{(\overline{X })}^{2}}$$
(8)

The analysis of emerging hotspots identifies sixteen distinct spatial–temporal clusters using the Mann-Kendell test statistics (ESRI 2021b). A "New Hot Spot" is recognized for the first time as a statistically significant hot spot in the latest observed time step without any previous record of such classification. On the other hand, a "Consecutive Hot Spot" is defined by achieving significant hot spot status for at least two sequential time steps towards the end of the observation period, without prior instances and with less than 90% of observations in this category. An "Intensifying Hot Spot" is noted for its continuous recognition as a significant hot spot in more than 90% of the time steps, including the most recent one, with a statistically significant increase in the intensity of clustering. The "Persistent Hot Spot" retains its significant status across more than 90% of the time steps without a discernible trend in the intensity of clustering, whereas a "Diminishing Hot Spot" is observed in more than 90% of the periods as well but with a significant decline in clustering intensity. The "Sporadic Hot Spot" appears in the last time step without regular previous significance, indicating a variable pattern, and the "Oscillating Hot Spot" switches between hot and cold statuses, being significant in less than 90% of the intervals. A "Historical Hot Spot" has lost its current significance but was significant in at least 90% of earlier intervals. For cold spots, similar categories exist, including "New," "Consecutive," "Intensifying," "Persistent," "Diminishing," "Sporadic," "Oscillating," and "Historical Cold Spots," which mirror the hot spot criteria but focus on areas of low counts or clustering. This approach highlights the intricate patterns of spatial–temporal variation and their importance in the fields of geography and environmental studies.

2.5 GWR

We used GWR to evaluate the local relationship between pollution and LST. GWR is useful approach in this context because it considers variations at a local scale rather than utilizing a single, global measure like traditional regression models (Brunsdon et al., 1996; ESRI 2019; O’Sullivan 2003). In our study, we opted for a distance band over a fixed number of neighbors. This decision was based on the understanding that all features within a certain distance can be relevant to our analysis, irrespective of their number (Brunsdon et al., 1996). To find the optimal neighborhood size, we applied the golden search neighborhood selection methods (Kiefer 1953). We utilized robust prediction as a strategy to lessen the impact of outliers, which could otherwise skew our regression results (Huber 1992). As for our choice of weighting scheme, we went with the bisquare weighting scheme. We believe this scheme is suitable as it gives more weight to closer observations, which often hold more relevance for our analysis (Cleveland 1979). We opted to use the z-score value of LST as the dependent variable, and the z-score values of air pollutants that are both generated from the Emerging Hotspot Analysis (Sect. 2.4). We do this to add a more dynamic component to the analysis. Specifically, the Z-score from the Emerging Hotspot indicates the level of significance of each feature while simultaneously signifying whether there is an increasing or decreasing trend. A Z-score value ranging from 0 to more than 2.74 indicates a significant hotspot, suggesting that the value of that feature is increasing over time. Conversely, a value ranging from less than -2.74 to 0 means the value is decreasing over time. In short, we can assess how an increase (positive z-score) or decrease (negative z-score) in pollution over time contributes to LST over that same time period. Formally, the GWR formula is:

$${y}_{i}={a}_{i0}+\sum_{k=1,m}{a}_{ik}{x}_{ik}+{\varepsilon }_{i}$$
(9)

where yi is the ith observation of the dependent variable (LST z-score), xik is the ith observation of the kth independent variable (pollution z-score), the \({\varepsilon }_{i}\) are independent normally distributed error terms with zero means, and each ak must be determined from a sample of n observations. In Ordinary Least Squares (OLS), the coefficient estimates minimize the sum of the squared differences between the predicted and observed dependent variable (Brunsdon et al., 1996). In weighted least squares, a weighting factor (w) is assigned to each squared difference before minimizing the errors, ensuring that inaccuracies in specific predictions are penalized more heavily than (Ziegel 2003). In many weighted regression models, the wi values remain constant, necessitating only a single calibration to generate a set of coefficient estimates. However, in this particular case, the weighting factor (w) varies with each observation (i), resulting in a distinct calibration for every point in the study area (Brunsdon et al. 2002). In this instance, the estimating formula for coefficients might be expressed more generically as:

$$a\left(i\right)={\left({x}^{t}w\left(i\right)x\right)}^{-1}{x}^{t}w\left(i\right)y$$
(10)

2.6 PCA

To address the complex interplay between various air pollutants and their cumulative impact on LST, the Pollutant Impact Index (PII) was developed using PCA conducted in the GeoDa software package. PCA is particularly advantageous for this study because it effectively reduces the dimensionality of complex, multivariate datasets while retaining the most significant information, thus simplifying the analysis of pollutant impacts on LST (Thurston and Spengler 1985; Vu et al. 2020). Compared to other methods like Multiple Regression Analysis or Factor Analysis, PCA provides a more robust and clear-cut approach for handling high-dimensional data, ensuring that only the most impactful components are considered (Tenenbaum et al. 2000; Y. F. Wang and Tang 2014). The process began with standardizing the GWR coefficients for each pollutant via the Standardize (Z) transformation, ensuring uniformity in scale and comparability. PCA, executed through the Singular Value Decomposition (SVD) method, allowed for the extraction of principal components (PCs) from the standardized data. The selection of PCs was based on their eigenvalues, with a threshold set at values greater than 1, to focus on those most significant in explaining the variance. The utilization of eigenvalues greater than 1 as a threshold for selecting PCs is grounded in the Kaiser criterion, a commonly used rule of thumb in factor analysis and PCA. It is based on the idea that each principal component represents the amount of variance (or 'information') that it explains in the dataset. An eigenvalue of 1 indicates that the principal component explains an amount of variance equivalent to that of one original variable. Therefore, PCs with eigenvalues greater than 1 are considered significant as they explain more variance than a single variable, justifying their inclusion in the analysis (Stieb et al. 2008; Stylianou and Nicolich 2009). The formulation of the PII from these selected PCs provided a singular, quantifiable measure, encapsulating the combined impact of air pollutants on LST across different geographical areas. This index is instrumental in identifying regions with heightened pollution effects, thereby guiding targeted interventions and informed policy-making. By creating the PII, the study bridges the gap between multifactorial pollutant effects and their spatial representation, offering a vital tool for comprehending and addressing the spatial dynamics of air pollution in relation to LST.

2.7 PII Development

The PCA was conducted on standardized GWR coefficients of pollutants (AOD, O3, SO2, HCHO, CO, NO2) to integrate their varied impacts on LST into a singular PII. The standard deviation of the components indicated the spread of each component, with the first three components showing higher values (1.276, 1.211, 1.188), suggesting their greater importance in variance. The eigenvalues, which reflect the amount of variance accounted for by each principal component, showed that the first three components had values greater than 1 (1.628, 1.466, 1.412), satisfying the Kaiser criterion of retaining components with eigenvalues over 1. These three components cumulatively explained 75.11% of the variance.

The variable loadings (Table 2) indicated how each pollutant correlated with the principal components. For instance, O3 had a strong positive loading on PC1, whereas HCHO had a strong negative loading on the same. This reflects how each pollutant uniquely contributes to the overall variance captured by each component. The squared correlations (Table 3) provided insight into how well each pollutant was represented by the components. For instance, HCHO showed a high squared correlation with PC1, indicating that this component effectively captured the variance associated with HCHO.

Table 2 Variable Loadings on Principal Components—This table displays the loadings of each air pollutant (AOD, O3, SO2, HCHO, CO, NO2) on the six principal components derived from PCA
Full size table
Table 3 Squared Correlations of Pollutants with Principal Components—This table outlines the squared correlations between each air pollutant and the six principal components
Full size table

Based on these results, the PII was formulated by averaging the first three principal components, given their substantial contribution to the explained variance and their eigenvalues surpassing the Kaiser criterion. The index thus provides a comprehensive representation of the combined impact of multiple air pollutants on LST, enabling a more targeted approach in environmental analysis and policy-making.

3 Results

3.1 Spatial–Temporal Variation

Plotting the monthly average air pollutants concentration over time unveils a notable pattern throughout the year, as shown in Fig. 2. All pollutant concentrations peak from January through March, while they are at their lowest from July through September. This clear seasonal trend, with higher concentrations of air pollution during the winter months and lower concentrations during the summer, aligns with previous studies (S. N. Rahaman et al. 2023). HCHO and SO2 exhibit the highest seasonal variability in concentration levels, while NO2 and CO show the least. Regardless, there has been a general uptick in the overall concentration levels of NO2, CO, AOD, O3 over time. These pollutants exhibit a relatively parallel trend over time, suggesting a common underlying dynamic driving their presence.

Fig. 2
figure 2

Monthly average concentration (mol/m2) of air pollutants over Bangladesh. Air pollutants have visible monthly fluctuation with SO2 has the highest ups and downs. January and February are cold season for Bangladesh which has a high concentration of air pollutants where July and August have lower concentration

Full size image

Figures 3 and 4 present the results from the space–time cube and emerging hotspot analysis further elucidate regional patterns in air pollution trends over time. CO and NO2 present similar and distinct spatial and temporal patterns. Notably, persistent and intensifying hotspots coincide with the locations of major metropolitan areas of Bangladesh situated in the middle, northeast, northwest, southeast, southern, and southwest parts of the country (Fig. 3). Across all regions of Bangladesh, the levels of LST, AOD, and SO2 exhibit fluctuating hotspots and cold spots, suggesting their growth is not consistent, but rather highly variable. This pattern also reflects the seasonal trends identified in Fig. 2. Intriguingly, consecutive cold spots for both, NO2 and CO are found across rural and suburban areas in the south and east (NO2), and north (CO) regions of Bangladesh. This underscores the strong correlation between increased urbanization and these two air pollutants. However, the fluctuations of other pollutants (AOD, HCHO, O3, and SO2) seem to be less connected to urbanization and are perhaps more indicative of seasonal climate changes that have a more widespread spatial effect on air quality.

Fig. 3
figure 3

NO2 has the highest variation of temporal trend, focusing the capital Dhaka on the middle with persistent and intensifying hotspot. CO also has the variation, focusing major cities, Sylhet on the north-east, Rajshahi on the north-west, Khulna in the south-west, Barishal in the south and Chattagram in the south-east. Chattagram and Rajshahi have persistent hotspot where all the other cities have intensifying hotspot along with new hotspot areas. LST, AOD, SO2, and HCHO have mostly oscillating hotspot and cold spot, indicating their frequent ups and downs over the years from Fig. 1

Full size image
Fig. 4
figure 4

Detailed percent distributions of temporal trend for LST and each air pollutants. NO2 and CO have sporadic, persistent, and intensifying hotspot where only CO has consecutive hotspot

Full size image

Table 4 presents the distribution of various emerging hotspot patterns for different air pollutants and LST across several administrative divisions in Bangladesh. The LST data shows that the "Oscillating Hot Spot" pattern is dominant in all divisions, especially in Barisal (99.50%) and Khulna (98.13%). This indicates frequent fluctuations between high and low temperatures in these areas. For AOD, the "Oscillating Hot Spot" pattern is consistently at or near 100% across all divisions, reflecting frequent changes in aerosol concentrations. The "New Hot Spot" is almost negligible, showing no significant new areas of high aerosol concentration emerging recently.

Table 4 Division wise percentage of spatial–temporal pattern for LST and air pollutants
Full size table

The CO data highlights various patterns. The "No Pattern Detected" is notably high in Chittagong (62.75%) and Rangpur (57.88%), suggesting stable CO levels in these regions. The "Diminishing Cold Spot" is prominent in Barisal (30.67%) and Mymensingh (24.87%), indicating a reduction in low CO concentration areas. "Intensifying Hot Spot" patterns in Dhaka (15.96%) and Barisal (13.47%) show increasing CO concentrations. The "Oscillating Hot Spot" and "Sporadic Hot Spot" patterns are present but with lower percentages, indicating occasional fluctuations and irregular high CO levels. For HCHO, the "Oscillating Hot Spot" pattern is significant across all divisions, especially in Rangpur (79.12%) and Dhaka (71.71%), suggesting frequent changes between high and low formaldehyde concentrations.

The NO2 data shows a diverse pattern distribution. The "Oscillating Hot Spot" is prominent in Mymensingh (49.47%) and Rajshahi (37.77%), indicating frequent changes in NO2 levels. The "Persistent Cold Spot" is significant in Barisal (30.42%) and Sylhet (16.36%), reflecting consistently low NO2 levels. The "No Pattern Detected" is notable in Rangpur (30.44%) and Khulna (26.64%), suggesting stable NO2 concentrations. For O3, the "Oscillating Hot Spot" is consistently at 100% across all divisions, indicating frequent fluctuations in ozone levels. Lastly, the SO2 data shows a significant presence of the "Oscillating Cold Spot" pattern in Rangpur (66.19%) and Mymensingh (61.11%), suggesting frequent changes between low and high SO2 levels. The "No Pattern Detected" is notable in Rajshahi (30.28%) and Dhaka (35.16%), indicating stable SO2 concentrations.

3.2 Nexus with LST

The GWR estimates individual regression coefficients for each unit of analysis included in the local model along with measures of significance. We applied a local and global Moran's I test to the coefficient values assigned to each unit of analysis to depict overall patterns (either positive or negative) between the pollution variable of interest and LST. We provide the coefficient estimates in Appendix II. As previously mentioned, the trend Z-score of LST was the dependent variable, and trend Z-scores of air contaminants were used as explanatory variables. The Global R-square value of our GWR model was 0.6091, with Local R-square values ranging from 0.68 to 0. Supporting tests for local autocorrelation in favor of the GWR model are disclosed in Table 5.

Table 5 Global Moran's I, Local Moran's I, Local R-squared and Coefficient distributions. The percentages are of the total administrative area
Full size table

Our study indicates a significant environmental concern in Bangladesh, with over 30% of all air pollutant coefficient areas showcasing high-high clusters, which represent substantial pollution hotspot zones (refer to Table 5, Fig. 5). Air pollutant concentrations, notably NO2 and O3, are alarmingly high across the country, with 48.53% and 54.67% of the area respectively displaying a high coefficient cluster of LST and air pollutants. On average, these high-high clusters affect about 43% of Bangladesh's total area. The local R-squared value reinforces this, indicating a 47.36% high-high cluster region in the nation. Interestingly, the proportion of positive coefficients discloses that NO2 has an extraordinarily high coefficient percentage of 78.57%, followed by CO at 39.36% of the total area. Positive coefficients for all other air contaminants remain below 32%.

Fig. 5
figure 5

GWR coefficient cluster map of LST and air pollutants. Interesting is that four of the air pollutants (AOD, O3, SO2, and HCHO) have high-high cluster coefficient in the south-east part of Bangladesh, the Chattagram division. NO2 and CO has high coefficient over major cities. Overall Local R-squared connects the urbanized path of each major cities and isolate the southern coastal and south-east Chattagram

Full size image

Table 6 presents the division wise bivariate cluster categories of model strength along with coefficients between LST and air pollutants. Dhaka exhibits dominant HH clustering for Local R2 (76.94%), indicating a strong correlation between pollutants and LST. A notable portion of LL clustering (21.91%) is also observed. For pollutants, AOD shows significant HH (47.62%) and LL (50.06%) clustering. CO and HCHO display primarily LL clustering (71.54% and 83.49%, respectively). In Barisal, the Local R2 values predominantly fall into the LL category (84.93%), indicating that the coefficients of determination between pollutants and LST are generally low. A smaller portion (15.07%) shows HH clustering, indicating areas where both pollutants and LST are highly correlated. For pollutants, AOD also shows significant LL clustering (44.17%), while CO is mainly HH (84.59%). HCHO exhibits a very high HH clustering (96.91%), suggesting a strong correlation between HCHO levels and LST.

Table 6 Division wise bivariate cluster category percentage for model strength and air pollutant coefficients
Full size table

Chittagong shows a significant proportion of Local R2 values in the LL category (70.30%), with some areas in the HH category (29.07%). For AOD, LL clustering (56.54%) is predominant, while for CO, HH (13.82%) is less frequent compared to LL (85.43%). HCHO has a balanced distribution, with significant HH (54.51%) and LL (44.95%) clustering. In Khulna, Local R2 values are mostly in the LL category (58.83%), with a substantial HH clustering (41.17%). For pollutants, AOD shows significant HH clustering (75.33%), indicating strong correlations with LST. CO exhibits predominant LL clustering (95.57%), while HCHO shows a balanced distribution with 43.37% HH and 56.63% LL. Mymensingh has a balanced distribution of Local R2 values with 57.52% in the HH category and 42.48% in the LL category. For pollutants, AOD shows a significant HH clustering (56.38%). CO and NO2 exhibit very high LL clustering (93.92% and 100.00%, respectively), indicating low correlations with LST.

Rajshahi predominantly shows HH clustering for Local R2 (68.07%), indicating strong correlations between pollutants and LST. A significant portion of LL clustering (31.93%) is also present. For pollutants, AOD and HCHO exhibit notable HH clustering (77.91% and 47.16%, respectively). CO shows a balanced distribution with 29.24% HH and 70.76% LL. Rangpur demonstrates a high proportion of HH clustering for Local R2 (65.75%) and a significant Low-Low (LL) clustering (33.33%). For pollutants, AOD exhibits dominant HH clustering (94.80%), indicating strong correlations with LST. CO also shows a high proportion of HH clustering (98.59%). Sylhet predominantly displays HH clustering for Local R2 (94.28%), indicating strong correlations between pollutants and LST. For pollutants, AOD exhibits very high LL clustering (98.63%), while CO shows a significant HH clustering (95.49%). HCHO has a balanced distribution with 34.54% HH and 65.46% LL.

3.3 PII Scenario

Figure 6 displays the spatial distribution of the Pollutant Impact Index (PII) values across Bangladesh, showcasing a gradient of pollution intensity. The color-coded legend correlates with the PII values, ranging from low (blue) to high (red), indicating the combined impact of various air pollutants on LST.

Fig. 6
figure 6

Spatial distribution of the Pollutant Impact Index (PII)—The color gradient represents the PII from low impact (blue) to high impact (red) on Land Surface Temperature, highlighting regional variations in air pollution levels from November 2018 to June 2022

Full size image

Table 7 presents the division-wise percentage of different ranges of PII values. We divide PII into three distinct categories: Low (< 0.33), Medium (≥ 0.33 to < 0.66), and High (≥ 0.66). In Barisal, the majority of PII values fall within the Medium category (61.35%), followed by Low (38.40%), with a negligible presence in the High category (0.25%). Chittagong demonstrates a predominant Medium impact (81.36%), with High and Low impacts constituting 16.48% and 2.17%, respectively. Dhaka presents a more balanced distribution, with Medium and High categories both contributing approximately equally (47.72% and 26.14%, respectively), and the Low category also at 26.14%.

Table 7 Division-wise percentage of different ranges of PII values
Full size table

Khulna's PII values are predominantly Medium (89.41%), with Low and High categories making up 9.66% and 0.93%, respectively. In Mymensingh, Medium and High impacts dominate, accounting for 60.32% and 39.68%, respectively, with no Low category presence. Rajshahi shows a high prevalence of Medium category values (55.98%), followed by Low (43.40%) and a minimal High category (0.61%). Rangpur exhibits a majority in the Low category (68.85%), with the remaining values in the Medium category (31.15%), and no High category presence. Sylhet displays an overwhelming majority in the High category (93.92%), with very few values in the Low (0.79%) and Medium (5.29%) categories. These results highlight regional disparities in pollutant impacts on LST, with Sylhet showing the highest proportion of severe impacts, while Rangpur has predominantly low impacts, and other regions exhibit varying distributions between the categories.

4 Discussion

The results of this study paint a stark picture of the environmental challenges faced by Bangladesh, particularly with regard to the correlation between air pollutants and LST. The spatial–temporal analysis, culminating in the creation of the PII, has offered critical insights into the patterns and intensity of pollution across the country. The higher PII values in urban areas, especially in Dhaka, as compared to rural areas, are indicative of the heightened UHI effect exacerbated by pollutants such as NO2 and O3. These findings are in line with existing literature which suggests that urbanization, with its associated increase in built-up areas and decrease in vegetative cover, leads to an accumulation of heat, further intensified by the presence of air pollutants. This finding is echoed among existing literature, for example, in the work by Shobnom et.al (2023) who show a strong relationship between NO2 concentration and population density, alongside LULC impacts in the Dhaka region (Shobnom et al. 2023). Additionally, the research by Hua et al. (2008) and Qian et al. (2022) on the impact of urbanization on air temperature in China offers comparative insights that can enhance our understanding of the relationship between air pollutants and LST within the context of rapid urban development. These studies collectively highlight the necessity of accounting for geographic, economic, and policy variations when exploring the dynamic between air pollutants and LST. Building on this foundation, our study advances the discussion by pinpointing specific locations where increased LST due to air pollutants has been observed over time, effectively bridging the gap identified in previous research within this domain. Such comparative analyses highlight the need for localized environmental strategies that are tailored to the specific urban and industrial profiles of different regions within the Global South (Marcotullio et al. 2008; Qian et al. 2022).

This study's findings also bring to light the regional variability in air pollution levels and their impact on LST. The northwest regions of Bangladesh, which are primarily agricultural and less industrialized, show lower PII values, suggesting a lesser impact of air pollution on LST. In contrast, the eastern regions, which include Sylhet and its environs, exhibit higher PII values. This could be attributed to the combined effects of industrial activities and urbanization, which are prevalent in these regions. The significant impact of air pollutants on LST in the central regions around Dhaka highlights the consequences of rapid urbanization without adequate environmental regulations and urban planning. For example, Hassan et al. (2023) investigate the climatic determinants of population exposure to PM2.5, emphasizing the significant impact of urban areas on PM2.5 concentrations due to changes in land use and climatic variables. They note that urban regions showed the highest level of PM2.5 concentration in 2021, demonstrating a direct correlation between urbanization and air pollution levels (Hassan et al. 2023). The variations in PII values across different regions also reflect the complex interplay between land use, topography, and human activities. For instance, the Sundarbans mangrove forest in the southern part of the country, despite its proximity to industrial activities, shows moderate PII values, potentially due to the mitigating impact of this extensive forested area on pollution levels and LST. An in-depth comparison with similar studies in other regions of the Global South, such as those detailed by Vardoulakis et al. (2014) in their comprehensive review of UHI intensity and mitigation strategies, provides a broader context to our findings which includes adopting cool roofs to control temperature in small cities (Vardoulakis et al. 2014). This review article serves as a foundational comparison for understanding how methodologies and mitigation strategies applied across different regions can inform localized environmental strategies.

Our findings underscore previously investigated linkages between air pollutants, urban heat dynamics, and potential public health risks, necessitating the integration of air quality management with urban planning and public health policies. Using LST proxies to measure the potential footprint of urbanization contributes to initiatives aimed at enhancing urban greenery as a pivotal strategy for mitigating the adverse effects of air pollution on public health (Mueller et al. 2017). Furthermore, the examination by Lelieveld et al. (2015) of the relationship between air pollution and public health risks reinforces the imperative for comprehensive strategies that encompass stricter emissions regulations and the promotion of sustainable transportation options (Lelieveld et al. 2015). We acknowledge the socio-economic challenges unique to the Global South and the open-source approach taken by this research contributes to solutions that are both equitable and accessible. The convergence of strategies that connect air pollution and urban dynamics can not only mitigate the immediate health impacts identified in our study but also contribute to a resilient public health infrastructure capable of addressing emerging environmental hazards.

Finally, while our study focuses on the immediate impact of air pollutants on LST, this work has broader implications in the climate change arena. The interaction between air pollutants and urban heat dynamics, as detailed in our research, could exacerbate both local and global climate change effects, potentially leading to more severe weather events and temperature extremes. Supporting this notion, Demuzere et al. (2014) highlight the role of urban green infrastructure in mitigating climate change effects, underscoring the importance of integrating such infrastructure to offset the warming impacts of urban air pollutants (Demuzere et al. 2014). Furthermore, D'Amato et al. (2010) discuss how urban air pollution and climate change act as compounding environmental risk factors for respiratory infections, reinforcing the need for comprehensive climate resilience planning in urban environments (D’amato et al. 2001). Together, these studies provide a robust foundation to support our findings and emphasize the critical need for sustainable urban planning practices that enhance climate resilience while addressing public health concerns.

We also acknowledge several limitations to our work. The scope of the remote sensing data, while comprehensive, does not capture the complete array of pollutants or the full spectrum of their sources. Also, remotely-sensed datasets may introduce biases due to atmospheric interference, sensor limitations, or data processing algorithms and, in this work, we assume the accuracy of the data sources but acknowledge that such biases could affect the precision of our pollutant concentration and LST measurements. The spatial resolution of the datasets used may not capture microscale variations in air pollutant concentrations or LST and this limitation could lead to underestimation or overestimation of hotspot areas and their impacts. Our statistical analysis, including Emerging Hotspot Analysis, GWR, and PCA, relies on certain assumptions regarding the spatial continuity and distribution of environmental variables. While these methods provide a robust framework for analyzing complex spatial–temporal data, they may oversimplify the nuanced interactions between air pollutants and LST. Future studies could explore alternative statistical models or machine learning approaches to capture these dynamics more accurately. Future work should aim to incorporate a broader set of pollution data, including emerging pollutants and their secondary products, to provide a more detailed understanding of their environmental impact. High-resolution urban data could enhance our understanding of pollutant dispersion patterns and their interactions with urban morphology. Longitudinal studies are also needed to evaluate the effectiveness of urban planning interventions over time. Moreover, integrating socio-economic data could offer insights into the social determinants of pollution exposure and their correlation with public health outcomes. In-depth studies involving in-situ measurements would complement the remote sensing approach, providing validation for the models used and a ground-truth reference for the PII. Exploring the bi-directional relationship between LST and air pollution—how each influences the other over time—could also provide valuable feedback for refining urban climate models.

5 Conclusion

Our findings indicate that air pollution remains a persistent challenge in urban areas, exacerbating the UHI effect and potentially leading to adverse health outcomes. The positive correlation between air pollutants and LST underscores the role of pollutants in absorbing and re-radiating heat, contributing to the UHI effect and increasing surface temperatures. These findings are of particular concern given the dense population of Bangladesh and the vulnerability of its citizens to heat-related stress and diseases. The broader environmental implications of these results are significant. The elevation in LST associated with air pollution can lead to increased energy consumption for cooling, further contributing to the release of pollutants if the energy is derived from fossil fuels. Additionally, the impact on vegetation health can lead to a vicious cycle where reduced vegetation leads to less cooling and increased LST, which in turn can stress vegetation further. The PII serves as an essential tool for identifying the regions most affected by pollution and for understanding the dynamics of air pollution's impact on LST. This knowledge is invaluable for informing strategies to reduce pollution levels, enhance urban resilience, and protect public health and indispensable for policymakers and urban planners, providing a data-driven foundation to strategize effective interventions aimed at pollution control and urban heat mitigation. Such interventions could range from enhancing green spaces to optimizing urban design and improving emissions regulations, all of which could significantly reduce the UHI effect and improve urban livability.

This study contributes to the field of environmental science by elucidating the intricate relationship between air pollution and urban temperature dynamics. Furthermore, the study introduces empirical novelty in the field of spatio-temporal monitoring. The methodology employed in this study is comprehensive within the statistics field as it surpasses conventional methods such as correlation, linear regression, and spatial regression. It integrates a space–time cube along with GWR, offering vital insights into how and where air pollutants impact surface temperature over time. The model's flexibility also opens up further opportunities to monitor other factors affecting surface temperature changes, including vegetation dynamics, land cover change, meteorological factors, and climate. The study highlights areas of concern, particularly in rapidly urbanizing regions of the Global South, and sets the stage for future research to further unravel the complexities of this relationship. The ultimate goal remains clear: to inform policy and practice that will lead to healthier, more sustainable urban environments for all.